2015 Volume 101 Issue 10 Pages 536-545
2015 Volume 101 Issue 10 Pages 536-545
Possibility of the occurrence of secondary recrystallization in high purity material without containing inhibitor elements was investigated experimentally. Only in the sample with primary recrystallization annealing performed at 900°C, onset of secondary recrystallization was observed. The orientation of secondary recrystallized grains proved to be {110} <001> (Goss) orientation. It was also shown that normal grain growth was suppressed in the sample in which secondary recrystallization occurred. Narrow grain size distribution and strong texture accumulation were considered to help the stabilization of the matrix grains.
Texture development during secondary recrystallization in the absence of inhibitors was discussed based on proposed growth models. It was shown from Grain Boundary Character Distribution (GBCD) analysis that the High Energy (HE) boundary model was applicable to secondary recrystallization and the Solid State Wetting (SSW) model was applicable to normal grain growth. The HE boundary was related theoretically to high mobility through high grain boundary diffusion coefficient. It was considered that reducing impurity elements exerted inherent high mobility of the HE boundary and hence led to the onset of the secondary recrystallization.
方向性電磁鋼板は,1930年台初頭にGossによって発明された1)。以来,よく知られているように多くの技術革新がなされてきた。現行の製造技術に共通する点としては,インヒビタと呼ばれる鋼中に均一微細に分散した析出物を利用して,圧延面に{110}面,圧延方向に磁化容易軸〈001〉を有するGoss方位を,二次再結晶により高度に発達させる点にある。インヒビタは最終仕上焼鈍工程において粒界移動を制御して,Goss方位を有する結晶粒の二次再結晶を発現させる上で重要な役割を担っている。
May and Turnbull2)は1958年に二次再結晶の発現のためには,微細分散したMnS析出物が必須であることを示した。MnS析出物の役割として,正常粒成長を抑制して二次再結晶の駆動力を維持することが指摘されている。Swift3)は,拡散律速によるMnS析出物の成長挙動と二次再結晶の開始を関連付けて述べた。このインヒビタとしてMnSを用いる技術は,今日でも汎用性方向性電磁鋼板(CGO)の製造方法として広く用いられている。May and Turnbull2)の指摘以来,多くの種類の正常粒成長を抑制する析出物や偏析元素の探求がなされてきた。析出物の具体例としては,Fiedler4)によるVN,Taguchi and Sakakura5)によるAlN,Matsuoka6)によるTiC,VN,NbC,Fiedler7)によるMnSeが挙げられる。Saitoは8,9),添加元素の影響を広範囲にわたって調査し,正常粒成長を抑制して二次再結晶粒方位のGoss方位への集積度を向上させる元素として,Pb,Sb,Nb,Ag,Te,Se,Sの添加が有効であることを報告した。
以上述べた析出物や偏析元素の中で,下記の方法が高磁束密度方向性電磁鋼板(HGO)製造に用いられた。
まずは,AlNとMnSを複合して用い,1回冷延法で最終板厚に仕上げる方法が実用化された10)。1回冷延法で高冷延圧下率の場合,AlNとMnSを複合添加した試料のみ正常粒成長を抑制できたという知見に基づいている。
さらに,HGO製造の別な方法として,MnSeとSbをインヒビタとして用い,2回冷延法で最終冷延圧下率をCGOよりは高めの60-70%とする方法も工業化された11)。
方向性電磁鋼板は,1990年ごろまでは上記の三種類の方法で製造されていた。それらに共通する製造技術として,熱延前のスラブ加熱を1300°Cを超える高温として,インヒビタ成分を完全固溶させて熱延中に微細分散させる技術がある。このような高温スラブ加熱は,補修を含む設備コストが高い他,スケールロスによる歩留り低下も引き起こす。そのため低温スラブ加熱による製造方法の開発が当時の方向性電磁鋼板開発の主流となっていた。1996年に1150°Cといった低温のスラブ加熱で,脱炭焼鈍工程の後半で窒化処理を施す方法が新たに開発された12)。窒化処理の次工程である最終仕上焼鈍工程における昇温過程でAlNインヒビタを形成して,二次再結晶を発現させる技術である。
インヒビタを使用する技術のもう一つの問題点は,Al,N,B,Se Sといったインヒビタ成分が,最終仕上焼鈍後に鋼中に残存すると磁気特性が劣化するために,インヒビタを除去する目的で,1100°Cを超える温度での水素雰囲気による純化焼鈍を施すことにある。このような高温での純化焼鈍は,コイル下部での座屈等により歩留り低下を引き起こす。
以上に述べたインヒビタに起因する問題点を解決するため,インヒビタを用いない,方向性電磁鋼板の製造方法開発が強く求められている。本論文では,インヒビタを含まない高純度鋼における二次再結晶発現と,その発現メカニズムについて述べる。
Table 1に実験に用いた真空鋼塊の化学成分を示す。
| C | Si | Mn | S | Al | Ti | Nb | N | P | O |
|---|---|---|---|---|---|---|---|---|---|
| 10 ppm | 3.3% | 0.08% | 4 ppm | 20 ppm | 6 ppm | 10 ppm | 10 ppm | 20 ppm | 11 ppm |
SiとMnを除く元素は極力低減した。Saitoの調査結果8,9)によると,SiとMnは,二次再結晶を発現させる効果がほとんど認められない元素である。
鋼塊は1120°Cで20分加熱した後,熱間圧延で2.6 mmに仕上げた。続いて熱延板焼鈍を1000°Cで60秒間施した後,冷間圧延で0.35 mmの最終板厚に仕上げた。続いて窒素雰囲気で一次再結晶焼鈍を700°Cから1050°Cの温度範囲で60秒間施した。続いて最終仕上焼鈍を,室温から850°Cまでは200°C/hで昇温し,続いて1150°Cまで2.5°C/hで昇温するヒートパターンにて実施した。冷間圧延したサンプルのうち一つは,一次再結晶焼鈍を施さずに直接最終仕上焼鈍を行った。一次再結晶焼鈍後のミクロ組織は光学顕微鏡を用いて観察した。冷間圧延後,一次再結晶焼鈍後,および最終仕上焼鈍後の試料の集合組織をX線回折により,{100},{110},{211}極点図を作成して調査した。これらの極点図のデータより,結晶方位分布関数(ODF)をPawlik13)による方法にて計算した。すべての集合組織は板厚中心層で調査した。
粒界性格分布(Grain Boundary Character Distribution)の調査のため,Morawiecら14)が提案した計算方法により,隣接していると考える結晶粒方位のペアを,ODFにおける結晶方位の存在量(f(g))に比例する確率で発生させて調査した。結晶粒方位はそれぞれオイラー角で表され,隣接粒間の粒界方位差角と回転軸とを計算した。ODFを用いた結晶粒方位発生法の統計的な妥当性は,EBSDよる結晶方位粒測定結果と比較することにより既に確認済みである15)。
一次再結晶焼鈍後,すべての試料は完全に一次再結晶していた。平均一次再結晶粒径と一次再結晶焼鈍温度の関係をFig.1に示す。Fig.1によると一次再結晶焼鈍温度を高めるほど結晶粒径は大きくなっている。一次再結晶焼鈍後,最終仕上焼鈍を施したが,一つの試料は,一次再結晶焼鈍を施さずに,冷間圧延後直ちに最終仕上焼鈍を施した。最終仕上焼鈍後の平均結晶粒径をFig.2に,マクロ組織をFig.3に合わせて示す。

Grain size of the samples after the primary recrystallization annealing at temperatures ranging from 700°C to 1050°C for 60 seconds.

Grain size of the samples after the final annealing. The primary recrystallization annealing at temperatures ranging from 700°C to 1050°C was performed before the final annealing.One of the samples was directly given the final annealing after cold rolling without being performed recrystallization annealing.

Macrostructure of the samples after the final annealing. The recrystallization annealing was performed at (a) 700°C, (b) 900°C (c) 1000°C before the final annealing, and (d) recrystallization annealing was omitted.
Fig.3に示されるように,一次再結晶焼鈍を900°Cで行った試料のみ,最終仕上焼鈍後に二次再結晶粒が発現し,結晶粒径は10 mm程度に発達した。他の試料では,正常粒成長して数百μmの結晶粒径となった。一次再結晶焼鈍を900°Cで実施し,最終仕上焼鈍後に二次再結晶した試料の結晶粒方位を,X線背面ラウエ法により2 mm間隔で測定した。方位測定結果をFig.4に示すが,二次再結晶粒方位はGoss方位であることが分かる。Fig.5には,理想Goss方位からのND,TD,RD回転軸に関してのずれ角の分布を示す。ほとんどの二次再結晶粒方位のずれ角は13°以内に収まっている。平均のずれ角はND,TD,RD回転軸に対して,5.8°,5.3°,4.9°であった。理想Goss方位からのずれ角(ND軸ずれ角とTD軸ずれ角を合成した〈100〉からのずれ角)は,HGOで3~4°,CGOのずれ角は7~10°程度である16)。今回の〈100〉からの平均ずれ角は7.9°となるため,平均ずれ角はHGOよりは大きいが,CGOなみのずれ角である16)。最終仕上焼鈍前後での集合組織(ODF)の変化をFig.6に示す。試料のうち一つは,一次再結晶焼鈍を施さずに直ちに最終仕上焼鈍を実施した。Fig.6の左最上部に示した冷間圧延集合組織の主方位はα-fiber組織(RD//〈110〉)であり,一次再結晶集合組織の主方位はγ-fiber組織(ND//〈111〉)であった。最終仕上焼鈍後の集合組織は,一次再結晶焼鈍を900°Cで行った試料以外は,一次再結晶後での主方位成分がさらに強まった結果となった。

Orientations of secondary recrystallized grains for the specimen with primary recrystallization annealing at 900°C measured by back-reflection Laue diffraction method at an interval of 2 mm expressed by {100} and {110} pole figures.

Deviation angle distributions from ideal Goss orientation around ND, TD and RD axis for the specimen with primary recrystallization annealing at 900°C.

The cross-section of ODFs (Φ2=45°) of the samples before and after the final annealing. One of the samples was directly given the final annealing after cold rolling without being performed recrystallization annealing.
ここで,二次再結晶開始までの粒成長挙動を調査する目的で,一次再結晶焼鈍後の試料を用い,200°C/Hの速度で850°Cまで昇温して50時間等温保持する追加の等温焼鈍実験を行った。Fig.7に等温焼鈍前後での平均結晶粒径を示す。Fig.7によると,一次再結晶焼鈍を900°Cまたは1050°Cで行った試料は,正常粒成長が抑制されていることが分かる。また,一次再結晶焼鈍を施さない試料や,一次再結晶焼鈍を700°Cで行った試料では,等温焼鈍後の平均結晶粒径は900°Cで一次再結晶焼鈍を行った試料よりも大きくなった。このことは,一次再結晶焼鈍温度が900°Cよりも低い場合には正常粒成長が抑制されないことを意味している。一次再結晶焼鈍を700°Cで行った試料と900°Cで行った試料のミクロ組織をFig.8に示す。Fig.8に示されるように,700°Cで焼鈍した試料は平均結晶粒径が10.2 μmであり,900°Cで焼鈍した試料の平均結晶粒径37.8 μmよりも小さくなっている。900°Cで焼鈍した試料の平均結晶粒径37.8 μmは,インヒビタを使用した鋼での一次再結晶粒径10 μm2)に比べてはるかに大きくなっていることは注目に値する。Fig.8中に指し示すように,700°Cで焼鈍した試料においては,比較的微細な一次再結晶粒が集団をなしている点にも特長がある。画像解析ソフトで求めた一次再結晶粒径分布をFig.9に示す。Fig.9において縦軸の頻度は面積率で表され,横軸のDは,平均結晶粒径Dに対する比で示されている。900°Cで焼鈍した試料の結晶粒径分布は,700°Cで焼鈍した試料よりも狭い。700°Cで焼鈍した試料においては,平均結晶粒径の2.5倍以上の結晶粒径を有する結晶粒の割合が2.7%となっているのに対し,900°Cで焼鈍した試料では,そのような粗大な結晶粒は全く存在しない。一次再結晶粒径の不均一さは,冷間圧延組織における結晶方位による蓄積エネルギーの不均一さに起因するものと考えられる。再結晶焼鈍温度が低い場合には,蓄積エネルギーの高いγ-fiber組織が,蓄積エネルギーの低いα-fiber組織よりも早く再結晶核形成することはよく知られている17)。

Grain size of primary recrystallized sheet and that after isothermal annealing at 850°C for 50 hours.

Microstructure of the sample with primary recrystallization annealing at (a) 700°C and (b) 900°C.

Grain size distribution of the samples with primary recrystallization annealing at 700°C and 900°C obtained using image analyzing software.
May and Turnbull2)の調査等により,インヒビタを含まない鋼では二次再結晶しないことが示されていた。それらの従来知見と異なり,本論文の実験では,インヒビタを含まない高純度成分系の鋼において,Goss方位粒の二次再結晶が発現した。まず,二次再結晶が発現した試料の一次再結晶集合組織の粒界性格分布の解析を行った。粒界性格分布を取り扱う二次再結晶発現のモデルとしては,主として3種類のモデルが存在する。
まず第1の対応粒界モデルでは,対応粒界のうちΣ518),Σ719),Σ920)粒界が高易動度であるとみなしている。Goss方位粒の周囲では対応粒界の存在頻度が高く,これらの対応粒界の移動速度が大きいので二次再結晶に至るというモデルである。対応粒界モデルは,元来,高純度鋼において,微量の固溶元素を添加した際に観察された選択的な粒界移動に基づいて提案された。対応粒界は規則構造を有しており,固溶元素が侵入しにくいので相対的に高易動度になるという考えである。その後,対応粒界モデルは,粒界エネルギーが低いことで,インヒビタによるピン止め力が減少して高易動度となるという考え方で,インヒビタ存在下においても提示された。
第2の高エネルギー粒界モデル21)では,粒界方位差角が20°から45°の範囲である粒界を,Dunnらの実験結果22,23)に基づいて,高エネルギー粒界であると定義している。そして,一次再結晶集合組織において,Goss方位粒周囲での高エネルギー粒界の存在頻度が,その他の全ての方位を有する結晶粒の中で最大であることを示した。高エネルギー粒界は,乱雑な構造を有しており,粒界拡散が速いことが高易動度に結びついていると考えられている24)。すなわち,最終仕上焼鈍時,高エネルギー粒界上でのインヒビタの粗大化が速く,優先的にピン止めがはずれて移動を開始する25)という考えである。そのため,最大の高エネルギー粒界頻度を有するGoss方位粒が二次再結晶するものと考えられている。高エネルギー粒界モデルと同等な,方位差角20-45°の範囲の粒界が高易動度であるというモデルは,既にTitorov26),Gubernatorov27)によって提示されていた。対応粒界のうち,Σ5,Σ7,Σ9粒界の方位差角は,いずれも20-45°の範囲内にある。しかし,高易動度となる理由が,対応粒界モデルでは,粒界エネルギーが低いことによるのに対して,高エネルギー粒界モデルでは,粒界エネルギーが高いことを根拠にしている違いがある。
第3のモデルは最近提示された,Solid State Wetting(SSW)モデル28,29)である。SSWモデルでは,低傾角(Σ1)粒界と双晶粒界(Σ3)といった,低エネルギー粒界が重要であるというモデルである。引用文献28)中のFig.2に示されているように,粒界三重点において,低エネルギー粒界によって囲まれている結晶粒が,高エネルギー粒界により接している別の結晶粒間を,Wettingを起こしたように侵入して,高エネルギー粒界により接していた結晶粒を分断して成長するモデルである。そして,低エネルギー粒界を多く持つGoss方位粒が成長するものとしている。
対応粒界モデルに基づき,二次再結晶が発現した,一次再結晶焼鈍を900°Cで行った試料のODFを用い,様々な方位を有する結晶粒周囲における対応粒界(Σ5,Σ7,Σ9の総計)の存在頻度を計算した。対応粒界の判定にはBrandonの基準30)を用いた。計算結果をオイラー空間(Φ2=45°断面)上で表示した結果をFig.10に示す。Goss方位は比較的高い対応粒界の存在頻度(4.7%)を有するが,最大ではない。最大値(6.7%)をとるのはGoss方位から20°ND軸回転した{110}〈113〉方位である。そのため,対応粒界モデルでは,Goss方位のみが選択成長することが説明できない。
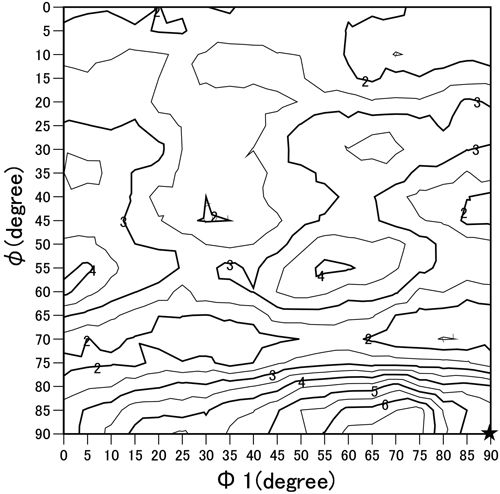
The frequency (%) of CSL (Σ5 + Σ7 + Σ9) boundaries around grains having various orientations in Euler space (Φ2=45° cross-section) in primary recrystallization texture of the sample with primary recrystallization annealing at 900°C. ★ denotes the Goss orientation.
高エネルギー粒界モデルに基づき,一次再結晶焼鈍を900°Cで行った試料のODFを用い,様々な方位を有する結晶粒周囲における方位差角20-45°を有する高エネルギー粒界の存在頻度を計算した。計算結果をオイラー空間(Φ2=0°断面と45°断面)上で表示した結果をFig.11に示す。Fig.11によると,Goss方位に関して,高エネルギー粒界の存在頻度が最大であることが明らかである。この特徴は,以前に調査したインヒビタ成分を含むHGOおよびCGOにおける調査結果21)と同じである。

The frequency (%) of the HE boundaries around grains having various orientations in Euler space ((a) Φ2=0° cross-section (b) Φ2=45° cross-section) in primary recrystallization texture of the sample with primary recrystallization annealing at 900°C. ★ denotes the Goss orientation.
SSWモデルに基づき,一次再結晶焼鈍を900°Cで行った試料のODFを用い,様々な方位を有する結晶粒周囲における低エネルギー粒界,低傾角粒界(Σ1)と双晶粒界(Σ3)の総計を計算した。計算結果をオイラー空間(Φ2=45°断面)上で表示した結果をFig.12に示す。Fig.12によると,γ-fiber組織を有する方位について,低エネルギー粒界の存在頻度が最大であり,SSWモデルでは成長する結晶粒と考えられる。Fig.6の左側の図に示したように,一次再結晶焼鈍を900°C以外で行った場合についても,本論文の実験における一次再結晶集合組織はγ-fiber組織の強い集積度を有している。主方位であるγ-fiber組織は,〈111〉軸に60°回転したΣ3の関係にある対称成分を有しているので,低傾角(Σ1)粒界と双晶粒界(Σ3)の存在頻度が高くなるものと考えられる。

The frequency (%) of low energy (Σ1 + Σ3) boundaries around grains having various orientations in Euler space (Φ2=45° cross-section) in primary recrystallization texture of the sample with primary recrystallization annealing at 900°C. ★ denotes the Goss orientation.
本論文の実験結果においては,Fig.6の右側に示したように,正常粒成長した後での試料の方位がγ-fiber組織となっており,SSWモデルは正常粒成長に適用可能であるものと思われる。
上述した二次再結晶モデルに基づく粒界性格分布の解析結果によると,Goss方位粒が二次再結晶するという本論文による実験結果は,高エネルギー粒界モデルによってのみ説明可能である。
4・2 ミクロ組織の影響Dunnが指摘31)したように,二次再結晶発現の条件として,マトリックス粒の正常粒成長が抑制されることが指摘され,通常はインヒビタの存在により実現されている。本論文の実験においても,インヒビタ成分は含有していないが,正常粒成長が抑制された条件下で二次再結晶が発現している。Fig.9に示したように,二次再結晶が発現した一次再結晶ミクロ組織の結晶粒径分布は狭く,隣接粒間での粒径差が駆動力となるマトリックス粒の正常粒成長が抑制されやすいものと考えられる。
それに対して,冷間圧延後直ちに一次再結晶焼鈍を施した試料や,一次再結晶焼鈍を低温で施した試料は,正常粒成長し,二次再結晶が発現しなかった。既にFig.8およびFig.9に示したように,一次再結晶焼鈍を低温で施した試料には,微細な結晶粒が集団で存在する部分が存在する他,平均結晶粒径の2.5倍以上の粗大粒が2.7%の割合で存在している。Fig.6によると,一次再結晶集合組織中においてGoss方位はマイナー成分である。そのため,粗大粒中にGoss方位粒が含まれる確率は低いものと考えられる。正常粒成長の駆動力は隣接粒間での粒径差なので,平均結晶粒径の2.5倍以上の粗大粒がサイズ効果により成長する可能性はある。しかし,Srolovitzら32)が示したように,サイズ効果単独では,二次再結晶発現には至らない。そのため,冷間圧延後直ちに一次再結晶焼鈍を施した試料や,一次再結晶焼鈍を低温で施した試料においては,一次再結晶焼鈍後にサイズ優位性を持つGoss方位以外の方位を有する結晶粒が,正常粒成長的に成長したものと考えられる。また,一次再結晶焼鈍を1050°Cの高温で行った試料においても二次再結晶が発現しなかった。二次再結晶が発現しなかった試料の平均結晶粒径は55 μm以上であり,発現した試料の37.8 μmよりも大きい。Dunnが指摘31)したように,二次再結晶の駆動力は,二次再結晶粒によって食われるマトリックス粒の粒界エネルギーである。その駆動力の大きさは,マトリックス粒径の逆数に比例する。
二次再結晶が発現した試料と二次再結晶しなかった試料の駆動力の比は(1/37.8)/(1/55)=1.46となる。
そのため二次再結晶が発現しなかった試料おいては,一次再結晶粒が粗大化し,二次再結晶に必要な駆動力が不足したものと考えられる。
4・3 一次再結晶集合組織の集積度の影響以前の報告21)では,インヒビタ成分を含有するHGOとCGOの一次再結晶集合組織が調査された。調査を行ったODFをFig.13に示す。これらのODFをFig.6に示される,二次再結晶が発現した一次再結晶焼鈍を900°Cで行った試料のODFと比較すると,今回調査したODFの方位集積度のほうがやや高いことが分かる。ODF強度の最大値は,HGOについて12,CGOについては8,今回の一次再結晶焼鈍を900°Cで行った試料については16である。HGOおよびCGOの製造工程においては,インヒビタ成分の完全固溶のため,熱延前の加熱温度は1400°C以上である。そのため,熱延前での結晶粒は著しく粗大化する。二次再結晶に有害となる熱延{100}〈011〉バンド組織の発達を抑制するために,HGO,CGOともに成分中にCを添加して,熱延中に部分的にγ変態を起こす技術を適用している。これに対して,本論文中で使用した高純度鋼の場合,熱延前の加熱温度は1120°Cと低く,熱延前での結晶粒径はHGOやCGOに比べて小さい。冷間圧延後,HGOやCGOでは,元γ相に起因する硬質な粗大析出セメンタイトが,ランダム方位の一次再結晶粒の核形成サイトとなる。高純度鋼ではC量を10 ppmまで低減しており,γ相の生成は完全に抑制されているため,粗大析出セメンタイトは存在せず,ランダム方位の一次再結晶粒の核形成が抑制される。上述した,熱延前の加熱温度の低温化とC量の低減効果により,方位集積度の高いγ-fiber組織が一次再結晶集合組織として実現されたものと考えられる。方位集積度の高いγ-fiber組織は,いわゆるTexture-Inhibition効果33)を通じて,正常粒成長の抑制にも有利である。すなわち,γ-fiber粒同士の粒界は,いずれも低易動度粒界である低傾角粒界(Σ1)か双晶粒界(Σ3)を形成するためである。

The cross-section of ODF (Φ2=45°) of the primary recrystallized sheet of (a) HGO and (b) CGO investigated in previous work21). ★ denotes the Goss orientation.
前報21)において,HGOおよびCGOについて,様々な方位を有する結晶粒周囲における高エネルギー粒界の存在頻度を計算した結果をFig.14に示す。Fig.14(a)によると,HGOにおいてはGoss方位が最大の高エネルギー粒界頻度を有することが分かる。Fig.14(b)によると,CGOでは,高エネルギー粒界の存在頻度が最大(70.1%)である方位は,Goss方位から20°ND軸回転した{110}〈113〉方位である。Goss方位も最大値に匹敵する高い存在頻度(69.2%)を有している。Fig.15に,Goss方位に関する高エネルギー粒界存在頻度の比較を示す。Fig.15におけるHigh Purity鋼の値は,Fig.12に示した一次再結晶焼鈍を900°Cで施した試料に関する値である。方位集積度の高いγ-fiber組織により,高純度鋼における高エネルギー粒界存在頻度が,HGOやCGOよりも高くなっている。高エネルギー粒界モデルにおいては,高純度鋼の一次再結晶集合組織が最も二次再結晶に有利であると考えられる。しかし,既にFig.5に示したように,高純度鋼の二次再結晶粒方位のGoss方位からのずれ角度は,HGOよりは大きくCGOと同レベルである。HGOと比較した場合,インヒビタが存在しないことにより,高エネルギー粒界の粒界移動における優位性がHGOに比べて減少したものと考えられる。CGOと高純度鋼と比較した場合には,インヒビタが存在しないことによる不利な点を,高エネルギー粒界の存在頻度が高い一次再結晶集合組織を発達させることで補っているものと考えられる。

The frequency (%) of HE boundary around grains having various orientations in Euler space (Φ2=45° cross-section) in primary recrystallization texture of (a) HGO and (b) CGO investigated in previous work21). ★ denotes the Goss orientation.

Comparison of the frequency (%) of the HE boundaries around the Goss grain.
最終冷延圧下率は高純度鋼では86.5%,HGOでは85.3%,CGOでは55.0%である。最終冷延圧下率を高めることは,一次再結晶集合組織を発達させる上で重要である。この点で,インヒビタ成分を含まない鋼で,二次再結晶が発現しなかったMay and Turnbull2)による実験と異なっている。彼らの実験における最終冷延圧下率は50.0%であり,二次再結晶発現に充分な一次再結晶集合組織の発達が実現できなかったものと推定される。
Goss方位粒に関する高エネルギー粒界の存在頻度を,一次再結晶焼鈍温度を変更した試料のODFから計算した結果をFig.16に示す。一次再結晶焼鈍温度を高めると粒成長に伴ってγ-fiber組織が発達するため,Goss方位に関する高エネルギー粒界の存在頻度は高まる。二次再結晶の発現のためには,Goss方位粒に関する高エネルギー粒界の頻度が高いほど有利になると考えられる。一方,一次再結晶焼鈍温度を高めると,一次再結晶粒径は粗大化するが,二次再結晶駆動力が低下する点では二次再結晶発現に不利である。結局,集合組織の発達による高エネルギー粒界の存在頻度の増加と二次再結晶駆動力の低下が釣り合うことで,一次再結晶焼鈍温度900°Cの試料のみで二次再結晶が発現したものと考えられる。

The relation between the frequency (%) of HE boundaries around Goss grain calculated from the ODFs of primary recrystallized samples and recrystallization annealing temperature (°C).
高エネルギー粒界モデルの元々の考え21)では,高エネルギー粒界上での速い粒界拡散による,仕上焼鈍中でのインヒビタの粗大化促進効果を主張していた。インヒビタの粗大化が起こっている粒界では,微細な析出物が保たれている他の粒界に比べて,ピン止め効果が小さいことを仮定している。Goss方位粒はこれらのインヒビタが粗大化する高易動度粒界を,他の方位粒よりも多く持つことが報告されてきた。しかし本論文の実験において,高純度鋼はインヒビタ成分を含まない他,Si,Mn以外の固溶元素をも含んでいない。そのため二次再結晶発現のモデルとしては,インヒビタの役割を排除して考慮される必要がある。
元々の対応粒界モデルでは,微量の固溶元素の存在下で,対応粒界への偏析量が相対的に少ないことで高易動度となることが主張されていた。その後,対応粒界の粒界エネルギーが低いことで,インヒビタのピン止め力が低下するという主張もされている。Nakashimaら34)は,固溶Siの存在下でΣ9粒界が高易動度となる実験結果を報告している。本論文の実験においても,固溶Siの影響で対応粒界の高易動度が実現されている可能性も考えられる。しかし,本論文での一次再結晶集合組織の解析結果では,Goss方位粒に対する対応粒界の存在頻度は最大でなく,対応粒界が二次再結晶発現に寄与するというモデルは適用し難い。
SSWモデルにおいては,インヒビタや固溶元素との相互作用について議論されておらず,それらの影響は明らかでない。SSWモデルの仮定は,インヒビタの役割が主でない場合の正常粒成長に適用可能であると思われる。
粒界エネルギーと粒界易動度との関係について,最近の論文35)で議論を行った。粒界エネルギーはBorisovら36)により提示された(1)(2)式により,粒界拡散と関連づけられている。この関係の正当性についてはPelleg37)によって確かめられた。(1)式において,Tは絶対温度,kはボルツマン定数,Eは粒界エネルギー,mは粒界原子層の数,aは格子定数,δ=maは粒界の厚み,α,λは定数である。Borisovら36)は,λ=1,α=2,m=1と仮定している。(2)式において,Dgbは粒界拡散係数,Dlは体拡散係数である。
| (1) |
| (2) |
(1)(2)式から,高エネルギー粒界は粒界拡散係数が大きいことが導かれる。粒界易動度Mは,Sandstrom38)により提示された(3)式で示される。
| (3) |
(3)式において,δは粒界厚み,Dgbは粒界拡散係数,bはバーガースベクトル,kはボルツマン定数,Tは絶対温度である。
(3)式により,粒界易動度は粒界拡散係数に比例することが分かる。(1)~(3)式を組み合わせることで,粒界エネルギーが高いことは,粒界拡散係数が大きいことを通じて,粒界易動度が高いことに理論的に結びつけられる。そのため,高エネルギー粒界の高易動度は,インヒビタが存在しなくても実現されるべきものだと考えられる。(1)~(3)式を用いて計算した,方位差角と粒界易動度との関係を定量的に示す図を,前報35)において示している。それによれば,方位差角20-45°の範囲の高エネルギー粒界は,方位差角が15°未満の低傾角粒界や方位差角が45°を超える高傾角粒界と比較して,数倍高い易動度を持つことが示されている。
S,Pといった固溶元素を添加した場合,粒界の構造が乱雑で,粒界自由空間の大きい高エネルギー粒界へと固溶元素が優先的に偏析する結果,粒界エネルギーは低下するものと考えられる。その場合,(1)~(3)式により,粒界易動度差は減少する。よって,不純物元素を極力低減することで,高エネルギー粒界が本来的に有している高易動度が発揮されるものと考えられる。すなわち,狭い粒径分布を有するミクロ組織と,発達した集合組織によるTexture Inhibitionにより,マトリックスの正常粒成長が抑制された上で,素材の高純度化により,高エネルギー粒界が本来的に有している高易動度が発揮されてGoss方位粒の二次再結晶が発現したものと考えている。
(1)インヒビタ成分を含まない高純度3.3%Si鋼において,二次再結晶の発現が観察され,二次再結晶粒方位はGoss方位であった。
(2)最終仕上焼鈍において二次再結晶が発現した試料については,正常粒成長の抑制が認められた。狭い粒径分布を有するミクロ組織と,発達した集合組織によるTexture Inhibitionが正常粒成長を抑制したものと考えた。
(3)粒界性格分布を取り扱う3種類の二次再結晶発現のモデル,対応粒界モデル,高エネルギー粒界モデル,SSWモデルを検証し,高エネルギー粒界モデルは二次再結晶に,SSWモデルは正常粒成長に適用可能であることを示した。
(4)粒界エネルギーが高いことは,粒界拡散係数が大きいことを通じて,粒界易動度が高いことに理論的に結びけられる。狭い粒径分布を有するミクロ組織と,発達した集合組織によるTexture Inhibitionにより,マトリックスの正常粒成長が抑制された上で,素材の高純度化により,高エネルギー粒界が本来的に有している高易動度が発揮されてGoss方位粒の二次再結晶が発現したものと考えられた。