Proposal of Two-dimensional Local Curvature Multi-vertex Model for Grain Growth Simulation

Synopsis:

A local curvature multi-vertex model was developed. This model is a straightforward two-dimensional topological network model based on physical principles that consider the local curvatures of grain boundaries and the grain boundary tensions at triple junctions. Virtual vertices are set on the grain boundaries in order to calculate the driving forces of grain boundary and triple junction migration. Therefore, the accuracy of the developed model is higher than that of the conventional curvature model and the vertex model. In the proposed model, the generation and annihilation of virtual vertices maintained a proper configuration of virtual vertices, and high accuracy is expected with a suitable set of simulation parameters. The proposed model was verified by the grain growth simulation using adequately determined parameters for the artificially generated specimens with 5040 grains.

1. 緒言

鉄鋼などの金属材料の特性は集合組織に大きく影響されるため，集合組織を予測して制御することは，高品質な材料を造り込むために極めて重要である。正常粒成長や異常粒成長にともなう集合組織の変化を予測するために，種々のモデルが提案されている。その一つである統計論的手法は，例えば製鉄プロセスでの方向性電磁鋼板の方位選択的な異常粒成長のメカニズムを理解するのに用いられている¹⁾。しかし，個別の結晶粒ごとに結晶方位を考慮して検討することができないという課題があった。近年，後方散乱電子回析(electron backscatter diffraction:EBSD)技術の劇的な進展によって²⁾，結晶粒ごとに結晶方位と隣接粒との方位関係を二次元の範囲で比較的容易に解析できるようになってきた。その意味で，EBSD観察データを十分に活用する粒成長シミュレーションモデルの開発が望まれている。

結晶粒成長を記述するモデルとして，確率論的手法(モンテカルロ法)³⁾やフェーズフィールド法⁴⁾，フロントトラッキングモデル^5,6)やバーテックスモデル^7,8,9,10)のようなトポロジカルネットワークモデルが既に提唱され開発されている。これらのモデルは，個々の結晶粒の結晶方位を取り扱っている点では優れており，ある限られた条件においては結晶粒成長の記述に成功している。

確率論的手法では，粒界特性とピン止め力が数学的に取り扱われている。そのため，異常粒成長を，物理的イメージをもって十分に表現できていないという課題がある。

フェーズフィールド法も結晶粒成長モデルに適用されているが，粒界を有限の幅に設定しなければならないという課題がある。そのため，多くの微小結晶粒が存在する結晶成長の初期段階では，計算精度が必ずしも十分とは言えない。また，三重点の張力バランスのような物理原理を導入することは容易ではない。

フロントトラッキングモデルは，粒界が曲線で近似され曲率中心に移動するモデルである。二次元のフロントトラッキングモデルでは，2つの三重点の間の粒界上にいくつかの仮想点(二重点，vertex)を配置して，粒界を多項式で表される曲線で近似することで，粒界の局所曲率を計算することができる。ここで，局所的な粒界，つまり粒界上の二重点p_iは移動速度$\overrightarrow{v}$_gb,iで移動する。   

$${\overrightarrow{v}}_{gb,i}=M_{gb,i}{\overrightarrow{F}}_{gb,i}$$(1)

  

$${\overrightarrow{F}}_{gb,i}={\gamma }_i{\overrightarrow{\kappa }}_{gb,i}$$(2)

M_gb,iは二重点p_iが属する粒界の易動度，$\overrightarrow{F}$_gb,iは粒界に作用する単位長さ当たりの駆動力で，その方向は二重点p_iから曲率中心へ向かう方向である。γ_iは粒界の単位長さ当たりの粒界エネルギー，$\overrightarrow{\kappa }$_gb,iは二重点p_iでの粒界の曲率を大きさとし，二重点p_iからその曲率の中心へ向かう方向を有する曲率ベクトルである。しかしながら，実在点である三重点は物理的に取り扱われておらず数学的に取り扱われているという課題がある。三重点では粒界エネルギーによる粒界張力が平衡となる角度で粒界が交わるように，三重点の位置が数学的に調整される⁵⁾。例えば，3つの粒界エネルギーが等しい場合には，交差角度は120°に調整される。

初期のバーテックスモデルでは，粒界は常に直線で近似されており^7,8)，結晶粒成長のための駆動力は，三重点に作用する粒界張力である。本モデルでは，式(3)および式(4)に示すように，粒成長を粒界三重点p_iの移動速度$\overrightarrow{v}$_tp,iでの移動で表現している。   

$${\overrightarrow{v}}_{tp,i}=M_{tp,i}{\overrightarrow{F}}_{tp,i}$$(3)

  

$${\overrightarrow{F}}_{tp,i}=\sum _{j=1}^3{\gamma }_{ij}\frac{{\overrightarrow{q}}_{ij}}{\Vert {\overrightarrow{q}}_{ij}\Vert }$$(4)

ここで，M_tp,iは三重点p_iの易動度，$\overrightarrow{F}$_tp,iは三重点p_iに作用する駆動力，γ_ijは三重点p_iと隣接する三重点p_jが属する粒界の単位長さ当たりの粒界エネルギー，$\overrightarrow{q}$_ijは三重点p_iから隣接する三重点p_jへのベクトルである⁷⁾。単位長さ当たりのエネルギーの単位は力の単位と同じである。したがって，式(4)の右辺は三重点に作用する力であり，三重点の移動は物理的に正確に記述されている。しかし，初期のバーテックスモデルでは通常直線でない粒界を直線で近似している点に問題がある。

この初期のバーテックスモデルは，粒界上に仮想点を配置すること，つまりマルチバーテックス化によって改善された^9,10)。この改善によって粒界は折れ線で近似される。それぞれの仮想点の運動は，粘性項または摩擦項を含む運動方程式に基づく変分原理で記述される。この改善されたバーテックスモデルは物理原理に基づいているので，結晶粒成長を記述するのに適していると考えられる。しかしながら，粒界を曲線ではなく折れ線で近似しているために，粒界上の仮想点が少ない場合には大きな誤差を生じる。例えば，孤立したn角形の収縮では，改善バーテックスモデルで記述された仮想点の移動速度は，フロントトラッキングモデルの曲率から計算される移動速度の約1/cos(π/n)²倍速い⁹⁾。n→∞の極限において両者は等しくなるものの，n=10の場合には約11%の誤差を生じることになる。

本論文においては，改善されたバーテックスモデルのこのような問題を解決でき，物理原理を直接的に表現した，新しい二次元のトポロジカルネットワークモデル，すなわち局所曲率マルチバーテックスモデルを提案することを目的とした。特に，本モデルのコンセプト，シミュレーションにあたっての空間や時間間隔や三重点の取り扱いに関する工夫と条件の適正化，およびモデルの検証に本論文では焦点を絞った。

2. モデルの提案 −局所曲率マルチバーテックスモデル−

2・1　粒界移動の原理

結晶粒成長を二次元でより正確且つ直接的にモデル化するために，Frostら⁵⁾およびFuchizakiら⁹⁾の方法と同様の方法を用いて2つのタイプの点を取り入れた。その1つは三重点で，これは実在点である。もう1つは粒界上に離散化して配置する仮想点である。この方法によって，線で表わされる粒界の移動を点の移動に変換することができる。仮想点は隣接する2つの点と便宜的に繋がれるので，二重点と呼ぶことができる。一方，実在点は隣接する3つの点と繋がれるので三重点と呼べる。仮想点および実在点の移動はそれぞれ式(1)，(2)および式(3)，(4)に従う。このとき局所曲率ベクトル$\overrightarrow{\kappa }$_gb,iは次式で計算される。   

$${\overrightarrow{\kappa }}_{gb,i}=-\frac{1}{R_i}\frac{{\overrightarrow{R}}_i}{\Vert {\overrightarrow{R}}_i\Vert }$$(5)

ここで，$\overrightarrow{R}$_iは粒界上の二重点p_iとその二重点に隣接する2つの点により定まる円C_iの半径を大きさとし，その円C_iの中心O_iから二重点p_iへ向かう方向を有する半径ベクトルである(Fig.1)。局所曲率ベクトル$\overrightarrow{\kappa }$_gb,iの方向は，$\overrightarrow{R}$_iと逆の方向となる。

Fig. 1.

 Proposed local curvature multi-vertex model.

なお，単位長さあたりの粒界エネルギーとして相互に隣接する2つの結晶粒の方位角度差にのみ依存すると仮定すると，式(2)および式(4)の駆動力は粒界エネルギーの勾配，つまり$\overrightarrow{F}$=−$\overrightarrow{\nabla }$Eから導出することができる。ここで，$\overrightarrow{F}$は駆動力，Eは粒界エネルギーである。したがって，式(1)~(5)は，物理原理に基づいた関係式と言える。但し，式(2)の駆動力の単位は単位長さ当たりの力と同じ単位であり，式(4)の駆動力の単位は力と同じ単位であることに注意する必要がある(付録を参照)。

また，粒界エネルギーについては多くの研究がなされており，小角粒界であるΣ1対応粒界のエネルギーは一般の高角粒界のエネルギー比べて小さく，Read & Shockleyの関係式が知られている¹¹⁾。また，高角粒界であってもΣ3対応粒界のような対応格子点密度の高い対応粒界のエネルギーは，Σ1対応粒界と同様に一般の高角粒界のエネルギーより小さいことが知られている¹²⁾。しかしながら，特にBCC金属については粒界エネルギーの定量的なデータが十分でないので，Σ3対応粒界等のエネルギーについては，Read & Shockleyの関係式を適用した。一方，対応格子点密度の高い対応粒界を除いて，一般の粒界のエネルギーは一定とした。

2・2　局所曲率マルチバーテックスモデルにおける仮想点の適正な配置方法

三重点および二重点の間隔は時間発展とともに変化する。計算精度を損ないようないようにするためには，これらの点の間隔が極端に長くなり過ぎたり短くなり過ぎたりしないようにする必要がある。本論文における新しいモデルでは，仮想点を生成・消滅させ，仮想点の間隔を適切な長さに保持することを提案する。以下に，その具体的な方法を示す。具体的な長さについては，2・3および2・5で述べる。

隣接する2つの点の間隔が規定した最大長さL_max以上になった場合には，隣接する2つの点の間に新しい仮想点を1つ生成させる。Fig.2(a)に示すように，点p₂と点p₃の間に仮想点p_aを生成させる。仮想点p_aは，線分p₂p₃の垂直二等分線上で，その曲率κ_aが仮想点p₂の曲率κ₂と仮想点p₃の曲率κ₃の平均とする。このとき，点p₂，点p₃，および点p_aの曲率中心の位置が線分p₂p₃に対して同一の位置関係となるように配置する。異なる位置関係のときは，曲率に符号を付けることで取り扱うことができる。

Fig. 2.

 Generation and annihilation of virtual vertex (double junction).

一方，隣接する2つの点の間隔が規定した最小長さL_min以下になった場合には，隣接する2つの点の間に新しい仮想点を1つ生成させ，元々あった2つの仮想点を消滅させる。結果としては，仮想点を1つ消滅させることになる。Fig.2(b)に示すように，仮想点p₂と仮想点p₃の間に仮想点p_bを生成させ，仮想点p₂と仮想点p₃を消滅させる。仮想点p_bは，線分p₁p₄の垂直二等分線上で，その曲率κ_bが仮想点p₂の曲率κ₂と仮想点p₃の曲率κ₃の平均とする。このとき，点p₂，点p₃，および点p_bの曲率中心の位置が線分p₁p₄に対して同一の位置関係となるように配置する。異なる位置関係のときは，曲率に符号を付けることで取り扱うことができる。

このような点の生成および消滅によって，隣接する2つの点の間隔Lは，   

$$L_{\min }<L<L_{\max }$$(6)

となる。このとき，点の生成および消滅を安定して実行するためには，最大長さL_maxは最小長さL_minの2倍より長く設定する必要がある。   

$$2L_{\min }<L_{\max }$$(7)

上記のような単純な仮想点の生成と消滅の処理，および式(6)と式(7)の条件により，結晶粒成長の時間発展の際に，点の間隔が極端に長くなり過ぎたり短くなり過ぎたりすることを防ぐことができ，点の間隔を安定させることができるので，計算精度を維持できると考えられる。

2・3　局所曲率マルチバーテックスモデルにおける仮想点間隔の適正化

2・2では局所曲率マルチバーテックスモデルの仮想点の適正な配置方法を述べた。ここでは，仮想点間隔が計算精度に及ぼす影響を検討する。計算精度への影響は，仮想点間隔の絶対値ではなく，粒界の長さつまり結晶粒径に対する相対値で整理できると考えられる。ここでは，平均結晶粒径を基準とすることとし，鋼板で観察される結晶粒径は数10 μm程度であることが多いことから，初期の結晶粒の半径を10(arbitrary units)とした。また，実際の結晶粒成長では粒界と三重点の移動が同時に進展するが，ここでは簡単のために粒界の移動にのみ着目して検討した。検討には，Fig.3に示す両端が固定された半径10の円弧状の粒界を用いた。白丸はピン止めされた固定点を，黒丸は仮想点を示す。ここで，固定点は三重点をイメージしており，三重点が移動しない場合の粒界(仮想点)の移動を評価することになる。このとき，固定点の位置を，円周の長さに対する円弧の長さが1/2~1/12となるようにした。更に，その円弧を2分割から最大96分割するように円弧上に仮想点を等間隔に配置したものを初期状態とした。分割数は常に偶数として，2つの固定点のちょうど中間にある，2つの固定点を結んだ弦から最も離れた位置の仮想点の移動を評価した。例えば，分割数2では隣接する2つの仮想点間隔は14.14，分割数96では仮想点間隔は0.33となる。

Fig. 3.

 Arc grain boundary for accuracy validation. (a) Half circular arc divided into 8 segments by 7 virtual vertices. (b) One-sixth circular arc divided into 6 segments by 5 virtual vertices.

半円の中間仮想点の位置と速さの時間発展を評価した結果をFig.4に示す。ピン止めされていない，孤立した完全な円形状の粒界の移動についてもFig.4に示す。粒界移動開始時の中間仮想点の速さはすべて同じであった。両端が固定された半円状の粒界の中間仮想点は，移動の初期段階ではピン止めの影響を受けないことから，この結果は正しいと考えられる。仮想点間隔が最も短い0.33(分割数96)の場合を基準に，分割数を2から96の範囲で変化させ仮想点間隔を小さくした場合の中間仮想点の位置と速さの差異を誤差(error)と定義して，初期の仮想点間隔に対する位置および速さの最大誤差をFig.5に示す。半円の場合，位置の最大誤差を1%以下にするためには仮想点間隔を約4.2以下(分割数を7以上)に，さらに速さの最大誤差も1%以下にするためには仮想点間隔を約2.4以下(分割数を12以上)にすればよいことがわかる。

Fig. 4.

 Grain boundary migrations of half circles calculated by the local curvature multi-vertex model and of isolated full circle calculated by conventional curvature model. (a) Time evolution of position. (b) Time evolution of speed. The radius of the initial circle is 10.

Fig. 5.

 Calculation errors of the position and speed of grain boundary migration as a function of the initial distance between adjacent vertices on half circular arc, on the basis of the initial distance 0.33. (a) Position error. (b) Speed error. The radius of the initial circle is 10.

以上の結果は円周の長さに対する円弧の長さが1/2の場合の結果であるが，同様のシミュレーションを円周の長さに対する円弧の長さが1/3~1/12の場合についても行った。円周の分割数に対して，位置および速さの最大誤差が1%および2%となる初期の仮想点分割数および仮想点間隔を評価した結果をFig.6に示す。初期の結晶粒径が同一で，固定点間の距離が異なり中間仮想点の移動距離が異なるような場合においても，最大誤差は円周の分割数にあまり依存しないことがわかる。位置の最大誤差を1%以下にするためには，2つの固定点つまり2つの三重点の間の分割数を6程度以上に，速さの最大誤差異を1%以下にするためには分割数を10程度以上にすればよいことがわかる。二次元では粒界特性(粒界エネルギー，粒界易動度)が均一の場合，1つの結晶粒にある三重点の数つまり円周分割数が7以上の場合には結晶粒は大きくなることが多く，5以下の場合には結晶粒は小さくなることが多いので¹³⁾，中間の6の場合で具体的な仮想点間隔を決めることが良いと考えられる。具体的には，Fig.6より位置の計算精度を1%としたい場合には，仮想点間隔を約2.0以下(仮想点分割数を6以上)に設定すればよい。速さの計算精度を2%とするためには仮想点間隔を約1.6以下(仮想点分割数を7以上)に，1%とするためには約1.2以下(仮想点分割数を9以上)にする必要がある。

Fig. 6.

 Calculation error against initial virtual vertex condition. (a) Errors of position and speed are presented as a function of the division number of the circle and division number of the circular arc. (b) The errors are presented as a function of the division number of a circle and the initial distance between adjacent vertices.

以上の議論で明らかなように，仮想点間隔の絶対値より，2つの三重点に対する相対的な仮想点間隔，つまり分割数により，大凡の計算精度が決まることがわかる。しかしながら，2・5で述べるように，時間発展間隔と総合的な適正化を考える場合には，仮想点間隔の相対値ではなく，絶対値が重要となるので，両者を考慮する必要がある。

2・4　局所曲率マルチバーテックスモデルにおける時間発展間隔の適正化

局所曲率マルチバーテックスモデルの時間発展間隔が計算時間精度に及ぼす影響を検討した。時間発展間隔Δtを小さくすることは，計算精度の観点からは好ましいことであるが，計算時間が膨大となり，場合によっては計算の実行が非現実的になることがあり得る。一方，時間発展間隔Δtを大きくすることは，計算精度を劣化させるという問題がある。粒界上の点p_iの時間発展は，式(8)および式(9)で計算することができる。   

$${\overrightarrow{r}}_i\left(t+\Delta t\right)={\overrightarrow{r}}_i\left(t\right)+\Delta {\overrightarrow{r}}_i\left(t\right)$$(8)

  

$$\Delta {\overrightarrow{r}}_i\left(t\right)={\overrightarrow{v}}_i\left(t\right)\Delta t$$(9)

ここで，tは時間，Δtは時間発展間隔，$\overrightarrow{r}$_i(t)は時間tにおける粒界上の点p_iの位置ベクトル，Δ$\overrightarrow{r}$_i(t)は時間tにおける粒界上の点p_iの位置ベクトルの変化，$\overrightarrow{v}$_i(t)は時間tにおける粒界上の点p_iの速度である。$\overrightarrow{v}$_i(t)は二重点では式(1)に，三重点では式(3)に従うので，二重点については従来の曲率モデルと，三重点については従来のバーテックスモデルと比較することで検討を行った。検討を単純化するために，曲率モデルとバーテックスモデルのそれぞれの場合について，時間tにM_gb,iγ_iまたはM_tp,iγ_ijを乗じたものを，粒界特性を考慮した時間として取り扱った。

2・4・1　曲率モデルにおける時間発展間隔の適正化

はじめに，孤立した円形状の結晶粒の時間発展を評価して，曲率モデルの計算時間精度を検討した。初期の結晶粒半径を10として，曲率モデルに関係する式(1)，(2)，(5)，(8)，(9)を用いて，結晶粒半径の時間発展を計算した。Fig.7にその計算結果と曲率モデルの解析解を示す。解析解では時間t=50で結晶粒が消滅するのに対して，シミュレーションでは時間発展間隔Δtによって誤差に違いが生じることがわかる。Fig.8に解析解で得られる結晶粒消滅時間t=50に対する誤差を示す。時間発展間隔Δtを0.2程度以下とすると，計算時間精度を1%以下にできると言える。

Fig. 7.

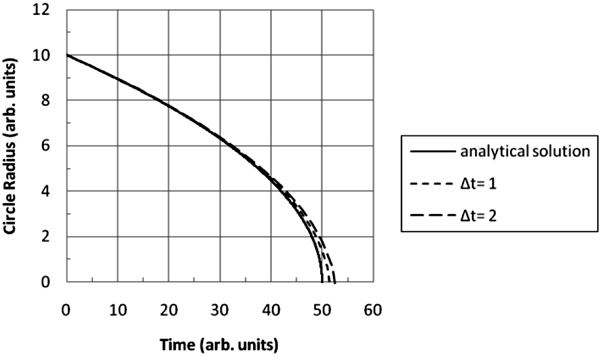
 Time evolution of isolated circle.

Fig. 8.

 Calculated error in time evolution of grain growth with an isolated circle shape.

2・4・2　バーテックスモデルにおける時間発展間隔の適正化

Fig.9(a)に示すような三重点の時間発展を評価して，バーテックスモデルの計算時間精度を検討した。ここでは，3つの粒界の特性はすべて等しいとした。この場合，平衡状態である最終状態では三重点の交差角はすべて120°となる(Fig.9(b))。平衡状態での三重点とその隣接点の間隔をすべて10とし，隣接点は固定されているとして，バーテックスモデルに関係する式(3)，(4)，(8)，(9)を用いて，三重点の時間発展を計算した。Fig.10にその計算結果を示す。Fig.9(a)の三重点の時間発展の解析解を求めるのは困難であるので，時間発展間隔Δt=0.001の条件まで計算を行い，時間発展が収束することを確認し，この時間発展を基準にして検討した。曲率モデルと同様に，シミュレーションでは時間発展間隔Δtによって誤差に違いが生じることがわかる。平衡状態となるのに無限の時間を要すると考えられるので，平衡状態からの距離が，初期状態と平衡状態の距離5の1%つまり0.05となる位置に三重点が移動するまでの時間で評価した。Fig.11に時間発展間隔Δt=0.001で得られる移動時間に対する誤差を示す。曲率モデルの場合と同様に，時間発展間隔Δtを0.2程度以下とすることで，計算時間精度を1%以下にできると言える。

Fig. 9.

 Time evolution of triple junction. Solid circles are triple junctions. Open circles are fixed. (a) Initial stage. (b) Final stage.

Fig. 10.

 Time evolution of triple junction calculated by vertex model.

Fig. 11.

 Calculation error in time evolution of triple junction.

以上の検討より，提案モデルで結晶粒成長シミュレーションを実行する際には，初期の結晶粒の半径を10 μm程度と想定した場合，時間発展間隔を0.2程度以下とすることで，計算速度を確保しつつ，1%程度の計算時間精度が得られることが確認された。

2・5　局所曲率マルチバーテックスモデルにおける隣接点間隔と時間発展間隔の総合的な適正化

2・3では仮想点間隔(空間)適正化を，2・4では時間発展間隔(時間)の適正化を行った。ここでは，両者の総合的な適正化について検討する。

2・5・1　結晶粒成長トポロジー変換，および変換条件

離散化された結晶粒成長の時間発展の過程では，トポロジー変換が要求される。Weygandらがバーテックスモデルにおいて既にトポロジー変換を整理しているので，本提案モデルにおいてもその変換を用いる¹⁰⁾。代表的なトポロジー変換をFig.12に示す。Fig.12(a)は2つの三重点のスイッチングであり，Fig.12(b)と(c)は結晶粒の消滅である。連続的な実現象を離散的なシミュレーションで再現するには，三重点のスイッチングや結晶粒の消滅のトポロジー変換を実行する臨界粒界長さを設定する必要がある。以下においては，シミュレーションを安定して行うための，臨界粒界長さと時間発展間隔の関係を検討した。さらに，仮想点間隔と時間発展間隔の関係についても検討した。

Fig. 12.

 Topological transformations. (a) Switching of triple junctions. (b) Annihilation of triangle grain. (c) Annihilation of a grain with two triple junctions.

2・5・2　バーテックスモデルにおける三重点の制約条件の検討

三重点の時間発展は式(3)，(4)，(8)，(9)で計算できる。これらの式を用いて，三重点のスイッチング条件，結晶粒の消滅条件，および三重点の平衡位置通過回避条件を検討した。

(1)三重点のスイッティング条件

2つの三重点のスイッチングを実行する臨界粒界長さと時間発展間隔の関係を検討するにあたり，Fig.12(a)に示す非平衡位置の2つの三重点の移動を考えた。このとき，2つの三重点の位置関係が逆転しない(例えば，Fig.12(a)の2つの三重点の左右または上下の位置関係が反対にならない)ための三重点スイッチングの臨界粒界長さL_cr,swは，Table 1の式(10)を満たさなければならない。ここで，M_tp,maxは三重点の易動度の最大値，γ_maxは単位長さ当たりの粒界エネルギーの最大値である。式(10)は対象とする三重点間の粒界エネルギーのみを考慮し，それ以外の粒界エネルギーを0とした最も厳しい条件と言える。さらに，スイッチングの際には2つの三重点の間の粒界には仮想点がない方が好ましいことから，Table 1の式(11)を得ることができる。

Table 1. Summary for conditions of space interval, time interval and critical length for triple junction switching and grain annihilation in the local curvature multi-vertex model.

Constraint items	Condition of vertex model	Condition of curvature model	Parameters
Triple junction switching	2Mtp,maxγmaxΔt < Lcr,sw (10) Lcr,sw < Lmax (11)	–	Δt, Lcr,sw, Lmax
Annihilation of grain with three triple junctions	3Mtp,maxγmaxΔt < Lcr,an (12) Lcr,an < Lmax (13)	$\sqrt{2}\sqrt{M_{gb,\max }{\gamma }_{\max }\Delta t}$ < Lcr,an(iso) (17) Lcr,an(iso) < Lmax (18)	Δt, Lcr,an, Lmax
Annihilation of grain with two triple junctions	2Mtp,maxγmaxΔt < Lcr,an2 (14) Lcr,an2 < Lmax (15)	–	Δt, Lcr,an2, Lmax
Prevention of virtual vertex overrun from equilibrium position	2Mtp,maxγmaxΔt < Lmin (16)	2Mgb,maxγmaxΔt < Lmin (19)	Δt, Lmin
Generation and annihilation of double junction	Lmin < L < Lmax (6) 2Lmin < Lmax (7)		L, Lmin, Lmax

(2)結晶粒の消滅条件

結晶粒は消滅する際には，その結晶粒を取り囲む粒界の長さが徐々に短くなり，既に2・2で述べた仮想点の消滅処理によって，多くの場合最終的には三角形となって消滅することになる。Fig.12(b)に示す結晶粒の消滅を実行するにあたって，臨界粒界長さと時間発展間隔の関係を検討した。ここでは，結晶粒消滅の条件として，3つの粒界がすべて臨界粒界長さ以下となることとした。

消滅する直前の結晶粒が正三角形の場合を考える。結晶粒のそれぞれの三重点が正三角形の外接円の中心を超えて移動しないようにしなければならないことから，結晶粒消滅の臨界粒界長さL_cr,anは，Table 1の式(12)を満たさなければならない。式(12)は式(10)と同様に，対象とする結晶粒の粒界エネルギーのみを考慮し，それ以外の粒界エネルギーを0とした最も厳しい条件と言える。さらに，三重点スイッチングの際と同様に，結晶粒消滅の際には2つの三重点の間の粒界には仮想点がない方が好ましいことから，Table 1の式(13)を得ることができる。結晶粒が正三角形でなく二辺が長く一辺が短い三角形や一辺が長く二辺が短い三角形の場合においても，式(12)および式(13)を満たしていれば十分である。

また，三角形の結晶粒の一辺が三重点スイッチングの臨界粒界長さL_cr,swより短い場合には，三重点のスイッチングを行って，Fig.12(c)の2つの三重点を持った結晶粒に変換される。便宜的に粒界を曲線で描写しているが，提案モデルでは2つの粒界とも粒界上に仮想点がない場合，粒界は直線となり2つが重なって面積が0の結晶粒となる。この場合も，Fig.12(c)の結晶粒の消滅のトポロジー変換によって結晶粒が消滅することになるが，結晶粒消滅の臨界粒界長さL_cr,an2は，Table 1の式(14)を満たさなければならない。結晶粒が2つの三重点を持った結晶粒になる場合には，2つの三重点を持つ結晶粒の2つの粒界のエネルギーの和が，その結晶粒に属さない粒界のエネルギーより大きくなるということは考えにくいことから，式(14)を得ることができる。結晶粒消滅の際には2つの三重点の間の粒界には仮想点がない方が好ましいことから，Table 1の式(15)を得ることができる。

(3)三重点の平衡位置通過防止条件

三重点の移動の計算を安定して行うためには，三重点に隣接する3つの点が固定されているという条件の下では，三重点が平衡位置を通過しないようにした方が良いが，仮に通過した場合でも通過前の三重点の位置と平衡位置の距離より，通過後の三重点の位置と平衡位置の距離が長くならないようにしなければならない。そのための隣接点間隔と計算時間間隔の関係を検討した。

Fig.13(a)に示すように，3つの粒界エネルギーが等しい場合における三重点の非平衡位置から平衡位置への移動を考える。このとき，非平衡位置の三重点に作用する駆動力F_tp1,iは，F_tp1,i≅(3ΔL₁/2L)γ_iと近似できる。ここで，Lは隣接点間隔，ΔL₁は非平衡位置と平衡位置の間隔，γ_iは粒界エネルギーである。三重点が平衡位置を通過しない，より厳しい条件を満足するためには，M_tp,i(3ΔL₁/2L)γ_iΔt≤ΔL₁を満たさなければならない。また，Fig.13(b)に示すように，1つの粒界エネルギーが0で他の2つの粒界エネルギーが0でなく且つ等しい場合における三重点の非平衡位置から平衡位置への移動を考える。このとき，非平衡位置の三重点に作用する駆動力F_tp2,iは，F_tp2,i≅(2ΔL₂/L)γ_iと近似できる。ここで，ΔL₂は非平衡位置と平衡位置の間隔である。三重点が平衡位置を通過しない，より厳しい条件を満足するためには，M_tp,i(2ΔL₂/L)γ_iΔt≤ΔL₂を満たさなければならない。以上から，より厳しい条件である後者の条件から，Table 1の式(16)を得ることができる。

Fig. 13.

 Triple junction migration from nonequilibrium (broken lines) to equilibrium (solid line) position. (a) Three grain boundary energies are equal. (b) One grain boundary energy is zero, while the other two are not zero and equal.

2・5・3　曲率モデルにおける制約条件の検討

仮想点の時間発展は式(1)，(2)，(5)，(8)，(9)で計算できる。これらの式を用いて，孤立結晶粒の消滅条件，および仮想点の平衡位置通過回避条件を検討した。

(1)孤立結晶粒の消滅条件

孤立した結晶粒は一般的にはあまり多くは存在しないが，粒界特性の差異などの影響から結晶粒成長の過程で発生することはあると考えられる。孤立した結晶粒は仮想点のみから成り，三重点を持つ結晶粒と同様に消滅の際，消滅する結晶粒を取り囲む粒界の長さは徐々に短くなり，仮想点の消滅処理によって，多くの場合最終的には三角形となって消滅する。3つの仮想点からなる三角形の孤立した結晶粒の消滅を実行するための臨界粒界長さと時間発展間隔の関係を検討した。ここでも，結晶粒消滅の条件として，3つの粒界がすべて臨界粒界長さ以下となることとした。ただし，仮想点が3つ以下の孤立結晶粒では，仮想点の消滅は行わないこととした。

孤立した結晶粒の消滅処理を確実に実行するためには，仮想点が結晶粒の消滅位置である外接円の中心を通り過ぎないようにした方が良いが，仮に通過した場合でも，通過前の三角形の結晶粒の外接円の半径より，通過後の三角形の結晶粒の外接円の半径が短くならなければならない。孤立結晶粒であることから，後者の条件としても粒界が交差する等の問題は生じないことから，この条件を用いた。結晶粒消滅の臨界外接円半径R_cr,isoは，M_gb,i(γ_i/R_cr,an(iso))Δt<2R_cr,an(iso)，つまり$\sqrt{M_{gb,i}{\gamma }_i\Delta t/2}\le R_{cr,an\left(iso\right)}$を満たさなければならない。ここで，孤立結晶粒消滅の臨界粒界長さをL_cr,an(iso)とすると，結晶粒が正三角形の場合は$\sqrt{3}{R}_{cr,an\left(iso\right)}=L_{cr,an\left(iso\right)}$であり，三角形の一辺が最も長い場合は2R_cr,an(iso)=L_cr,an(iso)である。より厳しい条件は後者であることから，孤立結晶粒消滅の臨界粒界長さL_cr,an(iso)と計算時間間隔Δtは，Table 1の式(17)を満たさなければならない。さらに，結晶粒消滅の際には3つの仮想点からなる三角形であることが好ましいことから，Table 1の式(18)を得ることができる。

(2)仮想点の平衡位置通過抑制条件

仮想点の移動の計算を安定して行うためには，仮想点に隣接する2つの点が固定されているという条件の下では，仮想点が平衡位置を通過しないようにした方がよいと考えられる。そのための隣接点間隔と計算時間間隔の関係を検討した。Fig.14に示す仮想点の移動について考える。仮想点に隣接する2つの点はいずれも固定されている。仮想点が平衡位置を通過しないためには，M_gb,i(γ_i/R)Δt≤δを満たす必要がある。また，Fig.14から関係式δ=R−Rcos(θ/2)，L=2Rsin(θ/4)が成り立つ。したがって，安定計算の条件として，隣接点間隔の最小長さL_minと計算時間間隔Δtは，Table 1の式(19)を満たさなければならない。

Fig. 14.

 Migration of virtual vertex (solid circle) whose adjacent vertices (open circle) are fixed.

以上，局所曲率マルチバーテックスモデルにおける隣接点間隔と時間発展間隔の適正化に関する総合的な検討結果をまとめたものが，Table 1である。これらはシミュレーションを安定して実行するための時間発展間隔，隣接点間隔，三重点スイッチングの臨界粒界長さ，および結晶粒消滅の臨界粒界長さに関する制約条件である。

3. 結晶粒成長の時間発展に関する提案モデルの検証

新しく開発した局所曲率マルチバーテックスモデルを結晶粒成長シミュレーションに適用した。各種のシミュレーションパラメータは，上記で検討した制約条件を満たすように決定している。具体的には，平均結晶粒径10のときの位置の計算精度は約1%を，速度の計算精度は約2%を狙って，以下の通りパラメータを設定した。   

$$M\gamma \Delta t=0.2,L_{\min }=0.7,L_{\max }=1.5,L_{cr,sw}=L_{cr,an}=L_{cr,an2}=0.7$$

このパラメータセットはTable 1の条件をすべて満足する。また，モデルの検証を目的としたシミュレーションに用いた結晶組織は人工的に作成したものである。試料のサイズは210 μm×216 μmで，その中に約3 μm×約3 μmのほぼ正方形の結晶粒が二次元的に5,040個配置されている。正確には四角形の各角の位置を正方形の各角の位置からランダムに微小にずらした。結晶粒方位についてはランダムに付与し，ここでは粒界エネルギーおよび粒界易動度は結晶方位角度差に依らず一定とした。二重点の易動度には粒界易動度を用いた。一方，三重点の易動度は方位が異なる3つの結晶粒が関与しているので粒界易動度とは異なるが，三重点の易動度に関するデータが十分でないことから，三重点に繋がる3つの粒界の易動度の平均値とし，ここでは結晶方位角度差依存性はないとしているので，粒界易動度と同じ値とした。初期の結晶粒の形状を四角形としたのは，ランダムな人工データを作成するのが簡単であるからである。シミュレーションの最初の時間ステップで四重点を2つの三重点に分割する必要があるので，結晶粒の形状を正方形としなかった。四重点の三重点への分割は，三重点のトポロジー変換と同等の規則に従って行った¹⁰⁾。

提案モデルを適用した四重点分割後の初期組織および粒成長のシミュレーション結果の一例をFig.15に示す。結晶粒成長が安定して計算できており，結晶粒の平均結晶粒面積つまり平均結晶粒径の二乗は，時間にほぼ比例していることがわかる。この結果はピン止め粒子のない条件での結晶粒成長を再現していると言える。実際には試料内の四角形の各角のずらし方を変化させて数種類の初期組織を人工的に作成してシミュレーションを行い，上記と同様の結果を得た。このときの傾きは，0.99±0.02であり，狙いとした精度が得られていると思われる。したがって，仮想点の生成・消滅を含む提案モデルは結晶粒成長に適用可能であることが確認できた。実測した再結晶粒の粒成長への本モデルの展開や粒界エネルギーや界面易動度の粒界性格依存性を考慮したモデルの構築，および二次再結晶プロセスへの応用についても，今後報告の予定である。

Fig. 15.

 Grain growth simulation by the local curvature multi-vertex model showing time evolutions of grains. The initial number of grains is 5040. The average grain areas are (a) 9.0 (initial), (b) 50.6 and (c) 324.0. (d) Time evolution of average grain area.

結晶粒成長は二次元と三次元とでは様相がことなる部分があることから，さらなる高精度化のためには三次元化が求められる。三次元モデルは二次元モデルに比べてかなり複雑になると推測されるが，面を三角形のメッシュで表現し，メッシュの各点について直交する二方向の曲率を計算することで，メッシュの各点つまり面上の各点の移動を計算することが可能となる。

4. 結言

二次元の局所曲率マルチバーテックスモデルを開発した。このモデルは，結晶粒界の曲率と三重点での結晶粒界エネルギーと三重点での粒界張力を考慮した物理原理に基づいた，直接的に粒成長を表現した二次元トポロジカルネットワークモデルである。提案モデルは，粒界上にいくつかの仮想点を配置して局所曲率および粒界張力を用いた駆動力から粒界および三重点の移動を計算する。この点で，従来の結晶粒成長を記述する曲率モデルやバーテックスモデルより，精度良く結晶粒成長を予測することができる。また，結晶粒成長に伴って，仮想点の生成および消滅を行うことで，仮想点を適切に配置することができる。さらに，平均結晶粒径に応じて，仮想点間隔を適正化することで，位置および速さの計算精度を確保できることを確認した。時間発展間隔については平均結晶粒径に応じて適正化することにより，計算速度を確保しつつ計算時間精度を確保できることを確認した。結晶粒成長に伴い結晶粒のトポロジー変換が必要となるが，三重点スイッチングおよび結晶粒消滅の臨界粒界長さ，隣接点間隔，時間発展間隔を適切に設定することで，計算を安定して実行できることを確認した。これらの検討結果を踏まえて，平均結晶粒径10のときの位置の計算精度として約1%を，速度の計算精度として約2%を見込めるシミュレーションパラメータのセットを示した。このように適正化したパラメータを用いて人工的に作成した5040個の結晶粒の粒成長シミュレーションを，提案モデルを用いて実行した。結晶粒成長が安定して計算でき，結晶粒成長時間発展において平均結晶粒面積が時間にほぼ比例していることを確認した。仮想点の生成・消滅を含む提案モデルは結晶粒成長に適用可能であることが確認できた。

付録

提案した二次元局所曲率マルチバーテックスモデルの単位について考察する。式(1)~(4)の各項目の定義と単位をTable 2に示す。式(2)は粒界に作用する駆動力を，式(4)は三重点に作用する駆動力を示している。線である粒界に作用する駆動力は単位長さ当たりの粒界に作用する力で定義され，単位は[N/m]となる。一方，点である三重点に作用する駆動力は単なる力で定義され，単位は[N]となる。粒界の移動速度の単位はいずれも[m/s]であるので，式(1)と式(3)に表れる粒界の易動度と三重点の易動度の単位は異なり，それぞれ[(m/s)/(N/m)]と[(m/s)/N]となる。

Table 2. Definitions and units of physical properties related to triple junction and grain boundary in the two-dimensional model.

Triple junction of grain boundary (point)		Grain boundary (line)
Symbol Unit	Definition	Symbol Unit	Definition
γij [J/m]	Grain boundary energy per unit length.	γi [J/m]	Grain boundary energy per unit length.
$\overrightarrow{F}$tp,i [N]=[J/m]	Driving force acting on triple junction.	$\overrightarrow{F}$gb,i [N/m]=[J/m2]	Driving force per unit length, acting on grain boundary.
Mtp,i [(m/s)/N]	Mobility of triple junction. Speed of triple junction applying the driving force of 1N on it.	Mgb,i [(m/s)/(N/m)]	Mobility of grain boundary. Speed of grain boundary applying the driving force of 1N on the grain boundary of unit length.
$\overrightarrow{v}$tp,i [m/s]	Velocity of triple junction.	$\overrightarrow{v}$gb,i [m/s]	Velocity of grain boundary.

謝辞

本研究におきまして，NSプラント設計株式会社の西俊二殿にはシミュレータのコーディングにおいて，株式会社アドウィンの吉田峻殿にはシミュレーションの実行においてサポート頂きました。感謝いたします。

文献

• 1)   Y.  Ushigami and  T.  Nakayama: Mater. Sci. Forum, 157(1994), 1081.
• 2)   S.I.  Wright and  M.M.  Nowell: Microsc. Microanal., 12(2006), 72.
• 3)   M.P.  Anderson,  D.J.  Srolovitz,  G.S.  Grest and  P.S.  Sahni: Acta Metall., 32(1984), 783.
• 4)   D.  Fan and  L.Q.  Chen: Acta Mater., 45(1997), 611.
• 5)   H.J.  Frost,  C.V.  Thompson,  C.L.  Howe and  J.  Whang: Scr. Metall., 22(1988), 65.
• 6)   H.J.  Frost,  C.V.  Thompson and  D.T.  Walton: Acta Metall. Mater., 38(8)(1990), 1455.
• 7)   A.  Soares,  A.C.  Ferro and  M.A.  Fortes: Scr. Metall., 19(1985), 1491.
• 8)   K.  Kawasaki,  T.  Nagai and  K.  Nagashima: Philos. Mag. B, 60(1989), No.3, 399.
• 9)   K.  Fuchizaki,  T.  Kusaba and  K.  Kawasaki: Philos. Mag. B, 71(1995), No.3, 333.
• 10)   D.  Weygand,  Y.  Bréchet and  J.  Lépinoux: Philos. Mag. B, 78(1998), No.4, 392.
• 11)   F.J.  Humphreys: Acta Mater., 45(1997), No.10, 4231.
• 12)   D.G.  Brandon: Acta Metall., 14(1966), 1479.
• 13)   S.G.  Kim,  D.I.  Kim,  W.T.  Kim and  Y.B.  Park: Phys. Rev., E74(2006), 061605.