Effect of Cr on Lamellar Spacing and High-Temperature Stability in Eutectoid Steels

Synopsis:

In order to clarify refinement of lamellar spacing and high temperature stability of lamellae in pearlite by the addition of Cr, we investigated in terms of supercooling, diffusion coefficient of C and Cr, and spheroidizing of cementite using Fe-0.8%C binary and Fe-0.8%C-Cr ternary steels.

Equilibrium transformation temperature of pearlite was increased by the addition of Cr. At a fixed pearlite transformation temperature, pearlite lamellar spacing of Cr addition steel was refined by increasing of supercooling compared with Fe-0.8%C steel. On the other hand, in spite of the same supercooling, lamellar spacing was refined by increasing of Cr content. This is caused by decreasing of the diffusion coefficient of C in the austenite by addition of Cr.

Spheroidizing of cementite in pearlite at high temperature was inhibited by inceasing of Cr content. Spheroidizing rate reduced by the addition of Cr. Spheroidizing of cementite in pearlite by increasing of Cr content was inhibited by increasing of the contribution of diffusion of Cr for the coarsening reaction of cementite.

1. 緒言

0.8%Cを含む共析鋼をオーステナイト状態に加熱後，A1温度以下に冷却されると，オーステナイトがフェライトとセメンタイトに分解する共析変態を生じ，パーライト組織となる¹⁾。パーライト組織は，フェライトとセメンタイトが交互に層状をなすラメラー，ラメラーの方向は異なるがフェライトの結晶方位が同じ領域のブロック，ラメラーが同一方向に並んだ領域のコロニーから構成される²⁾。共析鋼は，優れた強度特性や耐摩耗性を有するため，レール鋼などに使用されている³⁾。しかし，近年，使用環境が過酷化⁴⁾し，レール鋼の耐摩耗性向上が求められているが，耐摩耗性を向上するにはレール鋼の高強度化が有効であると報告されている⁵⁾。共析鋼の強度に影響を及ぼす組織因子として，ラメラー間隔が着目されており，降伏応力や硬さとラメラー間隔にはHall-Petchの関係式が成立すると報告されている^6,7,8,9)。そのため，ラメラー間隔を微細化することで共析鋼の高強度化を図ることができる。しかしながら，オーステナイトからパーライトが生成する際，体積的な自由エネルギーは低下するが，フェライト/セメンタイト界面を形成するため，ラメラーが微細化するほど界面エネルギーの上昇は大きくなり，微細化には限度がある¹⁰⁾。

フェライト/セメンタイトの界面エネルギーに費やすことができるエネルギーは，パーライトの変態駆動力の大きさになるため，化学的な駆動力の大きさは，パーライト平衡変態温度(T_e:Fe-0.77%Cでは996 K)からの過冷度(ΔT)に比例する。したがって，ΔTを大きくすることによってラメラーの微細化を図ることができる^11,12)。ここでΔTは，T_eとパーライト変態温度(P_s)の差(T_e−P_s)とT_eの比で定義される¹³⁾。T_eは合金元素により変化し，P_sは合金元素と冷却速度により変化する。そのため，合金元素の添加によりT_eを上昇させ，冷却速度を大きく，より低温側でパーライト変態させることで，ΔTを大きくすることができる。

しかし，置換型元素を添加すると，ΔTが同等であってもラメラー間隔が変化することがある。Takahashiら¹³⁾は，添加するCr量が増加すると，ΔTが同等であってもラメラーが微細化すると報告している。また，Capdevilaら¹⁴⁾は，Si，Cr，Moの添加量が増加するとラメラーが微細化し，Mn，Niの添加量が増加するとラメラーが粗大化すると報告しているが，いずれの報告においても，ラメラーが微細化するメカニズムについては明確でない。

そこで本研究では，添加するCr量の増加によるラメラー間隔の微細化に注目し，同等ΔTにおけるパーライト変態に対して，熱力学的観点からラメラー間隔微細化のメカニズムを検討した。また，ラメラーは873 K以上の高温域で形成されるため，高温域でのパーライトラメラーの安定性について，セメンタイトの球状化の速度論の観点からCrの影響を検討した。

2. 実験方法

2・1 供試鋼

Table 1に供試鋼の化学成分を示す。Fe-0.8%C鋼をBase鋼として，Cr量を0.18%，0.57%，0.99%の3水準に変化させたFe-0.8%C-Cr鋼を高周波真空溶解炉により25 kg鋼塊で溶製し，1273 Kで3.6 ks加熱した後，熱間圧延により厚さ25 mmの鋼板に加工した。

Table 1.  Chemical compositions of steels. (mass%)

Steel	C	Si	Mn	P	S	Cr	N
Base	0.80	0.01	0.01	< 0.001	0.0010	0.01	0.0026
0.2Cr	0.84				0.0003	0.18	0.0014
0.6Cr	0.83				0.0004	0.57	0.0013
1.0Cr	0.84				0.0004	0.99	0.0012

2・2 熱処理条件

はじめに，Cr量によるラメラーの微細化を熱力学的観点から考察するために，圧延した供試鋼の圧延方向から80 mm×75 mm×15 mmの板状試験片を採取し，富士電波工機製急速熱サイクル再現装置により熱処理を行った。熱サイクルをFig.1に，その条件をTable 2に示す。本研究では，このときに得られたパーライト組織を初期組織と定義した。次に，ラメラーの高温安定性に及ぼすCrの影響について検討するために，熱処理後の板状試験片の中心部から，10 mm角の試験片を採取し，873 K，923 K，973 Kの各温度に加熱し，3.6~1080 ks間の等温保持(球状化熱処理)を行い，その後，急冷させた。

Fig. 1.

 Schematic diagram of thermal process.

Table 2.  Isothermal transformation holding times (t₁) to obtain pearlitic structure.

Steel	873, 923 K	973 K
Base	100 s	1000 s
0.2Cr	100 s	1000 s
0.6Cr	100 s	700 s
1.0Cr	100 s	300 s

2・3 ミクロ組織観察および解析方法

ラメラー間隔は，熱処理後の10 mm角の試験片を研磨し，3%ナイタルにて腐食後，試験片中央部を走査型電子顕微鏡(SEM)で倍率10000倍にて各々9視野ずつ組織観察を行った。各視野でラメラー間隔が狭い箇所を選び，2 µm中のラメラーの本数からその間隔を測定し，平均ラメラー間隔を求めた。球状化パーライト組織も同様に，熱処理後の10 mm角の試験片を研磨し，3%ナイタルにて腐食後，試験片中央部をSEMで倍率10000倍にて各々9視野ずつ組織観察を行った。球状化パーライトの総界面は，各視野で直線交差線分法(JIS G 0552)によりフェライト/セメンタイト界面との交点数から，DeHoff and Rhinosの方法¹⁵⁾により各視野の界面の面積を求めて平均化後，単位面積あたりに換算した値を界面の総面積と定義した。

2・4 分配係数

分配係数は，初期組織ならびに球状化処理を行った試験片を用いて，EDX分析ならびに抽出残渣分析により，フェライト中，セメンタイト中のCr量を求め，(セメンタイト中のCr量/フェライト中のCr量)をもって分配係数を求めた。抽出残渣分析は，10%アセチルアセトン−メタノール電解抽出を行い，その残渣を用いてICP発光分析法で測定を行った。

3. 実験結果

3・1 平衡変態温度(T_e)に及ぼすCrの影響

平衡変態温度に及ぼすCr量の影響をFig.2に示す。平衡変態温度はThermo-Calc¹⁶⁾を用いて，Fe-0.8%C鋼をベースにCr量の影響を計算した。Base鋼と1.0%Cr鋼の平衡変態温度はそれぞれ999 Kと1009 Kであり，Cr量の増加により平衡変態温度が上昇した。Fig.3に，過冷度(ΔT)とCr量の関係を示す。過冷度は，(1)式により算出した^11,13)。   

$$\Delta T=\frac{T_e-P_s}{T_e}$$(1)

Fig. 2.

 Calculation results of Cr content and equilibrium transformation temperature.

Fig. 3.

 Influence of Cr content on ΔT.

ここで，P_sはパーライト変態温度である。923 KではBase鋼のΔTは7.6×10⁻²であったのに対して，1.0%Cr鋼は8.5×10⁻²であり，Cr量の増加によりT_eが上昇しΔTが大きくなった。

3・2 ラメラー間隔に及ぼすCrの影響

Fig.4に873 Kから973 Kで変態したラメラーのSEM観察結果，ならびにFig.5にラメラー間隔に及ぼすCr量の影響を示す。973 KではBase鋼が0.27 µmであったのに対して，1.0%Cr鋼は0.17 µmであり，Cr量の増加によりラメラー間隔が微細化した。一方，パーライト変態温度が973 Kから873 Kに低下すると，Base鋼のラメラー間隔は0.27 µmから0.15 µmに，1.0%Cr鋼は0.17 µmから0.10 µmに微細化した。

Fig. 4.

 SEM micrographs of initial lamellar structures at 873, 923, 973 K of Fe-C binary and Fe-C-Cr ternary eutectoid steels.

Fig. 5.

 Effect of Cr content on lamellar spacing transformed at 873, 923 and 973 K.

一般にラメラー間隔(λ)は(2)式で記述でき，過冷度の逆数(1/ΔT)に比例することが知られている¹¹⁾。   

$$\lambda =\frac{2\sigma }{V_M\cdot \Delta H}\cdot \left(\frac{T_e}{T_e-P_s}\right)=\frac{2\sigma }{V_M\cdot \Delta H}\cdot \frac{1}{\Delta T}=a\cdot \frac{1}{\Delta T}$$(2)

ここで，ΔHはパーライト変態のエンタルピー変化，V_Mはパーライトのモル体積，σはフェライトとセメンタイトの界面エネルギー，aは定数である。そこで，λと1/ΔTとの関係をFig.6に示す。例えば1.0%Cr鋼では，1/ΔTが28から7.4に減少，すなわち，ΔTが増加すると，λが微細化した。また，1/ΔTがほぼ同一の約12において，Base鋼のλは0.19 µmであるのに対して，1.0%Cr鋼は0.11 µmであり，1/ΔTが同等であってもCr量が増加するとλが微細化した。

Fig. 6.

 Effect of ΔT^–1 on lamellar spacing of Fe-C binary and Fe-C-Cr ternary eutectoid steels.

3・3 ラメラーの球状化に及ぼすCrの影響

Fig.7に923 Kで球状化熱処理での組織変化を示す。また，フェライト/セメンタイトの総界面を求めた結果をFig.8に示す。Base鋼の総界面は，球状加熱処理初期は11285 mm⁻¹であったのに対して，1080 ks後には400 mm⁻¹に減少した。一方，1.0%Cr鋼においては，初期は19380 mm⁻¹から2916 mm⁻¹に減少した。初期の組織はラメラーであったが，熱処理時間の増加とともに球状化が進行した。また，Cr量の増加により，パーライトの球状化が遅延し，1080 ks経過後も一部ラメラーが残存していた。

Fig. 7.

 SEM micrographs of Fe-C binary and Fe-C-Cr ternary eutectoid steels spheroidized at 923 K.

Fig. 8.

 Temporal evolutions of interface area in Fe-C binary and Fe-C-Cr ternary eutectoid steels by holding temperature at 923 K.

ラメラーの球状化過程における速度式は，(3)式で表される¹⁷⁾。   

$${\left(\frac{1}{S}\right)}^3-{\left(\frac{1}{S_0}\right)}^3=k^s\times t$$(3)

ここで，Sは界面の総面積，S₀はt=0における界面の総面積，k^sは球状化速度定数，tは保持時間である。Fig.9にFig.8と(3)式を用いてk^sを求め，Cr量で整理した結果を示す。923 KでのBase鋼の球状化速度定数は，1.6×10⁻¹⁴ mm⁻³・t⁻¹であったのに対して，1.0%Cr鋼は，3.8×10⁻¹⁷ mm⁻³・t⁻¹であり，Cr量を増加することで球状化速度定数が小さくなり，Ishidaらの報告¹⁷⁾と同様の傾向が確認できた。

Fig. 9.

 Relationships between spheroidization rate constant k^s and Cr content by holding temperature at 873, 923 and 973 K.

ラメラーの球状化に及ぼすCr量の影響について，Ishidaら¹⁷⁾は，球状化速度k^sは球状化を律速する原子の拡散係数，界面エネルギー，分配係数に依存し，分配係数の効果が顕著であると報告している。Fig.10に873 Kで保持した場合のCrの分配係数の時間依存性を示す。球状加熱処理初期はパラ平衡状態にあり，時間経過とともにCrがセメンタイトに分配される。Fig.11に1080 ks.保持後の分配係数を示す。Cr量が増加しても分配係数はほぼ同等であった。本研究で得られた分配係数は，Koら¹⁸⁾の報告に比べ，約1/2の値であったが，本研究の結果から，Cr量の増加による球状化抑制効果に対して，分配係数は大きな影響を与えなかった。

Fig.10.

 Temporal change of partition coefficient for Cr in Fe-C-Cr ternary eutectoid steel.

Fig. 11.

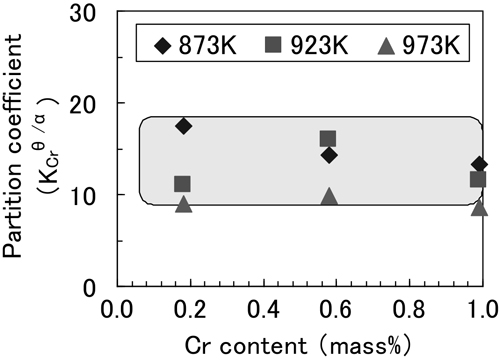
 Effect of Cr content on partition coefficient of Cr by holding temperature at 873, 923, 973 K.

4. 考察

4・1 Cr添加によるラメラー間隔微細化のメカニズム

ラメラー間隔(λ)は，(2)式に示すようにΔTが大きくなると微細化することが知られている。鋼の成分が同じ場合，T_eは同じ値となるためΔTの値はP_sで決まる。一方，パーライト変態温度(P_s)が同じ場合，ΔTはT_eで決まる。しかしながら，ΔTが同じ場合，Cr量が増加するとλが微細化しており，ΔTではλの微細化が説明できない。Takahashiら¹³⁾は，Cr量の増加によるλの微細化作用は，CrがΔHを上昇させる，あるいはσを減少させる効果によると報告している。一方，Tajimaら¹⁹⁾は，Cr量が増加しても鋼のΔHは同等であると報告している。そのため，Cr量の増加によるλの微細化作用は，σを減少させるためと考えられる。

σが減少すると(2)式中のaの値が小さくなり，aはFig.6の直線の傾きを示すため，σが減少するとFig.6の傾きが小さくなると予想される。そこで，各成分での傾きを求め，Cr量で整理した結果をFig.12に示す。Cr量の増加によるaの値の減少は認められず，Cr量の増加によるλの微細化作用は，Crによるσの低下によるとは考えにくい。したがって，同一ΔTにおけるCr量の増加によるλの微細化作用は，他の因子によるものと考えられる。

Fig. 12.

 Relationship between constant “a” in eq. (2) and Cr content.

λは，鋼の成分が同じ場合には(2)式で整理できるが，異なる場合には，必ずしも(2)式で整理できるとは限らない。これは，例えばパーライト変態は，拡散変態であるにも関わらず，拡散の効果など熱力学的影響が考慮されていないことが原因であると考えられる。そこで，γ中のCの拡散の影響を考慮した式として，(4)式に示すZener-Hillertの式²⁰⁾がある。   

$$v=\frac{D_C^{\gamma }}{b}\cdot \frac{{\lambda }^2}{{\lambda }^{\alpha }\cdot {\lambda }^{\theta }}\cdot \frac{C_e^{\gamma /\alpha }-C_e^{\gamma /\theta }}{C^{\theta /\gamma }-C^{\alpha /\gamma }}\cdot \frac{1}{\lambda }\cdot \left(1-\frac{{\lambda }_0}{\lambda }\right)$$(4)

ここで，vはパーライトの成長速度，D_c^γはγ中のCの拡散係数，λはラメラー間隔，C_e^γ/α，C_e^γ/θはそれぞれγ/α界面，γ/θ界面におけるγでのCの平衡濃度，C^α/γ，C^θ/γはそれぞれα，θ中のCの濃度である。λ₀はv=0となるラメラー間隔であり，Zener¹¹⁾は，(4)式を最大とするλが選ばれると考え，(5)式を導いている。   

$$\lambda =2{\lambda }_0$$(5)

λ^α，λ^θはそれぞれラメラー中のα，θの厚さであり，(6)式，(7)式で表される。   

$${\lambda }^{\alpha }=f^{\alpha }\times \lambda$$(6)

  

$${\lambda }^{\theta }=f^{\theta }\times \lambda$$(7)

ここで，f^α，f^θはそれそれフェライト分率，セメンタイト分率である。(5)−(7)式を(3)式に代入すると(8)式が得られる。   

$$v\lambda =\frac{1}{2b}\frac{1}{f^{\alpha }{f}^{\theta }}\frac{C_e^{\gamma /\alpha }-C_e^{\gamma /\theta }}{C^{\theta /\gamma }-C^{\alpha /\gamma }}\cdot D_C^{\gamma }$$(8)

Cr量の増加によるλの微細化作用を(8)式を用いて検討する。(8)式中のf^α，f^θ，C_e^γ/α，C_e^γ/θ，C^α/γ，C^θ/γはThermo-Calcにより計算を行い，λは，本研究で得られた結果を用いた。bは0.72とした²¹⁾。また，パーライト成長速度vは，Sharmaら²²⁾の結果からTable 3に示す値を用いた。以上より，(8)式からD_c^γを求めることができる。Fig.13に923KにおけるD_c^γに及ぼすCr量の影響を示す。Base鋼の拡散係数は，5.28×10⁻⁶ mm²/sであるのに対して，1.0%Cr鋼は0.79×10⁻⁶ mm²/sであり，Cr量の増加によりD_c^γが減少した。このことから，Cr量の増加によるλの微細化作用は，γ中のCの拡散係数の低下によるものと考えられる。Krishtal²³⁾は，Cの拡散係数に及ぼす合金元素の影響について検討し，Cr増加によりCの拡散係数が小さくなると報告しており，本研究と同様の傾向になっている。以上のことから，Cr量増加によるλの微細化作用は，オーステナイト中のCの拡散係数が減少し，Cの拡散距離が短くなったためと考えられる。

Table 3.  Pearlite growth rate using calculation²²⁾.

Steel	Pearlite growth rate v (×10–2 mm/sec)
Base	2.00
0.2Cr	1.69
0.6Cr	1.08
1.0Cr	0.62

Fig. 13.

 Relationship between Cr content and diffusion coefficient of C in γ calculated by eq. (8).

4・2 Cr添加による高温でのラメラー安定化のメカニズム

Cr量の増加によるラメラーの球状化遅延効果は，球状化を律速する原子の拡散係数，または界面エネルギーに依存すると考えられる。界面エネルギーについては，前節で示したようにCr量が変化しても変化しないと推定されるため，球状化を律速する原子の拡散係数の観点から検討を行う。

球状化速度定数は，オストワルド成長式よりFe-C2元系では(9)式，Fe-C-Cr3元系では(10)式で記述できる¹⁷⁾。   

$$k_1^s=\frac{8\sigma VD{x}_c}{9RT\times {\left(3f^{\theta }\right)}^3}$$(9)

  

$$k_2^s=\frac{8\sigma V{D}_{Cr}}{27RT\times {\left(K_{Cr}^{\theta /\alpha }-1\right)}^2\times X_{Cr}\times {\left(3f^{\theta }\right)}^3}$$(10)

ここで，k₁^s，k₂^sは球状化速度定数，Rは気体定数，Tは温度，DはCの拡散係数，D_crはCrの拡散係数である。x_c，X_Cr，f^θはそれぞれフェライトにおけるCの原子分率，Crの原子分率，セメンタイト分率である。K_Cr^θ/αはCrの分配係数，Vはセメンタイトのモル体積，σは界面エネルギーである。ここで，(9)式は(11)式に，(10)式は(12)式に書き換えることができる。   

$$\begin{array}{c}{k}_1^s=A\cdot D_0\exp \left(-\frac{Q_1}{RT}\right)\\ \ln k_1^s=\ln \left(A\cdot D_0\right)+\left(-\frac{Q_1}{R}\right)\frac{1}{T}\end{array}$$(11)

  

$$\begin{array}{c}{k}_2^s=B\cdot D_0^{Cr}\exp \left(-\frac{Q_2}{RT}\right)\\ \ln k_2^s=\ln \left(B\cdot D_0^{Cr}\right)+\left(-\frac{Q_2}{R}\right)\frac{1}{T}\end{array}$$(12)

ここで，A，Bは定数，D₀，D₀^Crは頻度因子，Q₁，Q₂は活性化エネルギーである。(11)式，(12)式より，球状化速度定数の対数(lnk^s)は，1/Tに比例し，傾きが−Q/Rとなる。そこで，Fig.14に球状化速度定数の対数(lnk^s)と1/Tの関係を示す。Base鋼の傾きは15494であるのに対して，1.0%Cr鋼は36743であり，Cr量の増加により，傾きが大きくなった。この結果から活性化エネルギーを求め，Cr量で整理した結果をFig.15に示す。図中には，フェライト中のCの拡散の活性化エネルギー，フェライト中のCrの拡散の活性化エネルギーを示した²⁴⁾。Fe-C2元系の場合は，フェライト中のCの拡散の活性化エネルギーに近い値を示すが，Cr量の増加とともにその値から外れ，フェライト中のCrの拡散の活性化エネルギーに推移した。以上のことから，Cr量の増加によるパーライトの球状化抑制効果は，粗大化反応に対するCrの拡散の寄与が大きくなるためと考えられる。本検討では，SEMによる2次元観察結果を用いて解析したが，近年，電子顕微鏡や解析ソフトウエアの発達により3次元観察も可能となった。Adachi²⁵⁾は，ラメラー間隔，表面積の2次元/3次元評価結果の比較を行い，2.5倍の差があると報告している。本検討結果の傾向には大きな影響がないと考えられるが，3次元での評価に関しては今後の課題である。

Fig. 14.

 Relationship between lnk^s and 1/T in Fe-C binary and Fe-C-Cr ternary eutectoid steels.

Fig. 15.

 Effect of Cr content on activation energy Q.

5. まとめ

Fe-0.8%C系，Fe-0.8%C-(0.2-1.0)%Cr系共析鋼を用いて，ラメラー間隔，高温でのラメラーの安定性に及ぼすCrの影響を調査した結果，以下のことが明らかになった。

(1)Fe-0.8%C系に対して，Crを1.0%添加することで，パーライトの平衡変態温度は10K上昇した。

(2)同一パーライト変態温度において，Cr量の増加に伴いラメラー間隔は微細化した。一方，同一過冷度において，Cr量の増加に伴いラメラー間隔は微細化した。

(3)Cr量の増加により，γ中のCの拡散係数の値が減少した。γ中のCの拡散係数の値が減少したことにより，Cの拡散距離が小さくなるために，ラメラー間隔が微細化したと考えられる。

(4)高温におけるラメラーの球状化は，Cr量の増加によって抑制された。

(5)分配係数に及ぼすCr量の影響は認められなかった。ラメラーの球状化抑制効果に対して，Crの分配係数の寄与は小さいと考えられる。

(6)Cr量の増加によるパーライトの球状化抑制は，粗大化反応に対するCrの拡散の寄与が大きくなるためであると考えられる。

謝辞

本研究に関して，有益なご助言をいただいた株式会社豊田中央技術研究所 三田尾眞司博士(前 JFEスチール(株)スチール研究所)に感謝致します。

文献

• 1)  例えば，H.K.D.H.Bhadeshia and S.R.Honeycombe: Steels (Third Edition), Elsevier, Butterworth-Heinemann, UK, (2006), 53.
• 2)   T.  Takahashi,  M.  Nagumo and  Y.  Asano: J. Jpn. Inst. Met., 42(1978), 708.
• 3)   T.  Kimura,  M.  Takemasa and  M.  Honjo: JFE Tech. Rep., 26(2010), 11.
• 4)   H.  Yokoyama,  S.  Mitao and  M.  Takemasa: NKK Tech. Rep., (2002), No.176, 59.
• 5)   Y.  Kataoka,  J.  Furukawa,  M.  Ueda and  T.  Horita: 1992 Rail Steel Symposium Proceedings, Iron and Steel Society, Inc., USA, (1992), 11.
• 6)   H.  Tashiro and  H.  Sato: J. Jpn. Inst. Met., 55(1991), 1078.
• 7)  古川直宏，阿南吾朗，難波茂信:変形特性の予測と制御，日本鉄鋼協会，東京，(1994), 269.
• 8)   A.R.  Marder and  B.L.  Bramfitt: Metall. Trans. A, 24A(1975), 365.
• 9)   T.  Gladman,  I.D.  Mcivor and  F.B.  Pickering: J. Iron Steel Inst., 210(1972), 916.
• 10)  山本定弘:第161・162回西山記念講座，日本鉄鋼協会，東京，(1996), 215.
• 11)   C.  Zener: Trans. AIME, 167(1946), 550.
• 12)   N.  Ridley: Metall. Trans. A, 15A(1984), 1019.
• 13)   T.  Takahashi,  Y.  Asano and  M.  Nagumo: Tetsu-to-Hagané, 62(1976), S368.
• 14)   C.  Capdevila,  F.G.  Caballero and  C.  García de Andrés: ISIJ Int., 45(2005), 229.
• 15)   T.  DeHoff and  F.N.  Rhines: Quantitative Microscopy, McGraw-Hill, USA, (1968), 79.
• 16)   B.  Jansson,  M.  Schalin,  M.  Selleby and  B.  Sundman: Computer Software in Chemical and Extractive Metallugy, ed. by C.W.Bale et al., The Metall. Soc. CIM, Quebec, (1993), 57.
• 17)   K.  Ishida,  M.  Ohkubo,  M.  Yong Wey and  T.  Nishizawa: J. Jpn. Inst. Met., 52(1988), 388.
• 18)   M.  Ko,  T.  Sakuma and  T.  Nishizawa: J. Jpn. Inst. Met., 40(1976), 593.
• 19)   M.  Tajima,  Y.  Nishimoto,  K.  Shima and  Y.  Mantani: Tetsu-to-Hagané, 90(2004), 807.
• 20)   M.  Hillert: Jernkont. Ann., 141(1957), 757.
• 21)   M.P.  Puls and  J.S.  Kirkaldy: Metall. Trans. A, 3A(1972), 2777.
• 22)   R.C.  Sharma,  G.R.  Purdy and  J.S.  Kirkaldy: Metall. Trans. A, 10A(1979), 1129.
• 23)   M.A.  Krishtal: Diffusion Processes in Iron Alloys, Israel Program for Scientific Translations, Jerusalem, (1970), 103.
• 24)  改訂4版金属データブック，日本金属学会編，丸善，東京，(2004), 21.
• 25)   Y.  Adachi: J. Jpn. Inst. Light Met., 61(2011), 78.