2015 Volume 101 Issue 3 Pages 228-235
2015 Volume 101 Issue 3 Pages 228-235
Internal fatigue crack growth rate was measured by using beach marks resulting from
repeated two-step fatigue tests for JIS-SCM440 low-alloy steel. This material showed
internal fractures under stress ratio of R = 0, and the inclusion sizes of
the internal fracture origins ranged from 14 to 40 μm. Two types of beach marks were
observed: One was small beach marks indicating internal cracks at an initial stage of
fatigue. The other was large ones indicating the internal cracks at a final stage. The
internal crack shape at the initial stage was a half-ellipse and asymmetric, while that at
the final stage were a circle and symmetric. The asymmetric internal crack shape requires
three-dimensional modeling, and therefore, an extremely slow crack growth rate, smaller
than the lattice length, is expected in two-dimensional modeling. The growth rate of the
asymmetric internal crack was evaluated by
引張強度が1200 MPa以上の高強度鋼1)では介在物を起点とした内部破壊2,3)(フィッシュアイ破壊)が生じ,通常の疲労限が消滅する。この場合,S-N曲線は二段の折れ曲りとなり,折れ曲がり点以降では内部破壊が主となる4)。そのため,高強度鋼における疲労限の消滅は内部破壊の出現によると理解されている5,6)。通常の疲労は表面破壊となるため内部破壊は特異な破壊形態であるが,特性も内部破壊と表面破壊では大きく異なる。疲労限の有無も大きな違いであるが,水素の影響7,8)や寸法効果9,10)等でも違いが認められる。特に寸法効果に関しては,内部破壊の場合には疲労試験結果が試験片寸法に依存するほど大きくなる。このことは,単に疲労試験でS-N曲線を求めただけでは材料の疲労特性を一意的に評価できないことを意味している。そのため,高強度鋼のギガサイクル疲労特性を評価するためには内部破壊機構を解明し,新たな評価法を構築する必要がある。
内部破壊に関する研究は近年盛んに行われてきたが,先ずはき裂の発生支配と伝ぱ支配に分けて考える必要がある。疲労き裂が発生するまでの寿命が全寿命の大半を占める場合がき裂発生支配で,発生した疲労き裂が伝ぱする寿命が大半を占める場合がき裂伝ぱ支配である。き裂発生支配とする説11,12)では,ギガサイクル域で試験片が破断する現象をき裂伝ぱ支配で説明しようとすると矛盾が生じることが指摘されている。き裂伝ぱ速度(1サイクルあたりの伝ぱ量)の最小値は格子間隔程度と考えられているが,仮に最小値のまま伝ぱしたとしても,109回の繰返しを与えるとき裂長さが試験片寸法よりも遥かに大きくなってしまう。そのため,き裂発生に寿命の大半を消費しなければギガサイクル域での破断を説明できないとするのがき裂発生支配説の主な根拠である。しかし,き裂発生を考える場合には応力集係数が主なパラメータとなる材料力学の問題として取扱うこととなる。この場合,起点となる介在物の形状が強く影響する反面,相似則が成立するため介在物の寸法の影響は小さくなる。このことは,内部破壊の場合には介在物の寸法の影響を強く受けるという実験結果2,13,14)と矛盾する。従って,き裂発生支配説に基づくと疲労寿命を予測するための合理的な解を得ることが困難となる。
介在物寸法の影響を考慮すると,応力拡大係数を主なパラメータとする破壊力学を用いることが合理的である。応力拡大係数ではき裂長さが変数の一つとなるため,介在物寸法を初期き裂長さとすることで介在物寸法の影響を考慮することができる。破壊力学を用いる場合には,更に二通りの方法が考えられる。一つは,き裂の停留現象に着目して,下限界応力拡大係数範囲ΔKthを用いる方法である。この方法では村上の式2)が有名であるが,介在物寸法を考慮した疲労限の予測式を導くことができる。この方法でギガサイクル疲労を表現するためには,ODA15,16)(Optically Dark Area)の影響を考慮する必要がある。すなわち,ΔKthを用いた予測式では疲労限を算出してしまうが,ODA寸法をき裂長さとして代入すれば疲労限の消滅を表現することができる。しかし,実際にはODAの評価に課題がある。先ず,ODA形成機構に関しては種々の説15,16,17,18)が提案されているが,厳密に解明されたとは言い難い。更に,ODAの成長を律する経験則を導くことも容易ではない。これらの理由により,ΔKthを用いる方法も現時点では合理的な疲労寿命の予測式を導ける状況にはない。
破壊力学を用いるもう一つの方法は,き裂の伝ぱに着目し,パリス則19)を用いてき裂の伝ぱ寿命を算出する方法である。これは,き裂伝ぱ支配となる場合に有効な方法である。この方法を最初に内部破壊に適用し,ギガサイクル疲労寿命の予測法を提案したのはTanaka and Akiniwaである20)(以下,田中・秋庭モデルと呼ぶ)。田中・秋庭モデルでは,S-N曲線から内部き裂の伝ぱ曲線を逆計算する点が特徴である。内部き裂の伝ぱ曲線を実験的に求めることは容易ではないが,田中・秋庭モデルではそれを実験的に求める必要はない。また,内部き裂の伝ぱ曲線をより簡便に求める方法がOmataによって提案された21)。Omataの方法ではS-N曲線と内部破壊起点となった介在物寸法から内部き裂の伝ぱ曲線を求めることができるため,実用的で使い易い方法といえる。しかし,田中・秋庭モデル(Omataの方法)では格子間隔よりも遥かに小さい,極低速でのき裂伝ぱを計算上で仮定する必要がある。このような極低速でのき裂伝ぱの存在を実験的に実証できていない点が問題であった。
以上のように,内部破壊機構の解明では内部き裂伝ぱの評価が鍵であった。具体的には,内部き裂の伝ぱにおいて,格子間隔よりも遥かに小さい極低速でのき裂伝ぱが存在するか否かが重要な論点であった。そこで著者は,二段多重の変動応力疲労試験により破面上にビーチマークを作製することで,内部き裂伝ぱの様子を可視化する方法を提案した22)。ビーチマークとは変動応力が作用した際に破面上に形成される模様であるが,周期的に変動応力を与えることで時々刻々のき裂前縁の様子をビーチマークとして破面上に残すことができる。ビーチマークを疲労き裂伝ぱの解析に適用した研究例23)はあったが,内部き裂の解析に適用した例は無かった。ここでは,起点となった介在物寸法と同程度の極めて微細なビーチマークを作製することに成功し,発生初期の内部き裂の伝ぱの様子を可視化することができた。その結果,発生初期の内部き裂は二次元でのモデリングが可能なリング状ではなく,介在物の一部から発生した半楕円形状となっていることが分かった。この場合,三次元でき裂をモデリングする必要があるが,二次元での伝ぱ量に換算した場合には極低速でのき裂伝ぱを想定し得る。すなわち,局所的な伝ぱ速度が格子間隔以上であったとしても,平均値として二次元での伝ぱ量に換算した場合には格子間隔以下となることがあり得ることが分かった。
このような内部き裂伝ぱの可視化技術を用いて,本研究では内部疲労き裂伝ぱ速度の評価を行った。すなわち,前報では一本の試験片を用いて内部き裂伝ぱの定性的な議論のみを行ったが,本研究では多数の試験片を用いてビーチマークから内部き裂伝ぱ速度を測定することで定量的な議論を行う。それにより,内部破壊の基本的なメカニズムを明らかにすると同時に,ギガサイクル疲労特性の予測法を確立するための指針を得ることを目的とした。
Table 1に供試材の化学成分を示すが,供試材は低合金鋼SCM440の熱間圧延丸棒である。熱処理は,1153 K×30 min,油冷で焼入れ行った後,473 K×60 min,空冷で焼戻しを行った。これらの熱処理は,直径12 mmの丸棒形状に下加工した後に行った。熱処理後のビッカース硬さはHV604で,3.26 HVの関係から推定した引張強度は1969 MPaである。本研究では引張試験を実施していないが,SCM440鋼に同様の熱処理を施した場合の引張特性は文献24)で参照可能である。Fig.1に旧オーステナイト粒界を出現させた組織写真を示す。組織は焼戻しマルテンサイトの様相を呈し,旧オーステナイト粒径は20 μm程度であった。
| Steel | Element (mass%) | ||||||
|---|---|---|---|---|---|---|---|
| C | Si | Mn | P | S | Cr | Mo | |
| SCM440 | 0.40 | 0.21 | 0.71 | 0.009 | 0.009 | 0.96 | 0.16 |

Microstructure of the tested steel.
疲労試験は通常の一定応力振幅の疲労試験によりS-N曲線を取得した後に,二段多重変動応力疲労試験を行い,ビーチマークの観察を行った。変動応力疲労試験の基本波形をFig.2に示す。応力振幅がσaで平均応力がσm=σaとなる条件(R=0)を試験応力とし,それに応力振幅がσa,ILの変動応力を周期的に与える。その際,変動応力の平均応力は試験応力のそれと同一とする。変動応力の繰返し数はNi,IL回とし,それを試験応力の繰返し数がNi回となる毎に周期的に与える。Fig.2では変動応力が試験応力より大きくなるように書いているが,実際には変動応力のほうが小さくなる条件もある。二段多重変動応力疲労試験の条件は予備試験でビーチマークが観察される条件を特定した上で決定したが,通常のR=−1の条件よりも圧縮応力の作用しないR=0の条件のほうが明瞭なビーチマークが観察された。 また,試験応力と変動応力の平均応力を同一とした理由は試験機の制御の都合である。

Basic wave form of the repeated two-step fatigue test.
疲労試験は,超音波疲労試験25,26,27,28,29)により繰返し速度20 kHzで行った。使用した試験機は平均応力付与機構30)を備えた島津製作所製超音波疲労試験機USF2000であるが,変動応力疲労試験を行うために制御ソフトは独自に作製した。また,試験中は発熱を防ぐために試験片を空冷した。空冷には,5.5 kW級のコンプレッサー(流量600 L/min.)とボルテックスチューブ型のクーラーを使用した。試験片は,Fig.3に示すような直系が3 mmの砂時計型のものを使用した。試験部表面の最終仕上げはバフ研磨である。超音波疲労試験では繰返し速度の影響が問題となる場合があるが,高強度鋼で内部破壊となる場合には繰返し速度の影響は無視できるほど小さい。過去の研究では,高強度鋼で内部破壊となる条件で超音波疲労試験による20 kHzでの結果と通常の試験による100 Hzでの結果を比較したが,両者はよく一致した31,32,33)。

Profiles of specimens in mm.
破面観察は,主に光学顕微鏡を用いて行った。走査型電子顕微鏡(SEM)で観察した場合よりも,光学顕微鏡で観察した場合のほうが,ビーチマークをより明瞭に識別できたためである。焦点深度の浅い光学顕微鏡で凹凸の大きい破面を観察すると視野の全体についてピントを合わせることはできないが,焦点をずらしながら撮影した複数枚の写真から画像処理によりピントが合っている部分だけを貼り合わせるマルチフォーカス機能により,視野全体についてピントの合った光学顕微鏡写真を得た。
Fig.4にS-N曲線を示す。通常の一定応力振幅の疲労試験の結果を○印で示しているが,試験片は全て内部破壊となり,内部破壊の起点は酸化物系の介在物であった。起点となった介在物の寸法は14~40 μmの範囲であった。ここでは,破断しなかった試験片(図中の矢印付記号)についても高い応力振幅で強制的に内部破壊させることで介在物寸法を測定している。破断した試験片のみに着目すれば,寸法の範囲は18~40 μmとなり,平均値は27 μmである。Fig.4の結果では107回以降でもS-N曲線が下降しているため通常の疲労限は消滅しているが,108~109回付近でS-N曲線が折れ曲がるような傾向を示している。すなわち,109回以降で試験片の破断は認められず,ギガサイクル域において疲労限を示しているように見える。

S-N curve.
Table 2に二段多重変動応力疲労試験の条件と結果を示す。二段多重変動応力疲労試験では試験条件のパラメータが多いため,組合せにより無数の試験条件が考えられる。ここでは,ビーチマークが明瞭に観察される条件に絞って疲労試験を実施した。変動応力は疲労試験結果に影響を与え,高い変動応力は寿命を短くする方向に作用し,低い変動応力はコーキシング効果34)により寿命を長くする方向に作用する。今回は,高い変動応力の場合には試験応力の繰返し数に対して変動応力の繰返し数を十分に少なくし,低い変動応力の場合には変動応力を十分に低くすることで影響が小さくなるように配慮した。ただし,超音波疲労試験では応力を高くした場合の立ち上がりに103回程度,応力を低くした場合の減衰に104回程度を要する。そのため,103~104回の短い周期で応力を変動させる場合に材料に作用する応力が正確に追従している保証は無く,その場合には試験機を制御する上での設定値とみなすべきである。 Fig.4では二段多重変動応力疲労試験の結果を×印でプロットしているが,通常の疲労試験の結果との差は小さく,ばらつき程度の差しかなかった。なお,ここでは破断繰返し数のうち,試験応力の繰返し数(Nf)でプロットしている。また,二段多重変動応力疲労試験でも試験片は全て内部破壊となり,内部破壊の起点は酸化物系介在物であった。
| Specimen | Test stress | Irregular stress | Number of cycles to failure | Inclusion size | ||||
|---|---|---|---|---|---|---|---|---|
| σa (MPa) | Ni (cycles) | σa,IL (MPa) | Ni,IL (cycles) | Nf (cycles) | NIL (cycles) | Total (cycles) | ||
| TP-1 | 500 | 106 | 900 | 104 | 1.24 × 107 | 1.24 × 105 | 1.25 × 107 | 18 |
| TP-2 | 500 | 106 | 800 | 104 | 9.38 × 107 | 9.38 × 105 | 9.47 × 107 | 22 |
| TP-3 | 500 | 106 | 800 | 104 | 4.73 × 107 | 4.73 × 105 | 4.78 × 107 | 19 |
| TP-4 | 560 | 106 | 800 | 104 | 6.85 × 106 | 6.85 × 104 | 6.92 × 106 | 28 |
| TP-5 | 560 | 106 | 800 | 104 | 4.65 × 107 | 4.65 × 105 | 4.70 × 107 | 20 |
| TP-6 | 590 | 4.0 × 103 | 400 | 4.0 × 103 | 2.73 × 107 | 2.73 × 107 | 5.46 × 107 | 15 |
| TP-7 | 620 | 2.0 × 103 | 400 | 4.0 × 103 | 7.48 × 106 | 1.50 × 107 | 2.25 × 107 | 23 |
| TP-8 | 620 | 4.0 × 103 | 400 | 4.0 × 103 | 1.07 × 107 | 1.07 × 107 | 2.14 × 107 | 18 |
σa and Ni: Stress amplitude and interval cycles of test stress.
σa,IL and Ni,IL: Stress amplitude and interval cycles of irregular stress.
Nf and NIL: Test and irregular cycles number, respectively.
Fig.5にビーチマークを観察した破面写真の代表例を示す。(a)は介在物寸法と同程度の小さなビーチマークが観察される場合の代表例である。この場合,低倍で観察しても(b)のような大きなビーチマークは観察されない。このようなビーチマークはTP-1~5の試験片で観察された。(a)のビーチマークでは,内部き裂が介在物の一部から発生し,最初は半楕円形状だった内部き裂が成長に伴いリング状へと変わっていく様子が示されている。すなわち,発生初期の内部き裂の伝ぱの様子を示している。(b)はリング状の大きなビーチマークが観察される場合の代表例である。この場合には,拡大しても(a)のようなビーチマークは観察されない。このようなビーチマークはTP-6~8の試験片で観察された。TP-6~8の試験片では数千回の変動応力が作用しているが,観察されたビーチマークは数本程度である。従って,寿命末期の内部き裂伝ぱの様子を示していると考えられる。なお,Fig.5ではビーチマークは規則的に並んでいるため,周的に与えている変動応力の1ブロックが1ビーチマークに対応していると考えられる。 また,Fig.5の(a)では黒く見える模様,(b)では白く見えるリング状の模様が変動応力によるき裂進展領域と判断している。(a)では高い変動応力を与えているが繰返し数が少なく,(b)では繰返し数は同程度であるが低い変動応力を与えているため,いずれの場合も試験応力によるき裂進展領域よりも変動応力によるき裂進展領域のほうが小さいと考えられることが判断の根拠である。

Typical fracture surface of the repeated two-step tests at around the internal fracture origin observed by an optical microscope.
このように,高い変動応力を与えるTP-1~5の条件は発生初期で速度の遅い内部き裂伝ぱの様子をビーチマークで捉えるためのもので,低い変動応力を与えるTP-6~8の条件は寿命末期で速度の速い内部き裂の伝ぱの様子を捉えるためのものである。速度の遅い小さな内部き裂を捉えるためには,変動応力を与える間隔を広くすると同時に,高い応力で明瞭なビーチマークを作製する必要がある。この場合,内部き裂が大きくなると伝ぱ速度が急激に増すため,大きなビーチマークは観察されなくなる。他方,速度の速い大きな内部き裂を捉えるためには狭い間隔で変動応力を与える必要があり,その場合には変動応力で破壊することを防ぐために低い応力を用いる必要がある。この場合には,応力が低い上に多数のビーチマークが重なるため,小さなビーチマークは観察されなくなる。このように,二段多重変動応力疲労試験の条件はビーチマークで内部き裂を捉える上でのピントのような働きをし,対象とする内部き裂に合わせた条件設定を行う必要がある。
Fig.6にビーチマーク寸法を測定した結果を示す。ここでは,各ビーチマークを楕円近似し,代表寸法として

Beach mark size measured on the fracture surface.
小さなビーチマークと大きなビーチマークの様子をそれぞれスケッチした図をFig.7に示す。それぞれから,発生初期と寿命末期の内部き裂の伝ぱの様子を読み取ることができる。初期の内部き裂は介在物の一部から発生し,半楕円形状となっている。それに対して,寿命末期の内部き裂は起点介在物を中心としたリング状となっている。内部き裂の形状がリング状の場合,軸対称形状であるため,二次元でのモデリングが可能である。しかし,発生初期の内部き裂のように半楕円形状となっている場合には非軸対称形状であるため,原理的には二次元モデルで現すことはできない。この場合,前報22)で指摘したように,平均値として二次元での伝ぱ量に換算した場合には格子間隔以下となる極低速でのき裂伝ぱが起こり得る。これらの点を考慮すると,き裂伝ぱ速度が格子間隔以上という理論的な条件は寿命末期の内部き裂のような軸対称の内部き裂の場合には当てはまるが,発生初期の非軸対称の内部き裂の場合には当てはまらない。従って,内部破壊機構を考える上で,格子間隔以下の極低速のき裂伝ぱを仮定している点はき裂伝ぱ支配説を否定する根拠にならない。

Schematic illustration of the beach marks.
一方,非軸対称の内部き裂伝ぱを評価するためには通常とは異なるパラメータを用いる必要がある。通常,無限板中のき裂伝ぱを評価する際にはき裂の半長aをパラメータとして,da/dN(1サイクルあたりの伝ぱ量)で評価する。しかし,非軸対称の内部き裂の場合にはき裂の半長aを一意的に定義することができないため,aをパラメータとして用いることができない。この問題を解決する最良の方法は,
| (1) |
ここで,KI maxはモードI応力拡大係数の最大値,σ0は遠方応力である。更には,田中・秋庭モデル(Omataの方法)では式(1)と
田中・秋庭モデルでは,S-N曲線から内部き裂の伝ぱ曲線を逆計算することを提案している。田中・秋庭モデルではODAの領域とその外側の領域を区別して解析するが,実際にはODAの領域で寿命の大半を消費する。そこで,Omataは両者の区別を無くすことでより簡便に内部き裂の伝ぱ曲線を求める方法を提案した。この方法では,ODA領域の内部き裂伝ぱ曲線に近い結果が得られる。本研究では,内部き裂の伝ぱ速度を評価することで田中・秋庭モデル(Omataの方法)の妥当性を検証しようとしている。そこで,先ずは本研究の実験結果を用いてOmataの方法による内部き裂の伝ぱ曲線を求めることとした。
計算の出発点は,次の式(2)で表されるパリス則である。
| (2) |
ここで,Cとmは定数であるが,これらの定数の値を求めることが内部き裂の伝ぱ曲線を求めることとほぼ等価となる。内部き裂の応力拡大係数範囲ΔKを求める際には式(1)を用いるが,具体的には以下のような形で求める。
| (3) |
完全両振りとなるR=−1の条件では応力範囲Δσの代わりに応力振幅σaを用いることもあるが,本研究では完全片振りのR=0の条件で試験を行っているためΔσを用いる。また,式(3)を式(2)に代入すると式(2)の左辺のda/daは自動的に
| (4) |
ここで,ΔKincは
| (5) |
Fig.8に本研究のΔKincと
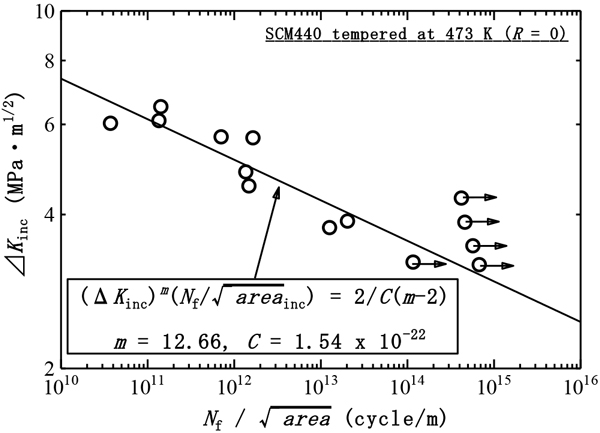
ΔKinc vs.

Fatigue strength predicted by Eqn. (5), compared with the experimental results.
上述のように,田中・秋庭モデルによる疲労強度の予測法は完成度が高く,Omataの方法により計算も簡便となった。しかし,大前提として格子間隔以下の極低速での内部き裂の伝ぱを仮定しており,その点が実験的に実証されていない点が問題である。そこで,本研究で測定したビーチマーク寸法から内部き裂伝ぱ速度を求め,田中・秋庭モデル(Omataの方法)による内部き裂の伝ぱ曲線との比較を行った。
Fig.10にビーチマーク寸法から内部き裂伝ぱ速度を求めた結果を示す。白抜きの丸印(○)は小さなビーチマークから求めた結果であるが,この場合は内部き裂の形状が非軸対称となることを考慮して

Internal crack growth rate measured by beach mark sizes.
小さなビーチマークにより求めた非軸対称内部き裂の伝ぱ速度は格子間隔より遥かに小さく,Omataの方法による内部き裂伝ぱ曲線に近い値を示している。Omataの方法ではき裂発生寿命を考慮していないため,実際よりも低速側のき裂伝ぱ速度を算出する傾向がある。従って,内部き裂伝ぱ速度の実測値がOmataの方法よりも高速側となる点は妥当な傾向である。また,実測値は低ΔK側でばらつきが大きくなる傾向があるが,小さなビーチマークは識別が難しく誤差が大きくなるためである。これらの結果から,格子間隔以下の極低速の内部き裂伝ぱが存在することが実証され,Omataの方法により求めたき裂伝ぱ曲線が概ね妥当であることが明らかとなった。
一方,大きなビーチマークによる結果に着目すると,小さな内部き裂に比べて不連続的に速度が増し,格子間隔以上の伝ぱ速度となっている。点線のCT試験片による結果と比較すると低速度側となっているが,内部き裂が真空環境となることを考慮すると,真空中では大気中よりも伝ぱ速度が遅くなるため整合する。従って,大きな軸対称の内部き裂は通常のき裂と同様の伝ぱ挙動を示している。また,ΔKに着目すると,小さな内部き裂と大きな内部き裂の境界は通常のΔKthに対応しているといえる。この場合も,真空環境でΔKthが高くなることを考慮すると,より良く一致する傾向となる。従って,小さな非軸対称の内部き裂はΔKth以下の領域で格子間隔より遥かに小さい量で成長するが,ΔKthに達して軸対称の内部き裂に変化すると通常のき裂と等価になる。これは,田中・秋庭モデルで提案されているき裂伝ぱと全く同じである。
田中・秋庭モデルでは,ΔKth以下で伝ぱする領域はODAの領域とされている。従って,ODAの領域を本研究の議論に基づいて再定義すれば,小さな内部き裂がΔKth以下で伝ぱする領域となる。本研究では圧縮応力の作用しないR=0の条件で試験を行っているため,通常の一定応力振幅試験の破面を見てもODAは不明瞭である。従って,ODAの領域が黒くなる(粗くなる)メカニズムはNakamura and Oguma39)が提案しているように真空中で極めて多くの回数の圧縮を受けたことによる破面の荒れである可能性があるが,ΔKth以下で小さな内部き裂が伝ぱする領域と再定義すればODAには物理的な意味があることになる。すなわち,ODAの領域が黒く見えるのは結果に過ぎず,厳密な定義としてはΔKth以下で小さな内部き裂が極低速で伝ぱする領域とすべきである。
以上の議論をまとめると,格子間隔以下となる極低速の内部き裂伝ぱの存在と田中・秋庭モデルの妥当性が実証された。また,Omataの方法により求めた内部き裂の伝ぱ曲線も概ね妥当であることが明らかとなった。これらにより,高強度鋼のギガサイクル疲労特性を評価する指針が得られたといえる。
本研究では,低合金鋼SCM440を供試材として二段多重変動応力疲労試験を実施し,ビーチマークを観察することで内部き裂伝ぱ速度の評価を行った。その結果,次のような結論を得た。
1)通常の一定応力振幅疲労試験の結果,全ての試験片が酸化物系介在物を起点とした内部破壊となり,起点介在物寸法は14~40 μmの範囲であった。また,通常の疲労限は消滅しいているものの,ギガサイクル域で疲労限を示しているような傾向が認められた。
2)二段多重変動応力疲労試験でも同様の内部破壊となり,破面にはビーチマークが観察された。ビーチマークには,半楕円形状の内部き裂を示す小さなものと,リング状の内部き裂を示す大きなものがあった。また,ビーチマーク寸法を
3)リング状の内部き裂は軸対称であるため二次元でのモデリングが可能であるが,発生初期の小さな内部き裂は半楕円形状(非軸対称)であるため,原理的には二次元でのモデリングはできない。この場合,平均値として二次元での伝ぱ量に換算した場合には格子間隔以下の極低速でのき裂伝ぱが起こり得る。また,非軸対称の内部き裂の場合には通常のda/dNではき裂伝ぱを評価できないため,代わりに
4)ビーチマーク寸法から内部き裂伝ぱ速度を求めた結果,リング状の大きな内部き裂は通常のき裂と同様の伝ぱ挙動を示していたが,非軸対称の小さな内部き裂は格子間隔以下の極低速でのき裂伝ぱを示した。その際,両者の境界は通常のΔKthにほぼ対応した。また,非軸対称の小さな内部き裂の伝ぱ速度はOmataの方法により通常の疲労試験結果から求めた内部き裂の伝ぱ曲線と一致する傾向を示した。
5)以上により,き裂伝ぱ支配説を基礎とする田中・秋庭モデルとOmataの方法の妥当性が実証され,高強度鋼の内部破壊によるギガサイクル疲労特性を評価する指針が得られた。
本研究の一部はJSPS科研費23760106の助成を受けて行われたものである。ここに謝意を表する。