Impact of the Different Friction Coefficients on the Tools on the Mechanics of the Mannesmann 2-roll Tube Piercing

Abstract

A numerical parametric study on friction in cross-roll tube piercing is reported in this paper, in order to assess the role of the different friction coefficients on the different parts of the complex tooling of this process (friction on cross-rolls, Diescher disks, piercing plug). Their effects on entrainment speed, state of strain and stress are quantitatively evaluated using the 3D Finite Element Method (FEM). This knowledge allows measures to be taken in case of friction-dependent defects occurring on the piercing mill. Simple regression formulae are proposed which highlight which friction coefficient(s) most impact feed efficiency, twist angle, piercing plug force and torques on the different tools. Based on these relations, a strategy is developed, involving measurements to be performed and equations to be used for an unambiguous friction coefficients identification procedure.

1. 緒言

穿孔工程はシームレス管製造の第一ステップであり，後続のプロセスとして拡管，減肉加工，縮径・定径等を経て製管が可能となる¹⁾。穿孔方法として，ドリル，プレス鍛造，またはFig.1に示すようなマンネスマン交差ロール穿孔圧延方法が挙げられる。後者の場合，熱間円柱ビレットは2本の逆回転する円すいロールにて噛み込まれる(したがって圧延工程である)。このとき，交差ロールは互いにオフセットしており，数度の傾斜角が付いている。したがって，被圧延材はらせん状の動きとなり，固定式穿孔プラグの先端に押しつけられる。ロール直下での材料直径と接触長との比はビレットの応力三軸度が高くなるよう設計されており，延性破壊による空隙開口，いわゆるマンネスマン効果が発生する。さらに，ピアサプラグはこの空隙を広げ，最終的にビレットは中空管になる。交差ロールからの圧下力により変形，穿孔中の断面形状は楕円となる。したがって，二つの幅方向ガイドを設け，楕円形状を修正，あるいは制御することで，軸対称のシェル断面形状を得る。これらのガイドは，固定式ガイドシューによる場合と，駆動するディッシャーディスク(Diescher disks)による場合がある。

Fig. 1.

(a) Schematic configuration of a cross-roll piercing mill. (b) Description of cone angles β' and β'' on a roll profile. (c) Description of the feed angle α.

寸法高精度化と良好な材質および表面性状を得るためには，数多くの工具設計パラメータが重要となる。交差ロールはバレル状あるいは円すい状¹⁾であり，様々な傾斜角が付けられる。ピアサプラグの形状，そして最も重要なのは，交差ロールバイトに対するプラグ先端位置が，マンネスマン効果と表面性状およびプラグ摩耗に大きな影響を与える。

本プロセスでは，摩擦は重要な役割を果たす。穿孔プラグの摩擦は管の進行を妨げるため，ビレット-交差ロール間の摩擦はビレットを進行させるに十分な大きさである必要がある。穿孔プラグの先端は固定棒(マンドレル)の軸方向に自由に回転できるため，穿孔方向の摩擦抵抗のみが重要となる。幅ガイドについては，ガイドシューによって全方向の摩擦抵抗となる(すべり摩擦)。ディッシャーディスクを使用した場合には，軸方向速度はシェルの速度よりも速くなるため，摩擦はシェルを前進させる力(駆動力)と，回転方向に逆らう力となる(制動作用)。ここで，この前進力は平均材料速度から90°-αの角度で押されるため，メタルフローには大きな影響を及ぼさないと考えられる。

プラグ摩擦による抵抗力およびロール摩擦による駆動力とのバランスが圧延に非常に大きな影響を与える。これは，板圧延や長尺製品の圧延の場合の，出側におけるマイナス張力(back-push)に相当する。その結果，ビレット温度と酸化状態および鋼種に依存した噛込み不良の問題が発現する。この問題に対しては，実用的には，交差ロールの一部ないし全体にローレット加工を施し非常に大きな粗度を与え，摩擦力を最大化することで対応可能である²⁾。さらに，高摩擦係数はビレット軸上の引張応力三軸度を助長するため，マンネスマン効果を制御する上で好都合である。一方で，ピアサプラグ表面は抵抗力を一定値に抑えるために平滑面となっている。また，交差ロールの出側半分は，プラグからの膨脹を抑える役割があるが，その表面はミルの設定に応じた平滑状態となっている。

本プロセスは非常に複雑であり，近年3次元FEMを用いた部品設計と設定およびそれらがパイプ寸法と内部組織に及ぼす影響が，Komori³⁾の定常解析を皮切りに，数多く検討されている。これらの殆どの論文が，マンネスマンき裂開口または最終的な内部組織の推定を実施しており，塑性加工発熱による温度上昇や，延性破壊モデルの適正な選択が重要な検討内容であると考えられてきた。ロール間の最小ギャップ²⁾に関連したピアサプラグの先端位置は重要である。すなわち，もしプラグ先端が上流から遠い位置にあった場合，き裂は上流部で開口せず，ビレットはプラグ先端部で強制的に穿孔されるため，プラグ先端に異常な摩耗を生じる。一方，もしプラグ先端が下流から遠い位置にあった場合，き裂は早期に開口し，その表面が酸化され，内部表面欠陥に至る。

Cerettiら^4,5)はLathamとCockroftの延性損傷モデルを用いて，き裂開口のモデル化を行った。次いで，Faniniと共同研究者ら^6–10)はいくつかの延性損傷モデルを比較し，Lemaitreモデルが最適であるとした⁸⁾。簡単のため，本検討では穿孔プラグは省略され，き裂の発生に重点が置かれた。ここで，マンネスマン効果はロールによる圧縮と垂直を成す方向の引張り応力によって発生するとした。また，最も重要な結論の一つとして，ビレット中央部における鋳造によるポロシティや材質上弱い部分が大きな影響を与えるとした^6,9)。

Skrinpalenkoと共同研究者らは，一般化したLathamとCockroftモデルを提案した¹¹⁾。彼らは，プラグの形状やより一般的には管壁の加工が最終的な凝固ポロシティに及ぼす影響について検討を実施した^12,13)。Romanenkoと共著者ら^14,15)，Zhangら¹⁶⁾は，材質を担保する基準として最高温度に着目した。

これらの特徴は，多かれ少なかれ摩擦に大きく影響を受ける。シミュレーションにおいては，表面状態は全ての部品で均一でかつ一定とする。しかし実際は，上記の通り，噛み込み促進のために各部品で表面状態を積極的に変化させており，いくつかの論文にこの疑問に関する言及がある。Pater and Kazanecki¹⁷⁾はすべり速度依存型の摩擦モデルを導入した。また，工具毎に異なる摩擦係数が与えるより重要な影響に対し，近年Murillo-Marrodánら¹⁸⁾による詳細な研究がなされた。実機データから得られた交差ロール荷重・交差ロールトルク(電力消費)・出側速度(穿孔効率)・シェルのねじり(ねじり変形)から同定された摩擦係数についても示されている。

本論文では，有限要素(FE)シミュレーション(FORGENxtソフト)を用い，交差ロール，穿孔プラグおよびディッシャーディスクにおける不均一摩擦について検討する。ここで，特に，ロールの噛み込み性を示すシェルの出側速度について検討を実施する。この数値解析と実験結果から，各接触部での適切な摩擦係数の範囲(指針)を提案する。

2. 有限要素法モデル

2・1　工具設計

Fig.1に寸法を示す。ビレットサイズはΦ120 mm×L400である。交差ロールはバレル形状であり，その最大径はΦ_rolls=420mmである。ここで，入側と出側のロール面角，β'およびβ''はそれぞれ3°と4°である。交差ロール間の最小ギャップは105 mmであり，傾斜角α=8°であるディッシャーディスクは幅方向のガイドとして用いられるが，その径はΦ_D=955 mmである。ディッシャーディスク間の距離は120 mmであり，加工後のシェル外径(outer diameter: OD)は130 mm以下となる。回転角速度はそれぞれ，ω_rolls=80 rev/min(8.38 rad∙s^-1)，ω_D=12 rev/min(1.25 rad∙s^-1)となる。穿孔プラグの最大径は94 mmであるが，その先端位置は最小交差ロールギャップ(HP)位置の73 mm上流に位置する。穿孔プラグに平行移動の自由度は無い。プラグバーはその軸を中心に自由に回転するため，正放線方向の“フローティング工具”としてモデル化する。このとき，穿孔プラグ軸はゼロトルク条件(従動)とし，その回転速度はシミュレーションのアウトプットとして得られる。

2・2　有限要素離散化

圧延スタンドは高剛性で工具は非常に大きいため，本プロセスにおける工具の熱弾性変形は重要で無いと見なされる。したがって，すべての工具は三角平面を表面に持つ剛体要素としてメッシュ分割する(Fig.2)。標準的なメッシュサイズは8 mmである。接触状態が誤って変化しないよう，工具メッシュは空間に固定されており(回転しない)，境界条件として接線速度ω_roll，r(x)の回転が考慮される。

Fig. 2.

Typical mesh of tools and preform (initial setting). (Online version in color.)

ビレットについては，4節点4面体“mini-element”を用いる¹⁹⁾。ここで“bimesh”オプションを有効化させる。本手法により，メッシュ毎に異なる関数系を用いることで，計算時間の短縮ができる。このように，変形解析の支配方程式は，予め設定した塑性変形領域を含む領域の外側は(4倍程度まで)粗メッシュ化したサブメッシュを用いて解くことになる。温度分布については，接触位置から遠い部分であっても大きな温度勾配よりメッシュ依存性が高いため，全ての領域で6 mmの細分メッシュで計算を実施する。この細分メッシュは計算領域の正確な保存先としても利用する。詳細はRamadanら²⁰⁾の参考文献を参照されたい。

ある要素におけるひずみが1に達した際に，都度リメッシュを実行する。計算時のタイムステップは，ソフトウェア内で，速度や温度変化や収束状況を元に10^-3 - 10^-1間で自動的に設定される。

2・3　構成モデル

ビレットはS355(0.27 w% C, 0.55 w% Si, 1.6 w% Mn)を1240°Cで90分間保持しオーステナイト化したものから製作する。通常の熱間成形でなされる通り，純粋な粘塑性則(Norton-Hoff則)を仮定する。また，応力の温度，ひずみ，ひずみ速度依存性をFig.3に示す。

Fig. 3.

Constitutive model chosen for S355 steel in the relevant ranges of temperature, strain and strain rate. (Online version in color.)

2・4　接触と摩擦

要素の接触非接触条件はペナルティ法¹⁹⁾を用いて近似的に解く。ここで要素の貫通量(重なり)は常に0.01 mm未満を維持する。

摩擦に関しては，Trescaモデル$\tau =\overline{m}\overline{\sigma }/\sqrt{3}$によって表現される。ここで，τは摩擦応力，mは摩擦せん断係数，σはvon Misesの相当応力である。通常，交差ロール上でm_R=1，穿孔プラグ上でm_plug=0.3，その他の工具上ではm_D=0.45とした。以下では，これらのパラメータを変化させた場合についての試行結果を示す。

2・5　熱伝達

ここでは，変形-温度の連成解析を実施する。ただし，本論文では温度についての詳細な検討は実施しない。また，変形と温度の計算を互いにずらした双方向計算を実施する。すなわち，各タイムステップにおいて，まず力学計算を実施し，続いて散逸エネルギーと変形を元に温度計算を実施する。

ビレットの初期温度は，加熱炉温度である1240°C均一状態とする。圧延機の測定結果から実際の平均温度を見積った結果から，計算を通じて交差ロール，ディッシャーディスクの温度は80°Cとし，穿孔プラグの温度は500°Cで一定とする。

熱伝達係数は全ての工具でh=10 kW∙m^-2∙K^-1の一定値を用いる。この近似は，大きな寸法で接触時間が短い場合においては，結果に大きな影響を与えないことを確認しており，このため，本論文の主眼として摩擦を取り扱っている。

摩擦発熱の工具と圧延材への分配は，熱拡散率の割合に応じて行う。すなわち，実質的には等配分(鋼/鋼の接触)とする。

3. 結果

3・1　標準摩擦状態:遷移挙動

交差ロールによる穿孔圧延は，Fig.4に示す通りビレットの先端および尾端部にかけての軸方向速度と外径形状の大きな遷移を伴う工程である。Fig.4(a)のように，ビレットはまず交差ロールの上流部でグリップされる(t=0.5 s)。圧延材は大きな軸速度で引き込まれるが，圧延材の肉厚としてはロールによってわずかに減肉される。次いで，穿孔プラグとの接触(t=1 s)およびプラグ軸力の増加によって，圧延材の急激な速度低下をもたらす(Fig.4(b))。これにより，断面に抗力が生じ，減肉と拡管が可能になる。ビレットの先端部分がロールの最小間隙部(HP)に到達までの間隔tが約1.6 sまでは圧延材の速度は大きくならず，この間，プラグの軸力Fplugはプラグ形状に応じて上昇する。次に，圧延材はロールの下流側の面と接触し，ロールによる引き込み性が向上し，圧延材の軸速度が再び上昇する。特に出側速度(V_output)が大きく増大し，入側速度(V_input)はわずかに増大する。この入側と出側の差は断面の減肉と前進方向の延伸増大によって生じる。最後に，ビレットの終端がプラグの最大径の部分に達し(Fig.2参照)，ほぼ同時にロールから離れ(t~2.5 s)，定常状態となる。

Fig. 4.

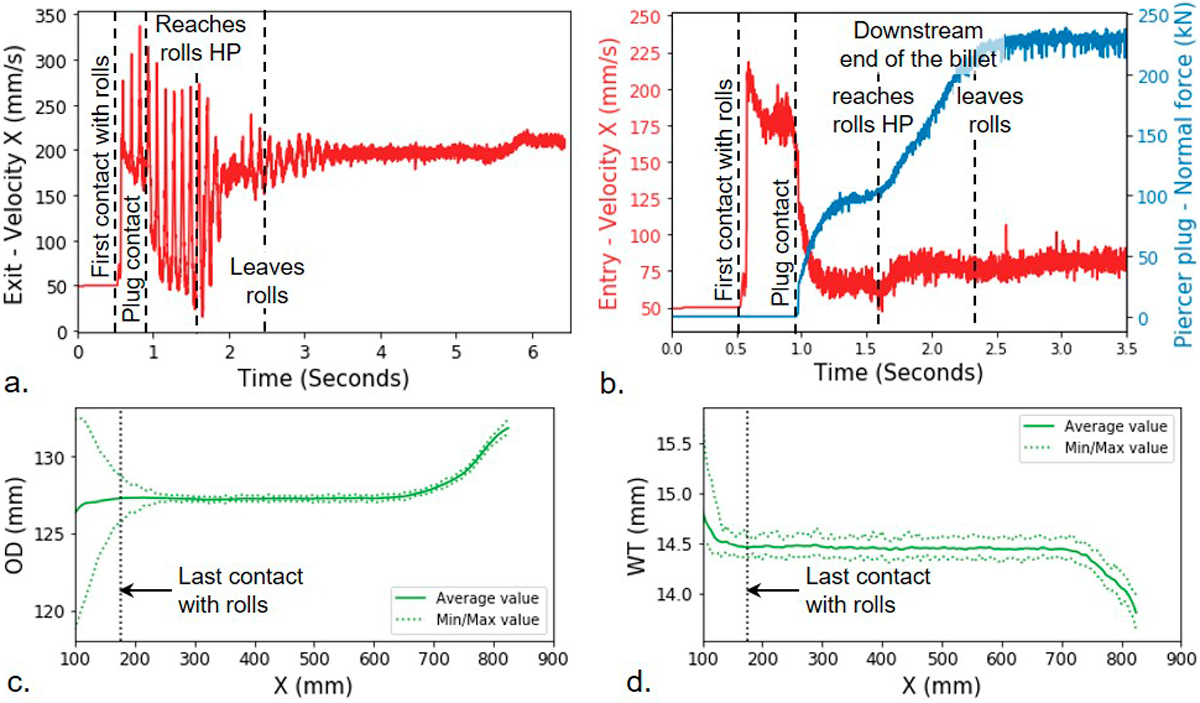
Some aspects of transient evolution and steady state of the process. (a) Time evolution of the tube exit velocity, showing transients and a steady state on which the following analyses focus. (b) Correspondence between entry velocity (back end of the billet) and plug force, showing the different stages in a different way. (c) Outer diameter and (d) wall thickness (WT) profile of the pierced tube. (Online version in color.)

Fig.4(c)はシェル先端部における過拡管状態を幾何学的に表現したものである。次に，径は定常状態に至るまでに4 mm減少し，圧延機内における遷移変化が明らかに確認される。定常状態に至るまでの遷移状態は約200 mmの長さ(およそt=2.5 sに相当)である。ここで，同時同位置において，最薄部の先端部で13.9 mmであった肉厚は，長手方向に若干100 mm程で肉厚14.5 mmの定常状態となる(Fig.4(d))。

また，ビレット尾端にも別の遷移(非定常)状態があるが，本論文では定常状態について着目する。

この一連の速度変化は，引き込み性の向上(交差ロールとの摩擦領域)と，プラグ反力(プラグ上の摩擦)とのバランスに明確に関係する。このバランス，すなわち圧延機の圧延・穿孔能は，ロール，プラグプロフィールと位置(以下では一定とする)，および摩擦係数によって左右されるが，摩擦係数の変化について本論文では検討する。

3・2　標準摩擦状態:静力学，動力学的定常状態の表現

標準摩擦状態とは，交差ロール上の一定のせん断摩擦係数m_R=1，m_plug=0.3およびm_D=0.45とする。この場合，計算された定常部外径(OD)は約128 mmであり，交差ロール計算荷重，ディッシャーガイドディスク(F_D)荷重，穿孔プラグ(F_plug)荷重はそれぞれ620，105，197 kNである。管の出側速度はv_output=214 mm∙s^-1である。穿孔効率と，ロールのビレット巻き込み能を評価するため，ビレットの出側を最大軸速度で規格化した比率，穿孔効率E_feedを導入した。すなわち，

  

$$\begin{array}{l}{E}_{feed}=\frac{v_{output}}{\pi \times {\varphi }_{\text{rolls}}\times \text{sin}\left(\alpha \right)\times {\omega }_{rolls}}\\ \left(=0.88\text{for}{\text{v}}_{\text{output}}=214\text{mm}\cdot {\text{s}}^{-1}\right)\end{array}$$(1)

である。Fig.5(a)はロール軸に沿って広がるビレットと交差ロールとの高圧接触域を示す。接触は接線方向(θ)全域で小さな角度で広がるが，プラグ先端では急激に広がっている(縦の黒線)。また，2つの応力の極大点が確認できる。1つ目は(図の左側)交差ロールの上流部分からの引き込み(ロール入側面角3°)によるものである。その後応力は交差ロール出側のロール出側面角(4°)と交差角(傾斜角8°)の両方によってロールギャップが開いている後半部分で減少する。しかし同時に，プラグにより拡管された材料は，最終的にディッシャーディスクおよび交差ロールの下流部分へ押し付けられる。これにより，2つ目の極大点が形成される。このような圧力分布は，プラグのプロフィールと位置に大きく依存する。

Fig. 5.

Assessment of friction effects from computed field variables, uniform roll friction (m_R=1 everywhere, m_plug=0.3 and m_D=0.45). The contact zone boundary is outlined in black. The dotted vertical line represents the position of the tip of the plug. From left to right and top to bottom: contact pressure field, σ_n; axial velocity field of the billet, v_x; rotational velocity field of the billet, v_θ; twisting of the billet under the rolls (the variable is the initial position of each material point on the vertical axis, Z₀); torsion strain (L_θx component of the Green-Lagrange strain tensor) ; equivalent strain. (Online version in color.)

θ方向については，通常の熱延(低形状比)で見られるように，接触の入口側で最大応力が確認できる。ここで，板圧延や棒圧延を参考にする場合は，支配的なθ速度方向を考慮し，本論文でのx方向と接線方向はそれぞれ板の幅方向と圧延方向に相当する。

このロールとビレット間の接触全域において，前進方向(x軸)のビレット速度V_xとその回転速度V_θはそれぞれ244および1742 mm∙s^-1であり，その位置における交差ロールの速度よりも小さい(Figs.5(b)および(c))。このことは，ビレットはロールによって圧延されるが，穿孔プラグによる抗力によって，全ての領域で後進域となっていることを示す。換言すると，穿孔プラグによる抗力“back-push”により，板圧延のような中立線の存在が無い。このことは，穿孔圧延において厳しい引き込み性の問題がしばしば生じ，特別な処置が必要であることの理由の一つである³⁾。

回転速度V_θ(Fig.5(c))は入側で~1600-1610 mm∙s^-1であり，その後~1550 mm∙s^-1まで減少し，下記の複合的な理由で周方向に大きく分布を持つ;

-ディッシャーディスクとの接触開始直前のビレットの回転方向の初期減速が起こる。ディッシャーディスクの摩擦は穿孔方向の駆動力であるが，シェルの回転の抗力でもある。

-プラグと交差ロール上流部の間のアップセット(V_xマップでも明らか)により，材料回転方向V_θの流れを+θ方向にも-θ方向にも加速させるため，Fig.5(c)に示す材料下部の低値と上部の高値が生じる。このことから局所的な大きなこう配を生むが，このこう配はせん断を含む材料流れの再配置によって，よりθ方向に遠い位置で消滅する。

-さらに，ビレット断面は楕円形状となり(すなわち局所半径rはθに依存)表層から見えるV_θを変化させる，下流側プラグによる拡管による交差ロール下流部における管外径の再拡大と同時に，終端部(図の右側)でV_θを~1660 mm∙s^-1まで再加速させる。

-V_xは入側領域(Fig.5(b))で非常に不均一となる。交差ロールとの初期の接触によりメタルはx方向に局所的に加速するが，この効果はロールとプラグ間でのアップセット(上記参照)によって拡大する。この不均一により変形のせん断成分が非常に強くなる。さらなる下流側では，プラグ周りの減面により材料送り方向の最終的な加速を生じる。

局所角速度(ω_x=v_θ/r)についても，一旦減少し，再加速し，わずかに正の，そして負のこの交互のねじれ(Fig.5(d))は，Green-LagrangeひずみテンソルLの成分L_θxの成分によっても示される(Fig.5(e))。最終的に角速度とねじりは互いにほぼ平衡状態となり，ビレット表面の流線は直線に保たれ，残留ねじり(以下では”ツイスト”と呼ぶ)はほぼゼロとなる。

相当塑性ひずみマップ(ε)をFig.5(f)に示す。回転による影響で，εは最終的には均一状態となり，7(700%)以上に達する。

3・3　穿孔プラグの摩擦低減が及ぼす効果

本検討では，交差ロール状の摩擦を均一摩擦としてm_R=1，m_plug=0.0およびm_D=0.45と設定する。Fig.6(a)に示す通り，接触面積や交差ロール上の接触面圧は大きく変化していないことが分かる。しかし，穿孔プラグの摩擦が小さくなったことで，下流側からの力“back-push”を減少させ，E_feed=1.03という高い穿孔効率をもたらす。言い換えると，軸方向速度が大きくなり，さらに，交差ロールの軸方向速度成分をも超える。つまり，接触域の下流側における先進域が発現する(Fig.6(b))。一方で，回転速度に変化は生じていない(Fig.6(c))が，これはプラグはビレットの動きに対する抵抗にはならないことから，容易に想到される。シェルのねじり角(Fig.6(d))やひずみの変化も見られない。

Fig. 6.

Assessment of friction effects from computed field variables, uniform roll friction (m_R=1 everywhere), low piercing plug friction case (m_plug=0) ; m_D=0.45. The contact zone boundary is outlined in black. The dotted vertical line represents the position of the tip of the plug. From left to right and top to bottom: contact pressure field, σ_n; axial velocity field of the billet, v_x; rotational velocity field of the billet, v_θ; twisting of the billet under the rolls (the variable is the initial position of each material point on the vertical axis, Z₀). (Online version in color.)

3・4　交差ロールにおける不均一摩擦の影響

交差ロール表面の不均一摩擦の影響を調査するため，上記の通常状態と，上流側での高い摩擦せん断係数(m_R,up=1)・下流側でのより平滑な表面(m_R,down=0.45)とを比較する。ただし，m_plug=0.3およびm_D=0.45である。

このとき，穿孔効率はE_feed=0.76となり，通常ケースのE_feed=0.88に比べ大幅に低くなる。このことは，m_R,downは押込み力として作用するため，この値が高値であることが出側速度にプラスの大きな影響を与えることを意味する。一方で，接触面圧にほぼ変化はない(Fig.7とFig.5(a)あるいはFig.6(a)との比較)。軸方向速度は入側で同速度であるが，当然，出側では遅くなる。また，低い摩擦力の影響により，2回目の高v_xゾーンは明瞭ではなく，同程度のせん断を付与することができない(Fig.7(a))。同様のことは回転についても言える(Fig.7(b))。つまり，下流側で回転抗力を補償するには，m_R,downが小さすぎ，2回目の逆ねじりはほぼ消滅し(Fig.7(c))，シェルの大きなツイストとなる(Fig.7(c))。この点が最も明瞭な摩擦の影響の差異であり，実際の現場では摩擦変化の指標として実用されている。このことは，ひずみ成分L_xθにおいても確認できる。

Fig. 7.

Assessment of friction effects from computed field variables, non-uniform roll friction m_R,up=1, m_R,down=0.45 ; m_plug=0.3, m_D=0.45. The contact zone boundary is outlined in black. The dotted vertical line represents the position of the tip of the plug. From left to right and top to bottom: axial velocity field of the billet, v_x; rotational velocity field of the billet, v_θ; twisting of the billet under the rolls (the variable is the initial position of each material point on the vertical axis, Z₀); torsion strain (L_θx component of the Green-Lagrange strain tensor); ; normal contact stress. (Online version in color.)

3・5　ディッシャーディスク上の摩擦

Fig.5からFig.7に示すv_θのマップは，ディッシャーディスクとの接触によりはシェルの回転速度が遅くなるということを示している。このことを考慮し，m_D=0としてシミュレーションを実施する。すなわち，ディッシャーディスクがシェルの円形を保つように作用するが，軸方向力や回転トルクの抗力としては作用しない。

Fig.5と比較すると，Fig.8では交差ロールが均一摩擦(m_R,down=m_R,up=1)であれば影響は小さく，m_D=0の場合にv_θが少し速い値となり，上記の記述を裏付けている。また，軸方向の速度またはE_feedが少し遅くなる(0.89から0.86となる。付録のTable A1参照)。これはディッシャーディスクの摩擦による前方への押出し力が働かないためであると考えられる。なお，外径変化は非常に小さく(Table A1)，外径変化ではv_θの推移を説明できない。

Fig. 8.

Assessment of friction effects from computed field variables: zero Diescher disk friction with uniform roll friction (m_R,up=1, m_R,down=0.45) ; m_plug=0.3. Compare with the same variables in Fig. 5 to 7. (Online version in color.)

m_R,down=0.45の場合，Fig.9(m_D=0)はFig.7(m_D=0.45)に比べて，圧延機出側において回転速度の約3%の上昇を示している。その結果，ツイストは大きく減衰する(17.4°と32.6°)。驚くべきことに，ディッシャーディスクからの摩擦による前方への押出しが無いにも関わらず，m_D=0の場合にも軸方向の速度またはE_feedが上昇する(0.76から0.78まで，Table A1参照)。E_feedのこの変化に関する違いは，m_D=0における数値パラメータ検証点数が過少であり，この段階で明らかでない。

Fig. 9.

Assessment of friction effects from computed field variables: zero Diescher disk friction with non-uniform roll friction m_R,up=1, m_R,down=0.45 ; m_plug=0.3. Compare with the same variables in Fig. 5 to 8. (Online version in color.)

4. 考察：摩擦せん断係数の同定

本章では，0.2 ≤ m_plug ≤ 0.45および0.2 ≤ m_R,down ≤1(m_D=0.45)まで拡張して考察する。また，m_D=0およびm_R,up=0.8の場合についても考察する。付録のTable A1に得られた結果の一覧を示し，全体の傾向についてはTable 1に示す。以下のセクションではTable A1のデータを試行的に定量回帰し，摩擦せん断係数と観測値の相関を抽出し，どの測定の組み合わせがm_R,up，m_R,down，m_plugおよびm_Dの正確な同定が可能であるかを検討する。シミュレーションを実施したケースに限りがあるため，本取り組みは実行可能性の調査と位置付ける。

Table 1. Variations of the main mechanical and kinematical observables with friction coefficients. The friction factor on the upstream part of the roll is kept constant, m_R,up=1.

	Efeed [–]	vθ [m.s‒1]	Θtwist [°]	OD [mm]	Froll [kN]	Fplug [kN]	FD [kN]	Troll [N.m]	TD [N.m]
mR,down	$$\nearrow \nearrow$$	$$\nearrow$$	$$\searrow \searrow$$	$$\to$$	$$\nearrow$$	$$\nearrow$$	$$\nearrow$$	$$\nearrow$$	$$\to$$
mplug	$$\searrow \searrow$$	$$\searrow$$	$$\nearrow$$	$$\searrow$$	$$\searrow$$	$$\nearrow \nearrow$$	$$\searrow$$	$$\searrow$$	$$\to$$
mD	$$\to$$	$$\searrow$$	$$\nearrow$$	$$\to$$	$$\to$$	$$\nearrow$$	$$\nearrow$$	$$\nearrow$$	$$\nearrow$$

以下に示す関係の係数と定数は，プロセスの本質的な特徴ではなく，第一に工具設計に依存するものであり，次に金属の構成特性(構成式)に依存する。この工具設計と構成式は，本研究においては固定値としている。この相関関係と係数は本シミュレーションを実施した特定の操業条件下でのみ有効である。今後，実験的な調査を実施し，摩擦せん断係数を明確に同定できるようにする予定である。このことは，以下のいくつかの点で有効である:

-同様の操業条件下で，摩擦係数が変化しやすい場合，例えば部品の表面状態(研削や摩耗等)によって変化する場合，力，トルク，寸法および動力学的変数は，理論上は既知であるが，これらの値を実験によっても確認できる。

-穿孔される鋼管の種類によって摩擦状態が大きく変化しない場合，つまり鋼種には依存するものの，少なくとも炭素鋼では大きく依存しない場合，同様の摩擦せん断係数が期待でき，他の同様の穿孔についても全体の傾向を与えることができる。

4・1　観測可能な動力学係数に関する分析:穿孔効率とツイスト角

下記の計算式により，穿孔効率E_feedにおける数値計算結果との強い相関(R²>0.95)が得られた。

  

$$E_{feed}~a_1{\left({\overline{m}}_R-{\overline{m}}_{plug}\right)}^{p_1}{\overline{m}}_R=\frac{{\overline{m}}_{R,up}+{\overline{m}}_{R,down}}{2},p_1~1/3$$(2)

このことは，交差ロールの平均摩擦で表される駆動力が大きいほど，出側速度が上昇していることを示している。プラグの摩擦が抗力としてv_outputを下げる方向に働くため，これらの摩擦応力の差は，シェルの押出しを支配している。これらの結果を注意深く分析すると，m_R,downが低摩擦値では穿孔効率E_feedに大きく影響し，高摩擦値になると飽和する(Fig.10(a))一方，m_R,upは高摩擦値においても大きな影響を与えることが分かる(m_R,up=0.8の場合と，m_R,up=1.0の場合との比較)。E_feedは軸方向の運動(多くの影響因子が含まれる)であるにも関わらず，本シミュレーション結果ではm_Dに大きく依存していない。

Fig. 10.

Effects of the piercer plug and cross rolls friction coefficients on two practical observables, feed efficiency (a) and twist angle (b). For all these cases, m_R,up=1 and m_D=0.45. (Online version in color.)

ツイスト角(Θ_twist)の変化をFig.10(b)およびFig.11に示す。一定のm_R,up=1.0(高駆動力)については，以下(R²>0.98)のように結論づけられる。

  

$$\begin{array}{l}if\left(2{\overline{m}}_D-3{\overline{m}}_{R,down}\right)<-2{\Theta }_{twist}(°)~7.4\\ else{\Theta }_{twist}(°)~7.4+28\left({\overline{m}}_D-3{\overline{m}}_{R,down}+1.9\right)\end{array}$$(3)

Fig. 11.

Impact of friction on the rear side of the rolls m_R,down and on the plug (m_plug) on the plastic twisting of the tube, materialized by Z₀ contour lines. For all these cases, m_R,up=1 and m_D=0.45. (Online version in color.)

ここでも，m_R,downの最大値において，E_feedの飽和が確認できる。この解釈としては，下流のロール摩擦はシェルがディッシャーディスク溝を横切る方向の回転を生じさせるに十分な力である必要があるためと考えられる。ここでのm_Dはシェルの回転に対する抗力となり，シェルを塑性変形(ツイスト)させるトルクを付与する。

4・2　荷重・トルク

交差ロール荷重F_rollはE_feed(または同様にm_R-m_plug)と強い相関があり，E_feedの補完関係とはならないが代替手段としてのパラメータ同定に資することが分かった。接触域が小さいと，そこに含まれる有限要素の数も少ないことから慎重に判断すべきだが，この相関はむしろ接触域の変化(接触応力の変化は小さい)によると考えられる。高E_feed下での接触域の増加は，同時に起こるシェル外径の増大と関係があると考えられる。

一方で，F_plugは以下の式に示す通り重要な情報を与える。

  

$$\begin{array}{cc}{F}_{plug}\left(kN\right)~a_2+a_3{\overline{m}}_{plug}\left(1+3E_{feed}\right)& \left({\text{R}}^2=0.99\right)\end{array}$$(4)

右辺第一項は摩擦が無い状態での拡管による塑性変形に要するエネルギー(力)である。また，第2項は摩擦力に対する反力であるが，これは穿孔効率に大きく依存するものであり，プラグとの接触域および接触応力に対するE_feedの影響と関連する。しかし，現実的な穿孔条件下では，E_feedの変化は大きくはならないことを付言する。

ディッシャーディスクの荷重F_Dとの相関は，得られたデータベース中には見られないが，興味深い関係がトルクT_Dから以下のように導かれる。

  

$$\begin{array}{cc}{T}_D\left(kN\cdot m\right)~a_4{F}_D{\overline{m}}_D& \left({\text{R}}^2=0.93\right)\end{array}$$(5)

この理由は以下の通り説明できる。一般的な圧延理論では，$T_D~K\cdot \left({\varphi }_D/2\right)\cdot {\overline{m}}_D\cdot \overline{\sigma }/\sqrt{3}\cdot S_{c,D}$である。ここで，σ･S_c,D~F_D(S_c,Dはシェルとディッシャーディスクとの接触面積である)。この関係は，板圧延における有名な公式であるT=μ∙F∙Rと類似している。この式によって，強制的に負の先進率とした場合におけるクーロン摩擦係数(μ)が測定可能となる。ここで，ディッシャーディスク速度(600 mm∙s^-1)はシェルの軸速度v_x(~240 mm∙s^-1)に比べて非常に速いものであることを再確認したい。式(4)は，m_Dを独立に推定するためには，ディッシャーディスク力とトルクが同時に測定できる環境が最適であると示している。

もしF_rollによって上記に示す同定精度が向上しない場合，対応するトルクT_rollはE_feedおよびm_Dに対して敏感であると考えられ，上記で計算した摩擦因子のクロスチェックが可能となる。すなわち，

  

$$\begin{array}{l}{T}_{roll}\left(kN\cdot m\right)~a_5{\left({\overline{m}}_R-{\overline{m}}_{plug}+{\overline{m}}_D/2\right)}^{p_2}\\ \left({\text{R}}^2=0.92\right){\text{p}}_2~0.23\end{array}$$(6)

となる。ここで，右辺最初の2項はE_feedを連想させる。すなわち，通常の圧延の通り，トルクは単位時間に変形する材料の量に応じて増加する。また，第3項(m_D)はディッシャーディスク抵抗トルクがm_Dに比例して，シェルの回転を妨げる。これは，板や棒圧延に必要な後方からの力による付加的エネルギーが必要なように，機械的エネルギー源であるトルクが増加することと同様である。

4つの摩擦せん断係数の同定は，上記の数式により可能となる。“周辺の工具”の摩擦せん断係数m_Dおよびm_plugは式(3)と(4)から計算可能であり，ツイスト角(式(2))は下流のロール摩擦m_R,downを与える。ロール粗度がm_R,down=1と異なる場合には，式(1)および(5)を用いて同定を完了することができる。

5. 結言

交差ロール穿孔プロセスの一連の数値計算により，プロセスを支配する動力学的な，あるいは機械的な変数である4つの摩擦せん断係数に関する係数の感受性を示した。回帰的に得られたものではあるが，これらの関係は圧延理論解析と一致するものである。これを用いて，異なる工具・工具部品における摩擦の同定の方法として，以下を提示する:

-プラグの摩擦はプラグ荷重から計算可能である(プラグ軸回転が自由なためプラグトルクはゼロ)。

-ディッシャーディスクの摩擦同定には，ディッシャーディスクの荷重とトルクの同時測定が必要である。一方で，精緻な計算においても，他の変数は明確に決定できるほどm_Dに依存しないものと考えられる。

-駆動工具である交差ロールの摩擦は，板圧延における先進率測定による摩擦測定のように，動力学変数であるE_feedおよび${\Theta }_{\text{twist}}$を用いて決定することが最適である。

摩擦の同定によって，摩擦係数と動力学的/機械的変数との相関関係を得て，駆動と抵抗力とのバランスを最適化することでプロセス改善に役立てることができる。

付録　理論結果のまとめ

Table A1に，動力学変数・荷重・トルクに与えるまさつ係数の影響に関する数値計算結果をまとめる。

Table A1. Influence of friction coefficients on mechanical and kinematical observables. All values are taken in the steady state.

mR,down	mplug	mD	mR,up	Efeed	Frolls	Trolls	FD	TD	Fplug	vplug	OD	WT	Θtwist
				[‒]	[kN]	[kN.m]	[kN]	[kN.m]	[kN]	[rpm]	[mm]	[mm]	[°]
0.2	0.2	0.45	1	0.70	591.4	38.7	94.0	3.7	161.3	254	128.4	14.5	55.4
	0.3			0.62	568.2	37.0	90.9	3.6	175.7	259	127.8	14.4	55.5
	0.45			0.52	540.2	34.9	85.5	3.4	192.7	266	126.8	14.2	55.7
0.3	0.2	0.45	1	0.76	609.9	40.6	104.3	3.9	165.1	261	128.3	14.5	47.4
	0.3			0.68	585.1	38.8	99.2	3.7	181.2	266	127.7	14.4	47.7
	0.45			0.58	556.0	36.6	92.7	3.5	200.1	271	126.8	14.3	48.2
0.45	0.2	0.45	1	0.84	627.3	42.6	113.2	3.9	168.7	272	128.1	14.5	31.3
	0.3	0		0.78	614.5	37.4	107.1	0.0	185.2	288	128.0	14.4	17.4
		0.45		0.76	602.2	40.8	107.0	3.7	186.8	274	127.6	14.4	32.6
	0.45	0.45		0.66	575.3	38.7	100.0	3.6	209.8	277	126.9	14.3	35.0
0.6	0.2	0.45	1	0.90	631.0	43.5	114.7	3.7	169.5	281	128.0	14.5	18.2
	0.3			0.83	612.8	42.2	109.0	3.6	191.5	282	127.5	14.4	19.2
	0.45			0.73	588.4	40.3	102.4	3.5	217.6	284	126.9	14.4	21.2
0.7	0.2	0.45	1	0.92	633.2	43.9	114.2	3.6	170.2	284	128.0	14.5	13.9
	0.3			0.86	615.6	42.6	108.3	3.5	193.2	285	127.5	14.5	14.5
	0.45			0.77	593.5	41.0	101.8	3.4	221.9	286	126.9	14.4	15.8
0.8	0	0.45	0.8	0.98	636.9	43.5	106.1	3.4	107.7	0	128.5	14.5	2.7
	0.2			0.88	617.1	41.9	98.8	3.3	164.5	285	127.6	14.4	5.3
	0.45			0.72	574.5	38.5	84.2	2.9	212.4	288	126.6	14.4	6.7
1	0	0.45	1	1.03	668.7	46.7	121.1	3.4	112.6	0	128.9	14.5	3.1
	0.2			0.94	642.1	45.0	111.6	3.5	173.0	288	128.1	14.5	9.4
	0.3	0		0.86	628.4	39.5	100.6	0.0	190.8	294	127.9	14.5	7.4
		0.45		0.89	622.9	43.7	105.7	3.4	196.6	289	127.8	14.5	8.5
	0.45	0		0.79	613.5	38.7	94.8	0.0	225.4	296	127.5	14.4	7.3
		0.45		0.81	606.5	42.6	99.8	3.3	231.2	291	127.3	14.5	8.6

謝辞

本研究はVallourec S.A.のサポートを受け，また併せてデータ開示許可も頂いた。

文献

• 1)  K.-H.Brensing and B.Sommer: Steel Tube and Pipe Manufacturing Process, https://pdfs.semanticscholar.org/1e72/45a6f6c8e88a7db893d5b311feb5f8083d7d.pdf?_ga=2.94978270.356729499.1577025450-670639474.1577025450, (accessed 2020-07-15).
• 2)  E.Ceretti, C.Giardini and F.Brisotto: Proc. NUMIFORM 2004, eds. by S. Ghosh et al., AIP Conf. Proc., Vol.712, AIP Publishing, Melville, NY, (2004), 1154.
• 3)  K.Komori: Int. J. Mech. Sci., 47(2005), No. 12, 1838.
• 4)  E.Ceretti, C.Giardini and F.Brisotto: Proc. 8th Int. Conf. Technology of Plasticity, ed. by P. Bariani, Edizioni Libreria Progetto, Padova, (2005), 281.
• 5)  E.Ceretti, C.Giardini and A.Attanasio: Proc. NUMIFORM 2007, eds. by J. M. A. Cesar de Sa and A. D. Santos, AIP Conf. Proc., Vol.908, AIP Publishing, Melville, NY, (2007), 413.
• 6)  S.Fanini, A.Ghiotti and S.Bruschi: Proc. 10th Esaform Conf., eds. by E. Cueto and F. Chinesta, AIP Conf. Proc., Vol.907, AIP Publishing, Melville, NY, (2007), 709.
• 7)  S.Fanini, A.Ghiotti and S.Bruschi: Proc. NUMIFORM 2007, eds. by J. M. A. Cesar de Sa and A. D. Santos, AIP Conf. Proc., Vol.908, AIP Publishing, Melville, NY, (2007), 1407.
• 8)  Y.Chastel, A.Diop, S.Fanini, P.-O.Bouchard and K.Mocellin: Int. J. Mater. Form., 1(2008), No. 1 (suppl.), 355.
• 9)  S.Fanini: Ph.D. Dissertation, Padua University, (2008), http://paduaresearch.cab.unipd.it/1552/, (accessed 2020-10-29).
• 10)   A. Ghiotti,  S. Fanini,  S. Bruschi and  P.F. Bariani: CIRP Ann., 58(2009), 255.
• 11)   B.A. Romantsev,  M.M. Skripalenko,  T.B. Huy,  M.N. Skripalenko,  Y.A. Gladkov and  A.A. Gartvig: Metallurgist, 61(2018), 729.
• 12)   M.M. Skripalenko,  B.A. Romantsev,  S.P. Galkin,  M.N. Skripalenko,  L.M. Kaputkina and  T.B. Huy: Metallurgist, 61(2018), 925.
• 13)   M.M. Skripalenko,  V.E. Bazhenov,  B.A. Romantsev,  M.N. Skripalenko,  T.B. Huy and  Y.A. Gladkov: Mater. Sci. Technol., 32(2016), 1712.
• 14)   V.P. Romanenko,  P.L. Alekseev,  E.A. Kharitonov,  A.A. Yandimirov and  A.A. Sevastyanov: Metallurgist, 55(2011), 28.
• 15)   V.P. Romanenko and  D.V. Sizov: Metallurgist, 57(2014), 830.
• 16)   Z. Zhang,  D. Liu,  Y.H. Yang,  Y. Zheng,  Y.H. Pang,  J.G. Wang and  H.P. Wang: Arch. Civ. Mech. Eng., 18(2018), 1451.
• 17)   Z. Pater and  J. Kazanecki: Arch. Metall. Mater., 58(2013), 717.
• 18)   A. Murillo-Marrodán,  E. Garcia and  F. Cortés: AIP Conf. Proc., 2113(2019), 040003.
• 19)   L. Fourment,  J.-L. Chenot and  K. Mocellin: Int. J. Numer. Methods Eng., 46(1999), 1435.
• 20)   M. Ramadan,  L. Fourment and  H. Digonnet: Int. J. Mater. Form., 7(2014), 207.