Ductile Fracture Behavior for Two-phase Steel under Tensile Deformation with Strain Path Change

Abstract

In this study, we investigated the strain-history dependence of ductile fracture behavior in ferrite–pearlite (FP) two-phase steels. The mechanism of this dependence was analyzed using finite element (FE) simulation. The orthogonal strain path changes were subjected to single-phase ferrite steel, two types of FP steels with different pearlite fraction, and single-phase pearlite steel. After the tensile pre-deformation, secondary tensile deformation was applied in the same direction or orthogonal to the first direction. The results showed that the elongation was higher when the secondary deformation was applied in the direction orthogonal to the pre-deformation, compared with that in the no-path change case. The elongation improvement due to the path change was greater with higher pre-deformation and pearlite fraction. The mechanism was investigated by analyzing the localization behavior of plastic deformation in the microstructure via FE simulation using a three-dimensional heterogeneous microstructure model. The simulations showed that the deformation path change in FP steel suppressed local accumulation of damage by changing the strain localization region owing to strength heterogeneity between the two phases.

1. 緒言

近年，自動車の軽量化と衝突安全性の観点から自動車用鋼板の高強度化が図られている。しかし，鉄鋼材料は通常，強度を上げると延性は低下する傾向にある。このため，プレス成形や衝突の際に破断が生じることを防ぐために，高強度鋼板の強度・延性バランスの向上が求められている。その手段の一つとして，強度の異なる二種類の相を含み，材料組織の不均質性を積極的に利用した二相組織鋼の開発が進められている^1–6)。また，複雑形状の自動車用部品は，通常，多工程で成形されるため，材料の受ける変形経路が大きく変化する場合を含めた多様な変形下での延性破壊の予測と，その機構の解明が求められている。

二相組織鋼の延性は，各構成相の特性だけでなく，第二相の体積分率^7,8)や形状⁹⁾などの組織形態に加え，材料の変形様式¹⁰⁾や負荷方向¹¹⁾にも依存して変化することが知られている。例えば，Avramovic-Cingaraらは，引張試験中のその場観察により，二相組織鋼のマルテンサイト形態とボイド生成挙動の関係を調査し，細長い形状のマルテンサイトが破壊の起点になっていることを示している⁹⁾。また，Kikuzukiらは，二相組織鋼の引張方向に並んだマルテンサイト間のフェライト領域にひずみが集中し，ボイドが発生することを報告している¹¹⁾。一方，微視組織内の不均一な変形は，ミクロ組織形態を考慮したシミュレーションにより再現することができ，この結果から，破壊に至る素過程を検討することができる。例えば，Tasanらは，二相組織鋼の結晶塑性解析により，DIC(Digital Image Correlation)により測定した変形の不均一分布が再現できることを示している¹²⁾。また，Matsunoらは，二相組織鋼の組織形態と二相の界面の特性を表現したシミュレーションによりボイドの発生箇所を再現できることを示している¹³⁾。このように，これまでの研究により，二相組織鋼の延性破壊の特徴とその機構の理解が進みつつあるが，これら一連の研究は，変形経路が変化しない比例負荷での延性破壊に関するものであり，ひずみ経路が変化したときの延性破壊については十分に検討がなされていない。

変形経路が変化したときの破断に対する余裕度は，板材成形では一般に，板厚減少率や成形限界線図(FLD: Forming Limit Diagram)を用いて判断される。このうち，薄板の破断限界ひずみを示すFLDは変形経路に依存し変化することが知られている。例えば，Nakazimaら¹⁴⁾やKikuma and Nakazima¹⁵⁾は2つの比例負荷を組み合わせた複合負荷経路の実験においてFLDの変形経路依存性を報告しているが，成形性の変化を念頭に置いた現象論的な報告にとどまっている。一方，二相組織鋼の延性破壊挙動の変化経路依存性に関する過去の知見としては，Ishiguroらによる引張後の圧縮変形下の延性破壊に関する報告¹⁶⁾や，Yoshinariらによる圧縮後の引張変形下の延性破壊に関して報告¹⁷⁾がなされている。しかし，これらの研究は，変形経路が変化したときの延性破壊の予測技術を対象とした検討であり，材料の組織変化と微視的損傷を関連付けた延性破壊に関する知見はない。

そこで本研究では，二相組織鋼を対象に，1次変形として15%，30%の引張予ひずみを施した後，2次変形として1次引張方向に対して90°方向を変化させた引張試験を実施し，延性破壊挙動におよぼす変形経路の影響を検討した。さらに，二相組織鋼の不均一構造を考慮した連続体損傷力学に基づく有限要素解析により微視組織変化と損傷の発展を関連付け，変形経路変化下の延性破壊挙動の機構を明らかにする。

2. 実験方法

2・1　供試材

二相組織鋼の延性は，構成相の粒径¹²⁾や強度差¹⁸⁾により変化することが報告されている。これらの影響を極力排除し，二相組織鋼の不均一構造の影響を評価するため，粒径と各構成相の硬さを同等としつつ，構成相の分率を変化させたフェライト―パーライト鋼を作成した。二相組織鋼の延性破壊のひずみ経路依存性に及ぼす硬質相の体積分率の影響を検討するために，パーライトの体積分率の目標値を20%および65%としたフェライト-パーライト鋼(以下，FP20材，FP65材)を供試材として用いた。また，各構成相の材料特性を同定するため，フェライト単相鋼(以下，F材)およびパーライト単相鋼(以下，P材)を作製した。供試材の化学組成をTable 1に示す。ここでは，C以外の元素をほとんど含まず，ボイド発生起点となる介在物が極めて発生しにくい化学組成とした。また，材料の異方性と鋳造時に生じる引け巣等の欠陥を極力排除するために，真空溶解した電解鉄に対しTable 2に示す温度と時間で，圧力を196 MPaとしてHIP(Hot Isotropic Pressing)処理を行った。また，各供試材で目標の組織分率と同等の粒径を得つつ，さらに構成相の硬さを各素材で統一するために焼鈍を実施した。

Table 1. Chemical compositions of two-phase steels and its constituent Ferrite and Pearlite single-phase steels.

Chemical composition (mass%)
	C	Si	Mn	P	S	Cu	Al	N
F	0.021	< 0.003	< 0.003	< 0.002	< 0.003	< 0.003	< 0.002	< 0.0005
FP20	0.143	< 0.003	< 0.003	< 0.002	< 0.003	< 0.003	< 0.002	< 0.0005
FP65	0.490	< 0.003	< 0.003	< 0.002	< 0.003	< 0.003	< 0.002	< 0.0005
P	0.765	< 0.003	< 0.003	< 0.002	< 0.003	< 0.003	< 0.002	< 0.0005

Table 2. Heat treatment condition for steel making. (A.C.: Air cooling, F.C: Furnace cooling, R.T.:Room temperature)

	Hot Isotropic Pressing	Annealing
F	920°C × 1 h	950°C × 15 min → A.C. to R.T.
FP20	920°C × 4 h	950°C × 15 min → A.C to 680°C → 950°C × 5 min → A.C to 680°C → 950°C × 5 min → F.C to 680°C → A.C. to R.T.
FP65	920°C × 1 h	950°C × 15 min → A.C to 680°C → 750°C × 5 min → A.C to 680°C → 750°C × 5 min → 727°C × 5 min → F.C to 680°C → A.C. to R.T.
P	920°C × 1 h	750°C × 15 min → F.C. to 680°C → A.C. to R.T.

作製した二相材と各相を構成する単相材の組織をFig.1に示す。FP20材とFP65材のパーライト分率はそれぞれ17.2%および66.4%であり，想定した通りの組織分率の素材が得られた。

Fig. 1.

Microstructure of materials. (a) F, (b) FP20, (c) FP65, and (d) P.

次に，EBSD(Electron Back Scattered Diffraction Pattern)法により，F材，FP20材およびFP65材のフェライト粒径を測定した。まず，IQ(Image Quality)値が300未満となる測定点をフェライトとみなした。次に，隣接測定点間の結晶方位差が5°以内であれば，同じ結晶粒に属すると定義し，フェライトの平均粒径を算出した。その結果，F材，FP20材およびFP65材の平均粒径は86.7 μm, 85.3 μmおよび82.8 μmであり，同程度の大きさの粒径を有していた。

さらに，押し込み荷重0.245 Nでビッカース硬さ(以下，硬さ)を測定した。ここでは各相の硬さの異方性の有無を確認するため，素材の長手方向(L方向)およびそれに直交する方向(T方向)の二方向から測定した。また，粒径に対して十分広い範囲で測定するため，測定範囲を試料の中心から7 mmとし，間隔を0.2 mmとした。その結果をFig.2に示す。二方向から測定した硬さに大きな差はなく，試験方向の影響は認められなかった。次に，各供試材の構成相の平均硬さをTable 3に示す。FP20材とFP65材では，構成相の分率に基づき各相の平均硬さを算出した。すなわち，FP20材では上位17.2%を，FP65材では上位66.4%をパーライトとみなし，残部をフェライトとみなして各相の硬さの平均値を求めた。その結果，FP20材とFP65材の中に存在するパーライトの硬さは，パーライト単相のP材に比べて若干高い傾向を示すものの大きな差がないことを確認した。このことから，各供試材を構成するフェライトおよびパーライトの硬さが同等であることがわかる。

Fig. 2.

Comparison of Vickers hardness distribution in steels used. (a) F, (b) FP20, (c) FP65, and (d) P.

Table 3. Average Vickers hardness.

	Average Vickers hardness (Hv)
	Ferrite	Pearlite
F	117	−
FP20	122	213
FP65	121	191
P	−	178

次に，供試材について，機械的特性と延性破壊限界を測定するために，L方向とT方向が引張方向となるように，Fig.3(a)の形状の微小引張を採取し，1 μm/sの引張速度で試験を行った。このとき試験中央の標点間距離2.5 mmの変化をCCDカメラにより測定し，公称ひずみを算出した。また，試験機の荷重と試験片の初期断面積から公称応力を算出した。その結果をFig.4に示す。各方向の加工硬化挙動と破断時全伸びはほぼ一致しており，供試材の初期異方性が小さいことを確認した。

Fig. 3.

Geometry and size of specimens. (a) round-bar specimen, and (b) flat-tensile specimen.

Fig. 4.

Effect of loading direction on the nominal stress nominal-strain curve. (a) F, (b) FP20, (c) FP65, and (d) P.

2・2　延性の変形経路依存性評価試験

延性の変形経路依存特性を評価するために，Fig.5に示す手順で試験を実施した。まず，素材のL方向が長手方向となるように切り出したFig.3(b)の平滑丸棒引張試験片に引張の予変形(以下，予変形)を施した後，平滑丸棒引張試験片の中央部から引張方向がL方向およびT方向となるようにFig.3(a)の微小引張試験片(以下，LL試験片およびLT試験片)を採取し，引張変形(以下，二次変形)を与えた。予ひずみ量ε_preはF材，FP20材については真ひずみで0.30とした。FP65材については，ε_preの依存性を検討するため，ε_preは真ひずみで0.15および0.30の二水準とした。なお，P材については破断真ひずみが0.30より小さいため，ε_preは真ひずみで0.15とした。ここでは素材，予ひずみの大きさおよび微小引張試験片の採取方向によって各微小引張試験片の名称をTable 4のように定めた。予変形では，クロスヘッド変位速度0.5 mm/min(ひずみ速度約0.02/min)で所定の予変形を与え，試験片のくびれ底断面の直径を測定して真ひずみを算出した。二次変形では，変位速度1 μm/sの変位を与え，荷重と平行部の長さを測定し公称ひずみε_Nと公称応力σ_Nを算出した。

Fig. 5.

Test procedure for the effect of strain history on ductility.

Table 4.

Types of micro-tensile specimens.

3. 実験結果

Fig.6に二次変形の公称ひずみ-公称応力を示す。まず，LL試験片とLT試験片の違いが最も明確に現れたFP65-30LLとFP65-30LTの結果(Fig.6(c))に着目し，加工硬化挙動の特徴を述べる。LL試験片では降伏直後に最大引張強度を示し，一様伸びは1.1%でありほとんど消失していた。これに対し，LT試験片では，降伏応力が低下するバウシンガー効果が生じ，ラウンドハウス型の降伏挙動を示した。その結果，一様伸びが4.6%となり，LL試験片よりも大きかった。

Fig. 6.

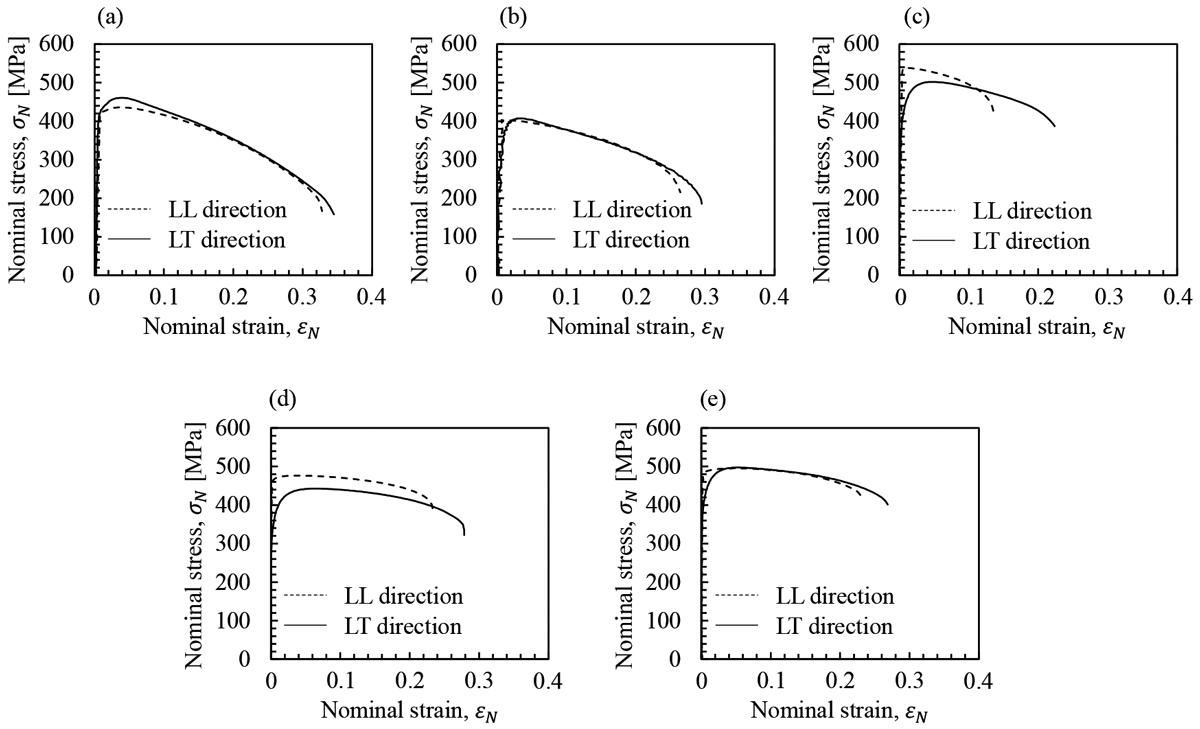
Effect of loading history on the nominal stress-nominal strain curve. (a) F-30LL and F-30LT, (b) FP20-30LL and FP20-30LT, (c) FP65-30LL and FP65-30LT, (d) FP65-15LL and FP65-15LT, and (e) P-15LL and P-15LT.

これらの特徴は，Fig.6(a)に示す通り，フェライト単相鋼では明確に現れないが，Fig.6(b)~(d)に示す通り，パーライトを含む鋼で観測された。また， Fig.6(b)とFig.6(c)の比較から，二相材におけるパーライトの分率が大きいほど，Fig.6(c)とFig.6(d)の比較から，ε_preが大きいほど，LL試験片とLT試験片の差が大きかった。

また，LL試験片よりLT試験片のほうが，破断直前に公称応力が急激に低下する際の二次変形時の公称ひずみ(以下，ε_Ncr)が大きく，延性のひずみ履歴依存性が認められた。各素材のLL試験片のε_Ncr(以下，ε_Ncr(LL))とLT試験片のε_Ncr(以下，ε_Ncr(LT))の比を求め，Fig.7に示した。単相材のF材では，延性にひずみ履歴依存性がほとんどないのに対し，二相材のPF20材およびFP65材の延性はひずみ履歴依存性を示した。また，その傾向はパーライト体積分率が大きいFP65材で顕著に現れた。また，0.15および0.30のε_preを与えたFP65材の結果を比較すると，ε_preが増加するほど延性のひずみ履歴依存性が明確に表れることが分かる。次に，延性破壊限界の代表値として，ε_Ncrにおいて除荷した微小試験片におけるくびれ部の断面積から二次変形による真ひずみ(以下，ε_2nd)を算出し，ε_preとε_2ndの和から破断に至るひずみ(以下，ε_cr)を求めた。ここで，くびれ部の断面積は，幅が最小となる長手方向位置の幅と厚さを測定し，試験片断面が長方形であるという仮定のもとで算出した。各素材のε_cr(LL)とε_cr(LT)の比を求め，Fig.8に示した。ε_Ncrと比較して比は小さいものの，ε_crも同様の傾向を示した。

Fig. 7.

Strain-history dependence on ductility and on the effect of volume fraction of pearlite.

Fig. 8.

Strain-history dependence on fracture strain and on the effect of volume fraction of pearlite.

4. 考察

本研究で供試材として用いたフェライト-パーライト鋼は，予変形と二次変形の引張方向によって延性が異なり，顕著なひずみ履歴依存性を示した。しかし，巨視的な力学的応答からは，その発生メカニズムを推定することは困難であった。そこで，本章では，引張後の破面を観察するとともに，Ohataらによって提案された延性損傷モデル¹⁹⁾を用いた数値シミュレーションを行ってミクロ組織内の損傷分布を評価し，二相組織鋼の延性のひずみ履歴依存性のメカニズムの解明を試みた。

4・1　破面観察による破壊機構の検討

本節では，ひずみ履歴の変化が破断形態に与える影響を調べるため，ε_Ncrの差が大きい0.30の予ひずみを与えたFP65材(FP65-30LLおよびFP65-30LT)の試験片の破面を観察し，F材(F-30LL)およびP材(P-15LL)の破面とともにFig.9に示した。FP65-30LLおよびFP65-30LTでは，破面の全ての領域でディンプルが形成されており，延性破壊により破断に至ったと考えられる。また，いずれもF材とP材と同等の大きさのディンプルが混在しており，延性き裂がフェライト相とパーライト相の両方の相で発生・進展して破断に至ったとものと推察される。一方，FP65-30LLおよびFP65-30LTの破面観察の結果からは，ディンプルの発生挙動に変形経路に依存した特徴は現れなかった。

Fig. 9.

Fracture surfaces of the micro-tensile specimens. (a) F-30LL, (b) P-15LL, (c) FP65-30LL, and (d) FP65-30LT.

さらに，破断に至るまでに形成されるマイクロボイドやき裂の発生位置を比較するために，FP65-30LLおよびFP65-30LTをε_Ncrで除荷した試験片の腐食断面を光学顕微鏡で観察した(Fig.10)。FP65-30LL(Fig.10(a))およびFP65-30LT(Fig.10(b))ともに主にフェライト相とパーライト相境界部近傍でマイクロボイドが発生してき裂状に成長しており，強度が異なる二相による応力やひずみの局在化挙動が，損傷挙動に影響を与えていることが伺われた。一方，ディンプルの観察と同様に，マイクロボイドの発生挙動に変形経路に依存した特徴は現れなかった。

Fig. 10.

Ductile crack behavior observed on the etched cross-section of the micro-tensile specimens (FP65). (a) magnified position of FP65-30LL specimen, (b) magnified position of FP65-30LT specimen, (c) micro void observation of FP65-30LL specimen, and (d) micro void observation of FP65-30LT specimen.

4・2　延性損傷シミュレーションによるひずみ履歴依存性のメカニズムの検討

4・1節に示す破面の観察結果から，強度が異なる二相のひずみや応力の局在化によって損傷挙動が影響を受けていることが推察された。一方，その結果から変形経路に依存した破壊機構の差異を考察することは困難であった。そこで，本節では，ミクロ組織内に生じる損傷分布をシミュレーションにより可視化し，メカニズムの考察を試みた。

4・2・1　延性損傷数理モデル

ミクロ組織内に生じる損傷は，Ohataらが提案する延性損傷数理モデル¹⁹⁾を用いた。これは対象鋼材の延性き裂を支配していると考えられるマイクロボイドの発生を，材料損傷の蓄積によるナノ・サブミクロンサイズボイドの発生・成長と仮想し表現したものである。単位ユニットセルの体積ひずみの増加に伴って損傷が増加し，損傷がある一定値に達すると損傷が加速されてマイクロボイドが形成されると想定している(式(1)，(2))。さらにGurson-Tvergaardの損傷モデル^20,21)をベースとした式(3)に示す新しい塑性ポテンシャル関数を提案することで，マイクロボイドが発生するまでの損傷の増加と材料の弾塑性挙動を連成させて同時解析を可能としている。

  

$$dD=\left(1-D\right)d{E}_m^p$$(1)

  

$$D^{\text{*}}=\{\begin{array}{cc}D& \text{for}D\le D_c\\ D_c+K\left(D-D_c\right)& \text{for}D<D_c\end{array}$$(2)

  

$$\Phi ={\left(\frac{\overline{\Sigma }}{\overline{\sigma }}\right)}^2+a_1{D}^{\text{*}}exp\left(a_2\frac{{\overline{\Sigma }}_m}{\overline{\sigma }}\right)-1=0$$(3)

ここで，Dは損傷度，D_cは加速限界損傷度，Kは損傷加速パラメータ(=4)，E_m^pはユニットセルの体積ひずみの塑性成分，a₁，a₂は損傷パラメータ，D*は有効損傷度Σは損傷を含むユニットセルの相当応力，σは材料マトリックスの降伏強度，Σ_mはユニットセルにかかる平均垂直応力である。ここで，本塑性ポテンシャルに従うと，マイクロボイドやマイクロクラックが形成しはじめる塑性ひずみ(E_p)_iと応力多軸度Σ_m⁄σが式(4)のような関係にあることから，種々の応力多軸度下におけるマイクロボイド発生限界ひずみから損傷パラメータa₁，a₂が一義的に決定できる。

  

$$\underset{D_0}{\overset{D_c}{{\displaystyle \int }}}\frac{1}{\left(1-D\right)D}dD={\displaystyle \underset{0}{\overset{{\left({\overline{E}}_p\right)}_i}{\int }}\frac{1}{2}{a}_1{a}_2\text{exp}\left(a_2\frac{{\overline{\Sigma }}_m}{\overline{\Sigma }}\right)\frac{\overline{\sigma }}{\overline{\Sigma }}d{\overline{E}}_p}$$(4)

4・2・2　シミュレーションのための材料特性の同定

4・2・2・1　加工硬化パラメータの同定

二相組織鋼について延性損傷シミュレーションを行うために，フェライト単相材，およびパーライト単相材の実験で得た均一伸びまでの応力-ひずみ曲線から，各構成相の加工硬化特性を同定した。各構成相の加工硬化特性は，F材，P材の予ひずみ試験の一様伸びまでの範囲の結果を下記の式(5)のSwift式で回帰して定めた。

  

$$\overline{\sigma }={\sigma }_{0.2}{\left(1+{\overline{\epsilon }}_p/\alpha \right)}^n$$(5)

ここで，σは相当応力，ε_pは相当塑性ひずみ，σ_0.2，α，およびnは材料定数である。得られた各構成相の加工硬化パラメータをTable 5に，各種応力と相当塑性ひずみの関係をFig.11に示す。なお，Table 3に示した通り，パーライト単相材の硬さは二相材中のパーライト粒の硬さよりも低いため，P材と二相材中のパーライト相の硬さ比から，P材の応力を1.14倍に補正した。

Table 5. Work hardening parameters of ferrite and pearlite steels.

	σ0.2	α	n
Ferrite	103	0.0023	0.270
Pearlite	132	0.0004	0.206

Fig. 11.

Combined hardening material models of the single-phase steels used for FE analysis.

4・2・2・2　損傷パラメータの同定

各構成相の損傷パラメータ²²⁾を求めるために，平滑丸棒引張試験片(Fig.12(a))と，切欠き底半径が2.0 mm，1.5 mmおよび1.0 mmである三種類の円周切欠き丸棒引張試験片(Fig.12(b))を用いて引張試験を行った。さらに，全ての試験片を対象に弾塑性FEM解析を実施し，延性破壊に達するまでの応力多軸度の履歴を算定した。なお，弾塑性FEM解析は4節点軸対称要素を用い，解析コードABAQUS Standard 6.12を使用した。

Fig. 12.

Configurations of the tensile specimens. (a) smooth round-bar specimen and (b) notched round-bar specimen.

全ての試験片に対し，破断時の応力多軸度と相当塑性ひずみをFig.13(a)に示す。また，破断に至る相当塑性ひずみの90%でマイクロボイドの形成が加速されるとし，その際の応力多軸度と相当塑性ひずみと，それまでの履歴を破線で同図に示した。次にマイクロボイドの形成が加速したと想定した相当塑性ひずみと応力多軸度の関係から式(4)の損傷パラメータa₁，a₂を同定し，Table 6に示した。以上により，得られた各構成相の応力多軸度と損傷加速限界ひずみの関係をFig.13(b)に示す。

Fig. 13.

Stress triaxiality dependence of ductility in ferrite and pearlite single-phase steels. (a) simulation results and (b) damage parameters determined from the triaxiality dependent ductility. F: Ferrite, P: Pearlite.

Table 6. Damage parameters of ferrite and pearlite steels.

	a1	a2
Ferrite	3.183	0.936
Pearlite	5.765	1.389

4・2・3　二相組織鋼のミクロ組織内の損傷分布解析

複合組織鋼の応力・ひずみの局在化挙動を再現するには，組織間の強度差に起因する塑性拘束の影響を考慮する必要性から三次元モデルを用いることが望ましい。そこで，三次元組織形態を再現した「三次元二相組織形態モデル」に4・2・1節に示す延性損傷数理モデルを適用して，実験を模擬した有限要素解析を行った。

FP65材のLL試験片およびLT試験片の平行部の1/4領域を模擬した三次元不均質組織形態モデルを，Ohataら²²⁾と同様の手順で作製した。すなわち，組織観察の結果に基づき，平均結晶粒径が約85 μmとなるような結晶粒数に相当する母点をランダムに三次元空間に分布させた後，Voronoi tessellation法によって三次元結晶粒モデルを作製した。そして，パーライトの体積分率が65%となるようにパーライト粒をランダムに選択した。解析領域は，平均要素サイズ5 μmの4節点4面体アイソパラメトリック要素で分割した。LL試験片では，真ひずみ0.30を付与しても一様に変形していると仮定し，実験で使用した微小引張試験片の形状から0.30の予ひずみを付与した後，標点を取り直してから引張荷重を与えた(Fig.14(a))。LT試験片では，0.30の予ひずみ付与後に実験を行った微小引張試験片と同じ形状，寸法となるようにした初期モデルを作製して予ひずみを付与した後，引張負荷を与えた(Fig.14(b))。三次元FEM解析はABAQUS Standard Ver.6.12を用い，式(3)の拡張塑性ポテンシャル関数をUser subroutine UMATを使って導入した。

Fig. 14.

FE-model the of micro-tensile specimens (FP65). (a) LL specimen and (b) LT specimen.

シミュレーションで得られた二次変形時の公称応力-公称ひずみ曲線を実験結果とともにFig.15に示す。また，均一伸びを同図に矢印で示した。負荷方向が変化しないLL試験片は実験結果と良い一致を示している(Fig.15(a))。一方，負荷方向が90°変化するLT試験片では，明確なラウンドハウス型の応力―ひずみ応答は生じておらず，降伏応力や最大引張強度が実験結果よりも高い。このため，LL試験片との降伏応力や最大引張応力の差が再現されていない。これらは，本研究のシミュレーション手法ではフェライト相やパーライト相のバウシンガー効果を考慮していないためと考えられる。しかしながら，実験で測定した加工硬化挙動の特徴やε_Ncrの差を再現しており，本手法を用いることで二相組織鋼の延性破壊挙動のひずみ履歴依存性を考察可能であるものと考えた(Fig.15(b))。すなわち，実験と同様に，LT試験片ではLL試験片に対して降伏初期の応力がわずかに低下し一様伸びが再度現れた。また，Fig.16の通り，実験と解析のε_Ncrの差は小さく10%以内であり，LT試験片ではLL試験片に対してε_Ncrが大きい傾向が定量的に再現された。

Fig. 15.

Comparison between stress-strain curves obtained by experiments and damage simulation (FP65). (a) LL specimen and (b) LT specimen. Arrows indicate the uniform elongation.

Fig. 16.

Reproducibility of experimental ductility by analysis.

次に，二次変形前後のフェライトの損傷度Dの分布をFig.17に示す。パーライトは同図中に灰色で示した。図中中央部のパーライト相の周囲のフェライト相の損傷分布に着目すると，二次変形前は，負荷方向とパーライトの交点(L1やL2)で主に損傷が蓄積する傾向にある(Fig.17(a))。また，二次変形後は，LL試験片では，同様の領域(L1やL2)でさらに損傷が増加したが(Fig.17(b))，LT試験片では，予変形時にひずみ量が少なかった別の箇所(L3)で損傷が増加した(Fig.17(c))。このようなミクロ組織内の変形領域の差異により，LT試験片とLL試験片の延性および加工硬化挙動の差がもたらされたと考えられる。すなわち，LT試験片では，ミクロ組織内のより広い範囲に損傷が分散することで局所的な変形集中が抑制され，ε_crが高まったと考えられる。また，二次変形開始時に，より変形量の小さい領域が変形することで，降伏応力が低下し，一様伸びが再度現れたものと考えられる。

Fig. 17.

Damage distribution in the microstructure during secondary deformation (FP65). (a) before secondary deformation, (b1) after secondary deformation (LL specimen), and (b2) after secondary deformation (LT specimen).

また，FP65材では，ε_Ncr(LT)/ε_Ncr(LL)は，ε_preの増加とともに大きくなった(Fig.6)。これは，ε_preが大きいほど，予変形時のミクロ組織内の損傷の差が大きくなるため，二次変形時の変形領域の違いの影響がより強く表れたと考えられた。

上述の機構は，構成相間の硬度差がある複相組織鋼特有のものであると考えられる。一方，単相組織であるP材でも同様にε_Ncr(LT)/ε_Ncr(LL)が1以上となった。このため，上述のメカニズム以外の要因も考えられた。Fig.6の通り，P材ではF材よりも降伏応力が低くバウシンガー効果が大きい。また，FP20材とFP65材の比較から，大きなバウシンガー効果を示すパーライトの構成比率が高まるほど，LL試験片とLT試験片のε_Ncrの差が大きくなる。本研究で用いたシミュレーション手法により，LL試験片とLT試験片の延性の差が概ね表現されたことから，その主要因はFig.17に示す変形領域の変化であると考えられるが，バウシンガー効果によっても，延性が高まることが示唆された。

5. 結言

本研究では，フェライト-パーライト鋼を対象に延性のひずみ履歴依存性を実験的に測定し，延性損傷シミュレーションによりメカニズムを検討した。その結果，以下の知見を得た。

(1)フェライト-パーライト複相鋼において，予変形と方向の異なる2種類の二次変形下の破断限界ひずみを調査した結果，二次変形を予変形に対して平行に与えた場合に対し，直交方向に与えた場合のほうが，延性が高くひずみ履歴依存性が現れた。

(2)延性のひずみ履歴依存性は，フェライト単相鋼では小さいが，フェライト-パーライト二相鋼では明確に認められた。また，その程度は，パーライトの分率が高いほど大きかった。

(3)延性損傷シミュレーション手法を用いて，上述の実験を模擬した変形を与えた際のミクロ組織内の変形分布を解析した。その結果，二次変形を予変形に対して直交方向に与えた場合は，予変形時に損傷が小さい領域が二次変形時に変形することで，より広い範囲に損傷が分散したため，延性が高まったと考えられる。

文献

• 1)   A. Uenishi: Nippon Seitetsu Giho, 412(2019), 8 (in Japanese).
• 2)   R. Kuziak,  R. Kawalla and  S. Waengler: Arch. Civ. Mech. Eng., 8(2008), 103. https://doi.org/10.1016/S1644-9665(12)60197-6
• 3)  T.Inoue and S.Kinoshita: Tetsu-to-Hagané, 62(1976), 90 (in Japanese). https://doi.org/10.2355/tetsutohagane1955.62.1_90
• 4)  T.Inoue and S.Kinoshita: Tetsu-to-Hagané, 62(1976), 875 (in Japanese). https://doi.org/10.2355/tetsutohagane1955.62.7_875
• 5)   H. Qiu,  H. Mori,  M. Enoki and  T. Kishi: ISIJ Int., 39(1999), 358. https://doi.org/10.2355/isijinternational.39.358
• 6)  T.Ishiguro, Y.Yoshida, N.Yukawa, T.Ishikawa, H.Yoshida and N.Fujita: Tetsu-to-Hagané, 97(2011), 136 (in Japanese). https://doi.org/10.2355/tetsutohagane.97.136
• 7)   T. Matsuno,  D. Maeda,  H. Shutoh,  A. Uenishi and  M. Suehiro: ISIJ Int., 54(2014), 938. https://doi.org/10.2355/isijinternational.54.938
• 8)  K.Hasegawa, Y.Toji, H.Minami, H.Ikeda, T.Morikawa and K.Higashida: Tetsu-to-Hagané, 98(2012), 320 (in Japanese). https://doi.org/10.2355/tetsutohagane.98.320
• 9)   G. Avramovic-Cingara,  Y. Ososkov,  M.K. Jain and  D.S. Wilkinson: Mater. Sci. Eng. A, 516(2009), 7. https://doi.org/10.1016/j.msea.2009.03.055
• 10)   J. Samei,  D.E. Green,  J. Cheng and  M. Soares de Carvalho Lima: Mater. Des., 92(2016), 1028. https://doi.org/10.1016/j.matdes.2015.12.103
• 11)  M.Kikuzuki, K.Hayashi, Y.Tsunemi, S.Yabu and T.Matsuno: Tetsu-to-Hagané, 106(2020), 224 (in Japanese). https://doi.org/10.2355/tetsutohagane.TETSU-2019-111
• 12)   C.C  Tasan,  J.P.M. Hoefinagels,  M. Diehl,  D. Yan,  F. Roters and  D. Raabe: Int. J. Plast., 63(2014), 198. https://doi.org/10.1016/j.ijplas.2014.06.004
• 13)   T. Matsuno,  C. Teodosiu,  D. Maeda and  A. Uenishi: Int. J. Plast., 74(2015), 17. https://doi.org/10.1016/j.ijplas.2015.06.004
• 14)   K. Nakazima,  T. Kikuma and  K. Hasuka: Yawata Tech. Rep. 264(1968), 8517.
• 15)  T.Kikuma and K.Nakazima: Trans. Iron Steel Inst. Jpn., 11(1971), Suppl., 827.
• 16)  T.Ishiguro, E.Abe, K.Ueno, N.Yukawea, M.Fujiwara, H.Yoshida and T.Ishikawa: J. Jpn. Soc. Technol. Plast., 54(2013), 993 (in Japanese). https://doi.org/10.9773/sosei.54.993
• 17)  H.Yoshinari, K.Enami, M.Kan and S.Kaneda: J. Soc. Mater. Sci. Jpn., 54(2005), 296 (in Japanese). https://doi.org/10.2472/jsms.54.296
• 18)   M. Azuma,  S. Goutianos,  N. Hansen,  G. Winther and  X. Huang: Mater. Sci. Technol., 28(2012), 1092. https://doi.org/10.1179/1743284712Y.0000000006
• 19)   M. Ohata,  M. Suzuki,  A. Ui and  F. Minami: Eng. Fract. Mech., 77(2010), 277. https://doi.org/10.1016/j.engfracmech.2009.08.011
• 20)   A.L. Gurson: J. Eng. Mater. Technol., 99(1977), 2. https://doi.org/10.1115/1.3443401
• 21)   V. Tvergaard and  A. Needlman: Acta Metall., 32(1984), 157. https://doi.org/10.1016/0001-6160(84)90213-X
• 22)  M.Ohata, H.Shoji and F.Minami: Tetsu-to-Hagané, 99(2013), 573 (in Japanese). https://doi.org/10.2355/tetsutohagane.99.573