2023 Volume 109 Issue 6 Pages 501-512
2023 Volume 109 Issue 6 Pages 501-512
Most production systems are operated in a human-in-the-loop fashion, and it is sometimes argued that the human decisions involved make it possible, or at least easier, for the systems to cope with various stationary and nonstationary variations. However, it has not been well-studied and understood how this positive contribution of human decisions work, what factors determine its effect, how the function should be supported or fostered, etc. This paper first briefly reviews conventional production systems simulation techniques and discusses why it is difficult for them alone to address aforementioned questions. This next points to some recent attempts, in production systems engineering and related areas, to study human decisions and their effects by complementally using gaming simulation and agent-based simulation and highlights the potential of combining such behavioral and computational scientific approaches. Then, the paper introduces a cognitive framework model composed of interface, interaction, and incentive dimensions. It can be used for formally characterizing the decisions made by an individual facing a problem situation in operating a production system, and functions as a bond connecting behavioral and computational analyses of the decision maker. The paper further presents some example ongoing research projects worked on by the author’s team in this direction and discusses some future perspective.
生産システムとは,一般に,複数の物理的な資源(例えば,加工や運搬のための機械設備や作業者)で構成され,それらが対象(例えば,原材料,部品,製品など)に対して,様々な作業を分担して実行していくことによって機能する分業系として捉えることができる。この意味では,生産システムは,製品の製造を担う工場に限定されるものではなく,複数の事業体にまたがるサプライチェーン,顧客にサービスを提供する店舗などを含むと考えてもよい。生産システムの性能(例えば,生産率,納期遵守率,製造コストなど)は,それがどのような資源で構成されているか,だけで決まるものではなく,それをどのように運用するか,にも依存する。ここに,生産システムの運用とは,不確実性を伴う現実の環境の中でそのシステムを動かすことであり,その本質は「いつ,どの資源に,どの対象に向けて,どの作業を,実行させるか」についての動的な意思決定にあるといえる。
生産システム運用の意思決定は,何らかのアルゴリズムに基づいて計算機で機械的に行われることもあるが,現実では,その多くを(少なくとも部分的に)人が担っている。この意味で,生産システムには「人の意思決定」が埋め込まれているといえる。「人の意思決定」は,参照する入力情報,出力可能な選択肢の集合,入力から出力を導くための手続き,意思決定を下すタイミングなどを,必ずしも事前に完全に規定しておく必要がないという点で柔軟である。この柔軟性こそが,生産システムの不確実性への対応を可能にしているという面がある。ここで言う「不確実性への対応」には,「定常的な変動の中でシステムが安定して稼働し続けられること」に加えて,「非定常的な変動の影響を受けた後,速やかに安定状態に復帰できること」も含まれる。これらの間の絶対的な線引きは難しいが,本稿では,前者を「ロバストネス」,後者を「レジリエンス」と呼び分けることにする。特に,少なくとも現状では,生産システムに後者の能力を具備させるために人の関与は不可欠である,という見方に大きな違和感はないだろう。
生産システムの運用への人の関与は,上述のように,不確実性への緩衝として働くこともあれば,逆に,新たな不確実性の源泉になってしまうこともある。例えば,サプライチェーンでは,需要量が予想よりも多かった(少なかった)際に,それに伴う在庫量の減少(増大)を確実にオフセットしようとして,在庫管理の担当者が発注量を過剰に増大(減少)させる傾向があり,それがブルウィップ効果の原因の一つであると言われている。また,「人の意思決定」は,柔軟であることの裏返しとして,属人的になりがちであり,その出力は,類似の状況下でも担当者によって異なり得る。特に,熟練者と新人の差異がしばしば問題視される。さらに,ヒューマンエラーの問題も存在する。こうしたマイナス面を解消,または,緩和するために,従来から,「人の意思決定」を自動化するための研究が数多くなされてきた。属人的な運用の意思決定を自動化して「機械の意思決定」に置き換えてしまえば,意思決定の質は向上する,あるいは,少なくとも安定するものと期待されるというわけである。しかし,その一方で,人の関与を排除しすぎると,上述のロバストネスやレジリエンスが阻害されてしまうことが懸念される。
昨今のデジタル化の流れは,インダストリー4.0,DXなどのキーワードとともに,生産システムにも押し寄せてきている。その結果,いわゆるIOTデバイスの普及が進み,実時間でセンシング可能な情報が増えている。また,サイバーフィジカルシステム(CPS)やデジタルツインといったコンセプトのもと,センシングしたデータを統合することでシステム全体の状況をより詳細な粒度で把握できるようになってきている。そして,そうして大量に蓄積されていくデータの履歴,いわゆるビッグデータに基づいて,様々な予測モデルの構築,改善が進んでいる。さらに,それによって,これまで「人の意思決定」固有の強みの一つとみなされていた「経験からの学習」は,少なくとも部分的には,「機械の意思決定」にも可能になりつつある。これらの変化は,機械に置換え可能な運用の意思決定を増加させる方向に作用する。しかし,上でも述べたように,可能なものをすべて「機械の意思決定」に置き換えてしまうことが得策であるという保証はない。生産システムのロバストネスやレジリエンスを確保するためにどの意思決定を人に残すべきか,人に残した意思決定をどのように支援するべきか,などの問いに向き合うことの重要性がますます高まってきているといえる。
そのためには,「人の意思決定」が埋め込まれた生産システムの性能,特に,そのロバストネスやレジリエンス,それらを決定づける上で「人の意思決定」が果たしている役割やその効果を左右する要因,などについての理解を深めることが必要である。そこで本稿では,そのための計算科学的,および,行動科学的なアプローチについて,著者らのグループのものを中心にレビューする。
生産システムの状態の時間発展を解析的に求めるのは難しいことが多く,その評価には,通常,シミュレーションが用いられる。生産シミュレーションについての研究は数多く,それらのレビュー論文もいくつか発表されている1–5)。例えば,文献4)では,生産シミュレーションの主な技法を,離散事象シミュレーション,システムダイナミクス,エージェントシミュレーションの3つに大別し,離散事象シミュレーションが最も一般的であるとしている。生産システムの離散事象シミュレーションでは,資源(機械設備,作業者など)と対象(原材料,部品,製品など)の状態が,作業(加工,運搬など)の完了,故障の発生,といった(確率的,あるいは確定的な)事象の生起にともなって変化していく様子を追跡していく。そして,それを繰り返すことによって,例えば,作業時間や故障の発生間隔などの確率的な変動のもとでのシステムの性能尺度の平均や分散,分布などを評価することになる。
こうした典型的な従来の生産シミュレーションでは,生産システムに埋め込まれた「人の意思決定」は,暗黙的に,例えば,ディスパッチングルールなどの,計算機で実行可能な何らかの計算手続き,すなわちアルゴリズムとしてモデル化されている。したがって,それらと「機械の意思決定」は,明確には区別されていないことが多い。そこで,「人の意思決定」の関与を明示するために,生産シミュレーションから,あえてその部分を切り出してみると,Fig.1の2層モデルが得られる。

Two-layer model of human-in-the-loop operation of a production system.
図では,第1層が,生産システムの機械的な挙動を表す層であり,第2層が,切り出された「人の意思決定」に対応している。第2層は,第1層の状態を観測し,それに基づいて下した意思決定を第1層に返すという図式になっている。第1層を環境(Environment)に,それとのやり取りを知覚(Percepts)と行為(Actions)に対応させると,第2層はまさに文献6)の意味でのエージェント(Agent)であることがわかる。
実際には,生産システムの運用には単一ではなく複数の意思決定者が関わることが多く,その場合は,厳密には,エージェントが複数存在する図式になる。また,各エージェントが観測する知覚には,対象生産システムの物理的な資源の状態だけではなく,事前に策定された生産計画や生産スケジュールなどの情報資源の状態も含まれる。CPSでは,環境のうち,前者の物理資源をPhysical,後者の情報資源をCyberと呼び分けている,また,後者を前者に対応させて統合化したものをデジタルツインと呼んでいる,などと理解することもできる。さらに,ICTの発展に伴って,顧客に今までよりも密に生産システムの運用に関わってもらうことも可能になりつつある。そうした試みを実践している生産システムでは,顧客も運用に関与する意思決定者,すなわちエージェントに含めた図式が有用になることもある(顧客包含型モデル)。
生産システムのエージェントシミュレーションの一つの形態は,この第2層を,第1層とは別のモジュールのアルゴリズム,すなわち,計算機エージェントで実装したものである。文献6)では,さらに,計算機エージェントを実現するためのアルゴリズムを複雑さの異なるいくつかのクラスに分類している。一方で,生産システムに埋め込まれた「人の意思決定」も,知覚(生産システムの状態)から行為(意思決定の結果)を導出するという働き,すなわち,このエージェントの機能,を担っているとみなすことができる。これらから,生産システムの運用に関する「機械の意思決定」と「人の意思決定」は,単にそれらのアルゴリズムとしての複雑さが異なるだけであるという見方も可能である。この見方によると,計算機エージェントのアルゴリズムを複雑化・高度化していけば,いつか「機械の意思決定」によって「人の意思決定」と等価な貢献が可能になるということになる。
これに対して,本稿では,少なくとも現状では,生産システムの運用に関する「機械の意思決定」と「人の意思決定」の間には単なるアルゴリズムの複雑さの違いだけでは捉えきれない,本質的な差異があるという立場をとる(これは,「少なくとも現状では」ということであり,この本質的な差異が将来的にアルゴリズムの中に完全に回収されてしまう可能性を否定するものではない)。この立場に立つと,現状では,上述のエージェントシミュレーションのように,意思決定者を計算機エージェントに置き換える,計算科学的なアプローチだけでは,「人の意思決定」が果たしている役割を見逃してしまう恐れがあるということになる。
これに対して,Fig.1の第2層を実際の人に担当してもらうという,行動科学的なアプローチが考えられる。これは,参加型シミュレーション,ゲーミングシミュレーションなどと呼ばれ,教育や訓練に加え,研究の手段としての活用も広がってきている。初期の最もよく知られた活用例の一つは,「人の意思決定」がサプライチェーンのブルウィップ効果に及ぼす影響を分析したビールゲーム7)であろう。一方,Meijerは,文献8)で,ゲーミングシミュレーションを研究手段として用いることの意義を論じている。そして,それをサプライチェーンの研究に,さらに,文献9)で,鉄道システムの研究に,それぞれ適用している。著者らも,上工程の1工場と下工程の3工場を持つ架空の製鉄企業の社内サプライチェーンを題材にしたシリアスゲーム,ColPManを開発した10)。それら複数の工場,および,本社の間で生産計画を協調させていく際の「人の意思決定」を分析するために,このゲームを用いたゲーミングシミュレーションが活用されている11,12)。なお,シリアスゲームとは,教育,訓練など,遊興以外の目的をもつゲームのことであり,このように,ゲーミングシミュレーションのプラットフォームとして活用することができる。
ゲーミングシミュレーションは,「人の意思決定」を生産シミュレーションに取り込むための最も直接的な方法であるといえる。しかし,このアプローチでは,「人の意思決定」は「人の意思決定」のまま,すなわちブラックボックスのままであり,残念ながら,それだけでは,「人の意思決定」の「機械の意思決定」との本質的な違い,その効果を左右する要因などは見えてこない。ゲーミングシミュレーションにおける「人の意思決定」を,何らかの数理モデルに基づいて理解する試みが必要になる。
この方向の従来研究として,例えば,Anandら13)は,都市交通システムを対象にして,ゲーミングシミュレーションの結果に基づいて,エージェントシミュレーションの妥当性を検証している。また,Nishinoら14)は,メンバーシップサービスを対象にして,参加者の選好を厳密に統制して行うゲーミングシミュレーションとも解釈できる,経済学実験を実施し,その結果をエージェントシミュレーションの結果と対比している。著者ら15)も,上述のシリアスゲーム,ColPManにおける「人の意思決定」を,数理最適化モデルと関連付けて分析することを試みた。しかし,ゲーミングシミュレーションでの「人の意思決定」のデータに基づいて,エージェントシミュレーション内の計算機エージェントのパラメータ値を調整するだけでは,両者の本質的な違いに迫ることは難しい。
2・2 生産システム運用の意思決定のモデル化人が直面する意思決定状況を,文献16)では,「単一主体・複数主体」および「静学的・動学的」の2軸で分類している。そして,最も単純な「単一主体・静学的」の場合の合理的な意思決定者の振舞いを次のように表現している。すなわち,可能な選択肢を洗い出し,そのそれぞれについて,それを採用した結果を想定し,その結果の好ましさが最も高くなる選択肢を選ぶ。これはまさに(数理)最適化のモデルにほかならない。
例えば,生産システム運用上の任意の意思決定において,実行可能な選択肢の集合をDx(∋x),生産システムの状態を捉える特徴量空間をDy(∋y),ある選択肢xを選択したときの状態yの値を与える関数をf(x),状態yの好ましさを評価する多属性効用関数をh(y)とおくと,この意思決定者の振舞いは,形式的に次式で表現することができる。
| (1) |
この数理最適化のモデルは,生産システムの運用に関する「人の意思決定」を捉えるための自然な数理モデルの一つである。しかし,式(1)が与えられたもとで,解x*を得ること(求解)だけが「人の意思決定」の働きであるというわけではない(もしそうなら,多くの場合,「機械の意思決定」に任せればよいということになるだろう)。
「人の意思決定」が果たしている役割について考察するために,運用の意思決定とは,解くべき問題のクラスを定義し,状況に応じてそのクラスのインスタンスを構成し,ある解法を適用してそのインスタンスの解を得ること,と考える。すなわち,意思決定を,「クラス定義」,「インスタンス構成」,「求解」の3フェーズに分解して捉える。ここに,インスタンスとは,必要な関数の形状やパラメータの値が指定された具体的な問題,クラスとは,それらは未指定のまま構造のみが規定された抽象的な問題,である。意思決定者は,例えば,まず,クラス定義フェーズで,実行可能な選択肢の集合Dx,生産システムの状態を捉える特徴量空間Dy,状態についての選好h(y)などを想定し,次に,インスタンス構成フェーズで,生産システムの状態を観察することなどを通じてf(x)の具体的な関数形を把握した後,最後に,求解フェーズで,何らかの暗黙的なヒューリスティック解法によってx*を選択している,というわけである。実際には,人は,必ずしもそれらのフェーズを意識的に切り分けて段階的に進めているというわけではないが,運用の意思決定には,少なくとも,それら三つの機能が含まれていると考えられる。
運用の意思決定をこのようにフェーズ分けすると,それを人が担当することの意義を,「機械の意思決定」と対比しながら,フェーズ別に検討することが可能になる。まず,求解フェーズに限れば,多くの場合,数理最適化のためのアルゴリズムを利用できる「機械の意思決定」に分があると考えられる。しかし,まれに,「機械の意思決定」が苦手とする,ある種の難しい問題に対して,人の暗黙的なヒューリスティック解法が有効に機能することがある。次に,インスタンスの構成は,「機械の意思決定」では,センサなどで取得した情報を,クラスを規定するパラメータに代入することによって行われる。それに対して,「人の意思決定」では,対応するセンサが未設置の情報を五感で取得すること,ブラックボックス関数を主観的に評価すること,なども可能であり,それらが有効に働く可能性がある。最後に,クラス定義は,少なくとも現状では,「機械の意思決定」に任せることは困難であると考えられる。現実には,解くべき問題のクラス自体をゼロから定義する必要があるような場面はまれかもしれないが,現場の状況に応じて,クラスを適応的に再定義しながら対処していくことは珍しくない。例えば,状況によって,新たな打ち手を考える,普段は気に留めない特徴量を確認する,交渉によって制約条件を緩和する,などの行為は,解空間や目的関数,制約条件の変更につながるものであり,単なるインスタンスの調整ではなく,クラスの再定義とみなすことができる。
求解フェーズに限れば,囲碁の世界でも計算機が熟練者を凌駕するようになってきており17),生産システムの運用においても,「人の意思決定」が貢献できる余地は消え去りつつあると考えられる。インスタンス構成フェーズでは,例えば,上述の五感センシングは,IOT機器の普及によって,また,ブラックボックス関数の主観評価は,機械学習技術の発展によって,それぞれ「機械の意思決定」に侵食されてきている。したがって,(少なくとも当面の間)人に残ると予想される貢献の余地の大部分は,クラス定義フェーズにあると考えられる。
したがって,以下では,主にこのクラス定義フェーズにおける「人の意思決定」の働きに焦点をあてる。ただし,多くの場合,人は,このフェーズで,クラスの構造を明示的に定義しているわけではない。むしろ,無意識的,かつ暗黙的に,問題の捉え方を決めていると考える方が自然である。この問題の捉え方が,その人にとってのクラスの定義に相当することになる。そこで,この「人が,直面している問題状況をどのように捉えているか」を表すためのフレームワークとして,インタフェース,インタラクション,インセンティブの3軸からなる,問題状況の「認知フレーム」を導入する。
インタフェースとは,知覚,すなわち,状態の捉え方,についての人の認識である。これは,例えば,式(1)の数理最適化モデルでは,特徴量空間Dyの設定の仕方に対応する。インタラクションとは,実行可能な行為とその影響についての認識である。これは,式(1)では,選択肢集合Dxの設定の仕方や,選択肢の影響f(x)の捉え方ということになる。インセンティブとは,結果の好ましさについての認識であり,式(1)では,多属性効用関数h(y)にあたる。これらは,完全な形で外から与えられるものではなく,少なくとも部分的には,意思決定者自身が意識的,あるいは無意識的に選び取っていると考えるわけである。
ここまでは,意思決定状況として,「単一主体・静学的」の場合を想定してきた。文献16)も指摘しているように,意思決定状況が「複数主体」になると,主体間の戦略的な相互作用を考慮する必要が出てくる。これは,生産システムの運用を,(ゲーム理論の意味での)ゲームとして分析する必要が生じるということである。一方,「動学的」になると,意思決定を下した後,それを受けて生産システムの状態が変化し,そのもとで次の意思決定を行う,という具合に,意思決定の介入を受けながら変化する生産システムの状態遷移を考慮することが必要になる。そのための代表的な数理モデルとして,文献16)は,マルコフ決定過程(MDP)を挙げている。さらに,「複数主体・動学的」の場合は,例えば,MDPに複数の主体が介入する状況をゲームとして分析することになる。そうした状況を捉える数理モデルとしては,例えば,DecPOMDP18)などが挙げられる。このように,意思決定状況の分類によって,それを捉えるための数理モデルは異なる。しかし,後述するように,それらの状況における「人の意思決定」の働きやその効果は,上述の「単一主体・静学的」の場合と同様のフレームワークで捉えることができると考える。
2・3 計算科学と行動科学の相互補完による接近Fig.2に,対象とする生産システムの運用を模擬したシリアスゲームと,上述の「認知フレーム」によって,エージェントシミュレーション(計算科学的手法)とゲーミングシミュレーション(行動科学的手法)を接合し,それらを補完的に活用することによって,「人の意思決定」の働きやその効果を左右する要因を解明していく,著者らの研究アプローチの概要を示す。

Combined approach of behavioral and computational means towards understanding human control decisions through cognitive framework.
図の中央には,対象システムの運用を模擬したシリアスゲームが置かれている。これが,ゲーミングシミュレーションとエージェントシミュレーションに共通のプラットフォームになる。そして,その左側に,このゲームを実際の人にプレイしてもらうゲーミングシミュレーションが,右側に,計算機エージェントにプレイさせるエージェントシミュレーションがそれぞれ位置づけられている。シリアスゲームモデルの妥当性の確認・調整,計算機エージェントモデルの妥当性の確認・調整,「認知フレーム」についての仮説検証,などには,実際の「人の意思決定」を反映したデータがある程度は必要であり,それらの収集は,ゲーミングシミュレーションの側に委ねられる。一方,エージェントシミュレーションの側には,ゲーミングシミュレーションと比べて,一般に,実験回数を増やしやすく,「認知フレーム」の指定や変更も容易である,という強みがある。
したがって,本アプローチでは,それらを相互補完的に用いて,例えば,異なる「認知フレーム」のもとでの意思決定の性能を比較・分析することによって,適切な「認知フレーム」の特徴を明らかにし,その結果を「人の意思決定」の効果的な支援や教育・訓練のための手段,生産システム全体の性能向上や安定化のための制度設計,などにつなげていくことを目指す。
人による生産システムの運用は,大抵の場合,ある意思決定を反映させてシステムの稼働が進み,その状態が変化した後,次の意思決定が必要になる,というサイクルで進む,動的な意思決定プロセスになる。この「単一主体・動学的」の意思決定状況を表現するのに適した数理モデルの一つが,2・2でも触れた,MDPである(なお,例えば,セミマルコフ決定過程(SMDP)19)など,より一般的なモデルの方が適している場合も考えられるが,本稿では,簡単のため,通常のMDPで捉えられる状況を想定する)。このモデルを利用する場合,Fig.2の中心にあるシリアスゲームの裏に,対象生産システムの運用をモデル化したMDPが置かれることになる。
本稿のアプローチでは,意思決定者は,このMDPに直接,対峙するのではなく,その人の「認知フレーム」を介して認識した(主観的な)問題状況に直面していると考える。すなわち,裏にあるMDPは同じであっても,人によって直面している問題状況は異なり得るということであり,それはまた,客観的には等しい意思決定状況に置かれたときの人による振舞いの違い(の一端)をその「認知フレーム」の差異に基づいて説明しようということでもある。
Fig.3は,この「単一主体・動学的」の状況を捉える数理モデルの一例である。裏にあるMDPでのある時点tの状態,そこで取り得る行動の集合,それによって獲得する即時報酬がそれぞれSt,A,Rt+1であるのに対して,意思決定者が認識している状態,行動集合,即時報酬が

Single-agent dynamic model for capturing human decisions through cognitive framework.
このモデルに基づくエージェントシミュレーションでは,意思決定者を表す計算機エージェントとして,様々なモデルフリーの強化学習アルゴリズム20)を用いることができる。そうした計算機エージェントに与える「認知フレーム」は,指定に合わせて,直接,変更することができる。近年,深層強化学習技術の発展に触発されて,生産システムの分野でも強化学習の応用が活発化している21,22)。特に,Ouら23),Altenmüllerら24),Kuhnleら25)は,本稿のアプローチとは目的は異なるものの,強化学習エージェントに与える状態や即時報酬の定義を変更して,エージェントの性能を比較している。一方,このモデルに基づくシリアスゲームを利用したゲーミングシミュレーションの側では,被験者の頭の中にある主観的な問題状況の捉え方を直接,操作することは難しい。したがって,被験者に見せる情報,シリアスゲーム内で実行可能なアクションやそのタイミング,ゲームスコアの定義,などを,指定された「認知フレーム」に合わせて変更することで,間接的に制御することになる。そして,そのもとでの被検者の振舞いを行動科学的に分析していく。
なお,生産システムの運用が厳密には動的な意思決定プロセスであるとしても,近似的に,毎期の意思決定を独立に静学的な最適化問題として取り扱っている状況は多い。例えば,ローリングホライズンで生産計画を更新していくような状況はそれに相当する。また,Fig.3のモデルにおける意思決定者の方策をパラメータで規定し,当面,同じパラメータの値を使い続けるような状況では,適切なパラメータ値を決定する問題は静学的な最適化問題として捉えられる。例えば,在庫管理における発注点や補充点の決定問題はそれにあたる。このように,前節で導入した「単一主体・静学的」モデルは,生産システムの運用の意思決定を捉える上で全くの的外れというわけではない。
3・2 加熱炉前スラブヤード運用の事例Fig.3の「単一主体・動学的」モデルを適用した研究の一例として,製鉄所の加熱炉前スラブヤードを対象とした事例を紹介する26,27)。このスラブヤードは,上工程から送られてくるスラブを加熱炉に装入するまで保持しておくバッファの役割を果たしており,そこには,スラブを積み上げた置場が複数存在する。下に積まれたスラブを取り出すためには,その上に積まれているスラブを,一旦,取り除く必要があり,それぞれの置場は後入れ先出し(LIFO)のバッファとして捉えられる。スラブの置場間での移動(配置換え)や,加熱炉への装入は,1個ずつクレーンで行われる。各スラブには,寸法や材質などの属性と納期が付与されており,納期を守りながら,加熱炉やその下流の圧延工程から要求される条件をなるべく満たす順序で,スラブを装入していくことが求められる。また,そのために,事前に配置換えしておくことが有利に働くこともある。本事例の現場では,この装入と配置換えの最終的な意思決定は,クレーンオペレータに委ねられている。
類似のスラブヤードにおけるクレーン操作のスケジューリング問題に取り組んだ従来研究は数多く存在する。例えば,Tangら28,29),Singh and Tiwari30),Tang and Ren31),Cheng and Tang32),Tangら33)は,スラブの初期配置が与えられ,それ以降はスラブの到着がないという条件のもとで,スラブの配置換えと装入のスケジュールを検討している。また,Konigら34),Kimら35),Luら36),Rei and Pedroso37,38)は,新しいスラブの到着を考慮したもとで,同様の問題を扱っている。ただし,これらの従来研究は,最終的にはクレーンスケジューリングを自動化することを目指したものであり,クレーンオペレータの「人の意思決定」の性能を左右する要因を解明し,それを効果的に支援することを目指している本事例とは目的が異なる。
本事例では,このスラブヤード運用の意思決定を,人にプレイしてもらいやすいシリアスゲームに仕立てるために,その本質的な特徴を維持しつつ,なるべく単純化して,Fig.4のようにモデルした。
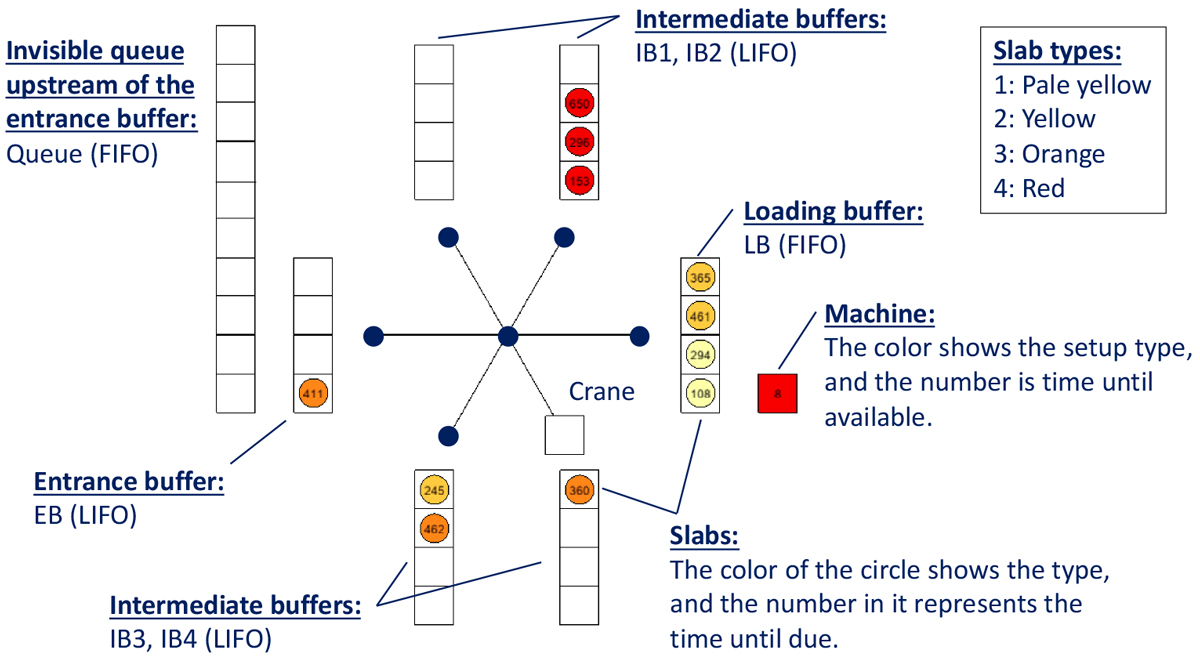
Simplified slab yard model utilized as the basis of the serious game.
このゲームモデルでは,加熱炉とその下流の圧延工程はグループ化され,架空の1台の機械として扱われている。そして,スラブヤードは,その機械と,いくつかのバッファ,そして1台のクレーンで構成されている。バッファは,受入バッファ,中間バッファ4個,および,装入バッファに分類され,さらに,受入バッファの前に,到着するスラブの待ち行列が置かれている。受入バッファと中間バッファはLIFO,装入バッファと待ち行列はFIFOである。また,待ち行列は無限容量,それ以外のバッファの容量は全て4個に設定されている。スラブは1個単位で確率的に到着し,待ち行列に入る。スラブの到着間隔は指数分布に従い,平均到着間隔(MTBA)はシミュレーションのパラメータとして扱われる。待ち行列内のスラブは,受入バッファに余裕があれば,所定のサイクルタイムで,FIFOで自動的に受入バッファに移される。
図中のスターグラフは,クレーンの軌道を表しており,その各葉ノードが,受入,中間,装入の各バッファに対応している。クレーンは,中央ノードからいずれかの葉ノードに移動し,その最上段のスラブを持ち上げ,中央ノードを経由して別の葉ノードに移動し,保持しているスラブをその最上段に降ろした後,再び中央ノードに戻る,というサイクルを繰り返す。この動作のサイクルタイムは一定である。
スラブには4個のタイプがあり,各スラブのタイプはランダムに指定される。機械が同じタイプのスラブを連続して処理している限り段取りは不要であるが,タイプを変更する際には段取りが必要であり,それには所定の時間がかかる。この段取り時間は,タイプを昇順に変更する場合よりも,降順に変更する場合の方が極端に長い設定になっている。スラブの機械での処理時間はタイプによらず一定である。装入バッファ内のスラブは,前のスラブの処理が完了し,もし段取りが必要ならそれも終えて,機械が空いたときに,FIFOで自動的に機械に移される。なお,スラブには納期が指定されており,もしそれまでに機械に装入できなければ,納期遅れに比例したペナルティがかかる。ゲームスコアは,機械にスラブを装入する毎に得られる固定額のボーナスから,この納期遅れペナルティを減じた値である。
このシリアスゲームを,MTBAの値と「認知フレーム」を変化させて,強化学習エージェントにプレイさせる実験を行ってきた。結果の詳細は文献26,27)に譲るが,これまでにいくつかの興味深い傾向が得られている。例えば,「認知フレーム」のインタフェースを介してエージェントに入力する,生産システムの状態を表す特徴量について,必ずしもそれを増やせばよいというわけではないことや,効果的な特徴量の組合せがMTBAの値に依存すること,などである。こうした傾向を,ゲーミングシミュレーションで検証することや,それをクレーンオペレータの教育・訓練,作業支援ツールの開発などに役立てることが今後の課題である。
生産システムの運用には,一般には,複数の意思決定者が関与していることが多い。この場合,2・2で指摘したように,生産システムの運用を(ゲーム理論の意味での)ゲームとして分析する必要が生じる。異なる事業体で構成されるサプライチェーンなどの場合は,各事業体を運用する担当者はそれぞれ自社利益の最大化を目指すと考えられるため,意思決定者間に利害対立が生じ得る。そのため,ゲーム理論分析の必要性は理解されやすい39,40)。しかし,例えば,同一工場の部署間などでは,少なくとも大きな利害対立は無さそうなので,ゲームとして分析することの有用性を訝る向きもあるかもしれない。しかし,どの部署の担当者も工場全体の利益最大化を目指してしていたとしても,それぞれの意思決定は,主に自部署の状態についての限られた情報のみに基づいて下されることになるため,結果として,予期せぬ合成の誤謬につながってしまうことがある。そうした状況の分析には,やはりゲーム理論の視点が有用になる。
例えば,3・2で取り上げたスラブヤードに複数のクレーンがあり,それらをそれぞれ独立に異なる意思決定者が操作しているとする。このとき,操作者間に大きな利害対立はなかったとしても,取得できる情報や保持している知識には違いがあると考えられるため,ゲーム理論的な状況が現れる。このような「複数主体・動学的」の状況は,例えば,Fig.3のモデルを,システムの状態遷移に単一ではなく複数のエージェントが介入する図式に拡張することによって捉えられる。その場合,エージェントシミュレーションで,上と同様に,強化学習エージェントを利用しようとすると,マルチエージェント環境での強化学習アルゴリズムが必要になる。例えば,Oroojlooyjadidら41)は,2・1で紹介したビールゲームにマルチエージェント強化学習を適用している。また,Chenら42)は,マルチエージェント強化学習で,ランダムに発生する荷物のピックアップ要求のディスパッチング方策の獲得を試みている。
一方で,3・1でも述べたように,各エージェントの方策をパラメータで規定し,そのパラメータ値を決定する問題を考えると,この動学的な状況を,静学的な意思決定問題として扱うことが可能になる。以下では,これにあたるような「複数主体・静学的」の場合を考えていく。この場合の意思決定状況は,外形的には標準型や展開型のゲームとしてモデル化することができる16)。各意思決定者がゲームのプレイヤであり,その意思決定者の方策を規定するパラメータの値が戦略,そのパラメータ値で規定される方策で生産システムを運用したときに獲得できる利益の期待値が利得,などということになる。
この利得の値は一般には未知であり,指定された戦略の組合せのもとで生産シミュレーションを実施して各プレイヤの利益の標本値を取得し,それに基づいて推定する必要がある。計算科学の側では,その推定値に基づいて,ナッシュ均衡などのゲームの解概念を求めることになる。ただし,均衡を同定する直接的な方法は,プレイヤ数や戦略数など,ゲームの規模が小さくないと適用しづらい。より一般的な場合には,例えば,進化ゲーム43)などに基づく数値計算が必要になる。そこで,著者らも,効率的な均衡探索のための数値計算アルゴリズムを検討している44)。一方,行動科学の側からは,例えば,Erev and Roth45)が,同じゲームを繰り返しプレイする人の学習過程が,強化学習アルゴリズムの挙動でよく説明できることを示している。
4・2 食品サプライチェーン運用の事例「複数主体・静学的」モデルに基づく研究の一例として,製鉄所からは離れるが,食品サプライチェーンの制度設計を検討した事例46)を紹介する。2015年の国連サミットで採択されたSDGsの中に食品廃棄半減の目標が掲げられたこと,食品サプライチェーンの持続可能性向上が急務になっていること,などを受けて,食品の流通過程でのロス削減が課題となっている。一方,我が国の食品業界では,「1/3ルール」と呼ばれる商習慣が広く根付いている。これは,食品の製造から賞味期限までの期間を3等分し,1/3の時点に小売店への納品期限を,2/3の時点に消費者への販売期限を,それぞれ設定するものである。納品,あるいは,販売されずにそれらの期限を超えた食品は廃棄されてしまうため,この商習慣が流通過程で生じる膨大な食品廃棄の主な原因になっていると指摘されてきた。しかし,2013年に行われた,これらの期限を緩和する社会実験では,廃棄が削減された食品ばかりではなく,逆に,小売店での廃棄が微増した食品もあった。
食品サプライチェーン全体を一つの生産システム,それを構成する食品メーカーや小売店など(の担当者)を意思決定者,発注,廃棄,出荷,値決めなどの方策を規定するパラメータ値を決定変数,などと考えると,このサプライチェーンの運用にまつわる意思決定状況は,上述の「複数主体・静学的」モデルに当てはめることができる。このとき,納品期限や販売期限を規定する商習慣は,取り得る方策の自由度を縛るものであり,「認知フレーム」(のインタラクション軸)に外から制限を加えていると考えることができる。このように考えると,本稿のアプローチは,「認知フレーム」への外からの介入やその設計,すなわち,生産システムの制度設計の検討にも適用することができる。
Fig.5に,本事例で,牛乳のサプライチェーンを対象に,納品期限や販売期限の影響を検討するために用いたゲームモデルの概要を示す。

Game model between manufacturer and retailer in milk supply chain, where their payoffs are evaluated through running simulation.
図中のメーカーと小売店がゲームのプレイヤである。メーカーの戦略空間は,出荷順(∈{FIFO,LIFO}),古い牛乳への値付け(∈{Regular,Discounted}),安全在庫の水準(∈{Low,High})の直積,小売店の戦略空間は,棚出し順(∈{FIFO,LIFO}),古い牛乳への値付け(∈{Regular,Discounted}),安全在庫の水準(∈{Low,High})の直積,となっている。これに対して,下に示す,統計的なゲーム理論分析の手順を適用した。
Step 1: 全ての戦略の組合せを調査し終えていれば,Step 3に進む。そうでなければ,未調査の戦略の組合せを一つ選択し,Step 2に進む。
Step 2: 選択された戦略の組合せのもとで生産シミュレーションを所定の回数実施し,両プレイヤの利益額の標本値を得る。Step 1に戻る。
Step 3: 一方のプレイヤの戦略毎に,他方のプレイヤの全戦略の利益額の標本値間に多重比較を適用し,前者のプレイヤの各戦略に対する,後者のプレイヤの「統計的な」最適反応を特定する。
Step 4: 互いに「統計的な」最適反応になっている戦略の組合せを「統計的な」ナッシュ均衡と呼び,それを抽出する。
廃棄量を支配する最大の要因は,メーカーの出荷順であり,廃棄量を減らすためには,それが(LIFOではなく)FIFOになることが望ましい。結果の詳細は文献46)に譲るが,これまでに確認できた,興味深い傾向の一つとして,「1/3ルール」を課すことが,メーカーがLIFOで出荷する均衡を消す効果を持つことがあることがわかった。これは,「1/3ルール」が廃棄量を増やすだけでなく,減らす方向にも働くことがあるということである。なお,これは,必ずしも「1/3ルール」を維持するべきということではない。それを緩和する際には,他の条件との兼ね合い次第では,期待とは逆の効果を生じ得るので,注意が必要であるということである。また,こうした計算科学的な検討と並行して,行動科学的な検討にも取り組んでいる。具体的には,牛乳のサプライチェーンにおけるメーカーと小売店をプレイヤとしたシリアスゲームを開発し,ゲーミングシミュレーションを進めている47,48)。
4・3 スケジューリングとゲーム理論最後に,今度の展望を兼ねて,生産スケジューリングとゲーム理論(および,メカニズムデザイン)とを掛け合わせた研究領域に簡単に触れておこう49–51)。これは,スケジューリング問題に登場する機械やジョブを,意思決定主体とみなすものである。例えば,複数の(中小の)製造企業が機械を提供し合うクラウドマニュファクチャリングのような環境は,各機械(の所有者)を意思決定主体としたモデルで捉えられる。また,顧客が,製品の納期と支払額の間にトレードオフのある選好を持っているような状況は,ジョブ(を依頼した顧客)を意思決定主体としたモデルで表される。なお,この後者の状況は,2・1で言及した,顧客をエージェントとして扱う,顧客包含型モデルになっていることにも注意したい。このように,顧客包含型モデルは,サービス産業だけではなく,製造業の生産システムにおいても,有効に活用できる可能性がある。
このような状況では,生産スケジュールの作成者は,(モデルの中で機械やジョブとして表されている)各意思決定者から,機械の使用原価や,ジョブの納期別の支払い意思額といった私的情報を引き出す必要がある。一方,意思決定者の側には,なるべく自分に有利になるように,申告する情報を操作しようとする誘引が働く。すなわち,意思決定者の間に,何を申告するかを戦略としたゲームが現れる。このゲームのルール(すなわち,メカニズム)を,例えば,全ての意思決定者の正直申告の組合せが支配戦略均衡になるように定めること,などがここでの問題になる。なお,本稿で導入した「認知フレーム」のインタフェース,インタラクション,インセンティブは,このメカニズムを規定する設計変数のフレームワークとして捉えることもできる。
これに対して,例えば,(いくつかの条件のもとで)正直申告を促すことのできる代表的なメカニズムとして,VCGメカニズム52–54)が知られている。著者らは,これを製造業の生産システムの運用に応用することを試みている55,56)。また,類似のアプローチは,サービス分野の予約システムにも応用されている57,58)。
本稿では,生産システムに「人の意思決定」が埋め込まれていることを指摘した上で,それを運用していく上での「人の意思決定」の役割やその効果を左右する要因を解明していくための,計算科学的,および,行動科学的なアプローチについて,著者らのグループのものを中心に述べてきた。今後,生産システム運用の自動化や知能化は否応なしに進展していくだろう。しかしその一方で,「人の意思決定」を完全に排除することは,(少なくとも当面は)難しいものと考えられる。その結果,自動化・知能化の進む生産システムに「人の意思決定」を適切に埋め込むことの重要性と困難性はますます増していくと予想される。そうした課題への挑戦に,本稿で述べた考え方やアプローチが少しでも貢献できることを期待したい。