Determination of Distribution and Structures of Manganese Aqua and Chloro Complexes in Hydrochloric Acid Solutions at 298 K

Abstract

As part of the research on metal aqua and chloro complexes in hydrochloric acid solutions, which is one of the fundamentals in the development of marine resource and the hydrometallurgical process, we have investigated distributions and structures of metal aqua and chloro complexes have been analyzed. The adsorption behavior of manganese species on anion exchange resin was investigated to understand the approximate distribution of manganese aqua and chloro complexes and found that anionic manganese complexes are formed in the concentrated hydrochloric acid solutions. The UV-vis absorption spectra of the manganese species in hydrochloric acid solutions at 298 K were collected for analysis of complex formation behavior. It was determined that the number of complex species to be three using the first derivative test. A series of UV-vis absorption spectra was analyzed using the thermodynamic model fitting analysis. As the results, the distribution of manganese aqua and chloro complexes and their stability constants were determined. The XANES and EXAFS spectra of individual species were obtained dividing a series of the spectra by the distribution of complexes in matrix form. The individual EXAFS spectra were examined using FEFF fitting analysis. The three manganese aqua and chloro complexes are [Mn^II(H₂O)_x]²⁺ (x = 4, 5, or 6), [Mn^IICl₂(H₂O)₄]⁰, and [Mn^IICl₄]²⁻. Only [Mn^IICl₂(H₂O)₄]⁰ was confirmed to have an octahedral structure. The structures of the rest of complexes were not clearly determined.

1. 緒言

酸性水溶液中の金属イオンの錯体分布は，湿式法による金属の分離，製錬法の構築，確立に欠くことのできない重要な知見である。HCl水溶液中では，金属イオンごとにClの配位挙動が異なるため，例えばイオン交換反応を利用して金属イオンを分離するのに，非常に便利が良い¹⁾。

従来，塩酸水溶液中の金属塩化物錯体分布は，Cl配位数が0，1，2，3，...，のように1ずつ増加するモデルに基づいて解析されてきた^2,3,4,5,6)。著者らにより開発された解析法によれば，平衡状態ではCl配位数が飛び飛びの値を取り，その組み合わせが金属イオンごとに異なる結果が報告された^7,8,9)。ただし，Cr^III塩化物錯体では，平衡状態では観察されない[Cr^IIICl₂(H₂O)_x]⁺が水和過程で生成されており⁷⁾，錯形成過程においてはCl配位数が1ずつ変化する可能性が示唆される。解析に使用する試料は，過塩素酸でイオン強度を調整した溶媒を用いることが多い¹⁰⁾。過塩素酸–HCl混酸水溶液中では，単純なHCl水溶液中に比較してCl配位の駆動力であるCl活量が大きくなるため，同じCl濃度でも生成される金属塩化物錯体が異なる^5,10)。錯安定度定数とCl活量を正しく把握できれば，異なる酸水溶液中でも実際の錯体分布を再現可能である。しかし，過塩素酸–HCl混酸水溶液中のCl活量の詳細は明らかにされておらず，単純なHCl水溶液中の錯体挙動の推測には注意を要する。これまでのイオン交換反応や電解挙動などの錯体が関与する反応では，単純なHCl水溶液を使用していても，イオン強度を調整した試料を用いて解析した実際とは異なる分布を基に考察を行い，研究開発がなされてきた。

そこで，金属イオンへのCl配位挙動について単純なHCl水溶液を用いて調査し，現実的な錯安定度定数および金属塩化物錯体分布を求めることが重要であると考え，これまでにCr^{III 7)}，Fe^{III 8)}，Co^{II 9)}の塩化物錯体分布について研究し，報告してきた。研究の過程で，熱力学モデル最適化法を開発した^{7,8,9,11,12,13,14,15)}。熱力学モデル最適化法で得られる錯体分布を応用して，一連の電磁波吸収分光を理論的に錯体個別の吸収スペクトルに分解できるようになった。その結果，紫外可視吸収分光解析結果をX線吸収分光解析に応用し，解析の妥当性を相互に補完しあうという新しい解析法の開発につながった^7,8,9,14,15)。著者が独自に開発した解析法を遷移金属全般に応用してHCl水溶液を中心に錯体分布を調査し，錯体が関わるイオン交換，溶媒抽出，電解などの反応の効率改善に寄与する基礎的知見を提供することを目的に研究を展開している。

本研究で扱うMn^II塩化物錯体の分布と構造は，これまでにもX線/紫外可視吸収分光^3,16)やX線回折¹⁷⁾により解析されている。従来の解析では，室温での最大Cl配位数は2とされている。Cl配位数が3である錯体は300°Cまでは確認できず，より高温，高圧の条件で初めて生成する¹⁶⁾。しかし，Mn^IIイオンは室温でCl濃厚領域において陰イオン交換樹脂に若干吸着する挙動が報告されており¹⁸⁾，室温で最大Cl配位数を2とする報告とは矛盾する。陰イオン交換樹脂への吸着は，陰イオン錯体の存在を示唆するが，最大Cl配位数が2では陽イオン錯体，中性イオン錯体しか生成しない。陰イオン交換挙動を合理的に説明するためには，Mn^II塩化物錯体分布を改めて明らかにする必要がある。

ところで，HCl水溶液中の金属イオンの塩化物錯体分布は，金属製錬だけではなく，深海における金属イオン分布のシミュレートにも必要な知見である¹⁹⁾。海底熱水鉱床，コバルトリッチクラスト，レアアース泥，マンガン団塊などの海洋鉱物資源は，陸上の鉱山に替わる資源として半世紀以上にわたって注目されている²⁰⁾。コバルトリッチクラスト，レアアース泥，マンガン団塊は，海底熱水鉱床から噴出した有価金属を含む熱水が深層海流などにより周辺に分布，沈殿した結果であると推測可能だが，成長機構などは明らかになっていない。マンガン団塊の成長速度は100万年に1 mmとも言われており，決して無限の資源ではない。そこで，マンガン団塊の成長や分布の機構を解明し，深海における金属資源の分布をシミュレートできれば，新たな海洋鉱物資源発見の可能性が大きくなる。

以上の背景から，本研究は，HCl水溶液中の金属イオンの塩化物錯体分布研究の一環として，Mn^IIの塩化物錯体分布を調査する。本研究で得られた知見は，製錬技術開発だけではなく，資源開発にも核となる基礎的知見を提供し，持続可能社会の実現に大きく貢献する。

2. 解析方法概要

Fig.1に解析の流れを示す。紫外可視吸収分光を測定し，第一導関数検定^7,13)により錯体種の数を決定して，熱力学モデルとして錯形成反応を仮定する。錯体種の数と配位可能なCl配位数範囲から，複数の錯体形成反応式が構築される。Mn^IIイオンのHCl水溶液からの陰イオン交換挙動を調べ，陰イオン錯体生成の可否を確認し，不適切な熱力学モデルを解析対象から外す。熱力学モデル最適化法^{7,8,9,11,12,13,14,15)}により，紫外可視吸収分光を再現するように錯体形成反応式の錯体安定度定数などの熱力学パラメータを最適化する。この時，誤差をできるだけ小さく紫外可視吸収分光を再現するものが，求める熱力学モデルの候補である。熱力学モデル最適化法は数学的処理であるため，誤差が最小のものが適切であるという保証はない。熱力学モデル最適化法により求めた熱力学パラメータを基に，錯体個別のX線吸収端構造（XANES：X-ray absorption near edge structure）スペクトルと広域X線微細構造（EXAFS：Extended X-ray absorption fine structure）スペクトルを求め，錯体構造解析を行う。錯体分布を導出する熱力学モデルではCl⁻配位数のみを仮定し，H₂O配位数は考慮しない。一方，構造解析で使用する構造モデルでは，Cl⁻配位数に加えてH₂O配位数を仮定して錯体をより具体化する。

Fig. 1.

Analysis flow of determination of distribution and structures of Mn^IICl_n complexes in HCl solutions.

本研究で扱う解析で最も重要な点は，紫外可視吸収分光の熱力学モデル最適化法により求めた錯体分布を使用して，錯体個別のXANESスペクトルとEXAFSスペクトルを求め，構造解析することにある。同じ電磁波吸収分光である紫外可視吸収分光と，XANESスペクトルとEXAFSスペクトルの元となるX線吸収分光において，錯体分布は共通であるために可能になる解析手法である。観察されたすべての吸収分光を合理的に説明できる熱力学モデルと錯体構造モデルの組み合わせが，実際の錯体分布と構造を再現する最も確度の高いモデルであると考えられる。したがって，紫外可視吸収分光とX線吸収分光の錯体分布を介した関係性から，EXAFSスペクトルを用いる構造解析²¹⁾は熱力学モデル妥当性の判断基準として使用可能である。

3. 実験方法

3・1　陰イオン交換挙動

HCl水溶液からのMn^IIイオンの陰イオン交換体への吸着挙動をバッチ法で調べた²²⁾。試料の作製には，富士フィルム和光純薬株式会社から購入した特級Mn^IICl₂·4H₂O，マンガン標準液（1000 mg·dm⁻³），特級HCl，蒸留水をイオン交換した純水（比抵抗17.8 MΩ·cm）を用いた。陰イオン交換体には，三菱ケミカル株式会社製強塩基性陰イオン交換樹脂DIAION SA10^TMを用いた。

Mn^IIイオン濃度を90 mg·dm⁻³とし，HCl濃度が2.0，5.0，8.0，10.0 mol·dm⁻³である水溶液を以下の手順で作製した。Mn^IICl₂·4H₂Oを純水に溶解して作製した4500 mg·dm⁻³–Mn^II水溶液1 cm³と所定量のHCl溶液を混合し，50 cm³にメスアップした。試料水溶液調製後，3日間25°Cに保持した後，陰イオン交換樹脂と接触させた。陰イオン交換樹脂は，遠心分離機を用いて回転数3000 r.p.m.で10分間水分を分離して²²⁾，試料水溶液との振盪接触に備えた。

試料水溶液15 cm³と陰イオン交換樹脂5 cm³を共栓三角フラスコ内で混合し，恒温振盪槽中で25°C，120 r.p.m.で1時間振盪接触させた。30~40分間の振盪接触で試料水溶液中の金属濃度は一定となる²²⁾。振盪接触後，濾過して水溶液と陰イオン交換樹脂を分離した後，試料水溶液中のMn^IIイオン濃度を誘導結合プラズマ発光分光分析（ICP-OES：Inductively coupled plasma optical emission spectrometry）で定量した。標準溶液は，Mn^II濃度を0，5，10，20 mg·dm⁻³，HCl濃度を1 mol·dm⁻³に調整した。試料水溶液を10倍に希釈し，HCl濃度を標準溶液と同じ1 mol·dm⁻³に調整して分析に供した。

1時間の振盪接触後の分配係数$K_{{\text{D}}_{\text{1h}}}$は次式により求めた。

  

$$K_{{\text{D}}_{\text{1h}}}=\frac{\overline{c_{\text{1h}}}}{c_{\text{1h}}}=\frac{\frac{V_{\text{s}}\left(c_{\text{initial}}-c_{\text{1h}}\right)}{V_{\text{r}}}}{c_{\text{1h}}},$$(1)

ここで，C_initialとC_1hは，接触前と1時間の振盪接触後の水溶液中のMn^IIイオン濃度である。上線は樹脂相中の濃度であることを示す。V_sとV_rは，それぞれ水溶液と樹脂相の容積を示す。

3・2　紫外可視/X線吸収分光測定

3・2・1　測定試料準備

紫外可視/X線吸収分光を測定する試料水溶液の組成をTable 1に示す。Mn^IIイオン濃度は，それぞれの測定に最適な濃度を選択した。Clイオン濃度範囲を0.5 mol·dm⁻³から11.5 mol·dm⁻³とした。試料作製後，10日以上25°Cに保持してから測定を行なった。

Table 1. The compositions of the sample solutions. The Cl concentrations were assessed as the sum of Cl from HCl and MnCl₂∙4H₂O. The concentrations of HCl were analyzed using neutralization and those of Mn^II were determined by mass of charge.

UV-vis absorption			X-ray absorption
Total Cl / mol∙dm−3	Total MnII / mol∙dm−3	Path length, lUV-vis / mm	Total Cl / mol∙dm−3	Total MnII / mol∙dm−3	Path length, lXAFS / mm
0.51	0.25	50	1.86	0.35	1.0
1.08	0.25	50	3.02	0.35	0.5
1.66	0.25	50	4.18	0.35	0.5
2.24	0.25	50	5.34	0.35	0.5
2.82	0.25	50	6.46	0.35	0.5
3.40	0.25	50	7.56	0.30	0.5
3.98	0.25	50	8.72	0.30	0.3
4.56	0.25	50	9.18	0.30	0.3
5.14	0.25	50	9.47	0.30	0.3
5.72	0.25	50	10.0	0.30	0.3
6.30	0.25	50	10.6	0.30	0.3
6.88	0.25	50	11.0	0.30	0.3
7.46	0.25	50	11.2	0.30	0.3
8.04	0.25	50
8.62	0.25	50
8.20	0.25	50
9.78	0.25	50
10.3	0.25	50
10.9	0.25	50
11.5	0.25	50

3・2・2　紫外可視吸収分光測定

紫外可視吸収分光測定は，日本分光株式会社製紫外可視近赤外分光光度計V–770を用いて測定した。ベースライン補正とダーク補正を実施し，光路長は50 mmとした。ベースライン補正には，測定試料と同じ塩素濃度でMn^IIイオンを含まない水溶液を用いた。190 nmから1400 nmの範囲で分解能1 nmで5回測定し平均を求めた。Cl濃度変化に伴ってスペクトルが変化する範囲である312 nmから610 nmを解析対象とし，波長から波数へ変換した。波数範囲は16400 cm⁻¹から32000 cm⁻¹で，分解能は200 cm⁻¹である。変換の際，吸収aは3次スプラインによる内挿により補正した。解析の際，光路長lを考慮しなくて済むように，吸収を光路長で除し，モル吸光係数εとモル濃度cの積εcを使用する。

  

$$\begin{array}{l}\text{Beer-Lambert law:}a=\epsilon cl,\\ \therefore a^{\prime }=\frac{a}{l}=\epsilon c\end{array}$$(2)

Mn^II塩化物水溶液のモル吸光係数とモル濃度の積$\epsilon c_{{\left[{\text{Mn}}^{\text{II}}{\text{Cl}}_n\right]}^{2-n}}$をFig.2に示す。吸収は可視光域にあるが，吸収はFe^{III 8,13)}やCu^II錯体^11,14)に比較して非常に小さく，肉眼での確認は難しい。25000 cm⁻¹，28000 cm⁻¹，30000 cm⁻¹付近の吸収は，Cl濃度が濃くなるにつれて低波数側にシフトする。6 mol·dm⁻³以上になると，31500 cm⁻¹付近に，10 mol·dm⁻³以上になると23500 cm⁻¹付近に吸収が現れる。以上の吸収の特徴の変化から，複数の錯体が存在することが示唆されるが，定性的解析では錯体種の数を推定することは難しい。

Fig. 2.

The product of the molar attenuation coefficient and the molarity of Mn^IICl_n as functions of wavenumber. (Online version in color.)

3・2・3　X線吸収分光測定

Fig.3に得られたXANESスペクトルとEXAFSスペクトルを示す。MnのK吸収端のXAFSスペクトルはPhoton FactoryのビームラインBL-9Cを使用して透過法で測定した。直径15 mmまたは20 mmの円を切り抜いた厚さ1.0 mm，0.5 mm，0.3 mmの硬質塩化ビニル製の板に，窓材として厚さ25 µmのポリイミド膜を両面にはり，試料セルとして用いた。試料セルの厚さは光路長に相当する。入射X線は，Si(111)を利用した二結晶分光器により単色化される。入射X線と透過X線測定イオンチェンバー内は，それぞれN₂，15%Ar–N₂に調整した。

Fig. 3.

X-ray absorption spectra of manganese aqua and chloro complexes in hydrochloric acid solutions. The XANES spectra (a) and the EXAFS spectra (b). (Online version in color.)

XANESスペクトルのホワイトライン強度は，Cl濃度が濃くなるにつれて弱くなっている。この傾向はこれまでに報告した遷移金属塩化物錯体でも観察されている。プレエッジピークの強度は徐々に強くなっているが，形状はほとんど変わらない。Fe^III塩化物錯体⁸⁾とCo^II塩化物錯体^9,12)の場合は，Cl濃度が濃くなるにつれてプレエッジピーク強度は非常に強くなり，錯体構造の対称性が悪くなることを示唆したが，Mn^II塩化物錯体構造の対称性に大きな変化はない可能性を示す。

波数が10 Å⁻¹以上のEXAFSスペクトルは，S/N比が悪い。そこで，スペクトル品質が良好な3 Å⁻¹から9 Å⁻¹の範囲について構造解析を試行する。

XANESスペクトル，EXAFSスペクトルから判断できることは，複数のMn^II塩化物錯体が存在することであり，どのような錯体が生成するのかは，熱力学モデル最適化法を基に行う解析を通して解析する。

4. 解析および考察

4・1　Mn^IIイオンの陰イオン交換樹脂への吸着特性

第2章で説明した熱力学モデル最適化法^{7,8,9,11,12,13,14,15)}は純粋に数学的処理である。得られる解析結果を確度の高いものとするためには，錯体が関与する実際の反応を観察・検証する必要がある。本節でMn^IICl_nの陰イオン交換樹脂への吸着挙動を調査し，錯体分布の概要を把握する。

試料水溶液と陰イオン交換樹脂の接触前後のMn^IIイオン濃度をFig.4上部に，分配係数$K_{{\text{D}}_{\text{1h}}}$を下部に示す。溶離法で解析されたMn^IIの陰イオン交換挙動¹⁸⁾より分配係数は小さいが，傾向は一致している。

Fig. 4.

Anion-exchange behavour of manganese species in hydrochloric acid solutions. Adsorption of manganese species demonstrated at the top and the distribution coefficient obtained in the present study and by Kraus and Moore¹⁸⁾ at the bottom. The average of manganese species in the initial solutions is displayed as the dashed green line. The green band along the average line in the top figure indicates the deviations from the average. The determination limit of distribution coefficient is displayed in the bottom figure. (Online version in color.)

バッチ試験における初期水溶液中のMn^IIイオン濃度は90 mg·dm⁻³で同一のはずだが，図に示すように実測値の平均は95 mg·dm⁻³で，およそ3.5%のバラツキがある。分析値の有意差が5%以上と仮定すると，分配係数$K_{{\text{D}}_{\text{1h}}}$決定の下限は0.05であると考えられる。2 mol·dm⁻³–HCl中の分配係数$K_{{\text{D}}_{\text{1h}}}$は0.02から0.1であると示されているが，決定下限と同等であること，5 mol·dm⁻³–HCl中では吸着が認められないことを考慮すると，2 mol·dm⁻³–HCl中でも吸着しないと判断できる。一方，8 mol·dm⁻³以上のHCl水溶液中では，Mn^IIイオンが陰イオン交換樹脂に吸着し，HCl濃度が濃い方がより吸着する傾向が認められる。従って，Mn^IIは5 mol·dm⁻³以下で陰イオン錯体を生成せず，濃厚HCl水溶液中で生成する。さらにHCl濃度が濃くなるにつれて陰イオン錯体の割合が増加する傾向があると結論できる。

従来のMn^II塩化物錯体の室温での最大Cl配位数は2であると報告されているが¹⁶⁾，Fig.4に示す陰イオン交換挙動から，Cl配位数が3以上である陰イオン錯体の生成が確認できた。

4・2　錯体分布解析

4・2・1　錯体種の数の決定 ─ 第一導関数検定 ─

第一導関数検定^7,13)は，Fig.2に示した一連の紫外可視吸収分光の行列表現A′の特異値分解により得られるユニタリ行列の列ベクトルの数学的滑らかさを比較して，成分数を決定する方法である。A′は式（2）で定義したa′を要素に持つ行列である。列ベクトルの順位は成分数を表す。各列ベクトルの滑らかさを反映する要素の差分商の総和を成分数の関数としてプロットしたものが，Fig.5である。

Fig. 5.

The results of the first derivative test. (Online version in color.)

成分数3から4にかけて，差分商の総和が急激に大きくなる。このことは，ユニタリ行列の4列目，随伴行列の4行目以降は測定誤差等を表現するためのベクトルであり，A′の再現には不要であることを意味する。それぞれの行列の1列目から3列目までと1行目から3行目のベクトルを用いることでA′を適切に再現できることは，考慮している系において3つのスペクトルの異なる錯体種を仮定して解析することができる。

4・2・2　錯体分布解析 ─ 熱力学モデル最適化法 ─

（1）熱力学モデルの構築

熱力学モデルとして式（3a）に示す錯体形成反応式を仮定すると，Cl配位数nの錯体の安定度定数β_nは式（3b）のように表される。

  

$${\text{Mn}}^{\text{II}}+n{\text{Cl}}^{-}={\left[{\text{Mn}}^{\text{II}}{\text{Cl}}_n\right]}^{2-n},$$(3a)

  

$${\beta }_n=\frac{a_{{\left[{\text{Mn}}^{\text{II}}{\text{Cl}}_n\right]}^{2-n}}}{a_{{\text{Mn}}^{\text{II}}}\cdot a_{{\text{Cl}}^{-}}^n}=\frac{{\gamma }_{{\left[{\text{Mn}}^{\text{II}}{\text{Cl}}_n\right]}^{2-n}}}{{\gamma }_{{\text{Mn}}^{\text{II}}}\cdot {\gamma }_{{\text{Cl}}^{-}}^n}\cdot \frac{m_{{\left[{\text{Mn}}^{\text{II}}{\text{Cl}}_n\right]}^{2-n}}}{m_{{\text{Mn}}^{\text{II}}}\cdot m_{{\text{Cl}}^{-}}^n},$$(3b)

ここで，aは活量，γは活量係数，mは質量モル濃度を表す。式（3b）を用いてβ_nを変数として質量モル濃度で錯体分布を算出できる^{7,8,9,11,12,13,14,15)}。得られた錯体分布を容量モル濃度に変換し，式（5）で使用する錯体分布行列Cを求める。各イオン種の活量係数は，Debye–HückelモデルとPitzerモデルを組み合わせた経験式¹³⁾を用いて，中性イオンの活量係数はSetchénowモデル²³⁾で算出する。

解析に使用する熱力学モデルを構築するためには，錯体種の数とCl⁻が配位可能な配位数の範囲を決定しておく必要がある。錯体種の数は，前項で3種類と決定した。配位数の範囲は，MnCl₂·4H₂OのCl濃度が0.01 mol·dm⁻³である水溶液への溶解の様子とShannonによるイオン半径²⁴⁾から推定する。

MnCl₂·4H₂Oは0.03 mol·dm⁻³–Clである水溶液へ完全に溶解した。Cl濃度は0.03 mol·dm⁻³で，塩化物錯体を形成するほどに大きくはない。すなわち，Cl希薄領域では，Mn^IIイオンはCl配位数0である水和錯体として存在していると判断した。Cl⁻とMn^IIのイオン半径と半径比についてTable 2にまとめた。Cl⁻は配位数6の場合のイオン半径を，配位数4と8の錯体の限界半径比の算出にも使用した。配位数4，8の場合のCl⁻のイオン半径は報告されていない。配位数8の場合，Cl⁻とMn^IIのイオン半径比Rは限界半径比の範囲から外れており，8配位は困難であることが分かった。配位数4，6の場合は，Rは限界半径比範囲内におさまっている。そこで，可能な最大Cl配位数を6とした。

Table 2. Ionic radii of Cl⁻ and Mn²⁺ and their radius ratios²³⁾.

Ion	Coordination number	Ionic radius, r / pm	$R=\frac{r_{{\text{Cl}}^{-}}}{r_{{\text{Mn}}^{2+}}}$	Critical radius ratio
Cl−	(6)	181	—	—
Mn2+	4	66	2.742	2.414 < R < 4.449
	6	83	2.181	1.366 < R < 2.414
	8	96	1.885*	R < 1.366

*The value of R is out of critical radius ratio.

前項の結果からCl⁻配位数が異なるMn^II塩化物錯体が3種類存在する。式（3a）から導出されるnの異なる3つの錯体形成反応式を熱力学モデルとして解析に使用する。3つのCl⁻配位数をn₁，n₂，n₃とし，それぞれの熱力学モデルを（n₁n₂n₃）モデルとして記述する。可能性のある熱力学モデル（n₁n₂n₃）を式（4）に列挙する。ただし，第4・1節で考察したように，Mn^IIは濃厚HCl水溶液中で陰イオン錯体を形成することが分かっている。そこで，陰イオン錯体を含まない(012)モデルを解析から除外する。

  

$$\begin{array}{l}\sout{\left(012\right)},\left(013\right),\left(014\right),\left(015\right),\left(016\right),\\ \left(023\right),\left(024\right),\left(025\right),\left(026\right),\\ \left(034\right),\left(035\right),\left(036\right),\left(045\right),\left(046\right),\left(056\right)\end{array}$$(4)

（2）熱力学モデルの最適化

物質による電磁波の吸収は式（2）で示すBeer–Lambertの法則に従う。Beer–Lambertの法則を行列で表現すると，式（5）のようになる。

  

$$\begin{array}{l}{a^{\prime }}_{\tilde{\nu }k}={\displaystyle \sum }_{i=1}^N{c}_i{\epsilon }_{\tilde{\nu }}\\ A^{\prime }=C^{\text{tr}}\times E,\end{array}$$(5)

$a_{\tilde{\nu }k}{}^{\prime }$は，測定試料kの波数 $\tilde{\nu }$ での吸収aを光路長lで割った値であり，Nは錯体種の数を表す。A′とEは，それぞれ$a_{\tilde{\nu }k}{}^{\prime }$とモル吸光係数εをまとめた行列表現である。“tr”は転置行列を示す。式（5）から，一連の電磁波吸収分光は錯体分布とモル吸光係数に分解できることが分かる。

熱力学モデル最適化法では，式（5）を成立させるように錯体分布C，つまり熱力学パラメータであるβ_nを最適化する。本研究では式（4）に列挙した組み合わせの中から，元の紫外可視吸収分光を誤差なく再現できる組み合わせを抽出する。元の紫外可視吸収分光と各組み合わせにより再現する紫外可視吸収分光の差の指標として次式のようにR因子を定義する。

  

$$R\text{-factor}={\displaystyle \sum {\left(A^{\prime }-A_{{\beta }_n}{}^{\prime }\right)}^2}$$(6)

$A_{{\beta }_n}{}^{\prime }$は，最適化した熱力学パラメータを用いて再現した紫外可視吸収分光である。R因子をCl配位数の組み合わせで整理したものをFig.6に示す。

Fig. 6.

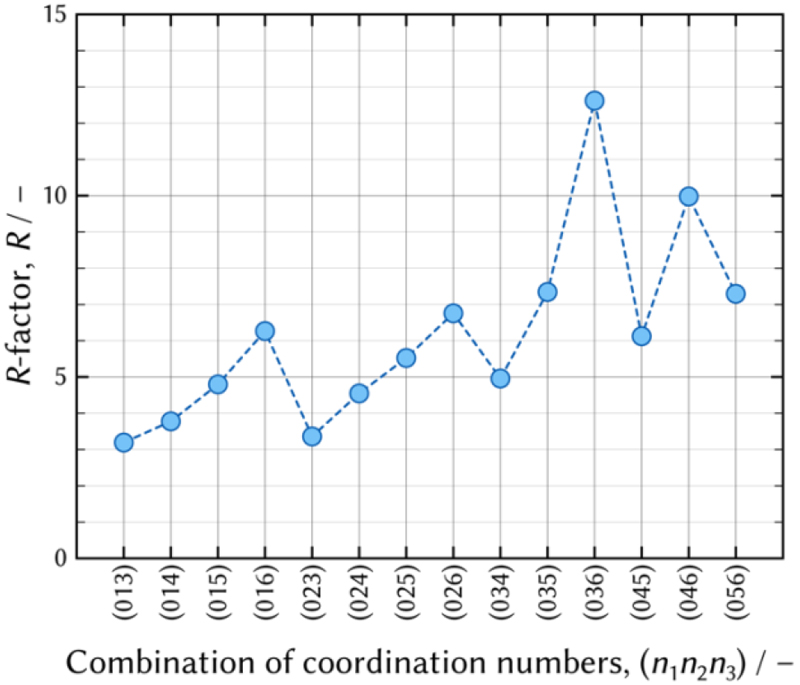
R-factor vs. the combinations of Cl coordination numbers. (Online version in color.)

(013)，(023)，(014)，(024)の順にR因子が小さい。この中で，(023)モデルに基づく錯体分布では，[Mn^IICl₂]⁰の最大分率は0.01でほとんど存在しないため，錯体種の数は実質2種類である。同じ原子，イオンから構成される錯体のモル吸光係数は同等の大きさになると考えられるが，[Mn^IICl₂]⁰のモル吸光係数は他の2つの錯体の100倍の大きさであり，容認することは難しい。従って，熱力学モデルとしては不適切であると判断し，(023)モデルを除外する。

Cl配位数(024)の熱力学モデルを基に求めたMn^IICl_n錯体分布と各錯体のモル吸光係数をFig.7に，錯体安定度定数をTable 3に示す。この解析ではH₂Oの配位数は考慮しないため，それぞれの錯体への配位数をx，y，zで表現する。Mn^IICl_n錯体分布とモル吸光係数を用いて，一連の紫外可視吸収分光を再現した結果も併せて示す。

Fig. 7.

The series of the product of the molar attenuation coefficient and the molarity of species (a), the distribution (b) and the molar attenuation coefficients (c) of manganese chloro-complexes in hydrochloric acid solutions following the model (024). (Online version in color.)

Table 3. Logarithm of the formation constants for manganese chloro complexes. Coordination of H₂O ligands is omitted for simple expression.

Formation reaction	log10 βn
[MnII]2+ + 2Cl− = [MnIICl2]0	−1.22
[MnII]2+ + 4Cl− = [MnIICl4]2−	−4.99

Setchénow coefficient for neutral species of [Mn^IICl₂]⁰, $b_{\gamma ,{\left[{\text{Mn}}^{\text{II}}{\text{Cl}}_2\right]}^0}$= −0.02.

解析結果を用いて再現された一連の紫外可視吸収分光は，Cl濃度が2.24 mol·dm⁻³以上で測定スペクトルを良く再現している。Cl濃度希薄域で26000 cm⁻¹以上の波数では，測定スペクトルとのズレが観察された。紫外可視吸収分光測定の際，HCl水溶液を用いてベースライン補正をしている。Table 1に示すようにMn^II濃度0.25 mol·dm⁻³相当のMn^IICl₂·4H₂Oを溶解すると，試料水溶液のCl濃度は0.5 mol·dm⁻³濃くなり，適切なベースラインからのズレを生じてしまう。Cl濃度が濃くなるにつれてズレは解消されると考えられる。

陰イオン交換体に吸着して水相の[Mn^IICl₄(H₂O)z]²⁻が減少すると，水相中の平衡を維持するために式（3a）の錯体形成反応式が右へ移動して新たに[Mn^IICl₄(H₂O)z]²⁻が生成し，樹脂相と水相の[Mn^IICl₄(H₂O)z]²⁻が平衡に達するまで錯形成が繰り返される。結果として水相中の吸着可能種のモル分率よりも大きい割合の[Mn^IICl₄(H₂O)z]²⁻が陰イオン交換体に吸着されることになる。実際のところ，Fe^III塩化物錯体⁸⁾，Co^II塩化物錯体⁹⁾でも吸着可能種のモル分率が1/100程度でも分配係数が1（吸着率換算50%）以上あることが確認されている²⁵⁾。Fig.7（b）に示されるMn^II塩化物錯体分布では，4 mol·dm⁻³–Cl以上の濃度域で陰イオン交換体に吸着可能な[Mn^IICl₄(H₂O)z]²⁻が生成する。Fig.4に示されるように，5 mol·dm⁻³–Clでは陰イオン交換樹脂への吸着は認められず，吸着挙動と分布が矛盾する。

陰イオン交換挙動との矛盾を考慮すると，測定スペクトルをより精確に再現できるモデル構築のためには，新たなパラメータの導入を検討する必要がある。従来研究³⁾と本研究では，H₂Oの配位挙動を考慮していない。H₂O配位挙動はH₂O活量に依存するが，HCl水溶液中のモル分率基準のH₂O活量²⁶⁾は多くの報告があるが，式（3b）に適用可能な質量モル濃度基準のH₂O活量の報告はない。今後，熱力学モデル最適化法の精度を高めるためにも，質量モル濃度基準のH₂O活量の理論的取扱の発展が期待される。

4・3　[Mn^IICln·xH₂O]²⁻ⁿ錯体構造解析

第2章で述べたように，構造解析の可否は熱力学モデルの妥当性の検証に使用可能である。そこで，仮定した構造モデルが全て不適切であった場合，基となる熱力学モデルを候補から除外し，適切な構造モデルを有する熱力学モデルを採用する。

EXAFSスペクトルを用いて構造解析をするには，錯体個別のEXAFSスペクトルを求める必要がある。紫外可視吸収分光の分解を示す式（5）は，X線吸収分光でも成立する。Fig.3に示す一連のXANESスペクトルM，EXAFSスペクトルXに適用すると，次式が得られる。

  

$$M=C_{\text{XAFS}}^{\text{tr}}\times \mu ,$$(7a)

  

$$X=C_{\text{XAFS}}^{\text{tr}}\times \chi ,$$(7b)

ここで，µ，χは錯体個別のXANESスペクトル，EXAFSスペクトルを示す。C_XAFSはX線吸収分光測定水溶液中の規格化されたMn^IICl_n錯体分布を示す。XANESスペクトル，EXAFSスペクトルは，測定スペクトルを規格化して得られるスペクトルなので，分布も規格化したものを使用する。

式（7a）と（7b）において，両辺にC^trの逆行列を左から乗ずると，µとχが得られる。

  

$$\mu =C_{\text{XAFS}}^{\text{tr}}{}^{-1}\times M,$$(8a)

  

$$\chi =C_{\text{XAFS}}^{\text{tr}}{}^{-1}\times X,$$(8b)

Cl配位数(024)の場合のC_XAFS，µ，χをFig.8に示す。後述する構造解析の結果，水和錯体のH₂O配位数を特定するには至らず，Cl配位数2である錯体のH₂O配位数は4であり，Cl配位数4である錯体にはH₂Oが配位していないことが分かった。得られた結果に従って，これ以降Mn^II塩化物錯体を[Mn^II(H₂O)_x]²⁺，[Mn^IICl₂(H₂O)₄]⁰，[Mn^IICl₄]²⁻と記述する。

Fig. 8.

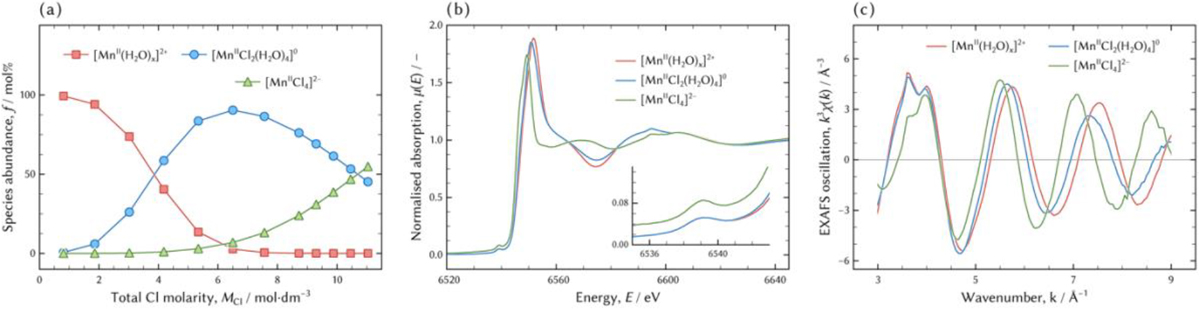
The distribution (a), the XANES spectra (b), and the EXAFS spectra (c) of the individual manganese chloro-complexes in hydrochloric acid solutions following the model (024). (Online version in color.)

Fig.8（b）から，[Mn^II(H₂O)_x]²⁺と[Mn^IICl₂(H₂O)₄]⁰のXANESスペクトルは非常によく似ており，一方[Mn^IICl₄]²⁻のそれは，プレエッジピークのエネルギーは一致しているが，その他の部分で全く異なるスペクトルを示す。このことから，[Mn^II(H₂O)_x]²⁺と[Mn^IICl₂(H₂O)₄]⁰の錯体構造は似ており，[Mn^IICl₄]²⁻は異なることが示唆される。

得られた錯体個別のEXAFSスペクトルに対して，FEFFによるフィッティング解析^27,28)を実施する。解析には，Demeter 0.9.26 ²⁹⁾を使用した。構造モデルの配位子の配位数を固定し，パラメータの一つである中心原子と配位子との距離の変位が初期値から±0.01 Å以内に収まるように調整する。仮定した構造モデルの適切性は，Calvin³⁰⁾により提唱された基準を基に判断した。仮定した構造モデルから再現したEXAFSスペクトルと観察されたEXAFSスペクトルとの差異を表すR因子が0.05より大きい場合，不適切なモデルであると判定する。R因子に加えて，吸収端の変動ΔEが±10 eV以内，Debye–Waller因子σ²が0.002 ≤ σ<0.03に収まる構造モデルを適切なモデルであると判定した。

第4・2・2項で構築した熱力学モデルでは，Cl配位数しか仮定しておらず，H₂Oの配位数に関する情報はない。そこで，H₂O配位数が異なる複数の構造モデルを仮定する。また，構造異性体も仮定し，可能性のある構造モデルすべてについて解析を実施した。一つのCl配位数に対して仮定した構造モデル全ての解析が失敗した場合，基となる熱力学モデルが不適切であると判断した。

前節の解析結果より，Cl配位数の組み合わせが(013)，(023)，(024)である熱力学モデルを用いて錯体構造解析を行なった。Cl配位数が1である構造は，仮定した構造モデル全てでR因子が0.05以下に収束しなかったため，(013)，(014)モデルを適切な熱力学モデルの候補から除外した。(024)モデルにおける構造解析結果をTable 4に，解析の成功例をFig.9に示す。

Table 4. The results of FEFF fitting to resultant EXAFS spectra of the individual manganese aqua and chloro complexes in hydrochloric acid solutions following the model (024). The underlined values are out of recommended ranges.

Cl coord. number	Assumed model			FEFF fitting result
	species*	Geometric configuration	Point group	R-factor, R / –	Path	Coord. number	ΔE to model, ΔE / eV	Shell distance, R / Å	Debye-Waller factor, σ2 / Å2
0	[MnII(H2O)6]2+	octahedron	Oh	0.0426	Mn–O	6	−1.57±1.27	2.168±0.011	0.0099±0.0008
	[MnII(H2O)5]2+	trigonal bipyramid	D3h	0.0314	Mn–O	5	−1.43±1.13	2.167±0.009	0.0075±0.0006
	[MnII(H2O)4]2+	planar square	D4h	0.0460	Mn–O	4	−0.98±1.39	2.168±0.010	0.0049±0.0007
	[MnII(H2O)4]2+	tetrahedron	Td	0.0458	Mn–O	4	−1.00±1.38	2.168±0.010	0.0049±0.0007
2	[MnIIClax2(H2O)eq4]0	distorted octahedron	D4h	0.0188	Mn–Oeq	4	−3.58±3.15	2.177±0.031	0.0111±0.0028
					Mn–Clax	2	−3.59±5.00	2.414±0.045	0.0140±0.0044
	[MnIIClax2(H2O)eq3]0	trigonal bipyramid	D3h	0.0198	Mn–Oeq	3	−2.01±10.75	2.148±0.052	0.0078±0.0071
					Mn–Clax	2	−10.6±26.5	2.397±0.083	0.0091±0.0119
	trans-[MnIICl2(H2O)2]0	planar rhombus	D2h	0.0260	Mn–O	2	−3.20±14.66	2.117±0.027	0.0023±0.0088
					Mn–Cl	2	−9.97±21.23	2.404±0.079	0.0061±0.0105
	[MnIICl2(H2O)2]0	distorted tetrahedron	C2v	0.0258	Mn–O	2	−3.21±14.64	2.117±0.027	0.0023±0.0088
					Mn–Cl	2	−9.97±21.24	2.405±0.079	0.0061±0.0105
4	[MnIIClax4(H2O)eq2]2−	distorted octahedron	D4h	0.0139	Mn–Oax	2	0.06±2.80	2.291±0.015	0.0018±0.0018
					Mn–Cleq	4	5.34±2.14	2.508±0.026	0.0200±0.0037
	[MnIICl4]2−	planar square	D4h	0.0454	Mn–Cl	4	−2.21±1.20	2.469±0.010	0.0106±0.0007
	[MnIICl4]2−	tetrahedron	Td	0.0273	Mn–Cl	4	−2.43±0.99	2.467±0.008	0.0105±0.0005

*Recommended parameter ranges; R ≤ 0.05, |ΔE| ≤ 10, and 0.002 < σ² ≤ 0.03.

Fig. 9.

The results of the FEFF fitting analysis of an octahedron of [Mn^II(H₂O)₆]²⁺ (a), a distorted octahedron of [Mn^IICl₂(H₂O)₄]⁰ (b), and a tetrahedron of [Mn^IICl₄^]2− (c) in hydrochloric acid solutions following the model (024). (Online version in color.)

Cl配位数が0である水和錯体で，H₂Oの配位数が6，5，4の構造を仮定して解析した。いずれの解析でもR因子，吸収端の変動ΔE，Debye–Waller因子σ²が適切な範囲に収束したため，どの錯体構造が水溶液中で存在する可能性が最も確からしいかは判断出来なかった。

  

$$\begin{array}{ll}\text{八面体構造}:{\left[{\text{Mn}}^{\text{II}}{\left({\text{H}}_{\text{2}}\text{O}\right)}_6\right]}^{2+}& \text{適切}\end{array}$$(9a)

  

$$\begin{array}{ll}\text{三方両錐構造}:{\left[{\text{Mn}}^{\text{II}}{\left({\text{H}}_{\text{2}}\text{O}\right)}_5\right]}^{2+}& \text{適切}\end{array}$$(9b)

  

$$\begin{array}{ll}\text{平面正方形構造}:{\left[{\text{Mn}}^{\text{II}}{\left({\text{H}}_{\text{2}}\text{O}\right)}_4\right]}^{2+}& \text{適切}\end{array}$$(9c)

  

$$\begin{array}{ll}\text{正四面体構造}:{\left[{\text{Mn}}^{\text{II}}{\left({\text{H}}_{\text{2}}\text{O}\right)}_4\right]}^{2+}& \text{適切}\end{array}$$(9d)

Cl配位数が2である塩化物錯体では，H₂O配位数が4，3，2である構造を仮定した。H₂O配位数が3または2である場合，Mn–ClのEXAFS振動の吸収端の変動ΔEがおよそ−10±20 eVで，実質±10 eVを超えるため，適切な構造モデルではないと判断した。一方，H₂O配位数が4で歪んだ八面体構造の解析パラメータは適切な値に収まり，R因子も0.0188であり，仮定した構造モデルが妥当であることが示された。

  

$$\begin{array}{ll}\text{八面体構造}:{\left[{\text{Mn}}^{\text{II}}{\text{Cl}}_2{\left({\text{H}}_{\text{2}}\text{O}\right)}_4\right]}^0& \text{適切}\end{array}$$(10a)

  

$$\begin{array}{ll}\text{三方両錐構造}:{\left[{\text{Mn}}^{\text{II}}{\text{Cl}}_2{\left({\text{H}}_{\text{2}}\text{O}\right)}_3\right]}^0& \text{不適切}\end{array}$$(10b)

  

$$\begin{array}{ll}\text{平面正方形構造}:{\left[{\text{Mn}}^{\text{II}}{\text{Cl}}_2{\left({\text{H}}_{\text{2}}\text{O}\right)}_2\right]}^0& \text{不適切}\end{array}$$(10c)

  

$$\begin{array}{ll}\text{正四面体構造}:{\left[{\text{Mn}}^{\text{II}}{\text{Cl}}_2{\left({\text{H}}_{\text{2}}\text{O}\right)}_2\right]}^0& \text{不適切}\end{array}$$(10d)

Cl配位数が4の場合は，H₂Oの配位数が2，0の構造を仮定して解析した。歪んだ八面体構造である[Mn^IICl₄(H₂O)₂]²⁻では，Debye–Waller因子σ²が推奨範囲を外れたため，不適切なモデルであると判断した。Cl配位数4である平面正方形構造，正四面体構造ともに適切な解析結果が得られた。どちらが実際の構造を反映しているかは，本研究での解析では決定出来なかった。

  

$$\begin{array}{ll}\text{八面体構造}:{\left[{\text{Mn}}^{\text{II}}{\text{Cl}}_4{\left({\text{H}}_{\text{2}}\text{O}\right)}_4\right]}^{2-}& \text{不適切}\end{array}$$(11a)

  

$$\begin{array}{ll}\text{平面正方形構造}:{\left[{\text{Mn}}^{\text{II}}{\text{Cl}}_4\right]}^{2-}& \text{適切}\end{array}$$(11b)

  

$$\begin{array}{ll}\text{正四面体構造}:{\left[{\text{Mn}}^{\text{II}}{\text{Cl}}_4\right]}^{2-}& \text{適切}\end{array}$$(11c)

以上の解析結果を基に，HCl水溶液中に存在する可能性の高いMn^II水和錯体，Mn^II塩化物錯体をFig.10に示す。

Fig. 10.

Possible manganese aqua- and chloro-complexes in hydrochloric acid solutions. (Online version in color.)

Mn^II錯体構造では，Table 4に示すように総じて中心原子であるMn^IIと配位子間距離が長い。これまでに著者らが報告してきたCr^{III 7)}，Fe^{III 8)}，Co^{II 9)}の水和錯体では中心原子と水和水の距離は2 Å未満であるのに対し，本報告でのMn^II水和錯体では2.17 Åであった。Tianらによる解析¹⁶⁾でも2.15 Å程度と報告されている。Cl配位子距離も従来報告では2.3 Å前後であるのに対し^7,8,9)，[Mn^IICl₄]²⁻では2.4 Å以上である解析結果が得られている。従って，Mn^II錯体の中心原子と配位子間距離は，他の3d遷移金属に比較して長いことが分かった。錯体構造に強く影響する電子軌道が他の3d遷移金属のそれと異なって特異なものである可能性を示唆する。原因の解明には，配位子場理論や第一原理計算を用いる理論的考察が必要である。

5. 結言

陰イオン交換樹脂への吸着挙動からおおよその錯体分布を把握した上で，紫外可視吸収分光を熱力学モデル最適化法を用いて解析し，HCl水溶液中におけるMn^II水和塩化物錯体の分布とモル吸光係数を決定した。得られた錯体分布を応用して，錯体個別のXANESスペクトルとEXAFSスペクトルを得て，FEFFを用いた錯体構造解析を行った。

その結果，HCl水溶液中での各錯体の安定度定数を決定し，[Mn^II(H₂O)_x]²⁺ (χ＝4, 5, or 6)，[Mn^IICl₂(H₂O)₄]⁰，[Mn^IICl₄]²⁻が存在することが分かった。EXAFSスペクトル解析の結果，[Mn^IICl₂(H₂O)₄]⁰は八面体構造を有することが分かった。水和錯体の水和数と構造，[Mn^IICl₄]²⁻の構造を明確に決めるには至らなかった。

HCl水溶液中で形成されるMn^II塩化物錯体の構造をより詳細に決定するためには，紫外可視近赤外より広範囲の赤外分光，異なる原理に基づくラマン分光の観察や，第一原理計算によるスペクトル解析の必要がある。

謝辞

本研究におけるX線吸収分光は，高エネルギー加速器研究機構フォトンファクトリー共同利用プログラム（課題番号:2022G649）の支援を受けてBL-9Cで測定しました。

文献

• 1)  K.A.Kraus and F.Nelson: Proceedings of the International Conference on Peaceful Uses of Atomic Energy, Vol.7, United Nations, New York, NY, (1955), 113.
• 2)  P.J.Elving and B.Zemel: J. Am. Chem. Soc., 79(1957), 1281. https://doi.org/10.1021/ja01563a006
• 3)  C.H.Gammons and T.M.Seward: Geochim. Cosmochim. Acta, 60(1996), 4295. https://doi.org/10.1016/s0016-7037(96)00275-x
• 4)  W.Liu, B.Etschmann, J.Brugger, L.Spiccia, G.Foran and B.McInnes: Chem. Geol., 231(2006), 326. https://doi.org/10.1016/j.chemgeo.2006.02.005
• 5)  J.Bjerrum, A.S.Halonin and L.H.Skibsted: Acta Chem. Scand. A, 29A(1975), 326. https://doi.org/10.3891/acta.chem.scand.29a-0326
• 6)  J.Brugger, D.C.McPhail, J.Black and L.Spiccia: Geochim. Cosmochim. Acta, 65(2001), 2691. https://doi.org/10.1016/s0016-7037(01)00614-7
• 7)  M.Uchikoshi, D.Akiyama, K.Kimijima and K.Shinoda: RSC Adv., 12(2022), 32722. https://doi.org/10.1039/d2ra06279h
• 8)  M.Uchikoshi, D.Akiyama, K.Kimijima and K.Shinoda: ISIJ Int., 62(2022), 912. https://doi.org/10.2355/isijinternational.isijint-2021-323
• 9)  M.Uchikoshi, K.Shinoda and T.Matsumoto: Adv. X-Ray Chem. Anal., Jpn., 53(2022), 97 (in Japanese).
• 10)  L.H.Skibsted and J.Bjerrum: Acta Chem. Scand. A, 32A(1978), 429. https://doi.org/10.3891/acta.chem.scand.32a-0429
• 11)  M.Uchikoshi: J. Solution Chem., 46(2017), 704. https://doi.org/10.1007/s10953-017-0597-8
• 12)  M.Uchikoshi: J. Solution Chem., 47(2018), 2021. https://doi.org/10.1007/s10953-018-0831-z
• 13)  M.Uchikoshi: Bull. Chem. Soc. Jpn., 92(2019), 1928. https://doi.org/10.1246/bcsj.20190195
• 14)  M.Uchikoshi and K.Shinoda: Struct. Chem., 30(2019), 61. https://doi.org/10.1007/s11224-018-1164-7
• 15)  M.Uchikoshi and K.Shinoda: Struct. Chem., 30(2019), 945. https://doi.org/10.1007/s11224-018-1245-7
• 16)  Y.Tian, B.Etschmann, Y.Mei, P.V.Grundler, D.Testemale, J.-L.Hazemann, P.Elliott, Y.Ngothai and J.Brugger: Geochim. Cosmochim. Acta, 129(2014), 77. https://doi.org/10.1016/j.gca.2013.12.003
• 17)  K.Waizumi, T.Kouda, A.Tanio, N.Fukushima and H.Ohtaki: J. Solution Chem., 28(1999), 83. https://doi.org/10.1023/a:1021741911462
• 18)  K.A.Kraus and G.E.Moore: J. Am. Chem. Soc., 75(1953), 1460. https://doi.org/10.1021/ja01102a054
• 19)  J.Brugger, W.Liu, B.Etschmann, Y.Mei, D.M.Sherman and D.Testemale: Chem. Geol., 447(2016), 219. https://doi.org/10.1016/j.chemgeo.2016.10.021
• 20)  Technological development, Japan Organization for Metals and Energy Security, JOGMEC, https://www.jogmec.go.jp/english/stockpiling/metal_10_000002.html, (accessed on 2024-01-27).
• 21)  X-ray Absorption Fine Structure —Measurement and Analysis of XAFS—, Series of Spectrometry by The Spectroscopical Society of Japan, Vol.26, ed. by Y.Udagawa, Japan Scientific Societies Press, Tokyo, (1993), (in Japanese). ISBN978-4762257087
• 22)  T.Kékesi and M.Isshiki: Mater. Trans., JIM, 35(1994), 406. https://doi.org/10.2320/matertrans1989.35.406
• 23)  M.Setchénow: Z. Phys. Chem., 4U(1889), 117 (in German). https://doi.org/10.1515/zpch-1889-0409
• 24)  R.D.Shannon: Acta Crystallogr. A, 32(1976), 751. https://doi.org/10.1107/s0567739476001551
• 25)  T.Kékesi, K.Mimura and M.Isshiki: Hydrometallurgy, 63(2002), 1. https://doi.org/10.1016/s0304-386x(01)00208-0
• 26)  H.Majima and Y.Awakura: Shigen-to-Sozai, 106(1990), 109 (in Japa-nese). https://doi.org/10.2473/shigentosozai.106.109
• 27)  J.J.Rehr and R.C.Albers: Rev. Mod. Phys., 72(2000), 621. https://doi.org/10.1103/revmodphys.72.621
• 28)  M.Newville: J. Synchrotron Rad., 8(2001), 322. https://doi.org/10.1107/s0909049500016964
• 29)  B.Ravel and M.Newville: J. Synchrotron Rad., 12(2005), 537. https://doi.org/10.1107/s0909049505012719
• 30)  S.Calvin: XAFS for Everyone, CRC Press, Boca Raton, FL, (2013). ISBN978-1439878637