2024 Volume 110 Issue 3 Pages 217-226
2024 Volume 110 Issue 3 Pages 217-226
Medium-manganese steel that undergoes Lüders deformation exhibits good uniform elongation owing to large elongation with a yield plateau. To accurately predict the deformation behavior in engineering applications, the yield stresses of medium-manganese steel (5% Mn), exhibiting the transformation-induced plasticity (TRIP) effect were investigated during elongation under a multiaxial stress state (MSS). Compact tensile tests with real-time diameter measurements were conducted on smooth and notched, tiny round-bar specimens to evaluate the local yield stress and strain without the Lüders band propagation effect. Consequently, the true stress plateau was measured without the upper yield point for the smooth round-bar specimen, and the cross-sectional average true stress of the blunt notched round-bar specimens had the same plateau as the smooth round-bar specimen. The sharp-notched round-bar specimen exhibited a two-stage linear increase in true stress. The true stresses of the three specimens at the initial yield point were almost identical. Under the MSS, the hydrostatic stress typically increases the true stress at the initial yield point. The independence of the MSS indicates that the yield stress during elongation was independent of the shear-dominant crystal slip resistance. Finite element (FE) analysis using the Mises yield locus did not express the true stress plateau and its independence of the MSS. Additionally, the transformation rate of retained austenite was measured for mechanistic analysis; however, the TRIP effect did not contribute to this unusual independence because it started at the intermediate yield elongation stage. Thus, the stress criterion for the generation of mobile dislocations can determine yield stress.
自動車用の次世代高張力鋼として中Mn鋼が着目される。中Mn鋼は3~10%程度のMnを含む低炭素鋼であり,フェライト母相と残留オーステナイトよりなる組織形態を示す。残留オーステナイトの変態誘起塑性(Transformation induced plasticity: TRIP)効果により優れた延性を有する鋼材となる1,2)。その中でも冷延後に焼鈍したものは10%程度,あるいはそれ以上の大きなLüders変形(Lüders帯を伴う不均一変形)が生じる。Lüders変形分だけ加工硬化曲線はオフセットされたような形となり,高強度であるにもかかわらず極めて高い一様伸びを示す3,4,5)。一方でLüders変形はストレッチャーストレインのようなプレス成形時の不良となることが知られており6),その対策を考える上で精度の良い力学モデルが必要となる。
ここで,Lüders変形とこれに伴う降伏伸びは古くから知られる鋼材の降伏現象の基本的な特徴の一つである。Lüders変形においては負荷された応力が上降伏点に達した際に降伏を開始し,即座に公称応力は下降伏点まで低下,ある伸び量(降伏伸び)に達するまで加工硬化せずに一定の応力を保ったまま塑性変形が進む。そのメカニズムは未だ不明なところが多いが,炭素原子と転位との固着がはずれる7),あるいは可動転位の急激な増殖8,9)による降伏応力低下が引き起こす現象として理解されている。
Lüders帯は降伏応力の低下に起因する不均一変形によって生じたせん断帯であり,降伏伸び中において引張試験片の掴み部付近から生じたものが長手方向に複数回伝播することを繰り返す。このため,Lüders帯の伝播挙動やその内部の金属組織状態と塑性変形中の応力低下・停留は相関する10,11,12,13)。実際,Lüders帯の伝播とともに伸び量は増すので,せん断帯の挙動が引張試験結果(応力と伸びの関係)に大きく影響を与えることに間違いはない。その証として,測定される降伏伸び量はゲージ長さやひずみ速度に強く依存し,ゲージ長さが短くなるほど,そしてひずみ速度が小さくなるほど降伏伸びは減少することが報告されている14,15)。
力学的には一様変形中の隠された高次変形モードがLüders帯(せん断帯)として発現したものと捉えることができる16)。このような高次モードの発現は分岐現象として知られる。分岐現象としてのせん断帯発生は加工硬化率が特定の値以下になった際に必ず発生してしまうため,Lüders変形のような加工硬化率が0以下となる状況においてせん断帯発生は必然である。これらの知見をもとに流動応力の低下項を導入した構成則が既に提案されており17,18),有限要素解析(FEM)に組み込むことでLüders帯の発生と伝播,その結果としての降伏伸びが再現されている19)。ここで注意するべきは,これら提案された構成則において降伏伸びは0であり,単に降伏応力が低下するだけであるという点である。局所的には降伏伸びのような降伏応力一定の状態は存在せず,数値解析上は試験片上をLüders帯が伝播する過程において降伏伸びが生じたものとなる。
一方で,降伏伸びを単純に降伏応力低下とこれに伴うせん断帯発生・伝播として捉えられないとの結果も報告される。丸棒引張試験では伸びの代わりに直径変化を測定することでゲージ長さ0として変形抵抗を測定することができるが20,21,22,23),このようなゲージ長さ0の測定においても降伏伸びと同等の応力一定状態の変形(正確には伸びではないが,簡単のためにこのような変形も降伏伸びと呼ぶことにする)が観測される20,21)。この結果は,せん断帯の挙動に無関係に降伏伸びが生じるものと解釈することができる。
以上の背景のもと,本研究では中Mn鋼を対象としたLüders変形時の局所変形抵抗の測定を行った。これまでの報告20,21)と同様に,小型丸棒引張試験時の直径変化測定により不均一な変形場における局所変形抵抗を得た。本研究の特徴は,残留オーステナイト相を含む中Mn鋼に対し,切り欠き丸棒引張試験片を用いた引張試験を実施した点である。Lüders変形を示す素材であっても切り欠きを有する引張試験片では切り欠き底を結ぶ最小断面部が優先的に塑性変形するので24),切り欠き部の直径を測定する限りにおいてLüders帯が応力とひずみの測定結果に影響を与えることはない。これによって改めて局所変形抵抗において降伏伸びが出現するか検証するとともに,さらに切り欠きによって多軸場となった応力状態がLüders変形に与える影響を明らかにする。多軸場となることで静水応力が誘起されるので,平滑試験片に比べて切り欠き試験片では同じひずみ量であってもその分だけ真応力は高い21)。加えて,静水応力はTRIP効果を促進する25)。これにより切り欠き部(あるいはくびれ部)のような多軸応力場では加工硬化率そのものも高くなる23)。降伏初期からTRIP効果が発現すればLüders変形の消失が期待され,その知見はLüders変形による不良現象を解消する成形方法のヒントになり得る。しかしながら,中Mn鋼のようなTRIP効果を示す鋼材ではこのような多軸場における降伏伸び時の変形抵抗が測定された例はない。そもそも転位の固着や増殖等のメカニズムにより降伏伸び時の負荷応力が定まるのであれば,臨界滑りせん断応力を基にした相当応力(静水応力を除いた応力量)で定義される降伏基準が妥当であるかとの疑問もある。
本報ではさらにFEMによるシミュレーションと放射光回折による引張中の残留オーステナイト体積率測定を行った。この結果を用いて測定された多軸場Lüders変形下での応力・ひずみ挙動を考察した。
供試鋼としてMnを約5%含む中Mn鋼を用いた。その成分をTable 1に示す。溶製したインゴットを1200°C(仕上げ温度850°C以上)で8 mm厚まで熱間圧延した後に空冷し,さらに2 mm厚まで冷間圧延した。冷間圧延材を650°Cで30分間焼鈍することでLüders変形を示す素材として仕上げた。
| C | Si | Mn | P | S | Al | O | N |
|---|---|---|---|---|---|---|---|
| 0.092 | 0.04 | 4.91 | <0.002 | 0.002 | 0.024 | 0.005 | 0.001 |
金属組織はFig.1のごとくである。電子顕微鏡(SEM)像(Fig.1(a))とEBSD(Electron Back Scattering Diffraction)解析より得たIPF(Inverse Pole Figure)マップ(Fig.1(b))より粒径1 µm以下の微細組織が形成されていることが分かる。同じくEBSDより得たPhase map(Fig.1(c))からは観察視野の残留オーステナイト率は26%と測定された。この供試鋼は既報11,12)に用いられたものであり,さらに詳細な金属組織分析についてはこれら既報を参照されたい。既報11,12)における観察視野では20%程度の残留オーステナイト率となったので,残留オーステナイト率の測定値は視野ごとにばらつくものと考えられる。

SEM and EBSD images of microstructures obtained with acceleration voltage of 15 kV. Step size for EBSD analysis was 0.12 μm. Image qualities are overlayed on the IPF and phase maps. The specimen for observations was mechanically polished using a diamond paste. (Online version in color.)
JIS13B試験片を用いた通常の伸びを測定する引張試験の結果はFig.2のようになった。公称応力で見れば,772 MPaの上降伏点に達した後に707 MPaまで降伏応力は低下し,そのままの応力を保ったまま0.09ほど伸びている。最大引張強度は約880 MPaであり,一様伸びは0.25に達する。この強度クラスとしては,極めて大きな一様伸びである。

Nominal stress vs. elongation curve determined using a sheet-type JIS 13B specimen with a gauge length of 50 mm and tensile rate of 10 mm/min.
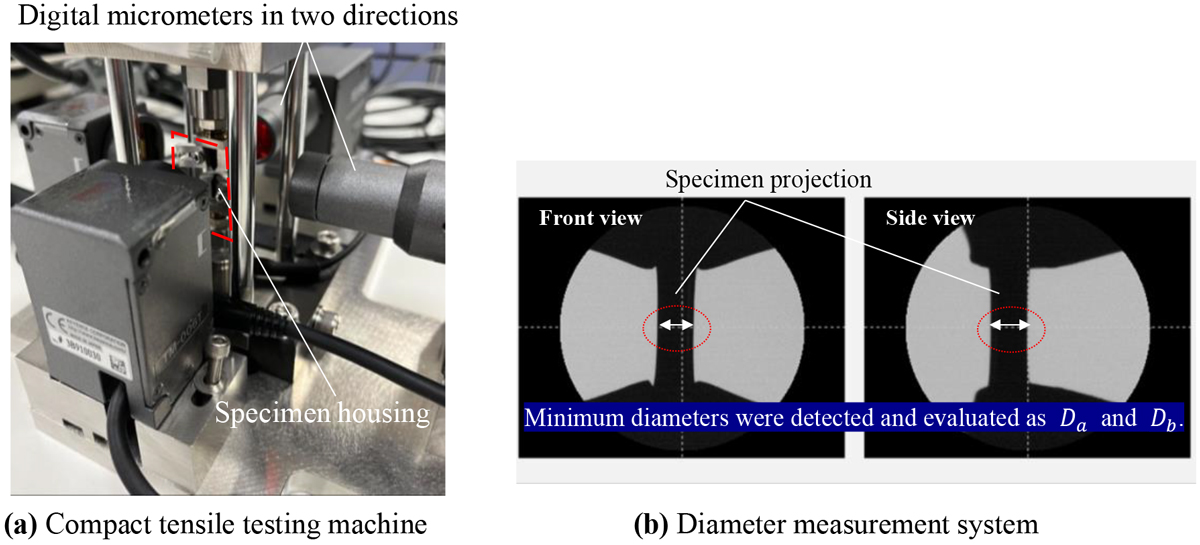
独自にカスタムメイドした(株)都島製作所製の小型引張試験機23,26)を用いた。Fig.3に示すように,小型引張試験機ではLED投影方式のデジタル形状測定器(Keyence製TM3000)2セットにより2方向から試験片の最小断面部の直径を測定する(Fig.3(a))。Fig.3(b)に計測画面の例を示すが,2方向から測定された最小断面部の直径はDa,Dbとして荷重Fとともにその履歴が保存される。元板の板厚方向がDbとなるように試験片を設置するので,異方性がある場合はDbを短軸とする楕円状に断面が減少していく。これより,最小断面部を楕円(Da=Dbの場合は真円)と仮定して最小断面部の平均真応力σtを以下のように算出することができる。
| (1) |
Local stress and strain determined by real-time diameter measurements. (Online version in color.)
小型化したがために本装置には伸びを測定する機構を組み込めていない。代わりに断面減少率ρを評価する。初期の試験片直径D0とDa,Dbの測定値を用いてρは以下のように算出される。
| (2) |
伸びた分だけ断面は減少するので,塑性変形部の体積が一定であることを仮定すればρは真ひずみに一致する。1章に述べたように,試験片くびれ以降は静水応力分だけ真応力が増す。そのため,降伏応力の評価に際してはσtに補正を加える必要がある27,28)が今回は実施しなかった。これは後述するようにFEMによるσt-ρ曲線の再現が不可能であったことによる。また,今回の実験においていずれの試験においても降伏伸びに相当するρ=0.09まではDa/Dbは最大で1.03程度であり,Da≈Dbとみなせる結果であった。本報の対象外のひずみ域とはなるが,破断までにこの値は1.3程度に上昇した。
引張試験は室温下で引張速度2 µm/sの準静的条件にて実施した。
小型丸棒引張試験片には平行部直径1.0 mmの平滑丸棒,および切り欠き半径10 mm(Notch A)と3.4 mm(Notch B)の2種類の小型切り欠き丸棒を用いた。Fig.4にその形状を示す。いずれも2 mm厚の供試鋼から引張方向が圧延直交方向に一致するように切り出した。供試鋼の厚みから直径2.5 mmの試験片把持部を切り出すことはできないため,把持部の一部には板面が残った形状となった。

Tiny round-bar shapes for compact tensile tests. Dimension is in mm.
Fig.5に小型平滑丸棒引張試験より得たσt-ρ線図を示す。参考のため,JIS13B引張試験より得たσtと真ひずみεt曲線も記載した。デジタル形状測定機器由来のノイズのためにばらつきがみられるものの,σt-ρ線図においてもJIS13B試験片引張中の伸び測定により得られたものと同様の降伏伸びが観測される。また,特徴的な点としてσt-ρ曲線では上降伏点が観測されない。σt-εt曲線ではσtが上降伏点に達した後に下降伏点まで値は降下し,降伏伸び中において徐々に上降伏点まで値が上昇する。一方,σt-ρ曲線ではほぼ一定のσt(≈σt-εt曲線における上降伏点)を保ったまま変形が進み,降伏伸び後に加工硬化を開始する。ここで,σt-εt曲線に対してσt-ρ曲線では降伏伸びが0.01程度小さい。降伏伸び後の加工硬化率もσt-ρ曲線におけるものがσt-εt曲線より高い。なお,JIS13B引張試験においてははっきりとしたLüders帯が観察された。その挙動の詳細については既報11,12)にて紹介をしている。

σt vs. ρ curve for the smooth tiny round-bar specimen determined by real-time diameter measurements. σt vs. true strain curves determined from the elongation measurement of JIS13B specimen is also shown. (Online version in color.)
小型切り欠き丸棒引張試験におけるσt-ρ線図はFig.6のようになった。降伏伸び域に限れば,小型平滑丸棒引張試験の結果に比べてNotch A(切り欠き半径10 mm)はほぼ同じσt-ρを示している。すなわち,切り欠き効果によるσtの上昇は観測されない。降伏伸び量も小型平滑丸棒とNotch Aでは一致している。降伏伸び以降のρにおいて,Notch Aのσtは小型平滑丸棒のものよりも高い。

σt vs. ρ curves of smooth and notched specimens. (Online version in color.)
その一方で,Fig.6よりNotch B(切り欠き半径3.4 mm)では降伏開始からρ=0.03程度までσtはあまり上昇せず,それ以降のρにおいて急激な上昇を示した。これにより降伏段を形成する結果となった。降伏段以降,ρ=0.09程度までは直線的なσtの上昇を示し,ρ>0.09より徐々にSwift型の累乗曲線に漸近していく。降伏段以降のσtはNotch Aのものよりも高いが,降伏段におけるσt,すなわち初期降伏点におけるσtは他の2つの試験片にほぼ同じである。つまり,より鋭い切り欠きを有するNotch Bにおいても切り欠き効果によるσtの上昇は表れないとの結果になった。これは他の鋼種(SS400)により測定された結果21)とは異なる。
なお,1種につき2本の試験片を用いて実験をした。これにより,上記の結果の再現性を確認している。
小型平滑丸棒の引張試験にて計測されたσt-ρ曲線により,供試鋼の局所的な特性として降伏応力一定にて変形する塑性域が存在することが改めて明らかとなった。JIS13B引張試験片によって測定されたような上降伏点や下降伏点以降のσtの上昇はσt-ρ曲線中には現れない。JIS13B引張試験より得られたこれらの挙動は,Lüders帯伝播による不均一変形が引き起こすゲージ長さに依存した測定上の誤差であるとみなせる。なお,誤差としたのはあくまでも局所的な変形抵抗に対してである。
ここで,降伏伸びのような加工硬化がほぼ起こらない状況ではくびれを起こしてしまう。そのため,σt-ρ曲線をそのまま変形抵抗(降伏応力Yと相当塑性ひずみεpの関係)として用いるには不十分である。くびれが生じれば変形場は不均一となるため,一般的な素材では切り欠き効果が発現してσtはYより高くなってしまう。
そこで,小型平滑丸棒引張試験を再現した弾塑性有限要素シミュレーション(FEM)を実施し,FEMがσt-ρ曲線の測定値を再現するものとしてY-εp(FEMへの入力)を求めることを試みた。FEMには商用の静的陰解法コードAbaqus/Standard(Dassault Simulia Corp.)を用い,軸対称2次元を仮定した一辺0.01 mm(最密部)の四辺形要素にて試験片をモデル化した。Hahn17)の構成則をはじめとする加工軟化による降伏伸びの表現(他には例えば29))がこれまでに行われるが,収束の問題がある。そのため,Fig.5より供試鋼のσt-ρ曲線は上降伏点が生じないことも受け,今回はMisesの降伏条件と関連流れ則のもとに単純にεp=εylの分だけオフセットさせたSwiftの加工硬化則30,31)を用いた。式(3)にこの加工硬化則を示す。
| (3) |
式(3)においてYpは初期降伏応力,F,ε0,nはSwift則における材料パラメータとなる。YpはFig.5のσt-ρ曲線より777.2 MPaとし,安定した収束を得るためにεp=εylまでに0.001 MPaだけ線形的に増加させている。残るパラメータについては合わせ込みの結果として,F=2022.9,ε0=0.0686,n=0.357,εyl=0.063と定めた。ただし,2・2節に述べたように降伏伸び域においてFEMは測定値を完全に再現するに至らなかった。なお,弾性変形についてはヤング率を206 GPa,ポアソン比を0.3としている。
Fig.7に小型平滑丸棒引張試験とFEMより得たσt-ρ曲線(プロット,およびFEMの入力とした式(3)のY-εp曲線を示す。ここで,FEMにおいても実験と同様に最小直径を該当位置の節点の座標より求め,荷重も上端部の節点力の和より算出をした。算出された荷重降伏伸び部以降のρ≥0.09においてFEMは測定結果によく一致している。しかしながら,ρ<0.09の降伏伸び域において双方の乖離が大きい。FEMでは降伏伸び域においても変形とともにσtが増しており,測定結果と異なっている。FEMにおけるσt-ρは2段階の折れ線となっており,Fig.7中に(b)として記入した点のあたりに折れ部が存在する。降伏伸び域では入力したY-εp曲線にも一致しない。

Input and output curves of the FE simulation for the smooth specimen. The FE meshes and measurements are also shown. Contour maps of the equivalent stress at (a)−(e) is presented in Fig.8. (Online version in color.)
想定通り,このようなFEMの結果は試験片のくびれによるものである。Fig.8(a)はFig.7中のポイント(a)におけるFEMにより解析された相当応力の分布である。概ね一様な相当応力分布であるが,若干くびれが生じている。このFEMにおいては,板材引張試験におけるLüders 帯伝播に相当するものはくびれ(不均一変形部)が引張方向に一様な変形となるように均されていく過程として現れた。このくびれにより切り欠き効果が大きくなることで,σtが徐々に上昇をしたものと考えられる。さらに変形が進みポイント(b)となれば,Fig.8(b)のごとく明らかに変形が不均一となる。中央部のεpがεylを超え,相当応力,すなわちεpが高い部位が生ずる。このような変形集中は引張中にくびれを起こした鋼材がその断面中心より破壊する現象としてよく知られる33)。さらに切り欠き効果が合わさり,2段階目のσt上昇が始まる。中心部の相当応力(またはεp)の集中部が試験片幅方向に伝播し終わり,ポイント(c)(Fig.8(c))のように再び試験片の長手中心部において均一な変形となった後にようやくσt-ρ曲線は式(3)のY-εp曲線に一致する。その後はポイント(d),(e)(Fig.8(d),(e))のように均一変形が継続する。

Contour maps of the equivalent stress at (a)−(e) shown in Fig.7. (Online version in color.)
測定値とFEMとの比較からは,Yが低下することで切り欠き効果によるσtの上昇を相殺する,あるいはそもそも切り欠き効果そのものが発現しない変形機構であることが示唆される。小型切り欠き丸棒引張試験より得たσt-ρ曲線において初期降伏応力が小型平滑丸棒のそれにほぼ一致したことを考慮すれば,後者の可能性が高い。Fig.9は式(3)の加工硬化則を用いて得た小型切り欠き丸棒のFEM解析結果(σt-ρ曲線)である。切り欠きにより初期降伏応力が明らかに増しており,切り欠き効果が発現していることが分かる。実験結果はFEMとは整合しないので,切り欠き効果は実際には発現しなかったものと考えざるを得ない。Misesの降伏条件ではせん断ひずみエネルギーがその閾値となるので,せん断応力に独立な静水応力成分は理論上降伏に寄与しない。これにより,多軸場では静水応力分だけσtが増すというのが切り欠き効果である。切り欠き効果が発現しないということは,降伏応力を決定づけるものはせん断支配ではない,すなわち臨界滑りせん断応力のようなものではないことを示す。本報の測定からは,ある所定のσtが加わりさえすればその際のせん断成分とは無関係に供試鋼は降伏してしまった。これは,降伏伸びにおける変形抵抗は滑りとは異なる機構によって定まることを意味する。変形が結晶内の滑りで起こることは観察結果から疑いようがない。ここではあくまでも変形に必要な応力に言及している。このような切り欠きに対する非依存性はMisesの降伏条件を基礎とする鉄鋼材料の塑性変形表現に対して極めて特異的な挙動となる。転位の固着が外れるために必要な応力場が主応力で支配される,あるいは可動転位の増殖の閾値となる応力が存在する,静水応力が駆動する残留オーステナイトの変態がこのような特異性を引き起こすものと考えられるが,本報告の段階ではそのメカニズムは分からない。

FE-simulated σt vs. ρ curves for smooth and notched specimens. (Online version in color.)
なお,切り欠き効果が発現せずともFig.8(b)のような部分的に塑性変形量がεylを超えることによるσtの上昇が見られるはずである。しかしながら,実験結果にはこのような上昇は見られず,むしろσtが低下するような挙動が窺える。よって,εpがεylに近づいた際には従来から言われるYの低下現象も起きたものと思われる。
4・2 残留オーステナイト率の推移4・1節に示したように,滑り変形の抵抗以外の機構が降伏伸び時の変形抵抗を定めることが考えられる。その一つとして残留オーステナイトの変態に伴う塑性変形の可能性がある。そこで,最も切り欠き効果が強く出るはずであったNotch B試験片を対象に平滑小型丸棒引張試験の降伏伸び域ρ≤0.08における残留オーステナイト体積率を測定した。
測定は大型放射光施設SPring-8のビームラインBL28B2にて実施した。白色X線の回折(回折角度2θ=10°)を用い,γ(2 0 0),γ(2 2 0),γ(3 1 1)ピークの積分強度それぞれから残留オーステナイト体積率を算出した。評価にはその後に平均化したものを用いている。測定に際しては試験片中央の最小断面部がゲージボリュームとなるように条件を定めた。ここでゲージボリュームは試験片長手方向に50 µmの厚みを持ち,直交方向に0.856 mm×0.3 mmの矩形となるように設定した。詳細は既報を参照されたい23)。ゲージボリュームサイズを除き,既報に同一の条件としている。
なお,供試鋼中の残留オーステナイトは変態を起こしやすいことから,引張負荷の都度除荷をし,X線回折取得後に再負荷をしている。また,X線の透過像を取得しておき,この画像よりX線回折測定時の断面減少率ρを算出した。ここで2・2節に述べたように降伏伸び中の断面のアスペクト比は1.0であったことから,式(2)中においてDa=Dbを仮定し,一方向からのみの直径変化よりρを算出している。
Fig.10にNotch B試験片変形途中の残留オーステナイト体積率の測定結果を示す。Fig.6のσt-ρ曲線も参考のために記載した。ρ=0.022程度までは残留オーステナイト率の減少はみられず,その値は17%前後である。Fig.1(c)における26%,あるいは既報11,12)における20%のEBSD測定値に比べれば小さい。しかしながら,測定方法の違いや狭い観察視野ごとのばらつきを考慮すれば初期値として概ね妥当な値であるとみなせる。それ以降のρ=0.06においては残留オーステナイト率の明確な低下が計測され,ρ=0.08付近では12.9%まで低下をしている。3章に述べたようにσtはρ=0.03あたりから2段目の直線状の上昇を示すので,この挙動は残留オーステナイト率が減少し始めたρに対応するとみなせる。

Volume fraction of the austenite phase during tensile deformation of the notch B type small round-bar specimen. The true stress in Fig.6 is also shown. (Online version in color.)
Fig.10から,変形初期ρ≤0.02において残留オーステナイトはほとんど変態していない。よって,TRIP効果は降伏伸び時の初期の変形抵抗に寄与していない。これは降伏伸び時の変形抵抗はフェライトと変態前のオーステナイトの挙動に支配されることを意味する。小型平滑丸棒やNotch Aと異なり,Fig.10のNotch Bではρ≤0.08においてσtが上昇する。その理由は,Fig.8(b)のような部分的にεpが増すためである。切り欠き形状は鋭いほど内部の不均一変形の程度は大きい。Fig.9のFEMの解析結果では2段階目の直線状のσt上昇はρ=0.06あたりからであるから,実験においてはFEMよりも小さなρで2段階目のσt上昇が始まったことになる。これは中心部において高い応力3軸度に誘起された残留オーステナイトの変態が不均一変形をさらに助長したためである。σt上昇が現れているのはNotch Bだけであるが,εp≥εylの断面における塑性変形量の均一化過程(断面内の変形伝播過程)(Fig.8(b),(c))が他の2種の試験片よりも著しいために降伏応力の低下を打ち消したものと思われる。
なお,平滑丸棒の結果では降伏伸び終盤における降伏応力の低下が示唆された。この段階ではかなりの割合のオーステナイトが変態していることから,降伏応力の低下は主にフェライトの挙動が主因であると考えられる。一つの仮説であるが,オーステナイトは一般的な加工硬化を示し,残り8割程度のフェライトが降伏応力低下と切り欠き非感受性を示しているのではなかろうか。相応力の測定により明らかにできると考えるが,供試鋼中のオーステナイトは不安定であるため,相当応力を得るための2軸応力測定をいかに短時間で実施できるかが鍵となる。
以上のように,多軸場の降伏伸びは様々な因子が関わる複雑な挙動を示す。Misesの降伏条件を含め,従来の結晶の滑り変形をもとにした塑性力学の考え方が適用できない。これまでは1,2%程度の小さな降伏伸びのLüders変形であったから,解析上は無視しても問題はなかった。しかしながら,供試鋼のように10%近くも降伏伸びをしてしまう鋼材においては無視できない。このような素材を使いこなすためにも,適切な力学モデルを構築することが肝要である。実際の鋼材の加工や自動車の衝突においては変形経路急変のような問題32)も考慮する必要がある。本報においてはヒントを得るにとどまったが,今後の課題としてこのような複雑現象を支配する力学因子を見出していきたい。
本研究では5%Mnを含む中Mn鋼を対象に,Lüders変形時の多軸状態における降伏伸び域の局所的な変形抵抗を調査した。供試鋼はTRIP効果を示す鋼材となり,10%程度の降伏伸びが合わさって高い均一伸びを有する。その手段として小型平滑丸棒と切り欠き丸棒を対象とした直径リアルタイム計測式引張試験を実施し,Lüders帯に影響を受けない状態で最小断面部の局所的な断面平均真応力と断面減少率(≅真ひずみ)を取得することに成功した。結果は以下の通りである。
(1)局所域であっても真応力一定のまま変形が進む降伏伸び挙動を示す。
(2)切り欠きによる初期降伏応力の上昇は起きず平滑,切り欠き丸棒ともに780 MPa程度で弾性から塑性に切り替わった。これはMisesのようなせん断応力をもとにした降伏条件により降伏伸び時の変形抵抗を表現することができないことを意味する。実際,Misesの降伏条件をもとにしたFEMでは降伏伸び時の真応力の挙動を再現することはできなかった。
(3)上記の切り欠き非依存性は結晶の滑り抵抗以外の因子が作用することによるものと思われる。その機構は本報では特定できていない。残留オーステナイトの変態率を放射光により測定したが,不均一変形を助長する以外の効果は見出せなかった。降伏伸び中の変形抵抗が決定づけられる因子を明らかにし,その因子に基づいた力学モデルを構築していく必要がある。
本研究は天田財団の重点研究開発助成(AF-2021003-A3)を受けてなされた。また,放射光を使った測定はJSPS科研費 JP20H02484の助成を受けてなされた研究成果の一部であり,大型放射光施設SPring-8の公募課題2020A1097 と2022A1385において実施されたものである。JASRIの梶原賢太郎氏および鳥取大学の固体力学研の卒業生と現メンバー:藤田大輝氏,近藤大樹氏,髙橋智也氏,上田裕也氏,清水太智氏,佐藤誉洋氏,横田秀就氏には実験の実施にあたって尽力をいただいた。供試鋼とJIS13B引張試験片を使った応力・ひずみ線図は日本鉄鋼協会「鉄鋼材料の不均一変形組織と力学特性」研究会の共通試料・データとして日本製鉄株式会社の吉武睦海氏より提供を受けたものとなる。ここに謝意を表する。