Crystal Plasticity Analysis on the Fundamental Processes of Strain Localization and Damage Formation in Pure Iron Polycrystals under Cyclic Fatigue

Abstract

By using finite element method for crystal plasticity, we investigated the accumulation behavior of dislocation and atomic vacancies introduced by non-uniform deformation in pure iron polycrystals. Dislocation density was calculated from the increment of plastic shear strain and spatial gradient of the slip systems for SS and GN dislocation densities. Vacancy density was calculated from the edge component of SS dislocation density and the incremental plastic shear strain by expanding the theory of Essmann and Mughrabi, in which atomic vacancies are released by the annihilation of edge dislocations, for each slip system. The cyclic loading analysis was performed under strain-controlled with 10 cycles between a tensile process up to 0.5% nominal strain and a compressive process down to 0%. For comparison, a monotonic loading analysis was also performed. The macroscopic mechanical responses were significantly different under the two conditions, and the work hardening rate under cyclic loading was less than half that under monotonic loading. The localization of plastic strain was more pronounced in the cyclic loading deformation than in the monotonic one. The low work hardening rate for cyclic loading deformation was attributed to the low accumulation of GN dislocations due to the relaxation of the plastic shear strain gradient caused by the load reversal. The average vacancy density was twice higher for monotonic loading deformation than for cyclic loading deformation. On the other hand, the maximum value of vacancy density was almost the same in both conditions, indicating that the cyclic loading deformation was more localized.

1. 緒言

結晶性金属材料中には多数の結晶欠陥（原子空孔，転位など）が存在し，結晶の塑性変形に伴い増大する。塑性変形中に増大した結晶欠陥は，材料の損傷へとつながり破壊の起点になることが考えられる。特に結晶欠陥の中でも原子空孔濃度の増大は，Voidの形成や微視亀裂の発生に関与するものと考えられており，材料の損傷に発展する。このような結晶中における損傷形成素過程は，結晶の微視組織構造，負荷経路や環境等の様々な要因によって異なる過程を示すものと考えられる。本論文では，このような損傷形成素過程について基礎的な検討を行うため，繰返し負荷と単調負荷の二つの負荷経路を用いて純鉄多結晶体の繰返し疲労に伴うひずみの局所化と損傷形成素過程について有限要素法結晶塑性解析を用いて検討する。従来，有限要素法結晶塑性解析を用いて繰返し疲労に伴う転位密度分布の形成を詳細に解析した例¹⁾はあるが，転位密度に加えて上記の原子空孔濃度分布にも注目した研究はない。そこでこの両者に着目して疲労損傷形成素過程の解析を行なったことが，本研究の特徴である。

原子空孔は結晶格子の格子点に本来あるべき原子が無いという点状の結晶欠陥である。原子空孔は熱的な平衡状態として結晶中に存在し，例えば300 Kの鉄（Fe）中においてその濃度は約6×10^－26である。ここで鉄に20%の引張変形を加え塑性変形させた後には，原子空孔濃度が10^－5のオーダーになったとの報告²⁾がある。つまりは結晶に塑性変形が加わると原子空孔が増加する。結晶の塑性変形は転位の運動によるすべり変形によって生ずる。すべり変形による原子空孔の発生は刃状転位の対消滅とらせん転位同士の切りあいによるジョグの引きずり運動の2つの機構がよく知られている。結晶の塑性変形によって転位が蓄積し転位密度が増加すると転位同士が出会う頻度が増加し，結果として前述の2つの機構によって原子空孔濃度も増加する。塑性変形に伴う原子空孔濃度の増加による Voidの形成や微視亀裂の発生は材料が破壊に至る原因となるため，結晶中に蓄積する空孔がどのように蓄積し分布するかを知ることは重要となる。

材料中の原子空孔濃度は電気抵抗測定³⁾や陽電子消滅寿命法で測定できるが，これらの方法では試料の平均的な値しか求めることができない。近年，千葉大学の藤浪らは，陽電子をマイクロビーム化することで十数µmの分解能で原子空孔濃度分布を測定する技術を開発した⁴⁾。しかし高強度化された鉄鋼材料の微視組織（超微細粒や粒子分散強化鋼など）はサブミクロンオーダー（~0.1 µm）のものもあり，実験的手法による空孔濃度測定の空間分解能はまだ十分とはいえない。そこで我々は，転位の対消滅により原子空孔が放出されるEssmann and Mughrabiの理論⁵⁾を，転位密度を基礎とした結晶塑性解析ソフトウェアコードに組み込み，結晶の塑性すべり変形に伴う原子空孔密度の発展を検討してきた^6,7)。ここでは，FCC銅単結晶モデルを用いて単調負荷および繰返し負荷条件における空孔密度の発展について様々な条件下で詳細に検討し，実験値とも一致する結果が得られている。本論文では，この手法をBCC純鉄多結晶体に適用し，多結晶体微視組織中で生ずる不均一変形とひずみの局所化およびそれに伴い蓄積する結晶欠陥として転位と原子空孔の密度について調査し，損傷形成素過程について検討する。また単調負荷と繰返し負荷の二つの負荷条件を与えて，負荷経路によって異なる力学特性および塑性ひずみの局所化，転位密度分布，原子空孔密度を生じさせ，それについて比較検討することで，純鉄多結晶体の繰返し疲労に伴う損傷形成素過程の基礎的な検討を行う。

2. 結晶塑性解析モデル

結晶の変形解析には，有限要素法を基礎とした3次元結晶塑性解析ソフトウェアコード^6,8,9,10)を用いた。本解析手法では，結晶の塑性すべり変形，それに伴い蓄積する転位，転位の蓄積に伴うすべり変形抵抗の増加すなわち加工硬化，転位の消滅により放出される空孔の蓄積を解析できる。

結晶の塑性すべり変形に伴い蓄積する転位は，統計的に蓄積する転位（Statistically Stored Dislocations，SS転位）と幾何学的に蓄積する転位（Geometrically Necessary Dislocations，GN転位）に分けて計算する。すべり系nにおけるSS転位密度ρ_Sの増分はKocks-Meckingモデル^11,12)により次式で与えられる。

  

$$\text{d}{\rho }_{\text{S}}{}^{\left(n\right)}=\left\{\frac{{\left(1+\alpha \right)}^2}{2\alpha }\frac{1}{\tilde{b}{L}^{\left(n\right)}}-\frac{D}{\tilde{b}}{\rho }_{\text{S}}{}^{\left(n\right)}\right\}\text{d}{\gamma }^{\left(n\right)}$$(1)

ここで，上添字（n）はすべり系の番号を表す。αは転位ループ形状のアスペクト比つまりは転位ループの刃状転位部とらせん転位部の運動距離の比¹³⁾であり本論文では1を用いる。$\tilde{b}$とLはそれぞれバーガースベクトルの大きさ，転位の平均自由行程である。Dは蓄積した転位の対消滅距離である。$D/\tilde{b}$の値として4.1~4.5程度の値¹⁴⁾が提案されており，本論文では$D/\tilde{b}=5$とした。γはすべり系の塑性せん断ひずみである。式（1）は塑性変形と共に増殖した転位ループが距離Lを運動したのちに材料中に蓄積されることと，その一方で，蓄積された転位密度ρ_Sが高くなればすべりを担う転位と距離Dにある反対符号の転位とが対消滅する描像に立脚している。

転位の平均自由行程Lは前述のように，すべり面上を運動する転位が障害物によって捕捉されるまでの距離である。障害物となりうるものとしてはまず，すべり系上の林立転位，すなわち注目するすべり系の転位からみて他のすべり系に蓄積する転位が考えられる。また結晶粒界や第二相などの界面も強力な障害物となりうる^15,16)。そこで転位の平均自由行程は，それまで結晶中に蓄積した転位の平均間隔と，結晶粒径のどちらか小さいほうに依存するものとし次式で与える。

  

$$L^{\left(n\right)}=\underset{}{\min }\left[\frac{c^{*}}{\sqrt{{{\displaystyle \sum }}_m{w}^{\left(nm\right)}\left({\rho }_{\text{S}}{}^{\left(m\right)}+\Vert {\rho }_{\text{G}}{}^{\left(m\right)}\Vert \right)}},d\right]$$(2)

ここで∥ρ_G^(m)∥はすべり系mに蓄積したGN転位の密度ノルムである。式（2）では，SS転位とGN転位が重みw^(nm)を介してすべり系nの転位の平均自由行程に関与する。ここでは林立転位を対象としているためすべり面が同じすべり系同士ではw^(nm)=0，すべり面が異なるすべり系同士ではw^(nm)=1とした。c*は運動転位に対する蓄積転位の抵抗に関する数値係数で経験的に10から100程度の値¹⁷⁾が良く使われ，本論文では15を用いた。

GN転位¹⁸⁾の密度ρ_Gはすべり系の塑性せん断ひずみの空間勾配の関数として下記のように求められる⁹⁾。

  

$$\begin{array}{cc}{\rho }_{\text{G,edge}}{}^{\left(n\right)}=-\frac{1}{\tilde{b}}\frac{\partial {\gamma }^{\left(n\right)}}{\partial {\xi }^{\left(n\right)}},& {\rho }_{\text{G,screw}}{}^{\left(n\right)}=\frac{1}{\tilde{b}}\frac{\partial {\gamma }^{\left(n\right)}}{\partial {\zeta }^{\left(n\right)}}\end{array}$$(3)

  

$$\Vert {\rho }_G{}^{\left(n\right)}\Vert =\sqrt{{\left({\rho }_{\text{G,edge}}{}^{\left(n\right)}\right)}^2+{\left({\rho }_{\text{G,screw}}{}^{\left(n\right)}\right)}^2}$$(4)

式（3）の刃状成分とらせん成分の密度は，それぞれγについてすべり面上においてすべり方向に平行な方向ξと垂直な方向ζでそれぞれ偏微分した値である。∥ρ_G⁽ⁿ⁾∥はGN転位の密度ノルム，別の言い方をすれば「GN転位密度の大きさ」であり，刃状成分とらせん成分からなっている。

すべり系nの臨界分解せん断応力（CRSS）は，拡張Bailey-Hirschモデル¹⁹⁾により次式で与えられる。

  

$${\theta }^{\left(n\right)}={\theta }_0{}^{\left(n\right)}\left(T\right)+{\displaystyle \sum _{m=1}{\Omega }^{\left(nm\right)}a\mu \tilde{b}\sqrt{{\rho }_{\text{S}}{}^{\left(m\right)}}+3\frac{\mu \tilde{b}}{d}}$$(5)

式（5）は3つの項で成り立ち，右辺第1項は温度Tに依存する格子摩擦応力θ₀⁽ⁿ⁾(T)の項，第2項は結晶中に蓄積した転位による変形抵抗を表すTaylorモデルの項，第3項は微視組織に依存する寸法効果を表すOrowan応力の項である。Ω^(nm)はすべり系nの運動転位とすべり系mに蓄積している転位の相互作用行列であり，運動転位と蓄積転位の相互作用がすべり系の組み合わせによって異なることを行列成分の値によって表現するもので，潜在硬化の大きさを示すものといえる。本論文では潜在硬化は微小なものを想定し，その値としてΩ^(nm)の対角項は1，その他の項は1.01とした。aおよびµはそれぞれ数値係数，せん断弾性係数である。Orowan応力項のdは微視組織の特徴長さで，多結晶組織の場合は結晶粒径となる。

異なるすべり面上にのった正負の刃状転位が対消滅するとき，対消滅と同時に原子空孔または格子間原子が結晶中に放出される。ただし格子間原子の形成エネルギーは原子空孔のそれよりも高く²⁰⁾，格子間原子は急速にsinkに吸収される。原子空孔の発生速度はEssmann and Mughrabiの理論⁵⁾をすべり系ごとに展開した次のモデル⁶⁾で表される。

  

$$\begin{array}{ccc}\text{d}{N}^{\left(n\right)}=\left(\frac{Z{D}^2{c}_e}{2}{\rho }_{\text{S},\text{edge}}^{\left(n\right)}-\frac{2y_p{c}_e}{\tilde{b}}\widehat{N}\right)\text{d}{\gamma }^{\left(n\right)} ,& \text{d}\widehat{N}={\displaystyle \sum }_n\text{d}{N}^{\left(n\right)},& \widehat{N}=\int \text{d}\widehat{N}\end{array}$$(6)

$\widehat{N}$とZはそれぞれ総原子空孔密度および原子数密度であり，dN⁽ⁿ⁾はすべり系nのすべり増分dγ⁽ⁿ⁾によって生じた原子空孔密度増分である。c_eはすべりに対する刃状転位の寄与割合で，0.5とした。y_pは転位の掃引により空孔の吸収が生ずる距離であり，バーガースベクトルの大きさに等しいものとした。式（6）のモデルを用いて，SS転位刃状成分の対消滅により形成する原子空孔密度の増分と転位の掃引による原子空孔密度の減少を評価し，塑性すべり変形と共に増大する総原子空孔密度を評価した。

本論文における相当塑性ひずみは次のように計算した¹⁰⁾。塑性仕事増分dW^pは各すべり系に生じた塑性せん断ひずみ仕事を足し合わせて次のように求められる。

  

$$\text{d}{W}^p={\displaystyle \sum _n{\theta }^{\left(n\right)}\text{d}{\gamma }^{\left(n\right)}}$$(7)

ここで，θ⁽ⁿ⁾は前述の通りすべり系nのCRSSであるが，塑性せん断ひずみが生ずるときそのすべり系は活性化しており，CRSSはすべり系に作用する分解せん断応力（RSS）と一致しθ⁽ⁿ⁾=RSSとなる。相当塑性ひずみ増分dε^p_eq.は，塑性仕事増分を相当応力σ_eq.で除すことで以下の通り求まる。

  

$$\text{d}{\epsilon }_{\text{eq}\text{.}}^p=\frac{\text{d}{W}^p}{{\sigma }_{\text{eq}\text{.}}}$$(8)

相当塑性ひずみε^p_eq.は相当塑性ひずみ増分を累積し次のように求めた。

  

$${\epsilon }_{\text{eq}\text{.}}^p={\displaystyle \int \text{d}{\epsilon }_{\text{eq}\text{.}}^p}$$(9)

よって引張と圧縮負荷を交互に与えて繰返し変形するときのように，引張と圧縮のひずみが打消しあうことで巨視的なひずみがゼロとなる場合においても相当塑性ひずみは繰返し数とともに増加する。

すべり系nに生ずる分解せん断応力τ⁽ⁿ⁾_RSSは，すべり系nのSchmidテンソルP_ij⁽ⁿ⁾および応力テンソルσ_ijより次式で与えられる。

  

$${\tau }_{RSS}^{\left(n\right)}=P_{ij}^{\left(n\right)}{\sigma }_{ij}$$(10)

ここですべり系nのSchmidテンソルは，すべり系のすべり面法線方向およびすべり方向の単位ベクトルv_i⁽ⁿ⁾およびb_i⁽ⁿ⁾を用いて次のように定義される。

  

$$P_{ij}^{\left(n\right)}=\frac{1}{2}\left(v_i^{\left(n\right)}{b}_j^{\left(n\right)}+v_j^{\left(n\right)}{b}_i^{\left(n\right)}\right)$$(11)

また本論文における相当応力は，次式で求めた。

  

$${\sigma }_{\text{eq}.}=\sqrt{\frac{1}{2}\left\{{\left({\sigma }_1-{\sigma }_2\right)}^2+{\left({\sigma }_2-{\sigma }_3\right)}^2+{\left({\sigma }_3-{\sigma }_1\right)}^2\right\}}$$(12)

ここで，σ₁~σ₃は主応力であり，応力テンソルの固有値である。

3. モデルおよび条件

Fig.1は，結晶塑性解析に用いた鉄多結晶の平板モデルである。モデルの寸法は103 µm×206 µm×2.3 µmの平板である。モデルは8節点複合要素²¹⁾で100×200×2の40000要素で分割されている。この要素分割モデルはボロノイ分割で30個の結晶粒に領域分割されている。ここで，モデル中の30個の結晶粒径を平均した平均結晶粒径は約30 µmである。結晶方位は，一様乱数を用いてランダムに与えた。Fig.1（b）~（d）の解析モデルの結晶粒の各色は，結晶方位を表している。結晶方位と色の関係は{100}-{110}-{111} 標準ステレオ三角形内にモデルのx，y，z軸の各方向をプロットした際の位置の色となっている。

Fig. 1.

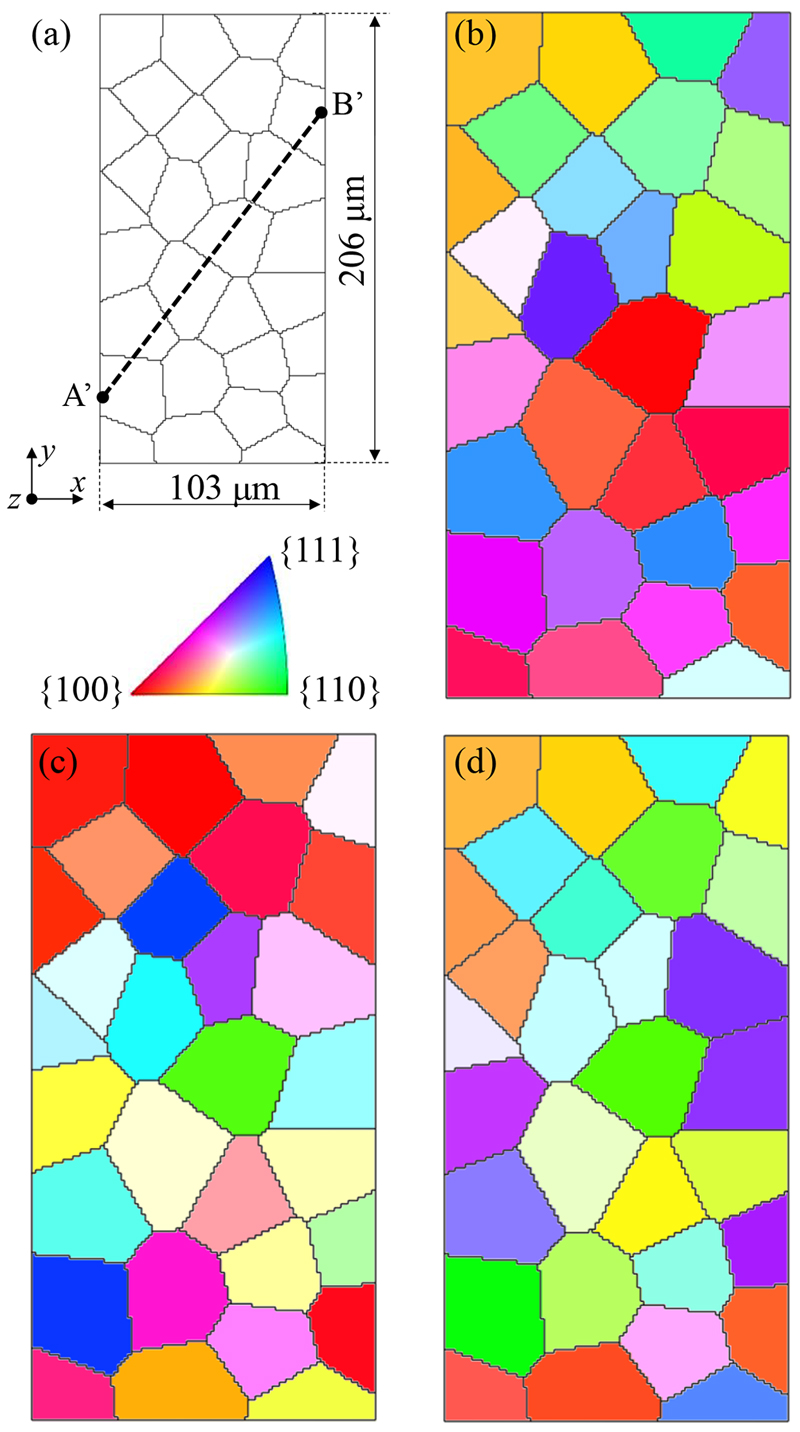
(a) The schematic of the analysis model. The model size is 103 μm×206 μm×2.3 μm. The model consists of 30 crystal grains and the average grain size is about 30 µm. Path line A’B’ is introduced to monitor the distribution of results along the line. (b), (c) and (d) are crystal orientation map of the x, y, and z direction, respectively. (Online version in color.)

解析に用いた主な材料定数をTable 1に示す。材料はBCC構造であるフェライトとし，弾性定数は室温における鉄単結晶の弾性コンプライアンス²²⁾を用いた。このとき，結晶の主軸方向{100}に関するヤング率は約130GPaとなる。すべり系は，{110}<111>すべり系と{112}<111>すべり系が活動するものとし，活動すべり系は計24通りとなる。格子摩擦応力は50 MPaとし，拡張Bailey-Hirschモデル（式（5）)の数値係数aは0.1とした。結晶粒径dは各結晶粒を円盤近似したときの直径とし，各結晶粒で異なる値を設定した。

Table 1. Material data used for the analysis.

		iron
Elastic compliance[×10−11 m2/N]	s11	0.772
	s12	−0.285
	s44	0.902
Magnitude of Burgers vector [nm]		0.248
Lattice friction stress θ0 [MPa]		50
Initial dislocation density [m−2]		24.0×109

鉄多結晶の平板モデルに繰返し変形を与えるため次に述べる負荷を与えた。Fig.1のモデル上下端面にy軸方向の均一強制変位を与え，公称ひずみ0.005となるまで引張変形させ，次に公称ひずみが0となるまで圧縮変形させる負荷を10サイクル与え繰返しの引張―圧縮変形解析（繰返し変形解析）を行った。また比較のため，繰返し変形解析の10サイクル後に生ずる相当塑性ひずみと同程度となるように公称ひずみ0.0614までの単調負荷による引張変形解析を行った。ここで，繰返し変形解析（繰返し負荷条件）と単調負荷による引張変形解析（単調負荷条件）の変形負荷終了時において生ずる相当塑性ひずみの平均値は，それぞれ0.05496と0.05494であった。

4. 結果と考察

Fig.2に単調負荷条件および繰返し負荷条件により得られた応力-ひずみ曲線の結果を示す。単調負荷条件による引張変形解析の結果を破線，繰返し負荷条件による引張―圧縮繰返し変形解析の結果を実線で示す。単調負荷条件では，巨視的な降伏後に線形的な加工硬化特性を示し負荷終了時である公称ひずみ0.0614のとき，公称応力は326 MPaであった。繰返し負荷条件では，サイクルが増加するとともに巨視的な降伏応力が増加するため弾性変形区間が増加し，それに伴い弾塑性変形による線形的な加工硬化特性を示す区間が減少する。最終サイクルにおける最大公称応力は，引張負荷区間で214.1 MPa，圧縮負荷区間で－214.7 MPaであった。Fig.2のグラフのように繰返し負荷条件と単調負荷条件の応力ひずみ曲線は全く異なる曲線となる。そこで単調負荷条件と繰返し負荷条件の結果を比較するため，公称応力の絶対値を平均相当塑性ひずみに対してプロットした公称応力-平均相当塑性ひずみ曲線をFig.3に示す。単調負荷条件による引張変形解析の結果を破線，繰返し負荷条件による引張―圧縮変形解析の結果を実線で示す。平均相当塑性ひずみがほぼ同じ状態において2つの結果を比較すると，繰返し負荷による変形では単調負荷による変形より塑性流動応力が低い値となり大きく異なる力学特性を示す。降伏応力をFig.3における0.2%耐力としたとき，それは繰返し負荷，単調負荷ともに150 MPaである。負荷終了時における繰返し負荷と単調負荷の公称応力の絶対値は，それぞれ214 MPaと326 MPaであり，0.2%耐力からの公称応力の増分Δσはそれぞれ64 MPaと176 MPaとなる。降伏から負荷終了時までの平均相当塑性ひずみの増分Δεは繰返し負荷と単調負荷でそれぞれ0.05296と0.05294である。加工硬化率をΔσ/Δεで計算すると単調負荷条件と繰返し負荷条件でそれぞれ3.32 GPaと1.21 GPaとなる。繰返し負荷による変形では単調負荷による変形に比べて半分以下の加工硬化率であった。

Fig. 2.

The nominal stress – strain curves. Solid and dashed lines show results of cyclic and monotonic loading conditions.

Fig. 3.

The absolute value of nominal stress plotted against average equivalent plastic strain. Points A and B are the end points of the tensile and compressive stages of the first cycle, respectively.

Fig.3に示す繰返し負荷変形の力学特性について注目すると，引張負荷から圧縮負荷へ負荷を反転した際に引張変形で生じた塑性流動応力に比べ低応力で降伏しており，バウシンガー効果が発現している。またサイクル数が増加していくと，さらに低応力からなだらかに降伏しており，より顕著にバウシンガー効果が発現している。バウシンガー効果の発生原因として知られているもの²³⁾の中で，本解析手法によって発生する可能性のあるものは転位の集積により生ずる長範囲の逆応力場（ただし本解析手法では転位による応力場を計算していないため，GN転位の集積と同等の現象である塑性せん断ひずみの不適合度によって生ずる応力場が起因となる）および結晶粒間の応力分配によって生ずる内部応力場である。そこで次に，バウシンガー効果発現の原因となる粒界近傍での内部応力の発生状況を明確化するため，いくつかの粒界を跨ぐ領域での内部応力場の位置変化を調べた。

Fig.4は，Fig.1（a）に示す参照線A’B’上に沿ったすべり系の分解せん断応力（RSSと称す），塑性せん断ひずみおよび相当応力の分布を示したものである。まずFig.4（a）と（b）は，それぞれ1サイクル目および10サイクル目における引張負荷時の公称ひずみ0.005，そこから除荷したとき，および負荷反転後の圧縮負荷時公称ひずみ0でのRSS分布の比較である。●のシンボルで引張負荷時，破線で除荷時，〇のシンボルで負荷反転後の圧縮負荷時の分布を示す。ここでGBと記した縦方向に沿う5本の点線は，結晶粒界を示している。またRSSは結晶粒ごとに異なるすべり系の値をプロットしており，プロットするすべり系の選択は各結晶粒ごとに各すべり系の塑性せん断ひずみの平均値から最も平均値の高いすべり系を用いた。そのため同じ参照線上でも結晶粒ごとにプロットする値のすべり系が異なるため正と負の値が混在している。Fig.4（a）に示す1サイクル目では引張負荷時の公称ひずみ0.005において±80 MPa前後のRSSが分布しており，また結晶粒界近傍で応力の集中がみられる。除荷時では応力レベルが全体的に低下するものの，残留応力が生じており粒界近傍での応力集中も見られる。また引張変形時に形成する応力場の符号と反符号の残留応力，つまり逆応力（分かりやすいようにグレーで塗潰し）の生ずる領域が一部ある。負荷反転後圧縮負荷時の公称ひずみ0では，引張負荷時に形成したRSS分布の符号を反転した状態とほぼ同様のRSS分布となっている。Fig.4（b）に示す10サイクル目の結果では，引張変形時に形成するRSS分布の応力レベルが全体的に増加し，粒内での応力差および粒界での応力集中が増加している。さらに除荷時にみられる逆応力も増加している。

Fig. 4.

Distribution of (a) the resolved shear stress (RSS) at 1st cycle, (b) the RSS at 10th cycle, (c) the plastic shear strain at 1st cycle and (d) the equivalent stress at 1st cycle and 10th cycle along the reference line A’B’ shown in Fig. 1 (a). The dotted lines GB represent the position of the grain boundary.

Fig.4（c）は，すべり系の塑性せん断ひずみ分布である。●のシンボルで引張負荷時の公称ひずみ0.005，〇のシンボルで負荷反転後圧縮負荷時の公称ひずみ0における結果を示す。プロットされる塑性せん断ひずみは結晶粒ごとに異なり，RSS分布と同じすべり系の値である。引張負荷時では粒界近傍での塑性せん断ひずみの抑制および粒内における大きな勾配が生じている。負荷反転後では塑性せん断ひずみが減少し引張負荷時に比べ平坦な分布となっている。これは引張変形時に生じた塑性せん断ひずみが負荷反転後の逆すべりによって塑性せん断ひずみが減少していることを示している。Fig.4（d）は，相当応力の分布である。円（●，〇）のシンボルで1サイクル目，三角（▲，△）のシンボルで10サイクル目の結果を示す。黒塗りのシンボルで引張負荷時の公称ひずみ0.005，白塗りのシンボルで負荷反転後圧縮負荷時の公称ひずみ0の結果を示す。RSS分布と同様に粒界での応力集中や粒内での応力の不均一性が生じている。また結晶粒ごとに担う応力レベルに差がみられる。また引張負荷時と圧縮負荷時で同様の応力場が形成している。これらの特徴は1サイクル目より10サイクル目の方が顕著であり，サイクルが進むほど顕著になるものと考えられる。

以上の結果をまとめると次のことがいえる。Fig.4（a）と（c）の比較より除荷時に見られた残留応力による逆応力は，塑性せん断ひずみの勾配が大きな領域（grain 2，grain 3，grain 5）に生じバウシンガー効果発現の要因となる。この逆応力場はサイクルが進むほど増大しておりバウシンガー効果の増大と整合する。また各結晶粒の担う応力レベルはサイクルが進むほど不均一性が増し，これら結晶粒間の応力分配によって生ずる内部応力場もバウシンガー効果発現の要因となる。次に応力場と塑性せん断ひずみの関係について述べる。RSSは，負荷反転後圧縮負荷時に引張負荷時とほぼ同程度の応力レベルで符号が反転し分布する。このため引張負荷変形と圧縮負荷変形で同じ領域において同程度の塑性すべり変形が生ずる。つまり引張負荷時に形成した塑性せん断ひずみは負荷反転後圧縮負荷時に逆すべり変形によって減少する。この逆すべりによって繰返し負荷条件ではサイクル数が増えても塑性せん断ひずみの不均一性がほとんど増大しない。

そこで次に繰返し負荷変形の加工硬化率が単調負荷変形の加工硬化率に比べて低い要因について検討する。Fig.5は，平均相当塑性ひずみに対して平均転位密度をプロットしたグラフである。単調負荷条件の結果を破線，繰返し負荷条件の結果を実線で示す。細い線でSS転位密度，太い線でGN転位密度の結果を示す。同じ平均相当塑性ひずみが生ずるときにSS転位，GN転位ともに繰返し負荷条件のほうが低い転位密度となった。これは引張変形時に生ずる不均一変形に起因し発展するGN転位密度が，圧縮変形時に不均一変形が緩和することで低下するためである。不均一変形が緩和する要因は前段のFig.4で述べた通りである。Fig.6はGN転位密度分布である。Fig.6のカラースケールは（a）（b）と（c）（d）で10倍値が異なることに注意する。Fig.6（a）は1サイクル目の引張負荷時の公称ひずみ0.005（Fig.3の点A）のときのGN転位密度分布である。なおFig.6（b）は1サイクル目の圧縮負荷時の公称ひずみ0（Fig.3の点B）のときのGN転位密度分布である。Fig.6（a）と（b）の比較から引張変形時に形成したGN転位の密度が負荷反転後の圧縮変形によって低下している様子が観察できる。Fig.6の（c）は繰返し負荷変形10サイクル終了後（平均相当塑性ひずみε_eq.=0.05496）におけるGN転位密度分布，（d）は単調負荷変形の負荷終了時（ε_eq.=0.05496）におけるGN転位密度分布である。Fig.6（c）と（d）を比較すると，繰返し負荷と単調負荷で同じ平均相当塑性ひずみが生じているにも関わらず繰返し負荷の（c）は単調負荷の（d）に比べて明らかに低いGN転位密度分布となっている。これは先にも述べたように繰返し負荷条件では各サイクルで引張負荷変形時に形成したGN転位を圧縮負荷変形時に緩和するということを繰返しながら塑性変形が進んでいくためである。したがって繰返し数とともに発達する塑性ひずみに対して繰返し負荷変形の際のGN転位密度は，単調負荷変形のGN転位密度に比べ小さい。

Fig. 5.

Density evolutions of SSDs and GNDs.

Fig. 6.

Distributions of GN dislocation density. (a) and (b) are the results of cyclic loading condition at point A and B in Fig. 3., respectively. (c) and (d) are the results of the cyclic and monotonic loading conditions at the end of 10th cycle, respectively. The color scale of (a) (b) and (c) (d) are 10 times different. (Online version in color.)

GN転位密度の増加は，式（3）の転位の平均自由行程を介してSS転位の増加率に寄与する。繰返し負荷変形は，単調負荷変形に比べGN転位密度の増加が緩やかであることで転位の平均自由行程の減少が起こりにくい。転位の平均自由行程が大きな値であることはSS転位の蓄積が生じにくいことを表し，つまりSS転位密度の増加率が小さく，それに伴い加工硬化率が小さくなることで低い塑性流動応力となる。以上のように，同じ微視組織においても負荷経路によって異なる転位密度分布となることで力学特性に大きな差異が発現することがわかった。また加工硬化率の低下は，塑性ひずみの局所化の要因となる²⁴⁾。そのため，同じ相当塑性ひずみが加えられる場合でも，繰返し負荷変形の方が早期に塑性ひずみの局所化が生ずるものと考えられる。

Fig.7（a）は平均相当塑性ひずみが約0.018（3サイクル終了時），0.035（6サイクル終了時）および0.055（10サイクル終了時）における相当塑性ひずみの頻度分布である。頻度分布は0から最大の相当塑性ひずみを含む範囲について0.001の幅で区切り，各区間（階級）の相当塑性ひずみ値に属する要素の個数を全要素数で除し100分率に変換した値を各区間の中間値（階級値）に対してプロットしたものである。Fig.7（a）より，単調負荷変形に比べ繰返し負荷変形の相当塑性ひずみ分布は，ばらつきが大きいとわかる。またこの塑性ひずみのばらつきは，変形の繰返しが進むごとに大きくなっている。

Fig. 7.

(a) Histograms of equivalent plastic strain obtained at the end of 3rd, 6th and 10th cycle. (b) Evolution of the standard deviation of the equivalent plastic strain divided by its average value.

ここで塑性変形の進行とともにひずみのばらつきが大きくなっていることを定量的に比較するための指標を考えよう。相当塑性ひずみは，塑性変形と共に増大していくため変形状態によってその平均値は異なり，平均値と共にばらつきも大きくなる。相当塑性ひずみの標準偏差sと相当塑性ひずみの平均値ε_eq.を用いて求められる次の量を考えよう。

  

$$\widehat{s}=\frac{s}{{\overline{\epsilon }}_{eq.}}=\sqrt{\frac{1}{n}{\displaystyle \sum }_{i=1}^n{\left(\frac{{\epsilon }_{i,eq.}}{{\overline{\epsilon }}_{eq.}}-1\right)}^2}$$(13)

ここで，nはデータ点数，つまり要素数である。ε_i,eq.は各要素における相当塑性ひずみである。$\widehat{s}$は，式（13）で示すように平均値で正規化された相当塑性ひずみの標準偏差である。Fig.7（b）は平均の相当塑性ひずみに対して，$\widehat{s}$をプロットしたグラフである。微視的な塑性変形開始直後ではε_eq.が非常に小さくても局所的には塑性すべりが生じているために$\widehat{s}$は極端に高い値となり，その後，巨視的な降伏に向けて徐々に値が低下する。そのためグラフの縦軸は1を最大値として示す。単調負荷条件の結果を破線，繰返し負荷条件の結果を実線で示す。Fig.7（b）より単調負荷条件では変形とともにひずみのばらつきを代表する$\widehat{s}$が減少しており，加工硬化を背景に塑性ひずみが伝播し均一化していくことがわかる。一方で，繰返し負荷条件では，変形とともに$\widehat{s}$が増大しており局所化がより進んでいる。

Fig.8は負荷終了時における相当塑性ひずみの分布図である。この図からも単調負荷変形時に比べ繰返し負荷変形時の塑性ひずみは，局所化していることが観察できる。このような塑性ひずみの局所化は，同じ相当塑性ひずみが生ずる変形であっても単調負荷に比べ繰返し負荷変形を受ける組織中においてGN転位，SS転位の蓄積が少なく加工硬化率が低いことにより生ずるものと考えられる。さらに繰返し負荷変形では，Fig.4で示すように引張変形過程で生ずる塑性せん断ひずみが負荷反転後の圧縮変形過程における逆すべりによって緩和する。また塑性せん断ひずみが緩和するため，圧縮負荷時から除荷した場合に生ずる残留応力が低下する。よって次のサイクルにおける引張変形過程は，最初のサイクルと同様に微視組織の弾性異方性にもとづく応力場を背景に塑性変形するため，初期サイクルと同領域で塑性せん断ひずみが生ずる。このようなサイクルを繰り返すことで，塑性ひずみが伝播せず局所化するものと考えられる。また同領域で塑性変形を繰返した場合においても，その領域での加工硬化率が高ければ，加工硬化することで塑性ひずみがその領域から伝播することは可能になると考えられる。しかし繰返し負荷変形では，塑性せん断ひずみの緩和によってGN転位密度が低く加工硬化率が低いことで塑性ひずみの伝播が生じ難く局所化の促進に寄与するものと考えられる。

Fig. 8.

Distribution of equivalent plastic strain. (a) and (b) are the results of the cyclic and monotonic loading conditions at the end of 10 cycle, respectively. (Online version in color.)

Fig.9は，負荷終了時における原子空孔密度の分布である。（a）は繰返し負荷条件の結果，（b）は単調負荷条件の結果である。負荷条件で異なる分布を示している。ここで原子空孔密度の最大値は，繰り返し負荷条件と単調負荷条件でそれぞれ1.18×10²⁴［1/m³］と1.20×10²⁴［1/m³］であり同程度の最大値となっている。一方で，負荷終了時における平均の原子空孔密度は，繰り返し負荷条件と単調負荷条件でそれぞれ0.859×10²³［1/m³］と1.81×10²³［1/m³］であり約2倍単調負荷条件の方が高い密度となっている。

Fig. 9.

Distribution of atomic vacancy density. (a) and (b) are the results of the cyclic and monotonic loading conditions at the end of 10 cycle, respectively. (c) and (d) are distributions of the results from (a) and (b), respectively, divided by the average vacancy density. (Online version in color.)

原子空孔の生成源となる転位の対消滅は，SS転位が高密度に蓄積するほど発生する。そのためFig.5で示す結果の通り単調負荷条件の方がSS転位密度は高く，単調負荷条件の方が高い原子空孔密度分布を示している。しかし平均で見れば半分程度の原子空孔密度である繰返し負荷条件において最大の原子空孔密度が単調負荷条件のそれと同程度となったのは，繰返し負荷条件における塑性ひずみの局所化が大きく寄与しているものと考えられる。原子空孔密度の平均値が2倍異なる分布結果を局所化という観点で比較しやすいようFig.9の（c）と（d）にそれぞれの平均値で除した原子空孔密度の分布を示す。繰返し負荷条件の方が局所化していることが良くわかる。

Fig.8の相当塑性ひずみの分布とFig.9の原子空孔密度の分布を比較すると，塑性ひずみの集中する領域と原子空孔密度の高い領域は必ずしも一致していない。塑性ひずみは結晶粒界近傍よりも少し離れた領域や粒内に集中している。一方，原子空孔密度では，粒界近傍でも高密度に蓄積する領域が見られる。転位の対消滅による原子空孔形成機構は正負の刃状転位同士がある距離（本論文では5$\tilde{b}$とした）に近づき対消滅することで原子空孔が放出されるものである。そのため刃状転位の密度が高いほど対消滅確率が高く原子空孔形成は促進される。ここでGN転位は幾何学的に必要な転位であり，塑性せん断ひずみ勾配によって同符号の転位の集団として導入されることから，正負の転位対が形成されることはない。つまり転位の対消滅はSS転位によってのみ発生する。SS転位は塑性すべり変形を担う運動転位がある間隔（これを平均自由行程と呼んでいる）で捕捉されることで，統計的に蓄積し密度が増加する。つまり運動転位のトラップサイトとなる林立転位の増加により転位の平均自由行程が短くなるほどSS転位密度は増加しやすく，対消滅により原子空孔形成頻度が増加する。このような原子空孔形成機構から粒界近傍において原子空孔密度が高い要因は次のように考えられる。多結晶体は，結晶の弾性異方性によって弾性変形中すなわち変形初期に結晶粒界で局所的な応力集中が生じ，その結果，粒界近傍で塑性変形が開始すると考えられている²⁵⁾。本解析においても同様に，応力集中の生じた結晶粒界から塑性変形が開始していた。応力集中が生じ，また隣接粒との変形の適合性を満たす必要がある粒界近傍では多重すべりも容易となり硬化する。変形が進むと硬化した粒界より単一すべりで塑性変形を担える粒内に塑性ひずみが集中する。しかし塑性ひずみが集中する粒内より，多重すべりが多く生ずることで林立転位が増加し転位の平均自由行程が減少する粒界近傍で高いSS転位密度となっていた。そのため高い密度で蓄積したSS転位の対消滅により原子空孔密度の増加が粒界近傍で多く生ずるものと考えられる。

本論文における繰返し負荷変形は，公称ひずみ0.005の引張変形を加えた後に公称ひずみ0となるまで圧縮変形を加え，この変形サイクルを10サイクル与えている。そのため10サイクルの変形終了後におけるみかけの変形は，Fig.8（a）でみられるように殆どない。しかし相当塑性ひずみは，変形サイクルが進行するとともに着実に増加する。塑性ひずみの増加に伴い結晶欠陥である転位密度および原子空孔密度も増加する。また塑性ひずみが局所化しやすいことにより，転位密度および原子空孔密度の平均値に対して原子空孔密度の最大値は高い結果となる。このような結晶欠陥の局所化による損傷の形成が，破壊の起点となるような損傷形成過程につながってゆくと考えられる。

5. 結言

純鉄多結晶体の繰返し疲労に伴うひずみの局所化と損傷形成素過程について基礎的な検討を行うため，繰返し負荷と単調負荷による鉄多結晶体中の塑性ひずみの発展とそれに伴う原子空孔密度の発展に着目し，結晶塑性解析を用いて比較検討した結果，以下のことが分かった。

（1）巨視的な力学特性は，繰返し負荷変形と単調負荷変形で大きく異なり，繰返し負荷変形の加工硬化率は単調負荷変形のそれの半分以下であった。繰返し負荷変形時の加工硬化率が低い要因は，引張と圧縮のひずみが繰返されることにより塑性ひずみの勾配が緩和されることでGN転位密度の増加が緩やかとなるためである。同じ微視組織においても負荷経路が単調負荷と繰返し負荷で異なることにより，巨視的力学特性，塑性ひずみ分布，転位密度分布，原子空孔密度分布はそれぞれ大きく異なる結果となる。

（2）単調負荷変形時に比べ繰返し負荷変形時の加工硬化率が低いことによって，繰返し負荷変形では塑性ひずみの局所化がより顕著に生ずる。また単調負荷変形は塑性変形と共にひずみが均一化していくのに対して，繰返し変形はひずみの局所化が進行する。

（3）原子空孔密度は単調負荷変形時の方が繰返し負荷変形時に比べ高い平均密度となる。その要因は単調負荷変形の方がGN転位の密度が高くSS転位の蓄積に寄与する転位の平均自由行程が小さいためである。SS転位が高密度に蓄積するほど転位の対消滅頻度が上昇し原子空孔密度が上昇する。繰返し負荷による変形では，原子空孔密度の平均値は単調負荷の場合に比べて低い一方，その最大値は殆ど変わらず，繰返し負荷変形時の方が局所化していた。

謝辞

本研究は，第29回鉄鋼研究振興助成の支援を受けて行われたものである。記して謝意を表す。また本研究の一部は，科学研究費補助金{基盤研究（B），（課題番号「20H02457」）}の支援を受けて行われたものである。記して謝意を表す。

文献

• 1)  N.Grilli, K.G.F.Janssens, J.Nellessen, S.Sandlöbes and D.Raabe: Int. J. Plast., 100(2018), 104. https://doi.org/https://doi.org/10.1016/j.ijplas.2017.09.015
• 2)  J.-i.Takamura, I.Takahashi and M.Amano: Trans. Iron Steel Inst. Jpn., 9(1969), 216. https://doi.org/10.2355/isijinternational1966.9.216
• 3)  S.Takenaka, R.Takahashi, K.Ishikawa and Y.Miyajima: Tetsu-to-Hagané, 109(2023), 927 (in Japanese). https://doi.org/10.2355/tetsutohagane.TETSU-2023-050
• 4)  M.Fujinami, S.Jinno, M.Fukuzumi, T.Kawaguchi, K.Oguma and T.Akahane: Anal. Sci., 24(2008), 73. https://doi.org/10.2116/analsci.24.73
• 5)  U.Essmann and H.Mughrabi: Philos. Mag. A, 40(1979), 731. https://doi.org/10.1080/01418617908234871
• 6)  T.Ohashi: Philos. Mag., 98(2018), 2275. https://doi.org/10.1080/14786435.2018.1478142
• 7)  T.Ohashi and Y.Okuyama: Philos. Mag., 99(2019), 3032. https://doi.org/10.1080/14786435.2019.1659517
• 8)  T.Ohashi: Philos. Mag. A, 70(1994), 793. https://doi.org/10.1080/01418619408242931
• 9)  T.Ohashi: Philos. Mag. Lett., 75(1997), 51. https://doi.org/10.1080/095008397179741
• 10)  T.Ohashi: Mathematical Modeling of Dislocation Behavior and its Application to Crystal Plasticity Analysis, Springer, Cham, (2024). https://doi.org/10.1007/978-3-031-37893-5
• 11)  U.F.Kocks: J. Eng. Mater. Technol., 98(1976), 76. https://doi.org/10.1115/1.3443340
• 12)  H.Mecking and U.F.Kocks: Acta Metall., 29(1981), 1865. https://doi.org/10.1016/0001-6160(81)90112-7
• 13)  T.Ohashi: Trans. Jpn. Inst. Met., 28(1987), 906. https://doi.org/10.2320/matertrans1960.28.906
• 14)  I.S.Yasnikov, A.Vinogradov and Y.Estrin: Scr. Mater., 76(2014), 37. https://doi.org/10.1016/j.scriptamat.2013.12.009
• 15)  Y.Yasuda and T.Ohashi: ISIJ Int., 57(2017), 573. https://doi.org/10.2355/isijinternational.ISIJINT-2016-612
• 16)  Y.Okuyama and T.Ohashi: Tetsu-to-Hagané, 102(2016), 396 (in Japanese). https://doi.org/10.2355/tetsutohagane.TETSU-2015-096
• 17)  D.Kuhlmann-Wilsdorf: Mater. Sci. Eng. A, 113(1989), 1. https://doi.org/10.1016/0921-5093(89)90290-6
• 18)  M.F.Ashby: Philos. Mag.-J. Theor. Exp. Appl. Phys., 21(1970), 399. https://doi.org/10.1080/14786437008238426
• 19)  T.Ohashi, M.Kawamukai and H.Zbib: Int. J. Plast., 23(2007), 897. https://doi.org/10.1016/j.ijplas.2006.10.002
• 20)  D.Hull and D.J.Bacon: Introduction to Dislocations, Butterworth-Heinemann, Oxford, UK, (2001). https://doi.org/10.1016/B978-0-7506-4681-9.X5000-7
• 21)  O.C.Zienkiewicz, trans. by M.Yoshiki and Y.Yamada: The Finite Element Method in Engineering Science, Baifukan, Tokyo, (1975), 99 (in Japanese).
• 22)  G.Simmons and H.Wang: Single Crystal Elastic Constants and Calculated Aggregate Properties, The MIT Press, Cambridge, MA, (1971), 34. ISBN978-0262190923
• 23)  T.Hasegawa: Bull. Jpn. Inst. Met., 15(1976), 509 (in Japanese). https://doi.org/10.2320/materia1962.15.509
• 24)  J.R.Rice: Theoretical and Applied Mechanics, Vol.1, North-Holland, Amsterdam, (1976), 207. ISBN978-0720405491
• 25)  M.A.Meyersm and E.Ashworth: Philos. Mag. A, 46(1982), 737. https://doi.org/10.1080/01418618208236928