2013 Volume 99 Issue 4 Pages 322-328
Austenitic stainless steel is widely used in important industries since it has excellent mechanical and chemical properties such as anti-corrosion, high ductility and high strength. In the past, it was reported that its extremely high energy absorption can be measured by the Charpy impact test. The mechanism of its energy absorption characteristic is still unclear and its rate sensitivity has not been discussed. In the present study, a rate sensitivity of energy absorption characteristic of austenitic stainless steel will be discussed experimentally by measuring J-integral under 3-point bending condition for a wide range of displacement rate. In the experiment, the direct current potential difference method is employed for sensing an onset of a stable crack extension. As a result, the positive rate sensitivity on the energy absorption can be observed and high energy absorption can be achieved by the high ductility of the steel.
オーステナイト系ステンレス鋼は高耐食性や光沢に優れているだけでなく，極低温での優れた加工硬化特性や高強度，常温付近で示す高延性および高じん性等優れた機械的性質を示すことから，非常に重要な工業用材料として広範に用いられている1,2)。この鋼は準安定オーステナイト組織を持ち，塑性変形に伴って組織の一部にマルテンサイト変態が生じる。この現象はひずみ誘起マルテンサイト変態と呼ばれる3)。通常，マルテンサイト変態を生じると，強度が向上する一方で延性は低下する。しかしながら，オーステナイト系ステンレス鋼の場合，引張変形の際に優れた均一伸びが得られ，結果的に強度のみならず延性，じん性も飛躍的に向上する1,3)。その一方で，溶接性やプレス成形性などの加工性を，材料の組織制御にて向上させるよう，難加工性材料に挙げられるオーステナイト系ステンレス鋼に対しては積極的な研究が行われている1)。
マルテンサイト変態は，外部から作用するエネルギーを消費あるいは散逸して発生すると考えられることから3,4)，力学的作用によって発生するマルテンサイト変態を伴う材料は，外環境から作用する力学的エネルギーの吸収特性が高いものと考えられる。その証拠に，過去に行われた研究5)では，種々のオーステナイト系ステンレス鋼を対象として，常温と極低温におけるシャルピー衝撃試験によって，吸収エネルギーに及ぼす圧延の際の圧下率の影響が評価されており，常温における未圧延材の結果によれば，軟鋼に比して2~3倍程度のエネルギー吸収能を持つことになる。
シャルピー衝撃値によって，準静的から衝撃までの広範囲の変形速度におけるエネルギー吸収能を議論しようとすれば，その試験装置の構造から困難である。また，シャルピー衝撃試験では，得られた衝撃値にき裂の進展による散逸エネルギーも含まれることになるため，材料の変形自体による吸収エネルギーを評価することは困難である。それに対して，広範囲のひずみ速度において引張試験を実施し，応力−ひずみ曲線が囲む面積を用いて吸収エネルギーを評価する方法がある。Tomita and Iwamoto6)は提案した構成モデルを用いた有限要素解析によって，オーステナイト系ステンレス鋼の均一伸びや強度に及ぼすひずみ速度の影響を検討しており，均一伸びはひずみ速度の増加に伴って減少することを示している。この結果は，不可逆仕事の増加に伴う熱発生の影響により，すなわちオーステナイト相の安定化により延性の低下を招くものと説明されている。この研究によって示されている応力−ひずみ曲線を用いて，それが囲む面積により吸収エネルギーの速度依存性を議論すれば，準静的試験の場合に比して，衝撃試験の場合のエネルギー吸収能は低下することになる。すなわち，前述のシャルピー衝撃試験の結果を考慮すれば，準静的試験下における吸収エネルギーは軟鋼の2倍をはるかに超える値となることが予想されることに疑問が生じる。
一方，同じひずみ誘起マルテンサイト変態が発生するTRIP鋼を対象として，Antolovich and Singh7)は応力拡大係数に着目し，平面ひずみ状態においてその温度依存性を実験的に明らかにした上で，熱力学を援用して変態による応力拡大係数向上の寄与分を算出している。また同時期に，Birat
and Gerberich8)は準安定オーステナイト組織を持つ鋼板の応力拡大係数を平面応力において測定し，約540MPa
の非常に高い値に達すると報告している。続いて，Gerberichら9)はその高い応力拡大係数がオーステナイト相の不安定化によってもたらされること，ならびに熱力学的な考察からオーステナイト相の安定化に伴う応力拡大係数の変動が，Antolovich
and Singh7)と同様に格子不変せん断ひずみに大きく依存していることを示した。本来，応力拡大係数等の破壊力学パラメータはき裂進展に対する抵抗力を示すが，き裂を単位面積進展させるのに必要なエネルギーとも考えられ，準静的から衝撃までの幅広い速度範囲にて，エネルギー吸収特性の評価に適用することが可能である。しかしながら，オーステナイト系ステンレス鋼における，エネルギー吸収能評価，ならびにその速度依存性の議論に破壊力学パラメータを用いた研究は極めて少ない。また，オーステナイト系ステンレス鋼は延性材料であり，小規模降伏状態を仮定した応力拡大係数より，J積分10)によって議論すべきである。このような観点から，Kobayashiら11)は，J積分値によって計装化シャルピー衝撃試験装置から得られたTRIP鋼の衝撃J積分値を測定し，MnおよびNi量が及ぼす影響を検討している。また，Iwamoto
and Tsuta12)は有限要素解析によって，オーステナイト系ステンレス鋼の高いJ積分値は，ひずみ誘起マルテンサイト変態によってもたらされることを明らかにし，Rodriguez-Martinezら13)はオーステナイト系ステンレス鋼板の貫通試験の結果，エネルギー吸収能はマルテンサイト変態によって向上されることを結論づけている。さらに，オーステナイト系ステンレス鋼を対象に，準静的14,15)およびシャルピー衝撃試験下16)においてJ積分値が測定されているが，その値は文献によって大きく異なり，準静的と衝撃試験では同レベルの値となる等，その速度依存性は検討されていないと言える。
そこで本研究では，オーステナイト系ステンレス鋼の一種であるSUS304を対象に，そのエネルギー吸収特性を，弾塑性破壊力学パラメータの1つであるJ積分を用いて実験的に評価する。まず，切欠き試験片を作成し，これに疲労予き裂を挿入する。次に材料試験機を用いて，クロスヘッド速度から算出した速度域にして10−4~10−1s−1にて準静的3点曲げ試験を行う。続いて，落錘型衝撃試験機を用いて約101s−1レベルの速度にて衝撃3点曲げ試験を行う。これらの結果をもとに各変形速度におけるJ積分値を算出し，オーステナイト系ステンレス鋼のエネルギー吸収能の速度依存性を実験的に評価することを目的とする。
供試材のミルシートより，本研究で用いたオーステナイト系ステンレス鋼SUS304の化学成分をTable 1に示す。試験片形状は3点曲げ切欠き試験片とする。試験片厚さならびにスパン間隔はそれぞれ12mmおよび80mmとし，これらを基準にASTM規格に準じて，板状の供試材に対し，Fig.1に示すような形状に機械加工を行う。なお，試験片は加工により組織変化を生じている可能性があるため，組織を均一なオーステナイト組織が得られるよう，1323Kで30分間加熱し，その後水中にて急冷する固溶化熱処理を施す。Fig.2は固溶化熱処理後の試験片の顕微鏡写真である。Fig.2を用いて切片法により求めた平均結晶粒径は約51μmとなる。
Chemical composition of SUS304.
Notched specimen made of SUS304.
Micrograph of the specimen after solution treatment.
各試験片の切欠き先端には，疲労試験機(島津製作所製，サーボパルサーE200kN)を用いて，ASTM規格に従い，最大繰返し荷重Pfmax=3.65kNを適用し，負荷周波数30Hzにて長さが2.4mmの疲労予き裂を挿入する。なお，各試験のn数は1とする。
2・2 直流電位差法ならびにJ積分値の算出法き裂進展に伴う試験片断面積の減少により，試験片の電気抵抗が増加する。Fig.3は安定破壊開始時の急激な電圧変化の一例を示している。試験中に定電流を供給することにより，安定破壊開始点のみならず，き裂進展の様子そのものを電圧変化として捉えることが可能となる17)。
Schematic illustration of changes in the load and the voltage during three-point bending test.
直流電位差法では，試験片形状に依存して，推奨される電流値が設定されている18)。本実験では，精度良く安定破壊開始点を検出するため，Fig.4に示すように6Aの定電流源(KENWOOD製，PA18-6A)を2台並列に接続し，12Aの定電流源として使用する。この時の電流密度は推奨電流値に近い値となる。
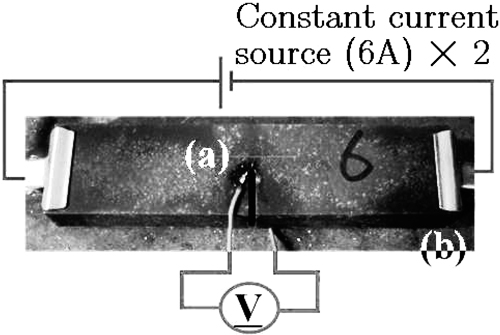
A photograph of notched specimen and probes for measurement of onset of stable crack extension by the direct current potential difference method.
実際の測定における電圧測定端子の試験片上の固定位置は，測定感度の点からFig.4に示す(a)の位置とし，スポット溶接機(近藤生産性技術所製，KTH-MWS)を用いて端子先端を試験片に固定する。この図に示すように，電圧測定端子は感度を可能な限り向上させるため，試験片の厚さ方向に予き裂を挟むよう対角に固定する方法を採用した。衝撃試験において，スポット溶接部の上からさらにビニールテープにより固定する。また，接触抵抗の影響を除去するため，4端子法を採用する。本実験では電流供給端子の位置は同図中(b)とし，試験片表面全体に均一に電流が流入可能なように端子を固定する。なお，電圧は直流増幅機能を有するシグナルコンディショナ(共和電業製，CDV-700A)により9000倍に増幅して測定を行う。
一方，J積分の測定について，Riceら19)は，き裂が深く，部材の荷重−荷重点変位線図がリガメント幅のみに依存する場合のJ積分簡便評価式を提案している。Riceら19)によると，曲げ変形が支配的な場合，J積分は次式のように表される。
 |
ここで，AはFig.3で示した荷重−荷重点変位曲線下のき裂進展開始までの面積であり，試験片に外部から作用する力学的エネルギーと同義である。Bは試験片厚さ，bはリガメント幅，Wは試験片高さを表し，疲労予き裂を含むき裂長さをa0とすれば，W=a0+bとなる。Fig.1に示す本研究で用いる試験片形状を考慮すれば，W=24mm，B=12mm，a0は切欠き長さ12mmに疲労予き裂長さ2.4mmを加えた14.4mmとなる。f(a0/W)はa0およびbに依存する関数を示す。この式によれば，J積分は試験片に加えられたエネルギーを，試験片のき裂部分を除いた初期断面積で除して一般化したパラメータであると言える。このことから，本研究ではJ積分を用いることによってエネルギー吸収能を評価可能であると考える。なお，ASTM規格に基づいた三点曲げ試験片の場合，f(a0/W)に対して2の一定値を用いる17)。以上より，各実験から荷重−荷重点変位線図および安定破壊開始点を検出することにより，式(1)を用いてJ積分を算出することが可能である。なお，シャルピー衝撃試験によって得られる衝撃値との相違点は，試験片形状ならびに疲労予き裂はもちろんのこと，Fig.3に示した荷重−荷重点変位曲線が描く面積の算出基準ならびにf(a0/W)=2の存在である。計装化シャルピー衝撃試験において計測される荷重−変位曲線の面積をSとすれば，衝撃値Iは以下のように計算することができる。
 |
もし，J積分値がシャルピー衝撃値と等価であれば，以下式が成立する。
 |
すなわち，試験片形状に関する相違点を除外して，安定き裂進展開始点までの面積の2倍が破壊後完全除荷された際の面積と等しくなれば，J積分値はシャルピー衝撃試験で得られた衝撃値と等価である。なお，前述のようにIはき裂の進展によるエネルギー吸収を考慮していることとなるので，一般には式(3)で示した単純な式が成立しないことを付記する。
2・3 準静的および衝撃試験準静的試験は，材料試験機(島津製作所製 オートグラフAG-250kNXplus)を用いて実施する。試験片の治具と接触する部分には，モリブデングリスを塗布することにより，試験片と治具間に生じる摩擦の影響を低減する。試験片に負荷した荷重は試験機に付属のロードセル，変位はクロスヘッド変位ならびにビデオカメラにより動画を撮影した上で，動画の画像処理によって測定する。また，クロスヘッド速度は0.2， 2， 20， 200mm/minの4種類に設定して，準静的試験を行う。この際，スパン長さを用いた無次元化荷重点変位速度は，クロスヘッド速度に対応して，それぞれ4.17×10−5，4.17×10−4，4.17×10−3および4.17×10−2/sとなる。荷重点変位速度の単位は[mm/s]であるが，これをスパン長さで無次元化した無次元化荷重点変位速度の単位は[/s]となる。
本研究では，落錐型衝撃試験装置を用いて衝撃3点曲げ試験も準静的試験と同様に行う。Fig.5に試験装置の概略を，Fig.6に装置の写真等詳細図を示す。Fig.5に示すように，本試験機は，電磁石(カネテック製 KE-7B)を介して，ウィンチにより重錘を所定の高さまで牽引した後，電磁石の操作によってガイドレールに沿って真直性を保ちながら試験片へ重錘を落下させる構造である。衝撃試験の際に生じる荷重は，Fig.6(c)に示すような検力ブロック20)を用いて測定した。検力ブロックには小突起が設けられ，その直下にある本体の断面積を小突起に対して十分大きく設定することにより，小突起に反射波が伝播し難い構造となっており，衝撃試験中も精度よく荷重の測定を可能とする20)。試験片に作用する荷重は，Fig.6(b)に示す3点曲げ用治具を介して，検力ブロックの小突起に貼り付けられたひずみゲージ(東京測器研究所製，UFLA-1-350-11)により，ひずみ波として検出し，き裂進展を検知する電圧信号とともにFig.6(d)に示すシグナルコンディショナにより増幅し，デジタルオシロスコープ(Iwatsu製，DS-5110)に出力する。重錘の高さは，試験片上部から重錘に設置したパンチ先端までの距離により定義し，本実験では700および900mmに設定する。また，衝突直前の落下速度は，Fig.6(e)に示すように50mm間隔で設置した2つのファイバーセンサ(KEYENCE製，FU-77V)が遮断される際に生じる，センサを接続した専用アンプ(KEYENCE製，FS-V31，FS-V32)からの信号の時間差により計測する。その結果，設定した重錘の高さに対応し，重錘の試験片衝突直前における落下速度はそれぞれ約3190および約3530mm/sとなった。これより無次元化荷重点変位速度を定義すると，それぞれ約40および約44/sとなる。なお，荷重点変位は最大8000fpsの高速度カメラ(Plextor製，PL1-C10)を用いて測定する。
Schematic of the structure of drop weight impact testing machine.
Photographs of (a) whole structure, (b) a part near jig, (c) load sensing block, (d) measurement devices and (e) optical fiber sensor in the impact testing machine.
Fig.7に，スパン長さで除した無次元化荷重点変位速度が(a)4.17×10−5，(b)4.17×10−2ならびに(c)40/sにおける荷重ならびに電圧−荷重点変位線図を示す。き裂の鈍化に伴って，材料組織内に空洞が形成されるため，本来ならば鈍化中にも微小な電圧上昇が観察されるものと考えられる。しかしながら，空洞が形成されることによって生じる階段状の電圧変化が観察できないことから，本実験で適用している電流値12Aでは空洞の形成現象を捕捉できているとは言えない。この図に示すように，変形初期段階に現れる電圧−変位曲線の直線部分からの変曲点を検出し，安定破壊開始点としてJ積分値を算出した。この図(a)~(c)を比較すると，無次元化荷重点変位速度の増加に伴って，安定破壊開始点における荷重には，無次元化荷重点変位速度の増加に伴う明確な差を観察し難いが，安定破壊開始点における変位が増加する傾向を確認可能である。
Load and voltage vs displacement at loading point for normalized displacement rate of (a) 4.17×10–5, (b) 4.17×10–2 and (c) 40/s.
Fig.8に，準静的3点曲げ試験および衝撃試験によって形成された破面を示す。この図(a)および(b)中にある灰色の実線は，疲労予き裂前縁ならびに安定き裂進展開始位置を容易に認識可能なよう描いた線である。また，Fig.8(a)に示す準静的試験から得られた破面においては，疲労予き裂前縁と安定破壊開始点はほぼ一致している。一方，Fig.8(b)に示す衝撃試験から得られた破面においては，疲労予き裂前縁と安定破壊開始点間に距離が存在していることがわかる。これは，準静的試験において，き裂の鈍化が疲労予き裂前縁付近の微小な領域で発生し，衝撃変形下においては，き裂の進展に抵抗し，き裂が大きく鈍化したためであると考えられる。さらに，Fig.8(c)および(d)から，き裂進展によって生成された破面を比較すると，準静的と衝撃試験では疲労予き裂前縁とき裂発生位置の差だけでなく，き裂進展後の破面の形状についても大きく異なっていることがわかる。準静的試験では，き裂の進展方向にディンプルが配向している様子が伺えるが，衝撃試験の場合，準静的試験の場合に比して非常に粗い破面を示している。この破面の違いは，変位速度の増加に伴ってき裂進展に伴う破壊の発生機構が異なっている可能性を示唆している。なお，破面の顕微鏡観察については今後の検討課題とする。
Photographs of fracture surface obtained by (a) quasi-static (4.17×10–5/s), (b) impact test (40/s), and different views of the specimens obtained by (c) quasi-static (4.17×10–5/s) and (d) impact test (40/s).
Fig.9に，得られたJ積分と無次元化荷重点変位速度の関係を片対数表示して示す。なお，図中の直線は近似直線である。この図に示すように，無次元化荷重点変位速度の増加に伴い，J積分値は直線的に増加していることがわかる。このことから，SUS304のエネルギー吸収能には，荷重点変位の増加に伴うJ積分値の増加という，正の速度依存性があると考えられる。これは，前述の破面観察における議論のように，安定破壊開始点までの鈍化過程に寄与する荷重点変位の増加に起因した，エネルギー吸収能の増加が考えられる。
Relationship between J-integral and normalized displacement rate.
Fig.10に安定破壊開始点における荷重および荷重点変位を無次元化荷重点変位速度に対して示す。安定破壊開始点における荷重は，荷重点変位速度の増加に伴って，ほぼ一定値を示しており，変位速度の増加に伴う強度の増加が，前述のエネルギー吸収特性の速度依存性に寄与しているとは考えがたい。一方，荷重点変位は，J積分値と同様に変形速度に対して増加する傾向にあり，これに起因してエネルギー吸収能が向上するものと考えられる。これは，前述した準静的および衝撃試験における安定破壊開始点の差異からも，同様の考察に至る。しかしながら，J積分値のひずみ速度依存性とは異なり，荷重点変位はある閾値を境目に，無次元化変位速度に対して急激に上昇する傾向にあることに留意する必要がある。
Displacement at the loading point and load at the point of onset of the stable fracture extension vs normalized displacement rate.
以上より，ひずみ速度の増加に伴ってオーステナイト系ステンレス鋼の延性が増加することを示しており，これが起因してエネルギー吸収能の向上に至るものと考えられる。前述のように，オーステナイト系ステンレス鋼の延性の増加には，ひずみ誘起マルテンサイト変態が寄与しており，Iwamoto and Tsuta12)ならびにRodrigues-Martines13)の解析や実験結果が示すように，引張試験とは異なる応力状態においても同様である。しかしながら，Tomita and Iwamoto6)による引張試験の解析結果におけるひずみ速度の増加に伴う延性の減少の結果と異なるものとなっており，今後の検討を要する。
本研究では，オーステナイト系ステンレス鋼SUS304を用いて疲労予き裂を挿入した切り欠き試験片を作成し，様々な変形速度の下，3点曲げ試験を行うことにより，そのエネルギー吸収能の速度依存性をJ積分により実験的に評価した。本研究で得られた結論を以下に示す。
(1)荷重点変位速度の増加に伴うJ積分の増加という，エネルギー吸収能に速度依存性の存在を確認した。
(2)安定破壊開始点における荷重ならびに荷重点変位を変形速度ごとに比較すると，荷重点変位速度の増加に伴って，荷重点変位が増加する一方で，荷重はほぼ一定値を示した。一般的に，ひずみ誘起マルテンサイト変態に起因する強度ならびに延性が向上するが，本研究では応力のひずみ速度依存性に見られるような強度の向上は確認することが困難であった。このことから，エネルギー吸収能の増加は，オーステナイト系ステンレス鋼の延性の向上に起因するものと考えられる。
本研究は文部科学省科学研究費補助金基盤研究(C)の補助を受けて遂行した。記して謝意を表する。
