2025 Volume 33 Issue 1 Pages 1-10
2025 Volume 33 Issue 1 Pages 1-10
Japan is a tourism-rich country with abundant water resources, and its archipelago landscapes are particularly important features. To capitalize on the trend of tourism recovery, the management and improvement of archipelago landscapes are crucial. However, in recent years due to fiscal constraints, many tourist areas have neglected green space management. The growth of trees and other vegetation has a significant impact on the landscape. This paper focuses on the Kujūku Islands as the main research subject. Additionally, this paper focuses on green space management, using the identifiable number of islands as an indicator to evaluate archipelago landscapes. Using mathematical models such poisson point process, we demonstrate that when the central field of view overlooking the landscape is obstructed, the number of visible islands decreases significantly. The influence of tree growth on the visible sea surface area and the visible islands is shown.
九十九島,平戸島,天草,瀬戸内海,松島の多島海景観は日本を代表する自然資源である.その醍醐味は,俯瞰景に映り込む島の数である.そのため,主たる視対象は海面ではなく島となる.一方で,近年樹木や雑草の繁茂など緑地管理不全が深刻となっている.その原因として,人口減少と高齢化による人手不足やコミュニティの希薄化,相続不調による山林放棄,さらには自治体の財政悪化がある.そのため,良好な多島海景観が広がっていても,生い茂る草木により眺望が阻害されている(例えば,濱久保ら,2022).そこで,本研究では,多島海景観を対象とし,樹木成長による眺望阻害を動的に分析する.
1995年に西海国立公園に指定された「九十九島」は,入り組んだリアス海岸と群島で構成される景勝地である(図1参照).日本で島々が最も密集しており,大地の栄養が豊富な海であり生物多様性の観点からも貴重な場所である.「九十九」とは,「数えきれないほどたくさん」という意味である.澤(2016)によれば,九十九島は200以上の島々から構成され,夕日や干満差による日々の変化が景観の特徴である.

九十九島のある佐世保市が策定した「令和3~5年度佐世保市観光アクションプラン」では,滞在型観光を推進している.一方で,佐世保市へのヒアリング(2024年2月16日)によれば,インバウンド観光の回復も遅れている.観光回復のために,沿道も含め展望台周辺などの眺望環境の整備は不可欠である.
図2は佐世保市の三階建ての石岳展望台3階から撮影した九十九島の景観である.展望台は垂直構造物であり,最上階である3階はパノラマ俯瞰景を享受できる場として設計された.しかし周辺の植生繁茂により視界が遮られている.そのため,1階という低所ではあるが,繁茂の影響を受けにくい海岸近くに訪問者が集まっている.このように,樹木成長は,垂直構造物の機能を弱めている.緑地管理不全は多島海景観のみならず多くの水辺景観を悪化させている.例えば,日本三大名園の1つである偕楽園周辺では,樹木成長が借景である千波湖への視界を遮り,見える千波湖の形を扁平にさせている(任ら,2023).

財政難により緑地管理に投入できる予算が年々縮減されている.他方,樹木は日々成長するため,剪定の先延ばしは将来負担をさらに増やしていく.良好な多島海眺望景観の確保のため,効果的な緑地管理の考え方が求められる.
1.2 研究の目的本研究では,俯角領域を,近景,中景,遠景と三区分に設定し,海面までの距離による見え方の違いに関する2つの特性に着目し,解釈を加えていく.図3に多島海景観の特徴をCGパース(Lumion 12.0.2 studentで作成)で示す.第一の特徴として,CGパースが示すように,同じ仰角幅でも,近景では,視対象は海域が支配的であるが,遠景に近づくほど海域より島嶼が目立ち,島嶼が支配的となる.そのため,近景では島数は少なく島々は分離して見える.遠景では多くの島が存在するが,視覚的に島々が重なり見かけ上の島は一つとなり,多島海として認識できない.第二の特徴として,樹木は成長するにつれて近景,中景,遠景の順で視野を狭窄していく.つまり,視界は近・中・遠景から中・遠景となり,最終的には遠景のみに限定される.これら2つの特性を組み合わせて緑地管理不全と認識できる島嶼数との基本的な関係を導出する.本研究の目的は,多島海景観の見え方を数理モデルで表現し,緑地整備や管理不全が多島海島嶼数の可視性へ与える影響を抽出することにある.そして,俯角中心領域での視界を確保する緑地整備の重要性を示す.

1.3 研究の位置づけ
多島海の俯瞰景について,脇水(1937)は,良い景観の条件として広い視野と適切な島の配置,視点場の高さの重要性を挙げ,瀬戸内海の魅力を説いている.篠原(1982)は視点場からの俯角を通じて景観の見え方を特徴づけた.窪田(1984)はメッシュデータを用いた可視分析を展開し,俯角が小さすぎると奥行き感が薄れることを指摘した.西田(1996)は,瀬戸内海の俯瞰景観の評価の変遷を整理した.伊藤(2010)は露出海域面積に対する島嶼総面積比率(島/海比率)を用い,さらに,樋口(1975)や篠原(1982)に基づき,俯角10°~8°の範囲が多島海俯瞰景観の中心領域であることを確認した.伊藤(2011, 2012)は,松島や九十九島における観光地整備と景観の歴史的変遷を考察した.さらに濱久保ら(2022)は,瀬戸内海の展望台を対象に,中心領域も含め俯角に応じた島々の分布状況を分析し,展望台管理を評価した.これらの研究は,俯瞰景の構造や俯角の影響,多島海景観の特性を総合的に理解するうえでの重要な知見を提供している.ただ,いずれの研究でも個別事例に応じた内容であり,しかも樹木成長による島嶼数の動的変化について論じていない.
既存研究と異なり,本研究は多島海俯瞰景と緑地管理との関係を単純な数理モデルで表現する.モデル化により,下記のような有用性が得られる.第一に,視点場位置,緑地高,干満差などの多数のパラメータの影響を感度分析として抽出できる.特に,視点場近傍での樹木成長は物理変化がわずかであっても,眺望遮蔽に与える影響は大きい.第二に,具体的な場所に限定されないため,現実の背後にある無数の緑地整備を比較することができ,有名展望台と同質を有する沿道景観など潜在的な観光資源を発掘できる.第三に,景観評価は感覚であり曖昧な議論になりがちとなるが,定量的で再現性に優れる数理モデルで得られた基本的関係は,緑地管理に関する合意形成に貢献できる.
一般的な知見を得るために,細部の異同より全体的な見え方に着目するため,視対象を「島嶼」と「海域」へと単純に二分割する.
図4の断面図が示すように,直線海面上に二等辺三角形の島が分布すると単純化する.視点場を中心とする現実の視野は三次元空間であり,水平方向の視野は扇形で表現される.樹木成長が影響を与えるのは鉛直方向の視野であるため,扇形の断面で単純化する.また,窪田(1984)が指摘するように,前方に実寸で大きな島が手前にあると多島海景観そのものが認識されず議論が複雑化する.島の形状の影響を取り除くため,同一な三角形の島形と仮定する.
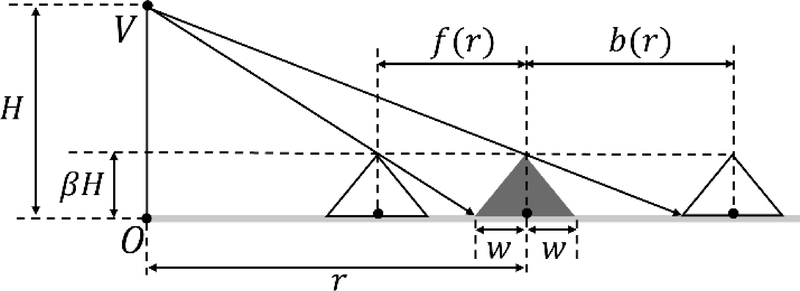
モデルでは,次の記号を導入する.V:視点場位置,O:視点場Vから水平面レベルへの垂線の足,r:原点Oから島中心までの水平距離,H:視点場高さ,βH(0≤β≤1):島の高さ,w:島の半径,ρ:島の密度(長さあたりの島数).
島の空間配置に関して,(1)等間隔,(2)ランダムを考える.窪田(1984)が指摘しているように,視点場から見える島の構図は距離ではなく,その島への俯角で定まる.したがって,距離と俯角との違いをより吟味するために,距離の側面から島密度を一定とする.そして,安定した結果を得るために,決定論的な(1)等間隔,確率論的な(2)ランダムの2通りという異なる考え方で分析を展開する.なお,これらは平面上の点パターンモデルとして標準的である.例えば,腰塚(1985)はポアソン分布を用いて都市施設の分布密度を分析した.本研究では,既存研究蓄積を基盤にモデルを構築する.
図5の断面図から,樹木位置(水平距離)xと樹木距離(視点場から樹頂点への鉛直距離)yで表現する.r0(r≥r0)をOから可視海域までの距離,視点場Vから手前可視海域までの俯角をθとすると,比例関係y:x=H:r0より,

| \[ r_{0}=H\frac{x}{y}=\frac{H}{\tan \theta }. \tag{1}\] |
視点場近傍の樹木成長や剪定による視野狭窄や拡大はyの大きさで表現される.yの増加(減少)は樹木剪定(成長)を意味し,俯角θは広く(狭く)なり,可視海域までの距離r0は縮み(伸び),海域が大きく(小さく)見える.
2.2 陸域数と独立数本研究では,多島海景観の審美性を島嶼数で数値化し,緑地管理の達成度合いを把握する.視点場Vから前後の島との間に海域が見える状況を分離,見えない状況を結合と呼ぶ.視点場の位置や高さに応じて分離や結合の状況は変動する.図6に示すように,前の島と分離している島を起点島,後ろの島と分離している島を終点島と呼ぶ.起点島かつ終点島となる島を独立と定義する.

本研究では,起点島と終点島を特定することで,島嶼数として,陸域数と独立数を求める.島間の海面により認識できる陸域の数(陸域数)は起点島数(水域数)と一致する.窪田(1984)は汀線が空間の奥行きを与える陸域数の意義を指摘している.そこで,見える陸域数が多い方が良いと考える.独立に見える島では,隣接する島間の空間的関係が曖昧とはならない.それぞれの島のそれぞれの歴史文化を一対一対応でき個々の島の生活が反映された景観から土地に思いを馳せることができる.そのため,その数の多い方が良いと判断する.なお,陸域数に関しては,既存研究(濱久保ら,2022)でも数値化されているが,独立数は多すぎるのも景観上単調となるという指摘もあり(脇水,1937;窪田,1984),著者らが知る限り指標化した研究はない.
ここで,f(r)とb(r)をそれぞれ距離rの島が分離するために必要な前の島,そして後ろの島までの距離とする.f(r)およびb(r)は前の山頂への俯角と後の手前汀線への俯角で定まる.図4の断面図から,f(r)の比例関係1:β=(r-w):(f(r)-w)とb(r)の比例関係(1-β):β=r:(b(r)-w)より,
| \[ f\left(r\right)=\beta \left(r-w\right)+w, \tag{2}\] |
| \[ b\left(r\right)=\frac{\beta }{1-\beta }r+w. \tag{3}\] |
直観に合うように,
| \[ b\left(r\right)>f\left(r\right) \tag{4}\] |
となり,前の島との分離条件(式(2))より,後ろの島との分離条件(式(3))が厳しくなる.
図7の例は2つの空間配置を比較している.等間隔(図7(a))では,陸域数が4,独立数が3となる.視点場から近いほど,島々の間に海面が見えやすいが,視点場から遠いほど,海面が見えなくなり,島々は一つの陸域と認識される.また,独立数は陸域数より1だけ小さい.ランダム(図7(b))では,陸域数が4,独立数が2となる.遠景も島々の前に海面が見えることが期待でき,一方で,近景でも必ず独立とはならないため,独立数は陸域数より大きく減る.

島が等間隔で並ぶと,島の間隔は1/ρとなる.中心が視点場から距離rに位置する島が前の島と分離される条件は1/ρ≥f(r)となり,式(2)を用いると,
| \[ r\leq \frac{1}{\beta }\left(\frac{1}{\rho }-\left(1-\beta \right)w\right). \tag{5}\] |
右辺の値を閾値 \( \overline{r_{f}} \) とする.
pE(r)を視点場Vから距離rの島が起点島と認識できる確率とする.閾値 \( \overline{r_{f}} \) を用いて,\( r_{0}\leq \overline{r_{f}} \) ならば,
| \[ p^E(r)=\left\{\begin{array}{lc} 0, & r \leq r_0 \\ 1, & r_0 \leq r \leq \overline{r_f}. \\ 0, & \overline{r_f} \leq r \end{array}\right. \tag{6}\] |
2.1節に述べたように,r0は樹木成長を数値化するyによって変化する.樹木成長(剪定)は定義域を通して確率を減少(増加)させる.r0と閾値 \( \overline{r_{f}} \) の間に密度ρで島が均等に分布するため,陸域数GpE(y)は次のようになる:
| \[ {G_{p}}^{E}\left(y\right)=\rho \left(\overline{r_{f}}-r_{0}\right). \tag{7}\] |
海面への俯角θは目に見える(実寸ではない)海面の長さを表す.そこで,海域長F(y)を
| \[ F\left(y\right)=\theta =\arctan \left(y/x\right) \tag{8}\] |
と定義し,yの関数として評価関数とする.樹木を剪定(成長)すると,海域長F(y)は長く(狭く)なる.式(1)から,
| \[ r_{0}=\frac{H}{\tan F\left(y\right)}. \tag{9}\] |
式(7),式(9)から,\( r_{0}<\overline{r_{f}} \) では,GpE(y)とF(y)との関係は,yをパラメータとし,次のように解析的に表現できる:
| \[ {G_{p}}^{E}\left(y\right)=\rho \left(\overline{r_{f}}-\frac{H}{\tan F\left(y\right)}\right). \tag{10}\] |
式(10)では,樹木成長や剪定を表す変数yが内生化されていることに注意したい.
本研究では,九十九島の面積や標高などの統計データに基づきパラメータを設定する.まず,九十九島を眺望する8つの展望台の高さの平均値(基盤地図情報データ)から視点場高さHをH=210(m)で与えた.また,現地調査に基づいて手前樹木までの距離xをx=20(m)とした.次に,基盤地図情報に示されている103個の島の地形データを用い,島の面積が中央値以上の広い島が島嶼の可視性へ影響を与えると考え,南九十九島の21個の広い島を抽出し,その平均値を求め,各島が円形になると想定し島半径wをw=167 mとした.また,基盤地図情報から前述の21個の島の標高データの平均値が26 mであるため,島高と視点場高の比例係数をβ=0.12と与えた.さらに,南九十九島の金重島,元ノ島,牧の島,松浦島,黒小島を囲む領域の島密度は1平方キロメートルあたり1.1個となる.各島が正方格子配置されていると想定し換算すると約900 mごとに1つの島があることから,島密度ρをρ=1/900とした.
樹木成長(剪定)と陸域数・独立数との関係を把握するために,横軸をy,縦軸をGpE(y), GqE(y)とするグラフを図8に,樹木成長(剪定)と海域長との関係を視覚化するために,横軸をy,縦軸をF(y)とするグラフを図9に示す.また,yの大きさで定まる俯瞰景観中心領域(8°~10°)を箱型で図示する.


両図から,樹木が成長(yが減少)し視野が狭くなるにつれて,海域長F(y)も島嶼数GpE(y), GqE(y)も減少することが読み取れる.そして,両図を比較すると,図9に示す海域長はほぼ線形で減少する.実際,式(8)のy/xに関するマクローリン展開を実施すると \( F\left(y\right)\approx \left(y/x\right)-\frac{1}{3}(y/x)^{3} \) により線形近似できる.一方で図9と異なり,図8の島嶼数は上に凸の帽子型の形状を有する.
また,横軸をF(y),縦軸をGpE(y)とし,海域長と島嶼数との関係(式(10))をグラフ化すると,図10の実線のようになる.ただし,5メートル間隔の樹木成長に応じた値を点線で示す.図10から2点を読みとれる.第一に,両者は線形関係とはならない.このように,奥行き感をもたらす島嶼数を,茫洋とした海面の量を測る海域長だけでは説明できない.第二に,樋口(1975),篠原(1982),伊藤(2010),濱久保ら(2022)が着目した中心領域を越えると(F(y)が0に近い側)島嶼数は大きく減少していく.このように,俯角10°~8°の重要性が本研究でも立証された.

なお,窪田(1984)では,CGモデルを用いて視点場位置の変更による可視空間率(平面図上での可視領域の面積と視野に収まる面積との比),と海面率を計算している.このモデルでは,視点場が高くなるあるいは海岸へ接近するにつれて,可視空間率も海面率も上昇する.本モデルでも,緑地樹木伐採剪定で視野が広がることで,可視空間率も海面率も上昇する.しかし両モデルは等価ではない.例えば,窪田(1984)ではどのような視点場高さあるいは距離でも近景を必ず含むが,本モデルでは,樹木成長した段階で近景を含まない.
3.1.2 独立数等間隔配置では,視点場から距離rに位置する島が独立となる条件は,後ろの島との分離条件と等価となるから,1/ρ≥b(r)となる.式(3)を用いると:
| \[ r\leq \frac{1-\beta }{\beta }\left(\frac{1}{\rho }-w\right)=\overline{r_{f}}-\frac{1}{\rho }. \tag{11}\] |
右辺の値を閾値 \( \overline{r_{b}} \) とすると,\( \overline{r_{b}}\geq \overline{r_{f}} \) となる.
qE(r)を距離rの島を独立と認識できる確率とする.閾値 \( \overline{r_{b}} \) を用いて,
| \[ q^E(r)=\left\{\begin{array}{lc} 0, & r \leq r_0 \\ 1, & r_0 \leq r \leq \overline{r_b}. \\ 0, & \overline{r_b} \leq r \end{array}\right. \tag{12}\] |
式(9)を用いると,独立数GqE(y)と海域長F(y)との関係は次のように表現できる:
| \[ \begin{split} {G_{q}}^{E}\left(y\right)&=\rho \left(\overline{r_{b}}-r_{0}\right)\\ &=\rho \left(\overline{r_{b}}-\frac{H}{\tan F\left(y\right)}\right)={G_{p}}^{E}\left(y\right)-1. \end{split} \tag{13}\] |
独立数は陸域数より1個だけ少ない.独立数GqE(y)と海域長F(y)との関係を図10の破線で示す.
3.1.3 最適俯角図10の帽子型関係を,図11を通して解釈する.見込角を固定し目線を上げていく(俯角θを小さくする)と,見える実寸の海域は長くなり,見える島は増えていくが,島々が重複して見えるようになる.このため,見込み角ϕを一定にして目線を足元から上げていくと,島嶼数は増えるが,ある俯角を境目に一転して減少していく.したがって,見込角ϕ一定で陸域数や独立数を最大化する俯角θp*とθq*が存在する.

次の二点を確認しながらθp*とθq*を求める.第一に,島数は実寸の海域の長さH(cotθ-cot(θ+ϕ))に比例するため,図11が示すように,俯角θを小さくするにつれて,陸域数も独立数も増えていく.第二に,式(4)と式(11)から,見込角ϕ内の島々を前の島と分離させる俯角θの条件は \( \frac{H}{\tan \theta }\leq \overline{r_{f}} \),後ろの島と分離させる俯角条件は \( \frac{H}{\tan \theta }\leq \overline{r_{b}} \) となる.俯角θが小さいとこの二つの条件も破綻する.このタイミングで陸域数・独立数が最も多くなり,\( H/\mathrm{t}\mathrm{a}\mathrm{n}{\theta _{p}}^{*}=\overline{r_{f}} \),\( H/\mathrm{t}\mathrm{a}\mathrm{n}{\theta _{q}}^{*}=\overline{r_{b}} \) となる.なお,最適俯角θp*とθq*は見込角ϕとは無関係となり,\( \overline{r_{b}}\geq \overline{r_{f}} \) からθp*>θq*が成り立つなる.
樹木が成長するにつれて,最初に見えていた近景が消失し,次に中景が消失して遠景だけとなる.したがって,島数が少ない近景では,樹木成長で陸域数GpE(y)も独立数GqE(y)も多少減少する.さらに樹木が成長し,近景より島数が多い中景が遮られることとなり,GpE(y)とGqE(y)はともに大幅に減少する.最後に,島々が結合する俯角が0に近い遠景では,GpE(y)とGqE(y)は0に収束する.
以上から,図10に示すように,樹木成長により海域長は近景,中景,遠景とは無関係に安定して減る.他方,海域や島嶼は近景,中景,遠景の違いがより反映される.このように,図10の結果は,図3で示すCGパースの様子と整合する.
3.2 ランダム 3.2.1 陸域数等間隔とは対比的に,島の中心が密度ρでランダム分布すると仮定する.島間隔に濃淡が発生するため,図7(b)が示すように近景でも必ずしも分離せず,遠景でも必ずしも結合しない.なお,島は重なる可能性もありそれを認めて分析を進めていく.
一次元ポアソン過程(小林ら,2004)から,距離rに位置する島が前方の島と分離する確率(見かけ陸と認識される確率)pR(r)は,長さf(r)の区間に島が1つも無い確率となるので,
| \[ p^R(r)=\left\{\begin{array}{lc} 0, & (r \leq r_0) \\ e^{-\rho f(r)}, & (r_0 \leq r) \end{array}\right.\!. \tag{14}\] |
pkを視点場Vからk番目に近い島が分離される確率とする.fk(r)を地点r0からのk次近隣距離の確率密度関数(Dacey, M., 1965)とすると,
| \[ f_{k}\left(r\right)=\frac{\rho ^{k}r^{k-1}}{\left(k-1\right)!}e^{-\rho r},~ ~ ~ ~ \left(r\geq 0\right). \tag{15}\] |
| \[ \begin{split} p_{k}&=\int _{0}^{\infty }e^{-\rho f(r+{r_{0}})}f_{k}\left(r\right)\mathrm{d}r \\ &=e^{-\rho f({r_{0}})}\int _{0}^{\infty }e^{-\rho (\beta (r-w)+w)}f_{k}\left(r\right)\mathrm{d}r \\ &=e^{-\rho (\beta {r_{0}}+2(1-\beta )w)}\frac{1}{(1-\beta )^{k}}. \end{split} \tag{16}\] |
式(16)から,pkは公比1/(1-β)の等比数列となり,べき乗則で順番kとともに逓減する.視点場と島との高さ比βが本質で,べき乗則で視点場から遠い島ほど重複して見えることが分かる.
よって,n個の島を観察したとき,陸域数の期待値Ep(n)は
| \[ \begin{split} E_{p}(n)&=\sum _{k=1}^{n}p_{k} \\ &=\frac{1}{\beta }\left(1-\frac{1}{(1-\beta )^{n}}\right)e^{-\rho (\beta {r_{0}}+2(1-\beta )w)}. \end{split} \tag{17}\] |
したがって,すべての島を観察した時の陸域数の期待値GpR(y)は
| \[ {G_{p}}^{R}\left(y\right)=E_{p}(\infty )=\frac{1}{\beta }e^{-\rho (\beta {r_{0}}+2(1-\beta )w)}. \tag{18}\] |
なお,Ep(∞)は次のように直接計算できる:
| \[ E_{p}(\infty )=\int _{0}^{\infty }e^{-\rho f(r+{r_{0}})}f(r)\mathrm{d}r. \tag{19}\] |
式(9)を用いて陸域数GpR(y)を可視海域長F(y)の関数で表現すると次のようになる:
| \[ {G_{p}}^{R}\left(y\right)=E_{p}\left(\infty \right)=\frac{1}{\beta }e^{-\rho \left(\beta \frac{H}{\tan F\left(y\right)}+2\left(1-\beta \right)w\right)}. \tag{20}\] |
距離rに位置する島が独立島と認識される確率qR(r)は,長さL(r)=f(r)+b(r)の2つの区間に島が1つも無い確率と等価なので,
| \[ q^R(r)=\left\{\begin{array}{lc} 0, & (r \leq r_0) \\ e^{-\rho L(r)}, & (r_0 \leq r) \end{array}\right.\!. \tag{21}\] |
よって,視点場Vからk番目に近い島が独立となる確率qkは次のようになる:
| \[ \begin{split} q_{k}&=\int _{0}^{\infty }e^{-\rho L(r+{r_{0}})}f_{k}\left(r\right)\mathrm{d}r \\ &=e^{-\rho L({r_{0}})}\int _{0}^{\infty }e^{-\rho (\beta (r-w)+w+\frac{\beta }{(1-\beta )}~ r+w)}f_{k}\left(r\right)\mathrm{d}r \\ &=e^{-\rho (2-\beta )(\frac{\beta }{(1-\beta )}~ {r_{0}}+2w)}\left(\frac{1-\beta }{1+\beta -\beta ^{2}}\right)^{k}. \end{split} \tag{22}\] |
式(22)から,qkは公比(1-β)/(1+β-β2)の等比数列となり,べき乗則で低減する.なお,1/(1-β)>(1-β)/(1+β-β2)から,qkはpkより速く減少する.
n個の島を観察したとき,独立数の期待値Eq(n)は
| \[ \begin{split} E_{q}(n)&=\sum _{k=1}^{n}q_{k} \\ &=\frac{\beta -1}{\beta \left(\beta -2\right)}(\frac{1-\beta }{1+\beta -\beta ^{2}})^{n}e^{-\rho (2-\beta )(\frac{\beta }{(1-\beta )}~ {r_{0}}+2w)}. \end{split} \tag{23}\] |
Ep(∞)も次のように直接計算できる:
| \[ E_{q}(\infty )=\int _{0}^{\infty }e^{-\rho L(r+{r_{0}})}f(r)\mathrm{d}r. \tag{24}\] |
よって,独立数の期待値GqR(y)は
| \[ {G_{q}}^{R}\left(y\right)=E_{q}\left(\infty \right)=\frac{\beta -1}{\beta (\beta -2)}e^{-\rho (2-\beta )(\frac{\beta }{(1-\beta )}~ {r_{0}}+2w)}. \tag{25}\] |
式(20)と式(25)との比較から,GpR(y)>GqR(y)を確認できる.
3.2.3 べき乗則べき乗則の振る舞いを観察するために,同じく九十九島データを用い,r0=0, β=0.12, w=167, \( \rho =\frac{1}{900} \) に対し,期待値Ep(n)とEq(n)を観察島数nの関数として,図12に示す.横軸を島数nとし,縦軸では陸域数の期待値を実線で,独立数の期待値を破線で示す.また,それぞれの漸近線を点線で示す.この図では,例えば,手前から10個の島を観察すると,島嶼数が5個,独立数が3個となるという,読み方となる.


図12の2本の曲線から,認識する陸域数や独立数が,点線で示した上限値に上に凸の形で収束していく様子を確認できる.漸近線の値から,九十九島では,多くの島があるが島の重なりが多く,見える島嶼数はかなり少なくなることが理解できる.
3.3 等間隔とランダムとの比較図13は,β=0.12, w=167, \( \rho =\frac{1}{900} \), r0=500に対し,確率pE(r), qE(r), pR(r), qR(r)を,距離rの関数としてグラフ化している.陸域となる確率を実線,独立となる確率を点線,等間隔とランダムを黒色線,灰色線で示す.pE(r), qE(r)の定義域は \( [r_{0},~ \overline{r_{b}}] \), \( [r_{0},~ \overline{r_{f}}] \),pR(r), qR(r)の定義域は[r0, ∞]となる.図13の陰影の面積と密度ρとの積が陸域数や独立数の期待値に対応する.
この図から二点読み取れる.第一に,これら確率の定義域はr0となるため,樹木成長により,r0が伸びると陰影部分が小さくなり分離確率の分布は左側から縮小していく.第二に,等間隔では近距離では1,遠距離は0となるが,ランダムでは,島が視点場から離れた場合でも分離されることがあるため,裾が長くなる.
式(10),式(13),式(20)および式(25)を用い,図10と同じパラメータに対し,海域長F(y)と島嶼数との関係をグラフ化すると,図14のようになる.陸域数を実線,独立数を破線,等間隔とランダムをそれぞれ黒色線,灰色線で示す.

この図から2点読み取れる.第一に,ランダム配置も島嶼数は帽子型となり,俯角中心領域付近で急激に変化する.つまり,緑地管理の影響では確率論的と決定論的というアプローチには本質的な違いはなく,俯角中心領域での視野確保が重要となる.第二に,等間隔配置と比べてランダムの方が島嶼数は少ない.そして,独立数の乖離は大きく,ランダムの値は等間隔の半分程度である.等間隔では,陸域数と独立数とは連動するが,ランダムではその連動がかなり弱まる.
高度成長時代では展望台建設などの視点場位置操作により,多島海眺望を獲得してきた.しかし成熟時代の現代での主たる操作可能な政策変数は緑地整備となる.このような背景から本研究を実施した.
多島海景観では,近景から遠景になるにつれて島は重なって見えていく.また,樹木成長は俯角領域を狭くかつ浅くし,近景,中景,遠景の順で多島海を見えなくしていく.これらの組み合わせを単純なモデルで表現した.その際,自然要素である島嶼の地理的分布を正確に表現するのではなく,島嶼への可視性に関する理解を促進させるために,海面上での島密度を一定として論を進めた.その結果,少なくとも次の2つの知見を得た.
第一に,樹木成長と島嶼数との関係を解析的に表現し,島間距離が決定論的にあるいは確率論的にと異なるアプローチでも,島嶼数は俯瞰景観の中心領域で急激に変化することを確認できた.したがって,島嶼数を確保するためには,俯角中心領域の視界が基本となる.なお,ランダム配置を視点場から近い順番で見ていく状況では,島嶼数や独立数はべき乗則に従い逓減し,漸近線に収束していくことを示した.この簡潔な結果は,多島海景観ならではの島の重なりの理解に役立つ.第二に,島嶼数と海中心の眺めで重視される海域長との差異を明確にした.両者の樹木成長に対する反応は異なり,例えば,樹木剪定が後手となり遠景のみで海域長を確保したとしても,島嶼数という多島海ならではの景観を堪能できなくなる.
本研究の実施にあたって,佐世保市都市整備部まち整備課,観光商工部観光課,平戸市まちづくり運営協議会と九十九島ビジターセンターから貴重なご意見を賜りました.伊藤弘先生(筑波大学),小林邦隆様(日本緑化センター)から,緑地管理と景観構造について,石井儀光先生(国土技術政策総合研究所),小林隆史先生(立正大学)から,モデル化について,それぞれ有意義なコメントをいただきました.