2021 年 10 巻 1 号 p. 29-44
2021 年 10 巻 1 号 p. 29-44
これまで,高齢者の特殊詐欺被害に対して認知機能の脆弱性にその原因が存在するとする立場から,認知機能の脆弱性を測定し判定が可能な論理を導き,詐欺抵抗力判定式として定式化した.従来の判定式ではロジスティック回帰式を用いたのに対して,本研究では高速倹約ヒューリスティクスを応用した決定木を用いた判定式への改良を提案する.高速倹約決定木を用いることによって,詐欺抵抗力判定の正解率が向上し,また,判定に基づくアドバイスの理解しやすさも向上する.更に,特殊詐欺被害者データを一般のデータと混在して分析するときに生じる不均衡データの問題及び特殊詐欺被害者データに必然的に伴う小標本の問題についても論じる.
So far, from the standpoint that the vulnerability of cognitive function causes the damageof special fraud in the elderly, we have derived the logic that can measure and judge the vulnerabilityof cognitive function, and formulate it as a fraud resistance judgment formula. Incontrast to the logistic regression which is used in our judgment formula, this study proposesan improvement to the judgment formula using a fast-and-frugal decision tree. By using adecision tree that applies fast-and-frugal heuristics, the accuracy of fraud resistance judgmentis improved, and the comprehension of advice based on the judgment is also improved.Furthermore, we discuss the problem of imbalanced data that occurs when analyzing specialfraud victim data mixed with general data and the problem of small samples that inevitablyaccompanies special fraud victim data.
個人によって異なるものの,われわれの認知機能には本来詐欺被害に遭いやすい特性が内在していると考え,何らかの方法によって詐欺被害に関連する認知機能の特性を把握できるならば,潜在的な詐欺被害者の予測さえ可能になると考えられる(永岑・原・信原, 2009).そのような考え方に立つと,被害に遭う可能性のある高齢者の認知機能からのアプローチによって,認知心理学が詐欺被害防止に貢献できる可能性が出てくる(Judges, Sara, Gallant, Yang, & Lee, 2017).
そこで,われわれは国立研究開発法人科学技術振興機構(JST)社会技術研究開発センター(RISTEX)の戦略的創造研究推進事業(社会技術研究開発)「安全な暮らしをつくる新しい公/私空間の構築」研究開発領域平成29 年度採択プロジェクト(https://www.jst.go.jp/ristex/pp/project/h29_5.html,以下RISTEX プロジェクト)において,高齢者の認知機能の特性を測定しそれに基づいて特殊詐欺に対する抵抗力の判定を行ってきた.プロジェクトの成果として,高齢者の特殊詐欺抵抗力を判定できる手法を開発し,現在それをアプリの形で提供している.
われわれは高齢者の認知機能と特殊詐欺に対する脆弱性に関する調査を,上記プロジェクト以前に過去20 年に亘って行ってきたが,その結果蓄積されたデータの中から,詐欺脆弱性に関係すると思われる認知機能に関する質問項目を選択し調査票を作成した.その調査票を用いて複数回調査を行い,分析結果に基づいて特殊詐欺抵抗力判定式を作成し,アプリへの実装を行った.
後述するように,2020 年3 月24 日にそれまでの質問項目を修正した新たな質問セットの入れ替えを行ったが,それ以前の旧質問セットでのアプリデータは2020 年3 月現在で9,237 件蓄積されている.アプリへは一般者でもアクセス可能であるため,回答者の特定は不可能である.そこで,回答者に対して研究用データの収集のために予め識別コードを振って回答を求めることを試み,アプリデータの中にはその回答者も含まれている.更に,関西地方のA 警察署によって識別コードを振って収集された警察署管内の特殊詐欺被害者の回答データも含まれている.本論文で分析の対象とするデータは,これらの予め識別コードを振って収集された研究用データとA 警察署が収集した特殊詐欺被害者データである.
前述のように,現在アプリで機能している特殊詐欺抵抗力判定式の作成には,アプリ作成以前にわれわれが過去20 年に亘って実施した調査によって収集したデータが用いられた.したがって,アプリ完成後にA 警察署によってアプリを用いて収集された特殊詐欺被害者データは用いられていない.そこで本研究ではA 警察署収集の特殊詐欺被害者データを用いて,詐欺抵抗力判定の正解率(全反応のうちで,真に陽性の反応を正しく陽性だと判断する事例と真に陰性の反応を正しく陰性だと判断する事例の合計の割合)によってアプリの正確さの検討を行い,アプリの精度の一層の向上を図るため新たな詐欺抵抗力判定式の作成を行う.アプリで現在機能している特殊詐欺抵抗力判定式と新判定式の正確さの比較については,既に渡部(2020)で述べた.また, 特殊詐欺抵抗力の尺度及び項目特性等の詳細については澁谷(2020)で述べた.そこで本研究では渡部(2020)とは異なった方法を用いて,新判定式の正確さについて検証を行う.
われわれが過去に行った研究によれば,特殊詐欺脆弱性と関連性のある変数として,未来展望(池内・長田, 2013),自己効力感,生活の質(QOL)が挙げられることが明らかにされた(渡部・澁谷, 2010: 渡部・澁谷・吉村・小久保, 2015).そこで,詐欺抵抗力判定アプリで採用する質問項目を決定するために,これらの質問項目を含んだ調査票を作成し最終調査を行った.
調査時期は2018 年12 月3 日~18 日で,調査対象者は秋田市・潟上市・男鹿市・青森市・弘前市・函館市の各シルバー人材センター会員計835 名(男性485 名,女性344 名,不明6 名)である.年齢については年齢区分(1. 60~64 歳,2. 65~69 歳,3. 70~79 歳,4. 80 歳以上)によって回答を求めたため,平均年齢等は計算できなかったが,年齢区分毎の人数は,1 が39 名,2 が149 名,3 が603 名,4 が37 名,不明が7 名であった.調査票は,デモグラフィック項目,詐欺場面における行動特性,読解力,未来展望(池内・長田, 2014),自己効力感,金融リテラシー(Lusardi & Mitchell, 2007, 2008),生活の質,詐欺シナリオ問題,悪徳商法シナリオ問題から構成され,全87 問である.未来展望と金融リテラシーの質問項目以外はオリジナルである.この中で,詐欺場面における行動特性とは,詐欺犯からアプローチがあった時にどのような反応をするかについて尋ねるもので,たとえば,「知らない人に強い口調で言われると,怯えてしまう」というような質問項目である.また,詐欺シナリオ問題は独立行政法人国民生活センターのウェブサイトに掲載された過去に高齢者から相談があった内容を参考に詐欺場面のシナリオを作成し回答を求めるものである.
古典的テスト理論及び項目反応理論(この中のrating scale モデル)を用いてこの調査データを分析した結果,デモグラフィック項目6 問,詐欺場面における行動特性項目9 問,未来展望項目10 問,自己効力感項目16 問,生活の質項目25 問,詐欺シナリオ問題12 問(特殊詐欺を構成するオレオレ詐欺・架空請求詐欺・還付金等詐欺・融資保証金詐欺の4 罪種につき3 問ずつのA~Lを設けた.なお,令和元年12 月の警察庁生活安全企画課の通知により,現在特殊詐欺の種類は10 種類と規定されているため,アプリでもこれらの罪種についても判定が出るように対応する予定である.)の合計78 問がアプリに採用された.この中で,詐欺場面における行動特性項目は前述のように詐欺に関連することを尋ねていることが明らかである問題であるが,未来展望項目・自己効力感項目・生活の質項目は一見すると特殊詐欺被害とは関連性がないと思われる項目であるものの,われわれの研究では有意な関係が認められている(渡部・澁谷, 2010).したがって,これらの質問項目は質問の意図が読み取りにくい項目であるため,回答者が意図的に本来の回答と異なる回答を行うことが困難であり,正直な回答を求めることができるという利点がある.質問項目に対する回答は,デモグラフィック項目のみ2~5 択で,その他の項目は全て4 択である.詐欺シナリオ問題においては,回答の数値が大きい程脆弱性が強いことを意味するが,Q11_H の問題のみ逆転項目である.表1 に詐欺シナリオ問題の属性を示す.また,その他の質問項目についても明示すべきであるが,アプリの実践的使用を考慮して,本稿では各質問文の明示は避け,質問項目の対応はアルファベット表記で示す.

先に述べたように,この調査票を用いて6 市のシルバー人材センターの会員に対して詐欺脆弱性の調査を行いデータの収集を行った.質問項目のうち,詐欺シナリオ問題のそれぞれについては4 択の回答を2 値に変換した値を目的変数に,また,未来展望項目・自己効力感項目・生活の質の項目については4 択の回答の数値を説明変数にして,ロジスティック回帰分析を行った.その結果8 本の重回帰式が得られたが,例として以下にその中の3 本を示す.重回帰式中の係数は全て有意な偏回帰係数である.これらの式において,右辺に現れるQ9は自己効力感項目,Q10は生活の質項目である.未来展望項目のうち有意な偏回帰係数を持つ項目はなかった.
Q11_A=(−1.763)+2.191×Q9_D+(−1.534)×Q9_E+(−1.660)×Q9_F+(−0.990)×Q9_J
Q11_B=(−5.320)+(−0.469)×Q9_A+0.542×Q9_B+0.675×Q9_D+0.714×Q9_K+(−0.651)×Q9_N
Q11_J=(−0.624)+0.951×Q10_B+(−1.158)×Q10_C+(−0.811)×Q10_I+(−0.746)×Q10_K+(−0.934)×Q10_P+1.489×Q10_U
得られた重回帰式の偏回帰係数を次式の各 に代入することによって確率
に代入することによって確率 を計算し,この値を特殊詐欺被害に遭う確率を表すと考え潜在詐欺被害確率と呼ぶことにする.そして,1 からこの値を引いたものを詐欺抵抗力の値とする.
を計算し,この値を特殊詐欺被害に遭う確率を表すと考え潜在詐欺被害確率と呼ぶことにする.そして,1 からこの値を引いたものを詐欺抵抗力の値とする.

このようにして得られた詐欺抵抗力の値に応じて,特殊詐欺抵抗力の最終的な判定が下されアプリの判定画面において表示される(抵抗力が最も低い危険レベルは赤色,注意は黄色,安全は緑色で表示).アプリではその後に,ロジスティック回帰式の偏回帰係数の大きな質問項目に基づいて簡単なアドバイスが表示される.しかし,1 本のロジスティック回帰式に含まれる値の大きな偏回帰係数は通常複数個存在し,それらに対応する質問項目についてアドバイスを作成し,それらを単純に結合して1 個のアドバイスを作成したのでは,理解困難な表現のアドバイスが作成されることになる.この点も改良の余地があると思われ,後述のようにわかりやすいアドバイスが作成できる決定木を詐欺抵抗力判定アルゴリズムとして採用することとした理由の一つである.
以上で説明した2018 年の調査で収集したデータは稼働する前の特殊詐欺抵抗力判定アプリの作成のために用いられた.一方,後述するifan 及びdfan の構築には,稼働した後の詐欺抵抗力判定アプリによって収集されたデータが用いられた.したがって,これら両データは質問項目群が一部重複するものの,異なるデータ群である.
高速倹約決定木(fast-and-frugal decision tree)は,Gigerenzer, Todd, & The ABC ResearchGroup(1999)の提唱する高速倹約ヒューリスティクス(fast-and-frugal heuristics)から考えられた決定木の一種である(Phillips, Neth, Woike, & Gaissmaier, 2017).
人間の規範的意思決定原理である期待効用最大化からの逸脱に注目するアプローチとしては次の2 つのアプローチが存在する.1 つは,Tversky とKahneman の一連の研究である(Kahneman & Tversky, 2000).彼らは,期待効用最大化の原則から逸脱する意思決定の具体的な姿を明らかにし,それらを種々のヒューリスティクスとして定式化した(Gilovich, Griffin, & Kahneman,2002).もう1 つのアプローチは,前述の高速倹約ヒューリスティクスである.高速倹約ヒューリスティクスの定義は,「最小限の時間・知識・計算によって現実環境における適応的決定を行う」ヒューリスティクスである(Gigerenzer et al., 1999, p.14).Tversky とKahneman がヒューリスティクスを期待効用最大化の原則からの逸脱というように否定的に考えたのに対して,Gigerenzerらの高速倹約ヒューリスティクスは,情報探索時間や計算の制約下での判断に注目し,制約下における上手な意思決定として肯定的に捉えたものであるといえる.また,Tversky とKahnemanがヒューリスティクスを認知バイアスの結果生み出されたものとして捉えそれ程積極的な価値を置いていないのに対して,Gigerenzer らはヒューリスティクスを用いた結果が時には合理的で規範的な方法で得た結果に勝ることもあるとして.肯定的な評価を下している点も異なる.
高速倹約ヒューリスティクスの前提として,(1)決定に関連する手掛かり(cue)が妥当性の高い順にわれわれの心内に存在し,(2)われわれはその手掛かりを妥当性の高い順に系列的に探索し,(3)選択肢が決定した時点で探索は終了することの3 点が挙げられる(中村, 2004).このような高速倹約ヒューリスティクスの前提を埋め込んで作成される決定木が高速倹約決定木である.高速倹約決定木は,他の決定木と同様にノード(node),枝(branch),葉(leaf)から構成される.ノードからは必ず2 本の枝が出ており,それぞれの枝の先にはノードかまたは葉がそれぞれ1 個付いている.ノードは判断の条件に該当し,葉は判断の結論に該当する.葉に到達することは結論に達して高速倹約決定木を脱することを意味するため,葉は高速倹約決定木の出口である.高速倹約決定木では,一番上のノードから出発し,判断の条件に応じて枝を辿ることによって分岐しながら順次下のノードに到達し,そのノードの判断の条件に従って更に分岐する.このように,枝を伝いながらノードに到達するたびに判断を繰り返しながら進む(Phillips et al., 2017).但し,高速倹約決定木の一番下のノードのみ,そこから出ている枝の先には2 個の葉が付いている.
高速倹約決定木のアルゴリズムとして最初にmax とzig-zag が提案された(Martignon, Vitouch,Takezawa, & Forster, 2003).max もzig-zag も,最初に一つ一つの手掛かりについて,その手掛かりを採用した場合としなかった場合について感度(sensitivity,真に陽性の反応のうちで陽性だと正しく判断する割合),特異度(specificity,真に陰性の反応のうちで正しく陰性だと判断する割合)をそれぞれ計算する(Phillips et al., 2017, p.348).次に,感度,特異度等の値を用いてそれぞれのアルゴリズムに従って各手掛かりを採用するか否かを決めて行く.max とzig-zag の違いは,感度や特異度等の値のうち,どの値をどの時点で採用するかが異なる.その後Phillips etal.(2017)によって,max とzig-zag では感度と特異度の重みが考慮されていない点と,考慮するノードの個数に制限がないため長い決定木が得られてしまう点が指摘されており,改良されたアルゴリズムとしてifan とdfan が提案された.
ifan は,各手掛かりについて閾値と均衡正解率(balanced accuracy,感度と特異度のそれぞれに0.5 の重みづけを与えて加えた値)に基づいて手掛かりを並べ,最上位の手掛かりを決める(Phillips et al., 2017, p.348).次に,最上位の手掛かりから予め決められた個数の決定木を作成し,プルーニングを繰り返しながら重み付き正解率(weighted accuracy,感度と特異度のそれぞれに任意の重みづけを与えて加えた値)が最大の決定木を残すというアルゴリズムである(Phillipset al., 2017, p.367~368).一方,dfan は手掛かりの間に関連性が存在する場合のアルゴリズムである(Phillips et al., 2017, p.368).
高速倹約決定木が他の分類法と異なる特徴として,効率性(efficiency)を考慮に入れている点が挙げられる.効率性は速度(speed)と倹約性(frugality)の2 個の測度によって判断される.速度は判断に実際に使用された手掛かりの個数の平均値を全ての対象について平均した値として定義される(Phillips et al., 2017, p.350).また,倹約性は判断に使用しなかった情報の割合として定義される(Phillips et al., 2017, p.350).更に,Martignon, Katsikopoulos, & Woike(2008)では高速倹約決定木が他の分類法と異なる特徴として,分類結果が決定的である(確率的ではない)こと,分類結果の時間的な継続性について定性的な回答しか与えられないこと,1 個の手掛かりは1 度しか用いられないことの3 点を挙げている.
高速倹約決定木の評価については,Phillips et al.(2017)においても標準的な決定木・ロジスティック回帰モデル・正則化回帰モデル・ナイーブベイズ・ランダムフォレスト・サポートベクターマシンとの比較で論じられており,10 課題の平均均衡正解率について2 番目に良い結果が得られている.また,Laskey & Martignon(2014)では,11 課題を用いて訓練用データの割合を変えながらmax アルゴリズムとzig-zag アルゴリズムの高速倹約決定木とナイーブベイズ・ロジスティック回帰モデル・標準的な決定木について分類の正確さの比較を行った.その結果,ナイーブベイズの成績が最も良く,高速倹約決定木はロジスティック回帰モデルとほぼ同様の成績にすぎなかった.但し,高速倹約決定木は訓練用データの割合が低い場合にナイーブベイズに匹敵する成績を出すことは注目に値する.Woike, Hoffrage & Martignon(2017)も11 課題について高速倹約決定木とナイーブベイズに対して分類の正確さと判別能力を示すROC(receiver operatingcharacteristic)曲線の2 つの比較を行っている.その結果,分類の正確さにおいては高速倹約決定木はナイーブベイズに次ぐ成績であったが,ROC 曲線では課題にもよるもののナイーブベイズに匹敵する成績をあげている.
このように,高速倹約決定木は認知心理学研究の成果より導かれたものであり,人間が日常の生活において認知的制約下や時間的制約下で意思決定を行う際に単純な決定規則にしたがうことを模したもので,ただ単に正確さを最大にすることを目的にするものではない.即ち,必要のない情報を捨てることによって部分的な情報を利用するにも関わらず,情報の全体を用いる方法よりも成績が良いという“less is more” を実現する有力な方法の一つとして高速倹約決定木の有用性がある.
R には高速倹約決定木を扱うパッケージFFTrees が用意されているが,このパッケージには決定木を作成する以外にも種々の機能が付いている.まず,決定木の決定結果に関する混同行列に伴って,決定の正確さの指標として感度,特異度,正解率(accuracy),重み付き正解率(この特別な場合として均衡正解率)が用意されており,既述したように重み付き正解率は高速倹約決定木の計算アルゴリズムにおいても用いられている.感度と特異度は両立することが不可能な指標であるため,この両者のトレードオフを表すROC 曲線が用意されている.また,速度の指標として決定に用いられた手掛かりの個数の平均値を表すmean cues used が,また倹約性の指標として判断に用いられなかった手掛かりの割合であるpercent cues ignored が用意されている.更に,高速倹約決定木のアルゴリズムの1 つであるfan アルゴリズム(ifan とdfan)のパラメータを変えながら作成した決定木の上位7 個と他の判定手法(標準的な決定木,ロジスティック回帰,ランダムフォレスト,サポートベクターマシン)をROC 曲線を用いて比較した図も表示可能である.
既述したように,詐欺抵抗力判定アプリで採用した詐欺抵抗力判定式は,ロジスティック回帰分析を用いて求めた偏回帰係数を用いて作成された.ロジスティック回帰式は変数の1 次式であるので,意思決定方略上は補償的方略に該当する.一方,高速倹約決定木では,あるノードに到達するとその判断条件によってノードから延びた枝に従って進んで行くために,その道筋以外の別の枝に付いているノードや葉に到達することはない.即ち,別の枝に付いているノードの判断条件を検討することはない.したがって,高速倹約決定木は非補償的方略に該当すると言える.このように,高速倹約決定木は一般的にはロジスティック回帰式よりも少ない条件を用いて判断を下す.ところが,少ない情報を用いて下す判断の方が,より多くの情報を用いて下す判断より勝っていることが高速倹約ヒューリスティクスの興味のある特徴である(Czerlinski, Gigerenzer, & Goldstein, 1999).
この節では,特殊詐欺抵抗力判定アプリで収集したデータから高速倹約決定木のアルゴリズムの一つであるifan を用いた詐欺脆弱性判定ルールの作成,及び,判定ルールの正確さの検証について述べる.
最初に,アプリで収集したデータから,研究用に回答時に予め識別コードを振ったデータを抽出する.これらのデータは,RISTEX プロジェクトにおいて回答の依頼を行って収集されたデータであり,青森県青森市で収集されたデータ94 件,神奈川県座間市で収集されたデータ318 件,関西のA 警察署管内の特殊詐欺被害者データ25 件の合計437 件である.アプリには過去の詐欺被害の経験を尋ねる項目はないため,青森市及び座間市で収集されたデータを詐欺被害に遭ったことがない回答者のデータとして扱う.なお,本研究は秋田県立大学研究倫理審査細則第5 条第2 項に基づき,2019 年5 月31 日付で研究倫理委員会の承認を得ている.
判定ルールの精度の検証は,10 分割交差検証によって行った.437 件のデータをランダムに並び替え,データの大きさがほぼ等しくなるように10 分割し,10 分割したデータの9 個を学習用データに,残り1 個の分割をテスト用データとして用いて交差検証を行った.交差検証は分割されたデータを交換しながら,1 個の分割すべてをテスト用データとして用いた.
詐欺脆弱性判定ルールの作成のために,アプリで採用した質問項目の中で,行動特性項目9 問,未来展望項目10 問,自己効力感項目16 問,生活の質項目25 問の合計60 問を用い,詐欺シナリオ問題12 問のそれぞれについて高速倹約決定木による分析を行った.高速倹約決定木による分析は,R のパッケージFFTrees verson1.4.0 を用いた.このパッケージの関数FFTrees のパラメータdecision.label はresistant(特殊詐欺抵抗力あり)とvulnerable(特殊詐欺抵抗力なし)であり,max.levels は10,algorithm はifan を用い,その他のパラメータの値は既定値を用いた.以上のようにして,詐欺シナリオ問題12 問のそれぞれについてFFTrees オブジェクトが数個得られた.FFTrees オブジェクトの作成は10 分割交差検証の学習用データを用いて行った.図1 に詐欺シナリオ問題Q11_B の5 番目のテスト用データを用いた場合に得られたFFTrees オブジェクトの結果を示す.

このFFTrees オブジェクトより,詐欺脆弱性が高い条件として,「Q7_G が1 以下でQ10_G が1 以下」,「Q7_G が1 以下で,Q10_G が1 より大きく,Q10_B が1 以下」,「Q7_G が1 以下で,Q10_G が1 より大きく,Q10_B が1 より大きく,Q8_E が1 より大きく,Q7_I が2 より大きい」,「Q7_G が1 以下で,Q10_G が1 より大きく,Q10_B が1 より大きく,Q8_E が1 より大きく,Q7_I が2 以下で,Q8_I が3 より大きい」のいずれかに該当する場合が得られる.また,図1 の下に示すように,このFFTrees オブジェクトによって,詐欺抵抗力があっても抵抗力がないと判断された者が134 名存在し,false alarm rate は0.348 になるが,詐欺抵抗力がなくても抵抗力があると判断された者はいなかったことを考えると,このFFFTrees オブジェクトによって得られた判定論理は保守的な特徴を持っていることになり,詐欺被害防止のためには望ましい.勿論,以上の評価はわずか1 個の結果のみに関するものであるため,色々なデータに関して評価を行うために以下の交差検証を行う.
得られたFFTrees オブジェクトを用いて,今度は10 分割交差検証のテスト用データを使い詐欺脆弱性に関する予測を行った.また,それとは別に,テスト用データについて,A 警察署管内の特殊詐欺被害者であるか否かによって2 分類を行った.最後に,FFTrees の予測とA 警察署管内の特殊詐欺被害者に基づいた2 分類を組み合わせて分割表を作成した.
次に,Jamil, Ly, Morey, Love, Marsman, & Wagenmakers(2017)にしたがって分割表に基づくBayes factor を求めた.分割表はデータの大きさがほぼ等しくなるように作成した10 分割交差検証のテスト用データに関して作成したものであるため,分割表全体のデータ数は一定であると考えてよい.よって,Jamil et al.(2017)のjoint multinomial sampling scheme にしたがってBayesfactor を作成した.Bayes factor の作成にはR のパッケージBayesFactor version0.9.12-4.2 を用いた.関数coningencyTableBF のパラメータsampleType はjointMulti で,関数posteriorのパラメータiterations は500000 であり,その他のパラメータの値は既定値を用いた.
以上の手続きによって,詐欺シナリオ問題12 問のA からL について,それぞれ正解率,感度,特異度,精度(precision)の事後分布が得られる.但し,Q11_H については逆転項目であることが高齢回答者によく理解できなかったと考えられ,逆転項目として理解した者とそうでない者の回答が混在していることがうかがわれ,また,得られた事後分布も一見して奇妙な形をしていた.そのため,以下の分析からQ11_H を除いた.
次に,詐欺シナリオ問題12 問のうちH を除くA からL のそれぞれについて,10 分割交差検 証のテスト用データ毎にそれぞれ10 個の正解率,感度,特異度,精度の値を求め,それらの平均 値及び標準偏差を算出しそれぞれ表2 と表3 に示す.


ここでは,特殊詐欺抵抗力判定アプリで収集したデータから高速倹約決定木のアルゴリズムの一つであるdfan を用いた詐欺脆弱性判定ルールの作成,及び,判定ルールの正確さの検証について述べる.ifan と異なり,dfan では決定に用いられる選択肢が持つ手掛かりの間が独立ではなく,それらの間に関連性があることを仮定している(Phillips et al., 2017, p.368).
これ以外の条件はifan における分析と同様である.図2 に詐欺シナリオ問題Q11_K の4 番目のテスト用データを用いた場合に得られたFFTrees オブジェクトの結果を示す.このFFTreesオブジェクトより,詐欺脆弱性が高い条件として,「Q9_O が2 より大きく,Q9_E が2 より大きく,Q9_D が2 より大きい」と「Q9_O が2 より大きく,Q9_E が2 より大きく,Q9_D が2 以下で,Q10_N が3 より大きい」のどちらかに該当する場合が得られる.また,図2 の下に示すように,このFFTrees オブジェクトによって,詐欺抵抗力があっても抵抗力がないと判断された者が47 名存在し,false alarm rate は0.121 になる.さらに,詐欺抵抗力がなくても抵抗力があると判断された者は1 名であった.
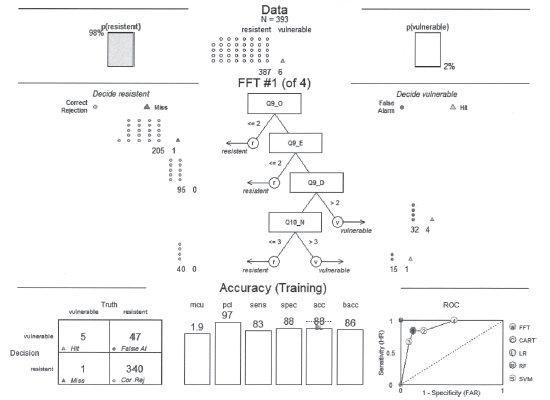
dfan を用いる場合にも,詐欺シナリオ問題12 問のA からL について,それぞれ正解率,感度,特異度,精度の事後分布が得られる.但し,Q11_H についてはifan の場合と同様に,逆転項目であることが高齢回答者によく理解できなかったと考えられ,逆転項目として理解した者とそうでない者の回答が混在していることがうかがわれたため,以下の分析からQ11_H を除いた.
次に,詐欺シナリオ問題12 問のうちH を除くA からL のそれぞれについて,10 分割交差検証のテスト用データ毎にそれぞれ10 個の正解率,感度,特異度,精度の値を求めそれらの平均値及び標準偏差を算出しそれぞれ表4 と表5 に示す.


本研究では,高齢者の特殊詐欺被害を単に犯罪被害として捉えるのではなく,高齢者の認知機能の弱点に注目し,特殊詐欺抵抗力の測定を行う認知心理学からのアプローチを試みた.そして,高齢者の認知機能の中で詐欺抵抗力に関連すると思われる変数を抽出し,高速倹約決定木によって詐欺抵抗力判定式を導いた.その結果,正解率がifan では0.735,dfan では0.768 の値を得ることができた.
Phillips et al.(2017)によれば,高速倹約決定木を用いるメリットがある場合として,決定アルゴリズムの実装容易性,時間的・金銭的・実行上の費用,アルゴリズムの透明性,予測の正確さの4 点が挙げられる.以下,特殊詐欺抵抗力判定式に高速倹約決定木を用いる場合についてこれら4 点を検討する.
決定アルゴリズムの実装容易性については,ロジスティック回帰式等を用いる場合と比較しても大差はないと思われる.高速倹約決定木であっても,ロジスティック回帰式であっても,適切なソフトウェアさえあれば,データからモデル式を組み立てる作業が異なるだけであり大きな差はない.したがって,この点に関して高速倹約決定木の優位性は小さいと思われる.
時間的・金銭的・実行上の費用については,すべての高齢者について,特殊詐欺被害に関連する項目の費用を算出すること自体が困難である点を上げなければならない.例えば,高速倹約決定木によって仮に「周囲の人とのつながりを持っている」という基準が抽出されたとすると,この基準の実現に要する費用の算出は極めて困難である.その理由は2 点あり,一つはこの費用を算出できる根拠や式を導き出すことが難しいことであり,もう一つは,そもそもすべての高齢者に共通の費用を想定すること自体が可能なことであるかどうかという点である.そのため,高齢者の特殊詐欺抵抗力において高速倹約決定木を応用するときには,費用の問題は含めない方がよいと思われる.但し,抽出された基準が,例えば「地域の防犯意識が高い」というように公共上の政策と関係するような場合には,政策の実現のために公的費用の支出が求められる場合もあるため,この費用を考えることも意味があると思われる.ただしこの場合も,特殊詐欺防止の社会的費用をどのように考えるかという新たな問題に発展する可能性が出てくるため,費用の算出法等を慎重に検討しなければいけない.
判定アルゴリズムの透明性の問題は,詐欺抵抗力判定に関連して提供するアドバイスのわかりやすさに関係してくる.ロジスティック回帰による判定の場合には,ロジスティック回帰式に含まれる値の大きな偏回帰係数に関係する項目からアドバイスが導かれる.1 本のロジスティック回帰式に含まれる偏回帰係数は通常複数個存在し,それらに対応する質問項目についてのアドバイスを単純に結合してアドバイスを作成しただけでは,アドバイスの理解が困難な表現になる.一方,決定木の場合にはこのようなことはなく,各ノードが表す基準を結合することによって自然に決定ルールを導くことができる.したがって,判定アルゴリズムの透明性が高い程,そこから導かれるアドバイスの理解容易性も高くなる.
最後に予測の正確さについては,渡部(2020)で述べたように,ロジスティック回帰による判定式を用いる場合より高速倹約決定木による予測は改善された.また,分析1 及び分析2 で報告したように,高速倹約決定木による判定の正解率は70%強の値を得ている.今後は更に正解率を向上することを目指したい.また,感度の値の改善が求められるが,感度の値は高速倹約決定木のアルゴリズムの問題というより研究に活用できる特殊詐欺被害者データを増やすことによって改善できる可能性が高い.この点については「今後の方向」で論じる.なお,特殊詐欺被害者データの収集については,A 警察署以外に新たに関西地方の警察に協力が得られることが決まった.更に各方面に働きかけて詐欺被害者データの収集に努めたい.
特殊詐欺抵抗力判定アプリの今後の改良のために,以下では不均衡データ(imbalanced data)及び小標本と高速倹約決定木による分析に関して論じる.
最新版の「特殊詐欺認知・検挙状況等(令和元年・確定値)について」(警察庁, 2020)によれば,令和元年の特殊詐欺認知件数は16,851 件である.勿論この数値の中には高齢者以外の被害者も含まれており,また,認知されていない被害もあるので,単純にこの数字を正確な特殊詐欺高齢被害者数として捉えることはできないが,被害者の概数として捉えてもそれ程大きな誤りではないだろう.そこで,令和元年の特殊詐欺高齢被害者が16,851 人いるものと考えると,65 歳以上の高齢者全体に対する特殊詐欺被害者の割合は約0.05%に過ぎないことになる.また,Baesens, Höppner,Ortner, & Verdonck(2020)はクレジットカード詐欺の件数はカード決済全体の0.5%以下であると記載している.このように,国内外において詐欺の被害者数や件数は極めて少ないのであるが,このような詐欺被害データの性質のためにデータの分析には不都合が出てくる.また,本研究のように,特殊詐欺高齢被害者という非常に稀なデータの中から,警察官によるデータ収集に協力した者では,更にデータの偏りが出てくる.一方,警察官が日常の業務において大規模に詐欺被害者データの収集を行うことは現在のところ想定されていないため,今後,研究に活用できる詐欺被害者データが大幅に増加することも期待できない.更に,詐欺被害者が被害を届けないために認知されない件数もある程度存在する.したがって,ごく少数の偏りのある特殊詐欺被害者データと多数の被害に遭っていない者のデータを用いて統計分析を行う状況は当分継続するものと考えられる.そこで,この問題を不均衡データ問題として捉え,高速倹約決定木作成に関係する問題について論じる.
本研究において用いたデータは,A 警察署管内の特殊詐欺被害者データ25 件に対して,詐欺被害に遭ったことがない回答者のデータが412 件であり,特殊詐欺被害者データ数がデータ全体の5.7%しかない不均衡データを構成している.本研究においては,高速倹約決定木に対する不均衡データの影響についての検討は行わなかったが,不均衡データ問題の解消は本研究で得られた高速倹約決定木の2 つのアルゴリズムによる正解率を高めるためのヒントを与える可能性があり,検討に値する問題である.
不均衡データ問題は,これまで統計分析と機械学習の両分野において研究されてきたが,本節では可能な限り統計分析からの視点から論じることにする.また,不均衡データ問題に対する対処法として,アルゴリズムレベル,データレベル,アンサンブル学習の3 分類や,サンプリングに基づく方法,コストに基づく方法,カーネルに基づく方法,能動学習に基づく方法の4 分類が用いられるが(Baesens et al., 2020; Zhu, Gao, Zhao, & vanden Broucke, 2019),ここでは対象データの性質に注目するデータレベルから検討することにする.
不均衡データ問題に対するデータレベルにおける対応には,標本の中の多数データのクラスからアンダーサンプリングを行う場合と,少数データのクラスからオーバーサンプリングを行う場合の2 つの場合がある.そして,この両サンプリングを行う際に,無作為に抽出を行うのか,何らかの情報(標本分布のカーネルや標本の近傍などの情報)を用いた抽出を行うのかによっていろいろな手法が提案されてきた.
ところが,高速倹約決定木に関するデータレベルの対応についての研究はほとんどないのが現状である.そこで,高速倹約決定木でない一般の決定木に関するデータレベルの対応についての先行研究を参考にしながら検討することが考えられる.
また,不均衡データ問題はいくつかの応用領域において論じられているが,その中に詐欺被害者の特定の問題があり多くの先行研究がある.そこで,詐欺被害者の特定の問題について,高速倹約決定木による特殊詐欺抵抗力判定の強化を行うために必要な点について検討することが求められる.
以上より,特殊詐欺抵抗力判定アプリの不均衡データの問題に関してまとめると,決定木における不均衡データの解消法としてデータレベルの対応法を取り上げ,その効果の評価法については機械学習ではなく主に統計的観点から論じることが目的となる.
そこでまずデータレベルの対応法としては,これまでの研究において用いられている技法の中から,R のライブラリーIRIC(Zhu et al., 2019)に含まれているオーバーサンプリング技法であるSMOTE(Chawla, Bowyer, Hall, & Kegekmeyer, 2002),MWMOTE(Barua, Islam, Yao, & Murase, 2014),ADASYN(He, Yang, Garcia, & Li, 2008),Random Oversampling 及びアンダーサンプリング技法のCLUS(Lin, Tsai, Hu, & Jhang, 2017),混合技法のSmoteENN(Batista, Prati, & Monard, 2004),SmoteTL(Batista et al., 2004),SPIDER(Stefanowski & Wilk, 2008)を取り上げることにする.これらの技法は,オーバーサンプリングやアンダーサンプリングを行う際にどのような情報に基づくかが異なるため,これらの技法を用いた不均衡データへの対応を行うことによって,高速倹約決定木の分類に対する影響を見ることができる.
次に,不均衡データの解消法の効果の評価について論じる.ここでも,本研究で用いたBayesfactor を用いた分割表の評価を行う(Jamil et al., 2017).更に,Baesens et al. (2020)は不均衡データを扱う場合には,AUC は評価結果が楽観的に出る傾向があるため,AUPRC(precisionrecallcurve)を勧めているので,AUPRC による評価も取り入れる.また,高速倹約決定木の特徴である効率性を表す「高速」と「倹約」の指標である速度と倹約性への影響も検討しなければいけない.
以上をまとめると,高速倹約決定木を用いた特殊詐欺抵抗力判定式導出に対する不均衡データの影響の検討は以下の方針で行うこととなる.
1. 不均衡データの解消法として,オーバーサンプリング技法であるSMOTE,MWMOTE,ADASYN,Random Oversampling,及びアンダーサンプリング技法のCLUS,混合技法のSmoteENN,SmoteTL,SPIDER を用いる.
2. 不均衡データの解消法の評価として,Bayes factor を用いた分割表の評価,AUPRC,速度と倹約性を用いる.
次に,小標本における分析について論じる.不均衡データ問題は,ターゲットとするデータ数に比べてターゲット群以外のデータの個数が多い場合の問題である.即ち,不均衡データ問題は,ターゲット群のデータとそれ以外の群のデータを一緒にして分析する場合に生ずる問題であるのに対して,小標本における分析の問題(以下,小標本問題という)は,ターゲットデータのみを用いて分析する際に,十分な個数のデータ収集が不可能なために生ずる問題である.
ここでは小標本を用いてベイジアン分析を行うときに絞って論じるが,このような場合データに対して事前分布の重要性が相対的に高まる.換言すれば,事前分布を上手く選択することによって小標本による情報の不足を補うことが可能であることを意味する.Zondervan-Zwijnenburg & Peeters(2017)は事前分布の選択の指針を示しており,その中で,先行研究や専門家の知見を参考にして色々な事前分布を作成し,それらを用いて試行的に分析を行い,その結果に関して感度分析を行うことを勧めている.実際にZondervan-Zwijnenburg & Peeters(2017)では潜在成長モデルに対してinformative prior とdefault prior を用いて比較した結果,informative prior を用いた場合の方が各パラメータの信用区間の幅が小さいという結果が得られている.
Zondervan-Zwijnenburg & Peeters(2017)で提案する感度分析の一つの方法としてWesner & Pomeranz(2020)は事前予測分布(prior predictive distribution)を用いることを提案している.この方法によれば,感度分析は以下の手順で行う.
(1)複数の事前分布の候補から超母数を生成する.
(2)生成した超母数を用いてモデルの母数を生成する.
(3)生成した母数を用いた事前分布よりデータを生成する.
(4)事前知識を用いて,生成したデータの評価を行う.
(5)評価の結果が悪い場合には,事前分布と尤度のどちらか,または両方を修正する.
(6)評価の結果が良い場合には,この事前分布よりデータを更に生成し,事後分布の推定に進む.
この方法は事前予測チェック(prior predictive check)を事前分布の評価に用いるものであり,特殊詐欺被害者データという小標本を用いた今後の分析においても有望な方法の一つになるものと思う.但し,(4)事前知識を用いたデータの評価は,特殊詐欺被害と心理要因に関する先行研究が極めて少ないため事前知識は期待できない.したがって,事前予測分布から生成したデータと実際の標本との類似度の測定も困難である.このような場合には,上記(3)までの仮定によって構成した事前分布とモデル(尤度)によってBayes factor を計算し,事前分布並びにモデルの選択を行うことが考えられる(Kennedy, Simpson, & Gelman, 2019).
本研究は国立研究開発法人科学技術振興機構(JST)社会技術研究開発センター(RISTEX)の戦略的創造研究推進事業(社会技術研究開発)「安全な暮らしをつくる新しい公/私空間の構築」研究開発領域平成29 年度採択プロジェクトとして研究活動費の助成を受けたものです.特殊詐欺抵抗力判定アプリを用いたデータ収集にご協力いただいた皆様方に厚くお礼申し上げます.