1996年,カナダのバンフで開かれた計量心理学会の会長演説で,その時点における数量化の問題点を拾い上げた(Nishisato, 1996).それからおよそ20年,問題は解決したか? 現時点に立って,もう一度落穂ひろいを試み,自説を繰り広げたい.数量化理論の基本的構造は双対の関係であり,独特な研究対象は行変数と列変数の同時解析にある.この独特の問題は従来の最小二乗法的アプローチでは解決できない問題をもたらす.最たる問題は行変数と列変数の多次元グラフの問題で,これは今でも未解決である.本文ではこれに焦点を当てて議論を進めたい.数量化の問題は探索的データ解析に不可欠な根本的理解を必要とするもので,カテゴリーデータの数量化に対応する量的データの主成分分析を理解するだけでは不十分なほど大きな問題を抱えている.というのは「数量化が変数間の相関行列の主成分分析と被験者間の相関行列の主成分分析を同時に解析することを趣旨としている」というのが筆者の立場であり,「双対」を主張してきたからである.この一見複雑な数量化の問題も,常識で十分理解できるように思われる.数式化に追われず,課題の根本的理解から始めよう.本文では,数量化の歴史で絶えず問題点として浮上した行変数,列変数の同時多次元グラフ問題に対する解決の案を再訪したい.
In the presidential address at the annual meeting of the Psychometric Society, held in Banff, Canada, Nishisato (1996) delivered his view on quantification theory under the title of “Gleaning in the field of dual scaling.” He identified a number of unsolved problems at that time. It is almost twenty years since then. Are those problems satisfactorily solved? Yes and no. From the current stage of progress, this paper was written about his view on the future perspectives of quantification theory. Given that the main purpose of quantification of categorical data lies in its strong desire to analyze both row variables and column variables on the equal footing, an immediate concern is around the current practice of multidimensional joint graphical display. This paper directs our attention to the difficulty underlying our joint graphical display of both row variables and column variables, where principal coordinates of both variables need to be plotted. The solution rests in the use of doubled multidimensional space, and the current paper recommends a step forward to total information analysis and the use of cluster analysis, instead of highly problematic multidimensional joint graph, an approach that most researchers, under the strong doctrine of `correspondence analysis,' have unsuccessfully pursued. In discussion, it was stated that the current practice of symmetric, non-symmetric scaling and biplot all fail to satisfy the basic premise of joint graphical display, that is, multidimensional plot of principal coordinates of both row and column variables. The paper emphasizes the importance of the understanding of the basic objective of joint analysis of row and column variables on the equal footing.
最近,素晴らしい数量化の本を読んだ( Nishisato, 2016).Wiley から出た Beh & Lombardo(2014) の560 ページにわたる数量化のあらゆる側面を網羅した大作である.しかし,この本を読んで私が気づいた最初の疑問は何故名前「correspondence analysis」が定着してしまったのか,ということである.残念ながら,上述の本にその答えは見つからない.
Beh が,数量化への関心は,学生の時, Greenacre (1984) の査読をアサイメントで出されたことに始まるとあるので,Greenacre が用いた「Correspondence analysis」(フランス語「Analysedes correspondances」の英訳)を,そのまま上述の本の題名に採用したのであろう.
数量化の名前に関しては,多くの代表的研究者提唱の独自の名前が世にでた. 林の数量化理論(1950) は大きな枠組みを持つ理論的なもので,素晴らしい名前で適名だ.しかし,correspondenceanalysis は,林の数量化理論の一部に過ぎなく,数量化3 類(飽戸弘先生命名)に対応する.
今からおよそ40 年前の1976 年,計量心理学会のシンポジウム「Optimal Scaling」(オーガナイザーForrest W. Young, 講演者Jan de Leeuw, Shizuhiko Nishisato, Gilbert Saporta, 指定討論者Joseph P. Kruskal)が開かれた.当時,北米では数量化の名前としてOptimal Scaling(Bock, 1960) が広く用いられていた.討論の中で,著名なJoseph Zinnes が「Optimal Scalingの名前はあまりにも一般的すぎる」と反対意見を述べた.これを機に,多くの数量化の名前と意味が議論された.そのなかで新たにNishisato が提案した「dual scaling」が大賛成を得たのに励まされ,拙著( Nishisato, 1980) で,dual scaling の名前がデビューした.当時多数の数量化の論文は出ていたが,専門書としては,Paul Horst (私信, 1986) が“the most comprehensive book onthe topic” と書いてくれたように, Nishisato (1980) が英語の唯一の単行本だったと思う.この本は,当時フランスで勉強中のGreenacre の博士論文委員会からの依頼に応え,Greenacre にも送呈されたが,四年後に出た Greenacre (1984) では,dual scaling が余り重要視されていない.Peter van der Heijden (私信, 1985) は,これを不服に親切な激励の書状をくれた.更に1986年,ソヴィエトアカデミーのBoris Mirkin,Sergei Adamov と数人の研究者が,数量化の本では Nishisato (1980) が最適として,そのロシア語訳を決定した.ロシア語版の出版は1990 年には翻訳も完成,著者もモスクワに招かれた.その2 月,トロント大学出版会とモスクワのFinansy iStatistika Publishing House の間に出版契約が調印されていた.しかし,1991 年の突然のソヴィエト連邦崩壊により,モスクワの出版社が倒産,出版の夢は消えた.もしロシア語版が出ていたら,と思わざるを得ない.この忘れられた双対尺度法の名前にもう一度光を与えたい.
数量化とは何かという疑問に対して,私は次のように説明する.
「もっとも重要な特徴はデータ行列の行と列を同時に解析することにある.後年H.O.Hartley の名で有名になった統計学者が若いときHirschfeld という名前で同時線型回帰法( Hirschfeld, 1935)を提唱した.彼の疑問は,「分割表が与えられたとき行 i に測度 x i を与え,列 j に測度 y j を与える場合,測度 x i の列への回帰,測度 y j の行への回帰が同時に線型になるような測度を見出せるか?」というものであった.彼の答えは「常に可能である」.そのような測度は上記の本 Nishisato(1980) に記された双対の関係式を満たす.

ここで統計量 ρ はHirschfeld の回帰係数,Guttman の測度間の最大の相関係数,標準化された分割表の特異値,Nishisato の行の列へ,列の行への射影子である」.
双対は対称を意味するので,同時線型回帰,交互平均法も包括するということで,双対尺度法(dual scaling)の名前が提唱された.上の双対関係式で,射影子の存在が,行空間と列空間の隔たりを明らかにしており,行変数と列変数の同時解析のグラフ表示に何が必要かを示唆している.
フランス語のCorrespondances の「双対」の意味はめったに使われない.はっきり「Dual Analysis」といったほうがわかりやすい.しかし,現実には,「Correspondence Analysis」が一般に受け入れられ,同時解析の焦点は希薄になった.「双対尺度法(Dual Scaling)」は,若輩の私が提唱したことのほかに,フランスのグラフ重視に呼応しなかった理由で,多くの研究者に無視されてきたのではないかと思われる.何故フランス流に呼応しなかったかが本文の中心的話題である.それは,双対式で浮上する射影子の存在に始まる.
数量化のグラフ表示には大きな問題があった.フランスの研究者がグラフ表示こそ数量化の神髄であるとして,グラフ表示を推進し,フランス仕込みの Greenacre (1984) もそれに従ったのに対し,グラフ表示の論理的根拠は不合理として Nishisato (1980) はグラフを避けた.これが,フランス勢を筆頭とする多くの研究者の Nishisato (1980) 批判,軽視となり,初めからグラフ法に重点を置かないdual scaling という言葉を回避したように思われる. Nishisato (1980) のグラフから遠ざかった根拠は, Nishisato (1996) に解説されているので,読者に再紹介したい.
Torgerson (1958) は数量化というのはカテゴリーデータの主成分分析であると述べている.両者の関係には Nishisato (1980) も触れている.そこで,いまデータが量的なものとして,その相関行列の主成分分析を考えよう. R = X′ Δ X の分解で, X は固有ベクトルの行列で 標準座標,ΔΔ 1/2 X は前者に特異値をかけたもので 主軸座標と呼ばれる.今,データが完全に2 次元構造を持つものなら,主軸座標を用いるとデータのすべての点が,直径1 の円上に分布する(各変数の分散は1).3 次元のデータなら,主軸座標をプロットすると,すべてのデータが直径を1 とする球体の表面に分布する.これが各変数の分散を1 として始まったデータのグラフで,これこそデータの多次元グラフであるということには異論がないと思われる.つまり「主軸座標はデータの多次元空間における無限に存在する座標の一つである」ということである.データが多次元空間に布置しても,各変数は原点から1 の距離にあるべきことは誰しも理解できる.換言すると,主軸座標は多次元解析においてデータの全情報を表現する一手段である.これに対して,標準座標をプロットすると,データが2 次元の場合,固有値の分布により円が歪められる.例えば,2 次元のデータで第一次元が80 パーセントの分散を担うなら,その円は2 次元軸で大きくひき延ばされ,一次元軸では狭まれ,縦に細長い円となる.この座標軸からは,変数の分散の情報が全く分からない.従って,標準座標はデータの真の姿(例,2 次元の場合の正円)を捉えない人為的に標準化したものであることがわかる.
数量化の場合,行変数と列変数を同時に解析するのが主目的で,これがグラフ表示にも当てはまらなくてはならない.上述のように,データの情報は主軸座標が捉えているが,双対式の射影子に見られるように,行変数と列変数が分布する空間には隔たりがある.その隔たりを全く無視して行の主軸座標,列の主軸座標を同じ空間にプロットするのがフランス流の対称スケーリング(symmetric scaling, French plot)で,大多数の研究者が今日使用しているが, Lebart, Morineau & Tabard (1977). は,このグラフからは行変数と列変数の正確な距離を計算できないと警告した.当然のことである.これが Nishisato (1980) の行,列変数のグラフ表示への躊躇の原点だった.明らかに誤ったグラフ法で支持できない.これに対し,片方の主軸座標と他方の標準座標のプロット(non-symmetric scaling と呼ばれる)では,片方を他方の空間に射影するということで,空間の違いの問題は出てこないので,「これこそ論理的なグラフ法だ」というのが,今でも数量化の研究者の多くの意見である.問題は射影した変数と他の変数のノルムが違うので,両者間の比較の拠点を失うことのほかに,一番重要なことは,一方はデータの座標,他はデータと関係のない座標であるということである.従って,「これこそ論理的なグラフ法だ」という定説に,私は異論を呈したい.数学的には正しい,論理的には正しいという説はわからないでもないが,「non-symmetricscaling もデータの表現法として論理的ではない」というのが真実である.それは多次元データの情報を担っていない行変数(あるいは列変数)の標準座標に列変数(行変数)を射影したグラフだからである.そのグラフ上での行変数と列変数の距離は全く無意味であるというのが私の主張である.敢えて論理的なものをというのであれば,「行(列)の主軸空間(データ空間)に列(行)の主軸座標を射影せよ」であるが,これには両者のノルムが違うという問題がまとうので,グラフ法の解決にはならない.
Biplot は統計学者(例えば, Gabriel, 1971; Gower & Hand, 1991)が推進してきた同時グラフ法である.行列の特異値分解を F = Y′ Λ X = Y′ Λ αΛ β X と書き換える.ただしΛαβαβαβαβ
以上のことから,現存の対称グラフ,非対称グラフ,バイプロットはデータの情報を忠実にグラフ化したものではないという結論に達する.行変数と列変数を同時に解析する数量化には,もっと論理的に正当化できるグラフが必要である.
データの多次元空間分解は行と列の主軸座標を合わせて表現されることは周知のことである.それなら,行と列の主軸座標を同時にプロットするのが正統であろう.しかし,従来の対称スケ―リングでは行と列を無理やり同一空間にプロットするという誤った強硬手段に頼っており,到底正当化できるものではない.行空間,列空間の隔たりを取り入れるには,次元数を増やすことしかない.つまり,第一次元のプロットには2 次元空間が必要である.行変数の軸と列変数の軸の隔たりは,cos −1 ρ 1 である.ただし, ρ 1 は第一成分の特異値である.同様に,第一,第二成分の行と列の同時グラフには4 次元空間が必要である.第二成分の行と列の隔たりはcos −1 ρ 2 で与えられる.これがNishisato ( 2012, 2014) の数量化の行変数と列変数の同時グラフ作成には多次元空間の次元数を二倍にするdoubled multidimensional space が必要だという主張の原点である.しかし,後学の為,一般には二倍でも不十分である可能性を記しておこう.
これまでのグラフに関する検討は,one-mode two-way の分割表の行と列のグラフの問題として,受け止められたかと思う.これに対して,多肢選択のようなデータはtwo-mode two-way 表なので,同時グラフは意味がないのでないかという疑問が出よう.この関係は, Nishisato (1980)に解説されているように,分割表のデータを被験者× 選択肢の形に書き替えた場合,後者の数量化には前者の数量化の二倍の次元の空間が必要であることが知られている.従って,one-modetwo-way の分割表であれ,two-mode wo-way の被験者× 選択肢の多肢選択データであれ,行と列変数の同時グラフの意味には違いが無い,というのが筆者の見解である.この二倍の次元数の空間が必要だということは,前述の話につながるものであり,興味深い.また,同時グラフということでは,因子分析において,被験者(被験者の因子得点)と変数(因子負荷量)をグラフにしようという場合,それは意味があるか,ないかという問題に通ずるのではないであろうか? Two-modetwo-way であっても,筆者は意味があると思っている.
Nishisato (1980) の詳しい記述にもかかわらず,CGS scaling ( Carroll, J.D., Green, P.E. & Schaffer, C.M., 1986) は,分割表のグラフの行と列の空間の違いの問題は,それを被験者× 選択肢(反応パタン表)に書き替えて数量化することにより,行と列の選択肢が同じ列に示されるので,同じ空間に行の選択肢と列の選択肢を表示できるとして提唱したが, Greenacre (1989) の鋭い批判を受け,CGS Scaling は失墜した.しかし,これは,すでに Nishisato (1980) が解説している問題で,どちらが間違っているともいえない.しかし,分割表を数量化しても,反応パタン表を数量化しても,両者が共有する成分の座標は完全に一致すること(つまり,one-mode two-wayでもtwo-mode two-way でも結果は同じ),しかし,反応パタン表の解析では,分割表の二倍あるいはそれ以上の次元が必要である( Nishisato, 1980) ことが解説されている(分割表の最大成分数は,行数と列数の小さいほうから1 を引いたもの,反応パタン表の最大成分数は,選択肢総数から項目数を引いたもの)が,Carroll, Green, Schaffer, Greenacre の四人は,この重要な違いを考えずに,無駄な論争をしていたというほかはない.換言すれば,CGS Scaling は,さらに多くの次元数の空間を使うという条件では正しく( Young & Householder, 1938),分割表の解析と同じ小次元で解析するというのであれば,Greenacre の批判が正しいことになる.
数量化の本分はデータ行列の行と列を同時に解析することである.すなわち,行変数と列変数を平等に解析することにあるといってよいであろう.しかし,従来の統計学の影響は非常に大きく,特に回帰分析のように,最小二乗法を使って一方から他方を推定しようとする研究法がデータ解析の大半を支配してきた.その影響が数量化理論の研究にも強い影響を与えてきた.例えば,non-symmetric scaling によるグラフ法を論理的だという証言である.しかし,データの行と列を対等に取り扱おうという数量化の研究にとって,最小二乗法は一方の変数を他方の変数空間に射影することで,行と列を対等に解析することにはならない.つまり,射影値のノルムは他の変数のノルムより通常小さいことから,変数とその射影値を多次元空間で比較するのは対等な扱いとは言えない.
一つの例を挙げよう.因子分析で変数の因子負荷量が得られたとしよう.その空間に被験者もプロットしたいということで,被験者の因子得点を変数の因子負荷量から最小二乗法で推定する.因子負荷量の多次元空間に被験者の因子得点をプロットしようという考えは,もっともな響きを持つが,後者は射影値であり,一般に前者よりノルムが小さく,因子負荷量と因子得点の比較には不適当である.対等の比較には行変数と列変数のノルムが等しくなくてはならない.それには二倍の空間が必要である.
射影という考えは,一つの空間から他の空間に両者の空間の隔たりが最小になるように決める一つの手段で,その前提には二つの空間がある.数量化の立場からいえば,射影ではなく,二つの空間をそのままグラフに用いなくてはならない.これが前章で述べた多次元空間を二倍にして行変数と列変数を同じノルムで検討しようという主張である.
この観点から,提唱されたのが全情報解析(総合的双対尺度法)( Nishisato & Clavel, 2010) である.データ行列から数量化によりすべての成分を抽出,それらすべてを用いて行内距離行列 D xx ,行列間距離行列 D xy , D yx ,列内距離行列 D yy を計算する(Nishisato & Clavel, 2003; Clavel & Nishisato, 2008).この大距離行列 D ,
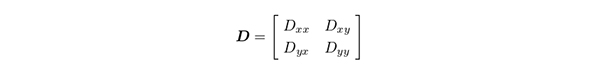
を完全に解析するには,数量化で用いる多次元空間の二倍の空間が必要なことは,数値計算でも証明できる.
現在の多次元グラフ法で一般に用いられる方法では,通常三次元グラフまでに限られている.しかし,行変数と列変数の主軸座標の布置には二倍,或はそれ以上の空間が必要であることを考えると,一成分のグラフに限られてしまう.これでは,データ解析の空間としては全く不十分であることは自明である.さらに,一般の多次元解析で,最初の二成分,三成分のみを検討することは,特異な情報を担う小さな成分を完全に見逃してしまうことにも通ずる.これらを考慮して,全情報解析では,行変数,列変数の多次元グラフ表示をあきらめ,二倍の全多次元空間における距離行列 D のクラスター解析を推薦している.つまり,一部の情報も落とさずに,距離行列を計算し,データのすべての情報をとらえる二倍の多次元空間で,どのような行変数,列変数がクラスターを構成するか,という問題の設定である.これで,長年の行変数,列変数のグラフ表示を追及しようとして突き当たった壁を乗り越えることができ,特異な反応結合も見逃すことのない多次元解析が出来るのではないかと思う.
クラスター解析による多次元空間の全情報解析は,次のようなケースに格好の処理法である.(1) 被験者 x 変数のデータが与えられ,被験者のクラスター解析と変数のクラスター解析が得られたとしよう.この場合,全情報解析は,これら二つのクラスター解析の結果を一つにまとめる役割を果たす.(2) 被験者x 被験者の相関行列の因子分析,変数x 変数の相関行列の因子分析が行われた場合,全情報解析では,二つの因子分析の結果を,一つの空間で対等に解釈してくれる.
回顧:1966 年,ノースカロライナ大学の著者の博士論文は「Minimum entropy clustering oftest items」で,指導教官はOptimal Scaling を提唱したR. Darrell Bock.そのあと研究は数量化に移っていたが,半世紀後の今,また出発点のクラスター解析に助けを求めることとなった.分類が科学の基礎をなすことを知らされた思いがする.
量的データの多次元解析では,主成分分析のように専ら行変数だけか列変数だけの多次元解析に目が向けられてきた.更に,その解析は殆どが線型解析にとどまる.これに対して,質的データの多次元解析では,行変数と列変数の対等な多次元解析に目が向けられ,変数間の関係は非線型でも,線型でも解析の対象となる.この第一の焦点の違いが,後者の場合には行変数と列変数のグラフ表示の問題をもたらした.いま,数量化でも行変数だけ,あるいは列変数だけの多次元解析をすると仮定して,これを量的データの主成分析の場合と比較してみよう.
主成分分析で相関行列( R )を解析するか,分散共分散行列( V )を解析するか,という問題が応用分野では良く持ち上がる.これは単に嗜好の問題ではない.何故なら, R の主軸と V の主軸の間には,通常1 対1 の関係がないからである.つまり, R の最初の主成分が同じデータの V の最初の主成分に対応するという保証は何もない(Nishisato & Yamauchi, 1974).すなわち,どちらを選ぶかにより結果が異なってくる.これは大変重要な問題であるが,どちらを選ぶべきかという問いに対する満足できる回答は見当らない.
これに対応する数量化の問題は,どういうことになるであろうか? R と V の違いは聞いたことがない.これは,数量化の過程で測度の単位,原点が任意に選ばれるからである.しかし,数量化の場合も,わずかであるが似たような問題に遭遇することがある.例えば,多肢選択データの或る質問に対し,多数の被験者のうち一人だけ選んだ選択肢があるとしよう.この場合,この選択肢が,分散を最大にする数量化では,outlier となり,これを持つ質問が最大分散を得,第一主軸を決定してしまうことがある.わずか一人の独特な反応が第一主成分を決めてしまうとは馬鹿げている.しかし残念ながら,現在の数量化の方法では.このようなことを避けることができない.対応策としてMethod of reciprocal medians,そのほかが提唱された( Nishisato, 1987)が,これらは実用に付されていない.同じように,多肢選択数の大きな質問ほど,全体の解析に及ぼす影響が大きい.このようなことを見て, Nishisato (1991) は数量化の多次元空間の一様化の案を出している.例えば,選択肢の影響を一定にすること,選択肢の反応分布を人工的に矩形化することで,選択肢数の影響,分布の偏りの影響を減少させることである.このいわばカテゴリーデータの標準化(この意味は量的データの標準化とは無関係である)は,現在のところ,案の提唱だけにとどまり,そのあと研究が続いていない.しかし,これは,さらに研究すべき課題ではないかと思われる.一般的な問題としては,例えば,すべての質問の選択肢の数を統一する,あるいは,あまり選ばれない選択肢を消去するなどである.このような実際的問題としては,データの取り方,データの代表性など,他にも沢山あるが,ここでは取り上げない.
連続変数の離散化は科学のあらゆる方面で研究されてきた.しかし,数量化の為に,どのように連続変量をカテゴリー化すべきか,という一般的な方法は見当たらない.カテゴリー化により,情報を失うという危惧は十分考えられる.しかし,カテゴリー化により,数量化にかけて比較的容易に非線型関係の多次元解析ができる,という大きな特典が待っている.量的データの多次元非線型解析がカテゴリー化以外には困難な現在,たとえ,情報消失がカテゴリー化の過程にあったとしても,多次元非線型解析の道が開かれるという可能性は捨てられないように思われる.
以上,思い付くままの落穂ひろいを試みた. Beh & Lombardo (2014) が強調しているように,R によるコンピューターのプログラムは,数量化の普及に大きな原動力になると思う.行と列の同時解析を主な目的とするデータ解析にとって,大きなデータを取り扱うプログラムは不可欠である.数量化の為のR のプログラムは,すでにいくつか出ている.著者の関係しているものとして,試みの第一号,多肢選択データの数量化が昨年出た( dualScale, authors Clavel, Nishisato & Pita, 2014, CRAN).そのあとの作業は現在進行中である.多くの研究が発表されると,さらに様々な実用上の問題が出てくるこことは当然である.これから20 年後の落穂ひろいには,どのような問題が浮上するであろうか?.
二人の査読者,審査担当の今泉忠先生から大変役に立つ好意的,建設的コメントをいただき,最終稿に改定された.ここに衷心より敬意とともに感謝の意を表したい.