2022 Volume 90 Issue 10 Pages 102001
2022 Volume 90 Issue 10 Pages 102001
Electrochemistry deals with the interrelationship between electrical and chemical energy. Various potentials appear in electrochemistry and pertain to one another in practical cells. Understanding the electrode potential is an important step in acquiring basic knowledge of electrochemistry and extending it to specific applications. This comprehensive paper outlines the fundamentals and related subjects of electrode potentials, including electrochemical cells and liquid junction potentials. Aqueous solution systems are ideal for connecting the theoretical background of electrode potentials to practical electrochemical measurements. Accordingly, the basic electrode chemistry in aqueous systems is described in this paper, as well as several advanced concepts introduced in recent studies.
Electrode potential is the most salient and puzzling concept in electrochemistry.1–10 Although electric potentials in physics certainly underlie the concept of the electrode potential, the thermodynamic connection of the electrode potential to Gibbs energy represents the direction and scale of a redox reaction. A basic understanding of the electrode potential is necessary for constructing an appropriate electrochemical system and extending it to different applications.
Historically, the electrode potential has a variety of backgrounds, and its definition is somewhat ambiguous. This comprehensive, instructive paper summarizes the fundamental aspects of the electrode potential, mainly in the equilibrium state. Section 2 starts by defining the different types of electric potentials required in electrochemistry and describes the thermodynamic aspects connecting the Gibbs energy and the cell potential. Next, the electrochemical potential, which considers the chemical and electrical contributions to the total energy of a charged species, is introduced and connected to the Nernst equation. A basic description of the electrochemical cell is presented, as well as the definitions of related terms and tips for the use of coin cells. At the end of the section is a description of the junction potential at the interface of two electrolytic solutions, and information on salt bridges.
Section 3 covers aqueous solution systems, which provide good examples of the fundamental concepts and are ideal for connecting the theoretical background to practical electrochemical measurements. Information is provided on the basic electrode chemistry in aqueous systems, including the Pourbaix diagram, electrochemical window, practical reference electrode, and mixed potentials, as well as several advanced concepts introduced in recent studies. Detailed slides for each section are provided in the Supplementary Material.
The electric potential of a charged species generally corresponds to work that brings it from the point at infinity to a specific point. Figures 1a and 1b summarizes the relationship between the inner, outer, and surface electric potentials and the Galvani and Volta potentials for metal M. The inner electric potential (ϕM) is the potential to bring a charged particle from the point at infinity (point O) to a specific point in the bulk of M (point B), and thus the difference between the two inner electric potentials (e.g., $\phi^{\text{M}_{1}}$ and $\phi^{\text{M}_{2}}$, where M1 and M2 are two different metals) provides the Galvani potential ($\varDelta \phi_{\text{M}_{1}}^{\text{M}_{2}}$). The outer electric potential (ψM) is a potential to bring a charged particle from the point of infinity (point O) to the surface of M (point A), and the difference between the two outer potentials ($\psi^{\text{M}_{1}}$ and $\psi^{\text{M}_{2}}$) is called the Volta potential ($\varDelta \psi_{\text{M}_{1}}^{\text{M}_{2}}$). The surface electric potential (χM) originates from the dipolar charge distribution at the surface of M. These three potentials are connected using Eq. 1; however, only ψM, which is the potential difference between two points in the same phase, is a measurable quantity.
| \begin{equation} \phi^{\text{M}} = \psi^{\text{M}} + \chi^{\text{M}} \end{equation} | (1) |

(a) Relationship between inner (ϕM), outer (ψM), and surface (χM) electric potentials of metal M. (b) Relationship between Galvani ($\varDelta \phi_{\text{M}_{1}}^{\text{M}_{2}}$) and Volta ($\varDelta \psi_{\text{M}_{1}}^{\text{M}_{2}}$) potentials for metals M1 and M2. (c) Electrode potential regarded as a potential difference between points in a metal M and a solution S.
When considering the following n-electron redox reaction (Eq. 2), the corresponding reaction Gibbs energy, ΔrG, is provided by Eq. 3 using the chemical potential, μi, and activity, ai, of two pairs of oxidants and reductants (Ox/Red and Ox′/Red′).
| \begin{equation} \text{Ox} + \text{Red}' \rightleftharpoons \text{Red} + \text{Ox}' \end{equation} | (2) |
| \begin{align} \Delta_{\text{r}}G & = \mu_{\text{Red}} + \mu_{\text{Ox${'}$}} - \mu_{\text{Ox}} - \mu_{\text{Red${'}$}}\\ & = (\mu_{\text{Red}}^{\circ} + \mu_{\text{Ox${'}$}}^{\circ} - \mu_{\text{Ox}}^{\circ} - \mu_{\text{Red${'}$}}^{\circ}) + RT\ln\frac{a_{\text{Red}}a_{\text{Ox${'}$}}}{a_{\text{Ox}}a_{\text{Red${'}$}}}\\ & = \Delta_{\text{r}}G^{\circ} + RT\ln Q \end{align} | (3) |
An important relationship between ΔrG and the cell potential, ε (the International Union of Pure and Applied Chemistry (IUPAC)13 recommends using the cell potential instead of the electromotive force, emf) for the corresponding electrochemical cell is introduced as follows (Eq. 4):
| \begin{equation} \Delta_{\text{r}}G = -nF\varepsilon \end{equation} | (4) |
| \begin{equation} \varepsilon = \varepsilon^{\circ} - \frac{RT}{nF}\ln Q \end{equation} | (5) |
When Red′ and Ox′ in Eq. 2 are $\frac{1}{2}$H2(g) and H+(aq), respectively, in their standard states, Eq. 3 can be written as follows (Eq. 6):
| \begin{equation} \Delta_{\text{r}}G = \Delta_{\text{r}}G^{\circ} + RT\ln\frac{a_{\text{Red}}}{a_{\text{Ox}}} \end{equation} | (6) |
Figure 2 shows the corresponding electrochemical cell, in which the working electrode potential is measured with respect to the reference electrode potential. The H+/H2 redox couple in the standard state is the universal reference electrode, known as the standard hydrogen electrode (SHE), and its standard electrode potential, E°, is zero at all temperatures (E°(H+/H2) = 0).13 Thus, ε in this case can be regarded as the electrode potential representing the half-cell reaction (Eq. 7) in question, and is simply called the electrode potential, E.
| \begin{equation} \text{Ox} + ne^{-}\rightleftharpoons \text{Red} \end{equation} | (7) |
| \begin{equation} E = E^{\circ} - \frac{RT}{nF}\ln\frac{a_{\text{Red}}}{a_{\text{Ox}}} \end{equation} | (8) |

Schematic of the standard hydrogen electrode (SHE) paired with an electrode W. The pressure of H2 and activity of H+ for SHE are 105 Pa and 1.0, respectively.
The chemical and electrochemical potentials (μ and $\tilde{\mu }$) defined in Eqs. 9 and 10 are important quantities for introducing the electrode potential under a constant potential and temperature. The two terms contain the word “potential;” however, their unit is J mol−1 and is different from the unit of the electrode potential (V).
| \begin{equation} \mu_{i} = \left(\frac{\partial G}{\partial n_{i}}\right)_{n_{j \neq i}} {}= \mu_{i}^{\circ} + RT\ln a_{i} \end{equation} | (9) |
| \begin{equation} \tilde{\mu}_{i} = \mu_{i} + z_{i}F\phi = \mu_{i}^{\circ} + RT\ln a_{i} + z_{i}F\phi \end{equation} | (10) |
| \begin{equation} \tilde{\mu}_{\text{Ox}} = \mu_{\text{Ox}} + z_{\text{Ox}}F\phi^{\text{S}} = \mu_{\text{Ox}}^{\circ} + RT\ln a_{\text{Ox}} + z_{\text{Ox}}F\phi^{\text{S}} \end{equation} | (11-1) |
| \begin{equation} \tilde{\mu}_{\text{Red}} = \mu_{\text{Red}} + z_{\text{Red}}F\phi^{\text{S}} = \mu _{\text{Red}}^{\circ} + RT\ln a_{\text{Red}} + z_{\text{Red}}F\phi^{\text{S}} \end{equation} | (11-2) |
| \begin{equation} \tilde{\mu}_{\text{e}} = \mu_{e}^{\circ} - F\phi^{\text{M}} \end{equation} | (11-3) |
| \begin{equation} \tilde{\mu}_{\text{Ox}} + n\tilde{\mu}_{\text{e}} = \tilde{\mu}_{\text{Red}} \end{equation} | (12) |
| \begin{align} &(\mu_{\text{Ox}}^{\circ} + RT\ln a_{\text{Ox}} + z_{\text{Ox}}F\phi^{\text{S}}) + n(\mu_{e}^{\circ} - F\phi^{\text{M}}) \notag\\ &\quad= \mu_{\text{Red}}^{\circ} + RT\ln a_{\text{Red}} + z_{\text{Red}}F\phi^{\text{S}} \end{align} | (13) |
| \begin{align} E & = \phi^{\text{M}} - \phi^{\text{S}}\\ & = -\frac{\mu_{\text{Red}}^{\circ} - \mu_{\text{Ox}}^{\circ} - n\mu_{\text{e}}^{\circ}}{nF} - RT\ln\frac{a_{\text{Red}}}{a_{\text{Ox}}}\\ & = E^{\circ} - \frac{RT}{nF}\ln\frac{a_{\text{Red}}}{a_{\text{Ox}}} \end{align} | (14) |
| \begin{align} E & = E^{\circ} - \frac{RT}{nF}\ln\frac{a_{\text{Red}}}{a_{\text{Ox}}}\\ & = E^{\circ} - \frac{RT}{nF}\ln\frac{\gamma_{\text{Red}}}{\gamma_{\text{Ox}}} - \frac{RT}{nF}\ln\frac{c_{\text{Red}}}{c_{\text{Ox}}}\\ & = E^{\circ\prime} - \frac{RT}{nF}\ln\frac{c_{\text{Red}}}{c_{\text{Ox}}} \end{align} | (15) |
The selected E° values at 25 °C are listed in Table 1.14 Although the H+/H2 couple (SHE) is defined as the reference for all the E° values, more convenient redox couples with a high reversibility are practically used as reference electrodes (details on practical reference electrodes are provided below). The ionic species in the list are assumed to be in an aqueous solution, which means that E° can be different in other solvents. The oxidizing power of the species on the left side decreases from high to low E°; F2 in F2/F− is the strongest oxidizer, and Li in Li+/Li is the strongest reducer in the list (Table 1).
| Half-cell reactions | E° |
|---|---|
| F2 + 2e− ⇌ 2F− | +2.87 |
| Ce4+ + e− ⇌ Ce3+ | +1.72 |
| MnO4− + 8H+ + 5e− ⇌ Mn2+ + 4H2O | +1.51 |
| Cl2 + 2e− ⇌ 2Cl− | +1.36 |
| Cr2O72− + 14H+ + 6e− ⇌ 2Cr3+ + 7H2O | +1.36 |
| O2 + 4H+ + 4e− ⇌ 2H2O | +1.23 |
| Br2 + 2e− ⇌ 2Br− | +1.07 |
| Ag+ + e− ⇌ Ag | +0.80 |
| Hg22+ + 2e− ⇌ 2Hg | +0.80 |
| Fe3+ + e− ⇌ Fe2+ | +0.77 |
| Cu2+ + 2e− ⇌ Cu | +0.34 |
| AgCl + e− ⇌ Ag + Cl− | +0.22 |
| 2H+ + 2e− ⇌ H2 | 0 |
| Pb2+ + 2e− ⇌ Pb | −0.13 |
| Sn2+ + 2e− ⇌ Sn | −0.14 |
| Fe2+ + 2e− ⇌ Fe | −0.44 |
| Zn2+ + 2e− ⇌ Zn | −0.76 |
| Al3+ + 3e− ⇌ Al | −1.68 |
| Mg2+ + 2e− ⇌ Mg | −2.36 |
| Na+ + e− ⇌ Na | −2.71 |
| Ca2+ + 2e− ⇌ Ca | −2.84 |
| K+ + e− ⇌ K | −2.93 |
| Li+ + e− ⇌ Li | −3.05 |
In electrochemical measurements, the electrode to be measured is called the working electrode (sometimes the indicator or test electrode) against the reference electrode. The electrode potential can be measured in a two-electrode cell when no current is flowing (Fig. 3a). However, a stable reference electrode (non-polarized) is necessary to correctly measure the potential of the working electrode under a current flow; thus, another electrode, called the counter electrode (or auxiliary electrode), is required. In such an arrangement, called a three-electrode cell (Fig. 3b), the current passes between the working and counter electrodes, and the reference electrode potential remains constant. When an ohmic drop occurs in the solution, iRs (i and Rs denote the current and solution resistance, respectively), and is not negligible under a current flow, the working electrode potential cannot be correctly measured. The ohmic drop can be minimized by placing the reference electrode near the working electrode. Although the use of Luggin-Haber capillary further reduces this contribution,15 the uncompensated potential drop still remains and needs to be corrected by instrumental techniques such as a positive feedback compensation scheme.16
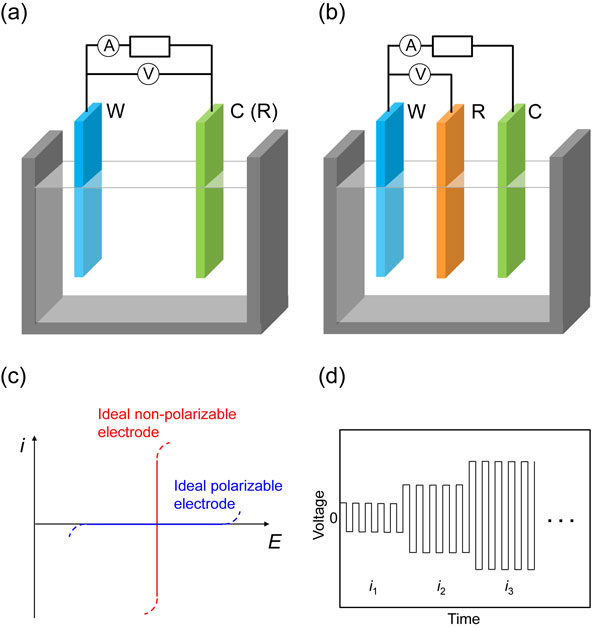
Schematics of (a) two-electrode and (b) three-electrode cells; the symbols W, C, and R denote working, counter, and reference electrodes, respectively. (c) Polarization curves of ideal polarizable and non-polarizable electrodes. (d) Relationship between time and voltage during metal deposition/dissolution cycles for a Li/Li symmetric cell.
The open-circuit potential (or rest potential) indicates the potential of a working electrode when no external current is flowing (see Section 3.4 for the open circuit potential under mixed potential). If no charge transfer (no redox reaction) occurs on a certain electrode in an electrolytic solution polarized from the open-circuit potential, the electrode–solution interface acts as a capacitor. Such an electrode is referred to as an ideal polarizable electrode and is used to investigate the double-layer behavior. On the other hand, an ideal non-polarizable electrode has an infinitely high exchange current density, and its potential does not change upon the passage of a current, indicating a potential determined by the Nernst equation. This behavior is preferable for use as the reference electrode. Figure 3c shows the relationship between the current and the potential for the ideal polarizable and non-polarizable electrodes.
Particular attention should be paid to electrochemical measurements using coin cells. Two-electrode coin cells are commonly used in batteries owing to their convenience. The solution resistance in coin cells can be minimized by placing the two electrodes close to each other (using a thin separator with a thickness of a few tens of micrometers) and increasing the electrode area. The performance of an electrode active material is often evaluated using a half-cell test with a metal counter electrode. For example, a lithium metal counter electrode in an electrolytic solution containing a lithium salt also works as a reference electrode in a two-electrode configuration in the form of Li+/Li. Although discussions are often based on the assumption that the Li+/Li equilibrium potential holds under a current flow, its non-zero charge transfer resistance certainly induces polarization (negatively during lithium metal deposition and positively during lithium metal dissolution). Consequently, the working electrode potential appears to be higher during delithiation and lower during lithiation (polarization also depends on various parameters such as the electrolyte and temperature). Thus, careful interpretation is required for measurements using coin cells, particularly at high current densities. Metal deposition/dissolution cycle tests for a Li/Li symmetric cell can provide useful information on the degree of polarization of the lithium metal electrode (Fig. 3d);17 polarization (response of voltage) is evaluated by increasing the direct current (DC) (i1 < i2 < i3 < ⋯) stepwise and repeating the deposition/dissolution up to a specific cycle number required in measurements where the Li metal counter electrode is used. Electrochemical impedance spectroscopy can provide similar information.
2.5 Liquid junction potentialThe liquid junction potential appears at the junction of two different electrolytic solutions. When both the cations and anions diffuse through the junction by the concentration gradient, the difference in their mobilities causes a charge separation, as shown in Fig. 4a.2,10 The liquid junction potential compensates for this charge separation (and thus this type of liquid junction potential is called a diffusion potential); it forms to slow down the faster ions and speed up the slower ions to satisfy charge neutrality, as shown in Fig. 4b. The liquid junction potential is defined as the Galvani potential between the right and left phases (the inner potential of the right phase with respect to that of the left phase in the case shown in Fig. 4b). Mass transfer in electrolytic solutions based on ion diffusion and migration is described by the Nernst-Planck equation (Eq. 16) by neglecting convection as follows:
| \begin{equation} J = -D\left(\frac{\text{d}c}{\text{d}x}\right) - \frac{z}{|z|}uc\left(\frac{\text{d}\phi}{\text{d}x}\right) \end{equation} | (16) |
| \begin{equation} \Delta\phi = -\cfrac{\displaystyle\sum\nolimits_{i}|z_{i}|\cfrac{u_{i}}{z_{i}}(c_{i,d} - c_{i,0})}{\displaystyle\sum\nolimits_{i}|z_{i}|u_{i}(c_{i,d} - c_{i,0})}\frac{RT}{F}\ln\left[\frac{\displaystyle\sum\nolimits_{i}(|z_{i}|u_{i}c_{i,d})}{\displaystyle\sum\nolimits_{i}(|z_{i}|u_{i}c_{i,0})}\right] \end{equation} | (17) |
| \begin{equation} \Delta\phi = -\frac{RT}{F}\ln\left[\frac{\displaystyle\sum\nolimits_{j}(\omega_{j}c_{j,d}) + \displaystyle\sum\nolimits_{k}(\omega_{k}c_{k,0})}{\displaystyle\sum\nolimits_{j}(\omega_{j}c_{j,0}) + \displaystyle\sum\nolimits_{k}(\omega_{k}c_{k,d})}\right] \end{equation} | (18) |

(a) Diffusion of ions from solution A (high concentration) to solution B (low concentration) at their boundary when u+ > u−. (b) Relationship between ion diffusion and liquid junction potential.
A prominent topic in this area is the use of an ionic liquid salt bridge proposed by Kakiuchi and coworkers.18,19 A hydrophobic ionic liquid ([C][A]) and an aqueous solution form a two-phase system. The liquid junction potential between these two phases ($\Delta\phi_{\text{IL}}^{\text{W}} $) is thermodynamically determined by the distribution potential (Eq. 19) and thus the ionic liquid salt bridge is distinct from the previously known ones, such as the KCl salt bridge, for which the phase-boundary potentials are determined by the non-thermodynamic diffusion potential.
| \begin{equation} \Delta\phi_{\text{IL}}^{\text{W}} = \frac{1}{2}({\Delta\phi(\text{C${^{+}}$})^{\circ}}_{\text{IL}}^{\text{W}} + {\Delta\phi(\text{A${^{-}}$})^{\circ}}_{\text{IL}}^{\text{W}}) + \frac{RT}{2F}\ln\frac{\gamma_{\text{A${^{-}}$}}^{\text{W}}\gamma_{\text{C${^{+}}$}}^{\text{IL}}}{\gamma_{\text{C${^{+}}$}}^{\text{W}}\gamma_{\text{A${^{-}}$}}^{\text{IL}}} \end{equation} | (19) |
The liquid junction potential in highly concentrated aqueous solutions was discussed in a recent study.22 Taking the equilibrated LiFePO4/FePO4 couple as an example of a Li+-insertion electrode, the difference in the electrode potentials in a highly concentrated LiCl aqueous solution (e.g., 18 mol kg−1 LiCl aq.) and reference electrolyte (e.g., 1 mol kg−1 LiCl aq.) (ΔE) is expressed by three different contributions (Eq. 20):
| \begin{equation} \Delta E = \Delta E_{\text{N}}^{c} + \Delta E_{\text{N}}^{\gamma} + \Delta E_{\text{LJP}} \end{equation} | (20) |
In electrochemical systems that use aqueous solutions as electrolytes, the pH ($ = - \log_{10}a_{\text{H}^{ + }}$) of the solution is often responsible for the potential-determining reaction and the equilibrium electrode potential. For example, zinc ions are dissolved as Zn2+ ions (more correctly, hydrated Zn(OH2)62+) in acidic solutions but precipitate mainly as Zn(OH)2 in neutral solutions, and [Zn(OH)4]2− is the main dissolved species in alkaline solutions. The redox reaction of zinc ions in acids is as follows:
| \begin{equation} \text{Zn$^{2+}$} + 2\text{e}^{-}\rightleftharpoons \text{Zn} \end{equation} | (21) |
| \begin{align} E_{\text{acid}} & = E_{\text{acid}}^{\circ} - \frac{RT}{2F}\ln \frac{a_{\text{Zn}}}{a_{\text{Zn${^{2+}}$}}} = E_{\text{acid}}^{\circ} + \frac{RT}{2F}\ln [\text{Zn$^{2+}$}]\\ & = E_{\text{acid}}^{\circ} + 0.0296\log [\text{Zn$^{2+}$}] \end{align} | (22) |
| \begin{equation} \text{[Zn(OH)$_{4}$]$^{2-}$} + 2\text{e}^{-}\rightleftharpoons \text{Zn} + \text{4OH$^{-}$} \end{equation} | (23) |
| \begin{align} E_{\text{base}} & = E_{\text{base}}^{\circ} - \frac{RT}{2F}\ln \frac{a_{\text{Zn}} \cdot a_{\text{OH${^{-}}$}}^{4}}{a_{\text{[Zn(OH)${_{4}}$]${^{2-}}$}}} = E_{\text{base}}^{\circ} + \frac{RT}{2F}\ln \frac{[\text{Zn(OH)$_{4}^{2-}$}]}{a_{\text{OH$^{-}$}}^{4}}\\ & = E_{\text{base}}^{\circ} + 0.0295\log[\text{Zn(OH)$_{4}^{2-}$}] + 0.118(14 - \text{pH}) \end{align} | (24) |
Therefore, a diagram showing the dissolved ionic or chemical species of the element of interest on a two-dimensional plane of the electrode potential vs. pH is a good guide for electrochemical reactions in aqueous solutions. The potential–pH diagram is also known as the Pourbaix diagram, named after the Belgian chemist Marcel Pourbaix (1904–1998). Initially, Pourbaix used the potential–pH diagram to study corrosion; today, potential–pH diagrams are available for almost all the elements. In addition, potential–pH diagrams for multiple elements can be drawn using commercial software with thermodynamic data.
For example, a potential–pH diagram for zinc is shown in Fig. 5.23 The two dashed lines in the figure are the standard potentials for the oxygen evolution and hydrogen evolution reactions and represent the theoretical stable region (potential window) of water. Potential windows are discussed in detail in the next section. The diagram can be divided into five regions where Zn2+, Zn(OH)2, [HZnO2]−, [Zn(OH)4]2−, and Zn are stable. The boundary line represents the equilibrium conditions (pH and electrode potentials), and the position of the boundary line may vary with the concentration of dissolved ion species (1.0 × 10−6 mol dm−3 in Fig. 5). Line (A) is a horizontal line, indicating that the potential-determining reaction is unaffected by changes in the pH, as shown in Eq. 21. Lines (E)–(G) have negative slopes because the electrode potential is affected by the pH. Lines (B)–(D) are not redox reactions (the oxidation number of zinc remains at +2) but are dissolution-precipitation reactions, and there is no change in the electrode potential.
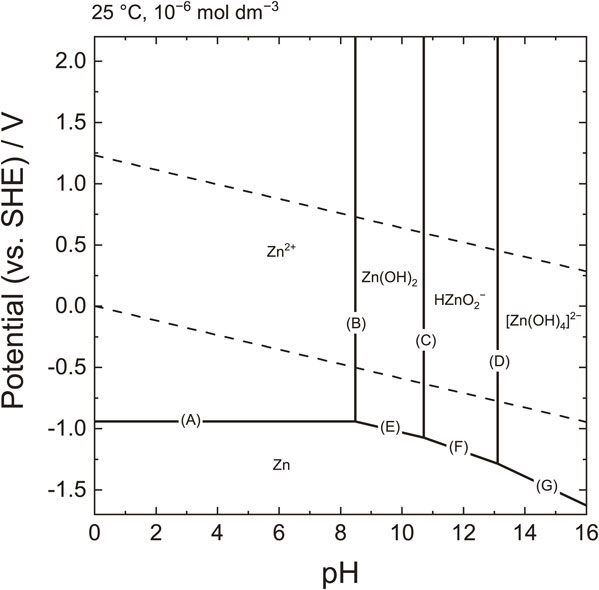
Potential–pH diagram for zinc. The concentration of Zn ion species is 1.0 × 10−6 mol dm−3.
The line types can be summarized as follows:
A simple potential–pH diagram can be derived relatively easily from thermodynamic data, but the calculation is complicated when multiple elements are considered. Density functional theory (DFT) calculations have recently been used to determine the total energy of chemical species, and the results provided the basis for the potential–pH diagram. However, when multiple elements are considered in DFT first-principles electronic structure calculations, numerous computational resources are required to search for candidate compounds. In recent years, algorithms for this purpose have been improved to search for convex hulls of stable candidate compounds. Many algorithms have been published that can be used together with the results of DFT calculations. For example, Fig. 6 shows a potential–pH diagram for zinc and manganese drawn by the Pourbaix diagram implemented in the Materials Project.24–26 As shown, the zinc and manganese compounds are drawn in a complex manner. An example code for drawing a Pourbaix diagram is provided in the Supporting Information.
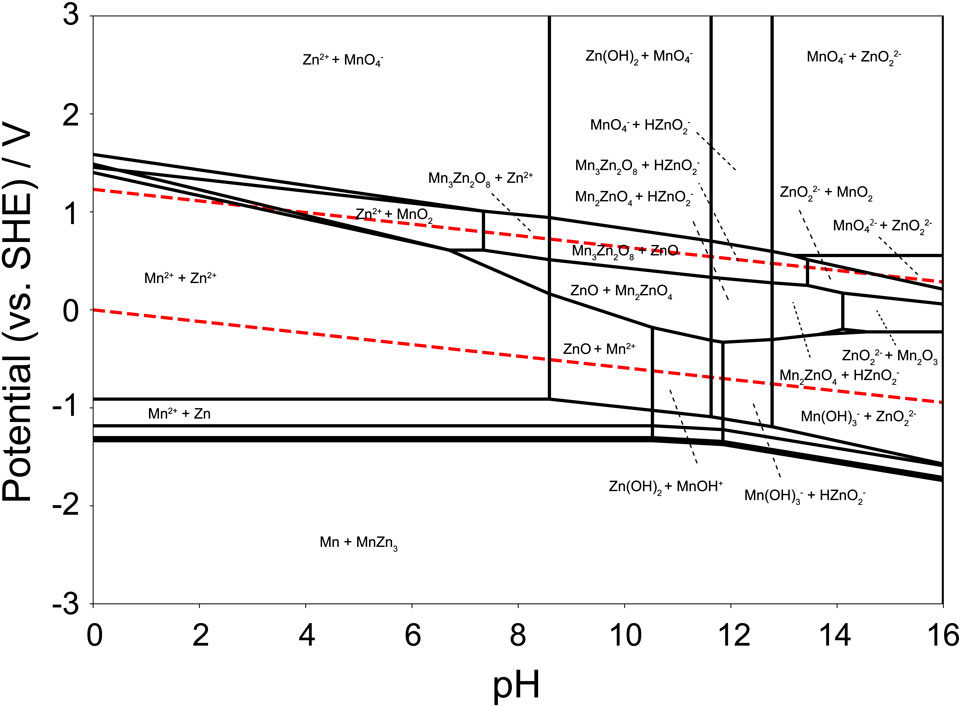
Potential–pH diagram for zinc and manganese, drawn by the Materials Project. The concentrations of Zn and Mn ion species are 1.0 × 10−6 mol dm−3.
The potential–pH diagram shows the region of the pH and potential where a compound is stable, and acts as a guide map when considering the electrochemistry of aqueous solutions.
3.2 Electrochemical windowIn an aqueous solution, oxygen and hydrogen evolution reactions occur when the electrode potentials are high and low, respectively. Therefore, the upper and lower limits of the electrode potential that can be applied in an electrochemical cell using an aqueous solution are determined by both reactions; this potential range is called the electrochemical window (or potential window). In the potential–pH diagram for zinc, the region sandwiched between the two dashed lines corresponds to the electrochemical window. The oxygen evolution reaction in acidic and basic solutions is described by Eqs. 25 and 26 as follows:
| \begin{equation} \text{2H$_{2}$O} \rightleftharpoons \text{O$_{2}$} + \text{4H$^{+}$} + 4\text{e}^{-} \end{equation} | (25) |
| \begin{equation} \text{4OH$^{-}$} \rightleftharpoons \text{O$_{2}$} + \text{2H$_{2}$O} + 4\text{e}^{-} \end{equation} | (26) |
The hydrogen evolution reaction in acidic and basic solutions is described by Eqs. 27 and 28 as follows:
| \begin{equation} \text{2H$^{+}$} + 2\text{e}^{-} \rightleftharpoons \text{H$_{2}$} \end{equation} | (27) |
| \begin{equation} \text{2H$_{2}$O} + 2\text{e}^{-} \rightleftharpoons \text{H$_{2}$} + \text{2OH$^{-}$} \end{equation} | (28) |
In practice, some overpotentials are required to allow the oxygen evolution and hydrogen evolution reactions to proceed, resulting in a larger potential window than the thermodynamic theoretical potential window of 1.23 V (25 °C). Owing to these overpotentials, a nominal voltage of 2.1 V is possible in lead–acid batteries.27 Conversely, water electrolysis, in which clean hydrogen can be produced, requires a voltage of 2 V or higher.
As a new topic regarding the potential window of aqueous solutions, research on the use of aqueous electrolytes in inexpensive and environmentally benign rechargeable batteries is gaining momentum. Compared with organic solvents and ionic liquids, aqueous solutions have a narrower potential window, which limits the operating voltage of the battery. Research on new aqueous electrolytes that achieve a wide potential window is underway by modifying the additives, electrolyte salts, and electrolyte concentration.28–31 Clarification of the origin of the wide potential window has been attempted by DFT calculations and analysis of the electrode/electrolyte interface, although no unified conclusion has been reached. However, it should be noted that the gap between the HOMO and LUMO obtained from the DFT calculations of water is extremely large (8.7 eV) and far from the actual thermodynamic data; therefore, the potential window cannot simply be obtained from the gap between the HOMO and LUMO.32
Although not discussed in detail in this paper, the potential window is important not only from a thermodynamic viewpoint but also from a kinetic viewpoint. Even if the electrode potential is outside the thermodynamic potential window, the kinetics of water decomposition may be sufficiently slow, in which case the aqueous electrolyte can be treated as apparently stable. Sufficiently slow kinetics is a state in which water molecules are unlikely to be supplied near the electrode, which is thought to be realized by the formation of a surface electrolyte interphase (SEI), which is a decomposition product of the electrolyte, or a local structure near the electrode in which water molecules are unlikely to be released.33
3.3 Practical reference electrodesThe reference electrode should be an ideal nonpolarizable electrode with a large exchange current density such that a small polarization allows a large current flow. The primary reference electrode used in aqueous solutions is the standard hydrogen electrode (SHE). However, SHE is an ideal device that cannot be realized experimentally. Therefore, reversible hydrogen electrodes (RHEs), which depend on the solution pH, are widely used.
The Nernst equation in Eq. 27 is as follows:
| \begin{align} E(\text{RHE}) & = E^{\circ} - \frac{RT}{2F}\ln \left(\frac{p_{\text{H${_{2}}$}}/p^{\circ}}{a_{\text{H${^{+}}$}}^{2}}\right)\\ & = -2.303\frac{RT}{2F}\left(\log \frac{p_{\text{H${_{2}}$}}}{p^{\circ}} + \text{2pH}\right) \end{align} | (29) |
Generally, an electrode of the second type, as shown below, is used as the reference electrode.
Silver–silver chloride electrode Ag/AgCl
| \begin{equation} \text{AgCl} + \text{e}^{-} \rightleftharpoons \text{Ag} + \text{Cl$^{-}$} \end{equation} | (30) |
| \begin{equation} \text{Hg$_{2}$Cl$_{2}$} + 2\text{e}^{-} \rightleftharpoons \text{2Hg} + \text{2Cl$^{-}$} \end{equation} | (31) |
| \begin{equation} \text{Hg$_{2}$SO$_{4}$} + 2\text{e}^{-} \rightleftharpoons \text{2Hg} + \text{SO$_{4}^{2-}$} \end{equation} | (32) |
| \begin{equation} \text{HgO} + \text{H$_{2}$O} + 2\text{e}^{-} \rightleftharpoons \text{Hg} + \text{2OH$^{-}$} \end{equation} | (33) |

Reference electrode potentials in aqueous solutions.
The open-circuit potential is measured with no current flowing to the working electrode; it is also known as the zero-current potential. When the potential-determining reaction is a single charge transfer reaction, the open-circuit potential shows an equilibrium potential according to the Nernst equation. However, when multiple charge transfer reactions are involved, the open-circuit potential cannot be described by the Nernst equation and it becomes a mixed potential. For example, when considering the oxidation of iron in an aqueous solution, the iron dissolution reaction is as follows:
| \begin{equation} \text{Fe} \to \text{Fe$^{2+}$} + 2\text{e}^{-} \end{equation} | (34) |

Schematic illustration of the relationship between mixed potentials and oxidation/reduction currents.
The former part of this comprehensive paper described the fundamentals of electrode potentials from both a theoretical and a practical viewpoint. Understanding the basic concepts, including the definition of the electrode potential, is essential for constructing an appropriate electrochemical system. The latter part provided important information regarding aqueous electrochemistry. The pH dependence, water stability region, practical reference electrodes, and mixed potentials were briefly summarized. New concepts and techniques appear together with the progress of electrochemistry, and a wide range of diverse methods are required for researchers. Detailed information on electrode potentials in nonaqueous and solid-state systems is available in the following comprehensive paper (Electrode Potentials Part 2: Nonaqueous and Solid-state Systems).
The data that support the findings of this study are openly available under the terms of the designated Creative Commons License in J-STAGE Data at https://doi.org/10.50892/data.electrochemistry.21353556. The authors' profiles of this paper can be found on the preface.34
Kazuhiko Matsumoto: Writing – original draft (Lead), Writing – review & editing (Lead)
Kohei Miyazaki: Writing – original draft (Lead), Writing – review & editing (Lead)
Jinkwang Hwang: Writing – review & editing (Equal)
Takayuki Yamamoto: Writing – review & editing (Equal)
Atsushi Sakuda: Writing – review & editing (Equal)
The authors declare no conflict of interest in the manuscript.
This paper constitutes a collection of papers edited as the proceedings of the 51st Electrochemistry Workshop organized by the Kansai Branch of the Electrochemical Society of Japan.
K. Matsumoto and K. Miyazaki: These authors contributed equally to this work.
K. Matsumoto, K. Miyazaki, J. Hwang, T. Yamamoto, and A. Sakuda: ECSJ Active Members