Linkage disequilibrium in a population undergoing periodic fragmentation and admixture

ABSTRACT

Glacial and interglacial cycles are considered to have caused the fragmentation and admixture of populations in many organisms. A simple model incorporating such periodic changes of the population structure is analysed in order to investigate the behaviour of neutral genetic variation at one and two loci. The equilibrium is reached very quickly in terms of cycles if the length of a cycle is long, as would be expected of the glaciation cycles. Heterozygosity and linkage disequilibrium are shown to depend on the length of time of the fragmented and admixed phases, population sizes, and number (n) of subpopulations in the fragmented phase. If the population size is small in the fragmented phase and its duration is long, the squared correlation coefficient of two loci (a measure of linkage disequilibrium) just after the admixture is approximated by 1/(n–1) for n > 1. After admixture, the correlation decays at a rate of approximately twice the recombination rate. Therefore, if post-glaciation admixture created linkage disequilibrium, we expect to observe linkage disequilibrium even between moderately linked loci, and its decay pattern along the chromosome is very different from that in a random mating population at equilibrium. This is especially true in organisms with long generation times such as trees.

INTRODUCTION

From about 0.7 million years ago (MYA), approximate 100-k year cycles of ice sheet expansion and recession have been continuous (Webb and Bartlein, 1992). For many species, these cycles (glacial-interglacial cycles) have caused contractions and expansions of their ranges and have resulted in changes in their population structures. More concretely, in one phase (the fragmented phase), the species might retreat to one or a few isolated refugia and their population sizes might become small. In the other phase (the panmictic phase), the subpopulations expand and admix to form a large panmictic population. As an example of approximate panmixis, currently many wind-pollinated plants show only weak population structure (Hamrick and Godt, 1996). Thus, the populations undergo fragmentation and admixture periodically.

In the fragmented phase, variation within subpopulations decreases and variation between subpopulations increases. Admixture merges the variation between subpopulations into variation in the whole population. In such cases, the equilibrium variation is determined by population sizes in the two phases and the time lengths. Jesus et al. (2006) quantified this situation and have shown that variation can be greater than that expected for a panmictic population of constant size even when the population size is small in the fragmented phase (the structured phase of Jesus et al., 2006). Moreover, because population admixture has been known to create linkage disequilibrium (Nei and Li, 1973), we expect to observe stronger linkage disequilibrium compared to that in a panmictic population, especially during the early portion of the panmictic phase.

In the present paper, an analysis of a simple model of genetic variation at one and two neutral loci under periodic admixture-fragmentation is presented. Specific questions asked are; 1. What would be the equilibrium diversity and linkage disequilibrium just after admixture? 2. How quickly is this equilibrium reached? 3. How does the dependency of linkage disequilibrium on the recombination rate under this model differ from that in a panmictic population?

MODEL

We consider a monoecious diploid population with discrete non-overlapping generations and assume that the population’s structure changes periodically. Each cycle consists of two phases in the following order: the panmictic and the fragmented phases (Fig. 1). At the beginning of the panmictic phase, existing subpopulations in the fragmented phase are merged in equal proportions to form a panmictic population with size N₁ and this state continues for t₁ generations. At the beginning of the fragmented phase, the population is subdivided into n subpopulations each of which has size N₂ and this state continues for t₂ generations. In this phase, there is no migration between subpopulations and mating is random in each subpopulation. This cycle is repeated with the same parameters. This model is the same as the one studied by Jesus et al. (2006). We would like to know the diversity measurements of the population at one and two loci (defined below) after k cycles of the fragmentation admixture.

Fig. 1.

One cycle of fragmentation admixture. A cycle consists of the panmictic and fragmented phases with lengths of t₁ and t₂ generations, respectively. In the panmictic phase, there is one large panmictic population with size N_1, and in the fragmented phase there are n subpopulations each with size N₂.

Consider two neutral loci A and B and the recombination rate between them is r. For mutations, the infinite allele model (Kimura and Crow, 1964) is assumed, and u (> 0) is the mutation rate per generation at each locus.

We compute the average heterozygosity at one locus (one-locus diversity measure) and joint heterozygosity (two-locus diversity measure) at two loci under the model by deriving their transition equations. Equivalent results can also be obtained by a genealogical approach as in Jesus et al. (2006) and McVean (2002) or using the diffusion approximation of the Wright-Fisher model as in Ohta and Kimura (1969) and Mano (2007).

ANALYSES

In the following, one- and two-locus diversity measures at the beginning of the kth cycle are calculated. Once they are obtained, it is easy to compute those measures at any time in the cycle using the measures at the beginning of the kth cycle as initial values.

One-locus diversity measures

Here, we consider one of the two loci. Let θ_k be the probability that two alleles randomly taken from the population at the beginning of the kth cycle are different. At this time point, the panmictic phase has just started. Let p_i be the frequency of the ith allele A_i. Then, θ_k is expressed as:   

where E[ ] denotes the expectation over the joint distribution of p_i’s. We will derive a transition equation that relates θ_k+1 to θ_k. Define the following quantities:   

where ν = (1–u)². ω_i is the probability that there is neither coalescence nor mutation of two alleles in one generation and θ_i∞ is the equilibrium value of the probability that two alleles randomly taken from a random mating population with a constant population size N_i are different.

First, we consider the panmictic phase and let θ_pt be the probability of sampling two different alleles from the population at the tth generation from the start of the panmictic phase. Then,   

(1)

(see, for example, Cockerham, 1984).

Next, we consider the fragmented phase and let θ_st and θ_dt be the probabilities of sampling two different alleles from the same subpopulation and different subpopulations, respectively, at the tth generation from the start of the fragmented phase of the kth cycle. Because two alleles taken at the beginning of the fragmented phase are samples from the panmictic population at the end of the panmictic phase irrespective of whether they are taken from the same or different subpopulations, we obtain:   

(2)

Because the size of each subpopulation is N₂,   

(3)

  

(4)

at the end of the fragmented phase.

Combining (2)–(4) and noting that the subpopulations contribute equally to the panmictic population at the beginning of the k+1th cycle, we obtain a transition equation:   

(5)

where   

(6)

Solving this transition equation, we obtain:   

(7)

where θ_∞ = A₁ / (1-Λ) and it represents the equilibrium value of θ_k.

Note that Λ is less than or equal to the larger of ω₁^t₁ω₂^t₂ and ω₁^t₁ν^t₂ and appreciably smaller than one unless t₁ + t₂ is small. Therefore, the approach to the equilibrium is fast and the equilibrium value is of practical interest. Numerical examples of the equilibrium value, θ_∞, as a function of t₂ /t₁ for various values of n when t₁ /(2N₁) = 0.1, N₂ /N₁ = 0.01 and 4N₁u = 0.04 are shown in Fig. 2. Here, we assumed N₁, N₂ >> 1 and u << 1, so that θ_∞ can be approximately expressed as a function of scaled times, t₁/(2N₁) and t₂/(2N₂), and the scaled mutation rate 4N₁u. The case with n = 1 is just the periodic size change circumstance, and thus θ_∞ decreases as t₂ increases. If n > 1, θ_∞ first decreases as t₂ increases, but then it increases and becomes larger than that expected in a randomly mating population with a larger size N₁. This is because variation within subpopulations is lost but variation between subpopulations accumulates as time passes in the fragmented phase. The accumulation of variation between subpopulations is faster when n is larger. When n = ∞, the initial decrease does not occur because two alleles taken at the beginning of the cycle never come from the same subpopulation in the fragmented phase. Jesus et al. (2006) have also shown these using a genealogical approach.

Fig. 2.

One-locus equilibrium diversity measure, θ_∞, as a function of t₂ /t₁ for various values of n are shown. Other parameters are u = 10^–7, N₁ = 10⁵, t₁ = 2 × 10⁴, N₂ = 10³.

Two-locus diversity measures

Next we consider two loci A and B. Let the alleles of the two loci be designated by A_i and B_j, respectively. Define g_ij, p_i, and q_j as frequencies of a gamete A_iB_j, allele A_i, and allele B_j, respectively.

In order to define the diversity measures for two loci, we introduce additional information. Assume that we sample two alleles a, a′ at the A locus and b, b′ at the B locus from the population. There are several ways in which sampled alleles are located on the chromosomes in the population (Weir and Cockerham, 1969). If alleles are on the same chromosome, we concatenate the two alleles. For example, if a and b are on the same chromosome, we write them as ab. If they are on different chromosomes from the same (sub)population, we separate the two alleles by a comma, such as a,b. Finally, alleles in the same (sub)population are put within parentheses. Thus, two alleles (a,b) are from the same (sub)population and (a)(b) are from two different (sub)populations. We indicate that two alleles x, y are different by x ≠ y.

With these notations, we define three two-loci diversity measures at the beginning of the kth cycle as (see Weir and Cockerham, 1969):   

and a column vector x_k = (Θ_k, Γ_k, Δ_k, θ_k,)^T where the superscript ^T denotes a transposition. The three measures, Θ_k, Γ_k, Δ_k, are called digametic, trigametic and quadrigametic measures because the alleles are located on two, three and four gametes, respectively.

In order to compute the transition from x_k to x_k+1, we first consider the panmictic phase. Let Θ_t, Γ_t, and Δ_t be the diversity measures at the tth generation from the start of the kth cycle. Here, we derive the transition equation for the digametic measure, which relates Θ_t+1 to Θ_t. Those for Γ_t, and Δ_t can be derived similarly. We consider three cases, (a) no mutation occurs at either locus (with a probability ν²), (b) mutation occurs at one of the loci and it does not occurs at the other loci (with a probability 2ν (1–ν)) and (c) mutation occurs at both loci (with a probability (1–ν)²).

In case (a), if neither of the two gametes is a recombinant (with a probability (1–r)²), both two allele pairs, (a, a′) and (b, b′), are different when the two gametes come from different chromosomes (with a probability 1–1/(2N₁)) and the digametic two allele pairs in the previous generation are different (with a probability Θ_t). If one of the two gametes is a recombinant but the other is not (with a probability 2r(1–r)), the two allele pairs are different when they come from different individuals (with a probability 1–1/N) and the trigametic two allele pairs in the previous generation are different (with a probability Γ_t). Note that if both gametes come from the same individual in the previous generation, either of the two allele pairs comes from the same allele in the previous generation. If both gametes are recombinants (with a probability r²), the two allele pairs are different either if they come from different individuals (with a probability 1–1/N) and the quadrigametic two allele pairs in the previous generation are different (with a probability Δ_t), or if both gametes come from the same individual (with a probability 1/N) but the alleles come from different alleles in this individual (with a probability 1/2) and the digametic two allele pairs in the previous generation are different (with a probability Θ_t).

In case (b), because one of the two allele pairs are different, only the other allele pair need to be different for the two allele pairs to be different. The other allele pair are different if they come from different alleles in the previous generation (with a probability 1–1/(2N)) and they are different (with a probability θ_pt). Note that recombination does not affect this case because whether the allele pair at the mutated locus come from the same allele in the previous generation or not does not affect the non-identity of the allele pair. Finally, in case (c), both allele pairs are different independent of how they come from the previous generations. Combining all those with some rearrangements, we obtain the transition equation for Θ_t as,   

where a = 1/(2N₁). If we set y_t = (Θ_t, Γ_t, Δ_t)^T, it satisfies the following transition equation (Serant, 1974):   

(8)

In this equation, 1 is a column vector with all elements as one and A is a 3 by 3 matrix,   

Note that y₀ = (Θ_k, Γ_k, Δ_k)^T. With this initial condition, (8) can be solved as   

(9)

where   

I is a 3 by 3 identity matrix. If we put t = t₁ in (9), we obtain the two-locus diversity measures at the end of the panmictic phase. For later use, we add a one-locus measure to the vector and redefine it as y_t = (Θ_t, Γ_t, Δ_t, θ_pt)^T. Noting that the initial condition for y_t is x_k, y_t at the end of the panmictic phase is expressed as a linear function of x_k,   

(10)

where elements of P₁ and q₁ are obtained from (9) and (1).

In order to calculate the transition equation in the fragmented phase, we need to introduce more two-locus diversity measures because there are several ways in which sampled alleles are located on chromosomes (Tachida and Cockerham, 1986). For simplicity, we assume that the initial condition is symmetric with regard to the two loci. Even with this assumption, we need 13 measures, two digametic, three trigametic and seven quadrigametic measures that are listed in Table 1 along with their allele arrangements.

Table 1. Two-locus diversity measures, Pr[a ≠ a′, b ≠ b′], of various allele arrangements in the fragmented phase.

subpopulation	digametic	trigametic	quadrigametic
One	Θ1t: (ab,a′b′)	Γ1t: (ab,a′,b′)	Δ1t: (a,b,a′,b′)
Two	Θ2t: (ab)(a′b′)	Γ2t: (ab)(a′,b′)	Δ2t: (a,b)(a′,b′)
		Γ3t: (ab,a′)(b′)	Δ3t: (a,b,a′)(b′)
			Δ4t: (a,a′)(b,b′)
Three		Γ4t: (ab)(a′)(b′)	Δ5t: (a,b)(a′)(b′)
			Δ6t: (a,a′)(b)(b′)
Four			Δ7t: (a)(a′)(b)(b′)

Only one representative arrangement is shown for each measure. For example, Γ_3t represents a measure for both (ab,a′)(b′) and (ab,b′)(a′).

Let t be the time from the beginning of this phase measured in generations. The initial condition for the measures are Θ_t1, Γ_t1, and Δ_t1 for digametic, trigametic and quadrigametic measures, respectively. We want to compute values of those measures z_t = (Θ_1t, Θ_2t, Γ_1t, ..., Δ_7t, θ_st, θ_dt)^T at the end of the fragmented phase (t = t₂). Although the computation is straightforward, the expressions become complex. Therefore, the derivations are explained in Appendix A. As in the panmictic phase, z_t is expressed as a linear function of the initial value   

(11)

where P₂ and q₂ can be computed from (A1)–(A8) in Appendix A.

Because n subpopulations contribute equally to the panmictic populations of the next cycle, we obtain the three two-locus diversity measures at the beginning of the k+1th cycle using elements of z_t2 as,   

We can express these along with (5) in a vector form:   

(12)

where H = (h_i,j) is a 4 by 15 matrix, whose non-zero elements are,   

All other elements are zero.

Finally, we combine (10), (11) and (12) to obtain the transition equation from k to k+1 as:   

(13)

The equilibrium values x_k is obtained as:   

(14)

Linkage disequilibrium

Here, we choose ρ² (r² of Hill and Robertson, 1968) as a measure of linkage disequilibrium and compute its approximate expectation using the diversity measures obtained in the preceding sections. The expectation of ρ² is expressed approximately as (Hill, 1975):   

(15)

The right-hand side of the equation is σ_d² of Ohta and Kimura (1969). For the accuracy of the approximation, consult Mano (2007). The denominator and numerator can be expressed using the two-locus diversity measures as:   

(see Weir and Hill, 1980). Therefore, E[ρ²] is approximately expressed as:   

(16)

We can compute E[ρ²] at the beginning of the panmictic phase by putting the equilibrium solution (14) or transient values computed from (13) into (16).

Before showing numerical examples using (16), we consider an extreme case where the recombination rate is large and the subpopulations in the fragmented phase are very small. More formally stated, we assume Nr >> 1 and t₂/(2N₂) >> 1. Then, at the end of the fragmented phase, each subpopulation becomes monomorphic. Therefore, all diversity measures involving two alleles at the same locus in the same subpopulation become zero. That is:   

(17)

(see Table 1). Here, we omitted subscript t₂ for simplicity. All other measures are approximately expressed as (θ_d)² because we assumed Nr >> 1. Putting those into (12) and using (16), we obtain   

(18)

This equation shows that, even for loci not tightly linked, we expect to observe linkage disequilibrium at the beginning of the panmictic phase and that its extent will be larger when the number of subpopulations is small.

Now let us examine linkage disequilibrium numerically using (13), (14) and (16). First, we ask how quickly the equilibrium state is reached. This can be answered by computing the eigenvalues of the matrix, HP₂P₁. Let λ_i (i = 1, ..., 4) be the eigenvalues of the matrix defined in decreasing order. Numerical values of λ₁ (the largest) and λ₂ (the second largest) are shown in Table 2. Numerical computations show that λ₁ is the eigenvalue of θ_k,   

(19)

where ω_i = (1 – u)²(1 – 1/(2N_i)) and ν = (1 – u)². Because λ₁ ≤ ν^t₁+t₂, the equilibrium is obtained fairly quickly unless 2u(t₁ + t₂) is very small. We can also see that λ₁ monotonically increases to ν^t₂ω₁^t₁ as n becomes larger. For large n, if we increase t₂ keeping t₁ + t₂ constant, λ₁ increases because ω₁ < ν. The second largest eigenvalue is also of interest because the behaviour of the two-locus measures also depends on them. As expected, λ₂ increases monotonically as r decreases and it achieves a value close to that of the largest eigenvalue when r is comparable to u.

Table 2. The largest and second largest eigenvalues of HP₂P₁

			n = 2		n = 5		n = 10
N2	t2	r	λ1	λ2	λ1	λ2	λ1	λ2
103	8 × 104	10–3	0.3704	0.1372	0.5927	0.3513	0.6667	0.4445
		10–5		0.2488		0.4122		0.4772
		10–6		0.2967		0.4749		0.5345
	5 × 104	10–3	0.3194	0.1017	0.5101	0.2602	0.5739	0.3293
		10–5		0.1723		0.3048		0.3601
		10–6		0.2481		0.3973		0.4474
	2 × 104	10–3	0.2744	0.0753	0.4391	0.1928	0.4939	0.2440
		10–5		0.1241		0.2295		0.2733
		10–6		0.2075		0.3326		0.3746
104	8 × 104	10–3	0.3772	0.1423	0.5954	0.3545	0.6681	0.4464
		10–5		0.2242		0.3899		0.4633
		10–6		0.2968		0.4694		0.5274
	5 × 104	10–3	0.3450	0.1190	0.5206	0.2710	0.5791	0.3354
		10–5		0.1724		0.3020		0.3567
		10–6		0.2638		0.3995		0.4452

Other parameters are N₁ = 10⁵, t₁ = 10⁵-t₂, u = 10^–6. λ₁ does not depend on r.

To see more directly how quickly E[ρ²] approaches equilibrium at the beginning of the panmictic phase, its change was computed along with the one-locus diversity measure θ_k. A typical example is shown in Fig. 3. We assumed that the population has been panmictic with size N₁ and in the equilibrium state before the start of the first cycle. In this example, λ₁ = 0.5927 and λ₂ = 0.4122. It takes several cycles to achieve the equilibrium state and E[ρ²] approaches the equilibrium more quickly than θ_k.

Fig. 3.

Changes of θ_k and E[ρ²] at the beginning of the panmictic phase. Parameters are u = 10^–6, r = 10^–5, N₁ = 10⁵, N₂ = 10³, t₁ = 2 × 10⁴, t₂ = 8 × 10⁴. Until the beginning of cycle 1, the population has been panmictic with size N₁ and in the equilibrium state.

Next we examine the equilibrium state. Figure 4 shows E[ρ²] at the beginning of the panmictic phase as a function of the recombination rate for various values of n. As shown in the figure, E[ρ²] decreases as r increases and approaches 1/(n–1) (see (18)) except in the case of n = 2, because t₂/(2N₂) = 8 used in the figure is very large. Therefore, strong linkage disequilibria are expected at the beginning of the panmictic phase when t₂/(2N₂) is large. As n increases, E[ρ²] decreases. When the length, t₂, of the fragmented phase becomes shorter, the level of linkage disequilibrium decreases as shown in Fig. 5. Note that admixture results in linkage disequilibrium even without fixation within subpopulations, although its absolute value is not large (see the case of t₂ = 2N₂).

Fig. 4.

Equilibrium values of linkage disequilibrium, E[ρ²], and the number of subpopulations. E[ρ²] is shown as a function of the recombination rate r. Four cases (n = 2, 3, 5, 10) are shown. Other parameters are u = 10^–7, N₁ = 10⁵, N₂ = 5 × 10³, t₁ = 2 × 10⁴, t₂ = 8 × 10⁴.

Fig. 5.

Equilibrium values of linkage disequilibrium, E[ρ²], and the length of the fragmented phase. E[ρ²] is shown as a function of the recombination rate r. Four cases (t₂ = 9N₂, 8N₂, 5N₂, 2N₂) keeping the total length of one cycle constant are shown. Other parameters are u = 10^–7, n = 2, N₁ = 10⁵, N₂ = 10⁴, t₁ = 10⁵-t₂.

Finally, we consider E[ρ²] at the tth generation since the start of the panmictic phase. Because the approach to equilibrium in terms of cycles of the fragmentation-admixture is rapid, only the equilibrium state will be considered. We can compute E[ρ²] using the equilibrium value, x_∞, as its initial condition and putting it into (9). When 2Nr >> 1, the time course of E[ρ²] can be approximately computed by ignoring the terms containing 1/(2N₁) in (9). In this case, the two-locus diversity measures are approximately expressed as:   

Therefore, we obtain:   

(20)

This relationship has been derived previously by Littler (1973) and shows that E[ρ²] is reduced by a factor (1–r)² every generation when 2Nr is large. One example of the time course of the decay of E[ρ²] is shown in Fig. 6. The straight and broken lines were computed from (9) and (20), respectively. The latter approximates the former quite well for large r and small t. We can see that linkage disequilibrium quickly decays when r is large, but it persists for a long time otherwise. The half-life of E[ρ²] is approximately -log2/(2log(1–r)) ≈ 0.347/r. Thus, for example, it would take about 350 generations for E[ρ²] of two loci 0.1 cM apart to decay to one-half of the values at the beginning of the panmictic phase. As t becomes large, E[ρ²] approaches the equilibrium value for a randomly mating population of size N₁, as approximately given by Ohta and Kimura (1971) when Nu is much smaller than 1,   

(21)

where R = N₁r. This value is quite small unless r is comparable to u (see Fig. 6).

Fig. 6.

The decay of linkage disequilibrium, E[ρ²], in the panmictic phase. Values of E[ρ²] at 0, 1000, 2000, 10000th generations since the beginning of the panmictic phase are shown as functions of the recombination rate, r. Straight and broken lines represent values of E[ρ²] computed from (9) along with (16), and (20), respectively. Approximate equilibrium values (Eq.) for N₁ = 10⁵ calculated from (21) are also shown. Parameters are u = 10^–7, N₁ = 10⁵, N₂ = 5 × 10⁴, t₁ = 2 × 10⁴, t₂ = 8 × 10⁴.

DISCUSSION

In this paper, the diversity measures at one and two loci, and a measure of linkage disequilibrium were investigated in a population undergoing periodic fragmentation and admixture. The study was motivated by the periodic nature of glaciation-interglaciation geological conditions. Under these circumstances, equilibrium is quickly approached and the size, N₂, of subpopulations and time length, t₂, of the fragmented phase, along with the number of subpopulations, strongly influence the levels of diversity measures and linkage disequilibrium. The parameters, N₂, n, and t₂, together determine the reduction of variation within subpopulations during the fragmented phase. After only one cycle of fragmentation and admixture, patterns of variation very different from those expected in panmictic populations are observed.

Such large linkage disequilibrium is also expected under models with geographically structured populations (Ohta, 1982; Tachida and Cockerham, 1986; De and Durrett, 2007). However, large estimates of F_ST (if subpopulations are recognized) or F_IS (if subpopulations are not recognized) are expected in geographically structured populations. On the other hand, estimates of those F-statistics are very small under the present model after admixture. Therefore, it is not difficult to discriminate the two types of models from the data. Incidentally, large estimates of linkage disequilibrium may lead to spurious detection of positive selection using the decay of the extended haplotype homozygosity as pointed out by De and Durrett (2007). Therefore, it is important to obtain information of the past population structure to infer actions of selection.

Because we made some simplifying assumptions in drawing those conclusions, we will briefly consider some of their effects here. First, we assumed that transitions between the phases are instantaneous in the model. In reality, the expansion after glaciation is not instantaneous, although it is not slow (Hewitt, 2000). For example, in the case of the Japanese cedar, Cryptomeria japonica, its expansion started from a few refugia about 15000 years ago and its maximum abundance and range was reached around 7000 years ago (Tsukada, 1982). Therefore, N₂ is not constant through time. To address this violation, we might use effective size such as the harmonic mean for N₂ because an important factor is the extent to which variation is reduced within subpopulations in the fragmented phase. For the change of linkage disequilibrium, formulas in Mano (2007) may be useful.

Second, although all parameters were assumed to be constant throughout the cycles in our model, some parameters might change between cycles. Indeed, glacial-interglacial cycles have been only quasi-periodic and some long-term trends might be imposed on them (see Webb and Bartlein, 1992). In addition, effective population sizes and number of subpopulations in the fragmented phase could fluctuate. Among those parameters, the time lengths are determined mainly by orbital-forcing of climatic oscillations and thus an approximate periodicity seems to be the case. Random factors, however, are likely to contribute to the resulting population sizes and the number of subpopulations as they are biological attributes. Therefore, their values might change randomly among the cycles of fragmentation and admixture. Especially important in determining the magnitude of linkage disequilibrium is the number, n, of subpopulations. Palynological studies (studies based on pollen and spores) have shown that some species were missing in some refugia in certain glacial periods (Bennett, 1997). Although a consideration of parameter fluctuation is important to understand the genetic diversity of organisms affected by repeated fragmentation-admixture, our results suggest that the most recent cycle is of primary importance because equilibrium is reached fairly quickly. Hence, the prediction of strong linkage disequilibrium from our model does not change qualitatively unless n in the most recent fragmentation phase is one.

Finally, although we assumed that n subpopulations in the fragmented phase equally contribute to the panmictic populations when admixture occurs, this is unlikely to be true in nature. Here, we consider the effects of an unequal contribution in the extreme case of Nr >> 1, and t₂/(2N₂) >> 1. For n = 2, E[ρ²] is still close to one because it is a correlation coefficient. To consider the case with n > 2, let x_i be the contribution from the ith subpopulation to the panmictic population. Then, instead of (18), we obtain:   

where   

Therefore, we might define an effective subpopulation number, n_e, by equating the right-hand side of this equation to 1/(n_e–1), as   

Because E[ρ²] is a decreasing function of n_e, any unequal contribution that reduces n_e will increase E[ρ²].

Many of the extant abundant taxa are considered to have experienced fragmentation during the glaciation period (Webb and Bartlein, 1992). Therefore, admixture of their fragmented subpopulations is considered to have occurred between approximately 5000 and 15000 years ago. Because the half-life of the linkage disequilibrium created by admixture is approximately 0.347/r generations, we expect to observe more than half the level of linkage disequilibrium at the beginning of the interglaciation between two markers less than 34.7/t cM apart, where t is the number of generations since the admixture. Therefore, extended linkage disequilibrium will be found in organisms having longer generation times. Recently, fine linkage maps have been developed in many organisms and total genome sequences are available in some model organisms. Thus, we can choose markers suitable for observing linkage disequilibrium as traces of past fragmentation. For example, if we assume that the generation time of a tree is 50 years, only one to three hundred generations have passed since the admixture after glaciation occurred. Then, we should be able to find linkage disequilibria between markers 0.35-0.11 cM or less apart if it existed when the admixture occurred. Because such markers are now available for trees (e.g. Brown et al., 2001; Tani et al., 2003; Tuskan et al., 2006), it would be interesting to survey those markers in natural populations to investigate their past population structure (see also Lascoux et al., 2008).

Appendix A

Two-locus diversity measures in the fragmented phase

Let t be the number of generations since the beginning of the fragmented phase. The initial conditions for the measures are Θ_t1, Γ_t1 and Δ_t1, for digametic, trigametic and quadrigametic measures, respectively. We want to compute values of those measures at the end of the fragmented phase.

The single population measures (Θ_1t, Γ_1t and Δ_1t) are computed using equation (9) but setting a = a₂ = 1/(2N₂).

Next we compute the two population measures. First, we consider Θ_2t, Γ_2t and Δ_2t. Note that no allele pair at the same locus is in the same subpopulation in these allele arrangements. Thus, no coalescence occurs between a pair of alleles at the same locus and we can obtain the explicit expressions for Θ_2t, Γ_2t and Δ_2t:   

(A1)

where   

and   

Next we consider Δ_4t for the allele arrangement (a,a′)(b,b′). It satisfies a transition equation:   

The solution for this is:   

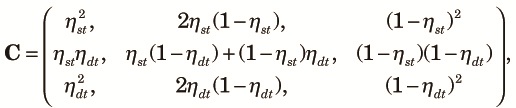(A2)

where   

The two population measures, Γ_3t and Δ_3t, satisfy transition equations,   

The solution for this equation is:   

(A3)

  

(A4)

where λ = ν²(1−r−a₂)(1−2a₂) and   

For the three-population allele arrangements (ab)(a′)(b′) and (a,b)(a′)(b′), again coalescence does not occur. Therefore, Γ_5t and Δ_5t are obtained using η_st and η_dt as:   

(A5)

  

(A6)

The transition equation for Δ_6t is:   

and the solution is:   

(A7)

Finally, we compute the four population measure Δ_7t. Again no coalescence occurs in this allele arrangement. Therefore, it is simple to obtain the solution:   

(A8)

ACKNOWLEDGMENT

I thank two anonymous referees for their helpful comments on earlier drafts of the manuscript. This work was partially supported by the Program for Promotion of Basic and Applied Researches for Innovations in Bio-oriented Industry (BRAIN) and by the Environment Research and Technology Development Fund (S-9-2) of the Ministry of the Environment, Japan.

REFERENCES

•  Bennet,  K. D. (1997) Evolution and Ecology; The Pace of Life. Cambridge University Press, Cambridge.
•  Brown,  G. R.,  Kadel,  E.E.III,  Bassoni,  D. L.,  Kiehne,  K. L.,  Temesgen,  B.,  van Buijtenen,  J. P., et al. (2001) Anchored reference loci in loblolly pine (Pinus taeda L.) for integrating pine genomics. Genetics 159, 799–809.
•  Cockerham,  C. C. (1984) Drift and mutation with a finite number of allelic states. Proc. Natl. Acad. Sci. USA 81, 530–534.
•  Cockerham,  C. C., and  Weir,  B. S. (1977) Digenic descent measures for finite populations. Genet. Res. Camb. 30, 121–147.
•  De,  A. and  Durrett,  R. (2007) Stepping-stone spatial structure causes slow decay of linkage disequilibrium and shifts the site frequency spectrum. Genetics 176, 969–981.
•  Hamrick,  J. L., and  Godt,  M. J. W. (1996) Effects of life history traits on genetic diversity in plant species. Philos. Trans. R. Soc. London B 351, 1291–1298.
•  Hewitt,  G. (2000) The genetic legacy of the Quaternary ice ages. Nature 405, 907–913.
•  Hill,  W. G. (1975) Linkage disequilibrium among multiple neutral alleles produced by mutation in finite population. Theor. Popul. Biol. 8, 117–126.
•  Hill,  W. G., and  Robertson,  A. (1968) Linkage disequilibrium in finite populations. Theor. Appl. Genet. 38, 226–231.
•  Jesus,  F. F.,  Wilkins,  J. F.,  Solferini,  V. N., and  Wakeley,  J. (2006) Expected coalescence times and segregating sites in a model of glacial cycles. Genet. Mol. Res. 5, 466–474.
•  Kimura,  M., and  Crow,  J. F. (1964) The number of alleles that can be maintained in a finite population. Genetics 49, 725–738.
•  Lascoux,  M.,  Pyhajarvi,  T.,  Kallman,  T., and  Savolainen,  O. (2008) Past demography in forest trees: what can we learn from nuclear DNA sequences that we do not already know? Plant Ecol. Div. 1, 209–215.
•  Littler,  R. A. (1973) Linkage disequilibrium in two-locus, finite, random mating models without selection or mutation. Theor. Popul. Biol. 4, 259–275.
•  Mano,  S. (2007) Evolution of linkage disequilibrium of the founders in exponentially growing populations. Theor. Popul. Biol. 71, 95–108.
•  McVean,  G. A. T. (2002) A genealogical interpretation of linkage disequilibrium. Genetics 162, 987–991.
•  Nei,  M., and  Li,  W.-H. (1973) Linkage disequilibrium in subdivided populations. Genetics 75, 213–219.
•  Ohta,  T. (1982) Linkage disequilibrium with the island model. Genetics 101, 139–155.
•  Ohta,  T., and  Kimura,  M. (1969) Linkage disequilibrium due to random genetic drift. Genet. Res. Camb. 13, 47–55.
•  Ohta,  T., and  Kimura,  M. (1971) Linkage disequilibrium between two segregating nucleotide sites under the steady flux of mutations in a finite population. Genetics 68, 571–580.
•  Serant,  D. (1974) Linkage and inbreeding coefficients in a finite random mating population. Theor. Popul. Biol. 6, 251-263.
•  Tachida,  H., and  Cockerham,  C. C. (1986) Analysis of linkage disequilibrium in an island model. Theor. Popul. Biol. 29, 161–197.
•  Tani,  N.,  Takahashi,  T.,  Iwata,  H.,  Mukai,  Y.,  Ujino-Ihara,  T.,  Matsumoto,  A., et al. (2003) A consensus linkage map for sugi (Cryptomeria japonica) from two pedigrees, based on microsatellites and expressed sequence tags. Genetics 165, 1551–1568.
•  Tsukada,  M. (1982) Cryptomeria japonica: glacia refugia and late-glacial and postglacial migration. Ecology 63, 1091–1105.
•  Tuskan,  G.,  DiFazio,  S.,  Jansson,  S.,  Bohlmann,  J.,  Grigoriev,  I.,  Hellstein,  U., et al. (2006) The genome of black cottonwood Populus trichocarpa (Torr. & Gray). Science 313, 1596–1604.
•  Webb,  T.III, and  Bartlein,  P. J. (1992) Global changes during the last 3 million years: climatic controls and biotic responses. Ann. Rev. Ecol. Syst. 23, 141–173.
•  Weir,  B. S., and  Cockerham,  C. C. (1969) Group inbreeding with two linked loci. Genetics 63, 711–742.
•  Weir,  B. S., and  Hill,  W. G. (1980) Effects of mating structure on variation in linkage disequilibrium. Genetics 95, 477–488.