Equilibrium Distribution Ratio of Phosphorus between Solid Iron and Magnesiowustite-saturated Al₂O₃–CaO–Fe_tO–MgO–SiO₂ Slag at 1623 K

Abstract

In the conventional iron-making process, the oxygen potential in the hearth of the blast furnace is determined only by the temperature because of the carbon-saturated conditions. As a consequence, impurities such as phosphorus are reduced and dissolved in the iron because of the excessively low oxygen partial pressure. The oxygen partial pressure can be controlled by using gas reductants such as hydrogen and carbon monoxide. Under these conditions, solid iron is obtained because of the low carbon content. In this study, the equilibrium distribution of phosphorus between the solid iron and molten slag is investigated at 1623 K as functions of the oxygen partial pressure and the basicity of the slag. The experimental results show that the phosphorus content in the solid iron is sufficiently low under the experimental conditions employed. The phosphate capacity is also evaluated, and a regression equation is obtained by comparing the results with those of previous studies.

1. Introduction

In recent integrated steelmaking works, iron ore is reduced to hot metal in a blast furnace, and then impurities such as C, Si, P, and S in the hot metal are removed in the steelmaking process by using hot-metal pretreatments, converters, and so on. Thus, the steelmaking process can be broken down into two parts: a reduction process and an oxidation process. In the blast furnace, the reduction process takes place, in which iron ore produces hot metal through the use of cokes. Because the hot metal and cokes coexist in the hearth of the blast furnace, the hot metal becomes carbon-saturated iron. In this case, on the basis of the C/CO equilibrium, the oxygen partial pressure is determined only by the working temperature. Generally, the temperature in the hearth is 1873 K, so the oxygen partial pressure in the hearth is approximately 10^–16 atm. This oxygen partial pressure is too low, and not only the iron oxide, but also the impurities are reduced in the iron ore. Therefore the hot metal contains impurities that must be removed in subsequent processes. If the oxygen partial pressure in the reduction process could be controlled to an appropriate value, it is possible that the iron oxide could be reduced without the reduction of impurities. Gas reductants such as hydrogen and carbon monoxide have the potential to reduce only the iron oxide, because the oxygen partial pressure can be controlled by changing the gas composition. Thus, the use of gas reductants might allow the production of steel that contains fewer impurities without the refining process, i.e., a “Direct Steelmaking Process” was proposed in our previous study.¹⁾ In this case, the melting point of iron is high compared with that of the hot metal, because the iron produced by a direct steelmaking process does not contain carbon, and the process temperature must be maintained higher than the melting point of iron to keep the hot metal in the molten state. This is an unrealistic condition, because the heat loss increases with process temperature, and refractory corrosion also increases. Kashiwaya et al. reported that the behavior of impurity when an iron ore was reduced by hydrogen or carbon at 1173–1373 K based on the concept of direct steel making.²⁾ In this case, iron ore was first reduced at lower temperature than melting point of iron, and then reduced iron was melted at 1873 K in a same crucible without slag removing. The results showed that the contents of silicon and manganese in the metal obtained by hydrogen reduction were lower than that obtained by carbon reduction. On the other hand, the difference of phosphorus content in metal between reducing agents was not so significant. This result showed that the phosphorus is easily moved to metal phase. However it is not clear whether the phosphorus is reduced at reducing period or at melting period.

Many researchers have reported the influences of slag composition, temperature, and oxygen partial pressure on the equilibrium distribution ratio of impurities between molten slag and molten steel.^3,4,5,6,7) These results showed that a low temperature, high oxygen partial pressure, and high CaO/SiO₂ ratio are advantageous for dephosphorization from steel. Thus, low-temperature processing has many advantages from the viewpoints of heat loss, refractory corrosion, and dephosphorization. In the direct steelmaking process, the reduction temperature is below the melting point of iron, and solid iron is obtained. In this process, iron ore is first melted to the molten oxide through the addition of some flux such as CaO. Then, the molten oxide is reduced under a controlled atmosphere at a temperature below the melting point of iron. This process is similar to smelting reduction processes such as direct iron ore smelting reduction process (DIOS).⁸⁾ The difference between the direct steelmaking process investigated in our previous study and such smelting reduction processes is that the reduction proceeds under a controlled atmosphere, and the reduced iron is solid because of the low-temperature and non-carbon-saturated conditions. For the establishment of a direct steelmaking process, the distribution ratio of impurities between the solid iron and molten oxide is important. Banya et al.,^9,10) Iwasaki et al.,¹¹⁾ Ito et al.,¹²⁾ Sano et al.,¹³⁾ Muraki,¹⁴⁾ and Jeoungkiu et al.¹⁵⁾ reported the distribution ratio of phosphorus between the solid iron and molten slag below 1700 K. These studies were carried out to investigate the influence of the slag composition on the dephosphorization ability in the hot-metal pretreatment process. They measured the distribution ratio of phosphorus between the solid iron and molten slag, and then converted this to the ratio between carbon-saturated molten iron and molten slag on the basis of the thermodynamics. In these cases, CaO–CaCl₂–CaF₂–Fe_tO–SiO₂–Na₂O–MgO–P₂O₅ slag was investigated, in which CaCl₂, CaF₂, and Na₂O were added to enlarge the liquid fraction of the slag. However, the slag assumed in this study contains some Al₂O₃, because this slag is produced directly from iron ore, and the phosphorus distribution between the solid iron and molten slag with Al₂O₃ has not previously been investigated. Therefore, the purpose of this study is to investigate the effect of the oxygen partial pressure and slag composition on the equilibrium distribution ratio of phosphorus between the solid iron and magnesiowustite-saturated molten Al₂O₃–CaO–Fe_tO– MgO–SiO₂ slag at 1623 K. Some of the experimental results have already been reported for the range P_O2 = 10^–12–10^–13.5 atm.¹⁾ In this study, the distribution ratio of phosphorus is measured in the range P_O2 = 10^–11.5–10^–14 atm and analyzed on the basis of thermodynamic principles. Finally, a regression formula for the phosphate capacity is proposed by comparing the results obtained with those from previous studies.^3,4,5)

2. Experimental Procedure

The method employed is based on that reported in previous studies,^{1,9,10,11,12,13,14,15)} in which iron foil is immersed into the slag. Figures 1 and 2 show the experimental apparatus and the procedure for measuring the equilibrium distribution ratio of phosphorus between the solid iron and molten oxide. Experiments were carried out in an electrical resistance furnace with a SiC spiral heating element and a mullite reaction tube with an inner diameter of 42 mm. The slag (10 g), prepared by mixing reagent-grade Al₂O₃, CaO, 3CaOP₂O₅, Fe, Fe₂O₃, MgO, and SiO₂, was set in the densely sintered MgO crucible (inner and outer diameters of 18 and 26 mm, respectively) and inserted in the furnace, which was kept at 1623 K. CaO was prepared by thermal decomposition of reagent-grade CaCO₃. The slag was melted under a suitable oxygen partial pressure. One hour later, iron foil (1 g) with a thickness of 0.1 mm was immersed into the molten slag. The preliminary experiment confirmed that the reaction reached equilibrium after 20 h.¹⁾ Therefore, the iron foil and slag were removed from the furnace after 20 h and quenched with water. The oxygen partial pressure was controlled by the CO and CO₂ gas mixture, and its ratio was determined by Eqs. (1), (2), (3):¹⁶⁾   

$$2\text{CO}\left(\text{g}\right)+{\text{O}}_2\left(\text{g}\right)=2{\text{CO}}_2\left(\text{g}\right)$$(1)

  

$$P_{{\text{O}}_2}={\left(\frac{P_{{\text{CO}}_2}}{P_{\text{CO}}}\right)}^2\times \frac{1}{K_1}$$(2)

  

$$\mathrm{\Delta }{G}^0=–565\hspace{0.17em}160+172.03 T \left(\text{J}/\text{mol}\right)=–\text{RT} \text{ln}\left(K_1\right)$$(3)

where P_M is the partial pressure of M (atm), K₁ is the equilibrium constant of Eq. (1) (–), and T is the temperature (K). The slag composition was determined on the basis of the composition of gangue minerals in iron ore. CaO was added to set the basicity, so that %CaO/%SiO₂ (C/S) = 0.5, 1.0, and 1.2. FeO was added to the equilibrium composition under the set oxygen partial pressure. The content of P₂O₅ was set to 5.0 wt% because of the limits of analytical sensitivity.

Fig. 1.

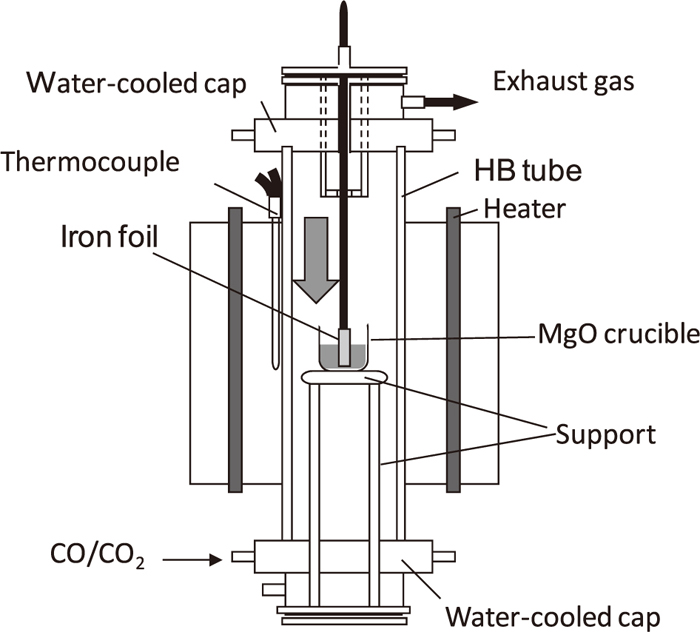
Schematic diagram of experimental apparatus for measuring equilibrium distribution ratio of phosphorus between solid iron and molten oxide.

Fig. 2.

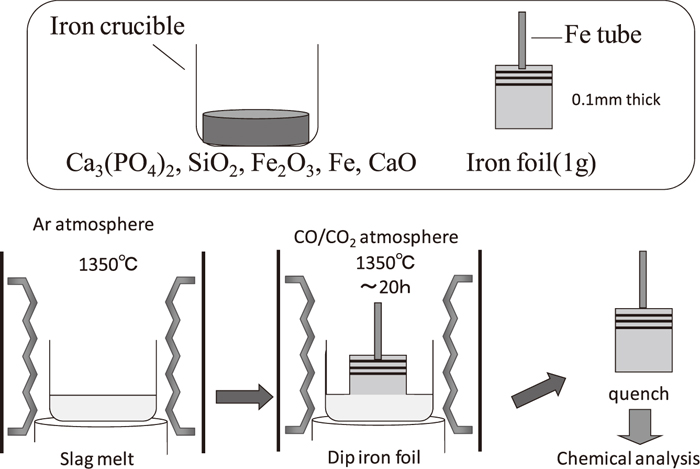
Experimental method for measuring equilibrium distribution ratio of phosphorus between solid iron and molten oxide.

The slag attached to the surface of the obtained iron foil was removed by using a diamond grinder. The phosphorus content in the iron foil was analyzed by inductively coupled plasma atomic emission spectrometry (ICP-AES) with an ultrasonic nebulizer after extraction of the iron from the sample solution with methyl isobutyl ketone (MIBK). The details of this analysis technique were described in a previous study.¹⁾ The slag was analyzed after removal of the fine particles of iron by Br-Methanol. The content of SiO₂ in the slag was determined by gravimetric analysis, and other contents were determined by ICP-AES. The cross-sectional view of the slag was analyzed using electron probe microanalysis (EPMA).

3. Experimental Results

Table 1 shows the analysis values of the slag and metal together with the basicity, C/S value, and equilibrium distribution ratio of phosphorus, L_P, which are defined by Eqs. (4) and (5):   

$$\mathrm{C}/\mathrm{S}=\left(\%\mathrm{C}\mathrm{a}\mathrm{O}\right)/\left(\%\mathrm{S}\mathrm{i}{\mathrm{O}}_2\right)$$(4)

  

$$L_{\text{P}}=\frac{\left(\%\text{P}\right)}{\left[\%\text{P}\right]}=0.44\frac{\left(\%{\text{P}}_{\text{2}}{\text{O}}_{\text{5}}\right)}{\left[\%\text{P}\right]}$$(5)

where (%M) and [%M] are the contents of M in the slag and the metal, respectively. In this experiment, a densely sintered MgO crucible was used. It is well known that a uniform layer of magnesiowustite is formed between the MgO crucible and the slag¹⁷⁾ when Fe_tO-containing slag comes into contact with the MgO. The iron foil was immersed into the slag and equilibrated under the CO/CO₂ atmosphere. Thus, the equilibrium experiment in this study was carried out in conditions under which magnesiowustite-saturated slag and solid iron coexisted. The MgO content in the slag increased with time until saturation, because MgO dissolved into the slag from the crucible. In the experiments, reagent-grade MgO powder was added to the slag so that the equilibrium content was reached in a short time. The equilibrium contents of MgO were 8.9–14.7 mass%.

Table 1. Compositions of slag and metal after reaching equilibrium, together with the distribution ratios of phosphorus between the molten slag and solid iron.

Sample Number	log (PO2)	Slag							Metal	LP
		(T-Fe)	(CaO)	(SiO2)	(Al2O3)	(MgO)	(P2O5)	C/S	[P]
1	–11.4	31.0	11.6	22.9	10.9	9.8	5.0	0.51	0.046	52.3
2	–11.9	21.2	13.7	27.5	13.2	9.0	4.9	0.50	0.270	8.9
3	–12.3	17.9	14.6	27.8	15.2	14.7	5.2	0.53	0.333	7.2
4	–12.8	11.3	17.8	34.8	12.6	13.6	4.3	0.51	0.326	6.1
5	–13.0	14.4	18.8	31.3	15.5	13.8	5.3	0.60	0.911	2.6
6	–13.2	10.5	18.9	35.3	13.8	13.3	4.5	0.54	0.924	2.2
7	–13.6	8.3	19.7	33.5	15.1	13.8	4.2	0.59	1.464	1.3
8	–12.5	5.2	30.4	30.9	13.5	11.9	5.3	0.98	0.076	31.2
9	–12.8	4.9	31.7	29.7	12.7	11.4	5.4	1.07	0.055	44.3
10	–12.9	6.4	33.7	31.0	14.8	11.8	5.0	1.09	0.124	17.0
11	–13.4	2.6	35.0	30.9	13.0	10.8	4.4	1.13	0.304	6.5
12	–13.5	3.5	34.2	31.4	14.8	12.8	4.9	1.09	0.618	3.4
13	–13.9	2.2	35.0	30.6	12.8	11.0	4.4	1.14	1.058	1.9
14	–14.0	2.5	34.8	30.9	13.8	10.3	4.7	1.13	1.057	2.0
15	–11.5	8.1	32.1	27.8	12.4	11.3	4.7	1.16	0.003	625.0
16	–11.9	6.2	35.0	28.3	11.5	11.1	4.7	1.24	0.002	996.5
17	–12.0	5.5	37.8	29.9	12.6	11.0	5.4	1.27	0.011	201.5
18	–12.3	4.7	36.9	29.4	13.7	8.9	4.4	1.26	0.016	124.0
19	–12.5	5.0	37.7	30.5	13.2	11.0	5.2	1.24	0.040	55.5
20	–12.8	3.6	39.5	29.7	12.7	9.9	4.7	1.33	0.147	13.8
21	–13.0	5.7	35.4	28.3	13.6	11.0	5.0	1.25	0.066	33.4
22	–13.2	2.7	39.5	29.6	12.7	10.4	4.8	1.34	0.214	9.8
23	–13.4	2.7	40.4	31.4	12.8	10.4	4.6	1.28	0.321	6.1
24	–13.5	2.5	38.2	30.8	14.6	11.2	5.0	1.24	0.259	8.2

The mineralogical phase in the slag sample was identified by observing the cross-sectional area of the sample. The compositions of the liquid and precipitated phases in the slag were analyzed by EPMA, and are listed in Table 2. In samples 1–15, uniform phases were observed. On the other hand, precipitated phases were observed in samples 16–24, for which the target C/S value was 1.2. Almost all the precipitated phases were Al₂O₃–MgO-type spinel, and these precipitated phases did not contain phosphorus.

Table 2. Composition of phases in slag analyzed by EPMA.

Sample Number	log (PO2)	Liquid Phase
		(T-Fe)	(CaO)	(SiO2)	(Al2O3)	(MgO)	(P2O5)	C/S
5	–13.2	10.5	18.9	33.7	13.8	14.0	4.5	0.56
6	–13.6	8.4	19.3	33.5	12.9	14.8	4.7	0.58
9	–12.8	1.9	38.7	30.3	13.3	9.7	4.4	1.28
11	–13.4	1.2	39.1	30.1	12.3	10.0	4.4	1.30
13	–13.9	2.1	35.6	32.4	13.6	11.5	4.3	1.10
15	–11.5	7.2	35.2	26.7	8.9	12.5	2.3	1.32
16	–11.9	2.8	37.6	29.1	9.1	11.4	2.2	1.29
18	–12.3	5.0	38.7	28.3	10.0	10.6	4.5	1.37
20	–12.8	6.6	33.8	29.5	10.4	11.2	4.9	1.15
22	–13.2	1.8	38.3	30.4	12.1	10.5	4.8	1.26
Sample Number	log (PO2)	Solid Phase
		(T-Fe)	(CaO)	(SiO2)	(Al2O3)	(MgO)	(P2O5)	C/S
16	–11.9	2.7	0.2	0.1	66.6	25.0	0.0	2.00
18	–12.3	4.4	0.7	0.3	67.6	25.4	0.1	2.33
20	–12.8	3.1	0.3	0.1	66.4	23.7	0.0	3.00
22	–13.2	0.3	43.3	30.6	18.8	6.4	0.2	1.42

Figure 3 shows the effect of the oxygen partial pressure on the total-Fe (T-Fe) content in the slag. Under our experimental conditions, the T-Fe content was 2–31 mass%. The logarithm of the T-Fe content increased linearly with the logarithm of the oxygen partial pressure, and the gradients were almost same at all C/S values. The content of T-Fe also increased with increasing C/S.

Fig. 3.

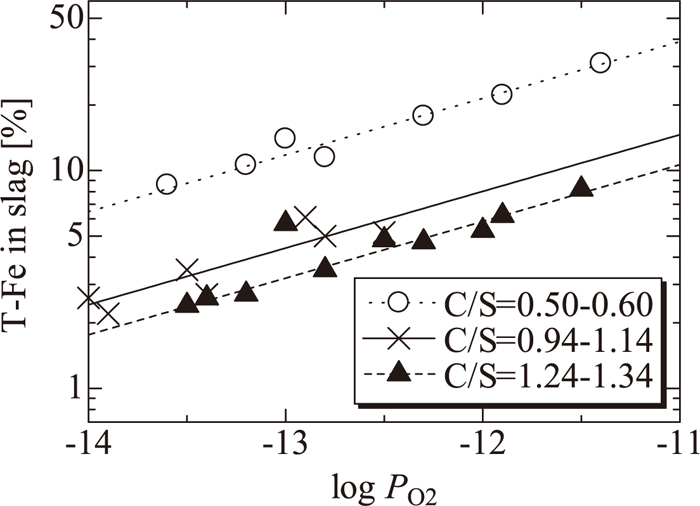
Relation between oxygen partial pressure and T-Fe content.

Figure 4 shows the influence of the oxygen partial pressure, P_O2, on the distribution ratio of phosphorus between solid iron and molten slag, L_P. L_P increased with increasing P_O2 and C/S. Note that the slag composition used in this study is varied with P_O2, though the influence of P_O2 on the L_P is generally discussed under the fixed composition of slag. When P_O2 was around 10^–11.5 atm, L_P was 67 at C/S = 0.5, 490 at C/S = 1.0 and 850 at C/S = 1.2. According to the blast-furnace operation, 1000 kg of iron and 300 kg of slag are obtained when 1600 kg of iron ore is reduced with 0.1% P₂O₅. The contents of phosphorus in the iron were 0.0043 mass% at L_P = 50, 0.002 mass% at L_P = 100, and 0.0002 mass% at L_P = 1000. These results indicate that the L_P values are large enough for solid iron to be obtained without the reduction of phosphorus.

Fig. 4.

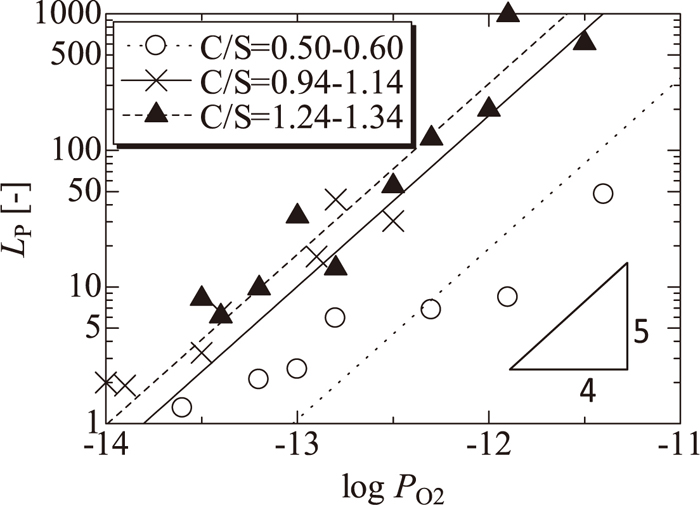
Relation between oxygen partial pressure and distribution ratio of phosphorus.

The phosphorus oxidation reaction is expressed by the following equation:   

$$\left[\text{P}\right]+\frac{5}{4}{\text{O}}_2\left(\text{g}\right)+\frac{3}{2}\left({\text{O}}^{2–}\right)=\left({\text{PO}}_4^{3–}\right)$$(6)

Thus, the gradient of log L_P as a function of log P_O2 might be 1.25 if the reaction in the slag proceeds as in Eq. (6). The lines fitted by a gradient of 1.25 are shown in the same figure. The fitted lines show good agreement with the experimental values.

Figure 5 shows the relation between the distribution ratio of phosphorus between the solid iron and molten slag, L_P and the FeO content in the slag which is estimated on the assumption that Fe is existed as FeO in slag. L_P increased with increasing FeO content and C/S value. The reaction between P and FeO can be expressed by the following equation:   

$$\left[\mathrm{P}\right]+2.5\left(\mathrm{F}\mathrm{e}\mathrm{O}\right)=\left(\mathrm{P}{\mathrm{O}}_{2.5}\right)+2.5\mathrm{F}\mathrm{e}$$(7)

Thus, the gradient of L_P as a function of FeO content might be 2.5 if the reaction in the slag proceeds as in Eq. (7). The lines fitted by a gradient of 2.5 are shown in Fig. 6. In the cases of C/S = 0.5–0.6 and 0.98–1.14, the fitted lines show good agreement with the experimental values. On the other hand, the gradient for the experimentally obtained L_P values at C/S = 1.16–1.34 is larger than that given by Eq. (7).

Fig. 5.

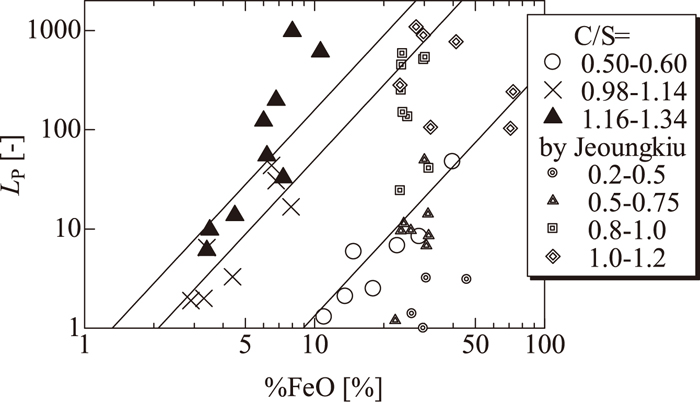
Relation between FeO content in slag and distribution ratio of phosphorus compared with the results reported by Jeoungkiu et al.¹⁵⁾

Fig. 6.

Relation between phosphate capacity and optical basicity and comparison with previous results.^3,4,5,15)

4. Discussion

Figure 5 shows the L_P results compared with the results reported by Jeoungkiu et al.¹⁵⁾ as a function of (%FeO) in the slag. Jeoungkiu et al. measured the phosphorus distribution ratio between the solid iron and molten slag at 1573 K, and converted this to the phosphorus distribution ratio between the hot metal and molten slag on a thermodynamic basis to estimate the dephosphorization behavior of the hot metal. In Fig. 5, the L_P results before this conversion are shown for comparison with those obtained in this study. The results of Jeoungkiu et al. were obtained using CaO–FeO–SiO₂–P₂O₅ slag with an FeO content of more than 15 mass%. Their L_P values are located near the fitted line when (%FeO) is around 20 mass%, although the slag composition and temperature are slightly different. In their case, L_P decreased slightly when the FeO content was increased from 23 mass% to 75 mass%. They explained this phenomenon by the fact that when the FeO content increases, the activity of Fe_tO, i.e., the oxygen partial pressure of the system, also increases, and the basicity decreases. Therefore, the effects of the oxygen partial pressure and basicity on the phosphorus distribution may compensate each other, leading to a slight decrease in the distribution ratio of phosphorus with an increase in FeO content.

The dephosphorization ability of the slag used in this study was evaluated using the phosphate capacity, ( $C_{{\text{PO}}_4^{3–}}$ ), which is defined by the following equations:¹⁸⁾   

$$1/2{\text{P}}_2\left(\text{g}\right)+3/2({\text{O}}^{2–})+5/4{\text{O}}_2\left(\text{g}\right)=({\text{PO}}_4^{3–})$$(8)

  

$$C_{{\text{PO}}_4^{3–}}\equiv \frac{\left(\%{\text{PO}}_4^{3–}\right)}{P_{{\text{P}}_2}^{1/2} P_{{\text{O}}_2}^{5/4}}=K_{{\text{PO}}_4^{3–}}\frac{a_{\left({\text{O}}^{2–}\right)}^{3/2}}{f_{{\text{PO}}_4^{3–}}}$$(9)

where $K_{{\text{PO}}_4^{3–}}$ is the equilibrium constant for Eq. (8), $f_{{\text{PO}}_4^{3–}}$ is the activity coefficient of the phosphate ion, and $a_{{\mathrm{O}}^{2–}}$ is the activity of the oxygen ion. This equation indicates that higher $a_{{\mathrm{O}}^{2–}}$ and lower $f_{{\text{PO}}_4^{3–}}$ values are effective for phosphate capacity. Although the partial pressure of phosphorus was necessary for calculating the phosphate capacity, to the authors’ knowledge, the standard Gibbs energy for the reaction between phosphorus gas and solid iron has not yet been reported. Here, the method reported by Jeoungkiu et al.¹⁵⁾ was employed. The phosphorus content in the solid iron was converted to the phosphorus content in the hot metal on the basis of the thermodynamics involved, and then the partial pressure of phosphorus was calculated by Eqs. (10) and (11), as reported for hot metal using the activity coefficient of phosphorus in hot metal:¹⁹⁾   

$$1/2{\text{P}}_2\left(\text{g}\right)\hspace{0.17em}=\hspace{0.17em}\text{P} \text{(mass}\% \text{in} \text{hot} \text{metal)}$$(10)

  

$$\mathrm{\Delta }{G}_{\text{P}}^0=–155\hspace{0.17em}700+5.4 T \left[\text{J}/\text{mol}\right]$$(11)

Figure 6 shows the relation between $C_{{\text{PO}}_4^{3–}}$ and the optical basicity, Λ, which was obtained by Eq. (12):   

$$\Lambda =\frac{{{\displaystyle \sum }}^{}{x}_1{n}_1{\Lambda }_{\text{th}1}+x_2{n}_2{\Lambda }_{\text{th}2}+x_3{n}_3{\Lambda }_{\text{th}3}+\cdots }{{{\displaystyle \sum }}^{}{x}_1{n}_1+x_2{n}_2+x_3{n}_3+\cdots }$$(12)

where x_i is the molar fraction of component i, n_i is the number of oxygen atoms in the molecule, and Λ_thi is the optical basicity of component i, as listed in Table 3.¹⁹⁾

Table 3. Optical basicity of various oxides.

Oxide	Al2O3	CaO	FeO	MgO	P2O5	SiO2
Λth	0.6	1.0	0.51	0.78	0.4	0.48

The logarithm of phosphate capacity increased linearly with increasing optical basicity. The results obtained by Jeoungkiu et al.¹⁵⁾ are also plotted in this figure. The phosphate capacity of CaO–FeO–SiO₂ slag at 1573 K was larger than that of Al₂O₃–CaO–FeO–MgO–SiO₂ slag at 1627 K.

The phosphate capacity has been measured by many researchers at steelmaking temperatures. Suito et al.,^3,4) Ishii et al.,⁵⁾ and Li et al.⁶⁾ measured the phosphate capacity at 1823–1873 K, and their results are shown in the same figure. The logarithm of phosphate capacity increases linearly with increasing optical basicity in all cases. The phosphate capacity at 1823 K is larger than that at 1873 K regardless of the presence of Al₂O₃. The effect of Al₂O₃ on the phosphate capacity can be expressed by the optical basicity, because the results for Al₂O₃-containing slag lie on the extension of the fitted line for the slag without Al₂O₃.

The gradients of plots of the logarithm of phosphate capacity as a function of optical basicity are similar. Figure 7 shows the relation between the y-intercept and the reciprocal of the temperature. A linear relation was observed, and the following regression equation was obtained:   

$$log\hspace{0.17em}{C}_{{\text{PO}}_4^{3–}}=20.67\Lambda +66\hspace{0.17em}204/T–32.01$$(13)

Fig. 7.

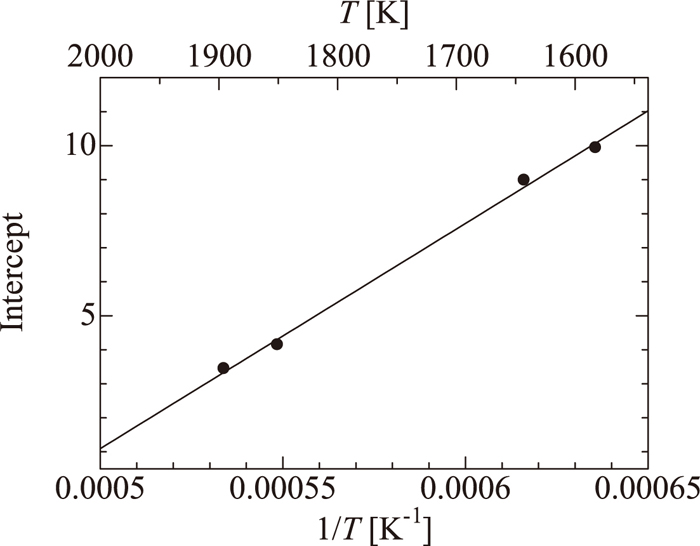
Relation between the intercept of log $C_{{\text{PO}}_4^{3–}}$ as a function of optical basicity and reciprocal of temperature.

5. Conclusions

The effects of slag composition and oxygen partial pressure on the equilibrium distribution ratio of phosphorus between solid iron and magnesiowustite-saturated Al₂O₃–CaO–FeO–MgO–SiO₂ molten slag at 1627 K were investigated, and the following conclusions were drawn:

(1) The phosphorus distribution ratio increases with increasing oxygen partial pressure, T-Fe content in the slag, and basicity.

(2) The Al₂O₃–MgO phase is precipitated at a basicity of 1.15–1.34, and the gradient of a plot of L_P as a function of FeO content in this slag is different from that for slag of lower basicity.

(3) The phosphate capacity increases with increasing optical basicity, Λ, and with decreasing temperature. The effect of Al₂O₃ on the phosphate capacity is expressed by the optical basicity, although the phosphate capacity decreases with Al₂O₃ addition. The following regression equation is obtained:   

$$log\hspace{0.17em}{C}_{{\text{PO}}_4^{3-}}=20.67\Lambda +66\hspace{0.17em}204/T-32.01$$

Acknowledgements

This study was supported in part by a grant from the JFE 21^st Century Foundation, KAKENHI (No. 22760574), and an ISIJ Research Promotion Grant. These grants are gratefully appreciated.

References

• 1)   N.  Maruoka,  S.  Ono,  H.  Shibata and  S.  Kitamura: Bull. Advanced Materials Processing Building, IMRAM Tohoku Univ., 66 (2010), 15.
• 2)   Y.  Kashiwaya and  M.  Hasegawa: ISIJ Int., 52 (2012), 1513.
• 3)   H.  Suito,  R.  Inoue and  M.  Takada: Trans. Iron Steel Inst. Jpn., 21 (1981), 250.
• 4)   H.  Suito and  R.  Inoue: Trans. Iron Steel Inst. Jpn., 24 (1984), 47.
• 5)   H.  Ishii and  R. J.  Fruehan: Iron Steelmaker, 24 (1997), 47.
• 6)   G.  Li,  T.  Hamano and  F.  Tsukihashi: ISIJ Int., 45 (2005), 12.
• 7)   H.  Suito,  R.  Inoue and  M.  Takada: Tetsu-to-Hagané, 67 (1981), 75.
• 8)   Y.  Kitagawa: Tetsu-to-Hagané, 88 (2002), No. 8, 430.
• 9)   S.  Ban-ya and  T.  Watanabe: Tetsu-to-Hagané, 63 (1977), No. 12, 1809.
• 10)   S.  Ban-ya and  R.  Nagabayashi: Tetsu-to-Hagané, 68 (1982), No. 2, 261.
• 11)   K.  Iwasaki,  N.  Sano and  Y.  Matsushita: Tetsu-to-Hagané, 67 (1981), 536.
• 12)   K.  Ito and  N.  Sano: Tetsu-to-Hagané, 69 (1983), 1747.
• 13)   N.  Sano: Tetsu-to-Hagané, 69 (1983), No. 3, 378.
• 14)   M.  Muraki,  H.  Fukushima and  N.  Sano: Tetsu-to-Hagané, 71 (1985), No. 6, 693.
• 15)   J.  Im,  K.  Morita and  N.  Sano: ISIJ Int., 36 (1996), No. 5, 517.
• 16)   O.  Kubaschewski and  C. B.  Alcock: Metallurgical Thermochemistry, 5th ed., Pergamon Press, Oxford, New York, (1979).
• 17)   J. D.  Shim and  S.  Banya: Tetsu-to-Hagané, 67 (1981), No. 10, 1735.
• 18)   C.  Wagner: Metall. Trans. B, 6B (1975), 405.
• 19)  Thermodynamic Data for Steelmaking, Tohoku University Press, Sendai, (2010), 248.
• 20)  Slag Atlas, 2nd ed., Verlag Stahleisen GmbH, Düsseldorf, (1995), 11.