Hot Deformation and Dynamic Recrystallization of 17-4 PH Stainless Steel

Abstract

The hot deformation behavior of a 17-4 PH stainless steel was investigated by compression tests. The typical single-peak dynamic recrystalization (DRX) behavior and also a transition state between single and multiple peak (cyclic) behaviors were seen in the resultant flow curves. The application of constitutive equations for determination of hot working constants was critically discussed. As a result, the deformation activation energy and the stress multiplier in the hyperbolic sine equation were determined as 337 kJ/mol and 0.011, respectively. The Zener-Hollomon parameter (Z) exponents for peak stress and peak strain based on the power relationships were determined as 0.18 and 0.11, respectively. The normalized critical stress and strain for initiation of DRX were respectively found to be 0.89 and 0.47. The prior austenite grain boundaries (PAGB) were revealed by electrolytic etching of the martensite in order to study the microstructure of hot deformed samples. Significant grain refinement occurred as a result of necklace DRX mechanism. The average dynamically recrystallized grain size was related to Z and peak stress by power equations with exponents of –0.25 and –1.24, respectively. A DRX map was developed to show the effect of deformation conditions on the occurrence of DRX and on the final grain size.

1. Introduction

The properties of materials can be deduced from knowledge of their microstructure. The shape, size, distribution, and orientation of phases and imperfections are important microstructural features. Among them, imperfections such as grain boundaries, which determine the grain structure, are of special interest. Two independent studies on the factors influencing the mechanical properties of steels by Hall¹⁾ and on the brittle failure of steels by Petch²⁾ resulted to development of the famous Hall-Petch relationship, which mathematically represents the grain size dependence of strength. It is well known that refining grain size is a method to increase the strength while maintaining the ductility properties.³⁾

Hot deformation processing of steels plays an important role in the industry for production of steels with required mechanical properties while maintaining the production costs as low as possible. The main idea is enhancing the properties of the material by processing not by alloying. Therefore, the parameters of the forming process must be carefully controlled to produce a fine microstructure with desired shape, size, distribution, and orientation of phases. Different strategies can be applied to refine the microstructure during and after hot deformation of steels, which are based on phenomena such as dynamic recrystallization (DRX), metadynamic recrystallization (MDRX), Static recrystallization (SRX), austenite pancaking, precipitation, and phase transformation.⁴⁾

During the course of hot deformation, grain refinement can be achieved by dynamic recrystallization.^5,6) In some materials such as aluminum, the dynamic recovery (DRV) can balance work hardening, and a plateau is achieved. However, in many materials such as austenite phase in steels, the kinetics of DRV is low and the work hardening can not be balanced only by DRV. As a result, the dislocation density increases gradually by strain and eventually the recrystallization occurs during deformation. DRX is one of the most important softening mechanisms in hot deformation processing and has profound effects on the microstructure and grain size. Based on this importance, the present work is focused on the evolution of the microstructure of 17-4 PH stainless steel (AISI 630) during hot compression and its refinement by DRX.

17-4 PH is more common than any other type of precipitation hardening (PH) stainless steels. Its ability to develop high strength without the catastrophic loss of ductility and its superior corrosion resistance to other steels of similar strength, have made it very attractive to designers and engineers.⁷⁾ Hot deformation processing such as forging for this steel is conducted in the temperature range of stability of austenite phase.⁸⁾ Due to the low stacking fault energy of austenite in the 17-4 PH stainless steel, the major restoration process during hot deformation is dynamic recrystallization (DRX). In our literature survey, there was not found any information on DRX microstructures of this important engineering alloy. Also, it should be indicated that the reported works on grain refining of PH stainless steels are scant.^9,10)

2. Experimental Materials and Procedures

2.1. Hot Compression Test

The chemical composition of the 17-4 PH stainless steel used in this study is shown in Table 1. Cylindrical samples with diameter of 5 mm and height of 10 mm were used as hot compression specimens, which had the Rastegaev design⁸⁾ to hold glass powder as a lubricant material at the contact surface of anvils and specimen. A Baehr DIL-805 deformation dilatometer was used for hot compression test. Before this test, the specimen was austenitized at 1180°C for 10 min and cooled with the rate of 1.5°C/s to deformation temperature and held there for 5 min. The austenite grain size just after this step was D₀ =105 µm (Fig. 1(a)). Afterwards, single-hit hot compression tests were carried out at temperatures of 950–1150°C with strain rates of 10^–3–10 s^–1 under true strain of about 0.9.

Table 1. Chemical composition (wt. %) of the experimental 17-4 PH stainless steel.

C	Cr	Ni	Cu	Mn	Si	Nb	Mo	V	S	P
0.03	15.14	4.53	3.4	0.6	0.54	0.25	0.19	0.05	0.02	0.02

Fig. 1.

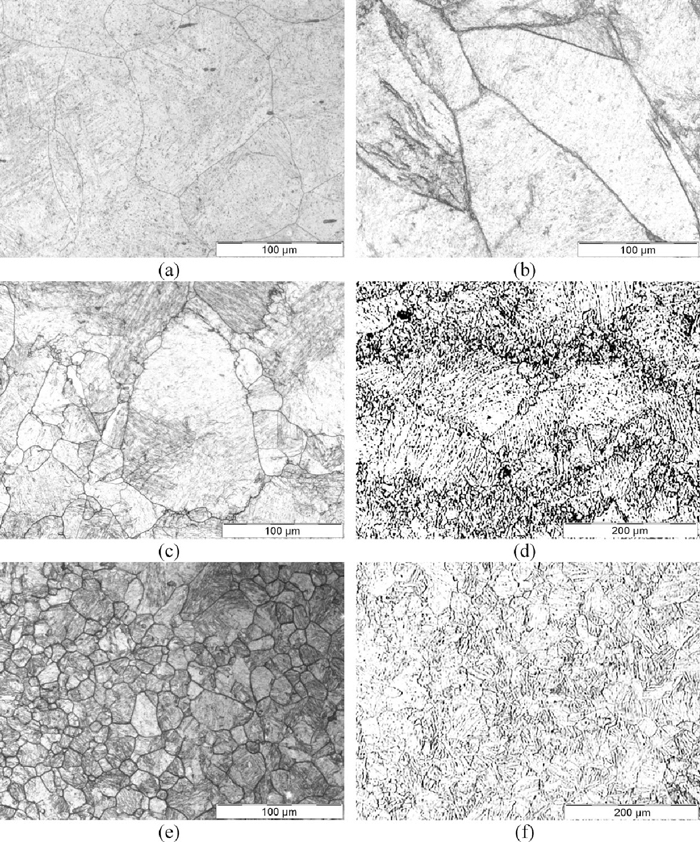
Optical micrographs of the 17-4 PH stainless steel: (a) initial microstructure, and deformed microstructures at (b) T=1000°C and $\dot{\epsilon }$ =10 s^–1, (c) and (d) T=1000°C and $\dot{\epsilon }$ =0.1 s^–1, and (e) and (f) T=1150°C and $\dot{\epsilon }$ =10 s^–1. Samples (d) and (f) were etched by superpicral.

2.2. Metallography

The microstructure of 17-4 PH stainless steel is essentially martensitic at room temperature.^7,11,12) However, in order to characterize hot deformed samples, the prior austenite grain boundaries (PAGBs) should be revealed. The difficulty to reveal the PAGBs in steels is mainly due to the existence of martensite microstructure. The efficiency of techniques to reveal the PAGBs in steels depends significantly on the chemical composition, heat treatment, deformation condition, and other unknown factors.^13,14,15,16) In the present work, two etching techniques were found to be able to reveal the PAGBs in 17-4 PH stainless steel. The first is the electrolytic etching in 60% HNO₃,¹⁷⁾ which has been originally developed for austenitic stainless steels, and the second is the hot supersaturated picric acid (superpicral),^12,17) which is a general etchant for revealing the PAGBs. The details of the etching solutions and methods used are shown in Table 2. These etching techniques can be used to reveal the PAGBs in the annealed (Fig. 1(a)), work-hardened (Fig. 1(b)), partially-recrystallized (Figs. 1(c) and 1(d)), and completely recrystallized (Figs. 1(e) and 1(f)) samples. Since the results of the electrolytic etching are significantly better, this technique was used for subsequent microstructural analyses.

The microstructure of the 17-4 PH stainless steel used in this work is free of δ-ferrite stringers in the martensite matrix. This can be ascribed to the fact that the amounts of chromium and nickel are respectively near the minimum (15<wt% Cr<17.5) and maximum (3<wt% Ni<5) allowable values. The chemical composition of this alloy falls within that of the 15-5 PH stainless steel, which is a ferrite-free version of 17-4 PH stainless steel.

Table 2. Etching solutions and methods used to reveal the prior austenite grain boundaries in 17-4 PH stainless steel.

Etchant	Composition	Details	Etch time (s)
Superpicral	5–10 g picric acid + 100 ml ethanol + drops of HCl	Temperature of the solution: 50–70°C	5–20
Electrolytic	60% HNO3 solution	1 volt, 316 SS electrode	50–70

Table 3. Measured and calculated values required to find the values of m.

$\dot{\epsilon }$	T	R0	H0	Rm	Hf	Rf	ΔHf	RT	ΔR	b	m
0.001	1150	2.49	10.02	3.96	4.21	3.841423	5.81	3.592548	0.37	0.28	0.11
0.001	1000	2.48	10	3.98	4.15	3.849707	5.85	3.574902	0.41	0.30	0.13
0.1	1150	2.51	10.06	4	4.25	3.861697	5.81	3.569051	0.43	0.33	0.14
0.1	1100	2.49	10	3.98	4.24	3.823987	5.76	3.491108	0.49	0.38	0.16
1	1150	2.5	9.96	4.06	4.15	3.872983	5.81	3.468833	0.59	0.44	0.19
1	1100	2.51	10.04	4.1	4.15	3.90406	5.89	3.479233	0.62	0.45	0.20
0.1	1000	2.51	10.04	4.12	4.15	3.90406	5.89	3.431656	0.69	0.50	0.22
10	1150	2.49	10	4.05	4.26	3.815	5.74	3.295099	0.75	0.59	0.25
0.1	950	2.5	10.04	4.07	4.24	3.847016	5.80	3.356901	0.71	0.54	0.23
1	1000	2.51	10.02	4.08	4.25	3.854012	5.77	3.3567	0.72	0.55	0.24
1	950	2.5	10.06	4.13	4.15	3.892377	5.91	3.367196	0.76	0.55	0.25
10	1000	2.5	10.04	4.09	4.25	3.842487	5.79	3.292099	0.80	0.61	0.27

2.3. Preparation of Flow Curves

After removal of the elastic portion, each flow curve was corrected for friction and then was smoothed in order to eliminate the irregularities and fluctuations as described below.

The application of suitable lubricants in the hot compression test may significantly reduce friction, but the lubricants are unable to eliminate it completely. Therefore, the effect of friction should be considered in the raw stress data to form the friction-corrected data. Based on the upper-bound theory, a simple theoretical analysis of the barrel compression test for determination of the constant friction factor (m) has been proposed by Ebrahimi and Najafizadeh.¹⁸⁾ The required expressions are shown below:   

$$\frac{H}{8bR}\times \frac{P}{\sigma }={\left(\frac{1}{12}+{\left(\frac{H}{Rb}\right)}^2\right)}^{3/2}+\left(\frac{m}{24\sqrt{3}}\times \frac{e^{-b/2}}{e^{-b/2}-1}\right)-{\left(\frac{H}{Rb}\right)}^3$$(1)

  

$$\{\begin{array}{l}H=H_{0}exp\left(-\epsilon \right)\\ R=R_{0}exp\left(-\epsilon /2\right)\\ b=4\times \frac{R_M-R_T}{R_f}\times \frac{H_f}{H_f-H_0}\\ m=\frac{R_f}{H_f}\times \frac{3\sqrt{3}}{12-2b}\times b\\ R_f=R_0\sqrt{\frac{H_0}{H_f}}\\ R_T=\sqrt{3\times \frac{H_0}{H_f}\times R_0^2-2R_M^2}\end{array}$$(2)

where σ is the corrected true stress, P is the external pressure applied to sample in compression (uncorrected stress), b is the barrel parameter, m is the constant friction factor, R and H respectively are the values of radius and height of sample during the test (strain dependant variables). R₀ and H₀ are the initial values of radius and height of sample, respectively. H_f is the height of sample after deformation, R_M is the radius at middle high of deformed sample, R_f is the average radius of sample after deformation, and R_T is the top radius of deformed sample. The values of R₀, H₀, H_f, R_M were measured using the samples before and after hot compression, while the values of R_T, R_f, b, and m were calculated using Eq. (2). Afterwards, based on Eq. (1) and the dependence of R and H on strain, the values of σ were calculated. Table 3 shows the summary of friction-correction calculations. As can be seen in this table, by decreasing the deformation temperature and increasing the strain rate, the friction becomes more effective. This effect can be better seen in friction-corrected curves as shown in Fig. 2(a). These figures also show that the effect of friction is more pronounced at higher strain values, especially after the peak stress point.

Fig. 2.

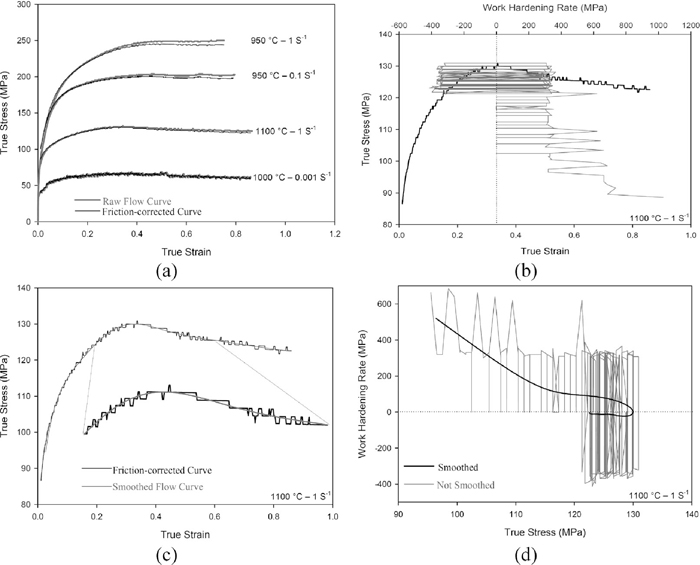
Preparation of flow curves: (a) the friction-corrected versus experimental flow curves, and for the deformation condition of T=1100°C and $\dot{\epsilon }$ =1 s^–1: (b) the θ–σ plot from friction-corrected flow data showing the effects of irregularities and fluctuations of experimental flow stress data, (c) the smoothed versus friction-corrected flow curve, (d) the comparison between the θ–σ plots from friction-corrected and smoothed flow data.

The occurrence of DRX is traditionally identified from the presence of stress peaks in flow curves.¹⁹⁾ However, not all materials display well-defined peaks when tested under hot working conditions. It has been shown by Ryan and McQueen²⁰⁾ and Poliak and Jonas^21,22) that the onset of DRX can also be detected from inflections in plots of the strain hardening rate against stress. The derivative of the true stress with respect to true strain yields the work hardening rate, θ (Eq. (3)). Therefore, this technique requires the differentiation of the stress-strain curve, but short range noise in flow curves can render such differentiation calculus impossible (such as the one showed in Fig. 2(b)). In order to solve this problem, the flow stress data were smoothed in order to eliminate the irregularities and fluctuations in the experimental curves (Fig. 2(c)) and make them differentiable (Fig. 2(d)).^22,23)

  

$${{\theta |}_i=\frac{d\sigma }{d\epsilon }|}_i=\frac{{\sigma |}_{i+1}-{\sigma |}_{i-1}}{{\epsilon }_{i+1}-{\epsilon }_{i-1}}$$(3)

3. Results and Discussion

3.1. Hot Working Behavior

Flow curves at different deformation conditions are shown in Fig. 3. Most of the curves exhibit typical DRX behavior with a single peak stress followed by a gradual fall towards a steady state stress.²⁴⁾ However, the peak becomes less obvious when the strain rate increases or the deformation temperature decreases. In the single peak behavior, new cycles of DRX initiate before completion of the first cycle. Therefore, different grains will be at different stages of the DRX process at any point of time. The flow curve will represent the averaged flow stress of grains at different stages of recrystallization in the form of a single peak curve. In some cases, such as deformation condition of T=1000°C and $\dot{\epsilon }$ =1 s^–1, the shape of flow curve resembles typical dynamic recovery behavior. However, inflections point in the θ–σ plots are considered as stronger indications of the occurrence of DRX.^21,22,25) Therefore, the θ–σ curve analysis was performed to reveal whether or not DRX occurred. The θ–σ curve for this deformation condition is shown in Fig. 4(a). This figure shows that this sample, despite the shape of its flow curve, has a clear inflection point (associated with a minimum in –dθ/dσ–σ curve as shown in Fig. 4(b)) that may be related to the occurrence of DRX. The microstructure of this sample is shown in Fig. 4(c). In this microstructure, some fine grains at serrated grain boundaries can be seen that confirms the occurrence of DRX in this case.²⁶⁾ For deformation condition of T=1000°C and $\dot{\epsilon }$ =10 s^–1, the shape of flow curve resembles typical DRX behavior (Fig. 3). However, neither an clear inflection point nor a minimum were determined on the θ–σ (Fig. 4(d)) and –dθ/dσ–σ curves (Fig. 4(e)), respectively. As shown in Fig. 4(f), the softening beyond the peak can be ascribed to adiabatic deformation heating at high strain rate of 10 s^–1. The straight grain boundaries in the microstructure of this sample (Fig. 1(b)) also signify the absence of DRX.

Fig. 3.

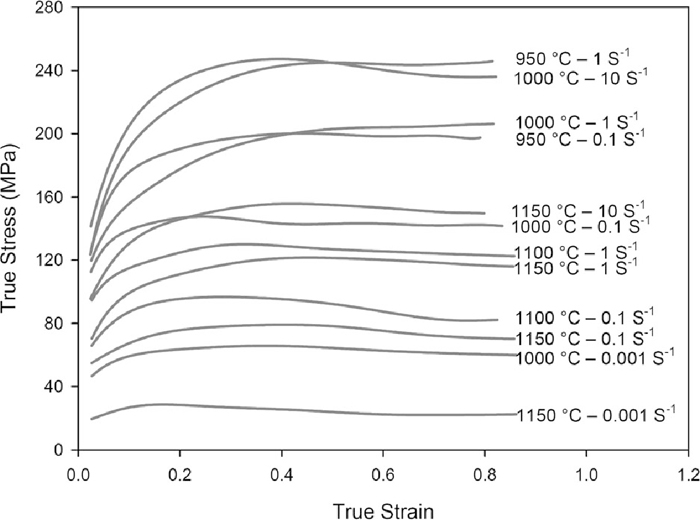
Flow curves at different deformation conditions.

Fig. 4.

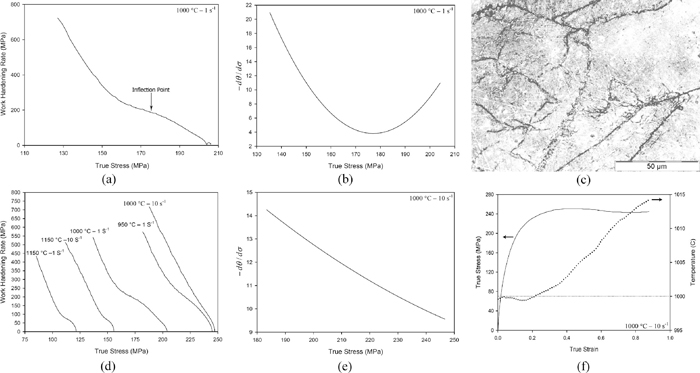
The comparison between two exceptional deformation conditions: (a) the θ–σ plot, (b) -dθ/dσ–σ plot, and (c) the hot deformed microstructure for T=1000°C and $\dot{\epsilon }$ =1 s^–1 as a sample that its flow curve exhibits typical DRV behavior, and (d) the θ–σ plot, (e) –dθ/dσ–σ plot, and (f) temperature change during deformation for T=1000°C and $\dot{\epsilon }$ =10 s^–1 as a sample that its flow curve exhibits typical DRX behavior.

At low stored energy, the nucleation of DRX is believed to begin at a critical strain,²⁷⁾ which corresponds to a critical dislocation density,^28,29,30) and by the bulging of pre-existing grain boundaries.^31,32) These may be the original grain boundaries, boundaries of dynamically recrystallized grains, or high angle boundaries created during straining (e.g. those associated with deformation bands or twins).³³⁾ This mechanism is often called strain-induced boundary migration (SIBM) and commonly used to explain the onset of DRX in polycrystals. However, at high stored energy, DRX begins by the growth of the high angle cell boundaries formed by dislocation accumulation.^34,35,36) The difference in dislocation density in front of and behind the boundary is the driving force for the growth of the DRX nuclei.^29,30,36)

In single peak DRX, such as the case of Figs. 1(c) and 1(d), nucleation occurs essentially along existing grain boundaries (necklace mechanism) and the growth of each grain is stopped by the concurrent deformation as a result of increasing the dislocation density of the new grains and reducing the driving force for their further growth.^26,37) The DRX process continues until the completion of the first layer of necklace to cover the entire grain boundary. Afterwards, the subsequent layers form at the recrystallization front between the recrystallized and unrecrystallized portions. ^26,32,33,34) If stress oscillations appear before reaching the steady state, then several recrystallization and grain growth cycles occur before the steady state strain, which tend to die out gradually, and the stress behavior is said to be of the cyclic or multiple peak type.^38,39,40,41) In this case, the growth of grains is stopped by boundary impingement and not by concurrent deformation.^24,42)

There is no evidence of classical multiple peaks in the flow curves of this work, even at very low strain rate of 0.001 s⁻¹ and high temperature of 1150°C. Although the flow curve associated with this deformation conditions can be classified as single-peak, the close view of the original flow curve (Fig. 5(a)) shows that it is not the conventional single peak flow curve. Several plateaus (horizontal stress lines) followed by a decrease in flow stress after each plateau are detected beyond the peak point of its flow curve. Each plateau represents a transient steady state period (similar to a peak point), and the decrease in flow stress after each plateau may be attributed to the progress of a new DRX cycle. This condition may be considered as a transition state between single and multiple peak behaviors and it was called the multiple transient steady state (MTSS) behavior.⁸⁾ As shown in Fig. 5(b), there may be an overlap between the end of a given cycle and the onset of the subsequent cycle of DRX. At the last stages of a cycle, the rate of recrystallization process is relatively low and the material work hardens under concurrent deformation. At the same time, the rate of the new DRX cycle increases and softening occurs. These simultaneous processes result to the appearance of several plateaus after the peak stress. The microstructures of this sample are shown in Fig. 5(c). The average prior austenite grain size was determined as about 81 µm. It is evident that there is no significant grain refinement in this case, which can be ascribed to the fact that this condition is a transition state between single and multiple peak behaviors and is related to a high temperature and low strain rate deformation condition. The latter reason will be discussed later. Figure 5(d) shows the flow curves resulted from the hot compression tests using an Instron type instrument for the same material under Zener-Hollomon parameters near that of the sample deformed under strain rate of 0.001 s^–1 and temperature of 1150°C. As can be seen in this figure, the MTSS behavior has occurred again and lower Zener-Hollomon parameters can result in cyclic behavior. Therefore, these results signify the aforementioned assumption that the MTSS behavior is a transition state between single and multiple peak behaviors. Since the single peak and cyclic behaviors are respectively responsible for grain refinement and grain coarsening, this transition state (MTSS behavior) has practical importance.

Fig. 5.

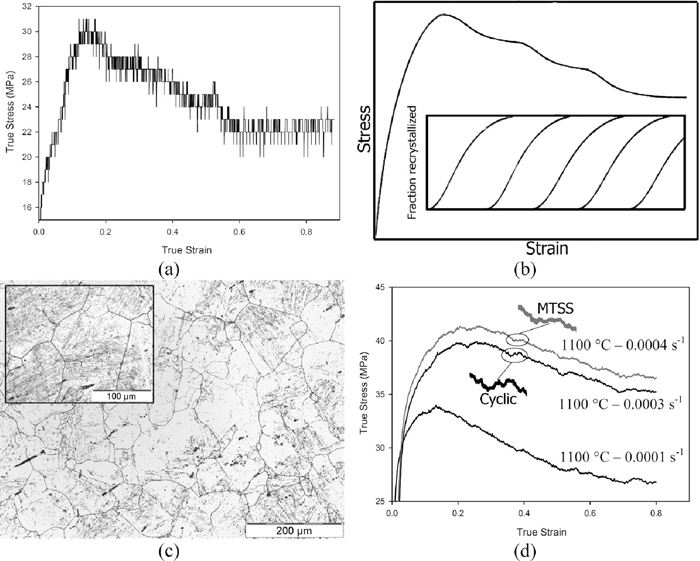
DRX behavior of the sample deformed at T=1150°C and $\dot{\epsilon }$ =0.001 s^–1: (a) a close view of the experimental flow curve, (b) schematic representation of the effect of recrystallization cycles on the flow curve, (c) hot deformed microstructures, (d) hot deformed flow curves using an Instron type instrument.

The drop in flow stress of Fig. 3 with deformation temperature may be attributed to the increase in the rate of restoration processes and decrease in the strain hardening rate. Since the formation of DRX nuclei becomes easier at higher deformation temperatures, the critical strain for initiation of DRX decreases. Moreover, the mobility of grain boundaries increases with increasing deformation temperature and hence the rate of DRX increases. Therefore, both the peak and steady state strains decrease with deformation temperature.⁴³⁾

The increase in the flow stress with strain rate can be ascribed to the decrease in the rate of restoration processes and increase in strain hardening rate.⁴³⁾ The rate of DRV also decreases with increasing strain rates. Since well-developed substructures by occurrence of DRV are observed in DRX microstructures and are the origin of DRX nuclei,^28,34,44,45) the increase in the critical strain for initiation of DRX with increasing strain rate is reasonable. The mobility of grain boundaries decreases with increasing strain rate, which in turn increases the peak and steady state strains.

3.2. Constitutive Analyses

It was shown by Sellars and Tegart,^46,47) using the hyperbolic sine function suggested by Garofalo,⁴⁸⁾ that hot working can be considered as a thermally-activated process and it can be described by strain rate equations similar to those employed in creep studies. Based on these works, the Zener- Hollomon parameter (Z),⁴⁹⁾ which is the temperaturecompensated strain rate, can be related to the flow stress in different ways (Eq. (4)): The power law at relatively low stresses, exponential law at high stresses, and hyperbolic sine law for a wide range of deformation conditions:   

$$Z=\dot{\epsilon }exp\left(\frac{Q}{RT}\right)=\{\begin{array}{l}{A}^{\prime }{\sigma }_P^{n^{\prime }}\\ A^{″}exp(\beta \sigma )\\ A{[sinh(\alpha \sigma )]}^n\end{array}$$(4)

where Q is the activation energy of hot working. A′, A″, A, n′, n, β and α (≈β/n′) are material constants. The stress multiplier α is an adjustable constant which brings ασ into the correct range that gives linear and parallel lines in ln $\dot{\epsilon }$ versus ln {sinh(ασ)} plots.⁵⁰⁾ In these expressions, the flow stress is related to both the absolute temperature during deformation and strain rate. However, the description of flow stress by these expressions is incomplete, because no strain for determination of flow stress is specified. Therefore, characteristic stresses that represent the same deformation or softening mechanism for all flow curves, such as steady state, peak, or critical stress for initiation of DRX, should be used for this purpose. It should be noted that the nature of material constants and equations are dependent on the characteristic stress used to derive them. In general, the peak stress is the most widely accepted one in order to find the hot working constants. By taking natural logarithm from each side of the expressions in Eq. (4), the following expressions could be derived for peak stress:   

$$lnZ=ln\dot{\epsilon }+\frac{Q}{R}(1/T)=\{\begin{array}{l}ln{A}^{\prime }+n^{\prime }ln{\sigma }_P\\ ln{A}^{″}+\beta \sigma \\ lnA+nln[sinh(\alpha \sigma )]\end{array}$$(5)

By partial differentiation of these expressions at constant temperature, equations of $n\prime ={[\partial ln\dot{\epsilon }/\partial ln{\sigma }_P]}_T$ , $\beta ={[\partial ln\dot{\epsilon }/\partial {\sigma }_P]}_T$ , $n={[\partial ln\dot{\epsilon }/\partial ln\left\{sinh\left(\alpha {\sigma }_P\right)\right\}]}_T$ can be derived and the value of α (≈β/n′) can be calculated. The required plots are shown in Fig. 6(a). The value of α = 0.011 can be calculated from these results. This value slightly differs from the conventional value of 0.012 for stainless steels.⁴³⁾ It is usual to take the value of α = 0.012 for steels that can be a source of error for analyses based on the hyperbolic sine law in hot deformation studies.

Fig. 6.

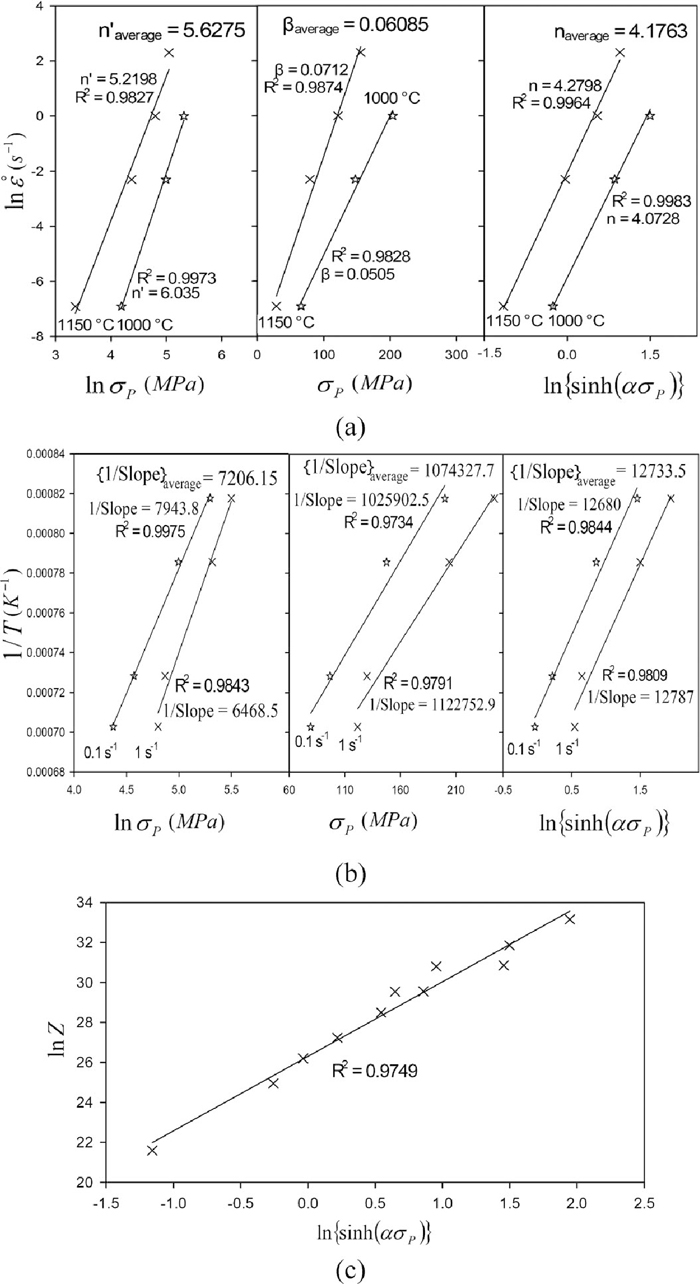
Constitutive analyses: (a) plots for calculation of hot working constants, (b) plots for calculation of deformation activation energy, (c) the hyperbolic sine plot for the peak stress.

By partial differentiation of the expressions shown in Eq. (5) at constant strain rate, the following expressions can be determined:   

$$Q=\{\begin{array}{l}R{n}^{\prime }/{\left[\partial (1/T)/\partial ln{\sigma }_P\right]}_{\dot{\epsilon }}\\ R\beta /{\left[\partial (1/T)/\partial {\sigma }_P\right]}_{\dot{\epsilon }}\\ Rn/{\left[\partial (1/T)/\partial lnsinh\left(\alpha {\sigma }_P\right)\right]}_{\dot{\epsilon }}\end{array}$$(6)

It is apparent that a greater dependence of flow stress on deformation temperature will result in greater value of deformation activation energy. It follows from these expressions that the slope of the plots of (1) ln $\dot{\epsilon }$ and 1/T against lnσ_P based on the power law, (2) ln $\dot{\epsilon }$ and 1/T against σ_P based on the exponential law, and (3) ln $\dot{\epsilon }$ and 1/T against ln {sinh(ασ_P)} based on the hyperbolic sine law can be used for obtaining the value of Q. The required plots are shown in Fig. 6(b). The average correlation coefficients for regression analysis of Fig. 6(b) in the case of power, exponential and hyperbolic sine equations were calculated as 0.991, 0.976 and 0.982, respectively. This indicates the appropriateness of power equation in the experimental conditions of present investigation, which resulted to the value of 337 kJ/mol for deformation activation energy. The values of 543 and 442 kJ/mol were also determined using the exponential and hyperbolic sine laws, respectively. Since the 17-4 PH stainless steel is austenitic at hot working conditions, its behavior can be compared to a similar austenitic stainless steel with the same level of alloying elements. The published values of deformation activation energy for austenitic stainless steels follow the relation Q_Calc = 13.5 × S ±25.⁵¹⁾ In this relation, S is the total weight percent of metallic solutes and Q_Calc is the activation energy in kJ/mol. For the 17-4 PH stainless steel in the case of present investigation (Table 1), S = 24.7 and hence Q_Calc = 333 ± 25 kJ/mol. Therefore, the value of 337 kJ/mol is reasonable. In many research works, one of the expressions of Eq. (6) is taken from the literature for calculation of apparent activation energy, and as shown in the abovementioned analyses, it may lead to significantly different values.

The value of 337 kJ/mol for deformation activation energy deviates from the self diffusion activation energy in austenite, which is about 280 kJ/mol.⁵²⁾ Although the hot working activation energy depends on the material being considered, it is usually referred to as apparent value, because no account is generally taken of the internal microstructural state and it is only derived from plots generated by experimental data and the assumption that the microstructure remains constant.

The value of 337 kJ/mol was used to calculate the Z parameter. According to Eq. (5), plots of lnZ against ln {sinh(ασ_P)} can be used for obtaining the appropriate values of n and A (Fig. 6(c)). These analyses resulted to the following constitutive equation:   

$$Z=\dot{\epsilon }exp\left(\frac{337\times {10}^3}{RT}\right)=2.64\times {10}^{11}\times {\left[sinh\left(\text{0}\text{.011}\times {\sigma }_P\right)\right]}^{\text{3}\text{.73}}$$(7)

This equation can be easily used to find the values of peak stress for a wide range of deformation conditions.

3.3. Characteristic Points of DRX Flow Curves

The onset of DRX was detected from the inflections in plots of the θ versus σ or from the minimum in plots of –dθ/dσ versus σ (before the peak stress for both type of curves).²²⁾ The latter curves were used to detect the critical stress for initiation of DRX (σ_C). Moreover, the peak (σ_P) and steady-state (σ_S) stresses, peak (ε_P) and steady-state (ε_S) strains, and the critical strain for the onset of DRX (ε_C) were detected from the θ–σ curves, θ–ε curves, and inflection points in θ–ε plots, respectively. Figure 7 shows the method used for determination of characteristic points of flow curves by using the work hardening rate. For example, the exact values of peak stress and strain were determined at the first occurrence of θ = 0 in the θ–σ and θ–ε curves, respectively. The characteristic points of flow curves were plotted versus Z in Fig. 8. Regression analysis of these curves and afterwards consideration of Z/A dimensionless parameter resulted in the following expressions:   

$$\{\begin{array}{l}{\sigma }_P=0.66\times Z^{0.18}=75\times {(Z/A)}^{0.18}\\ {\sigma }_C=0.59\times Z^{0.18}=67.1\times {(Z/A)}^{0.18}=0.89\times {\sigma }_P\\ {\sigma }_S=0.61\times Z^{0.18}=69.3\times {(Z/A)}^{0.18}=0.92\times {\sigma }_P\\ {\epsilon }_P=0.018\times Z^{0.11}=0.325\times {(Z/A)}^{0.11}\\ {\epsilon }_C=0.0084\times Z^{0.11}=0.151\times {(Z/A)}^{0.11}=0.47\times {\epsilon }_P\\ {\epsilon }_S=0.09\times Z^{0.08}=0.738\times {(Z/A)}^{0.08}\end{array}$$(8)

where the stress values are expressed in MPa. The Z exponent of 0.11 for the peak strain is consistent with the literature data which has a value between 0.09 and 0.22.^{22,53,54,55,56)} The normalized critical stress and strain can be expressed as σ_C/σ_P = 0.89 and ε_C/ε_P=0.47, respectively. Nearly similar value for normalized critical stress has been reported for AISI 304 austenitic stainless steel.⁵⁷⁾ The present investigation indicates that the DRX starts when the normalized strain reaches to the value of 0.47. This value is close to the previous reported value of 0.5 for AISI 304 stainless²³⁾ and it is within the general range reported for steels, which is between 0.3 and 0.9.^{22,53,58,59,60)}

Fig. 7.

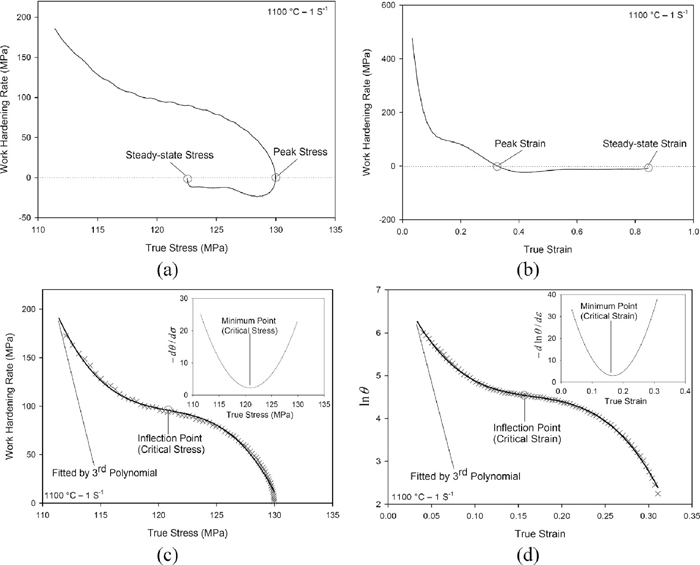
Methods used for determination of characteristic points of flow curves.

Fig. 8.

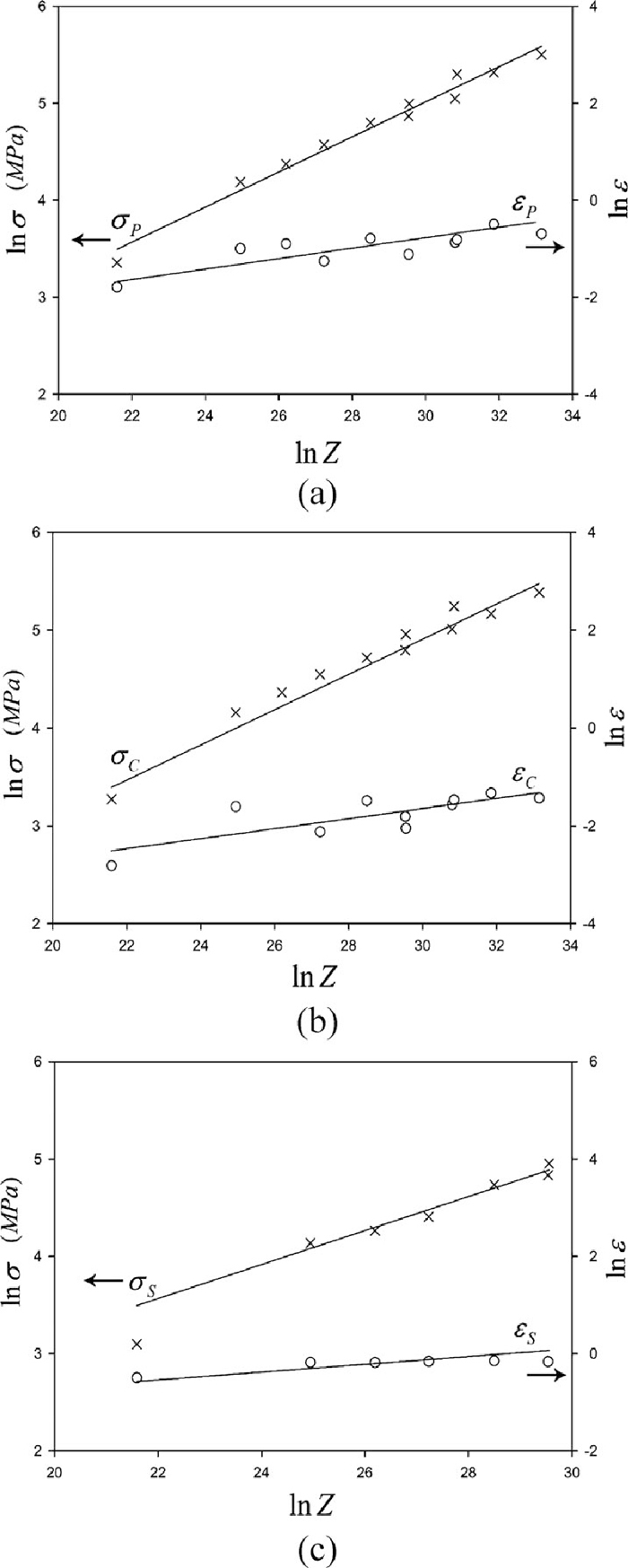
Dependence of the characteristic points of flow curves on Z.

3.4. Hot Deformed Microstructures

Microstructures obtained at deformation temperature of 1150°C and different strain rates are shown in Fig. 9. This figure shows that the average grain size increases with decreasing strain rate. Figure 10 shows the resultant microstructures at strain rate of 0.1 s^–1 and different deformation temperatures. Here, the average grain size increases with increasing the deformation temperatures. The increase in grain size with rising temperature and declining strain rate could be attributed to decline in dislocation density and increase in the mobility of grain boundaries and hence the growth rate.

Fig. 9.

Hot deformed microstructures at deformation temperature of 1150°C under strain rate of (a) 10, (b) 1, (c) 0.1 and (d) 0.001 s^–1.

Fig. 10.

Hot deformed microstructures under strain rate of 0.1 s^–1 at deformation temperature of (a) 950, (b) 1000, (c) 1100 and (d) 1150°C.

Since DRX involves repeated nucleation but limited growth of new grains, the mean DRX grain size varies slightly as recrystallization proceeds.³⁷⁾ However, in a partially recrystallized structure, deformed grains also contribute to the measurement of grain size. As a result, the average grain size ( $\overline{D}$ ) continuously decreases until the completion of DRX.⁶¹⁾ Therefore, partially recrystallized samples such as that deformed at 950°C with strain rate of 0.1 s^–1 under true strain of about 0.9, do not show their final DRX microstructure (Fig. 10(a)). In this case, the necklace DRX is underway and the boundaries of primary grains are highly serrated and decorated with small DRX grains pertaining to the necklace DRX (Fig. 11). Figure 11 shows that the given temperature/strain rate combination is suitable for DRX to occur and a significant grain refinement is probable for this sample if the straining continues.

Fig. 11.

Hot deformed microstructure of the sample deformed at T=950°C and $\dot{\epsilon }$ =0.1 s^–1 showing the serrated grain boundaries and very small DRX grains.

3.5. Grain Refinement

Figure 12 shows the average grain size ( $\overline{D}$ ) versus Z and peak stress. Only those cases when steady state was reached before quenching were used for this analysis. Therefore, the average grain size ( $\overline{D}$ ) was equal to fully dynamically recrystallized grain size (D_S). Based on the discussions in the previous section, the exclusion of partially recrystallized samples is crucial for removing the effect of strain on grain size and for developing correct relationship between dynamically recrystallized grain size and Z. As can be seen in this figure, the DRX grain size significantly decreases as Z or peak stress increases. The smallest grain size obtained in the present study is about 11 µm when the strain rate is 0.1 s^–1 and the deformation temperature is 1000°C. The data on Fig. 12 can be fitted to the following power relationships:   

$$D_S=\{\begin{array}{l}15\mathrm{\hspace{0.17em} }794\times Z^{-0.25}\\ 4\mathrm{\hspace{0.17em} }958\times {\sigma }_P^{-1.24}\end{array}$$(9)

  

$${\sigma }_P=904\times D_S^{-0.8}$$(10)

where D_S and σ_P are expressed in µm and MPa, respectively. The Z exponent of –0.25 in Eq. (9) is consistent with the classical literature data which has a value between –0.11 and –0.4 for steels.^{4,5,62,63,64,65)} Moreover, The D_S exponent of –0.8 in Eq. (10) is within the reported range of –0.7 to –0.8 for singlephase materials.^{20,24,33,66,67)}

Fig. 12.

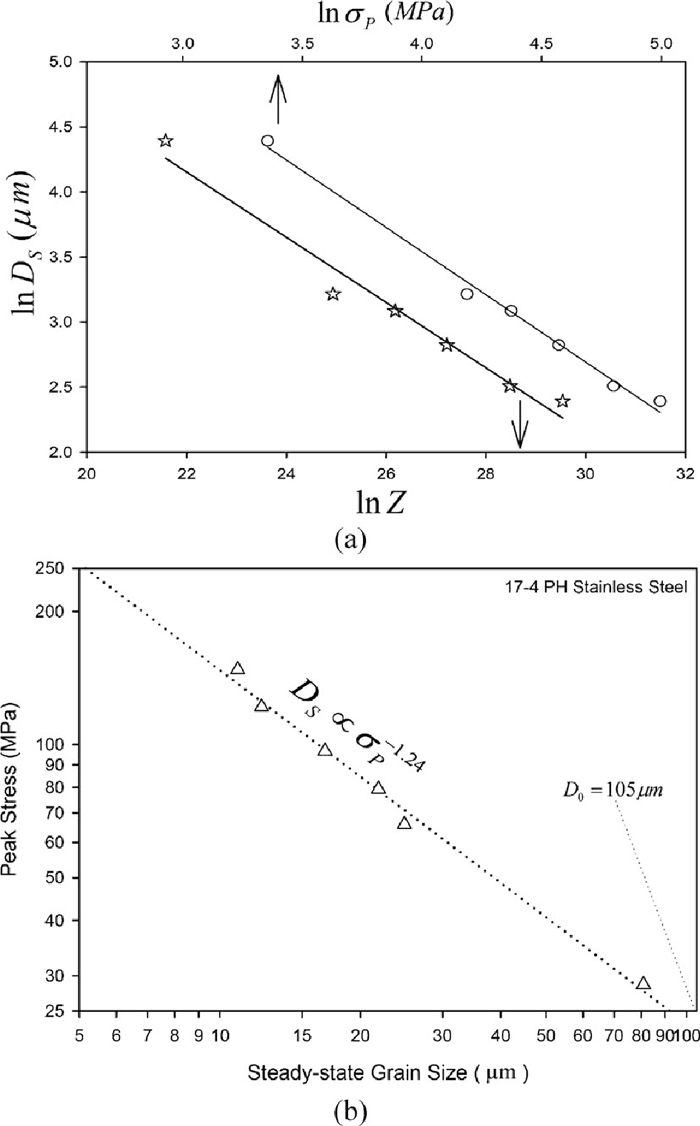
The dependence of the average steady-state grain size on Z and peak stress.

The highest Z and peak stress under DRX condition in this work was determined for the deformation condition of T = 950°C with strain rate of 1 s^–1; where, the steady state grain size and strain can be estimated as 5.4 µm by Eq. (9) and 1.27 by Eq. (8), respectively. Unfortunately, the strain of 1.27 is relatively large for hot compression test. However, bear in mind that these analyses were performed for initial grain size of 105 µm. This is an undisputable fact that the recrystallized grain size under conventional discontinuous dynamic recrystallization (DDRX) is virtually independent of initial grain size.³⁷⁾ However, by decreasing the initial grain size, both critical and steady state strains will decrease and full DRX under high Z parameters can be achieved at relatively lower strains. In other words, the higher grain boundary frequency in the finer initial microstructure will increase the potential nucleation sites, which in turn accelerates the recrystallization process of austenite.

3.6. DRX Map

Microstructural observations when combined with the flow curve analysis can be used to construct DRX maps as shown in Fig. 13. In order to draw this figure, the critical and steady state strains from flow curve analysis (Eq. (8)) were used to define the partial and fully DRX regions (solid lines). Moreover, microstructural studies were used to relate the DRX grain size with Z (dotted lines). The microstructural observations may also be used to determine the completion strain of DRX,⁶⁵⁾ but in the current work, due to difficulties in microstructural studies, the steady state strain was used as the completion strain of DRX. Since the flow softening related to the progress of DRX continues until reaching the steady state strain, this assumption is practically reasonable. As can be seen in Fig. 13, the critical and steady state strains increase with Z, while the DRX grain size decreases with increasing Z. The developed map can be used as a rough estimate to show the effects of deformation conditions on the occurrence of DRX and on the resultant grain size. However, it should be noted that this map is valid for the 17-4 PH stainless steel with initial grain size of 105 µm. For a different initial grain size, the critical and steady state strains (solid lines) will be different and hence another map should be developed. In other words, the effect of initial grain size on the extent of DRX in a given temperature and strain rate should be taken into account in hot deformation studies.

Fig. 13.

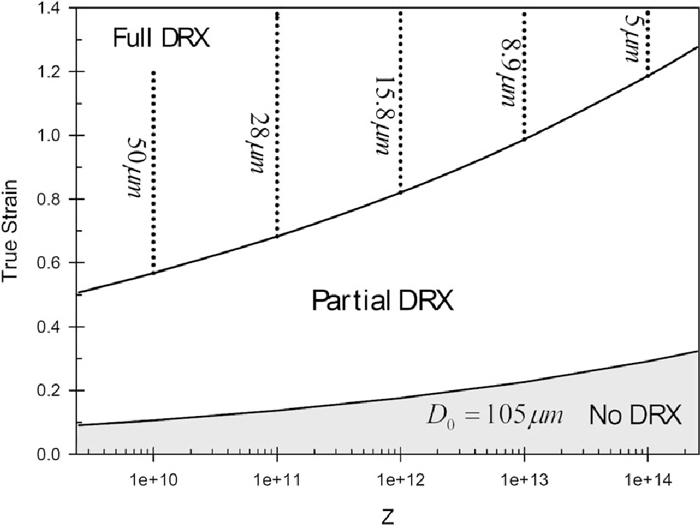
DRX map of the hot compressed 17-4 PH stainless steel with initial grain size of 105 µm.

4. Conclusions

(1) The majority of flow curves of 17-4 PH stainless steel under hot compression test exhibited typical dynamic recrystalization (DRX) behavior with a single peak stress followed by a gradual fall towards a steady state stress. A transition state between single and multiple peak behaviors was seen in this work and it was called the multiple transient steady-state (MTSS) behavior. Although some samples exhibited typical DRV or DRX behavior, the inflection analysis in the work hardening rate vs. stress plots and microstructural investigations proved the occurrence of DRX or DRV, respectively.

(2) After a critical discussion, the following constitutive equation was found, which can be used to express hot working characteristics of the 17-4 PH stainless steel during hot compression:   

$$Z=\dot{\epsilon }exp\left(\frac{337\times {10}^3}{RT}\right)=2.64\times {10}^{11}\times {\left[sinh\left(\text{0}\text{.011}\times {\sigma }_P\right)\right]}^{\text{3}\text{.73}}$$

(3) The Z exponents for peak stress and peak strain were determined as 0.18 and 0.11, respectively.

(4) The normalized critical stress and strain for initiation of DRX were found to be σ_C / σ_P = 0.89 and , ε_C / ε_P = 0.47, respectively.

(5) Significant grain refinement occurred as a result of necklace DRX mechanism. The average dynamically recrystallized grain size decreased with increasing strain rate and decreasing deformation temperature. It was related to Zener-Hollomon parameter and peak stress by power equations with exponents of –0.25 and –1.24, respectively.

(6) A DRX map, as a bridge between flow curve analyses and microstructural investigations, was developed to show the effects of deformation conditions on the occurrence of DRX and on the resultant grain size.

References

• 1)   E. O.  Hall: Proc. Phys. Soc. B, 64 (1951), 747.
• 2)   N. J.  Petch: J. Iron Steel Inst., 174 (1953), 25.
• 3)   R. E.  Reed-Hill and  R.  Abbaschian: Physical Metallurgy Principles, 3rd ed., PWS Publishing, Boston, MA, USA, (1994).
• 4)   I.  Tamura,  H.  Sekine,  T.  Tanaka and  C.  Ouchi: Thermomechanical Processing of High Strength Low Alloy Steels, Butterworths, London, UK, (1988).
• 5)   I.  Salvatori,  T.  Inoue and  K.  Nagai: ISIJ Int., 42 (2002), 744.
• 6)   F. H.  Samuel,  S.  Yue,  J. J.  Jonas and  K. R.  Barnes: ISIJ Int., 30 (1990), 216.
• 7)   H.  Mirzadeh and  A.  Najafizadeh: Mater. Chem. Phys., 116 (2009), 119.
• 8)   H.  Mirzadeh,  A.  Najafizadeh and  M.  Moazeny: Metall. Mater. Trans. A, 40 (2009), 2950.
• 9)   K. H.  Lo,  C. H.  Shek and  J. K. L.  Lai: Mater. Sci. Eng. R, 65 (2009), 39.
• 10)   Z.  Guo,  W.  Sha,  E. A.  Wilson and  R. W.  Grey: ISIJ Int., 43 (2003), 1622.
• 11)  Carpenter Technology, http:// www.cartech.com/techarticles.aspx?id= 1450, (2008).
• 12)  Metals Handbook, Vol. 9, Metallography and Microstructures, ASM, Metals Park, OH, USA, (1985).
• 13)   C.  García de Andrés,  M. J.  Bartolomé,  C.  Capdevila,  D.  San Martín,  F. G.  Caballero and  V.  López: Mater. Charact., 46 (2001), 389.
• 14)   D.  San Martin,  P. E. J.  Rivera Diaz del Castillo,  E.  Peekstok and  S.  van der Zwaag: Mater. Charact., 58 (2007), 455.
• 15)   A. W.  Brewer,  K.  Erven and  G.  Krauss: Mater. Charact., 27 (1991), 53.
• 16)   G.  Petzow: Metallographic Etching: Techniques for Metallotraphy, Ceramography, Plastography, 2nd ed., ASM International, OH, USA, (1999).
• 17)   G. F.  Vander Voort: Metallography: Principles and Practice, ASM International, Materials Park, OH, USA, (1999).
• 18)   R.  Ebrahimi and  A.  Najafizadeh: J. Mater. Process. Technol., 152 (2004), 136.
• 19)   H. J.  McQueen: Met. Forum, 4 (1981), 81.
• 20)   N. D.  Ryan and  H. J.  McQueen: Can. Metall. Q., 29 (1990), 147.
• 21)   E. I.  Poliak and  J. J.  Jonas: Acta Mater., 44 (1996), 127.
• 22)   E. I.  Poliak and  J. J.  Jonas: ISIJ Int., 43 (2003), 684.
• 23)   H.  Mirzadeh,  J. M.  Cabrera,  A.  Najafizadeh and  P. R.  Calvillo: Mater. Sci. Eng. A, 538 (2012), 236.
• 24)   T.  Sakai and  J. J.  Jonas: Acta Metall., 32 (1984), 189.
• 25)   H.  Mirzadeh and  A.  Najafizadeh: Mater. Design, 31 (2010), 1174.
• 26)   D.  Ponge and  G.  Gottstein: Acta Mater., 46 (1998), 69.
• 27)   C. M.  Sellars: Met. Forum, 4 (1981), 75.
• 28)   G.  Gottstein,  D.  Zabardjadi and  H.  Mecking: Met. Sci., 13 (1979), 223.
• 29)   R.  Sandström and  R.  Lagneborg: Acta Metall., 23 (1975), 481.
• 30)   W.  Roberts and  B.  Ahlblom: Acta Metall., 26 (1978), 801.
• 31)   G. J.  Richardson,  C. M.  Sellars and  W. J.  McG Tegart: Acta Metall., 14 (1966), 1225.
• 32)   C.  Ouchi and  T.  Okita: Trans. Iron Steel Inst. Jpn., 22 (1982), 543.
• 33)   F. J.  Humphreys and  M.  Hatherly: Recrystallization and Related Annealing Phenomena, 2nd ed., Elsevier, Oxford, UK, (2004).
• 34)   H. J.  McQueen and  S.  Bergerson: Met. Sci., 6 (1972), 25.
• 35)   M.  Ueki,  S.  Horie and  T.  Nakamura: Mater. Sci. Technol., 3 (1987), 329.
• 36)   G.  Gottstein,  L.  Chang and  H. F.  Yung: Mater. Sci. Technol., 7 (1991), 158.
• 37)   J. P.  Sah,  G. J.  Richardson and  C. M.  Sellars: Met. Sci., 8 (1974), 325.
• 38)   C.  Rossard and  P.  Blain: Mem. Sci. Rev. Metall., 156 (959), 285.
• 39)   M. J.  Luton and  C. M.  Sellars: Acta Metall., 17 (1969), 1033.
• 40)   S.  Sakui,  T.  Sakai and  K.  Takeishi: Trans. Iron Steel Inst. Jpn., 17 (1977), 718.
• 41)   T.  Sakai,  M. G.  Akben and  J. J.  Jonas: Acta Metall., 31 (1983), 631.
• 42)   C.  Roucoules: PhD Thesis, McGill University, Canada, (1992).
• 43)   H. J.  McQueen,  S.  Yue,  N. D.  Ryan and  E.  Fry: J. Mater. Process. Technol., 53 (1995), 293.
• 44)   P.  Karduck,  G.  Gottstein and  H.  Mecking: Acta Metall., 31 (1983), 1525.
• 45)   R. D.  Doherty,  D. A.  Hughes,  F. J.  Humphreys,  J. J.  Jonas,  D. Juul  Jensen,  M. E.  Kassner,  W. E.  King,  T. R.  McNelley,  H. J.  McQueen and  A. D.  Rollett: Mater. Sci. Eng. A, 238 (1997), 219.
• 46)   C. M.  Sellars and  W. J.  McG Tegart: Mem. Sci. Rev. Metall., 63 (1966), 731.
• 47)   C. M.  Sellars and  W. J.  McG Tegart: Acta Metall., 14 (1966), 1136.
• 48)   F.  Garofalo: Trans. Metall. Soc. AIME, 227 (1963), 351.
• 49)   C.  Zener and  J. H.  Hollomon: J Appl. Phys., 15 (1944), 22.
• 50)   J. L.  Uvira and  J. J.  Jonas: Trans. Metall. Soc. AIME, 242 (1968), 1619.
• 51)   N. D.  Ryan and  H. J.  McQueen: J. Mater. Process. Technol., 21 (1990), 177.
• 52)   H. J.  Frost and  M. F.  Ashby: Deformation-Mechanism Maps: The Plasticity and Creep of Metals and Ceramics, Pergamon Press, Oxford, UK, (1982).
• 53)   S. H.  Cho and  Y. C.  Yoo: J. Mater. Sci., 36 (2001), 4267.
• 54)   S. H.  Cho,  K. B.  Kang and  J. J.  Jonas: ISIJ Int., 41 (2001), 63.
• 55)   N. D.  Ryan and  H. J.  McQueen: Can. Metall. Q., 29 (1990), 147.
• 56)   A.  Laasraoui and  J. J.  Jonas: Metall. Trans. A, 22 (1991), 1545.
• 57)   A.  Najafizadeh and  J. J.  Jonas: ISIJ Int., 46 (2006), 1679.
• 58)   T. M.  Maccagno and  J. J.  Jonas: ISIJ Int., 34 (1994), 607.
• 59)   W. P.  Sun and  E. B.  Hawbolt: ISIJ. Int., 37 (1997), 1000.
• 60)   L. P.  Karjalainen,  T. M.  Maccagno and  J. J.  Jonas: ISIJ Int., 35 (1995), 1523.
• 61)   S. I.  Kim,  Y.  Lee,  D. L.  Lee and  Y. C.  Yoo: Mater. Sci. Eng. A, 355 (2003), 384.
• 62)   B.  Derby: Acta Metall., 39 (1991), 959.
• 63)   J. L.  Nazabal,  J. J.  Urcola and  M.  Fuentes: Mater. Sci. Eng. A, 86 (1987), 93.
• 64)   A. I.  Fernandez,  P.  Uranga,  B.  Lopez and  J. M.  Rodriguez-Ibabe: Mater. Sci. Eng. A, 361 (2003), 367.
• 65)   A.  Dehghan-Manshadi,  M. R.  Barnett and  P. D.  Hodgson: Metall. Mater. Trans. A, 39 (2008), 1359.
• 66)   T.  Sakai: J. Mater. Process. Technol., 53 (1995), 349.
• 67)   A.  Belyakov,  H.  Miura and  T.  Sakai: Mater. Sci. Eng., A, 255 (1998), 139.