2019 Volume 83 Issue 5 Pages 166-175
2019 Volume 83 Issue 5 Pages 166-175
Recrystallization, grain growth, and particle ripening behaviors of pre-deformed Fe-In alloy specimens in liquid-particle dispersion microstructures were investigated by microstructural observation. Liquid In particles were trapped by grain boundaries of recrystallized grains, and the trapped particles were dragged by the grain boundaries during grain growth. The recrystallization and the grain growth of the αFe matrix were extremely retarded by the addition of In. The controlling diffusion mechanism of the growth of matrix grains and the ripening of intergranular liquid In particles changed from interfacial diffusion between matrix and particles to impurity diffusion through liquid In particles with increasing volume fraction of liquid In particles.
Mater. Trans. 59(2018) 188-197に掲載
微量の液相Bi粒子が分散したAl-Bi二相合金が543 K以上で200%を越える超塑性を示すことが小池らにより報告された1).通常,濡れ性の高い液相が多結晶組織の結晶粒界上にフィルム状に存在する場合,液相による粒界脆化が生じるが,Al中のBiのように濡れ性の低い液相が粒状に分散したAl-Bi合金では超塑性変形中に結晶粒界への応力集中を低減する効果をもたらす.著者らはAl-Bi2)とFe-Bi3)合金における結晶粒成長の実験を行い,液相Biの分散粒子により母相結晶粒の成長が著しく抑制されることを明らかにした.Fig. 1に予加工後573 Kで熱処理したAl-Bi合金の典型的な組織を示す2).複数の粒界の曲率の外側に無析出物帯(precipitate-free zones: PFZs)が形成し,PFZを形成した粒界上に粗大な液相粒子が形成している.これらの組織変化は,粒内に分散していた液相Bi粒子が移動する粒界にトラップされ,さらに引き摺られた結果,オストワルド成長に加えてトラップ・ドラッグされた液相粒子の合体により液相Bi粒子の粗大化が生じることを示唆している.このようなPFZの形成を引き起こす粒界移動の駆動力が母相と液相粒子との界面エネルギーであり,液相粒子の引き摺り速度が液相粒子中の溶質原子の不純物拡散に依存することが理論的な解析により示されている2).さらに,粒内および粒界上の液相粒子の成長速度が従来のオストワルド成長理論により予測されることが報告されている3).Fig. 2に(a)全組成領域と(b)Feリッチ領域のFe-In二元系の状態図4)を示した.これらの状態図は,液相In粒子が偏晶反応により形成し分散することを示唆している.本研究ではFe-In合金の液相粒子分散組織におけるαFe相の再結晶と粒成長,および液相粒子の成長挙動を調査した.

Typical microstructure of pre-deformed Al-Bi alloy annealed at 573 K.

Fe-In binary phase diagrams4) of (a) whole system and (b) Fe-rich side.
体積分率が1,3および7.5 vol%となるように組成を調整したFe-In合金をアルゴン雰囲気中で高周波誘導炉により溶解し,直径が12 mmの円柱状鋳片を作製して,冷間圧延により厚さ6 mmの板状試料を得た.板状試料から試験片を切り出し,透明石英管に封入後,Inの融点(429 K)以上の1173 Kで再結晶と粒成長のための熱処理を施したのち,氷水中で急冷した.光学顕微鏡とSEMを用いて試料断面の組織を観察した.光顕観察のための腐食には,1 Nの硝酸水溶液とエタノールを1:1の体積比で混合したナイタール溶液を用いた.αFe母相結晶粒の平均半径を定量組織解析5)により導出し,1173 Kの熱処理温度で液相状態であったIn粒子の体積分率と平均半径を画像解析(Win Roof)により推算した.組織観察とマイクロビッカース硬さ測定により,再結晶の進行を評価した.αFe母相とIn粒子の化学組成をEPMAにより測定し,ZAF補正により濃度を決定した.5点以上の測定結果の平均値を両相の濃度として採用した.
Fig. 3に冷間圧延後,1173 Kで熱処理したFe-7.5 vol%In試料の硬さと熱処理時間の関係を,純Fe試料の測定結果と比較して示した.純Fe試料では冷間圧延後の硬さ185 HVが1173 Kで60 s熱処理した試料では76 HVまで急激に低下し,60 s以降ほぼ一定値に定常化した.この結果は純Fe試料では1173 Kで60 sの熱処理により再結晶がほぼ完了していることを示唆している.一方,Fe-7.5 vol%In冷間圧延試料では,圧延後の硬さ156 HVが1173 Kでの熱処理時間の増加に伴い徐々に低下し,600 sの熱処理後に105 HVまで低下し,900 sにおいて100 HVとほぼ一定値に定常化した.Fig. 4にFe-7.5 vol%In試料の(a)冷間圧延後,(b)1173 K・60 sの熱処理後,および(c),(d)1173 K・900 sの熱処理後の試料断面の光顕組織写真を示した.冷間圧延後の圧延方向に伸長した初期組織(Fig. 4(a))が,1173 K・900 sの熱処理による再結晶を経て,等軸なαFe+Inの二相組織(Fig. 4(c))に変化している.Fig. 4(d)に示した再結晶組織において,明るく見える相がIn粒子であり,黒く見える部分は試料表面の研磨中にIn粒子が一部剥離して形成したボイドである.大部分のIn粒子はαFe結晶粒界の三重点上に存在している.Fig. 3とFig. 4に示した結果はIn添加によりαFeの再結晶が抑制されることを示唆している.
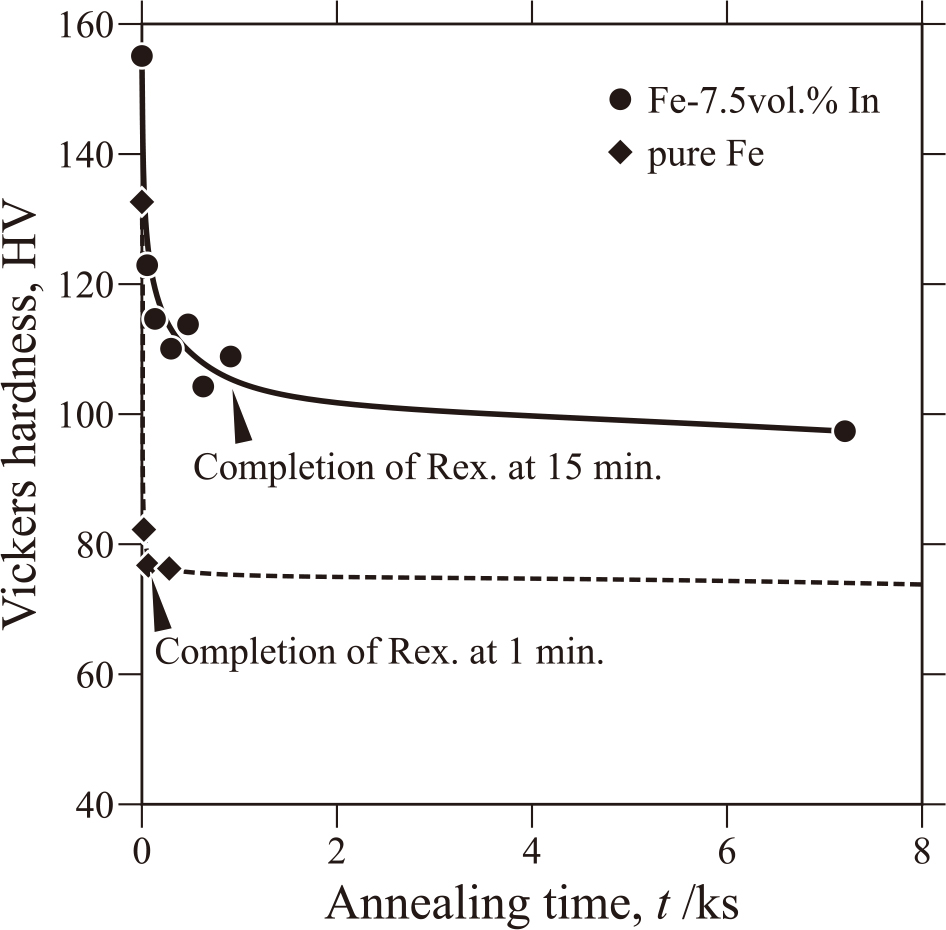
Vickers hardness of pre-deformed Fe-7.5 vol%In alloy annealed at 1173 K.

Optical micrograph of (a) as-rolled Fe-7.5 vol%In specimen, Fe-7.5 vol%In specimens (b) annealed at 1173 K for 60 s, (c) annealed at 1173 K for 900 s, and (d) enlarged micrograph of (c).
Fig. 5に冷間圧延したFe-7.5 vol%In試料を1173 Kで(a)1 dおよび(b)2 d熱処理した試料の断面組織を示した.大部分のIn粒子はαFeの結晶粒界上,特に粒界の三重点上に存在しており,αFeの結晶粒内には少量しか存在しない.この結果は1173 Kにおける熱処理の初期段階に液相のIn粒子がαFeの再結晶粒の界面にトラップされ,再結晶完了後,粒界がIn粒子を引き摺りながら移動して粒成長が進行することを示唆している.Fig. 6に(a)熱処理時間tと液相In粒子の平均半径$\overline{r}$の関係と(b)tとαFe結晶粒の平均半径$\overline{R}$の関係を純鉄の実験結果と比較して示した.tが大きくなるほど$\overline{r}$が大きくなり,特にFe-7.5 vol%In試料において,液相In粒子の成長速度が大きいことが分かった.$\bar R$もtの増加とともに大きくなるが,いずれの試料においても,純鉄の結晶粒径と比較すると成長が停滞しており,液相In粒子が母相結晶粒成長の抑制に大きな影響を及ぼすことが分かった.

Typical optical micrograph of pre-deformed Fe-7.5 vol%In alloy annealed at 1173 K for 1 day and 2 days.

Mean radius evolutions of (a) intergranular liquid In particles and (b) matrix grains in Fe-In alloys annealed at 1173 K.
Fe-In合金のαFeの静的再結晶を抑制する因子として,(i)液相In粒子による再結晶粒界面のピン止め効果,(ii)Inによる再結晶粒界面へのソリュート・ドラッグ効果,(iii)再結晶粒界面が液相In粒子を引き摺る効果が考えられる.ここでは,再結晶中の再結晶粒と未再結晶粒の界面移動速度から再結晶抑制効果を検討する.
物質移動の速度論の観点から,結晶粒の平均半径が$\bar R$の多結晶組織における界面の移動速度vは界面の易動度Mと駆動力Pの積として次式により表される.
| \[v=\frac{{\rm d}\bar R}{dt}=M\cdot P\] | (1) |
多結晶組織の母相中に体積分率f,平均半径$\bar r$の異相粒子がランダムに分散している場合,単位面積の界面に及ぼす粒子によるピン止め力の最大値$\varDelta G_{\rm p}$は次式により表される6).
| \[\varDelta G_{\rm p}=\frac{3\cdot f\cdot {\sigma_{\rm m}}}{2\cdot\bar r}\] | (2) |
| \[P=(\varDelta G_{\rm rex}-\varDelta G_{\rm p})\cdot V_{\rm m}\] | (3) |
| \[M_{\rm gb}=\frac{D_{\rm gb}}{\delta RT}\] | (4) |
式(3)と式(4)を式(1)に代入すると,分散粒子にピン止めされた粒界の移動速度は次式のように求められる.
| \[v_{{\rm pin}}^{{\rm cal}}=M_{\rm gb}\cdot(\varDelta G_{\rm rex}-\varDelta G_{\rm p})\cdot V_{\rm m}\] | (5) |
粒界の易動度は溶質原子のソリュート・ドラッグ効果により低減し,溶質原子の固溶度をx,偏析係数を$K_{\rm seg}^{\rm gb}$とすると,その易動度は次式により表される9).
| \[M_{{\rm sol}.{\rm drag}}=\frac{D_{\rm gb}}{\delta RT}\cdot\frac{1}{1+(K_{\rm seg}^{\rm gb})^2 \cdot x}\] | (6) |
| \[v_{{\rm sol}.{\rm drag}}^{\rm cal}=M_{{\rm sol}.{\rm drag}}\cdot \varDelta G_{\rm rex}\cdot V_{\rm m}\] | (7) |
GeguzinとKrivoglazは界面上の半径rの粒子が界面の移動により引き摺られるときの界面の易動度を拡散過程の相違により以下に示す三種類の律速過程に分類している10).
Case 1.球状粒子の周囲の母相中の体拡散により律速される場合,体拡散係数をDvとすると,界面の易動度は次式で表される.
| \[M_{{\rm particle}-{\rm drag}}^{\rm volume}=\frac{D_{\rm v}}{RT}\cdot\frac{V_{\rm m}}{r^3}\] | (8) |
Case 2.母相/球状粒子の界面拡散により律速される場合,界面拡散係数をDs,界面の幅をwとすると,界面の易動度は次式で表される.
| \[M_{{\rm particle}-{\rm drag}}^{\rm interface}=\frac{w\cdot D_{\rm s}}{10RT}\cdot\frac{V_{\rm m}}{r^4}\] | (9) |
Case 3.粒子中の溶質原子の不純物拡散により律速される場合,不純物拡散係数をDL,粒子中の溶質原子の固溶度をnp,粒子のモル体積をVpとすると,界面の易動度は次式で表される.
| \[M_{{\rm particle}-{\rm drag}}^{\rm impurity}=\frac{D_{\rm L}}{10RT}\cdot\frac{n_{\rm p}\cdot{V_{\rm m}}^2}{V_{\rm p}\cdot{r^3}}\] | (10) |
| \[v_{{\rm particle}-{\rm drag}}^{case-{\rm cal}}=\frac{M_{{\rm particle}-{\rm drag}}^{case \vphantom{f}}}{N_{\rm s}}\cdot\varDelta G_{\rm rex}\cdot V_{\rm m}\] | (11) |
Table 1にFe-In合金のαFeの再結晶における界面移動速度の計算値を実測値と比較して示した.ただし,再結晶の駆動力を$\varDelta G_{\rm rex}$ = 1 MPaあるいは10 MPaと想定し,計算に用いたその他の物性値を文末のAppendix A-1にまとめて示した.1173 Kで再結晶が完了する900 s熱処理した試料のαFe結晶粒の平均半径が,$\bar R$ ≒ 5.5 μmとなったことから,界面の移動速度の実測値はおおよそ次式のように見積もることができる.
| \[v_{{\rm rex.}}^{\rm exp}=\frac{5.5\times{10}^{-6}}{900}=6.1\times{10^{-9}}\ {\rm m}\cdot{\rm s}^{-1}\] | (12) |
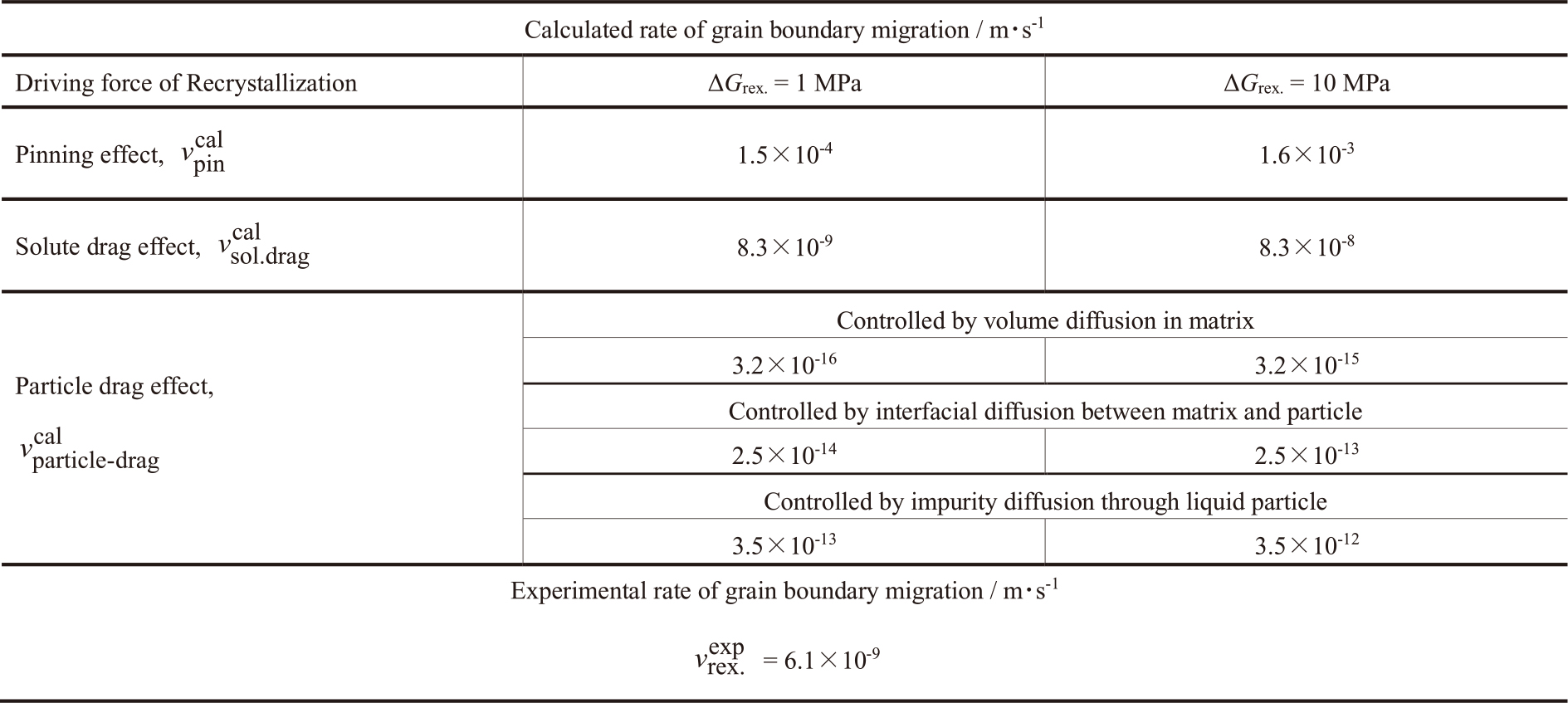
Comparison between experimental and calculated migration rates of interface boundary during recrystallization.
粒子分散組織における母相結晶粒の平均半径$\bar R$と分散粒子の平均半径$\bar r$の間には,定常状態において,分散粒子の体積分率fと定数β,mを介して次の関係式が成り立つ6,11,12).
| \[\bar R={\rm \beta}\cdot\frac{\bar r}{f^{\rm m}}\] | (13) |
| \[\bar R=2\cdot\frac{\bar r}{f^{1/2}}\] | (14) |
| \[\bar R=1.95\cdot\frac{{\bar r}}{{f_{{\rm gb}}}^{1/2}}\] | (15) |

Relationship between $\bar R$ and $\bar r/f^{1/2}$ in Fe-In alloys.
粒子分散組織における分散粒子の成長は,熱処理時間tにおける平均半径を$\bar r$,t = 0における初期平均半径を${\bar r_0}$とすると,次式により表される.
| \[{\bar r^3}-{\bar {r}_0}{}^3={k_3}\cdot t\] | (16) |
| \[k_3^{{\rm vol.}}=\frac{8D_x \cdot\sigma_{\rm mp}\cdot x\cdot V_{\rm p}}{9RT}\] | (17) |
| \[\bar r^4-{\bar{r}_0}{}^4=k_4^{\rm gb}\cdot t\] | (18) |
| \[k_4^{{\rm gb}}=\frac{9\delta\cdot D_{\rm gb}^{\rm impurity}\cdot\sigma_{\rm mp}\cdot N_x({\rm gb})\cdot V_{\rm p}}{32A\cdot B\cdot RT}\] | (19) |
| \[A=\frac{2}{3}+\frac{\sigma _{\rm m}}{2\sigma_{\rm mp}}+\frac{1}{3}{\left(\frac{\sigma_{\rm m}}{2\sigma_{\rm mp}}\right)^3}\] | (20) |
| \[B=\frac{1}{2}\ln\left({\frac{1}{f_{\rm b}}}\right)\] | (21) |
| \[k_4^{\rm gb}=\frac{9K_{\rm seg}^{\rm gb}\cdot\delta\cdot D_{\rm gb}^{\rm impurity}\cdot\sigma_{\rm mp}\cdot x \cdot V_{\rm p}}{32A\cdot B\cdot RT}\] | (22) |
| \[k_4^{\rm Yang}=\frac{4}{3}\cdot\frac{D_s \cdot\delta\cdot \sigma_{\rm \alpha\beta}\cdot V_{\rm m}}{RT}\] | (23) |

(a) cube and (b) fourth power of mean radius of intergranular liquid In particles versus annealing time of Fe-In alloys annealed at 1173 K.

(a) cube and (b) fourth power of mean grain radius versus annealing time of Fe-In alloys annealed at 1173 K.

Comparison between experimental and calculated rate constants of intergranular liquid In particles (eq.(17), (22), (29) and (26)) and those of matrix grains (eq.(28) and (25)) in Fe-In alloys.
液相In粒子のαFe母相の粒界移動に伴う引き摺りが母相/液相粒子の界面拡散に律速される場合,成長速度式は次式により表される.
| \[{\bar R}^4-{\bar R_0}{}^4=K_4^{\rm matrix}\cdot t\] | (24) |
| \[K_4^{\rm matrix}=\frac{4\pi\cdot D_s\cdot w\cdot\sigma_{\rm m}\cdot V_{\rm m}\cdot C}{5RT\cdot f}\] | (25) |
| \[{\bar r}^4-{\bar r_0} {}^4=k_4^{\rm particle-modify}\cdot t\] | (18') |
| \[k_4^{{\rm particle}-{\rm modify}}=\frac{K_4^{\rm matrix}}{C^4}=\frac{4\pi\cdot D_s\cdot w\cdot\sigma_{\rm m}\cdot V_{\rm m}}{5RT\cdot f\cdot C^3}\] | (26) |
一方,液相In粒子の引き摺りが液相中の溶質原子の拡散により律速される場合,成長速度式は次式により表される.
| \[{\bar R^3}-{\bar R_0}{}^3=K_3^{\rm matrix}\cdot t\] | (27) |
| \[K_3^{\rm matrix}=\frac{6\pi\cdot D_L\cdot n_{\rm p}\cdot\sigma _{\rm m}\cdot{V_{\rm m}}^2}{5RT\cdot V_{\rm p}\cdot f}\] | (28) |
| \[{\bar r}^3-{\bar r_0}{}^3=k_3^{{\rm particle}-{\rm modify}}\cdot t\] | (16') |
| \[k_3^{{\rm particle}-{\rm modify}} =\frac{K_3^{\rm matrix}}{C^3}=\frac{6\pi\cdot D_L\cdot n_{\rm p}\cdot \sigma_{\rm m}\cdot {V_{\rm m}}^2}{5RT\cdot V_{\rm p}\cdot f \cdot C^3}\] | (29) |
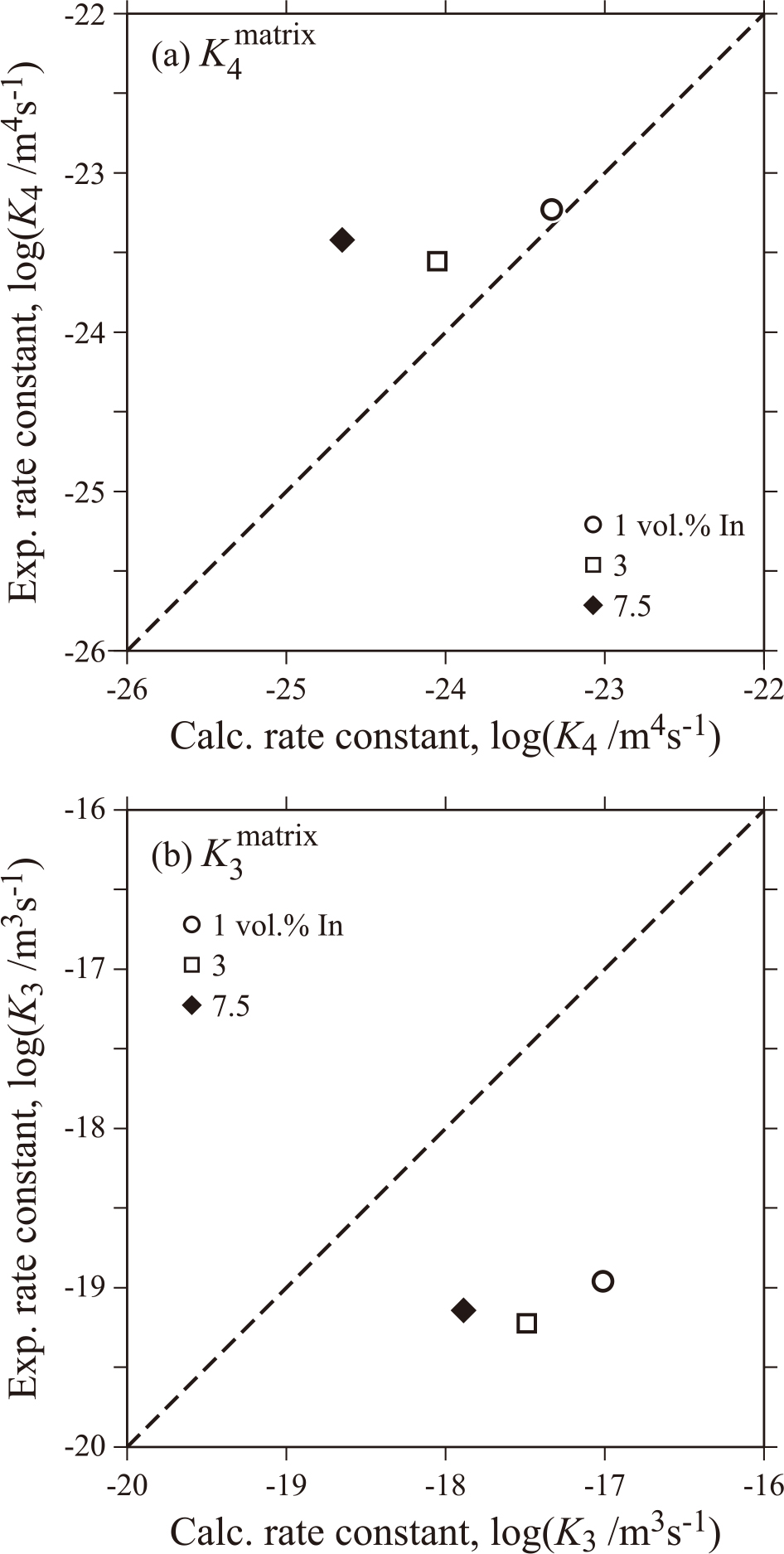
Comparison between experimental and calculated rate constants of matrix grains in Fe-In alloys.

Comparison between experimental and calculated rate constants of intergranular liquid In particles in Fe-In alloys.

Mobility of a spherical particle calculated by eqs.(9) and (10).
Fe-In合金のαFe母相の再結晶と結晶粒成長に及ぼす液相In分散粒子の影響を調査した結果,以下に示す結果が得られた.
(1) 約50%冷間圧延したFe-7.5 vol%In合金を1173 Kで熱処理した結果,900 sまでにαFe母相の再結晶が完了する.再結晶が完了した組織では,大部分の液相In粒子が母相の結晶粒界上に存在する.
(2) αFeの再結晶における界面移動を抑制する液相粒子によるピン止め効果,ソリュート・ドラッグ効果および界面による液相粒子引き摺り効果のうち,ソリュート・ドラッグ効果を律速過程と仮定した界面移動速度の計算値が実験値にほぼ一致した.この結果はFe-In合金のαFeの再結晶がInによるソリュート・ドラッグ効果により抑制されることを示唆している.
(3) 再結晶完了後,αFeの結晶粒界にトラップされた液相In粒子は,1173 Kの熱処理中に結晶粒界に引き摺られながら移動する.その結果,液相In粒子によりFe-In合金のαFeの結晶粒成長は著しく抑制される.
(4) Fe-In合金において,αFe結晶粒の平均半径($\bar R$)と液相In分散粒子の平均半径($\bar r$)の間には,全ての分散粒子が粒界上に存在している場合に理論的に導出される関係式$\bar R={2\bar r/}{f_{\rm gb}}^{1/2}$が成立する.
(5) αFeの結晶粒界に引き摺られながら成長する液相In粒子の成長速度定数は,αFe中のInの体拡散,αFe/液相In粒子の界面拡散,液相In粒子中のFeの体拡散を考慮した粗大化モデルの成長速度定数よりも2-3桁大きくなる結果が得られた.物質移動の式に基づき修正したYangのモデルにより算出した液相In粒子の成長速度定数が実験値にほぼ一致した.
(6) αFeの結晶粒成長は,$\bar R=2\bar r/{f_{\rm gb}}^{1/2}$式に従い,液相In分散粒子の粗大化過程に律速される.液相In粒子の体積分率と平均粒径が大きくなると,粒子の粗大化を律速する拡散過程がαFe/液相In粒子の界面拡散から液相In粒子中のFeの不純物拡散に遷移する.
αFeのFeの粒界拡散係数$\delta D_{\rm gb}$として,$\delta D_{{\rm gb},{\rm Fe\ in\ \alpha Fe}}=1.3\times 10^{-19}\ {\rm m}^3\cdot{\rm s}^{-1}$の文献値18)を,αFeのFeの体拡散係数$D_{\rm v}$として,$D_{\rm Fe\ in\ \alpha Fe}=4.1\times 10^{-15}\ {\rm m}^2\cdot{\rm s}^{-1}$の文献値19)を用いた.粒界の厚さδを三原子幅のδ = 0.75 nmと近似すると,$D_{\rm gb}=1.7\times 10^{-10}\ {\rm m}^2\cdot{\rm s}^{-1}$と算出される.αFe/液相In粒子のFeの界面拡散係数$D_{\rm s}$と液相In粒子中のFeの不純物拡散係数$D_{\rm L}$の報告値は存在しないため,$D_{\rm s}$と$D_{\rm L}$として液相Pb中のFeの不純物拡散係数$D_{{\rm Fe\ in\ Pb}\left({\rm L}\right)}^*\ =\ 5.4\times 10^{-9}\ {\rm m}^2\cdot{\rm s}^{-1}$ 20)を代替値とした.αFeのモル体積$V_{\rm m}$とIn液相のモル体積$V_{\rm p}$として文献値21)$V_{\rm m}=7.1\times 10^{-6}\ {\rm m}^3\cdot{\rm mol}^{-1}$と$V_{\rm p}=1.3\times 10^{-5}\ {\rm m}^3\cdot{\rm mol}^{-1}$を用いた.αFeの結晶粒界へのInの偏析係数$K_{\rm seg}^{\rm gb}$は,αFeへの各種元素の固溶度と偏析係数の関係9)に基づき,Inの固溶度xから${K_{\rm seg}^{\rm gb}}\ =\ 2\times 10^3$と見積もった.1173 KにおけるαFe中のInの固溶度xとIn液相中へのFeの溶解度$n_{\rm p}$には,本研究でEPMAにより測定した実測値の$x=5.0\times 10^{-3}$と$n_{\rm p}=1.5\times {10^{-2}}$を適用した.αFe/液相In粒子の界面幅wの値にはαFeの格子定数$a_{\rm \alpha Fe}$ = 0.3 nmを適用した.
Appendix A-2 液相In分散粒子の粗大化速度の数値計算データαFe/液相In粒子の界面エネルギー$\sigma _{\rm mp}$の値は,本研究における組織観察においてαFeの結晶粒界上で液相In粒子が形成する二面角θを測定し,Youngの式$\sigma_{{\rm \alpha Fe}/{\rm \alpha Fe}}=2\sigma_{{\rm \alpha Fe}/\ell{\rm In}}\cdot\cos\theta$から$\sigma_{\rm mp}$ = $\sigma_{{\rm \alpha Fe}/\ell{\rm In}}=0.55\ {\rm J}\cdot{\rm m}^{-2}$と見積もった.これより式(20)のAの値はA = 3.1と算出できる.式(21)のBの値はSEMによる組織観察の結果からfbの値を見積もった結果,B = 1.12(1 vol%In),0.85(3 vol%In)および0.62(7.5 vol%In)と算出した.αFe中およびその結晶粒界中のInの不純物拡散係数の報告例が無いため,Inの替わりにSnに関する拡散データを代用し,$D_{\rm x}=D_{\rm Sn\ in\ \alpha Fe}=3.2\times 10^{-14}\ {\rm m}^2\cdot{\rm s}^{-1}$ 22)と${K_{\rm seg}^{\rm gb}}\cdot\delta\cdot {D_{\rm gb}^{\rm impurity}}=3.9\times 10^{-19}\ {\rm m}^3\cdot{\rm s}^{-1}$ 23)を適用した.
易動度Mと駆動力Pにより構成される物質移動の式から,母相粒界にトラップされた液相粒子の移動速度(すなわち,母相粒界の移動速度)は次式により表される.
| \[\frac{{\rm d}\bar R}{{\rm d}t}=M\cdot\frac{P}{N_{\rm s}}\] | (B1) |
| \[M_{{\rm particle}-{\rm drag}}^{\rm interface}=\frac{w \cdot D_{\rm s}}{10RT}\cdot\frac{V_{\rm m}}{\bar r^4}\] | (B2) |
| \[P=\frac{2{\rm \sigma}_{\rm m}}{\bar R}\] | (B3) |
| \[N_{\rm s}=\frac{\bar R\cdot f}{2\pi\cdot \bar r^3}\] | (B4) |
| \[\frac{{\rm d}\bar R}{{\rm d}t}=\frac{\pi\cdot w \cdot D_{\rm s}\cdot V_{\rm m}\cdot{\rm \sigma}_{\rm m}}{5RT\cdot \bar R^2\cdot f \cdot \bar r}=\frac{\pi\cdot w \cdot D_{\rm s}\cdot V_{\rm m}\cdot{\rm \sigma}_{\rm m}\cdot C}{5RT\cdot \bar R^3\cdot f}\] | (B5) |
| \[{\bar R}^4-{\bar R_0}{}^4=\frac{4\pi\cdot w \cdot D_{\rm s}\cdot\sigma_{\rm m}\cdot V_{\rm m}\cdot C}{5RT\cdot f}\cdot t\] | (B6) |
| \[{\bar r}^4-{\bar r_0}{}^4=\frac{4\pi\cdot w \cdot D_{\rm s}\cdot \sigma_{\rm m}\cdot V_{\rm m}}{5RT\cdot f \cdot C^3}\cdot t\] | (B7) |
| \[M_{{\rm particle}-{\rm drag}}^{\rm impurity}=\frac{D_{\rm L}}{10RT}\cdot\frac{n_{\rm p}\cdot {V_{\rm m}}^2}{V_{\rm p}\cdot \bar r^3}\] | (B8) |
| \[{\bar R}^3-{\bar R_0}{}^3=\frac{6\pi\cdot D_{\rm L}\cdot n_{\rm p}\cdot \sigma_{\rm m}\cdot {V_{\rm m}}^2}{5RT\cdot V_{\rm p}\cdot f}\cdot t\] | (B9) |
| \[{\bar r}^3-{\bar r_0}{}^3=\frac{6\pi\cdot D_{\rm L}\cdot n_{\rm p}\cdot\sigma_{\rm m}\cdot {V_{\rm m}}^2}{5RT\cdot V_{\rm p}\cdot f\cdot C^3}\cdot t\] | (B10) |