Random Dirichlet series arising from records

抄録

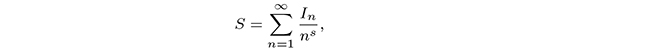We study the distributions of the random Dirichlet series with parameters (s, β) defined bywhere (I_n) is a sequence of independent Bernoulli random variables, I_n taking value 1 with probability 1/n^β and value 0 otherwise. Random series of this type are motivated by the record indicator sequences which have been studied in extreme value theory in statistics. We show that when s > 0 and 0 < β ≤ 1 with s + β > 1 the distribution of S has a density; otherwise it is purely atomic or not defined because of divergence. In particular, in the case when s > 0 and β = 1, we prove that for every 0 < s < 1 the density is bounded and continuous, whereas for every s > 1 it is unbounded. In the case when s > 0 and 0 < β < 1 with s + β > 1, the density is smooth. To show the absolute continuity, we obtain estimates of the Fourier transforms, employing van der Corput's method to deal with number-theoretic problems. We also give further regularity results of the densities, and present an example of a non-atomic singular distribution which is induced by the series restricted to the primes.