Change in size distribution of porewater and entrapped air with progression of water infiltration in sandstone

Abstract

Rocks have pores of various sizes. We investigated which pore sizes filled with water and in what order with the progression of water infiltration. The pore radii of the sandstone mainly ranges from a few µm to several tens of µm. Water was passed through the sandstone core at 25 °C, and water saturation, S, was adjusted to 63, 67, 71, 87, and 100%. At each S, the porewater radius distribution was measured using the water expulsion method, in which water in pores of a given pore radius was expelled by gas pressure. The results showed that the porewater radius distribution was approximately the same for S = 63-71%. As S increased from 71 to 100%, the pores with 4-10 and 10-20 µm radii were filled with water first, followed by pores with 20-52 µm radius. For S = 63-71%, water was considered to have entered via adsorption on the pore walls and capillary action at the corners of the pore. Because this water cannot be expelled by gas pressure, an increased amount of water was not detected by the water expulsion method. As for the results at S > 71%, a theoretical model of the dissolution of entrapped air, assuming a cylindrical shape, showed that the length of the trapped air decreases faster in pores with small radii than in those with large radii. This may be a major explanation for the experimental result, which showed that pores with small radii fill with water more quickly than those with large radii.

INTRODUCTION

Knowledge of the mechanism and rate of water infiltration into pores is fundamental to understand the various physical and chemical processes that occur in rocks and soils. Pores in geological media are generally of various sizes and shapes. When water infiltrates vacant pores, the pores are often not fully saturated with water, and that air becomes trapped (Guéguen and Palciauskas, 1994; Kumar et al., 2010; Yokoyama et al., 2020). This air is known to have a significant effect on the ease of water flow in rocks (Nishiyama et al., 2012). The thickness of the unsaturated zone at the Earth’s surface is estimated to range from a few meters to a few hundreds of meters (Zimmerman and Bodvarsson, 1989). The amount of entrapped air is generally small for soils (3-22% of pore spaces; Faybishenko, 1995 and references therein), probably because for poorly consolidated media pores are comparatively well-connected (Lowry and Miller, 1995) and the porosity is high (Al Mansoori et al., 2010). However, a larger amount of air is often trapped in rocks that have poorer pore connectivity and lower porosity than soils (10-60% of pore spaces; Kumar et al. 2010; Nishiyama et al., 2012). Compared with the total amount of air trapped in rocks, less is known about the amount of air trapped in each pore radius and how that amount changes when water continues to flow. In this study, we applied the water expulsion method (Nishiyama et al., 2012) to sandstone to examine the amount of water in each pore radius, and investigated the pore radius at which water increases and air decreases as water infiltration progresses. In addition, to account for the experimental results, we developed a model to assess the dependence of the rate at which trapped air dissolves in water on the pore radius.

SAMPLE

Fontainebleau sandstone from France was used for the experiments. Figure 1 shows a backscattered electron image of the rock sample obtained with a scanning electron microscope (TM3030, Hitachi). The mean diameter of mineral grains is approximately 248 µm. Energy-dispersive X-ray spectroscopy showed that the sample was composed almost exclusively of quartz. A sandstone core, 8.1 mm in height and 34.4 mm in diameter, was used. The lateral side of the core was filled with resin (Technovit4004) to allow water to flow in one direction. The porosity of the sample was 9.9% (connected pores), which was calculated from the rock volume (7.50 cm³) and the difference between the dry weight (33.916 g) and water-saturated weight (34.653 g) of the sample (density of water = 0.997 g cm⁻³). The water-saturated weight was measured after saturating the pores with water by vacuum impregnation, according to the procedure described by Yokoyama (2013).

Figure 1. Backscattered electron image of the surface of sandstone core.

METHOD

Adjustment of water saturation by water permeation

The sample was dried in an oven at 70 °C and cooled to room temperature. Then, to adjust the water saturation S (%), the sample was installed on a water permeation apparatus (Fig. 2a) for the permeation of ultrapure water (18.2 MΩ). Water pressure was maintained at a constant water head difference of 17.8 cm. The entire portion in Figure 2a was placed in an incubator at a constant temperature of 25 °C. As soon as the water began to flow, S reached 63% and continued to increase with time. To determine S, the sample was occasionally removed from the apparatus, excess water on the sample surface was wiped off with a pre-moistened tissue, and the sample was weighed. S is calculated by S = (wet weight − dry weight)/(water-saturated weight − dry weight) × 100. S was adjusted to 63, 67, 71, and 87%, and the porewater radius distribution measurement was started immediately (error in S was estimated to be within a few percent). At S = 100%, the sample was saturated with water by vacuum impregnation and not by water permeation.

Figure 2. (a) Water permeation apparatus for adjusting water saturation. (b) Outline of water expulsion method. γ is the interfacial tension and θ is the contact angle. (c) Conceptual diagram of trapped air when the radius (r) of the tube is assumed to be single at each diameter and (d) when the diameter of the tube changes in the middle.

Measurements of porewater radius distribution by water expulsion method

We used the water expulsion method (Nishiyama et al., 2012) to measure porewater radius distribution (Fig. 2b) after adjusting S by the above procedure. In this method, gas pressure is applied to the bottom of the sample and the water volume in each pore radius expelled from the top is quantified by increasing the gas pressure in a stepwise manner. The pore radius r (m) is determined by r = 2γcosθ/ΔP, where ΔP is the pressure difference (Pa) at top and bottom of the sample, γ is the interfacial tension (N/m), and θ is the contact angle (assumed to be 0°) (Nishiyama et al., 2012). The value of γ was calculated for the temperature at the time of measurement (20.0-26.0 °C) using the equation provided by Vargaftik et al. (1983). We selected four suitable ΔP [2.8 × 10³ Pa (52 µm), 7.3 × 10³ Pa (20 µm), 1.4 × 10⁴ Pa (10 µm), and 3.6 × 10⁴ Pa (4 µm), value in parenthesis was r for the ΔP] to evaluate the change in the porewater radius distribution when S is changed. The uncertainty in radius due to variation of ΔP was less than ±4% for each radius. For S = 100%, the same measurements were performed four times to check reproducibility. In the water expulsion method results, the measured radius and the radius of air coincide if the radii of each tube are assumed to be constant, as shown in Figure 2c. However, when the radii of the tubes change, as shown in Figure 2d, the radius of air is estimated to be smaller (Fig. 2d; left) or larger (Fig. 2d; right) than the actual. Because the extent of the situation shown in Figure 2d is difficult to estimate using the water expulsion method, a constant radius is assumed in the following discussion. A similar difference between the actual and measured radii occurs when using the mercury intrusion method, which is a popular method for measuring pore radius distribution.

RESULTS

Figure 3a shows the porewater radius distribution measured at each S, where the vertical axis is the water volume fraction ϕ_wat for each pore radius (= water volume in pore of each radius / whole rock volume × 100). The data points at 4, 10, 20, and 52 µm are the sum of the amount of water in pores with radii of 4-10, 10-20, 20-52, and >52 µm, respectively, and their ranges are shown in Figure 3a. Figure 3b shows how ϕ_wat changes with S. The sample has the highest pore volume around 10 µm radius (Fig. 3a; S = 100%). The four measurements at S = 100% show good reproducibility for three of the measurements. The repeatability error for all four measurements was ±7-39%, and the error that excluded the first measurement was ±6%. A possible reason for the difference between the first and subsequent three measurements at S = 100% is that the pore radius distribution changed owing to the movement of unstable grains during the course of the first water expulsion, but stabilized thereafter.

Figure 3. (a) Porewater radius distribution at water saturation S = 63-100% determined by water expulsion method. Shown in the upper right is the relationship between the amount of water and trapped air in pores with 10 µm radius for S = 63%. (b) Water volume fraction (ϕ_wat) in each pore radius plotted against S.

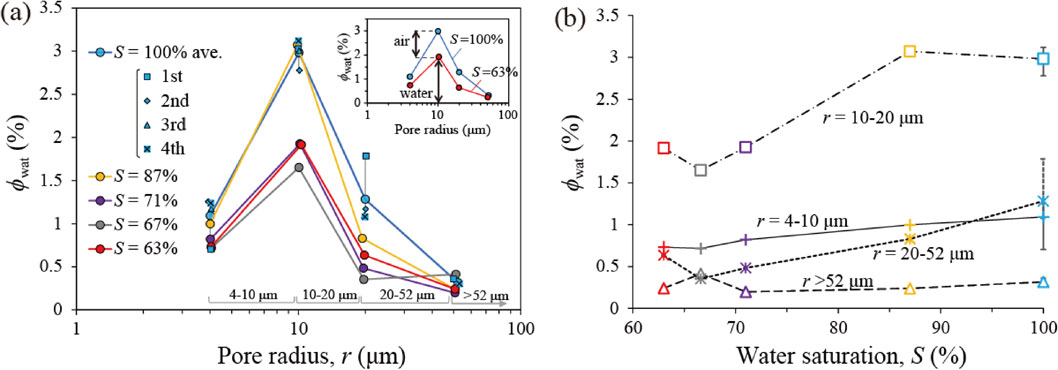
In Figure 3a, the data with S values between 63 and 71% are considered almost identical within the margin of error. However, when S increased to 87%, the relatively narrow pores of 4-10 and 10-20 µm radii were almost completely filled with water, while air still remained in the wider 20-52 µm radius pore. The trend in the widest pore radius of >52 µm is difficult to evaluate because of the large uncertainty due to small water volume, even at S = 100%.

DISCUSSION

Behavior of water and air at S = 63-71%

As shown in Figure 3a, the porewater radius distribution at S = 71% was approximately the same as that at S = 63%, although S increased by 8%. Water adsorbs on the pore wall and a water film of nanometer (nm) to submicron (µm) order of thickness is formed (Nishiyama and Yokoyama, 2013b), even in pores with entrapped air. For water in the pores to be expelled using the water expulsion method, the pores must be filled with water (Fig. 2b). When the pore wall surface is covered by only a water film (Fig. 2b), gas passes through the center of the pore, and water cannot be pushed out by the gas pressure. Therefore, the increase in S from 63 to 71% without a definite change in the porewater radius distribution is considered at least partly due to the formation of a water film.

The thickness of the water film on the pore wall surface of entrapped air is calculated as follows (Nishiyama and Yokoyama, 2013a):   

\begin{equation} \frac{\varepsilon_{r}\varepsilon_{0}}{2}\left(\frac{\pi k_{\text{B}}T}{eZ}\right)^{2}\frac{1}{h^{2}} - \frac{A_{\text{svl}}}{6\pi h^{3}} = \frac{2\gamma}{r} \end{equation} (1),

where ε_rε₀: dielectric constant of water (= 6.99 × 10⁻¹⁰ C² J⁻¹ m⁻¹), k_B: Boltzmann’s constant (= 1.38 × 10⁻²³ J K⁻¹), T: absolute temperature (= 298.15 K), e: elementary charge (= 1.60 × 10⁻¹⁹ C), Z: valence of dissolved ions (= 1), h: water film thickness (m), and γ = 7.2 × 10⁻² N m⁻¹. A_svl is the Hamaker constant of SiO₂ (= −1.0 × 10⁻²⁰ J) (Tokunaga, 2011). Substituting the dominant pore radius in the rock (r = 10 µm; Fig. 3a) into Eq. 1, h is calculated to be 12.7 nm (h = 8.1 nm for r = 4 µm and h = 17.9 nm for r = 20 µm). In addition, the specific surface area of the Fontainebleau sandstone is 0.1 m² g⁻¹ (Nishiyama and Yokoyama, 2013b). Assuming that a water film of the same thickness is formed on all surfaces, and using the measured density of the rock (2.38 g cm⁻³), the volume of water film per total rock volume is 0.3% (= 0.1 m² g⁻¹ × 12.7 × 10⁻⁹ m × 2.38 × 10⁶ g m⁻³ × 100). Using the porosity of the rock (9.9%), the increase in S owing to the formation of the water film is 3.1% (= 0.3/9.9 × 100). When using h for r = 4 µm and 20 µm, the increases in S are 2.0 and 4.3%, respectively. In practice, however, 63% of the pore is filled with water soon after water flow, and water film is not formed in pores filled with bulk water. Therefore, only a portion of the surface area of 0.1 m² g⁻¹ is covered by a water film. For an 8% increase in S from 63 to 71%, the contribution of the water film is estimated to be less than 2-4%.

Pores in rocks typically have corners. The capillary rise in the corners proceeds before the center of the channel is filled with water (Ponomarenko et al., 2011). Thus, the most likely form of water present in the air-trapping pores, other than the water film, is water filling the corners (Fig. 4). The water present in such a corner is not detected by our water expulsion method unless the radius of the meniscus of corner water exceeds 4 µm (maximum ΔP applied was ∼ 360 hPa). Because the contribution of the water film to the 8% increase in S is less than 2-4% from the above calculation, the remaining 4% (= 8-4%) or more is expected to be corner water.

Figure 4. Water film covering the pore wall and water filling the corner. The shape of the grain boundary is approximated by a triangular prism. Gas can flow through the center of the pore.

Behavior of water and air at S > 71%

As S exceeds 71%, the water volume fraction (ϕ_wat) increases and the air volume fraction ϕ_air decreases with increasing S for any pore of radii of 4-10, 10-20, or 20-52 µm (Figs. 3a and 3b) (ϕ_wat + ϕ_air = total pore volume in pore of each radius / whole rock volume × 100). In Figure 3a, narrow pores with 4-10 and 10-20 µm radii are almost fully filled with water at S = 87%, while much air remains in the pores of 20-52 µm radius. In other words, the experimental results showed that the air in the pores with small radii disappeared before the air in the pores with large radii. In the current experiment, before the water flows into the rock, it is considered to be in equilibrium with air, and additional dissolution of air is unlikely to occur at atmospheric pressure. However, the pressure of the trapped air P is greater than the atmospheric pressure P_a by the capillary pressure (2γ/r) (Fig. 5a). This P is expressed as   

\begin{equation} P = P_{a} + \frac{2\gamma}{r} \end{equation} (2).

According to Henry’s law, the amount of gas dissolved in water is proportional to pressure. This means that the amount of air that can dissolve in a pore of radius 4, 10, 20, and 52 µm is 36, 14, 7, and 3% greater, respectively, than the value in the water in equilibrium with atmosphere. Therefore, air in the small-radius pores is more soluble. A similar concept is described in Holocher et al. (2003), who developed a kinetic model for gas bubble dissolution in water. By extending this model, we created a model in which the entrapped air in a tubular pore with radius r and length l was dissolved in water at the meniscus, as shown in Figure 5a. According to Holocher et al. (2003), the rate at which air bubbles dissolve in water is given by   

\begin{align} J &= k\left(c_{w} - \frac{P}{RTK_{H}}\right) = k\left(\frac{P_{a}}{RTK_{H}} - \frac{P}{RTK_{H}}\right) \\&= -k\frac{2\gamma}{rRTK_{H}} \end{align} (3),

where J is the flux of mass transfer from air to water (M L⁻² T⁻¹) (M: mass, L: length, T: time), k is the mass transfer coefficient (L T⁻¹), c_w is the concentration of dissolved air in water (M L⁻³) (from Henry’s law, P_a = c_wK_HRT), R is the gas constant (L² T⁻² K⁻¹) (K: Kelvin), and K_H is the dimensionless Henry’s coefficient. In the original equation of Holocher et al. (2003), several parameters have a subscript specifying the type of gas i considered (k_i, C_w,i, P_i, K_H,i); however, we treat them collectively as air for simplification. Using the surface area of the meniscus, A (= 4πr²) (meniscus becomes a sphere when the two ends of air in Figure 5a are bound together), and by converting Eq. 3 to the rate of change of the dissolved mass of entrapped air (dn/dt), we obtain   

\begin{equation} \frac{dn}{dt} = -AJ = \frac{8\pi \gamma k}{RTK_{H}}r \end{equation} (4).

Eq. 4 can be converted to the rate of change of air volume (dV/dt) by using the density of air ρ (M L⁻³)   

\begin{equation} \frac{dV}{dt} = \frac{1}{\rho}\frac{dn}{dt} = \frac{8\pi \gamma k}{RT\rho K_{H}}r \end{equation} (5).

Meanwhile, from V = πr²l, we have   

\begin{equation} \frac{dV}{dt} = \pi r^{2}\frac{dl}{dt} \end{equation} (6).

Because Eq. 5 is equal to Eq. 6, we obtain   

\begin{equation} \frac{dl}{dt} = \frac{8\gamma k}{RT\rho K_{H}}\frac{1}{r} \end{equation} (7).

Eq. 7 denotes that with a smaller r, the rate at which the entrapped air length decreases (dl/dt) is greater. Holocher et al. (2003) showed that the expression for k differs between the no water flow case and the active flow case, but k increases with decreasing r in both. Therefore, even after incorporating the effect of flow condition, dl/dt increases with decreasing r. Note that Eqs. 6 and 7 correspond to a single air. Because there is more than one air in the rock, let N be the number of air and multiply Eq. 6 by N. The air length at the initial state is l₀, and by further dividing by the total initial volume of air in pores with radius r (V_tot = Nπr²l₀), we obtain   

\begin{equation} \frac{dV}{dt}\frac{N}{V_{\text{tot}}} = \frac{dl}{dt} \frac{1}{l_{0}} \end{equation} (8).

The value $\frac{dV}{dt}\frac{N}{V_{\text{tot}}}$ corresponds to the rate at which the total volume of air in pores of radius r decreases, normalized to the volume of air in the initial state for the same r. As for the value of l₀, Kumar et al. (2010) showed that 70-80% of the entrapped air in Fontainebleau sandstone has an equivalent diameter of 100-500 µm. If this data is applicable to the sample used in this study, most of the air would have a size of less than two grains. Here, we assume that l₀ is the same for all pore radii. From Eqs. 7 and 8, it is expected that $\frac{dV}{dt}\frac{N}{V_{\text{tot}}}$ is larger with a smaller radius. To obtain information on $\frac{dV}{dt}\frac{N}{V_{\text{tot}}}$ from the experimental results, Figure 5b plots the value of $\overline{\phi }_{\text{air}}$ (= ϕ_air/ϕ_{air_avg_S=63-71}), calculated by dividing the volume of air at each radius by the average of the volume of air at S = 63-71%, in which the volume of air at S = 63-71% is assumed to be equal to that before dissolution. Data for >52 µm radius were omitted due to large errors. In Figure 5b, decrease of $\overline{\phi }_{\text{air}}$ from S = 63 to 87% was 0.72, 1.08, and 0.43 for 4-10, 10-20, and 20-52 µm, respectively (green arrows). If we assume that τ is the time elapsed during which S to increases from 63 to 87%, the value corresponding to $\frac{dV}{dt}\frac{N}{V_{\text{tot}}}$ is 0.72/τ, 1.08/τ and 0.43/τ for 4-10, 10-20, and 20-52 µm, respectively. The lack of information on the value of l₀ for each pore radius makes definitive discussion difficult, but the experimental results suggest that $\frac{dV}{dt}\frac{N}{V_{\text{tot}}}$ at radii of 4-10 and 10-20 µm is larger than that at 20-52 µm, which is generally consistent with the predictions from Eqs. 7 and 8 (the reversed values of 4-10 and 10-20 µm are possibly due to the difference in l₀).

Figure 5. (a) Schematic of the model of dissolution of entrapped air in tubular pore. The red arrows indicate the interfacial tension generated at the contact point (circumference) between the meniscus and the pore wall. P is the pressure of entrapped air [= atmosphere pressure (P_a) + capillary pressure (2γ/r)]. (b) Normalized volume of entrapped air ($\overline{\phi }_{\text{air}}$) plotted against water saturation (S). See text for details of $\overline{\phi }_{\text{air}}$. Green arrows indicate the amount of reduction of air at S = 87% for each radius after time τ elapsed from the starting point (average of S = 63-71%).

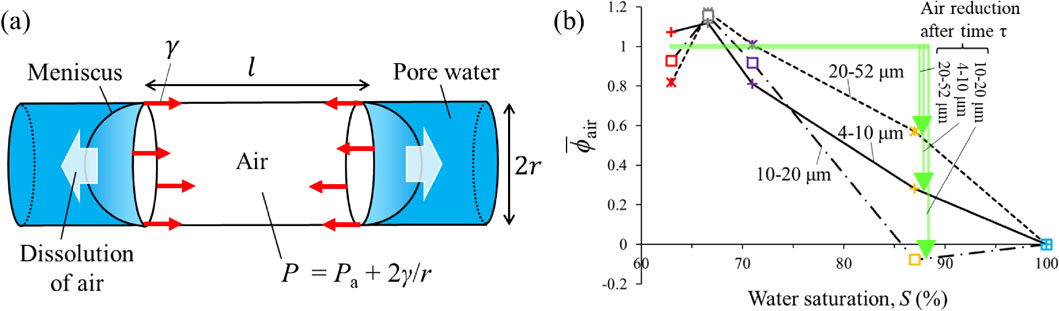
The above discussion strongly suggests that the experimental results that pores with small radii are filled with water quicker than pores with large radii can be explained primarily by the radius dependence of the dissolution rate of trapped air. Another possible explanation is air movement. However, if air movement accounted for the experimental results, air with a smaller radius should move more easily. Although no evidence was found for such air movement, the present results do not rule out this possibility. The evaluation of air movement in complex pore structure is a subject for future research.

CONCLUSIONS

Using Fontainebleau sandstone with the main pore radii, ranging from a few micrometers to several tens of micrometers, we applied the water expulsion method to investigate how air in the pores of each radius is replaced by water during infiltration. The results and interpretations are as follows:

1. 1)    S became 63% as soon as water began to flow in the rock; as S increased from 63 to 71%, water infiltrated the rock via water film formation and capillary action at the corners of the pores. In this S range, little change in the porewater radius distribution was detected using the water expulsion method.
2. 2)    For S > 71%, as S increased, the narrower pores with 4-10 and 10-20 µm radii were filled with water quicker than pores with 20-52 µm radius. A theoretical model of the dissolution of entrapped air showed the rate of length reduction of the air is faster when the radius of trapped air is smaller, which may be a mechanism governing the experimental results.

ACKNOWLEDGMENTS

We thank the two anonymous reviewers for their constructive comments.

REFERENCES

•  Al Mansoori,  S.K.,  Itsekiri,  E.,  Iglauer,  S.,  Pentland,  C.H., et al (2010) Measurements of non-wetting phase trapping applied to carbon dioxide storage. International Journal of Greenhouse Gas Control, 4, 283-288.
•  Faybishenko,  B.A. (1995) Hydraulic behavior of quasi-saturated soils in the presence of entrapped air: Laboratory experiments. Water Resources Research, 31, 2421-2435.
• Guéguen, Y. and Palciauskas, V. (1994) Introduction to the physics of rocks. pp. 294, Princeton University Press.
•  Holocher,  J.,  Peeters,  F.,  Aeschbach-Hertig,  W.,  Kinzelbach,  W. and  Kipfer,  R. (2003) Kinetic model of gas bubbles dissolution in groundwater and its implications for the dissolved gas composition. Environmental Science & Technology, 37, 1337-1343.
•  Kumar,  M.,  Senden,  T.,  Sheppard,  A.,  Middleton,  J. and  Knackstedt,  M. (2010) Visualizing and quantifying the residual phase distribution in core material. Petrophysics, 51, 323-332.
•  Lowry,  M.I. and  Miller,  C.T. (1995) Pore-scale modeling of nonwetting-phase residual in porous media. Water Resources Research, 31, 455-473.
•  Nishiyama,  N.,  Yokoyama,  T. and  Takeuchi,  S. (2012) Size distributions of pore water and entrapped air during drying-infiltration processes of sandstone characterized by water-expulsion porosimetry. Water Resources Research, 48, W09556.
•  Nishiyama,  N. and  Yokoyama,  T. (2013a) Estimation of water film thickness in geological media associated with the occurrence of gas entrapment. Procedia Earth and Planetary Science, 7, 620-623.
•  Nishiyama,  N. and  Yokoyama,  T. (2013b) Does the reactive surface area of sandstone depend on water saturation? — The role of reactive-transport in water film. Geochimica et Cosmochimica Acta, 122, 153-169.
•  Ponomarenko,  A.,  Quéré,  D. and  Clanet,  C. (2011) A universal law for capillary rise in corners. Journal of Fluid Mechanics, 666, 146-154.
•  Tokunaga,  T.K. (2011) Physicochemical controls on adsorbed water film thickness in unsaturated geological media. Water Resources Research, 47, W08514.
•  Vargaftik,  N.B.,  Volkov,  B.N. and  Voljak,  L.D. (1983) International tables of the surface tension of water. Journal of Physical and Chemical Reference Data, 12, 817-820.
•  Yokoyama,  T. (2013) Characterization of the reaction and transport properties of porous rhyolite and its application to the quantitative understanding of the chemical weathering rate. Geochimica et Cosmochimica Acta, 118, 295-311.
•  Yokoyama,  T.,  Yorimoto,  M. and  Nishiyama,  N. (2020) Flow path selection during capillary rise in rock: Effects of pore branching and pore radius variation. Transport in Porous Media, 135, 79-99.
•  Zimmerman,  R.W. and  Bodvarsson,  G.S. (1989) An approximate solution for one-dimensional absorption in unsaturated porous-media. Water Resources Research, 25, 1422-1428.