Decompressional spinel + plagioclase symplectite from Tenmondai Rock, Lützow-Holm Complex, East Antarctica: Implications for the garnet-aluminosilicate-spinel-plagioclase geobarometer

Abstract

Spinel + plagioclase symplectites in pelitic metamorphic rocks have been reported from many localities. We report in detail an occurrence of this texture from Tenmondai Rock, Lützow-Holm Complex, East Antarctica. This texture is produced by the following metamorphic reaction; garnet + sillimanite = spinel + plagioclase. This can be described as the following two net-transfer reactions; 5Grs + Alm + 12Als = 3Hc + 15An, and 5Grs + Prp + 12Als = 3Spl + 15An. We propose new geobarometers (GASpP) based on these equations. For example, one of these is P = (−155790 + 587.4T + RT lnK_Fe) / 29.378, for garnet + sillimanite + spinel + plagioclase assemblage in the CFASZn-system. Where P is pressure in bar, T is temperature in K, and R represents gas constant. The equilibrium constant is, K_Fe = (a_Grs⁵ a_Alm)/(a_Hc³ a_An¹⁵). Our proposed new geobarometers are free from quartz, corundum, orthopyroxene, and cordierite within these equations. These barometers are useful to estimate pressure conditions for spinel-bearing pelitic metamorphic rocks within a wide pressure-temperature range (andalusite, kyanite, and sillimanite fields). We estimate the metamorphic pressure-temperature (P-T) conditions at Tenmondai Rock by applying the GASP, GRIPS, GRAIL, GASpP geobarometers, and the Zr-in-Rt geothermometer. The metamorphic evolution of the rocks at Tenmondai Rock is characterized by a clockwise P-T-t path. The peak P-T condition is about 820 MPa and 850 °C. Spinel + plagioclase symplectite was produced during the decompressional stage of this metamorphic evolution, at about 450 MPa and 700 °C.

INTRODUCTION

Spinel is one of the common rock-forming minerals in pelitic metamorphic rocks. It mainly occurs in the sillimanite field, but also occurs in the kyanite field (e.g., Tuccillo et al., 1992; Zhang et al., 2005; Cruciani et al., 2019) and andalusite field (e.g., Perchuk et al., 1989; Xu et al., 1994; Carson et al., 1997; Kalt et al., 1998; Pitra and de Waal, 2001; Sawaki et al., 2001; Marien et al., 2019).

Spinel coexisting with quartz is commonly regarded as an ultrahigh-temperature (UHT) metamorphic mineral assemblage (e.g., Hensen and Green, 1971; Vielzeuf, 1983; Waters, 1991; Harley, 1998; Shimura et al., 2002; Ganguly et al., 2017) although additional minor chemical components such as Zn can extend the spinel + quartz stability to below 900 °C (Shimura et al., 2002; Harley, 2008; Clark et al., 2011). In spinel + quartz stable cases, spinel occurs in direct contact with quartz. On the other hand, in the case of lower grades, spinel does not occur in direct contact with quartz, although quartz is present in the rocks. In such rocks, spinel coexisting with cordierite is well known (e.g., Clarke and Powell, 1991; Komatsu et al., 1994; Pitra and de Waal, 2001; Johnson et al., 2004).

Sometimes spinel occurs in contact with plagioclase in pelitic metamorphic rocks (e.g., Hiroi et al., 1997; Rötzler and Romer, 2001; Álvarez-Valero et al., 2007; Shimizu et al., 2009; Saki, 2011; Baldwin et al., 2015). For example, Hiroi et al. (1997) reported spinel + plagioclase symplectite around a garnet porphyroblast. This spinel is not in direct contact with quartz. Rötzler and Romer (2001) and Baldwin et al. (2015) describe spinel + plagioclase symplectite occurrences around garnet or kyanite. Álvarez-Valero et al. (2007) observed spinel with a thin rim of plagioclase. Santosh et al. (2007) reported that spinel is surrounded by plagioclase, and is separated from quartz. Saki (2011) reported that spinel + cordierite symplectite occurs around andalusite, and this spinel has a thin rim of plagioclase. These textures suggest that the spinel + plagioclase assemblage may be produced by garnet + aluminosilicate breakdown reactions.

In this paper, we describe an example of microstructural relations between spinel and plagioclase from Tenmondai Rock, Lützow-Holm Complex, East Antarctica, and propose new geobarometers for spinel-bearing pelitic metamorphic rocks.

Abbreviations of minerals in this paper are after Whitney and Evans (2010).

GEOLOGICAL SETTING

The Lützow-Holm Complex (LHC) is located in eastern Dronning Maud Land, East Antarctica (Fig. 1) and is a medium P/T type metamorphic complex. SHRIMP U-Pb zircon dating of the LHC indicates that peak metamorphism occurred at about 600-500 Ma (Shiraishi et al., 2003, 2008; Dunkley et al., 2020). A two-stage metamorphic history with events at ∼ 600 Ma and 550-530 Ma metamorphism has been reported (e.g., Hokada and Motoyoshi, 2006; Kawakami et al., 2016).

Figure 1. Simplified metamorphic zone map of the Lützow-Holm Complex (LHC), East Antarctica (modified after Hiroi et al., 1991). South-westward progressive metamorphism from amphibolite- to granulite-facies has been documented by six isograds (Hiroi et al., 1991). Orthopyroxene sporadically occurs from the Opx-in (1) isograd, whereas orthopyroxene becomes much more common from the Opx-in (2) isograd (Hiroi et al., 1983). Tenmondai Rock is the locality where the first appearance of orthopyroxene in the LHC is documented (Shiraishi et al., 1984).

Across the LHC the metamorphic grade increases progressively south-westward from amphibolite-facies to granulite-facies (Hiroi et al., 1991). A clockwise metamorphic P-T-t path is reported by many authors (e.g., Hiroi et al., 1991; Kawakami and Motoyoshi, 2004; Yoshimura et al., 2004, 2008; Kawasaki et al., 2011). The highest-grade rocks of the LHC occur at Rundvågshetta (Fig. 1), where peak P-T conditions reached UHT, about 1.0-1.2 GPa and 1000-1100 °C (Motoyoshi and Ishikawa, 1997; Fraser et al., 2000; Yoshimura et al., 2008; Kawasaki et al., 2011; Takahashi et al., 2018). Spinel + quartz assemblages have been recognized at Rundvågshetta and Skallevikshalsen (Motoyoshi et al., 1985; Kawakami and Motoyoshi, 2004; Kawasaki et al., 2011).

Metamorphic zone mapping of the LHC (Fig. 1) has been studied based on matrix mineral assemblages (Hiroi et al., 1991). Recently, Suzuki and Kawakami (2019) proposed that metamorphism of Akarui Point (Fig. 1) near Tenmondai Rock occurred at higher P-T conditions than suggested by previous studies, and provided P-T estimates of about 1.05 GPa and 834 °C. They suggested that the P-T-t evolution of the LHC needs to be re-evaluated utilizing detailed petrochronological approaches.

Tenmondai Rock (68°26′S-68°28′S and 41°40′E-41°44′E) is one of the outcrops of the LHC (Figs. 1 and 2), and is the locality where the first appearance of pyroxene is noted in the progressive metamorphic zonation (Hiroi et al., 1991) (Fig. 1). Tenmondai Rock is underlain by gneisses, migmatitic rocks, granite and pegmatite (Shiraishi et al., 1985) (Fig. 2). Among the metamorphic rocks, biotite-hornblende gneiss and hornblende-biotite gneiss are predominant, and lesser amounts of garnet-biotite gneiss and amphibolite are intercalated (Shiraishi et al., 1985). Fe-rich amphibolites at Tenmondai Rock contain orthopyroxene, marking the first appearance of orthopyroxene in the progressive metamorphic sequence in the LHC (Shiraishi et al., 1984) [see isograd Opx-in (1) in Fig. 1]. All aluminosilicate polymorphs (kyanite, sillimanite, and andalusite) are reported from garnet-biotite gneiss from Tenmondai Rock (Hiroi et al., 1983; Shiraishi et al., 1985), and their occurrence is interpreted to result from a clockwise metamorphic P-T-t path (Hiroi et al., 1991; Takamura et al., 2020). Takamura et al. (2020) reported that zircon U-Pb ages from mafic metamorphic rock from Tenmondai Rock show a wide age range, between 582-481 Ma, and post-peak decompression possibly started around 560 Ma.

Figure 2. Simplified geological map of Tenmondai Rock (modified after Shiraishi et al., 1985).

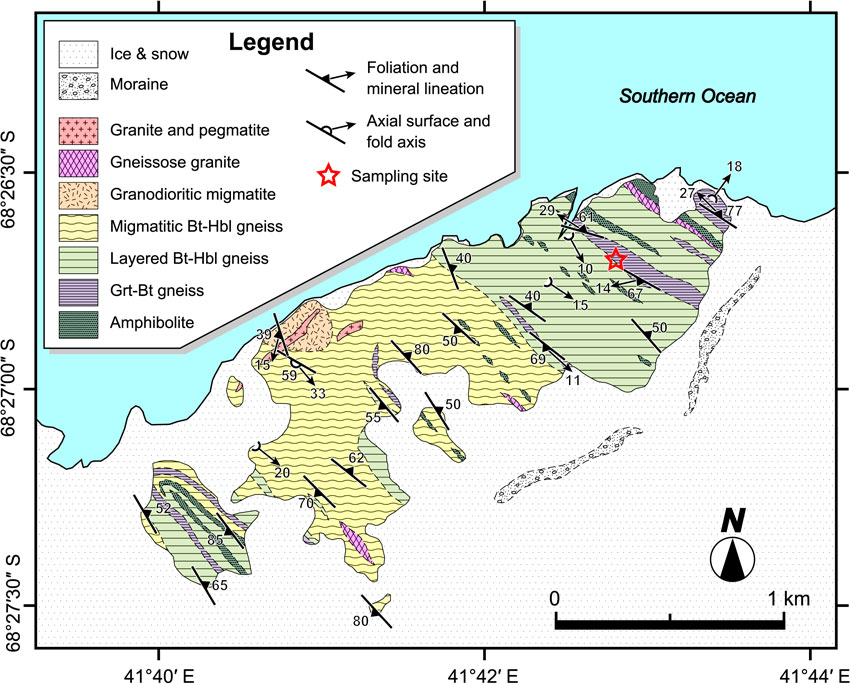
Garnet-biotite gneiss is developed mainly in the eastern area of Tenmondai Rock (Fig. 2). Reddish brown pegmatitic dykes intrude the gneiss (Shiraishi et al., 1985) (Fig. 3a). The garnet-biotite gneiss occurs as a layered migmatite structure composed of biotite-rich melanocratic layers and garnet-aluminosilicate rich leucocratic layers (Fig. 3b). Sample TMD40 (Fig. 3c) was collected from a garnet-sillimanite rich leucocratic layer (star in Fig. 2).

Figure 3. (a) Field occurrences of garnet biotite gneiss at Tenmondai Rock. (b) Close up of garnet biotite gneiss. The sample TMD40 was collected from a garnet- sillimanite- rich leucocratic layer. (c) A slab photograph of the sample TMD40. (d) close-up of spinel + plagioclase symplectite.

PETROGRAPHY

Analytical methods

SEM image photographing and qualitative analyses of minerals were carried out by JEOL JSM-6030LA and energy-dispersive X-ray spectroscopy (EDS) (JEOL JED-2300) at the Yamaguchi University. X-ray intensity mapping was also obtained by this EDS, using analytical conditions of 20 kV acceleration voltage, 3.45 nA probe current, 0.0002 s dwell time, 10 sweep time, and 2048 × 1536 pixels.

Quantitative analyses of minerals were carried out by wavelength-dispersive X-ray spectroscopy (WDS) (JEOL JXA-8230) at the Yamaguchi University. Five-channel spectrometers were used simultaneously. Natural and synthesized minerals and oxides were used as standards.

Operating conditions for analyses of garnet, spinel, biotite, feldspars and ilmenite were 15 kV accelerating voltage, 20 nA probe current, beam diameter was 2 µm, counting times were 10 s on the peak and 5 s on the background. Oxide ZAF correction procedures were used. Fe₂O₃, FeO, Fe³⁺, and Fe²⁺ of spinel and ilmenite are calculated by stoichiometry (e.g., Droop, 1987).

The measurement conditions for analyses of rutile referred to Zack et al. (2004). Our operating conditions are as follows; 20 kV accelerating voltage, 120 nA probe current, 5 µm beam diameter. Counting time for zirconium, 300 s on the peak and 150 s on the background. For titanium, 7 s on the peak and 3.5 s on the background. Hafnium was rejected because the measured data was lower than the detection limit in 100 s counting time. For other elements (Si, Sn, Al, Cr, V, Fe, Mg, Zn, Ca, Nb, Sb, Ta, and W), 50-170 s on the peak and 25-85 s on the background. Since the vanadium-LIF-Kα peak is overlapped by the titanium-LIF-Kβ peak, an interference correction was carried out on the intensity of the titanium-LIF-Kα peak. Oxide ZAF correction procedures were used. Quantitative analyses for rutile were confirmed by rutile standards R10 and R19 (Luvizotto et al., 2009).

Petrography and mineral chemistry of a spinel-bearing gneiss

The sample TMD40 is about 15 cm sized handspecimen (Figs. 3c and 3d). It is leucocratic medium-grained garnet-sillimanite gneiss. It is mainly composed of garnet, spinel, biotite, sillimanite, plagioclase, K-feldspar, quartz, ilmenite, and rutile (Figs. 4, 5, and 6). It has minor amounts of muscovite, apatite, zircon, and monazite. Very small amounts of hematite, pyrrhotite, pyrite, chalcopyrite, and chlorite occur as retrograde phases. Cordierite is absent.

Figure 4. (a) Occurrence of a garnet porphyroblast, in the thin section #S2 of TMD40, plane polarized light (PPL). The porphyroblast consists of three zones; inclusion-poor core, inclusion rich-mantle, and inclusion-poor rim. Almost all inclusions are quartz. Other small inclusions are apatite, rutile, ilmenite, zircon, biotite, and muscovite. Red-cross marks are analysis points for chemical zoning (see Fig. 7). A red circle indicates the highest grossular position in Figure 7. This porphyroblast garnet is in contact with both quartz and plagioclase. Large apatite crystals occur at the rim of the garnet. Pale-colored biotite, muscovite, pyrrhotite, pyrite, and hematite occur in the pressure-shadow (left side of this picture). (b) and (c) are SEM-backscattered electron (BSE) images of two green rectangles areas in (a). Red numbers represent Zr concentration in rutile (in ppm).

Figure 5. Occurrences of spinel + plagioclase symplectite in the sample TMD40 (a)-(i). Note the spinel and quartz are always separated by plagioclase, and spinel is not in direct contact with quartz. Garnet crystals near spinel + plagioclase symplectite are enveloped by plagioclase. On the other hand, garnet crystals in spinel-free domains are in contact with quartz [(a), (b), and Fig. 3]. (a) Matrix plagioclase + quartz + K-feldspar domain shows granoblastic texture, and spinel is absent. BSE image of thin section #S1. (b) Close-up of spinel + plagioclase symplectite of green rectangle area in (a). PPL. (c) BSE image of thin section #S2. (d) EDS SiKα X-ray intensity map of orange rectangle area in (c). (e) Close-up of spinel + plagioclase symplectite of yellow rectangle area in (c) and (d). PPL. Spinel + plagioclase symplectite of thin section #S1 (f) and thin section #S2 (g), PPL. (h) Close-up of red rectangle area in (g), BSE image. Note spinel + plagioclase produced along grain boundary of garnet and sillimanite. (i) occurrence of a rutile within the spinel + plagioclase symplectite of thin section #S1. BSE image. Occurrence of rutile + chlorite intergrowth around ilmenite (j and k), BSE image. (j) is close up BSE image of red rectangle in (a). (k) is close up BSE image of green rectangle in (j). Red numbers represent Zr concentration in rutile (in ppm).

Figure 6. Occurrences of spinel-free regions in the sample TMD40, thin section #S2. (a) and (c) are PPL. (b) and (e) are crossed polars. Sillimanite + ilmenite + quartz domain embayed into the garnet. The boundary of sillimanite and garnet is separated by quartz. Such garnet crystal is almost inclusion-free and is surrounded by quartz.

TMD40 is subdivided into two domains. One is a matrix domain consisting of plagioclase + quartz + K-feldspar (lower part of Fig. 5a). This domain shows granoblastic texture. Spinel does not occur in this domain. The other is a garnet- and sillimanite- rich domain. This domain contains spinel (upper part of Fig. 5a). Spinel occurs as vermicular intergrowth with plagioclase (Figs. 3d and 5a-5i). In this paper, we call such texture and related minerals as ‘spinel + plagioclase symplectite’, ‘symplectite spinel’, and ‘spinel-bearing plagioclase’, hereafter.

Representative chemical compositions of minerals are shown in Supplementary Table S1 (Supplementary Tables S1, S2, and S3 are available online from https://doi.org/10.2465/jmps.221130).

Generally, garnet occurs as porphyroblast (Figs. 3c, 3d, and 4a). Sometimes it is embayed by spinel + plagioclase symplectite (Fig. 5f) or by sillimanite + ilmenite + quartz (Fig. 6). Porphyroblastic garnet {X_Mg [= Mg/(Fe²⁺ + Mg)] = 0.244-0.306, Prp [= Mg/(Fe²⁺ + Mn + Mg + Ca) mol%] = 23.5-29.4, Grs [= Ca/(Fe²⁺ + Mn + Mg + Ca) mol%] = 2.01-3.63} is euhedral to subhedral (Figs. 4, 5, and 6). It encloses quartz, sillimanite, rutile, ilmenite, apatite and zircon (Fig. 4). Very small amounts of biotite and muscovite are occasionally enclosed (Fig. 4a). Chemical zoning in porphyroblast garnet is shown in Figure 7. The grossular content of porphyroblast garnet is rich in the core and decreases towards the rim. The X_Mg is low in the core and high in the mantle, and then decreases towards the rim.

Figure 7. Chemical zoning in a garnet porphyroblast of Figure 4a, exhibiting three-zones, (1) high-almandine and low-pyrope core, (2) low-almandine and high-pyrope mantle, and (3) high-almandine and low-pyrope rim. Grossular content decreases from core to rim.

Spinel + plagioclase symplectite occurs associated with garnet- and sillimanite- rich domains (Fig. 5). Garnet compositions near the symplectite are lower in Mg and Ca (X_Mg = 0.204-0.256, Grs = 2.11-2.75) than in the porphyroblasts (Fig. 8 and Table S1-1). Garnet compositions in contact with biotite or muscovite are lower in X_Mg (X_Mg = 0.156-0.286, Prp = 19.6-24.6, Grs = 1.97-2.69) (Fig. 8 and Table S1-1).

Figure 8. Chemical compositions of garnet of the sample TMD40 in the Grs-Alm-Prp diagram. Pyrope content of garnet near spinel + plagioclase symplectite is poorer than porphyroblast garnet.

Sometimes sillimanite + ilmenite + quartz domains are embayed into garnet (Fig. 6). In this case sillimanite and garnet are bounded by quartz (Fig. 6d). Spinel does not occur around such texture.

Sillimanite occurs as prismatic crystals (Figs. 5 and 6). Kyanite and andalusite are not found in sample TMD40, but these were reported from almost the same locality (Hiroi et al., 1983; Shiraishi et al., 1985).

Dark green spinel occurs as spinel + plagioclase symplectite (Fig. 5). Spinel and quartz are always separated by plagioclase and spinel is not in direct contact with quartz (Fig. 5). Garnet near this texture is enveloped by plagioclase (Figs. 5a-5f).

Oxide spinels (AB₂O₄) can be classified as ‘2-3 spinels’ (A²⁺B³⁺₂O₄) and ‘4-2 spinels’ (A⁴⁺B²⁺₂O₄) (e.g., Biagioni and Pasero, 2014; Colas et al., 2016). The spinel series is B = Al³⁺ solid solution and the general formula is (Fe, Mn, Mg, Zn, Ni)²⁺Al³⁺₂O₄ (e.g., Deer et al., 2013). Among naturally occurring spinels, A may include Fe²⁺, Mn, Mg, Ca, Zn, Ni, Co, and Cu, whereas B may include Al, Cr, V, Fe³⁺, Ti, and Si. R⁴⁺ is occupied in ‘4-2 spinel’ (A⁴⁺B²⁺₂O₄) structure, such as a result of the substitution R⁴⁺ + R²⁺ = 2R³⁺ (Deer et al., 2013), where R is a generalized symbol for a group of metal ions. Spinel in TMD40 has low X_Mg (= 0.201-0.313), Fe³⁺/Fe^total (= 0.084-0.147), and Fe³⁺/R³⁺ (= 0.033-0.062) in composition (Fig. 9 and Table S1-2). It is hercynite (FeAl₂O₄). It contains small amounts of ZnO (1.72-2.34 wt%), Cr₂O₃ (0.42-1.79 wt%), V₂O₃ (0.23-0.39 wt%), NiO (0.06-0.20 wt%), and CoO (0.07-0.18 wt%) (Fig. 9 and Table S1-2). CuO is lower than the detection limit.

Figure 9. Chemical compositions of spinel of the sample TMD40. (a) Zn-Fe²⁺-Mg triangle diagram. (b) Fe²⁺-Fe³⁺-Mg triangle diagram. Grids of solid line and dashed line are X_Mg = Mg/(Fe²⁺ + Mg) and X_Mg* = Mg/(total Fe + Mg), respectively.

Two main occurrences of plagioclase can be observed. One is ‘matrix-plagioclase’ (lower part of Fig. 5a) which shows granoblastic texture. The other is ‘spinel-bearing plagioclase’ (Fig. 5). Spinel-bearing plagioclase is richer in anorthite content (An = 25.4-31.2 mol%), compared with matrix-plagioclase which is poorer in anorthite content (An = 22.5-25.0 mol%) (Fig. 10 and Table S1-3). K-feldspar (Or = 81.5-90.9 mol%) (Fig. 10 and Table S1-3) represents granoblastic texture with plagioclase and quartz in the matrix (Figs. 4a and 5a).

Figure 10. Chemical compositions of feldspars of the sample TMD40 in the An-Ab-Or diagram. Anorthite content of symplectite plagioclase is richer than that of matrix plagioclase.

Large euhedral or subhedral biotite (X_Mg = 0.488-0.555) occurs in the matrix or cuts the garnet porphyroblasts, and it has X and Y = brown, Z = reddish brown pleochroism (right of Fig. 4a and Table S1-4). Sometimes small anhedral biotite (X_Mg = 0.625-0.631) occurs within spinel + plagioclase symplectite (Figs. 5b, 5f, 5g, and 5h). It has X and Y = light brown, Z = brown pleochroism. Composition of this biotite is rich in X_Mg and Al, and poor in Ti (Table S1-4). A small amount of fine-grained muscovite occurs in the pressure-shadows or along cracks in garnet (Fig. 4) or near areas with chlorite (Fig. 5j).

Ilmenite occurs in the matrix (Fig. 4a), in inclusions in garnet (Fig. 4c), in Sil + Ilm + Qz domains (Fig. 6), and with Spl + Qz symplectite (Fig. 5i). Representative chemical compositions of ilmenite are shown in Table S1-5.

Rutile occurs as subhedral large crystals in the matrix (Figs. 4a and 5c), or it occurs as small crystals in garnet porphyroblasts (Fig. 4). The c-axis of large rutile defines a weak lineation (Figs. 5c and 5f) and the zirconium content shows a relatively wide range (466-2821 ppm) (Figs. 5c, 11, and Table S1-6). Rutile inclusions in garnet porphyroblasts have relatively high zirconium content, Zr = 1251-2517 ppm (Figs. 4, 11, and Table S1-6). Rutile within spinel + plagioclase symplectite has relatively low zirconium content, Zr = 637-703 ppm (Figs. 5g, 11, and Table S1-6). Rutile occurs as very small euhedral crystals around ilmenite associated with chlorite (Figs. 5j and 5k). Sometimes this chlorite forms a fine-grained intergrowth with rutile (Fig. 5k). Such rutile has low zirconium content; lower than 622 ppm (Figs. 5j, 11, and Table S1-6).

Figure 11. Zirconium content in rutile (ppm) versus temperature of Zr-in-Rt thermometry (Tomkins et al., 2007; Kohn, 2020). Zirconium content in rutile is different in different textures. Rutile in the matrix has a relatively wider range of Zr content. The rutile with the highest Zr content (2821 ppm) is from the matrix, surrounded by quartz, in the spinel-free domain (see Fig. 5c). Rutile inclusions in garnet and rutile in contact with garnet have almost same range of Zr content. Rutile in spinel + plagioclase domains has a narrow range of Zr content (637-703 ppm). Rutile around ilmenite associated with chlorite (Figs. 5j and 5k) has low zirconium content, lower than 622 ppm. Ib, II, IIIa, IIIb, and IIIc are metamorphic stages (see Fig. 12 and text).

METAMORPHIC STAGES

We propose multiple metamorphic stages (Fig. 12) based on the textural evidence and mineral compositions documented in this study as well as previous petrological analyses of garnet-biotite gneiss at Tenmondai Rock. The main stages are the following; stage-I (prograde), stage-II (peak-temperature), and stage-III (retrograde).

Figure 12. Metamorphic stages of pelitic metamorphic rocks of Tenmondai Rock. Solid bars for each mineral indicate that the mineral was stable in the rock at that stage, not that it coexisted in equilibrium with other minerals. For example, spinel + quartz is not an equilibrium assemblage. Broken bars for each mineral indicate uncertain evidence from sample TMD40. Al₂O₃-FeO-MgO diagram and Al₂O₃-K₂O-(FeO + MgO) diagram for each stage are shown as composition -paragenesis diagrams. Solid tie-lines indicate equilibrium coexistence of connected minerals. Broken tie-lines indicate uncertain evidence from sample TMD40. Evidence of stages-Ia and IIIc is relatively poor in our sample TMD40. Since kyanite and andalusite are reported by Hiroi et al. (1983) and Shiraishi et al. (1984) from almost same locality, we refer their occurrences for these stages. The reaction garnet + sillimanite = spinel + plagioclase occurred at the retrograde (decompression) stage IIIb. See also CMAS tetrahedral diagram in Figure 13f for this reaction.

Stage-I is subdivided to the two sub-stages Ia and Ib. Stage-Ia is inferred from the presence of relict kyanite (Hiroi et al., 1983; Shiraishi et al., 1985). Stage-Ib is represented by the core of garnet porphyroblasts which enclosed quartz, sillimanite, rutile, ilmenite, apatite, and zircon (Fig. 4a). However, sample TMD40 preserves relatively poor evidence for the prograde stage, because the sample is re-equilibrated by later stage metamorphism.

Stage-II is a peak-temperature metamorphic stage. It is defined by a garnet + K-feldspar tie-line (Fig. 12). We interpret the composition of some matrix rutile to have been partially affected by subsequent stages of metamorphism and re-equilibration, and regard the matrix rutile that contains the highest zirconium content to provide the best estimate of Stage-II temperature conditions (Fig. 11).

Stage-III is subdivided into three sub-stages; IIIa, IIIb, and IIIc. Stage-IIIa is defined by disappearance of garnet + K-feldspar association (Fig. 12) and the occurrence of embayed garnet (Fig. 6). The embayed garnet is replaced by Ilm + Sil + Qz (Fig. 6). We interpret that rutile originally occurred as inclusions in garnet. This texture is interpreted as the beginning of a garnet breakdown reaction, Grt + Rt = Ilm + Sil + Qz. This is the GRAIL geobarometer reaction (Bohlen et al., 1983) progressing to the lower-pressure conditions. These garnet crystals which experienced the GRAIL reaction are separated from the matrix by quartz (Fig. 6). Since the garnet and sillimanite are separated by quartz, the formation reaction of spinel (Grt + Sil = Spl + Pl) does not occur. The reaction Grt + Sil = Spl + Pl is observed at grain boundaries between garnet and sillimanite (Figs. 5g and 5h). This can be understood using the tetrahedral diagram of Figure 13f. Quartz and spinel plot on opposite sides of the Prp/Alm-Grs-Als plane. As a result, such garnet constitutes a spinel-free domain.

Figure 13. Composition-paragenesis diagram of the spinel forming metamorphic reactions. (a)-(e) three-components (MgO + FeO)-Al₂O₃-SiO₂ system. (a) Crd = Spl + Qz. (b) Grt + Als = Spl + Crd. (c) Opx + Als = Spl + Crd. (d) Grt + Als = Spl + Qz. (e) Grt + Crn = Spl + Als. (f) four-components CaO-(MgO + FeO)-Al₂O₃-SiO₂ system. A spinel-anorthite tie-line goes through a pyrope/almandine-grossular-aluminosilicate plane. This diagram depicts the four-component reaction of this study: Grt + Als = Spl + Pl. The tetrahedral plot diagrams are drawn by the method of Shimura and Kemp (2015), at a condition of α = 0°, β = 0°, γ = 171°, and dip = 22°.

Stages-IIIb and IIIc are defined by appearance of spinel and disappearance of garnet, respectively (Fig. 12). Coexistence of garnet + sillimanite + spinel + plagioclase is restricted to stage-IIIb (Fig. 12), and the observed spinel + plagioclase symplectite (Fig. 5) is interpreted to have formed in this stage. Small amounts of fine-grained muscovite in the pressure-shadows around garnet (Fig. 4a) is produced at stage-IIIc (Fig. 12).

GEOBAROMETER

Geobarometers for spinel-bearing rocks

Many authors studied spinel-forming reactions in pelitic metamorphic rocks. Some of these were solved as net-transfer reactions (geobarometers). Many geobarometers have been proposed for spinel-bearing pelitic metamorphic rocks (Table 1). For example, net-transfer reaction in Table 1b and Figure 13b is, Grt + 2Als = Spl + Crd. This reaction means that the product minerals are spinel and cordierite. As a result, the spinel must be in contact with cordierite. Such textures are well-known from the amphibolite-facies or granulite-facies metamorphic rocks (e.g., Clarke and Powell, 1991; Komatsu et al., 1994). However, our sample TMD40 is cordierite absent.

Table 1. Spinel-forming net transfer reactions and related geobarometers

Reaction number	Net-transfer reaction	System	Als	Reference of geobarometer
(a)	Crd = 2(Hc, Spl) + 5Qz	FAS	-	Harris (1981)
		FAS	-	Seifert and Schumacher (1986)
		MAS
		MAS	-	Perchuk et al. (1989)
		FMAS	-	Vielzeuf (1983)
		FASZn MASZn	-	Nichols et al. (1992)
(b)	(Alm, Prp) + 2Als ​ = (Hc, Spl) + Crd	FAS	Sil	Harris (1981) Droop and Charnley (1985)
		MAS	Sil	Perchuk et al. (1989)
(c)	5En + 10Als = 2Spl + 4Crd	MAS	Sil	Harris and Holland (1984)
(d)	(Alm, Prp) + 2Als ​​ = 3(Hc, Spl) + 5Qz	FAS	Sil	Bohlen et al. (1986)
		MAS	Sil	Perchuk et al. (1989)
		FASZn MASZn	Sil, Ky	Nichols et al. (1992)
(e)	Alm + 5Crn = 3Hc + 3Als	FAS	Sil	Bohlen et al. (1986) Shulters and Bohlen (1989)
(f)	5Grs + (Alm, Prp) + 12Als ​​ = 3(Hc, Spl) + 15An	CFASZn CMASZn	And, Sil, Ky	This Study

On the other hand, net-transfer reactions which related spinel + quartz assemblage are, Crd = Spl + Qz (Fig. 13a and Table 1a) and Grt + 2Als = 3Spl + 5Qz (Fig. 13d and Table 1d). These equations mean that the product minerals are spinel and quartz. As a result, the spinel must be in contact with quartz directly (e.g., Vielzeuf, 1983; Shimura et al., 2002; Kawakami and Motoyoshi, 2004; Kawasaki et al., 2011). Generally, almost all pelitic metamorphic rocks contain quartz. However, spinel does not occur in contact with quartz in the amphibolite facies and/or in the granulite facies (lower than the UHT) conditions. One reason for this is that cordierite lies on the spinel-quartz tie line, in the composition-paragenesis diagram (Fig. 13a). Since the paragenesis is subdivided into two assemblages, cordierite + quartz and spinel + cordierite, spinel + quartz assemblage is not stable (Fig. 13a). Therefore, reactions (a) and (d) geobarometers cannot be used for such metamorphic conditions.

Reactions (b) and (c) in Table 1 and Figure 13 have cordierite as a product. Reactions (c) and (e) in Table 1 and Figure 13 have orthopyroxene and corundum as reactants, respectively. However, our sample TMD40 is absent of cordierite, orthopyroxene, and corundum. Therefore, for our sample TMD40, all spinel-related previously proposed geobarometers in Table 1a-e cannot be used. The pressure condition of our spinel-bearing texture cannot be solved by the those previously proposed geobarometers.

Garnet-aluminosilicate-spinel-plagioclase (GASpP) geobarometer

Textural evidence from our sample suggests that the reactants are garnet and sillimanite, and the products are spinel and plagioclase (Fig. 5). This texture implies the following reaction;   

\begin{equation} \text{Grt} + \text{Sil} = \text{Spl} + \text{Pl} \end{equation} (1).

This reaction can be explained within the CaO-FeO-Al₂O₃-SiO₂ system and the CaO-MgO-Al₂O₃-SiO₂ system. The four-component CFAS or CMAS system is illustrated by a tetrahedral-plot diagram (e.g., Shimura and Kemp, 2015) (Fig. 13f). In this diagram, garnet solid-solution is plotted on a (Prp/Alm)-Grs line. Reactants garnet solid solution + sillimanite are shown as a triangular plane of (Prp/Alm)-Grs-Sil. On the other hand, products spinel + plagioclase are shown as a tie-line of Spl-An. As shown in Figure 13f, the reactants plane is cut by the products line. It must be solved as a net-transfer reaction. We solved this reaction as the following two net-transfer reactions;   

\begin{align} &\text{CFAS system:} \\&\quad \text{5Grs} + \text{Alm} + \text{12Als} = \text{3Hc} + \text{15An} \\ &\quad \text{5Ca$_{3}$Al$_{2}$Si$_{3}$O$_{12}$} + \text{Fe$_{3}$Al$_{2}$Si$_{3}$O$_{12}$} + \text{12Al$_{2}$SiO$_{5}$} \\&\qquad= \text{3FeAl$_{2}$O$_{4}$} + \text{15CaAl$_{2}$Si$_{2}$O$_{8}$} \\ &\quad \text{and}\\ &\text{CMAS system:} \qquad \\&\quad \text{5Grs} + \text{Prp} + \text{12 Als} \\ &\qquad= \text{3Spl (Mg-endmember)} + \text{15An} \\ &\quad \text{5Ca$_{3}$Al$_{2}$Si$_{3}$O$_{12}$} + \text{Mg$_{3}$Al$_{2}$Si$_{3}$O$_{12}$} + \text{12Al$_{2}$SiO$_{5}$} \\&\qquad= \text{3MgAl$_{2}$O$_{4}$} + \text{15CaAl$_{2}$Si$_{2}$O$_{8}$} \end{align} (2).

Such reactions for sillimanite and kyanite were described by Ravindra Kumar and Chacko (1994) and Rötzler and Romer (2001), respectively. They solved the reactions by the TWQ program (Berman and Aranovich, 1996a, 1996b). We employed thermodynamic data from Holland and Powell (2011) (Table 2) for these reactions. Calculated results of parameters on CFAS and CMAS reactions are also shown in Table 2. We substitute these parameters in the geobarometer equation;   

\begin{equation} P = (\varDelta H - T\varDelta S + RT \ln K_{\text{eq}})/ (-\varDelta V) \end{equation} (3).

Consequently, we propose the following new garnet-aluminosilicate-spinel-plagioclase (GASpP) geobarometers:   

\begin{align} &P_{\text{[CFAS, Ky-bearing]}} \\&\quad = (-241950 + 730.2T + RT{\ln}K_{\text{Fe}})/36.242, \\ &P_{\text{[CMAS, Ky-bearing]}} \\&\quad = (-218730 + 707.0T + RT{\ln}K_{\text{Mg}})/36.163, \\ &P_{\text{[CFAS, Sil-bearing]}} \\&\quad = (-155790 + 587.4T + RT{\ln}K_{\text{Fe}})/29.378, \\ &P_{\text{[CMAS, Sil-bearing]}} \\&\quad= (-132570 + 564.2T + RT{\ln}K_{\text{Mg}})/29.299, \\ &P_{\text{[CFAS, And-bearing]}} \\&\quad= (-190350 + 619.8T + RT{\ln}K_{\text{Fe}})/27.374,\\ &\quad \text{and} \\ &P_{\text{[CMAS, And-bearing]}} \\&\quad= (-167130 + 596.6T + RT{\ln}K_{\text{Mg}})/27.295 \end{align} (4).

Where P is pressure in bar, T is temperature in K. R is gas constant, 8.3145 J mol⁻¹ K⁻¹. The equilibrium constant K_eq is   

\begin{align} &K_{\text{Fe}} = (a_{\text{Grs}}^{5}\ a_{\text{Alm}})/(a_{\text{Hc}}^{3}\ a_{\text{An}}^{15})\quad \\ &\quad \text{and} \\ &K_{\text{Mg}} = (a_{\text{Grs}}^{5}\ a_{\text{Prp}})/(a_{\text{Spl}}^{3}\ a_{\text{An}}^{15}) \end{align} (5).

Where a_i means activity of endmember i.

Table 2. Thermodynamic parameters for the garnet-aluminosilicate-spinel-plagioclase (GASpP) geobarometer

End-member	H (kJ/mol)	S (J/mol K)	V (J/bar)
Grs	−6643.01	255.0	12.535
Alm	−5260.70	342.0	11.525
Prp	−6281.96	269.5	11.313
Sps	−5693.49	335.3	11.792
Ky	−2592.97	83.5	4.414
Sil	−2585.79	95.4	4.986
And	−2588.67	92.7	5.153
Hc	−1953.03	113.9	4.075
Spl	−2301.19	82.0	3.978
An	−4232.69	200.5	10.079
CFAS-system	H (kJ/mol)	S (J/mol K)	V (J/bar)	ΔS/ΔV
5Grs + Alm + 12Ky	−69591.39	2619.0	127.168
5Grs + Alm + 12Sil	−69505.23	2761.8	134.032
5Grs + Alm + 12And	−69539.79	2729.4	136.036
3Hc + 15An	−69349.44	3349.2	163.410
Δ [Ky]	−241.95	−730.2	−36.242	20.15
Δ [Sil]	−155.79	−587.4	−29.378	19.99
Δ [And]	−190.35	−619.8	−27.374	22.64
CMAS-system	H (kJ/mol)	S (J/mol K)	V (J/bar)	ΔS/ΔV
5Grs + Prp + 12Ky	−70612.65	2546.5	126.956
5Grs + Prp + 12Sil	−70526.49	2689.3	133.820
5Grs + Prp + 12And	−70561.05	2656.9	135.824
3Spl + 15An	−70393.92	3253.5	163.119
Δ [Ky]	−218.73	−707.0	−36.163	19.55
Δ [Sil]	−132.57	−564.2	−29.299	19.26
Δ [And]	−167.13	−596.6	−27.295	21.86

Original thermodynamic dataset (H, S, V) of each endmembers of minerals are employed from Table 2a of Holland and Powell (2011) and their ‘tc-ds62’ file (which date description is 6 Feb, 2012) in the THERMOCALC.

Activity-composition relationships (a-x relation) of garnet are explained by the regular solution model by many authors (e.g., Ganguly and Saxena, 1984; Berman, 1990; Mukhopadhyay et al., 1997; White et al., 2014). Garnet solid solution can be written as A²⁺₃B³⁺₂Si₃O₁₂. The divalent cations such as Fe²⁺, Mn²⁺, Mg²⁺, and Ca²⁺ occupy the A-site, and the trivalent cations such as Fe³⁺, Cr³⁺, and Al³⁺ occupy the B-site. Wu (2015) described that ‘Fe³⁺ and Cr³⁺ cations in metapelitic garnet are negligible due to extreme dilution, therefore, only the mixing properties of the divalent cations on the dodecahedral sites are considered’. Wood and Fraser (1976) described that ‘it is rarely necessary to extend the symmetric solution treatment beyond three or four components despite the presence of many minor components in phases of geological interest’. Consequently, we consider garnet as pyralspite garnet, (Fe, Mn, Mg, Ca)₃Al₂Si₃O₁₂. Then;   

\begin{align} &X_{\text{Alm}} = \text{Fe}/(\text{Fe} + \text{Mn} + \text{Mg} + \text{Ca}), \\ &X_{\text{Prp}} = \text{Mg}/(\text{Fe} + \text{Mn} + \text{Mg} + \text{Ca}),\\ &\quad \text{and} \\ &X_{\text{Grs}} = \text{Ca}/(\text{Fe} + \text{Mn} + \text{Mg} + \text{Ca}) \end{align} (6).

Where X_A is mole fraction of endmember A.

Mukhopadhyay et al. (1993) and Berman (1990) described ternary (three components i, j, and k) asymmetric regular solution model;   

\begin{align} RT \ln \gamma_{\text{i}} &= 2(X_{\text{i}}X_{\text{j}}W_{\text{ji}} + X_{\text{i}}X_{\text{k}}W_{\text{ki}}) + X_{\text{j}}^{2}W_{\text{ij}} + X_{\text{k}}^{2}W_{\text{ik}} \\ &\quad - 2[X_{\text{i}}X_{\text{j}}(X_{\text{j}}W_{\text{ij}} + X_{\text{i}}W_{\text{ji}}) \\ &\quad + X_{\text{i}}X_{\text{k}}(X_{\text{k}}W_{\text{ik}} + X_{\text{i}}W_{\text{ki}}) \\ &\quad + X_{\text{j}}X_{\text{k}}(X_{\text{k}}W_{\text{jk}} + X_{2}W_{\text{kj}})] \end{align} (7).

Where γ_i is activity coefficient for component i, and W_ij or W_kj are Margules parameters for components i, j, and k. Since the ternary interaction parameters are often neglected (e.g., Anderson and Crerar, 1993), W_ijk is neglected in Equation 7. Other expressions for RT ln γ_i can be obtained by cyclically rotating the subscripts in the Equation 8 (i → j → k → i). Here, if we use i = Ca, j = Mg, and k = Fe, solution models of garnet are,   

\begin{align} RT{\ln}\gamma_{\text{Fe}} &= 2(X_{\text{Fe}}X_{\text{Ca}}W_{\text{CaFe}} + X_{\text{Fe}}X_{\text{Mg}}W_{\text{MgFe}}) \\ &\quad + X_{\text{Ca}}^{2}W_{\text{FeCa}} + X_{\text{Mg}}^{2}W_{\text{FeMg}} \\ &\quad - 2[X_{\text{Fe}}X_{\text{Ca}}(X_{\text{Ca}}W_{\text{FeCa}} + X_{\text{Fe}}W_{\text{CaFe}}) \\ &\quad + X_{\text{Fe}}X_{\text{Mg}}(X_{\text{Mg}}W_{\text{FeMg}} + X_{\text{Fe}}W_{\text{MgFe}}) \\ &\quad + X_{\text{Ca}}X_{\text{Mg}}(X_{\text{Mg}}W_{\text{CaMg}} + X_{\text{Ca}}W_{\text{MgCa}})], \\ RT{\ln}\gamma_{\text{Mg}} &= 2(X_{\text{Mg}}X_{\text{Fe}}W_{\text{FeMg}} + X_{\text{Mg}}X_{\text{Ca}}W_{\text{CaMg}}) \\ &\quad + X_{\text{Fe}}^{2}W_{\text{MgFe}} + X_{\text{Ca}}^{2}W_{\text{MgCa}} \\ &\quad - 2[X_{\text{Mg}}X_{\text{Fe}}(X_{\text{Fe}}W_{\text{MgFe}} + X_{\text{Mg}}W_{\text{FeMg}}) \\ &\quad + X_{\text{Mg}}X_{\text{Ca}}(X_{\text{Ca}}W_{\text{MgCa}} + X_{\text{Mg}}W_{\text{CaMg}}) \\ &\quad + X_{\text{Fe}}X_{\text{Ca}}(X_{\text{Ca}}W_{\text{FeCa}} + X_{\text{Fe}}W_{\text{CaFe}})],\quad \\ &\text{and}\\ RT{\ln}\gamma_{\text{Ca}} &= 2(X_{\text{Ca}}X_{\text{Mg}}W_{\text{MgCa}} + X_{\text{Ca}}X_{\text{Fe}}W_{\text{FeCa}}) \\ &\quad + X_{\text{Mg}}^{2}W_{\text{CaMg}} + X_{\text{Fe}}^{2}W_{\text{CaFe}} \\ &\quad - 2[X_{\text{Ca}}X_{\text{Mg}}(X_{\text{Mg}}W_{\text{CaMg}} + X_{\text{Ca}}W_{\text{MgCa}}) \\ &\quad + X_{\text{Ca}}X_{\text{Fe}}(X_{\text{Fe}}W_{\text{CaFe}} + X_{\text{Ca}}W_{\text{FeCa}}) \\ &\quad + X_{\text{Mg}}X_{\text{Fe}}(X_{\text{Fe}}W_{\text{MgFe}} + X_{\text{Mg}}W_{\text{FeMg}})] \end{align} (8).

  

\begin{align} &a_{\text{Alm}} = (X_{\text{Fe}}\ \gamma_{\text{Fe}})^{3},\ a_{\text{Prp}} = (X_{\text{Mg}}\ \gamma_{\text{Mg}})^{3},\ \\ &\quad \text{and}\quad a_{\text{Grs}} = (X_{\text{Ca}} \ \gamma_{\text{Ca}})^{3} \end{align} (9).

We employ Margules parameters as average values from Holdaway (2000). These are W_FeMg = −5672 J, W_MgFe = 11622 J, W_FeCa = 19932 J, W_CaFe = −1304 J, W_CaMg = 66114 J, and W_MgCa = 25759 J.

Feldspar is CaAl₂Si₂O₈-NaAlSi₃O₈-KAlSi₃O₈ solid solution. The a-x relation of plagioclase is not simple, because it has a miscibility gap by phase transition (e.g., Carpenter and McConnell, 1984). Holland and Powell (1992) describes the a-x relation of plagioclase based upon Darken’s quadratic formalism (e.g., Powell, 1987) and Landau’s theory of phase transitions (e.g., Carpenter and McConnell, 1984). The following equations (Eqs. 10-14) are after Holland and Powell (1992);   

\begin{align} &X_{\text{Ca}} = \text{Ca}/(\text{Ca} + \text{Na} + \text{K}),\quad \\ &\quad \text{and}\quad X_{\text{Na}} = \text{Na}/(\text{Ca} + \text{Na} + \text{K}) \end{align} (10).

For phase transition of plagioclase, they used two kinds of factors (X_An and X_b);   

\begin{equation} X_{\text{An}} = (1/16)\ X_{\text{Ca}}\ (1 + X_{\text{Ca}})^{2}\ (3 - X_{\text{Ca}})^{2} \end{equation} (11a)

  and   

\begin{equation} X_{\text{b}} = 0.12 + 0.00038T \end{equation} (11b).

Where X_b marks the location of the transition between different a-x relations, following Carpenter and McConnell (1984). And then;   

\begin{align} I_{\text{An}} &= -(W_{\text{c}} - W_{\text{i}})\ (1 - X_{\text{b}})^{2} \\&\quad- RT{\ln}\ [(1 + X_{\text{b}})^{2}\ (3 - X_{\text{b}})^{2}\ {/}16] \end{align} (12).

Where I_An is contiguity factor of transition boundary. W_c and W_i are interaction parameters, W_c = 5510 J and W_i = 9770 J for model 4 of Holland and Powell (1992).

Finally, for the anorthite a-x relations, they proposed two kinds of equations,

If X_Ca ≥ X_b conditions, a-x relation is;   

\begin{equation} RT{\ln}\gamma_{\text{An}} = W_{\text{c}}\ X_{\text{Na}}^{2} + I_{\text{An}}\quad \text{and}\quad a_{\text{An}} = X_{\text{An}}\ \gamma_{\text{An}} \end{equation} (13).

If X_Ca ≥ X_b conditions, a-x relation is;   

\begin{equation} RT{\ln}\gamma_{\text{An}} = W_{\text{i}}\ X_{\text{Na}}^{2}\quad \text{and} \quad a_{\text{An}} = X_{\text{Ca}}\ \gamma_{\text{An}} \end{equation} (14).

a-x relation of spinel was described by many authors (e.g., White et al., 2002; Holland and Powell, 2011). For our geobarometers, not only A-site composition, but also aluminum occupancy in the B-site is important, within the A²⁺B³⁺₂O₄ stoichiometry. Therefore, we use the approach of Harris (1981) and Goscombe et al. (1998);   

\begin{align} &X_{\text{Fe}} = \text{Fe}^{2+}/A^{2+},\ X_{\text{Mg}} = \text{Mg}/A^{2+},\ X_{\text{Zn}} = \text{Zn}/A^{2+},\ \\&\quad\text{and}\quad X_{\text{Al}} = \text{Al}/B^{3+} \end{align} (15).

Where A²⁺ and B³⁺ are total cation number of each site, in ideal chemical composition as A²⁺B³⁺₂O₄ of the spinel group. Moreover, we correct zinc content by using the non-ideal interaction parameter W from Nichols et al. (1992), W_MgFe = 1960 J, W_FeZn = −3800 J, and W_MgZn = −2600 J.   

\begin{align} &RT \ln \gamma_{\text{Hc}} = W_{\text{MgFe}}\ (X_{\text{Mg}}^{2} + X_{\text{Mg}}X_{\text{Zn}}) \\&\qquad\qquad\quad + W_{\text{FeZn}}\ (X_{\text{Zn}}^{2} + X_{\text{Mg}}X_{\text{Zn}}) \\&\qquad\qquad\quad + W_{\text{MgZn}}\ (-X_{\text{Mg}}X_{\text{Zn}}), \\ &RT \ln \gamma_{\text{Spl}} = W_{\text{MgFe}} (X_{\text{Fe}}^{2} + X_{\text{Fe}}X_{\text{Zn}}) \\&\qquad\qquad\quad + W_{\text{MgZn}} (X_{\text{Zn}}^{2} + X_{\text{Fe}}X_{\text{Zn}}) \\&\qquad\qquad\quad + W_{\text{FeZn}} (-X_{\text{Fe}}X_{\text{Zn}}), \\ &\quad\text{and}\\ &a_{\text{Hc}} = X_{\text{Al}}^{2}X_{\text{Fe}}\gamma_{\text{Hc}},\quad \text{and}\quad a_{\text{Spl}} = X_{\text{Al}}^{2}X_{\text{Mg}}\gamma_{\text{Spl}} \end{align} (16).

Because the ΔS/ΔV is very small (19.26-22.64) (Table 2), dP/dT slopes of the above-mentioned equations are very gentle, making these reactions good geobarometers (Fig. 14).

Figure 14. Pressure-temperature diagram contoured for equilibrium constant (K_eq) for the GASpP geobarometer. K_Fe = (a_Grs⁵ a_Alm)/(a_Hc³ a_An¹⁵) for CFAS system and K_Mg = (a_Grs⁵ a_Prp)/(a_Spl³ a_An¹⁵) for CMAS system.

Consistency of the GASpP barometer

As described earlier, previously proposed spinel-bearing geobarometers (Table 1a-e) cannot be used for the spinel-bearing texture of our sample TMD40. On the other hand, garnet-aluminosilicate-silica-plagioclase geobarometer (GASP) is represented by the reaction;   

\begin{align} &\text{Grs} + \text{2Als} + \text{Qz} = \text{3An}\quad \\ &\quad \text{and} \\ &\text{Ca$_{3}$Al$_{2}$Si$_{3}$O$_{12}$} + \text{2Al$_{2}$SiO$_{5}$} + \text{SiO$_{2}$} = \text{3CaAl$_{2}$Si$_{2}$O$_{8}$} \end{align} (17).

GASP was first proposed by Ghent (1976). After that, many authors proposed new models (e.g., see review in Holdaway, 2001). The GASP equation includes quartz, but does not include spinel (Eqs. 17). On the other hand, our GASpP equation includes spinel, but does not include quartz (Eqs. 1 and 2). Both geobarometers include garnet, plagioclase, and aluminosilicate. We arranged GASP by thermodynamic data (Holland and Powell, 2011) and their ‘tc-ds62’ file in the THEMOCALC. These equations are;   

\begin{align} &P_{\text{[Ky-bearing]}} = (40770 - 136.5T - RT{\ln}K)/(-6.605), \\ &P_{\text{[Sil-bearing]}} = (26290 - 112.5T - RT{\ln}K)/(-5.461),\ \\ &\quad \text{and} \\ &P_{\text{[And-bearing]}} = (32050 - 118.1T - RT{\ln}K)/(-5.127) \end{align} (18).

Where K = a_Grs/a_An³. Activity models of garnet and plagioclase are same as described above (Equations 6-9 for garnet, Equations 10-14 for plagioclase).

Figure 15a shows calculation results of GASpP geobarometer by 54 metamorphic samples in Supplementary Table S2. Figure 15b shows GASP versus GASpP calculation results with the same data. Although equilibrium conditions between spinel and quartz are not established for certain in GASP equations, except for UHT assemblages (see Table S2 and its references), the calculation results are consistent with wide P-T conditions (Fig. 15 and Table S2). GASpP is free from quartz, corundum, orthopyroxene, and cordierite (Table 1 and Fig. 13). The GASpP barometer is useful to estimate pressure conditions for spinel-bearing pelitic metamorphic rocks across a wide range of P-T conditions (andalusite, kyanite, and sillimanite fields) and mineral assemblages (Figs. 14, 15, and Table S2). P(GASpP, CFASZn)-P(GASpP, CMASZn) diagrams are also consistent (Fig. 15c). Calculation results of CFASZn and CMASZn from our TMD40 sample are almost the same (Table S2 and S3-4). We note that careful observations of petrography and quality of analysis data are important for such geothermo-barometric calculations.

Figure 15. Calculation results of the GASpP geobarometer for the 54 metamorphic samples from various areas (see Table S2). (a) P (GASpP) versus reference temperature diagram. The reference temperatures were referred from each original thesis. Phase relations of aluminosilicates are also shown. (b) P (GASP) versus P (GASpP) diagram by the same garnet and plagioclase compositions. (c) P (GASpP, CFASZn-system) versus P (GASpP, CMASZn-system) diagram.

Metamorphic conditions of Tenmondai Rock

Previous studies reported that the peak P-T conditions of Tenmondai Rock were about 750 °C and 720-750 MPa (e.g., Hiroi et al., 1983). Recently, several authors reported higher peak conditions of 750-800 °C and 800-900 MPa from pelitic metamorphic rock (Baba et al., 2019a, 2019b) or 850-860 °C and 780-840 MPa from mafic metamorphic rock (Takamura et al., 2019a, 2019b, 2020). Takamura et al. (2020) reported metamorphic rock from Tenmondai rock, and they described a clockwise P-T-t path.

For our sample TMD40, metamorphic P-T conditions of each stage (Fig. 12) are calculated from related textures and their mineral compositions (see Tables S1 and S3). For example, Stage-II pressure condition from mantle of porphyroblast garnet and matrix plagioclase by GASP (method by this study) and GRIPS (Ghent and Stout, 1984) barometers (Tables S3-1 and S3-2), and temperature by Zr-in-Rt thermometer (Fig. 11 and Table S1-6). Stage-IIIa pressure condition from embayed garnet texture (Fig. 6) by GRAIL barometer (Table S3-3) and temperature by Zr-in-Rt thermometer (Fig. 11 and Table S1-6). Stage-IIIb pressure condition from spinel + plagioclase symplectite texture by GASpP barometer (method by this study, Table S3-4) and temperature by Zr-in-Rt thermometer (Fig. 11 and Table S1-6).

The metamorphic peak (stage-II) P-T conditions are estimated as about 820 MPa and 850 °C (Fig. 16). These conditions are broadly consistent with recent studies of Tenmondai Rock (Takamura et al., 2020). The retrograde stage-IIIa P-T conditions are slightly lower than the peak P-T conditions (Fig. 16).

Figure 16. Metamorphic pressure-temperature path of Tenmondai Rock. Gray striped areas are P-T conditions estimated by several authors. These are; H83: Hiroi et al. (1983), B19: Baba et al. (2019a, 2019b), T19: Takamura et al. (2019a, 2019b), and T20: Takamura et al. (2020). Blue dashed lines are calculation results of geobarometers for stage II-IIIa, from related mineral compositions of each stage texture, by GASP (this study), GRAIL (Bohlen et al., 1983), and GRIPS (Ghent and Stout, 1984) barometers. Red dashed lines are calculation results by Zr-in-rutile thermometer (Tomkins et al., 2007; Kohn, 2020). The green box shows calculation results for stage IIIb using the GASpP barometer of this study. Phase relations of aluminosilicates are calculated by PERPLEX (Connolly, 2005). A reaction line of Ms + Qz = Als + Kfs+ V/L is from Vielzeuf and Holloway (1988) and Spear and Cheney (1989).

In contrast to the peak conditions, results from our GASpP geobarometer indicate a narrow range of pressure conditions, around 400-500 MPa. Occurrence of rutile in spinel + plagioclase symplectite texture (Fig. 5i) is rare; we found only two rutile grains in many thin-sections. The mineral paragenesis of rutile is not clear, and analyzed data of the rutile is poor, but the zirconium content is between that of inclusions in garnet and that around ilmenite associated with chlorite (Figs. 5j, 5k, and 11). As a result, we regard the Zr-in-Rt temperature of stage-IIIb to be lower than that of the lower limit of inclusions in garnet, and higher than that of the upper limit of around ilmenite (Fig. 11). We estimate the Stage-IIIb temperature is about 675-730 °C. The assemblage ‘garnet + sillimanite + spinel + plagioclase’ is stable only at stage-IIIb (Fig. 12). We interpret our spinel + plagioclase symplectite is produced by decompression from a garnet + sillimanite assemblage at stage-IIIb, at pressures defining the lower stability limit of garnet + sillimanite during the retrograde stage (Figs. 12 and 16).

Conclusions and implications

Decompressional metamorphic P-T-t paths produce spinel + plagioclase textures from the reaction of garnet + aluminosilicate (e.g., this study; Hiroi et al., 1997; Rötzler and Romer, 2001; Álvarez-Valero et al., 2007). An example is provided here from Tenmondai Rock, East Antarctica, which experienced a clockwise P-T-t path. In contrast, counter-clockwise metamorphic P-T-t paths produce garnet + aluminosilicate from reaction of spinel + feldspar assemblages (e.g., Boger and White, 2003; Zhang et al., 2012; Sarkar and Schenk, 2014).

We propose a new geobarometer (GASpP) based on the reaction ‘garnet + aluminosilicate = spinel + plagioclase’, with application across a wide range of P-T conditions. Application of this geobarometer provides new constraints on the magnitude of decompression at Tenmondai Rock.

ACKNOWLEDGMENTS

We (Tsuchiya, Shimura, and Fraser) visited Tenmondai Rock, 11-13 February 1994, during the geological field survey of the 35th Japanese Antarctic Research Expedition (JARE-35) (1993-1994). The sample TMD40 of this study was collected at that time. We wish to thank all members of JARE-35 and the crew of the icebreaker SHIRASE, and the National Institute of Polar Research, for their support in the fieldwork. We would like to thank all members of the JARE geology group for their fruitful discussions. We wish to thank Prof. George L. Luvizotto, who kindly distributed rutile standard samples to us. Mr. Youji Morihuku helped us with EPMA analysis. Constructive reviews by two anonymous reviewers and editorial comments by Prof. T. Kawakami improved the manuscript drastically and are gratefully acknowledged. Part of this study was supported by JSPS KAKENHI Grant Numbers JP24540509 and JP15K05343 to T. Shimura.

SUPPLEMENTARY MATERIALS

Table S1 (Representative mineral compositions) Table S2 and its references (original data of Figure 15), and calculation examples of geobarometers Table S3 (calculation examples of geobarometers) are available online from https://doi.org/10.2465/jmps.221130.

REFERENCES

•  Álvarez-Valero,  A.M.,  Cesare,  B. and  Kriegsman,  L.M. (2007) Formation of melt-bearing spinel-cordierite-feldspar-glass coronas after garnet in metapelitic xenoliths: reaction modelling and geodynamic implications. Journal of Metamorphic Geology, 25, 305-320.
• Anderson, G.M. and Crerar, D.A. (1993) Thermodynamics in geochemistry. The equilibrium model. pp. 588, Oxford University Press.
• Baba, S., Hokada, T., Kamei, A., Kitano, I. and Motoyoshi, Y. (2019a) Metamorphic conditions of pelitic gneisses in Prince Olav Coast, East Antarctica. The 126th Annual Meeting of the Geological Society of Japan, 205 (in Japanese).
• Baba, S., Hokada, T., Kamei, A., Kitano, I., et al. (2019b) New insights into the metamorphic evolution of the Lützow-Holm Complex along the Prince Olav Coast, East Antarctica. 2019 IAGR Annual Convention &16th International Conference on Gondwana to Asia, Abstract Volume, IAGR Conference Series No. 25, 1-2.
•  Baldwin,  J.A.,  Powell,  R.,  White,  R.W. and  Štípská,  P. (2015) Using calculated chemical potential relationships to account for replacement of kyanite by symplectite in high pressure granulites. Journal of Metamorphic Geology, 33, 331-330.
•  Berman,  R.G. (1990) Mixing properties of Ca-Mg-Fe-Mn garnets. American Mineralogist, 75, 328-344.
•  Berman,  R.G. and  Aranovich,  L.Ya. (1996a) Optimized standard state and solution properties of minerals: I. Model calibration for olivine, orthopyroxene, cordierite, garnet, and ilmenite in the system FeO-MgO-CaO-Al₂O₃-TiO₂-SiO₂. Contributions to Mineralogy and Petrology, 126, 1-24.
•  Berman,  R.G. and  Aranovich,  L.Ya. (1996b) Optimized standard state and solution properties of minerals: II. Comparisons, predictions, and applications. Contributions to Mineralogy and Petrology, 126, 25-37.
•  Biagioni,  C. and  Pasero,  M. (2014) The systematics of the spinel-type minerals: An overview. American Mineralogist, 99, 1254-1264.
•  Boger,  S.D. and  White,  R.W. (2003) The metamorphic evolution of metapelitic granulites from Radok Lake, northern Prince Charles Mountains, East Antarctica; evidence for an anticlockwise P-T path. Journal of Metamorphic Geology, 21, 285-298.
•  Bohlen,  S.,  Wall,  V.J. and  Boettcher,  A.L. (1983) Experimental investigations and geological applications of equilibria in the system FeO-TiO₂-Al₂O₃-SiO₂-H₂O. American Mineralogist, 68, 1049-1058.
•  Bohlen,  S.R.,  Dollase,  W.A. and  Wall,  V.J. (1986) Calibration and applications of spinel equilibria in the system FeO-Al₂O₃-SiO₂. Journal of Petrology, 27, 1143-1156.
•  Carpenter,  M.A. and  McConnell,  J.D.C. (1984) Experimental delineation of the C1 = I1 transformation in intermediate plagioclase feldspars. American Mineralogist, 69, 112-121.
•  Carson,  C.J.,  Powell,  R.,  Wilson,  C.J.L. and  Dirks,  G.M. (1997) Partial melting during tectonic exhumation of a granulite terrane: an example from the Larsemann Hills, East Antarctica. Journal of Metamorphic Geology, 15, 105-126.
•  Clark,  C.,  Fitzsimons,  I.C.W.,  Healy,  D. and  Harley,  S.L. (2011) How does the continental crust get really hot? Elements, 7, 235-240.
•  Clarke,  G.L. and  Powell,  R. (1991) Decompressional coronas and symplectites in granulites of the Musgrave Complex, central Australia. Journal of Metamorphic Geology, 9, 441-450.
•  Colás,  V.,  Padrón-Navarta,  J.A.,  González-Jiménez,  J.M.,  Griffin,  W.L., et al (2016) Compositional effects on the solubility of minor and trace elements in oxide spinel minerals: Insights from crystal-crystal partition coefficients in chromite exsolution. American Mineralogist, 101, 1360-1372.
•  Connolly,  J.A.D. (2005) Computation of phase equilibria by linear programming: A tool for geodynamic modeling and its application to subduction zone decarbonation. Earth and Planetary Science Letters, 236, 524-541.
•  Cruciani,  G.,  Franceschelli,  M.,  Scodina,  M. and  Puxeddu,  M. (2019) Garnet zoning in kyanite-bearing eclogite from Golfo Aranci: New data on the early prograde P-T evolution in NE Sardinia, Italy. Geological Journal, 54, 190-205.
• Deer, W.A., Howie, R.A. and Zussman, J. (2013) An introduction to the rock-forming minerals. 3rd edition. pp. 549, The Mineralogical Society.
•  Droop,  G.T.R. (1987) A general equation for estimating Fe³⁺ concentrations in ferromagnesian silicates and oxides from microprobe analyses, using stoichiometric criteria. Mineralogical Magazine, 51, 431-435.
•  Droop,  G.T.R. and  Charnley,  N.R. (1985) Comparative geobarometry of pelitic hornfelses associated with the Newer Gabbros: a preliminary study. Journal of the Geological Society London, 142, 53-62.
•  Dunkley,  D.J.,  Hokada,  T.,  Shiraishi,  K.,  Hiroi,  Y., et al (2020) Geological subdivision of the Lützow-Holm Complex in East Antarctica: from the Neoarchean to the Neoproterozoic. Polar Science, 26, 100606.
•  Fraser,  G.,  McDougall,  I.,  Ellis,  D.J. and  Williams,  I.S. (2000) Timing and rate of isothermal decompression in Pan-African granulites from Rundvågshetta, East Antarctica. Journal of Metamorphic Geology, 18, 441-454.
•  Ganguly,  J. and  Saxena,  S. (1984) Mixing properties of aluminosilicate garnets: constraints from natural and experimental data, and applications to geothermobarometry. American Mineralogist, 69, 88-97.
•  Ganguly,  P.,  Bose,  S.,  Das,  K.,  Torimoto,  J. and  Ghosh,  G. (2017) Origin of spinel + quartz assemblage in a Si-undersaturated ultrahigh-temperature aluminous granulite and its implication for the P-T-fluid history of the Phulbani Domain, Eastern Ghats Belt, India. Journal of Petrology, 58, 1941-1974.
•  Ghent,  E.D. (1976) Plagioclase-garnet-Al₂SiO₅-quartz: a potential geobarometer-geothermometer. American Mineralogist, 61, 710-714.
•  Ghent,  E.D. and  Stout,  M.Z. (1984) TiO₂ activity in metamorphosed pelitic and basic rocks: principles and applications to metamorphism in southeastern Canadian Cordillera. Contributions to Mineralogy and Petrology, 86, 248-255.
•  Goscombe,  B.,  Armstrong,  R. and  Barton,  J.M. (1998) Tectonometamorphic evolution of the Chewore Inliers: partial re-equilibration of high-grade basement during the Pan-African orogeny. Journal of Petrology, 39, 1347-1384.
•  Harley,  S.L. (1998) On the occurrences and characterization of Ultrahigh-Temperature (UHT) crustal metamorphism. Geological Society London Special Publications, 138, 81-107.
•  Harley,  S.L. (2008) Refining the P-T records of UHT crustal metamorphism. Journal of Metamorphic Geology, 26, 125-154.
•  Harris,  N. (1981) The application of spinel-bearing metapelites to P/T determinations: an example from south India. Contributions to Mineralogy and Petrology, 76, 229-233.
•  Harris,  N. and  Holland,  T.J.B. (1984) The significance of cordierite-hypersthene assemblages from the Beitbridge region of the Central Limpopo Belt; evidence for rapid decompression in the Archaean? American Mineralogist, 69, 1036-1049.
•  Hensen,  B.J. and  Green,  D.H. (1971) Experimental study of the stability of cordierite and garnet in pelitic compositions at high pressures and temperatures. I. Compositions with Excess Alumino-Silicate. Contributions to Mineralogy and Petrology, 33, 309-330.
•  Hiroi,  Y.,  Shiraishi,  K. and  Kizaki,  K. (1983) Aluminum silicates in the Prince Olav and Soya Coasts, East Antarctica. Memoirs of National Institute of Polar Research Special Issue, 28, 115-131.
• Hiroi, Y., Shiraishi, K. and Motoyoshi, Y. (1991) Late Proterozoic paired metamorphic complexes in East Antarctica, with special reference to the tectonic significance of ultramafic rocks. In Geological evolution of Antarctica (Thomson, M.R.A., Crame, J.A. and Thomson, J.W. Eds.). Cambridge University Press, Cambridge, 83-87.
• Hiroi, Y., Motoyoshi, Y., Shiraishi, K. and Mathavan, V. (1997) Local formation of hercynite-plagioclase symplectite after garnet and sillimanite in khondalite from Habarana, Sri Lanka: mineral textures. Proceedings of the NIPR Symposium on Antarctic Geosciences, 10, 153-164.
•  Hokada,  T. and  Motoyoshi,  Y. (2006) Electron microprobe technique for U-Th-Pb and REE chemistry of monazite, and its implications for pre-, peak- and post-metamorphic events of the Lützow-Holm Complex and the Napier Complex, East Antarctica. Polar Geoscience, 19, 118-151.
•  Holdaway,  M.J. (2000) Application of new experimental and garnet Margules data to the garnet-biotite geothermometer. American Mineralogist, 85, 881-892.
•  Holdaway,  M.J. (2001) Recalibration of the GASP geobarometer in light of recent garnet and plagioclase activity models and versions of the garnet-biotite geothermometer. American Mineralogist, 86, 1117-1129.
•  Holland,  T.J.B. and  Powell,  R. (1992) Plagioclase feldspars: Activity-composition relations based upon Darken’s quadratic formalism and Landau theory. American Mineralogist, 77, 53-61.
•  Holland,  T.J.B. and  Powell,  R. (2011) An improved and extended internally consistent thermodynamic dataset for phases of petrological interest, involving a new equation of state for solids. Journal of Metamorphic Geology, 29, 333-383.
•  Johnson,  T.,  Brown,  M.,  Gibson,  R. and  Wing,  B. (2004) Spinel-cordierite symplectites replacing andalusite: evidence for melt-assisted diapirism in the Bushveld Complex, South Africa. Journal of Metamorphic Geology, 22, 529-545.
•  Kalt,  A.,  Altherr,  R. and  Ludwig,  T. (1998) Contact metamorphism in pelitic rocks on the island of Kos (Greece, Eastern Aegean Sea): a test for the Na-in-cordierite thermometer. Journal of Petrology, 39, 663-688.
•  Kawakami,  T. and  Motoyoshi,  Y. (2004) Timing of attainment of the spinel + quartz coexistence in garnet-sillimanite leucogneiss from Skallevikshalsen, Lützow-Holm Complex, East Antarctica. Journal of Mineralogical and Petrological Sciences, 99, 311-319.
•  Kawakami,  T.,  Hokada,  T.,  Sakata,  S. and  Hirata,  T. (2016) Possible polymetamorphism and brine infiltration recorded in the garnet-sillimanite gneiss, Skallevikshalsen, Lützow-Holm Complex, East Antarctica. Journal of Mineralogical and Petrological Sciences, 111, 129-143.
•  Kawasaki,  T.,  Nakano,  N. and  Osanai,  Y. (2011) Osumilite and a spinel + quartz association in garnet-sillimanite gneiss from Rundvågshetta, Lützow-Holm Complex, East Antarctica. Gondwana Research, 19, 430-445.
•  Kohn,  M.J. (2020) A refined zirconium-in-rutile thermometer. American Mineralogist, 105, 963-971.
•  Komatsu,  M.,  Toyoshima,  T.,  Osanai,  Y. and  Arai,  M. (1994) Prograde and anatectic reactions in the deep arc crust exposed in the Hidaka metamorphic belt, Hokkaido, Japan. Lithos, 33, 31-49.
•  Luvizotto,  G.L.,  Zack,  T.,  Meyer,  H.P.,  Ludwig,  T., et al (2009) Rutile crystals as potential trace element and isotope mineral standards for microanalysis. Chemical Geology, 261, 346-369.
•  Marien,  L.,  Bayon,  B.L.,  Pitra,  P.,  Driessche,  J.V.D., et al (2019) Two-stage Variscan metamorphism in the Canigou massif: Evidence for crustal thickening in the Pyrenees. Journal of Metamorphic Geology, 37, 863-888.
•  Motoyoshi,  Y.,  Matsubara,  S.,  Matsueda,  H. and  Matsumoto,  Y. (1985) Garnet-sillimanite gneiss from the Lützow-Holm Complex, East Antarctica. Memoirs of National Institute of Polar Research Special Issue, 37, 82-94.
• Motoyoshi, Y. and Ishikawa, M. (1997) Metamorphic and structural evolution of granulites from Rundvågshetta, Lützow-Holm Bay, East Antarctica. In The Antarctic region: geological evolution and processes (Ricci, C.A. Ed.). Terra Antarctica Publication, Siena, 65-72.
•  Mukhopadhyay,  B.,  Basu,  S. and  Holdaway,  M.J. (1993) A discussion of Margules-type formulations for multicomponent solutions with a generalized approach. Geochimica et Cosmochimica Acta, 57, 277-283.
•  Mukhopadhyay,  B.,  Holdaway,  M.J. and  Koziol,  A.M. (1997) A statistical model of thermodynamic mixing properties of Ca-Mg-Fe²⁺ garnets. American Mineralogist, 82, 165-181.
•  Nichols,  G.T.,  Berry,  R.F. and  Green,  D.H. (1992) Internally consistent gahnitic spinel-cordierite-garnet equilibria in the FMASHZn system: geothermobarometry and applications. Contributions to Mineralogy and Petrology, 111, 362-377.
•  Perchuk,  L.,  Gerya,  T. and  Nozhkin,  A. (1989) Petrology and retrograde P-T path in granulites of the Kanskaya formation, Yenisey range, Eastern Siberia. Journal of Metamorphic Geology, 7, 599-617.
•  Pitra,  P. and  de Waal,  S.A. (2001) High-temperature, low-pressure metamorphism and development of prograde symplectites, Marble Hall Fragment, Bushveld Complex (South Africa). Journal of Metamorphic Geology, 19, 311-325.
•  Powell,  R. (1987) Darken’s quadratic formalism and the thermodynamics of minerals. American Mineralogist, 72, 1-11.
•  Ravindra Kumar,  C.R. and  Chacko,  T. (1994) Geothermobarometry of mafic granulites and metapelite from the Palghat Gap, South India: petrological evidence for isothermal uplift and rapid cooling. Journal of Metamorphic Geology, 12, 479-492.
•  Rötzler,  J. and  Romer,  R.L. (2001) P-T-t Evolution of ultrahigh-temperature granulites from the Saxon Granulite Massif, Germany. Part I: petrology. Journal of Petrology, 42, 1995-2013.
•  Saki,  A. (2011) Formation of spinel-cordierite-plagioclase symplectites replacing andalusite in metapelitic migmatites of the Alvand aureole, Iran. Geological Magazine, 148, 423-434.
•  Santosh,  M.,  Tsunogae,  T.,  Li,  J.H. and  Liu,  S.J. (2007) Discovery of sapphirine-bearing Mg-Al granulites in the North China Craton: Implications for Paleoproterozoic ultrahigh temperature metamorphism. Gondwana Research, 11, 263-285.
•  Sarkar,  T. and  Schenk,  V. (2014) Two-stage granulite formation in a Proterozoic magmatic arc (Ongole domain of the Eastern Ghats Belt, India): Part 1. Petrology and pressure-temperature evolution. Precambrian Research, 255, 485-509.
•  Sawaki,  T.,  Sasaki,  M.,  Fujimoto,  K.,  Takeno,  N., et al (2001) Corundum and zincian spinel from the Kakkonda geothermal system, Iwate Prefecture, northeastern Japan. Journal of Mineralogical and Petrological Sciences, 96, 137-147.
•  Seifert,  F. and  Schumacher,  J.C. (1986) Cordierite-spinel-quartz assemblages: a potential geobarometer. Bulletin of the Geological Society of Finland, 58, 95-108.
•  Shimizu,  H.,  Tsunogae,  T. and  Santosh,  M. (2009) Spinel + quartz assemblage in granulites from the Achankovil Shear Zone, southern India: Implications for ultrahigh-temperature metamorphism. Journal of Asian Earth Sciences, 36, 209-222.
•  Shimura,  T.,  Kawai,  T. and  Kagashima,  S. (2002) Granulite xenoliths from the Sumikawa Granite Body, Niigata Prefecture, Japan: finding of spinel + quartz assemblage from the Japanese Islands. Journal of the Geological Society of Japan, 108, 347-350.
•  Shimura,  T. and  Kemp,  A.I.S. (2015) Tetrahedral plot diagram: A geometrical solution for quaternary systems. American Mineralogist, 100, 2545-2547.
•  Shiraishi,  K.,  Hiroi,  Y.,  Moriwaki,  K. and  Onuki,  H. (1984) Orthopyroxene-bearing rocks from the Tenmondai and Naga-iwa Rocks in the Prince Olav Coast, East Antarctica: First appearance of orthopyroxene in progressive metamorphic sequence. Memoirs of National Institute of Polar Research Special Issue, 33, 126-144.
• Shiraishi, K., Hiroi, Y., Moriwaki, K., Sakaki, K. and Onuki, H. (1985) Geological Map of Tenmondai Rock, Antarctica. Antarctic Geological Map Series, Sheet 19 (with explanatory text). National Institute of Polar Research, Tokyo, Japan.
•  Shiraishi,  K.,  Hokada,  T.,  Fanning,  C.M.,  Misawa,  K. and  Motoyoshi,  Y. (2003) Timing of thermal events in eastern Dronning Maud Land, East Antarctica. Polar Geoscience, 16, 76-99.
•  Shiraishi,  K.,  Dunkley,  D.J.,  Hokada,  T.,  Fanning,  C.M., et al (2008) Geochronological constraints on the Late Proterozoic to Cambrian crustal evolution of eastern Dronning Maud Land, East Antarctica: a synthesis of SHRIMP U-Pb age and Nd model age data. Geological Society London Special Publications, 308, 21-67.
•  Shulters,  J.C. and  Bohlen,  S.R. (1989) The stability of hercynite and hercynite-gahnite spinels in corundum- or quartz-bearing assemblages. Journal of Petrology, 30, 1017-1031.
•  Spear,  F.S. and  Cheney,  J.T. (1989) A petrogenetic grid for pelitic schists in the system SiO₂-Al₂O₃-FeO-MgO-K₂O-H₂O. Contributions to Mineralogy and Petrology, 101, 149-164.
•  Suzuki,  K. and  Kawakami,  T. (2019) Metamorphic pressure-temperature conditions of the Lützow-Holm Complex of East Antarctica deduced from Zr-in-rutile geothermometer and Al₂SiO₅ minerals enclosed in garnet. Journal of Mineralogical and Petrological Sciences, 114, 267-279.
•  Takahashi,  K.,  Tsunogae,  T. and  Ugwuonah,  E.N. (2018) Fluid-induced high-temperature metasomatism at Rundvågshetta in the Lützow-Holm Complex, East Antarctica: Implications for the role of brine during granulite formation. Geoscience Frontiers, 9, 1309-1323.
• Takamura, Y., Tsunogae, T. and Tsutsumi, Y. (2019a) Petrology, U-Pb geochronology, and zircon REE geochemistry of granulites from Gondwana collisional orogens. The 126th Annual Meeting of the Geological Society of Japan, 59 (in Japanese).
• Takamura, Y., Tsunogae, T. and Tsutsumi, Y. (2019b). Petrology, U-Pb geochronology, and zircon REE geochemistry of granulites from Gondwana collisional orogens: Implications for the timing of rapid exhumation. 2019 IAGR Annual Convention &16th International Conference on Gondwana to Asia, Abstract Volume, IAGR Conference Series No. 25, 93-94.
•  Takamura,  Y.,  Tsunogae,  T. and  Tsutsumi,  Y. (2020) U-Pb geochronology and REE geochemistry of zircons in mafic granulites from the Lützow-Holm complex, East Antarctica: Implications for the timing and P-T path of post-peak exhumation and Antarctica-Sri Lanka correlation. Precambrian Research, 348, 105850.
•  Tomkins,  H.S.,  Powell,  R. and  Ellis,  D.J. (2007) The pressure dependence of the zirconium-in-rutile thermometer. Journal of Metamorphic Geology, 25, 703-713.
•  Tuccillo,  M.E.,  Mezger,  K.,  Essene,  E.J. and  Van Der Pluijm,  B.A. (1992) Thermobarometry, geochronology and the interpretation of P-T-t Data in the Britt Domain, Ontario Grenville Orogen, Canada. Journal of Petrology, 33, 1225-1259.
•  Vielzeuf,  D. (1983) The spinel and quartz associations in high grade xenoliths from Tallante (S.E. Spain) and their potential use in geothermometry and barometry. Contributions to Mineralogy and Petrology, 82, 301-311.
•  Vielzeuf,  D. and  Holloway,  R. (1988) Experimental determination of the fluid-absent melting relations in the pelitic system. Consequences for crustal differentiation. Contributions to Mineralogy and Petrology, 98, 257-276.
•  Waters,  D.J. (1991) Hercynite-quartz granulites: phase relations, and implications for crustal processes. European Journal of Mineralogy, 3, 367-386.
•  White,  R.W.,  Powell,  R. and  Clarke,  G.L. (2002) The interpretation of reaction textures in Fe-rich metapelitic granulites of the Musgrave Block, central Australia: constraints from mineral equilibria calculations in the system K₂O-FeO-MgO-Al₂O₃-SiO₂-H₂O-TiO₂-Fe₂O₃. Journal of Metamorphic Geology, 20, 41-55.
•  White,  R.W.,  Powell,  R.,  Holland,  T.J.B.,  Johnson,  T.E. and  Green,  E.C.R. (2014) New mineral activity-composition relations for thermodynamic calculations in metapelitic systems. Journal of Metamorphic Geology, 32, 261-286.
•  Whitney,  D.L. and  Evans,  B. (2010) Abbreviations for names of rock-forming minerals. American Mineralogist, 95, 185-187.
• Wood, B.J. and Fraser, D.G. (1976) Elementary thermodynamics for geologists. pp. 303, Oxford University Press.
•  Wu,  C.M. (2015) Revised empirical garnet-biotite-muscovite-plagioclase geobarometer in metapelites. Journal of Metamorphic Geology, 33, 167-176.
•  Xu,  G.,  Powell,  R.,  Wilson,  C.J.L. and  Will,  T.M. (1994) Contact metamorphism around the Stawell granite, Victoria, Australia. Journal of Metamorphic Geology, 12, 609-624.
•  Yoshimura,  Y.,  Motoyoshi,  Y.,  Miyamoto,  T.,  Grew,  E.S., et al (2004) High-grade metamorphic rocks from Skallevikshalsen in the Lützow-Holm Complex, East Antarctica: Metamorphic conditions and possibility of partial melting. Polar Geoscience, 17, 57-87.
•  Yoshimura,  Y.,  Motoyoshi,  Y. and  Miyamoto,  T. (2008) Sapphirine + quartz association in garnet: implication for ultrahigh-temperature metamorphism at Rundvågshetta, Lützow-Holm Complex, East Antarctica. Geological Society London Special Publications, 308, 377-390.
•  Zack,  T.,  Moraes,  R. and  Kronz,  A. (2004) Temperature dependence of Zr in rutile: empirical calibration of a rutile thermometer. Contributions to Mineralogy and Petrology, 148, 471-488.
•  Zhang,  H.,  Li,  J.,  Liu,  S.,  Li,  W., et al (2012) Spinel + quartz-bearing ultrahigh-temperature granulites from Xumayao, Inner Mongolia Suture Zone, North China Craton: petrology, phase equilibria and counterclockwise P-T path. Geoscience Frontiers, 3, 603-611.
•  Zhang,  J.X.,  Mattinson,  C.G.,  Meng,  F.C. and  Wan,  Y.S. (2005) An Early Palaeozoic HP/HT granulite-garnet peridotite association in the south Altyn Tagh, NW China: P-T history and U-Pb geochronology. Journal of Metamorphic Geology, 23, 491-510.