2021 Volume 1 Issue 2 Pages 37-46
2021 Volume 1 Issue 2 Pages 37-46
生体の細胞内では数千以上もの化学反応が、適切なタイミングで適切な量おこることにより、多様な機能が維持されている。代謝ネットワークは、細胞内の化学反応と化合物の関係をネットワークとして表現する。代謝ネットワークの種々の数理モデルの中でも、制約モデルを用いた流束均衡解析(Flux balance analysis: FBA)はゲノムスケールの代謝ネットワークに対しても高速なシミュレーションが可能であることが知られている。しかし所望の性質を持つ代謝ネットワークのFBAに基づく設計は、シンプルなFBAシミュレーションに比べて所用計算時間が激増するので、数理的な工夫をしなければ最新鋭の計算機システムを用いても実質的に計算不可能な場合が多い。本稿では、有用物質生産のための制約モデルに基づく代謝機能設計について、数理的側面を中心に、図例を用いながら基本的な問題設定やアルゴリズム、分野の動向等を解説する。
化合物を人工的に合成する方法として、化学工程を用いて製造する「化学合成法」と、微生物や植物等を利用して合成する「バイオ合成法」がある。低分子医薬品、低分子化学品や分子量が1万程度までの高分子化学品は化学合成法で製造可能であることが多いが、それを超える構造の化学合成には多段階操作が必要で、事実上不可能な場合も多い。一方、糖類、タンパク質・酵素、バイオ医薬品、食品等の大きくて複雑な構造を持つ化合物製造に関しては、バイオ合成法が優位である。低分子化合物であってもコハク酸のようにバイオ合成が優位な例もある。コハク酸の1kgあたりの製造コストは化学合成法が309円なのに対し、バイオ合成法が280円と試算されている[1]。
また化学合成による安価な大量生産が可能な化合物であっても、化石資源に依存する場合も多く、環境問題の観点からもバイオ合成の方法論の確立は重要である[2]。社会の持続的発展と脱炭素社会の実現に向け、情報科学的手法で生物機能をデザインし、ゲノム編集技術で機能発現が制御された遺伝子改変細胞による有用物質生産技術が注目されている。人工合成された遺伝子改変細胞はスマートセルと呼ばれ、生体内で機能を発現させて目的物質を取り出して利用する。このように生物制御技術と情報科学技術が組み合わさることにより、「第五次産業革命」と呼ぶに値する産業構造のパラダイムシフトが起こりつつある[1]。
情報科学的手法で生物機能をデザインするためには、細胞のふるまいを計算機を用いて予測・シミュレーションする必要がある。しかし現実におこる細胞内の複雑な事象を、計算機上ですべて完璧に再現することは事実上不可能である。そこで生物機能のデザインの良し悪しの判断に特に必要と思われる箇所のみを適切に抽出して予測・シミュレーションする必要がある。この抽象化されたデジタル疑似細胞は、計算機上において数理モデルにより表現される。数理モデルは簡素すぎると生物機能のデザインの良し悪しの判断の役に立たず、複雑すぎると計算機のメモリが足りなくなるエラーが出たり、人間の寿命と比較して現実的な時間のうちに計算結果を得ることができなくなる。この問題はスパコン等の高性能計算機システムを用いることである程度解決することもあるが、それでも組合せ爆発の観点から不可能な場合が多い。そこで複雑すぎず簡単すぎない数理モデルを用いて、細胞内の特徴的かつ重要な事象を逃さずに予測・シミュレーションして、遅くとも数日以内に(できれば数分以内に)所望の条件を満たす生物機能のデザインができることが肝要である。
代謝ネットワークは、細胞内で複雑に制御しあう数千以上の化学反応と化合物をネットワークとして表現する。代謝ネットワークには様々な数理モデルがあるが、ゲノムスケールの代謝機能デザインにおいては制約モデルと呼ばれる数理モデルを用いた流束均衡解析(Flux Balance Analysis: FBA)[3]がしばしば用いられる。FBAでは代謝の定常状態に焦点をあてて解析が行われる。
制約モデルは、例えるなら、水道の蛇口から一定速度で出てきた水が、迷路内の様々な経路をたどり最終的に排水口に流れ落ちていくようなイメージの数理モデルである。迷路内の経路の太さは地点により様々であるが、各地点において流入してくる水の量と、流出していく水の量が釣り合っている必要がある。
図1に制約モデルを用いたFBAの簡単な例を示す1。四角が反応で丸が化合物である。中でも黒い四角は外部とのやり取りのある反応で、白い四角は内部反応である。M1からM7は化合物で、R1,R8,R9は外部とのやりとりのある反応、R2からR7は内部反応である。x1からx9をそれぞれR1からR9の反応速度とする。内部反応においては各基質の消費速度と各生成物の生成速度は化学反応式における比率を満たす必要がある。例えばR6はM2+M3→2M6なので、R6の反応速度x6に対し、M2とM3の消費速度はx6で、M6の生成速度は2x6になる。また各化合物においては、消費される速度の和と、生成される速度の和が等しくなければならない。例えばM6はR6とR7から生成され、R8に消費されるので、2x6+x7=x8である。

制約モデルの例。四角は反応、丸は化合物を表す。ただし手法解説のために単純化されたトイモデルである。
R1はグルコース等の栄養源を取り込むための反応である。この例では栄養源を取り込む反応は1つしかないが、実際の制約モデルでは栄養等を外部から取り込むための多数の反応がある。図の各反応に付記された[a, b]の表記は、その反応の速度の下限値がaで、上限値がbであることを示す。この例では全ての反応速度の下限値は0であり、上限値はR5とR6を除いて10である。R5とR6の速度上限値は5である。可逆反応の下限値は負の値になる。
制約モデルを用いたFBAの大きな特徴のひとつは、細胞増殖を表現する仮想反応が組み込まれている点である。この細胞増殖反応は、様々な培地条件や遺伝子ノックアウト条件下で実際に計測された細胞増殖率と、シミュレーション値ができる限り合致するようにデザインされている。 図1ではR8が細胞増殖に対応する反応である。FBAによる最も標準的なシミュレーションでは、この細胞増殖反応の速度が最大化されるという仮定を用いる。その根拠は、微生物自体ができるだけ大きく増殖を目指すであろうということに加え、継代培養を繰り返すうちに細胞増殖率が大きくなる遺伝型が残りやすくなるということである。このように細胞増殖率最大化を仮定するのが、FBAにおける最も標準的な問題設定である。
図1の例において、細胞増殖反応の速度x8の最大値は10である。x8=10が達成されるのは、R1から上限値の10の栄養が摂取され、それがR2とR3に5ずつ分配された時である。R2やR3では5が入れば5が出てくるが、R6は化学反応式がM2+M3→2M6なので、M2とM3が5ずつ入るとM6が10出てくる。この場合はR4やR5には栄養が流れないので、R7からM6が作られることはなく、細胞増殖に対応するR8には10+0=10のM6が流れ込み、細胞増殖は10になる。R7を介してM6を作るためには、同量のM4とM5が必要だが、R7の化学反応式はM4+M5→M6+M7なので、R1から上限の10の栄養がR4とR5に5ずつ送られたとしても、M6は5しか作られない。したがって栄養をすべてR6へ送り込み、R7を使わない時が細胞増殖が最大になる。
上述のFBAを数学的に記述すると、以下のような線形計画問題として定式化される。
maximize
x8 /*細胞増殖最大化*/
such that
x1−x2−x3−x4−x5=0 /*M1の均衡*/ (1)
x2−x6=0 /*M2の均衡*/ (2)
x3−x6=0 /*M3の均衡*/ (3)
x4−x7=0 /*M4の均衡*/ (4)
x5−x7=0 /*M5の均衡*/ (5)
2x6+x7−x8=0 /*M6の均衡*/ (6)
x7−x9=0 /*M7の均衡*/ (7)
0≦x1≦10 /*R1の速度の上下限*/ (8)
0≦x2≦10 /*R2の速度の上下限*/ (9)
0≦x3≦10 /*R3の速度の上下限*/ (10)
0≦x4≦10 /*R4の速度の上下限*/ (11)
0≦x5≦5 /*R5の速度の上下限*/ (12)
0≦x6≦5 /*R6の速度の上下限*/ (13)
0≦x7≦10 /*R7の速度の上下限*/ (14)
0≦x8≦10 /*R8の速度の上下限*/ (15)
0≦x9≦10 /*R9の速度の上下限*/ (16)
線形計画問題は目的関数と制約式で記述され、目的関数は線形関数(1次関数)、制約式も線形関数による等式か不等式である必要がある。線形関数なので変数どうしの掛け算はできない。上述の例では細胞増殖最大化に対応するx8の最大化が目的関数である。such that以下の(1)-(7)に各化合物における流入・流出の均衡の制約が化学反応式の比率を満たすように記述されている。例えばM1はR1から生産(摂取)され、R2, R3, R4, R5に消費されるので、(1)のような制約式が課される。また例えばM6に関しては、R6の反応速度x6とR7の反応速度x7に対して2x6+x7が生成され、R8の反応速度x8の分だけ消費されるので(6)のような制約が課される。(8)-(16)は反応速度の上下限に関する制約である。これを解くと上述のようにx8=10が得られる。線形計画問題はゲノムスケールの制約モデルに対してもCPLEX[4]やGurobi[5]等のソルバを用いて高速に解ける。
FBAによるシミュレーションの目的のひとつに、遺伝子改変した微生物による物質生産がある。手法解説のためのトイモデルを図2に示す。図2のM4を目的物質とするとR7は目的物質生産反応である。継代培養により細胞増殖率の大きな遺伝型が残る前提により、FBAによる物質生産シミュレーションでは、細胞増殖率最大化時の目的物質生産率を評価することが多い。
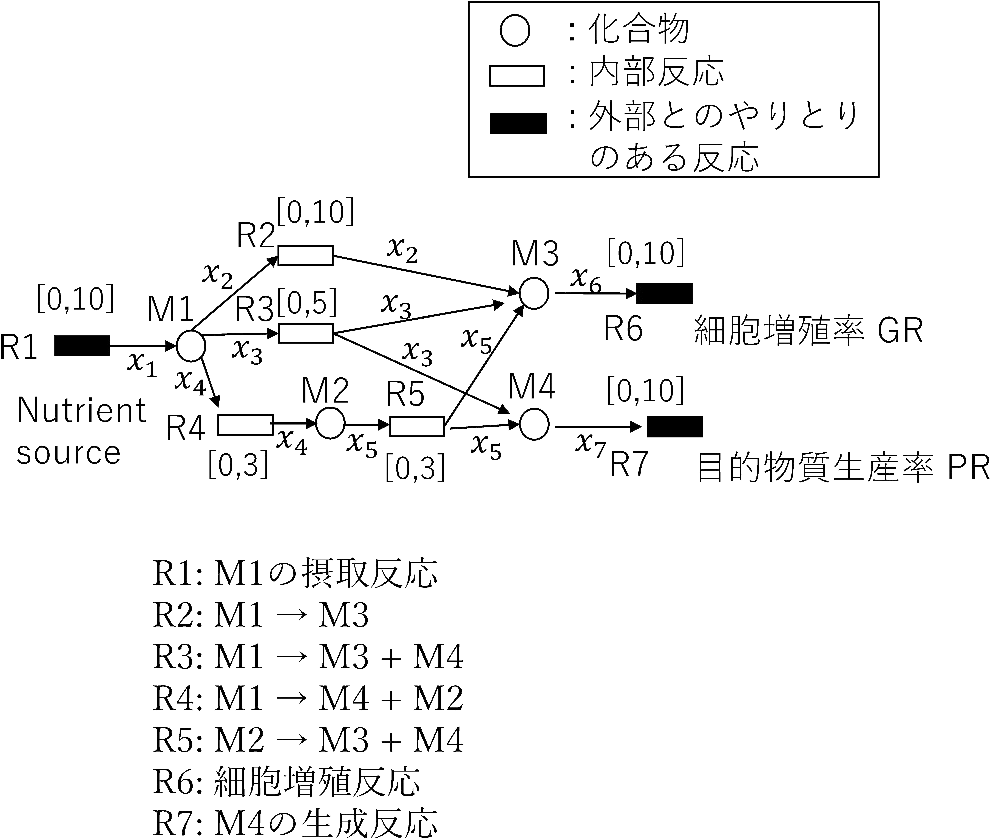
細胞増殖率最大化時の目的物質生産率が一意に決まらない例。ただし手法解説のために単純化されたトイモデルである。
図2のネットワークでは、例えばR1から摂取された栄養のうち、R3へ流れた分は、M3とM4へ自動的に分配され、細胞増殖と目的物質生産が同時におこる増殖連動型物質生産(growth coupling)が達成される。R1から摂取された栄養がR4, R5を通る時も同様である。しかしR1から摂取された栄養がR2を通る時は、すべて細胞増殖に使われ目的物質は生産されない。
3.1 反応削除による増殖連動型物質生産図2のネットワークで各反応を削除した時に、細胞増殖率を最大化した時の、目的物質生産率の最大値、最小値に対応する各反応の速度が表1に示されている。FBAの性質上、R4の削除とR5の削除は等価なので、反応削除のパターンは{R2}、{R3}、{R4}、{R2, R3}、{R2, R4}、{R3, R4}、{R2, R3, R4}のいずれかである。{R2, R3, R4}削除の時は各反応速度が0になるので表に含まれていない。
| 削除 | 目的物質生産率 | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| 最大 | 10 | 2 | 5 | 3 | 3 | 10 | 8 | |
| 最小 | 10 | 10 | 0 | 0 | 0 | 10 | 0 | |
| R2 | 最大 | 8 | 0 | 5 | 3 | 3 | 8 | 8 |
| 最小 | 8 | 0 | 5 | 3 | 3 | 8 | 8 | |
| R3 | 最大 | 10 | 7 | 0 | 3 | 3 | 10 | 2 |
| 最小 | 10 | 10 | 0 | 0 | 0 | 10 | 0 | |
| R4 | 最大 | 10 | 5 | 5 | 0 | 0 | 10 | 5 |
| 最小 | 10 | 10 | 0 | 0 | 0 | 10 | 0 | |
| R2, R3 | 最大 | 3 | 0 | 0 | 3 | 3 | 3 | 3 |
| 最小 | 3 | 0 | 0 | 3 | 3 | 3 | 3 | |
| R2, R4 | 最大 | 5 | 0 | 5 | 0 | 0 | 5 | 5 |
| 最小 | 5 | 0 | 5 | 0 | 0 | 5 | 5 | |
| R3, R4 | 最大 | 10 | 0 | 10 | 0 | 0 | 10 | 0 |
| 最小 | 10 | 0 | 10 | 0 | 0 | 10 | 0 |
図2の制約モデルにおいて、自然状態における細胞増殖率の最大値は10である。上述のようにR1から摂取された栄養はR2, R3, R4の3通りの経路に分配される可能性があるが、目的物質が最も生産されるのは、x2=2、x3=5、x4=3と流れた場合であり、目的物質生産率は8になる。すなわち図2のネットワークの自然状態で、細胞増殖率を最大化した時、目的物質生産率の最大値は8である。しかし細胞増殖率最大化時の目的物質生産率の最小値は、R1から摂取された栄養がすべてR2を通る場合の0である。
このように細胞増殖率が最大値になる場合でも、代謝の流れのパターンは複数ある可能性があり、それぞれ目的物質生産率が異なる場合がある。これは線形計画問題に複数の解があり得ることに起因する。flux variability analysis (FVA)は、細胞増殖率最大化時などにおいて各反応速度の上下限を求め、代謝の流れの多様性を解析する。表1が示すように、細胞増殖率最大化時の目的物質生産率の最大値を評価するのであれば、{R3, R4}と{R2, R3, R4}削除以外のすべて場合でgrowth couplingは達成される。しかし目的物質生産率の最小値を評価するのであれば、{R2}、{R2, R3}、{R2, R4}削除の時のみ達成される。
このように自然状態ではgrowth couplingが達成されなくても、反応を適切に削除すればgrowth couplingが達成されることがある。したがって制約モデルが与えられ、目的化合物が指定された時に、どの反応を削除するべきかを知ることが重要になる。しかし、この問題は組み合わせ最適化の観点からとても難しい場合が多い。
ゲノムスケールの代謝工学シミュレーションにおいてFBAが用いられる理由のひとつは、線形計画問題を高速に解くアルゴリズムが存在するからである。情報科学では、問題のサイズの多項式関数に比例する時間で解ける問題は効率良く解けるとみなし、問題のサイズの指数関数に比例する計算時間を要する場合は効率よく解けないとする基本的な考え方がある。上述のようにFBAは線形計画問題として表現可能であり、線形計画問題を解く多項式時間アルゴリズムが存在する。
しかしgrowth couplingを達成するためにどの反応を削除すれば良いかという問題は、元のFBAを解くよりも格段に難しくなる。FBAでは各反応速度は制約条件を満たす範囲内で任意の数値(実数)になることができるが、反応削除戦略の計算では、各反応を削除するかどうかを0(削除する)か1(削除しない)で表現するための0-1変数が必要になる。線形計画問題にこのような整数制約が加わった問題は混合整数線形計画問題(Mixed integer linear programming: MILP)と呼ばれるが、混合整数線形計画問題を解くための多項式時間アルゴリズムは知られていない。
しかし削除数が小さい時や、ネットワークが小さければgrowth couplingのための反応削除戦略の計算はそれほど難しくない。調べるべき組合せの数が計算機の能力と比べてそれほど大きくならないからである。一方で、ゲノムスケールの制約モデルに対して、多数の反応削除を認めると、適切な反応削除を見つけるのは難しくなる。そこでgrowth couplingを達成するための反応削除を見つける問題に対し、様々な手法が提案されてきた。(4節参照)
従来はウェット実験での遺伝子削除の手間やコスト等の観点から、削除する遺伝子数や反応数は少ない方が望ましいとされてきた。しかし合成生物学の発展等により、コアの部分のみ残して大半を削除してしまうという考え方も有望になりつつある。また制約モデルの数理的な解析という観点から、growth couplingに必要な最小ネットワークを見つけるための計算技術も盛んに研究されており以下に概要を説明する。
3.2 最小ネットワークによる増殖連動型物質生産指定された制約を満たす(0個ではない)極小反応数で構成される反応速度の分布を基準モード(elementary mode)という。基準モードは反応速度の上下限を考慮して基準ベクトル(elementary flux vector)[6]に拡張され使用されることが多いが、本稿では説明の簡単のため両者とも「基準モードに基づく手法」として記述する。図2のネットワークには表2に示す3つの基準モードが存在する。あるふたつの基準モードにおいて、片方の基準モードを定数倍すればもう片方と同じになる時、このふたつの基準モードは同一の基準モードとみなす。反応速度分布のすべてのパターンを、基準モードを組合せて足し合わせることにより表現する、というのが背景にある考え方である。
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | |
| 基準モード1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 |
| 基準モード2 | 1 | 0 | 1 | 0 | 0 | 1 | 1 |
| 基準モード3 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
growth couplingのための反応削除問題の有効な解き方として、細胞増殖反応と目的物質生産反応を両方含む基準モードを見つけて、基準モードに含まれない反応をすべて削除する方法がある。この場合、細胞増殖により強制的に目的物質が生産されるので、strong couplingと呼ばれる。 strong couplingが達成されると細胞増殖率と目的物質生産率が比例するので、細胞増殖率が最大化されなくても目的物質は生産される[7]。
基準モードをすべて列挙したうえで取捨選択して組み合わせれば、growth couplingを達成する様々な反応削除戦略を得ることができる。しかし基準モードの数はネットワークの大きさの指数関数に比例するので、ゲノムスケールの制約モデルに対して基準モードをすべて列挙するのはほぼ不可能である。そこで最短の基準モードを混合整数線形計画法を用いて計算する等の手法が用いられる。
基準モードでは与えられた制約に対し反応数極小の流れに着目するが、各反応速度の絶対値の総和に着目する手法もある。GridProd[8]は細胞増殖率と目的物質生産率の値に着目して解空間を分割して、それぞれの小さな解空間内で反応速度の絶対値の和が最小になる流れにおいて、使われなかった反応を削除する。図2のネットワークにおいて、細胞増殖率と目的物質生産率の必要最小値を1とした時に、解空間を細胞増殖率と目的物質生産率を用いてそれぞれ3つずつに分割した時のGridProdの動作を表3にまとめる。例えば細胞増殖率が1以上4以下で、目的物質生産率が1以上3.33以下の場合という制約の下で反応速度の絶対値総和を最小化すると、R2やR4は使わずにx3=1とする流れが得られる。この時R2, R4, R5は使われないのでR2, R4, R5を削除して細胞増殖率最大化すると、細胞増殖率=目的物質生産率=5が得られる。次に細胞増殖率が1以上4以下で、目的物質生産率が3.33以上5.67以下の場合という制約の下で反応速度の絶対値総和を最小化すると、やはりR2やR4は使われないがx3=3.33となり、R2, R4, R5を削除した結果、細胞増殖率=目的物質生産率=5が得られる。細胞増殖率が1以上4以下で、目的物質生産率が5.67以上8以下を満たす流れは存在しない。細胞増殖率が4以上7以下で、目的物質生産率が1以上3.33以下の制約の下で反応速度の絶対値総和を最小化するとx2=3、x3=1となりR4, R5が使われない。R4, R5を削除して細胞増殖を最大化すると、細胞増殖率=10、目的物質生産率(最小値)=0となってしまう。以下同様にすべての分割された解空間に対し、追加制約の下で線形計画問題を解き、使われなかった反応を削除してgrowth couplingを達成する反応削除を探索していく。
| 細胞増殖率 | 目的物質生産率 | ||||||||||
| 最小値 | 最大値 | 最小値 | 最大値 | x1 | x2 | x3 | x4 | x5 | x6 | x7 | |
| 1 | 4 | 1 | 3.33 | 反応速度絶対値総和最小 | 1 | 0 | 1 | 0 | 0 | 1 | 1 |
| 細胞増殖率最大 | 5 | 0 | 5 | 0 | 0 | 5 | 5 | ||||
| 1 | 4 | 3.33 | 5.67 | 反応速度絶対値総和最小 | 3.33 | 0 | 3.33 | 0 | 0 | 3.33 | 3.33 |
| 細胞増殖率最大 | 5 | 0 | 5 | 0 | 0 | 5 | 5 | ||||
| 1 | 4 | 5.67 | 8 | 反応速度絶対値総和最小 | - | - | - | - | - | - | - |
| 細胞増殖率最大 | - | - | - | - | - | - | - | ||||
| 4 | 7 | 1 | 3.33 | 反応速度絶対値総和最小 | 4 | 3 | 1 | 0 | 0 | 4 | 1 |
| 細胞増殖率最大 | 10 | 10 | 0 | 0 | 0 | 10 | 0 | ||||
| 4 | 7 | 3.33 | 5.67 | 反応速度絶対値総和最小 | 4 | 0.66 | 0.33 | 0 | 0 | 4 | 3.33 |
| 細胞増殖率最大 | 10 | 10 | 0 | 0 | 0 | 10 | 0 | ||||
| 4 | 7 | 5.67 | 8 | 反応速度絶対値総和最小 | 5.66 | 0 | 5 | 0.66 | 0.66 | 5.66 | 5.66 |
| 細胞増殖率最大 | 8 | 0 | 5 | 3 | 3 | 8 | 8 | ||||
| 7 | 10 | 1 | 3.33 | 反応速度絶対値総和最小 | 7 | 6 | 1 | 0 | 0 | 7 | 1 |
| 細胞増殖率最大 | 10 | 10 | 0 | 0 | 0 | 10 | 0 | ||||
| 7 | 10 | 3.33 | 5.67 | 反応速度絶対値総和最小 | 7 | 3.66 | 3.33 | 0 | 0 | 7 | 3.33 |
| 細胞増殖率最大 | 10 | 10 | 0 | 0 | 0 | 10 | 0 | ||||
| 7 | 10 | 5.67 | 8 | 反応速度絶対値総和最小 | 7 | 1.3 | 5 | 0.66 | 0.66 | 7 | 5.66 |
| 細胞増殖率最大 | 10 | 10 | 0 | 0 | 0 | 10 | 0 | ||||
このように9つのすべての解空間を調べた結果、{R2, R4, R5}を削除すれば細胞増殖率=目的物質生産率=5が得られ、{R2}を削除すれば細胞増殖率=目的物質生産率=8が得られることがわかる。すなわちGridProdで解空間全体を9分割した時に得られる最も良い反応削除戦略は{R2}の削除である。GridProdにおいては解空間を細かく分割すればするほど良い解は見つかりやすくなるが、その分、計算時間は増大する。iAF1260というゲノムスケールの制約モデルに対して細胞増殖率と目的物質生産率を25分割ずつして、全体を625分割した時が最も性能が良かったという実験結果もある[8]。
3.3 遺伝子削除による増殖連動型物質生産代謝ネットワークの化学反応の多くは酵素タンパク質により触媒されており、その酵素タンパク質は遺伝子の情報に基づき生成される。したがって遺伝子削除に基づく反応削除により代謝ネットワークを制御して、所望の物質生産を促進できる場合がある。遺伝子追加や反応追加も同様であるが、追加反応の候補もすべて含む大きな代謝ネットワークから不要な反応を削除していくと考えれば、遺伝子削除問題に一般化できる。
しかし、反応Aを削除したい時に、どの遺伝子を削除すれば良いかは一意に決まらない場合がある。例えば図1の反応6を触媒する酵素P6が遺伝子G1由来のタンパク質と遺伝子G2由来のふたつのタンパク質の複合体であるとする。この場合、G1とG2のどちらかが欠失すると、この酵素は作られなくなる。仮にG1が削除される時をG1=0、削除されない時にG1=1、またP6が作れる時をP6=1、作れない時をP6=0と表現することにすると、P6=1となるのはG1とG2が両方とも1の時のみとなる。
このように引数や計算結果が0か1にしかなれない関数をブール関数という。上述のようなP6の値を決定するG1とG2の関係は論理積(AND関数)と呼ばれ、P6=G1∧G2のように表現される。ここで∧はAND関数を表し、引数がすべて1の時のみ結果も1になる。P6=0の時はx6は強制的に0になる。逆にG1が作るタンパク質とG2が作るタンパク質がアイソザイムで、どちらも単独でR6を触媒できる場合はP6=G1∨G2と記述される。∨は論理和(OR関数)を表し、G1とG2が両方とも0の時のみP6=0となることを意味する。またブール関数には否定(NOT)を表す関数も存在して、0と1を反転させるような表現も可能である。制約モデルにおいて、タンパク質を介した遺伝子による反応の制御関係はGPRネットワークと呼ばれ、上述のようなブール関数で表現される。どのようなブール関数であっても、AND、OR、NOTの組合せで表現することができる。
図1の例において遺伝子と反応触媒酵素の関係が以下のように与えられたとする。
P2=G2∨G4
P4=G3∨G4
P5=G1
P6=G1∧G3
P7=G2
G1が削除されるとR5とR6が使えなくなる。R5が使えないとR7も使えなくなるので、代謝の流れはすべて止まる。G2が削除されるとR7が使えなくなるので、目的物質は生産されない。G3を削除するとR6が使えなくなるので、細胞増殖率最大化のためにはR7経由でR8に栄養を流す必要があり、強制的に目的物質が生産される。G4を削除する場合はすべての反応が使える状態なので、R1から摂取された栄養はR6経由ですべてR8へ流れて細胞増殖に使われ、目的物質は生産されない。1つの遺伝子のみ削除する場合は上記のようになるが、ゲノムスケールの制約モデルに対して多数の遺伝子削除する場合は、各遺伝子による反応への複雑な制御関係を考慮することになり、問題はとても難しくなる。
現在、高性能の計算機システムを用いれば、多くの目的物質に対してgrowth couplingを達成する反応削除戦略を基準モードを介して計算することが可能になりつつある[7]。しかし基準モードに基づき得られた反応削除戦略から遺伝子削除戦略を得るのは簡単ではない。
openCOBRAは制約モデルを用いた代謝シミュレーションのためのオープンソースのソフトウェア・パッケージであり、コミュニティにより開発されたMATLAB、Python、Juliaのコードが公開されている[9]。またCellNetAnalyzerは基準モードの計算やそれに基づく削除戦略を計算するソフトウェア等を公開している[10]。
制約モデルによるFBAは、ミカエリス・メンテン式のような微分方程式等を用いた代謝の動態解析は避けることにより、高速なシミュレーションを可能にしている。シミュレーションで用いるゲノムスケールの制約モデルは、従来は遺伝的、化学的な性質等を考慮しながらひとつずつ反応を追加して構築されてきたが、ゲノム配列からデータ科学に基づいて制約モデルを半自動的に構築する手法も盛んに研究されている[11]。1997年に解読されたゲノム配列[12]に基づき、最初に構成された大腸菌の制約モデルiJE660[13]は660遺伝子と627反応で構成されていた。2003年に発表された904遺伝子931反応からなるiJR904[14]ではGPRネットワークが追加された。その後、iAF1260, iJO1366, iML1515と更新されている[15, 16, 17]。また大腸菌以外にも様々な生物種に対するゲノムスケールの制約モデルがBiGGデータベース[18]等より利用可能である。また代謝ネットワークとGPRネットワークで構成される制約モデルを基礎として、様々な拡張を施した数理モデルが提案されている。転写や翻訳の過程を考慮したMEモデル[19]や、酵素量や酵素の回転数を考慮したGECKOモデル[20]、遺伝子発現や転写制御を考慮するモデル[21]、代謝物濃度から熱力学的に反応の方向を予測して制約を課すモデル[22]などが提案されている。いずれも数理モデルの詳細化により、ウェット実験によるデータとの整合性向上を果たしている。一方で数理モデルの拡張とともに、反応削除戦略や遺伝子削除戦略の計算が複雑化するという課題もある。
growth couplingのための反応削除や遺伝子削除を計算するその他の手法のいくつかを以下に簡単に説明する。多くの手法は小さいネットワークや少ない削除数を想定しているが、ゲノムスケールや削除数を限定しない場合でも計算できる場合もある。OptKnock はgrowth couplingのための反応削除の計算手法の草分け的な存在で、細胞増殖率最大化を仮定しながら目的化合物生産量も最大化する[23]。またGDLSは局所探索法を用いる[24]。Redirectorは目的関数に微調整を加えながら条件を満たす反応削除戦略を探索する[25]。EMILioは各反応の速度最適化と逐次線計画法を組み合わせて削除戦略を計算する[26]。GDBBは分枝限定法で遺伝子削除戦略を計算する[27]。pFBAは目的の流れを達成する際の貢献度に応じて各遺伝子を分類する[28]。IdealKnockは目的物質生産を最大化する理想の反応速度分布を計算して、使われなかった反応を削除する[29]。FastProsは感度分析を用いて各反応削除の影響を見積り、削除戦略を計算する[30]。また細胞増殖を優先するプロセスと目的物質生産を優先するプロセスを分ける二段階培養を想定した計算手法もある[31]。
化合物の合成方法には化学合成法とバイオ合成法があり、技術的・経済的な理由に加え環境問題の観点からも有用物質のバイオ合成の方法論の確立は重要である。また情報科学的手法で生物機能をデザインして、ゲノム編集技術で機能改変されたスマートセルにより、第五次産業革命と呼ぶに値する産業構造のパラダイムシフトが起こりつつある。情報科学的手法で生物機能をデザインするためには、数理モデルによる予測・シミュレーションを高速に行う必要がある。遺伝子改変による代謝制御のゲノムスケールのシミュレーションでは、代謝ネットワークとGPRネットワークを組み合わせた制約モデルがしばしば用いられる。制約モデルは代謝の定常状態を仮定した数理モデルであり、細胞増殖を最大化する線形計画問題として定式化される。制約モデルを用いた有用物質生産シミュレーションでは、細胞増殖最大化時に目的物質が生産されるgrowth couplingを達成する反応削除戦略や遺伝子削除戦略の計算が必要になる。ゲノムスケールの制約モデルでgrowth couplingを達成するための反応削除や遺伝子削除戦略は、様々な手法が提案され使われている。growth couplingのためのゲノムスケールの反応削除問題は基準モードに基づく手法で計算可能な場合が多いが、遺伝子削除問題への応用等の課題が残されている。表4に本稿で紹介した主な問題設定とアルゴリズムの特徴をまとめる。
| 記載箇所 | 問題設定 | 目的、特徴 |
| 2節 | FBAによる代謝シミュレーション | 細胞増殖率最大化時の各反応速度を計算 |
| 線形計画問題による定式化 | ||
| 3節冒頭 | FBAによる増殖連動型物質生産 | 細胞増殖率最大化時の目的物質生産率を評価 |
| FVAによる目的物質生産率のバラつき評価 | ||
| 3.1節 | FBAによる増殖連動型物質生産のための反応削除問題 | 上記のための反応削除戦略を計算 |
| 3.2節 | 基準モードによる増殖連動型物質生産 | 細胞増殖率が低くても目的物質が生産される反応削除戦略を計算 |
| 3.2節 | GridProdによる反応削除戦略の計算 | 細胞増殖率最大化時の目的物質生産率を評価 |
| 解空間の分割による計算高速化、反応速度絶対値総和を最小化 | ||
| 3.3節 | FBAによる増殖連動型物質生産のための遺伝子削除問題 | 代謝ネットワーク部分に加えてGPRネットワークも考慮 |
1 手法解説を目的としたトイモデルである。
 |
田村 武幸 京都大学化学研究所バイオインフォマティクスセンター准教授。アルゴリズム理論や組合せ最適化等を用いて遺伝子制御ネットワークや代謝ネットワークの数理的側面を研究している。京都大学大学院情報学研究科知能情報学専攻にて修士課程と博士課程の指導資格有。大学院生募集中。科研費基盤B「有用物質を効率的に生産する代謝ネットワークの設計アルゴリズム」代表(令和2年~)。 ホームページ:https://sunflower.kuicr.kyoto-u.ac.jp/~tamura/ |