Mathematics for Heterogeneous Biological Data Fusion Analysis with Matrix-Tensor Factorization

– Part II. Simultaneous Matrix Factorization –

Abstract

生命科学分野で取得されるデータ集合は、雑多（ヘテロ）な構造になり、ヘテロなデータ構造を扱える理論的な枠組みがもとめられている。本連載では、汎用的なヘテロバイオデータの解析手法である行列・テンソル分解を紹介していく。第1回では、1つの行列における代表的な行列分解PCA/SVD、NMF、ICAを紹介し、それらを「パターンの和としての行列分解」、「射影としての行列分解」という2つのアプローチで説明した。第2回でも引き続きこれらのアプローチを利用し、行列が複数ある時に適用できる、行列同時分解について説明する。

2行列での行列同時分解

同じ行を共有する2つの行列、すなわちn×pの行列Xとn×qの行列Yの同時分解を考える。ここでいう同時分解とは、1行列での行列分解手法を個々の行列に適用したり、複数の行列を一度1つの行列にマージしてから行列分解するようなことではなく、後述するように、1つの手法内で複数の行列を最適化時に互いに関連づけながら、同時に分解することを指す。2行列が行ではなく列を共有する場合は、それらを転置してから利用すれば同様に扱うことができる。このようなデータ集合の典型例としては、共通の空間（例：細胞、臓器、組織）から、トランスクリプトーム、プロテオームなど異なる種類のオミックスデータを取得する、マルチオミックスデータがある。このようなデータ構造は、マルチモーダル、マルチビューといった呼ばれ方もする。ここでは、第1回［1］のやり方を踏襲し、「射影としての行列同時分解」手法であるPartial Least Squares（PLS［2, 3］）、Canonical Correlation Analysis（CCA［4, 5, 6］）、「パターンの和としての行列同時分解」手法であるJoint Non-negative Matrix Factorization（JointNMF［7, 8, 9］）、Group Independent Component Analysis（GroupICA［10］）、Generalized Singular Value Decomposition（GSVD［11］）を紹介する。

射影としての行列同時分解

まずは「射影としての行列同時分解」手法として、PLS［2, 3］とCCA［4, 5, 6］を説明する。ここでは第1回［1］で説明した、「射影としての行列分解」のイメージが役に立つ。ここでは2行列X、Yはともに、列ごとに平均値が0になるように中心化されているものとする。行列X、Yは本来次元が異なる（p != q）行列同士なので、そのままでは値を比較することはできない。しかし、Xに行列V（p×k）をかけ、Yには行列W（q×k）をかけることで、共通のk次元空間に射影されるため、その空間内では類似度が計算できるようになる（図1）。この部分空間内におけるXのスコア（XV）とYのスコア（YW）間で共分散cov（XV,YW）が最大になるようにローディングV、Wを推定する手法がPLSであり、相関cor（XV,YW）が最大になるようにV、Wを推定する手法がCCAである。これらは、目的関数は同じであるが、拘束条件が異なり、ナイーブにPLSを解いた場合［12］はX、Yの相互共分散行列${\Sigma }_{\mathit{XY}}=\frac{1}{n}{X}^{T}Y$のSingular Value Decomposition（SVD、第1回［1］を参照）   

$$\begin{array}{}\text{（1）}& {{\Sigma }_{\mathit{XY}}=\mathit{VSW}}^T\end{array}$$

としてV、Wを求める事ができる（Sは特異値を対角要素にもつk×kの対角行列）。または、トレースを利用して、   

$$\begin{array}{}\text{（2）}& \underset{V,W}{\max }\mathit{tr}(V^T{\Sigma }_{\mathit{XY}}W)\end{array}$$

のように、Σ_XYの対角化ととらえることもできる。このような定式化は、Principal Component Analysis（PCA、第1回［1］を参照）の目的関数のΣ_XXをΣ_XYに置き換えただけなので、PCAの素直な2行列拡張ととらえる事もできる。このアプローチは、Co-inertia Analysis（CIA［13］）、またはPartial Least Squares-Correlation（PLS-C）［3］とも呼ばれる。

図１：CIA、PLS、CCA（射影としての行列同時分解）

共通のk次元空間に2行列を射影し、スコア間の共分散（または相関）が最大になるように、射影行列をもとめる。

PLSはPCAと異なる基準でスコアXV、YWとローディングV、Wを求めるが、圧縮次元数が2以上の時に、スコアとローディングのどちらに直交性をもたせるかで、幾つも最適化アルゴリズムが提案されている。上記のナイーブなPLSはローディングの列ベクトルを互いに直交にするが、実際に広く利用されているNonlinear Iterative Partial Least Squares（NIPALS）やStatistically Inspired Modification of Partial Least Squares（SIMPLS）といったPLSアルゴリズムは、スコアの列ベクトルの方を互いに直交にする［2］。これは、後述するようにPLSはPartial Least Squares-Regression（PLS-R）、Partial Least Squares-Discriminant Analysis（PLS-DA）など、圧縮次元先で予測モデルを構築するようなモデリングに利用されるため、多重線形性の観点から、ローディングVよりもスコアXVの方を直交化させたいという要請によるものである［2］。PCAではスコアも、ローディングもともに直交であるが、PLSの枠組みで両者を同時に直交化させることは難しく、著者の知っている範囲ではBi-orthogonal PLS ［14］というモデルだけがそのような直交化を行っている。

一方CCAの場合は、白色化（スコアの分散が1になるようにする前処理、第1回［1］のICAの項を参照）したX、Yの相互共分散行列のSVDから   

$$\begin{array}{}\text{（3）}& {\left({\Sigma }_{\mathit{XX}}\right)}^{-\frac{1}{2}}{\Sigma }_{\mathit{XY}}{\left({\Sigma }_{\mathit{YY}}\right)}^{-\frac{1}{2}}={\mathit{VSW}}^T\end{array}$$

として求める［15］。またはトレースを利用して   

$$\begin{array}{}\text{（4）}& \underset{V,W}{\max }\mathit{tr}(V^T{\left({\Sigma }_{\mathit{XX}}\right)}^{-\frac{1}{2}}{\Sigma }_{\mathit{XY}}{\left({\Sigma }_{\mathit{YY}}\right)}^{-\frac{1}{2}}W)\end{array}$$

と書くこともできる。

パターンの和としての行列同時分解

次に、「パターンの和としての行列同時分解」手法として、Non-negative Matrix Factorization（NMF、第1回［1］を参照）ベースのJointNMF［7, 8, 9］、ICA（第1回［1］を参照）ベースのGroupICA［10］、SVD（第1回［1］を参照）ベースのGSVD［11］を紹介する。ここでは第1回［1］で説明した「パターンの和としての行列分解」のイメージが役に立つ。射影としての行列同時分解では、2行列X、Yを低次元に射影するための行列V、Wを各々最適化していたのに対し、パターンの和としての行列同時分解での問題設定では、2行列に共通する因子行列Uと、各行列が各々もつ因子行列V_X、V_Yを最適化する（図2）。

図２：JointNMF、GroupICA、GSVD（パターンの和としての行列同時分解）

共通因子Uを仮定し、全因子行列を逐次的に更新。

JointNMFでは、図2のように、2行列X、Yを同時に分解する際に、共通の因子行列Uを仮定する。なお2行列はともに非負値だとする。後は、通常のNMFと同様に、Multiplicative Update Rule（MU則、第1回［1］を参照）で以下のように因子行列U、V_X、V_Yを逐次的に最適化する。

  

$$\begin{array}{}\text{（5）}& U\leftarrow U\circ (\frac{{\mathit{XV}}_X+{\mathit{YV}}_Y}{{\mathit{UV}}_X^T{V}_X+{\mathit{UV}}_Y^T{V}_Y})\end{array}$$

  

$$\begin{array}{}\text{（6）}& V_X\leftarrow V_X\circ \frac{X^{T}U}{V_X{U}^{T}U}\end{array}$$

  

$$\begin{array}{}\text{（7）}& V_Y\leftarrow V_Y\circ \frac{Y^{T}U}{V_Y{U}^{T}U}\end{array}$$

Independent Component Analysis（ICA、第1回［1］を参照）の最適化アルゴリズムの一つInfomaxの更新式を2行列に拡張した、Group ICA［10］では、2行列X、Yは実行列として、以下のように自然勾配法で2行列に共通する因子行列U_tを逐次的に最適化する（ただし、tは逐次最適化の反復ステップ、η（t）は定数か1/tなどの減衰関数、φ（A）はtanh（A）など何らかの非線形関数）。

  

$$\begin{array}{}\text{（8）}& U_{t+1}=U_t+\eta \left(t\right)\{I-\phi (X)X^T-\phi (Y)Y^T\}{U}_t\end{array}$$

SVDを2行列に拡張したGeneralized SVD（GSVD［11］）では、実行列であるX、Yを以下のように同時に分解する。

  

$$\begin{array}{}\text{（9）}& \begin{array}{c}X={\mathit{U\Lambda }}_X{V}_X^T\\ Y={\mathit{U\Lambda }}_Y{V}_Y^T\end{array}\end{array}$$

ただし、UはXとYで求めた共通する因子行列であり、Λ_Aは行列Aごとの対角行列、V_Aは行列Aごとの因子行列である。

1行列での行列分解と2行列での行列同時分解の違い

上記のような2行列の同時分解を利用することで、1行列の行列分解を個々に行った場合とで解析結果に差が出る可能性がある。例えば、射影としての行列同時分解（例：PLS、CCA）で考えてみると、2行列で別々にPCAを実行して2行列のスコア（XV、YW）を取り出した場合と、行列同時分解で2行列を互いに関連づけながら、2行列のスコアを取り出した場合とで比較すると、例え片方の行列で分散が大きいスコアがPCAで選ばれても、そのスコアがもう1つの行列のスコアと共分散や相関が低い場合、行列同時分解としてはそのようなスコアは選ばれない。パターンの和としての行列同時分解（例：JointNMF、GroupICA、GSVD）で考えても同様であり、個々の行列の解析だけでは、ある行列の中に含まれるパターンのうち、どれがもう片方の行列にも共通しているもので、どれがその行列に特異的なのかを区別することはできない。しかし、共通因子行列Uの推定に2行列を参加させることで、2行列に共通したパターンUにすることができる。

このようなモデリングは、複数のデータでの再現実験を自然と行ったことに相当し、個々のデータの解析だけで、一般的な結論を導こうとしたり、再現性がないテクニカルノイズを生物学的なシグナルだと勘違いしてしまう偽陽性の回避が期待できる。例えば、PCCA［16］という手法では、個人ごとのリンパ芽球細胞株の遺伝子発現データと、SNPデータの2行列をCCAで同時分解しており、遺伝子発現データのPCAではノイジーで検出できなかった集団構造を、SNPのデータと組み合わせることで、検出できるようにしている。

分子動力学分野では、シミュレーションでもとめたタンパク質を構成する原子の時間発展情報（トラジェクトリ）を行列データととらえ、PCAなど各種多変量解析手法を適用することで代表的な動きのパターン（モード）を検出することが行われているが、Functional Mode Analysis（FMA［17, 18］）という手法では、トラジェクトリ行列を説明変数、事前に設定したタンパク質の機能情報を目的変数として、PLS-R（後述）を適用しており、タンパク質の機能と関連するモードだけを取り出すことに成功している。

また、1細胞レベルでラマンスペクトルと、遺伝子発現量を同時計測したデータに対してPLS-Rを行った例［19］のように、一度同時計測したデータで予測モデルを構築しておけば、それ以降は計測しやすい方のデータ（例：ラマンスペクトル）を取得するだけで、もう片方のデータの予測値（例：遺伝子発現量）を手に入れることが可能である。

教師のありなしと恣意性に関する議論

2行列の同時分解において、Xをデータ行列、YをXのラベル情報（ダミー変数行列）とした場合、ラベルに関連したXのスコアを取り出すことができる（図3）。PLSは元々このような発想で生まれた手法であり、PCAのスコアとYの回帰（Principal Component Analysis-Regression; PCA-R）ではYの予測に不必要なスコアまでモデルに利用されてしまうため、予測に役に立つスコアだけをXから取り出そうとする。この時、Yがダミー変数の場合はPLS-DA、Yが連続量の場合はPLS-Rという［2, 3］。CCAのYがダミー変数の場合は、FisherのLinear Discriminant Analysis（LDA）と等価であることがわかっている［20, 21］。

図３：ダミー変数との行列同時分解

行列同時分解で、片方の行列をラベル情報（ダミー変数）にすることで、ラベルを反映するスコアを得ることができる。

このようなモデルで計算されたスコアやローディングを可視化に利用することもでき、教師あり次元圧縮と呼ばれることもある。なお、教師ありモデルの文脈では、ローディングは回帰係数とも呼ばれる。教師あり次元圧縮は、良くも悪くも人が最初に設定したラベルに関連した構造を取り出そうとするため、データのありのままの性質を見ておらず、恣意的であるとして、否定的な意見を持つ人が一定数いる。著者の見解としては、両アプローチともにメリット・デメリットがあり、うまく使い分けたり、組み合わせて利用することで、より解析の幅が広がると考えていることから、ここでは、可能な限り両者をフェアに比較してみることにする。

まず、そもそもの話として、教師あり学習と教師なし学習の境界はかなり曖昧である。例えば、教師あり学習と教師なし学習の違いを以下のように説明する人が多いと思われる。

1．状況による説明：事前知識がある状況で行うのが教師あり学習、事前知識なしで行うのが教師なし学習 2．タスクによる説明：新たなデータでの予測値を求めるのが教師あり学習、手元のデータに含まれるパターンを調べるのが教師なし学習 3．ラベルによる説明：モデルがラベルを使っているなら教師あり学習、使っていないなら教師なし学習

これらの説明は、全て例外があり、はっきりと区別できない場合が存在する。まず1. 状況による説明についてだが、真に教師なしの状況であれば、データXから得られたパターンYのその後の生物学的解釈も、手法の良し悪しも本来議論できない。ほとんどの場合、研究者は結果を解釈する別のラベル情報をヒントとして事前に持っており、手法の評価に利用することから、真に教師なしの状況で解析することなどほとんどありえない。

また、2．タスクによる説明については、教師あり次元圧縮を利用して教師なし学習のようにパターンを見る解析、例えば、ラベルの通りにクラスタが分離する部分空間が存在するかを確認するような解析もある［22］。また逆に、予測を教師なし学習の枠組みで行うことも可能であり、例えば、事前に学習データX_trainでPCAを行い、学習された射影行列V_trainを、新たに得られた行列X_newにかけてX_newのスコア（X_new V_train）とする解析もある。このような解析は、2017年にLi, H.らがReference Component Analysis（RCA［23］）と名付けたが、それより以前から情報検索の分野ではFolding-in［24］という名前で利用されている。NMFでも同様に、学習データXの分解で得られたV_trainをX_newの分解に利用する、NMFによる転移学習がある［25, 26, 27, 28, 29］。また、データ行列に含まれる計測されなかった欠損値を補完する解析の場合は、行列分解であっても、やっていることとしては予測問題である。まとめると、以上のことから、教師ありなしの違いは射影行列の推定にラベルを使ったかどうかの違いでしかなく、タスクで区別することは常にできるわけではない。

また、例え射影行列の推定にラベルを使ったとしても、どの程度そのラベルを参考にしたのかという議論もある。これが3. ラベルによる説明の曖昧さであり、線形回帰モデルのように、Yを定数（教師）として、データ行列XのスコアXVがこのYの値となるべく一致するように射影行列Vを最適化するのであれば議論はないが、PLS、CCAのように、XもYも一度低次元に射影してスコアにする行列同時分解においては、XのスコアもYのスコアも共に変数であり、最適化対象である。このような場合、YによりXの射影行列Vが学習されるだけでなく、XによりYの射影行列Wも学習されるため、これではXとYのどちらが教師で生徒なのかわからない。このようなモデルを教師あり学習というのは、実際にやっていることとニュアンスに乖離があり、Raj, B.は“Softly” Supervisedという言葉を使っている［30］。行列同時分解におけるラベル情報の影響は、あくまで程度問題であり、XにありもしないパターンがYからの一方的な影響により偽陽性的に作り出される訳ではないことに注意してほしい。

上記のように、教師ありなしという言い方は、時として本質を見失う危険性をはらんでいる。しかしながら、両アプローチで代表されるタスクや手法が各々あり、それらを指し示すインデックスとして便宜上そういった言葉が必要な場面があることも事実であることから、ここでは教師ありという言葉を、3．のように“Softly” Supervised なモデルも含め、モデルがラベル情報を使っているという意味で使うことにする。

教師あり学習のメリットとしては、教師あり学習の方が、研究者人口が多く、理論的発展が先行しており、Open Source Software（OSS）も良く整備されている印象がある。例えばscikit-learn［31］などの機械学習フレームワークでは、各教師ありモデルの実行ワークフローが素晴らしく体系化されている。また、機械学習分野でおそらく最も重要な概念である、汎化性能（X_newにおけるY_newの予測性能）は、Cross Validation（CV）で定量的に評価でき、目的がはっきりしているため作業に曖昧さが少なく、データXとラベルYのセットを用意できさえすれば、比較的誰でも参入しやすい。ただし、デメリットとしては、ラベルがないと使えない点、データが大規模になるほどラベル作成コストが無視できなくなる点、またラベル情報の作成に曖昧さや恣意性が入りやすい点が挙げられる。また、少数のサンプルで超高次元データを解析する状況（p>>n問題）や、誤ったラベルが含まれている状況では、精度が大幅に落ちることが報告されている［32］。良くも悪くもラベルの影響を受けるところが、教師あり学習の特徴だと言える。

一方、教師なし学習のメリットとしては、ラベルを利用しないモデルであるため、ラベル作成のコストを省いて取り組むことができ、また事前知識に寄らない新たなパターンの発見が期待される。データの品質管理（Quality Control）のためにまずは教師なし学習を試して、データの分布や性質を調べる探索的データ解析（Explanatory Data Analysis; EDA）は、その後どのようなモデリングを行うにせよ、まずは最初に行うべき作業である。一方、デメリットとしては、得られた結果（パターン）の解釈が経験的な要素が多く、主観が入りやすいことである。ラベルに従った構造をラベルがなくても取り出せるという主張は、多くの教師なしモデルの論文でよく見る論調であるが、「その研究者の望んだラベルに従うY」になるようにデータの選別や前処理、パラメーターを選べるため、手作業でモデルを過学習させてしまう危険性もあり、データや仮説検定手法を取捨選択して有意な結果を導こうとするp-hackingと同様、研究者にとって都合の良い解析結果を作成できる余地があることから、客観性の担保が難しい。また、あるデータで試行錯誤して、特徴量を抽出した手順は汎用的でない場合が多いため、別のデータでは意味をなさず、作業が煩雑になるほど職人芸化してしまい、解析の再現性が損なわれる点もある。ここで「再現できないものは科学ではない」［33］とまで言うのは厳しすぎるかもしれないが、誰かが開発した教師なしモデルを、別の研究者が別のデータで試す際に、同じことが再現できるか、開発者が想定している最高のパフォーマンスを引き出せているかがわからない。また職人芸は自動化できないので、「100個のデータで同じことをする」というタスクにも向かない。

上記のような両者のメリット・デメリットを理解した上で、お互いを連携させることで、より良い解析が期待できる。例えば、教師なし学習で教師あり学習をサポートする話として、教師あり学習の学習データの前処理として、教師なし学習（例：PCA）を行う特徴量エンジニアリングが挙げられる。一般的にデータの次元が大きいほどモデルの性能が落ちる「次元の呪い」という現象があるため、事前に教師なし学習で次元を減らすことで、教師あり学習の性能を改善できる。また深層学習のような複雑な構造のモデルでは、最適化するパラメーターの値が極端に小さくなることでアンダーフローを起こす勾配消失、または大きくなることでオーバーフローを起こす勾配爆発という現象があるが、事前の教師なし学習が計算の安定に寄与することが経験的に知られている［34］。また、前処理の教師なし学習のパラメーターも汎化性能が高くなるように選択すれば、教師なし特有の恣意的な作業もない。教師なし学習で得られた構造をデータのラベル作成（アノテーション）に活用しても良いので、その後は、ラベルを利用した教師ありモデルの活用も視野に入れることが可能となる。また、現実世界では、データの一部分だけラベルが付いているという状況もあるため、こういった状況では、半教師モデルという、両者のハイブリッドな手法が活躍する［35］。

逆に、教師あり学習で教師なし学習をサポートする話として、パラメーター推定の客観化・自動化が挙げられる。教師なし学習での試行錯誤の末、データXから取り出されたパターンYは、さらに様々な作業を経て妥当性が評価され、意味ある面白いパターンだと主張されるわけだが、最終的にデータXとラベル（“元”データから得られたパターン）Yがペアになった状態は、教師ありの状況に他ならない。この状況をうまく利用し、XからクラスタラベルYを生成し、XとYを別の教師あり学習でCVすることで、最適なクラスタ数を自動探索する手法が幾つか提案されている［36, 37］。このような方法は、自己教師あり学習とも呼ばれ、クラスタ数や興味があるパターンの選出を恣意的に行う教師なし学習の弱点を教師あり学習でうまくカバーしており、教師なし学習における自動化（AutoML）の鍵にもなるかもしれない。

Known/Unknown/Wanted/Unwanted分類

上記のように、教師あり学習はラベル作成時に、教師なし学習は結果の解釈時に恣意性が入る。また、そもそも自分が知りたいことだけを調べる研究という行為自体が、言ってしまえば恣意性の塊なので、我々は恣意性から逃れることはできないと思う。そのため、ここではやや開き直り、恣意性も肯定的にとらえた上で、上記の教師のありなしとは違った、もう少し役に立つ分類法も紹介する（図4）。

図４：Known/Unknown/Wanted/Unwanted分類

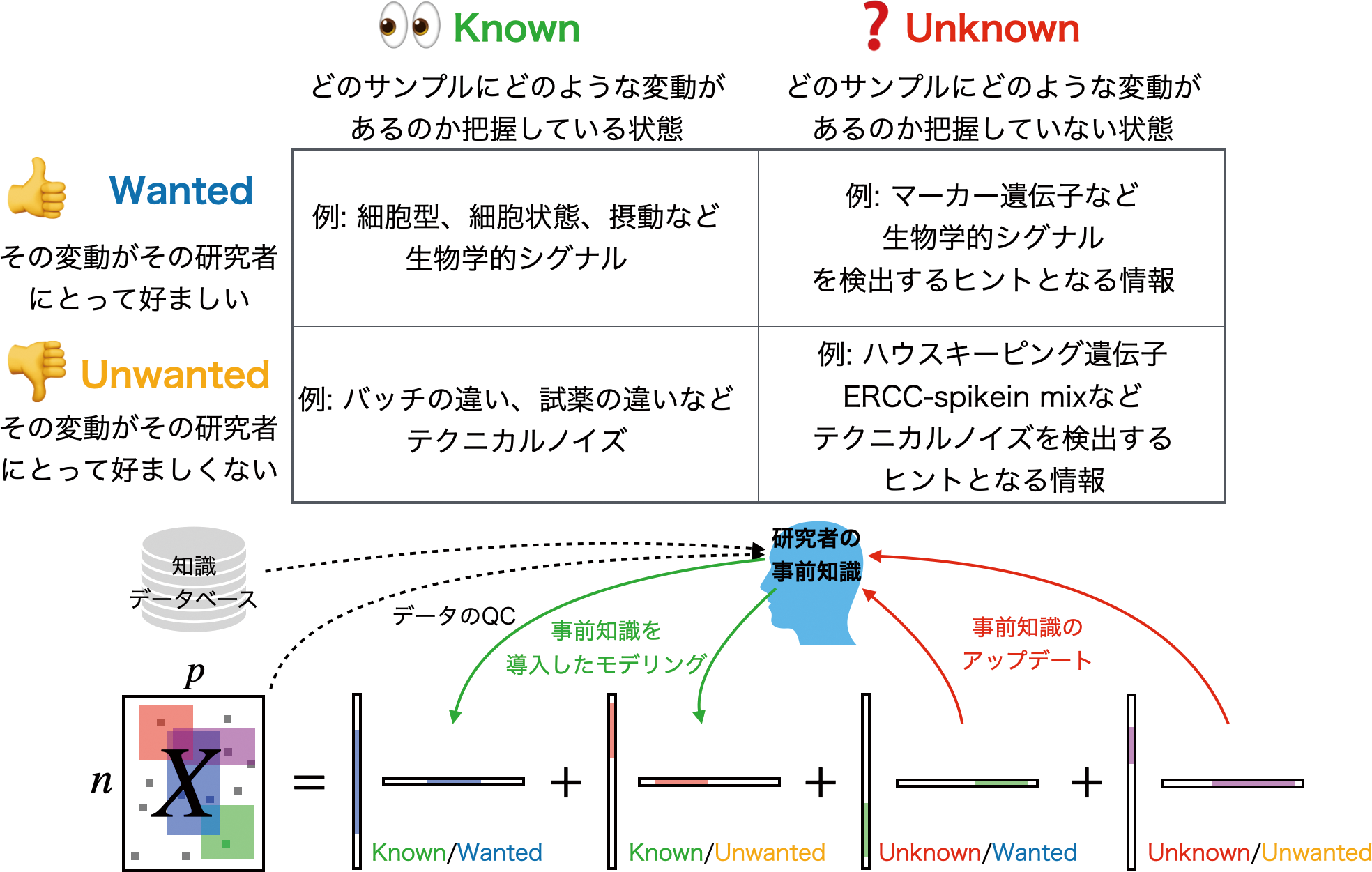
Wanted/Unwantedは、その変動がその研究者にとって好ましいか否か、Known/Unknownは、どのサンプルにどのような変動があるのかを研究者が把握しているか否かを意味する。

2017年にストックホルムで開催されたHuman Cell Atlas Computational Methods MeetingでNir Yosefは、データには4つの変動、すなわち、1．既知の望ましい変動（Known/Wanted）、2．既知の望ましくない変動（Known/Unwanted）、3．未知の望ましい変動（Unknown/Wanted）、4．未知の望ましくない変動（Unknown/Unwanted）が含まれると説明している［38, 39］。

ここでWanted/Unwantedの区別は、研究者が恣意的に決めるものである。例えば、1細胞RNA-Seqデータで細胞型ごとの変動を見たい時に、細胞周期による変動も含まれていた場合、その人にとって細胞周期は邪魔なUnwantedな変動だと言えるが、細胞周期を研究対象としている人にとっては、その変動こそがWantedであるため、これらの分類は研究者によって異なる。ここではその分類の仕方の優劣は議論しない。

Known/Unknownの違いは、そういう変動がデータに含まれていることを、その研究者が把握しているかどうかの違いである。例えば、細胞のラベル情報や、遺伝子のパスウェイ情報などは、そのデータに紐づいたKnownな情報である。データに含まれているかもしれないその他の変動要因は、まだ調べないとわからないのであればUnknownとする。ただし、前述したように、完全なUnknownな状況は手の施しようがないので、実際はあくまで手がかり程度の情報（例：マーカー遺伝子）はある状態を指す。

Wantedな変動をどうモデリングするかについてだが、前述の教師ありなし議論と関連付けると、Known/Wantedは教師あり学習、Unknown/Wantedは教師なし学習で取り出されるパターンである。EDAの過程で知識がアップデートされることでKnown/UnwantedやUnknown/Wantedが、Known/Wantedに切り替わることもある。データ解析でやりたいことは、あくまで最終的にその研究者のKnown/Wantedなパターンを取り出すことであり、それを取り出すためのヒントはなんでも使えば良い。例えば、細胞型が未知の1細胞RNA-Seqデータに含まれる細胞型を見つけたい問題などでは、マーカー遺伝子の発現がUnknown/Wantedな変動であり、Known/Wantedは細胞型が同定された時にその細胞型に従った変動である。Unknown/Wantedな変動をよく調べることで、細胞型が同定されることは、Unknown/Wantedな変動 がKnown/Wantedな変動に切り替わったことを意味する。このKnown/Wantedなラベルをさらにモデルに組み込むかというところで、上記のラベルの利用に関する恣意性で意見が分かれるところであるが、自分の見解としては、「ラベルという情報もノイズを含んだカテゴリカルな1データでしかないので、特に区別せず使えるものは何でも使えば良いのでは」と考えている。例えば、ラベルを与えて、ラベルを見つける問題をモデルに解かせるのはただのカンニングでしかないが、それ以外の解析、例えば、ラベルに従った特徴量の抽出や、もっと下流の解析への利用にその特徴量を利用する際においては、ラベルとは無関係な変動も多く含む教師なしパターンよりも、よりはっきりとしたパターンだけが取れてくる教師あり学習の方が便利な状況もあるだろう。

Unwantedな変動のモデリングについては、基本的な考え方はWantedと同じだが、最終的にそのUnwantedな変動を推定した後にデータから取り除く（Regress outという）ことでデータの値を補正したり、Unwantedな変動とWantedな変動を分離することで、よりWantedな変動検出の精度を向上させることを考える。行列同時分解は、データからKnown/Unwantedな変動を取り除くのに便利である。例えば、複数バッチある1細胞RNA-Seqをそのままマージして解析すると、細胞型など研究者が見たい変動よりも、計測器具、試薬、計測日など実験環境の微妙な違いによる人為的な変動の方が大きくなってしまうバッチ効果を例に挙げると、Seurat［40］やLIGER［41］といった手法では、バッチごとにデータ行列を分離しておき、「細胞型・細胞状態のような生物学的な変動はデータ間で再現性があるが、バッチごとの人為的な変動には再現性がない」という仮定のもとで、行列同時分解を適用することで、バッチ効果を回避することができる。また、データからUnknown/Unwantedな変動を除去する手法としては、対照群と処置群とでデータ行列が2つあった時に、処置の有無とは無関係に両群に含まれる交絡バイアスを取り除くscPLS［42］、Contrastive PCA ［43］といった手法がある。具体的にどのサンプルの遺伝子にそのような交絡因子があるのか把握していなくても、モデルとしてそのような仮定を入れることで、交絡バイアスを取り除いた結果だけを得ることができるのである。なお、行列同時分解的には、前者の解析は共通因子だけを見ようとする解析、後者の解析は共通因子を取り除こうとする解析に対応する。

Knownな変動もUnknownな変動も同時にモデルに組み込むことは可能である。例えば、Remove Unwanted Variation from RNA-Seq Data（RUV-Seq［44］）や、Surrogate Variable Analysis（SVA［45］）、Factorial Single-cell Latent Variable Model（f-scLVM［46］）などは、共に（1細胞）RNA-Seqデータにおける正規化やDifferential Expression Genes（DEGs）検出を行うツールであり、対照群と処置群のような群情報（Known/Wanted）に従って、変動する遺伝子群を検出するが、オプションでKnown/Unwanted（バッチの違い、QC尺度のばらつき）やUnknown/Unwanted（例：ERCC-spikein mixやハウスキーピング遺伝子のばらつき）も同時に考慮できる。また、例えUnknown/Unwantedのヒントが全くなくても、少なくとも完全にランダムなノイズではなく、なんらかの原因によって発生する、構造を持ったノイズだと想定されるため、データ行列からKnown/Unwantedな変動を差し引いた残差に対してSVDを実行し、分散が大きい成分をデータ行列からRegress Outするという考え方もある［44］。

正則化

上記の教師あり学習では、データXも事前情報Yも対等に扱っていたが、データと事前情報のどちらをどの程度信頼するのかを正則化の枠組みで調整できるモデルもある。通常正則化とは、過学習の解消や、多重線形性があるデータでの数値計算の安定化の目的で、目的関数とは別にペナルティ項（正則化項）を追加する機械学習のテクニックの総称である。一方、ここで紹介するグラフ（ラプラシアン）正則化［47］という手法は、正則化項を利用してさらに事前情報を取り組める。ここでは、X側はPCAやNMFなどの行列分解を適用し、Y側は事前情報のグラフデータとして、ラプラシアン固有マップという次元圧縮法を適用する。この時に、Xの行列分解で得られる因子行列とYのラプラシアン固有マップで得られる因子行列が共通だと仮定し（図5）、二つの目的関数を重み付けで足し合わせて1つの目的関数にした上で、まとめて最適化する。メインの目的関数側の最小化問題（行列分解）と、正則化項側の最大化問題（ラプラシアン固有マップ）は拮抗しており、これらのバランスは重みパラメーターλ（0≤λ≤1、大きい値にするほどより事前知識を反映した結果になる）によって調整される。このような目的関数を混ぜるアプローチは、機械学習分野では常套手段であり［48, 49］、両者の性質を併せ持ったような共通因子が得られるため、ノイジーなXであっても、Yでサポートすることで、望ましいパターンが取り出せる可能性がある。例えば、miRNAと疾患の関係［50］や、ヒトマイクロバイオーム（例：腸内細菌叢）と疾患の関係［51］など、一部の例を除いてほとんど何もわかっていないスパースなデータに対して、miRNA-miRNA類似度（例：ターゲット遺伝子の重複度合い）や、疾患-疾患類似度（例：疾患オントロジー上のセマンティック類似度）を事前知識としてグラフ正則化で取り込むことにより、上記の関係性の予測精度が向上した例がある。

図５：グラフ正則化

メインの行列分解の目的関数に、事前情報のラプラシアン固有マップの目的関数を重み付けで足し合わせる。両目的関数に共通因子を仮定することで、両者の性質を併せ持つ結果が得られる。

他にもグラフ正則化と類似したテクニックとして、ヘッシアン固有マップを利用したヘッシアン正則化［52］、事前情報がテンソルの場合のグラフ正則化であるハイパーグラフラプラシアン正則化［53］、Hilbert-Schmidt Independence Criterion（HSIC［54］）、Kernel Target Alignment（KTA［55］）、Maximum Mean Discrepancy（MMD［56］）など、カーネル関数で非線形に射影された高次元空間上でのX、Yの非類似度を正則化に利用したものがある。また、クロネッカー積カーネルによる正則化は、vecトリックというテクニックで、高速に計算できるエレガントな解法である（KronRLS［57］）。

3行列以上での行列同時分解

2行列での行列同時分解を拡張して、3つ以上の行列でも同時分解を行うことができる。なお、アルファベットが枯渇するため、ここでは3つ以上の行列は各々X_i（サイズ：n×p_i、1≤i≤m、m≥3）とし、2行列の時と同様に、これらは同じ行を共有しているとする。例えば、このようなデータ集合は、3つ以上のオミックスを、共通の空間で計測したものマルチオミックスデータ［58］や、同じ種類のデータであってもバッチが異なるデータ集合の解析［40, 41］などで利用されている。

CIAや、PLS、CCAの3行列以上の拡張としては、Multiple CIA（MCIA［59, 60］）、Multiset PLS（MPLS ［61］）、Multiset CCA（MCCA［40, 58, 62, 63, 64, 65］）がある。ここではMCCAだけを説明する。通常のCCAでは、中心化された2行列X、Yの射影先での相関最大化が目的関数であったのに対し、MCCAでは、中心化されたデータ集合X₁, X₂, ..., X_mの射影先での「総当たりの相関の和」が最大になるように射影行列をV₁, V₂, ..., V_m推定する（図6）。

  

$$\begin{array}{}\text{（10）}& \underset{V_1,V_2,\dots V_m}{\max }\sum _{i=1}^m\sum _{j=1,j\ne i}^{m}tr(V_i^T{\Sigma }_{\mathit{ij}}{V}_j)\end{array}$$

図６：m行列におけるMCIA、MPLS、MCCA

共通のk次元空間に全行列を射影し、総当たりでのスコア間共分散（または相関）の和が最大になるように、射影行列をもとめる。

ただし、${\Sigma }_{\mathit{ij}}=\frac{1}{n}{X}_i^T{X}_j$は、2行列X_i、X_jの相互共分散行列であり、拘束条件として、全てのiにおいて$V_i^T{\Sigma }_{\mathit{ii}}{V}_i=I_k$（I_k：k×kの単位行列）とする。なお、この総当たりの相関の和をどのように計算するのかは、最適化アルゴリズムによるところではあるが、一般化固有値分解（Generalized EVD; GEVD）を利用した手法Sum of Correlation（SUMCOR）［62, 63］では、全てのΣ_ijの対角化を以下のように一度に行う。まず、自分自身を含む1からmまでの全組み合わせでの相互共分散行列と、拘束条件に関係する行列を以下のように、ブロック行列としてまとめる。

  

$$\begin{array}{}\text{（11）}& C=\left[\begin{array}{ccc}\begin{array}{cc}{\Sigma }_{11}& {\Sigma }_{12}\\ {\Sigma }_{21}& {\Sigma }_{22}\end{array}& \cdots & \begin{array}{c}{\Sigma }_{1m}\\ {\Sigma }_{2m}\end{array}\\ ⋮& \ddots & ⋮\\ \begin{array}{cc}{\Sigma }_{m1}& {\Sigma }_{m2}\end{array}& \cdots & {\Sigma }_{\mathit{mm}}\end{array}\right]\end{array}$$

  

$$\begin{array}{}\text{（12）}& D=\left[\begin{array}{ccc}\begin{array}{cc}{\Sigma }_{11}& 0\\ 0& {\Sigma }_{22}\end{array}& \cdots & \begin{array}{c}0\\ 0\end{array}\\ ⋮& \ddots & ⋮\\ \begin{array}{cc}0& 0\end{array}& \cdots & {\Sigma }_{\mathit{mm}}\end{array}\right]\end{array}$$

次に、ラグランジュ未定乗数法より、以下のようにGEVDとすることで、V=（V₁, V₂, …, V_m）^Tを一度にもとめる。

  

$$\begin{array}{}\text{（13）}& \mathit{CV}=\mathit{\Lambda VD}\end{array}$$

ただし、Λは対角要素に全組み合わせのCCAの目的関数の値（相関係数）を格納した、（k×m）×（k×m）の対角行列である。

JointNMF［7, 8, 9, 41］の場合の3行列以上の拡張は、よりシンプルに行える（図7）。通常のNMFと同様、データ集合X₁, X₂, ..., X_mや、分解後に得られる因子行列U、V₁, V₂, ..., V_mが非負値と仮定した際に、以下のように共通因子Uの更新は、MU則においてX_iやV_iの数が増えるだけであり、   

$$\begin{array}{}\text{（14）}& U\leftarrow U\circ \frac{{\sum }_{i=1}^m{X}_i{V}_i}{{\sum }_{i=1}^m{\mathit{UV}}_i^T{V}_i}\end{array}$$

各V_iの更新も、X_iごとに以下のように更新するだけで良い。

  

$$\begin{array}{}\text{（15）}& V_i\leftarrow V_i\circ \frac{X_i^{T}U}{V_i{U}^{T}U}\end{array}$$

図７：m行列におけるJointNMF

共通因子Uを仮定し、MU則で全因子行列を逐次的に更新する。

上記のSeurat［40］やLIGER［41］は、既に3種類以上の1細胞オミックスデータに適用可能であり、各々MCCAとintegrative NMF（JointNMFの拡張）が利用されている。また、マルチオミックスデータ解析フレームワークであるmixOmics［58］が提供しているモデルの1つDIABLOも、MCCAの一種Generalized CCA（GCCA）を利用している。

よりヘテロな行列同時分解

上記のように、行が共通する複数の行列の同時分解は、これまで幾つも提案されてきている。一方、実際の生命科学データでは、行が共通する行列ばかりではなく、ある行列では列に関わる他のデータ行列があり、さらにその行列には、行が共通するデータ行列があり...という風に、より複雑な繋がり方をしている。ここでは、そういったよりヘテロなデータ構造にも適用できる行列分解アルゴリズムを紹介する。

まず、行列同時分解と、正則化項での事前知識の取り込みを組み合わせた手法が挙げられる。このようなアプローチは、行が共通した複数の行列同時分解がメインの解きたい問題として、他にも任意の行列の行・列に関する付加情報も加え、メインの問題を増強（Augment）するため、Augmented Multi-view Learningと呼ばれることもある［66］。例えばMCCAにラプラス正則化やヘッセ正則化を組み合わせたGraph Multi-view CCA［67］や、Hessian Multi-view CCA［68, 69］がある。Joint NMFでも同様に、Graph regularized Multi-view NMF［70］がある。また、複数行列とそれら全てにラベル情報も付随する状況では、複数の判別分析を同時に解くモデルを適用することもできる［58, 71, 72］。

Collective Matrix Factorization（CMF［73, 74, 75, 76, 77, 78］）というより汎用的な行列分解の定式化では、どの行列の分解もメインの目的関数、サブの目的関数（正則化項）とは区別せずに、統一的に分解する（図8）。多くのCMFの分解アルゴリズムはNMF（MU則）ベースであり、行・列問わず、繋がりがあるデータ同士で共通因子を設定することで、互いに関連づけた解を得る。このようなヘテロなデータを活用した例は、遺伝子に関するあらゆるデータをCMFで統合することで、遺伝子-疾患の予測精度を向上させた例［74, 75, 76, 78］や、1細胞RNA-Seqの欠損値補完に利用したもの［77］などが挙げられる。

図８：CMF

行・列問わず、繋がりがあるデータ同士では共通因子を設定することで、互いに関連づけた解を得ることができる。

おわりに

今回は、行列が2つ以上ある状況で、どのようなアルゴリズムが適用できるかを議論した。第1回で紹介したPCA/SVD、ICA、NMFは2行列以上にも拡張でき、第1回で導入した「パターンの和としての行列分解」、「射影としての行列分解」という2通りの理解の仕方が、ここでも役立つことを示した。複数の行列を取り込む際に、人が事前に設定したラベルを利用することに関しての恣意性に関してどのような議論があるのかを、著者の私見を交えて述べさせていただいた。

行列同時分解自体は、行を共有する行列が直線的に増えていくことに対応しているが、各種正則化テクニックと組み合わせたり、CMFに拡張することで、行だけでなく列を共有する行列さえも取り込める。ただしそれでも、これらが想定するデータが複雑化していく過程はあくまで平面的であり、遺伝子発現×疾患のような二項関係は表現できても、遺伝子発現×疾患×臓器のような多項関係を表現するのには限界がある。後者は、テンソル（多次元配列）というデータ構造であり、行列（同時）分解と同様に、テンソルに対しても分解アルゴリズムが存在し、データ中に含まれる因子行列（パターン）を取り出すことができる。第3回では、このテンソル分解を紹介する。

References

• [1]  Tsuyuzaki, K. (2021/4/24). Mathematics for Heterogeneous Biological Data Fusion Analysis with Matrix-Tensor Factorization – Part I. Matrix Factorization –. JSBi Bioinformatics Review, 1(2), 18-25. 10.11234/jsbibr.2021.1
• [2]  Boulesteix, A-L. & Strimmer, K. (2006/3/26). Partial least squares: a versatile tool for the analysis of high-dimensional genomic data. Briefings in Bioinformatics, 8(1), 32-44. 10.1093/bib/bbl016
• [3]  Krishnan, A. & Williams, L. J. & McIntosh, A. R. & Abdi, H. Partial Least Squares (PLS) methods for neuroimaging: a tutorial and review. (2011/3/15). Neuroimage, 56(2), 455-475. 10.1016/j.neuroimage.2010.07.034
• [4]  Morga, M. Canonical Correlation a Tutorial. (2001).
• [5]  Uurtio, V. & Monteiro, J. M. & Kandola, J. & Shawe-Taylor, J. & Fernandez-Reyes, D. & Rousu, J. (2017/10). A Tutorial on Canonical Correlation Methods. ACM Computing Surverys, 50(6):95. 10.1145/3136624
• [6]  Bie, T. D. & Cristianini, N. & Rosipal, R. (2005). Eigenproblems in Pattern Recognition. Handbook of Geometric Computing. Springer, 10.1007/3-540-28247-5_5
• [7]  Badea, L. (2008). Extracting gene expression profiles common to colon and pancreatic adenocarcinoma using simultaneous nonnegative matrix factorization. Pacific Symposium on Biocomputing. 279-290
• [8]  Kim, H. & Choo, J. & Kim, J. & Reddy, C. K. & Park, H. (2015/8/10-13). Simultaneous Discovery of Common and Discriminative Topics via Joint Nonnegative Matrix Factorization. Proceedings of KDD'15, 10.1145/2783258.2783338
• [9]  Zhang, S. & Liu, C. C. & Li, W. & Shen, H. & Laird, P. W. & Zhou, X. J. (2012/10). Discovery of multi-dimensional modules by integrative analysis of cancer genomic data. Nucleic Acids Res., 40(19), 9379-9391. 10.1093/nar/gks725
• [10]  Calhoun, V. D. & Adali, T. & Pearlson, G. D. & Kiehl, K. A. (2006/4/1). Neuronal chronometry of target detection: fusion of hemodynamic and event-related potential data. Neuroimage, 30(2), 544-53. 10.1016/j.neuroimage.2005.08.060
• [11]  Alter, O. & Brown, P. O. & Botstein, D. (2003/3/18). Generalized singular value decomposition for comparative analysis of genome-scale expression data sets of two different organisms. PNAS, 100(6), 3351-6. 10.1073/pnas.0530258100
• [12]  山本博之. （2015/10/3）. フリーソフトウェアを通じた多変量解析講習, 第2回メタボロームシンポジウム若手会
• [13]  Sankaran, K. & Holmes, S. P. (2019/8/28). Multitable Methods for Microbiome Data Integration, Frontiers in Genetics, 10(627), 10.3389/fgene.2019.00627
• [14]  Ergon, R. (2002), PLS score–loading correspondence and a bi-orthogonal factorization. Journal of Chemometrics, 16, 368-373. 10.1002/cem.736
• [15]  Jendoubi, T. & Strimmer, K. (2019/1/9). A whitening approach to probabilistic canonical correlation analysis for omics data integration. BMC Bioinformatics, 20(1), 15. 10.1186/s12859-018-2572-9
• [16]  Brown, B. C. & Bray, N. L. & Pachter, L. (2018/11). Expression reflects population structure. PLOS Genetics, 14(12), e1007841. 10.1371/journal.pgen.1007841
• [17]  Hub, J. S. & de Groot, B. L. (2009/8). Detection of functional modes in protein dynamics. PLOS Computational Biology, 5(8), e1000480. 10.1371/journal.pcbi.1000480
• [18]  Krivobokova, T. & Briones, R. & Hub, J. S. & Munk, A. & de Groot, B. L. (2012/8). Partial least-squares functional mode analysis: application to the membrane proteins AQP1, Aqy1, and CLC-ec1. Biophysical Journal. 103(4):786-96. 10.1016/j.bpj.2012.07.022
• [19]  Kobayashi-Kirschvink, K. J. & Nakaoka, H. & Oda, A. & Kamei, K. F. & Nosho, K. & Fukushima, H. & Kanesaki, Y. & Yajima, S. & Masaki, H. & Ohta, K. & Wakamoto, Y. (2018/6/20). Linear Regression Links Transcriptomic Data and Cellular Raman Spectra. Cell Systems, 7(1), 104-117.e4 10.1016/j.cels.2018.05.015
• [20]  Indahl, U. G. & Martens, H. & Næs, T. (2007), From dummy regression to prior probabilities in PLS‐DA. J. Chemometrics, 21: 529-536. 10.1002/cem.1061
• [21]  Barker, M. (2010/10/1). Partial Least Squares for Discrimination: Statistical Theory and Implementation. LAP LAMBERT Academic Publishing.
• [22]  Fan, J. GitHub, https://github.com/JEFworks/MUDAN
• [23]  Li, H. & Courtois, E. T. & Sengupta, D. & Tan, Y. & Chen, K. H. & Goh, J. J. L. & Kong, S. L. & Chua, C. & Hon, L. K. & Tan, W. S. & Wong, M. & Choi, P. J. & Wee, L. J. K. & Hillmer, A. M. & Tan, I. B. & Robson, P. & Prabhakar, S. (2017/3). Reference component analysis of single-cell transcriptomes elucidates cellular heterogeneity in human colorectal tumors. Nature Genetics, 49(5), 708-718. 10.1038/ng.3818
• [24]  Berry, M. W. & Drmac, Z & Jesup, E. R. (1999). Matrices, Vector Spaces, and Information Retrieval. SIAM Review, 41(2), 335-362. 10.1137/S0036144598347035
• [25]  Tamayo, P. & Scanfeld, D. & Ebert, B. L. & Gillette, M. A. & Roberts, C. W. & Mesirov, J. P. (2007/4/3). Metagene projection for cross-platform, cross-species characterization of global transcriptional states. PNAS. 104(14), 5959-64. 10.1073/pnas.0701068104
• [26]  Li, Y. & Ngom, A. (2013/4/16). The non-negative matrix factorization toolbox for biological data mining. Source Code for Biology and Medicine, 8(1), 10. 10.1186/1751-0473-8-10
• [27]  Stein-O’Brien, G. L. & Clark, B. S. & Sherman, T. & Zibetti, C. & Hu, Q. & Sealfon, R. & Liu, S. & Qian, J. & Colantuoni, C. & Blackshaw, S. & Goff, L. A, & Fertig, E. J. (2019/5/22). Decomposing Cell Identity for Transfer Learning across Cellular Measurements, Platforms, Tissues, and Species. Cell Systems, 8(5), 395-411.e8. 10.1016/j.cels.2019.04.004
• [28]  Rodriques, S. G.& Stickels, R. R. & Goeva, A. & Martin, C. A. & Murray, E. & Vanderburg, C. R. & Welch, J. & Chen, L. M. & Chen, F. & Macosko, E. Z. (2019/3/29). Slide-seq: A scalable technology for measuring genome-wide expression at high spatial resolution. Science, 363(6434), 1463-1467. 10.1126/science.aaw1219
• [29]  Song, D. & Li, K. A. & Hemminger, Z. & Wollman, R. & Li, J. J. (2021/2/9). scPNMF: sparse gene encoding of single cells to facilitate gene selection for targeted gene profiling. bioRxiv, 10.1101/2021.02.09.430550
• [30]  Raj, B. (2016/11/8). Machine Learning for Signal Processing Supervised Representations: Johns Hopkins Whiting School of Engineering, Class19.
• [31]  Pedregosa, F. & Varoquaux, G. & Gramfort, A. & Michel, V. & Thirion, B. & Grisel, O. & Blondel, M. & Prettenhofer, P. & Weiss, R. & Dubourg, V. & Vanderplas, J. & Passos, A. & Cournapeau, D. & Brucher, M. & Perrot, M. & Duchesnay, E. (2011). Scikit-learn: Machine Learning in Python. Journal of Machine Learning Research, 12, 2825-2830
• [32]  Taguchi, Y. H. (2020). Unsupervised Feature Extraction Applied to Bioinformatics A PCA Based and TD Based Approach, Springer, 10.1007/978-3-030-22456-1
• [33]  Buffalo, V. & 片山俊明 & 鈴木治夫 & 川島秀一 & 山本泰智 & 酒匂寛 & 山村吉信. （2020/9/19）. バイオインフォマティクスデータスキル ―オープンソースツールを使ったロバストで再現性のある研究
• [34]  Ankur, A. Patel, & 中田秀基 （2020/4/13）. Pythonではじめる教師なし学習 ―機械学習の可能性を広げるラベルなしデータの利用. オライリージャパン
• [35]  鹿島久嗣 & 加藤毅 & 山西芳裕 & 杉山将 & 津田宏治. （2009/4）. リンク伝搬法：リンク予測のための半教師付き学習法. Proceedings of 人工知能学会, 第73回人工知能基本問題研究会, 19-24
• [36]  Miao, Z. & Moreno, P. & Huang, N. & Papatheodorou, I. & Brazma, A. & Teichmann, S. A. (2020/6/17). Putative cell type discovery from single-cell gene expression data. Nature Methods, 17(6), 621-628. 10.1038/s41592-020-0825-9
• [37]  Shah, N. & Li, J. & Li, F. & Chen, W. & Gao, H. & Chen, S. & Hua, K. & Zhang, X. (2020/7/10). An Experiment on Ab Initio Discovery of Biological Knowledge from scRNA-Seq Data Using Machine Learning. Patterns, 1(5), 100071. 10.1016/j.patter.2020.100071
• [38]  Yosef, N. (2017/6/5). Nir Yosef at the Human Cell Atlas Computational Methods meeting – Stockholm, 1-2 June 2017. YouTube, https://www.youtube.com/watch?v=rCGr62Sk1CQ
• [39]  Cole, M. B. & Risso, D. & Wagner, A. & DeTomaso, D. & Ngai, J. & Purdom, E. & Dudoit, S. & Yosef, N. (2019/4/24). Performance Assessment and Selection of Normalization Procedures for Single-Cell RNA-Seq. Cell Systems, 8(4), 315-328.e8 10.1016/j.cels.2019.03.010
• [40]  Butler, A. & Hoffman, P. & Smibert, P. & Papalexi, E. & Satija, R. (2018/6). Integrating single-cell transcriptomic data across different conditions, technologies, and species. Nature Biotechnology, 36(5), 411-420. 10.1038/nbt.4096
• [41]  Welch, J.D. & Kozareva, V. & Ferreira, A. & Vanderburg, C. & Martin, C. & Macosko, E. Z. (2019/6/13). Single-Cell Multi-omics Integration Compares and Contrasts Features of Brain Cell Identity. Cell, 177(7), 1873-1887.e17.10.1016/j.cell.2019.05.006
• [42]  Chen, M. & Zhou, X. (2017/10/19). Controlling for Confounding Effects in Single Cell RNA Sequencing Studies Using both Control and Target Genes. Scientific Reports, 7(1), 13587 10.1038/s41598-017-13665-w
• [43]  Abid, A. & Zhang, M. J. & Bagaria, V. K. & Zou, J. (2018/3). Exploring patterns enriched in a dataset with contrastive principal component analysis. Nature Communication, 9(1), 2134. 10.1038/s41467-018-04608-8
• [44]  Risso, D. & Ngai, J. & Speed, T. P. & Dudoit, S. (2014/9). Normalization of RNA-seq data using factor analysis of control genes or samples. Nature Biotechnology, 32(9), 896-902. 10.1038/nbt.2931
• [45]  Leek, J. T. & Storey, J. D. (2007/9). Capturing heterogeneity in gene expression studies by surrogate variable analysis. PLOS Genetics, 3(9), 1724-35. 10.1371/journal.pgen.0030161
• [46]  Buettner, F. & Pratanwanich, N. & McCarthy, D. J. & Marioni, J. C. & Stegle, O. (2017/11/7). f-scLVM: scalable and versatile factor analysis for single-cell RNA-seq. BMC Genome Biology, 18(1), 212. 10.1186/s13059-017-1334-8
• [47]  Jiang, B. & Ding, C. & Luo. B. & Tang, J. (2013). Graph-Laplacian PCA: Closed-Form Solution and Robustness. IEEE Conference on Computer Vision and Pattern Recognition, 3492-3498. 10.1109/CVPR.2013.448
• [48]  van der Maaten, L. (2009). Preserving local structure in Gaussian process latent variable models. Proceedings of the 18th Annual Belgian-Dutch Conference on Machine Learning, 81–88.
• [49]  Goodfellow, I. J. & Pouget-Abadie, J & Mirza, M. & Xu, B. & Warde-Farley, D. & Ozair, S. & Courville, A. & Bengio, Y., Generative Adversarial Networks, Proceedings of NIPS'14, 2672-2680.
• [50]  Xiao, Q. & Luo, J. & Liang, C, & Cai, J. & Ding, P. (2018/1). A graph regularized non-negative matrix factorization method for identifying microRNA-disease associations. Bioinformatics, 34(2), 239-248. 10.1093/bioinformatics/btx545
• [51]  He, B. S. & Peng, L. H. & Li, Z. (2018/11/1). Human Microbe-Disease Association Prediction with Graph Regularized Non-Negative Matrix Factorization. Front Microbiol., 9(2560). 10.3389/fmicb.2018.02560
• [52]  Ma, Y. & Zhao, J. & Ma, Y. (2020/11/18). MHSNMF: multi-view hessian regularization based symmetric nonnegative matrix factorization for microbiome data analysis. BMC Bioinformatics, 21(Suppl 6), 234. 10.1186/s12859-020-03555-w
• [53]  Yu, N. & Gao, Y. L. & Liu, J. X. & Wang, J. & Shang, J. (2019/10/22). Robust hypergraph regularized non-negative matrix factorization for sample clustering and feature selection in multi-view gene expression data. BMC Human Genomics, 13(Suppl 1), 46 10.1186/s40246-019-0222-6
• [54]  Barshan, E. & Ghodsi, A. & Azimifar, Z. & Jahromi, M. Z. (2011). Supervised principal component analysis: Visualization, classification and regression on subspaces and submanifolds. Pattern Recognition, 44(7), 1357-1371, 10.1016/j.patcog.2010.12.015
• [55]  Marcou, G. & Horvath, D. & Varnek, A. (2016/1/25). Kernel Target Alignment Parameter: A New Modelability Measure for Regression Tasks. Journal of Chemical Information and Modeling, 56(1), 6-11. 10.1021/acs.jcim.5b00539
• [56]  Singh, R. & Demetci, P. & Bonora, G. & Ramani, V. & Lee, C. & Fang, H. & Duan, Z. & Deng, X. & Shendure, J. & Disteche, C. & Noble, W. S. (2020/06/13). Unsupervised manifold alignment for single-cell multi-omics data. bioRxiv, 10.1101/2020.06.13.149195
• [57]  Cichonska, A. & Ravikumar, B. & Parri, E. & Timonen, S. & Pahikkala, T. & Airola, A. & Wennerberg, K. & Rousu, J. & Aittokallio, T. (2017/8/7). Computational-experimental approach to drug-target interaction mapping: A case study on kinase inhibitors. PLOS Computational Biology, 13(8), e1005678. 10.1371/journal.pcbi.1005678
• [58]  Rohart, F. & Gautier, B. & Singh, A. & Cao, K-A. (2017/11/3). mixOmics: An R package for omics feature selection and multiple data integration. PLOS Computational Biology, 13(11), e1005752. 10.1371/journal.pcbi.1005752
• [59]  Meng, C. & Kuster, B. & Culhane, A. C. & Gholami, A. M. (2014/3/29). A multivariate approach to the integration of multi-omics datasets. BMC Bioinformatics, 15(162), 10.1186/1471-2105-15-162
• [60]  Min, E. J. & Long, Q. (2020/4/15). Sparse multiple co-Inertia analysis with application to integrative analysis of multi -Omics data. BMC Bioinformatics, 21(1), 141. 10.1186/s12859-020-3455-4
• [61]  Csala, A. & Zwinderman, A. H. & Hof, M. H. (2020/1/9). Multiset sparse partial least squares path modeling for high dimensional omics data analysis. BMC Bioinformatics, 21(1), 9. 10.1186/s12859-019-3286-3
• [62]  Parra, L. (2018). Multi-set canonical correlation analysis simply explained. arXiv, arXiv:1802.03750
• [63]  Deleus, F. & Van Hulle, M. M. (2011/4/15). Functional connectivity analysis of fMRI data based on regularized multiset canonical correlation analysis. Journal of Neuroscience Methods, 197(1), 143-57. 10.1016/j.jneumeth.2010.11.029
• [64]  Zhuang, X. & Yang, Z. & Cordes, D. (2020/9). A technical review of canonical correlation analysis for neuroscience applications. Human Brain Mapping, 41(13), 3807-3833. 10.1002/hbm.25090
• [65]  Tenenhaus, A. & Guillemot, V. (2017/5/10). The RGCCA package for Regularized/Sparse Generalized Canonical Correlation Analysis. Vignettes of RGCCA package
• [66]  Klami, A. & Bouchard, G. & Tripathi, A. (2013/12/25). Group-sparse Embeddings in Collective Matrix Factorization. ICLR 2014
• [67]  Chen, J. & Wang, G. & Giannakis, G. B. (2019/6/1). Graph Multiview Canonical Correlation Analysis. IEEE Transactions on Signal Processing, 67(11), 2826-2838, 10.1109/TSP.2019.2910475
• [68]  Zhou, B. & Wang, Y. & Liu, W. & Liu, B. (2018). Hessian-regularized weighted multi-view canonical correlation analysis for working condition recognition of sucker-rod pumping wells. Systems Science & Control Engineering, 6(3), 215-226. 10.1080/21642583.2018.1545610
• [69]  Liu, W. & Yang, X. & Tao, D. & Cheng, J. & Tang, Y. (2018). Multiview dimension reduction via Hessian multiset canonical correlations. Information Fusion, 41, 119-128. 10.1016/j.inffus.2017.09.001
• [70]  Yu, N. & Gao, Y.-L. & Liu, J.-X. & Shang, J. & Zhu, R. & Dai, L.-Y. (2018/11/28). Co-differential Gene Selection and Clustering Based on Graph Regularized Multi-View NMF in Cancer Genomic Data. Genes (Basel), 9(12), 586, 10.3390/genes9120586
• [71]  Shen, C. & Sun, M. & Tang, M. & Priebe, C. E. (2014). Generalized canonical correlation analysis for classification. Journal of Multivariate Analysis, 130, 310-322. 10.1016/j.jmva.2014.05.011
• [72]  Kan, M. & Shan, S. & Zhang, H. & Lao, S. & Chen, X. (2012). Multi-view Discriminant Analysis, Computer Vision – ECCV 2012. Lecture Notes in Computer Science, 7572. 10.1007/978-3-642-33718-5_58
• [73]  Singh, A. P. & Gordon, G. J. (2008/8). Relational Learning via Collective Matrix Factorization. KDD'08, 650–658. 10.1145/1401890.1401969
• [74]  Zitnik, M. & Zupan, B. (2016/6/15). Jumping across biomedical contexts using compressive data fusion. Bioinformatics, 32(12), i90-i100. 10.1093/bioinformatics/btw247
• [75]  Huang, F. & Qiu, Y. & Li, Q. & Liu, S. & Ni, F. (2020/4/9). Predicting Drug-Disease Associations via Multi-Task Learning Based on Collective Matrix Factorization. Frontiers in Bioengineering and Biotechnology, 8(218), 10.3389/fbioe.2020.00218
• [76]  Zakeri, P. & Simm, J. & Arany, A. & ElShal, S. & Moreau, Y. (2018/7/1). Gene prioritization using Bayesian matrix factorization with genomic and phenotypic side information. Bioinformatics, 34(13),i447-i456. 10.1093/bioinformatics/bty289
• [77]  Xu, J. & Cai, L. & Liao, B. & Zhu, W. & Yang, J. (2020/3/1). CMF-Impute: an accurate imputation tool for single-cell RNA-seq data. Bioinformatics, 36(10), 3139-3147. 10.1093/bioinformatics/btaa109
• [78]  Žitnik, M. & Zupan, B. (2015/1/1). Data Fusion by Matrix Factorization. IEEE Transactions on Pattern Analysis and Machine Intelligence, 37(1), 41-53. 10.1109/TPAMI.2014.2343973

略語リスト

・PCA

Principal Component Analysis

・SVD

Singular Value Decomposition

・NMF

Non-negative Matrix Factorization

・ICA

Independent Component Analysis

・PLS

Partial Least Squares

・CCA

Canonical Correlation Analysis

・MICA

Multimodal Independent Component Analysis

・JointNMF

Joint Non-negative Matrix Factorization

・GroupICA

Group Independent Component Analysis

・GSVD

Generalized Singular Value Decomposition

・CIA

Co-inertia Analysis

・PLS-C

Partial Least Squares Correlation

・NIPALS

Nonlinear Iterative Partial Least Squares

・SIMPLS

Statistically Inspired Modification of Partial Least Squares

・PLS-R

Partial Least Squares Regression

・PLS-DA

Partial Least Squares Discriminant Analysis

・MU則

Multiplicative Update Rule

・FMA

Functional Mode Analysis

・LDA

Linear Discriminant Analysis

・RCA

Reference Component Analysis

・OSS

Open Source Software

・CV

Cross Validation

・EDA

Explanatory Data Analysis

・RUV-Seq

Remove Unwanted Variation from RNA-Seq Data

・SVA

Surrogate Variable Analysis

・f-scLVM

Factorial Single-cell Latent Variable Model

・DEGs

Differential Expression Genes

・HSIC

Hilbert-Schmidt Independence Criterion

・KTA

Kernel Target Alignment

・MMD

Maximum Mean Discrepancy

・MCIA

Multiple Co-inertia Analysis

・MPLS

Multiset Partial Least Squares

・MCCA

Multiset Canonical Correlation Analysis

・GEVD

Generalized Eigen Value Decomposition

・SUMCOR

Sum of Correlation

・GCCA

Generalized Canonical Correlation Analysis

・CMF

Collective Matrix Factorization

著者略歴

露崎 弘毅 2015年、東京理科大学生命創薬科学科博士後期課程終了。博士（薬科学）。同年より、理化学研究所情報基盤センターバイオインフォマティクス研究開発ユニット（現在の所属1）に在籍。現在、基礎科学特別研究員及びJSTさきがけ研究員を兼任。パッケージングに特化したハッカソンBio “Pack”athonを主催。本年度BioconductorのアジアカンファレンスであるBioC Asia 2021を主催予定。 ホームページ：https://sites.google.com/view/kokitsuyuzaki