Efficient Algorithm of Monte-Carlo Simulation of Light Propagation for Optical Coherence Tomography

Abstract

入射光と同じ位置から出射する特定の長さの光路長の散乱光のみを効率的に解析することができるモンテカルロ法について解説する．均一な散乱媒質と散乱特性に空間分布がある散乱媒質に対するこのモンテカルロ法の適用方法を説明し，解析例を示す．このシミュレーションは光干渉断層撮影法で検出される散乱光の解析を効率的に行うことができる．

Translated Abstract

Efficient algorithm of Monte-Carlo simulation of scattered light which re-emerges from the incident point of light and has a specific pathlength is reviewed. Calculation procedures of this algorithm for uniform and nonuniform scattering media are explained and examples of simulation results are shown. This algorithm can efficiently analyze scattered light detected by optical coherence tomography.

1.  はじめに

光計測技術と計測機器の進展により光を用いて生体内部を可視化する生体光計測は大きく発展しており，さまざまな臨床診断への取り組みが行われている^1,2)．生体は光に対して強い散乱体であり，生体光計測において散乱は重要な問題である．生体からの多重散乱光（拡散光）を利用して生体内部を可視化する技術が拡散光トモグラフィー³⁾，および，光トポグラフィー⁴⁾である．前者は乳がんの診断装置⁵⁾として欧米で実用化されつつあり，後者は脳表面の血中酸素飽和度をイメージングする装置であり，うつ病や統合失調症などの精神疾患の診断に利用されている⁶⁾．一方，多重散乱光の影響を抑え準直進光のみを検出することで生体内部を可視化する技術が光干渉断層撮影法であり，眼底における網膜剥離の診断装置として普及している^7,8)．

生体光計測では，光計測技術と計測機器の進展と同時に，光計測で取得される信号から散乱体内部の情報を推定するための散乱光の光伝搬解析が重要である．生体内部の光伝搬は，輸送方程式によって表すことができる^9,10)．輸送方程式を解析的に解くことは難しい．光が十分に多重散乱され光の伝搬がほぼ等方的（拡散的）になっている場合は，光伝搬は拡散方程式に従うと近似することができる．これは拡散近似と呼ばれる．拡散方程式は解析解を求めることができ，半無限空間に広がる散乱体の一点にパルス光を照射したときの散乱光の時間波形や空間分布が得られる．また，有限要素法などを用いて数値解を求めることもできる．これらの解析は，拡散光トモグラフィーや，光トポグラフィーにおいて利用されている．しかし，拡散近似は，入射点近傍の空間分布や，早い領域の時間応答など，光が拡散的になる前の光の伝搬を正確に表すことはできない．

輸送方程式の解を統計的に求める方法がモンテカルロ法である¹¹⁾．モンテカルロ法の解析は，散乱体内部の散乱を乱数により発生させ，光の伝搬経路を決定する．非常に多数の伝搬経路を発生させることで，統計的に，光の伝搬を解くことができる．モンテカルロ法は近似解ではないため，拡散近似のような制限はなく，すべての領域の光伝搬を表すことが可能であり，準直進光の解析にも利用することができる．モンテカルロ法では，散乱光の光路長（伝搬時間）や出射位置は，実際の確率に従ってランダムに決まる．多数の経路を発生させることで統計的に光路長分布や出射位置が決定される．一方，特定の出射位置（検出位置）からの光，さらには，特定の光路長の光のみを解析しようとする場合には，興味のある伝搬経路は，発生させた多数の伝搬経路のごく一部となり，計算効率が低い．しかし，現在の計算機の能力を用いれば，これらの解析も可能ではある．

筆者らは，光干渉断層撮影法と同じ低コヒーレンス干渉計を用いて高濃度粒子溶液の粒子径計測を行う低コヒーレンス動的光散乱計測法の研究のなかで，入射点と同じ位置から出射する特定の光路長の伝搬経路のみを発生させるモンテカルロ法のアルゴリズムを提案した¹²⁾．さらに，光干渉断層撮影法への応用を考え，このモンテカルロ法を散乱媒質内部の伝搬解析へと展開している^13,14)．本解説では，特定の光路長の伝搬経路のみを発生させるモンテカルロ法のアルゴリズムと，それを用いた散乱媒質内部の伝搬解析について述べる．

2.  輸送方程式とモンテカルロ法

散乱体内の光の伝搬は，光のエネルギーの流れを表す輸送方程式で表すことができる⁹⁾．位置rでの $\widehat{s}$ 方向へ伝搬する単位面積，単位立体角，単位時間当たりの光のエネルギー（光強度）I(r, $\widehat{s}$)を用いると，輸送方程式は

  

$$\frac{dI\left(r,\widehat{s}\right)}{ds}=-{\mu }_{t}I\left(r,\widehat{s}\right)+{\mu }_s{\displaystyle {\int }_{4\pi }p\left(\widehat{s},{\widehat{s}}^{\prime }\right)}I\left(r,{\widehat{s}}^{\prime }\right)d{\omega }^{\prime }+\epsilon \left(r,\widehat{s}\right)$$（1）

と表すことができる．ここで，μ_t，μ_s，p($\widehat{s}$, ${\widehat{s}}^{\prime }$)，ω，および，ε(r, $\widehat{s}$)は，それぞれ，減光係数，散乱係数，位相関数，立体角，光源の光強度である．（1）式の輸送方程式の左辺は，光の伝搬に伴う光強度の変化であり，右辺1項目は散乱と吸収による光強度の減衰，2項目は $\widehat{s}$ 方向への散乱による光強度の増加，3項目は光源による増加をそれぞれ表している．光源がなく，散乱による光強度の増加が無視できる場合には，右辺は1項目のみとなる．これはランバート・ベール則であり，この時．光強度は，伝搬とともに指数関数的に減衰する．輸送方程式を解く1つの方法は，強い散乱体では光の伝搬はほぼ等方的であると仮定する拡散近似である．これについては参考文献9)と10)を参照されたい．

輸送方程式は1階の線形微分方程式であり，その一般解は

  

$$I\left(r,\widehat{s}\right)=C{\mathrm{e}}^{-\tau }+{\displaystyle {\int }_{-\infty }^{s}Q\left(r_1,\widehat{s}\right){\mathrm{e}}^{-(\tau -{\tau }_1)}d{s}_1}$$（2）

となる．ここで，Cは定数，$\tau ={\displaystyle {\int }_{-\infty }^s{\mu }_{t}ds}$ と ${\tau }_1={\displaystyle {\int }_{-\infty }^{s_1}{\mu }_{t}d{s}_1}$は，それぞれ，位置rとr₁までの光路長，

  

$$Q\left(r,\widehat{s}\right)={\mu }_s{\displaystyle {\int }_{4\pi }p\left(\widehat{s},{\widehat{s}}^{\prime }\right)}I\left(r,{\widehat{s}}^{\prime }\right)d{\omega }^{\prime }+\epsilon \left(r,\widehat{s}\right)$$（3）

は，位置rでの $\widehat{s}$ 方向への散乱と光源の強さを表している．（2）式の右辺の1項目は，ランバート・ベール則に従う項で，適当に境界条件を設定すれば，定数Cが決定できる．2項目は，散乱と光源による光の増加を表す項であり，位置r₁で散乱と光源により増加した光も，その後はランバート・ベール則に従い，指数関数的に減衰することを示している．（2）式で示される輸送方程式の一般解は光強度の分布を与える式ではあるが，右辺にも光強度が入っているので，そこから光強度を求めることは難しい．そこで，光強度を散乱回数ごとに分けて考えてみると，（2）式は

  

$$I_n\left(r,\widehat{s}\right)={\displaystyle {\int }_{-\infty }^s\left[{\mu }_s{\displaystyle {\int }_{4\pi }p\left(\widehat{s},{\widehat{s}}^{\prime }\right)}{I}_{n-1}\left(r_1,{\widehat{s}}^{\prime }\right)d{\omega }^{\prime }\right]e^{-(\tau -{\tau }_1)}d{s}_1}$$（4）

となる．したがって，（n − 1）回散乱の光強度がわかれば，n回散乱の光強度が計算できる．したがって，入射光の光強度から，1回散乱，2回散乱と順番に光強度を計算していけば，輸送方程式を解くことができる．これを行っているのがモンテカルロ法である．

ここで，モンテカルロ積分について説明する．定積分 ${\displaystyle {\int }_a^{b}f\left(x\right)dx}$ を数値積分することを考える．この積分を数値計算する1つの方法は，積分範囲内をN個（x₁, x₂, ..., x_N）に等分割し，それぞれの区間の面積（関数の値と幅の積）を足し合わせることで，以下の式より計算できる．

  

$${\displaystyle {\int }_a^{b}f\left(x\right)dx}\cong \frac{b-a}{N}{\displaystyle \sum _{i=1}^{N}f\left(x_i\right)}$$（5）

モンテカルロ積分は，積分範囲の中から乱数を用いてN個の点（ξ₁, ξ₂, ..., ξ_N）を選び，以下の式で定積分を計算する．

  

$${\displaystyle {\int }_a^{b}f\left(x\right)dx}\cong \frac{1}{N}{\displaystyle \sum _{i=1}^N\frac{f\left({\xi }_i\right)}{g\left({\xi }_i\right)}}$$（6）

ここで，g(x)は乱数の確率密度関数である．一様乱数を用いる場合，確率密度関数はg(x) = 1/(b − a)であり，（6）式と（5）式は同じ形である．一方，確率密度関数g(x) $\propto$ f(x)が被積分関数に比例する乱数を用いる場合は，総和の中は定数となり，被積分関数f(x)の値を評価する必要はなくなる．この時，積分への寄与が大きくなる被積分関数f(x)が大きな値となるようなxがより多く選ばれ，積分への寄与が少ないxの値はあまり選ばれなくなっている．このような乱数を用いると，積分の誤差が小さくなる．

光散乱のモンテカルロ法は，次の手順で行われる．媒質に入射された光は，散乱されるまで媒質内を直進する．この時，入射光（0回散乱光）の光強度は（2）式の右辺1項目で示されるように指数関数的に減衰する．1回目の散乱点の位置は0回散乱光の強度に比例するので，その強度分布に比例した確率密度関数を用いて散乱位置を決定する．散乱位置の決定は，取りえる光路長の範囲内の一様乱数を発生させ，その光路長に対応した減衰を重みとすることも可能である．しかし，この方法ではほとんど発生しない長い光路長を多く発生させることになり，精度が悪くなる．次に，散乱の位相関数に従う乱数を用いて，散乱方向を決定する．これも一様乱数で散乱角を決定し，その方向の散乱の強さを重みとすることも可能である．光が最初に散乱される点の位置とその点で散乱された光が進む散乱方向を乱数を用いて決定し，1回散乱の光強度を計算することは，（4）式をモンテカルロ積分で数値計算していることになる．これを散乱光が媒質から出射するまで繰り返すことで，各散乱回数の光強度を計算することができる．また，各散乱回数の散乱位置，出射光の出射位置，散乱回数，光路長等も評価することができる．

3.  特定の光路長の伝搬経路のみを発生させるモンテカルロ法

通常のモンテカルロ法による光散乱解析では，散乱光の出射位置と光路長（時間）はその発生確率に従ってランダムに決定される．しかし，特定の検出位置での光路長分布やパルス光を入射したときの時間波形を解析する場合には，対象となる散乱光の発生確率は低く，計算効率が悪い．特定の位置から出射される特定の長さの光路長をもつ伝搬経路のみをランダムに発生させることができると，計算効率が向上し，精度も高くなる．本章では，文献12)で提案されたモンテカルロ法について説明する．この方法は，光干渉断層撮影法と同じ低コヒーレンス干渉計で計測される多重散乱光の光路長分布を解析するために導入された．Fig.1に示されるような，散乱媒質に垂直に入射され，特定の長さの光路を伝搬し，入射点と同じ位置から垂直に出射する散乱光の伝搬経路のみを発生させ，モンテカルロ積分を用いて光伝搬を解析する．この解析では，各散乱回数ごとに出射光の光強度をそれぞれモンテカルロ積分で計算する．

Fig.1 

Configuration of scattering points and scattering processes in scattering medium. Light is normally incident on a scattering medium and re-emerges from the same point after propagation along path with pathlength of L and n times of scatterings.

直交座標系のxy平面を境界とし，z > 0の半無限空間に存在する散乱媒質に，原点から垂直に光強度I₀(0, $\widehat{k}$)の光が入射され，光路長Lの光路を伝搬した後，原点から垂直に出射されるn回散乱光の光強度I_n(0, $-\widehat{k}$; L)を考える．散乱媒質の散乱特性は均一である場合を考える．

初めに1回散乱光の光強度を考える．この場合，Fig.2(a)に示すように入射光軸上の深さL/2の位置が散乱点であり，そこで光は後方に散乱される．したがって，1回散乱光の光強度は

  

$$I_1\left(0,-\widehat{k}:L\right)=I_0\left(0,\widehat{k}\right){\mu }_s{e}^{-{\mu }_{t}L}p\left(-\widehat{k},\widehat{k}\right)$$（7）

で表される．

Fig.2 

Configuration of scattering points and scattering processes for (a) single scattering, (b) second-order scattering, (c) third-order scattering, and (d) fourth-order scattering.

Fig.2(b)に示す2回散乱光の場合は，1回目または2回目の散乱は，入射光軸上の深さL/2の位置で後方に散乱される．もう1つの散乱は，入射光軸上の深さL/2より近い位置で前方に散乱される．（4）式を用いると2回散乱光の光強度は

  

$$I_2\left(0,-\widehat{k}:L\right)=I_0\left(0,\widehat{k}\right){\left({\mu }_s\right)}^2{e}^{-{\mu }_{t}L}\left[{\displaystyle {\int }_0^{L/2}p\left(-\widehat{k},\widehat{k}\right)p\left(\widehat{k},\widehat{k}\right)ds}+{\displaystyle {\int }_0^{L/2}p\left(-\widehat{k},-\widehat{k}\right)p\left(-\widehat{k},\widehat{k}\right)ds}\right]$$（8）

の積分で表される．［　］内の1項目は1回目が前方散乱，2回目が後方散乱の場合を，2項目はその逆を表している．この被積分関数は定数であり，積分を実行すると，2回散乱光の光強度は

  

$$I_2\left(0,-\widehat{k}:L\right)=I_0\left(0,\widehat{k}\right){\left({\mu }_s\right)}^{2}L{e}^{-{\mu }_{t}L}$$（8）

となる．

3回散乱光の散乱点の配置をFig.2(c)に示す．この場合，1回目と3回目の散乱点は入射光軸上の深さL/2より近い位置である．また，光路長がLとなるためには，1回目と3回目の散乱点を焦点とし，入射光軸上の深さL/2の点を通る回転楕円体を考える．2回目の散乱点は，その回転楕円体の表面上でなければならない．したがって，3回散乱光の光強度は，1回目と3回目の散乱点の積分と1回目の散乱角の積分を用いて

  

$$I_3\left(0,-\widehat{k}:L\right)=I_0\left(0,\widehat{k}\right){\left({\mu }_s\right)}^3{L}^2{e}^{-{\mu }_{t}L}{\displaystyle {\int }_0^{1/2}{\displaystyle {\int }_0^{1/2}{\displaystyle {\int }_{4\pi }p\left(-\widehat{k},{\widehat{s}}_2\right)p\left({\widehat{s}}_2,{\widehat{s}}_1\right)p\left({\widehat{s}}_1,\widehat{k}\right)d{\omega }_{1}d{\widehat{s}}_{1}d{\widehat{s}}_3}}}$$（9）

と表される．ここで，積分変数の光路長 ${\widehat{s}}_i=s_i/L$ は全光路長Lで規格化している．そのため積分範囲は0から1/2であり，積分の前にL²が掛けられている．また，${\widehat{s}}_i$ はi回散乱光の伝搬方向の単位ベクトルである．（9）式をモンテカルロ積分で計算すると，3回散乱光の光強度が得られる．このモンテカルロ積分は光路長の長さに無関係であり，光路長ごとに計算する必要はない．一度この積分を実行するだけで，3回散乱光の光路長分布関数が得られる．

モンテカルロ積分を実行するためには，1回目と3回目の散乱点，および，1回目の散乱方向を乱数によって決定する．1回目と3回目の散乱点を決定するには，散乱間の光路長を乱数で発生させる．規格化された光路長は1であり，3回散乱光を考えているので，光路長を3点で4分割すれば，散乱間に光が直進する光路長を決定できる．したがって，［0, 1］の一様乱数を3つ発生させ，その最小値の乱数を選ぶことで，3回散乱の光路長の発生確率に合うようにランダムに決定することができる．この乱数の確率密度関数は

  

$$g\left(s\right)=n{\left(1-s\right)}^{n-1}$$（10）

で与えられる．ここで，nは散乱回数である．このように発生させた乱数が1/2より大きい場合は，再度，乱数を発生させる．1回目の散乱方向は一様乱数により決定する．1回目と3回目の散乱点を焦点とし，入射光軸上の深さL/2の点を通る回転楕円体の表面と1回目の散乱方向との交点が2回目の散乱点である．これで，1回目と2回目の散乱方向が決定され，（9）式の被積分関数の値が計算できる．この手順で，多数の散乱点の組み合わせを発生させることで，モンテカルロ積分により積分の値を求める．この方法での散乱点の発生では，散乱係数，減光係数，位相関数などの散乱媒質の特性は全く関係していない．したがって，一度発生させた散乱点の組み合わせは，様々な媒質の散乱光強度を計算に利用できる．これはこの計算方法の利点である．

次に，Fig.2(d)に示すような4回散乱光の散乱光強度を説明する．この場合，1回目と4回目の散乱点は入射光軸上の深さL/2より近い位置である．また，光路長がLとなるためには，2回目の散乱点は，1回目と4回目の散乱点を焦点とし入射光軸上の深さL/2の点を通る回転楕円体の内側でなければならない．次に，3回目の散乱点を考える．2回目の散乱点で考えた回転楕円体の表面と1回目の散乱方向との交点に3回目の散乱点があると光路長はLとなる．その点を通り，2回目と4回目の散乱点を焦点とする回転楕円体の表面上に3回目の散乱点があれば，光路長はLとなる．したがって，4回散乱光の光強度は，1回目，2回目と4回目の散乱点の積分と1回目と2回目の散乱角の積分を用いて，

  

$$I_4\left(0,-\widehat{k}:L\right)=A_4{I}_0\left(0,\widehat{k}\right){\left({\mu }_s\right)}^4{L}^3{e}^{-{\mu }_{t}L}$$（11）

  

$$A_4={\displaystyle {\int }_0^{1/2}{\displaystyle {\int }_0^{{s^{\prime }}_{2\_\max }}{\displaystyle {\int }_0^{1/2}{\displaystyle {\int }_{4\pi }{\displaystyle {\int }_{4\pi }p\left(-\widehat{k},{\widehat{s}}_3\right)p\left({\widehat{s}}_3,{\widehat{s}}_2\right)p\left({\widehat{s}}_2,{\widehat{s}}_1\right)p\left({\widehat{s}}_1,\widehat{k}\right)d{\omega }_{1}d{\omega }_{2}d{\widehat{s}}_{1}d{\widehat{s}}_{2}d{\widehat{s}}_4}}}}}$$（12）

と表される．（12）式の積分をモンテカルロ積分で計算するには，次の手順で散乱点を発生させればよい．はじめに，（10）式の確率密度関数を持つ乱数により1回目と4回目の散乱点を発生，次に，一様乱数で1回目の散乱方向を決定し，その散乱方向と（10）式の確率密度関数を持つ乱数により2回目の散乱点を決定，最後に一様乱数で2回目の散乱方向と3回目の散乱点を決定する．2回目の散乱点の決定の時に，散乱点が回転楕円体の外になった場合には，光路長を決めなおす．

n回散乱光の光強度は

  

$$I_n\left(0,-\widehat{k}:L\right)=A_n{I}_0\left(0,\widehat{k}\right){\left({\mu }_s\right)}^n{L}^{n-1}{e}^{-{\mu }_{t}L}$$（13）

  

$$A_n={\displaystyle {\int }_{{\widehat{s}}_1}^{}\cdots {\displaystyle {\int }_{{\widehat{s}}_n}^{}{\displaystyle {\int }_{{\omega }_1}\cdots {\displaystyle {\int }_{{\omega }_{n-2}}{\displaystyle \prod _{j=1}^{n}p\left({\widehat{s}}_j,{\widehat{s}}_{j-1}\right)}d{\omega }_1\cdots d{\omega }_{n-2}d{\widehat{s}}_1\cdots d{\widehat{s}}_n}}}}$$（14）

で表される．これまでと同様の手順で，散乱点の組み合わせを発生させ，モンテカルロ積分により（14）が計算できる．散乱回数の増加とともに積分が増えるため，モンテカルロ積分の精度は低下する．精度を高めるためには，より多くの散乱点の組み合わせを発生させる必要があり，計算時間が増加していく．

4.  均一な散乱媒質の光伝搬解析

散乱特性が均一な散乱媒質に対する，特定の光路長の伝搬経路のみを発生させるモンテカルロ法を用いた解析結果を示す．Fig.3は，1回散乱光から30回散乱光までの散乱光強度，および，それらの総和である全散乱光強度の光路長依存性を示す．これらの強度は入射光と同じ点から垂直に出射する散乱光の光強度である．横軸は平均自由行程lで規格化した光路長，縦軸は，光路長0での全散乱光強度で規格化した光強度である．ここで，平均自由行程は，散乱されずに光が直進する平均的な距離であり，減光係数の逆数である．散乱体は水中に懸濁する直径100 nmのポリスチレン球，入射光の真空中の波長は810 nmを仮定している．この時の散乱体の相対屈折率は1.20である．これらの条件をもとにミー散乱の位相関数を求め，モンテカルロ積分に用いている．この時の非等方性パラメータは0.046である．各散乱回数につき，1,000,000組の散乱点分布を発生させ，モンテカルロ積分を実行している．1回散乱光の光強度は光路長が0のとき1であり，光路長の増加とともに指数関数的に減衰する．2回以上の散乱光の光強度は，光路長が0のときは0であり，光路長の増加とともに増加し，散乱回数と平均自由行程の光路長あたりで最大となり，その後減少していく．全散乱光強度は，光路長が平均自由行程より長くなると，多重散乱光の影響により徐々に指数関数的な減衰から外れていく．また，この結果から特定の光路長を伝搬した散乱光の散乱回数分布も求めることができる．その結果，30回散乱光までの計算では，平均自由行程の20倍程度の光路長まで正確に計算できている．

Fig.3 

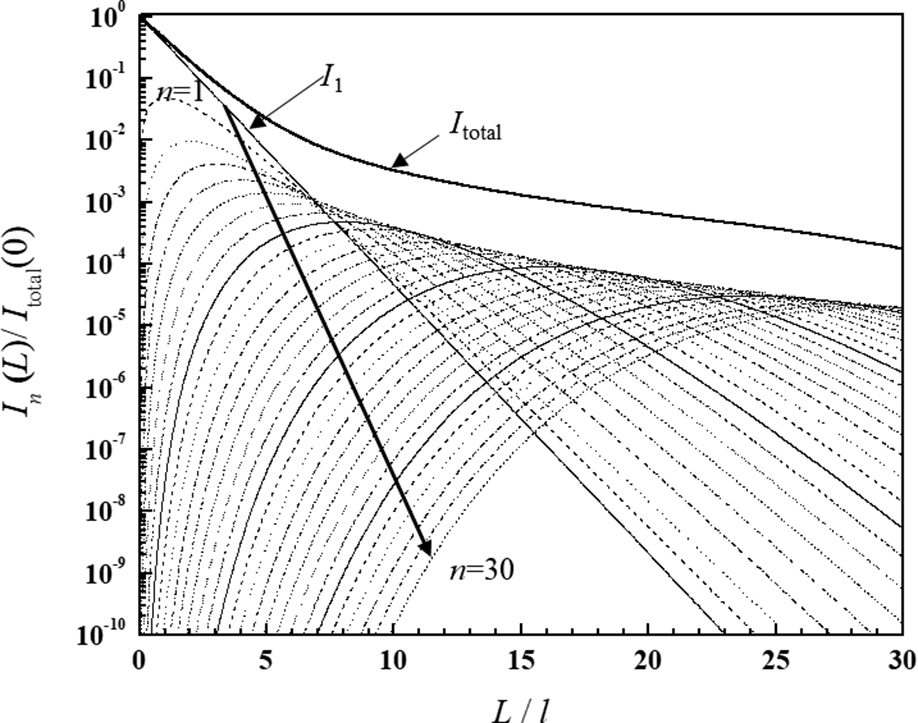
Path-length dependence of scattered light intensity of single scattered light to 30^th order scattered and total scattered light on path length. They are calculated using path-length-assigned Monte Carlo simulation.

Fig.4は，モンテカルロ積分で発生された光路長が1のときの散乱点の分布を積算した結果を示している．各散乱点には，（14）式の被積分関数である位相関数の積の値が重みとして掛けられている．これらの図は入射光の光軸を含む断面での散乱点分布であり，領域の大きさは1 × 1である．入射光は図の左側の中心から垂直に入射されている．この散乱点分布は，すべての散乱光の広がりを示しているのではなく，入射光と同じ位置から垂直に出射する散乱光が散乱される位置の分布を示していることに注意されたい．3章で説明したとおり，1回散乱光の散乱点は図中心の深さ1/2の一点であり，2回散乱光の散乱点は，入射点から中心までの光軸上に分布する．3回散乱光以上では，光軸上以外にも散乱点の分布が広がっている．散乱回数の増加とともに，光軸から遠い位置まで散乱点が広がり，より浅い位置の散乱点が増加していく．また6回散乱程度までは，光軸上の近くの散乱点が多いことがわる．この程度の散乱回数までは，準直進光の成分が多く残っていることを示している．また，散乱回数が15回程度を超えると，散乱点は入射点の近くに等方的に広く分布するようになる．これは，散乱光が拡散的になっていることを示している．

Fig.4 

Scattering points distributions of scattered light from single scattered light to 30^th order scattered, which is obtained from path-length-assigned Monte Carlo simulation.

Fig.5は，光路長が変化したときの入射点と同じ位置から垂直に出射する全散乱光の散乱点分布の変化を示している．図の縦と横の大きさは散乱光の光路長となっているので，散乱光の広がりは同じに見えるが，光路長の増加とともに散乱光は深い位置まで伝搬している．光路長が平均自由行程と等しい散乱光では，88%が深さL/2の点で散乱される1回散乱光である．光路長が平均自由行程の3倍の散乱光では60%，5倍の散乱光では30%，10倍の散乱光では1%程度と1回散乱光の割合は，光路長の増加とともに減少していく．それにともなって，散乱点の分布は光軸から遠い点まで広がり，浅い位置の散乱点が増加していく．それらの散乱点の分布から散乱点の重心位置を求めると，光路長が平均自由行程程度までは，光路長の増加に比例して散乱点の深さが増加する．この領域では直進成分の散乱光が検出可能である．光路長が平均自由行程程度の5倍程度までは，増加率は減少するが光路長の増加とともに散乱点の平均深さが増加していく．この領域では，準弾性散乱光の検出が可能である．光路長が平均自由行程程度の5倍を超えると散乱点の平均深さは，平均自由行程程度の1.5倍で変化しなくなる．これはその位置を中心にして，光が拡散的に広がっていることを意味している．平均深さが変化しないことは，光路長が増加してもそれ以上深い位置まで光が到達しないわけではない．散乱点分布の光軸方向の幅（標準偏差）は，光路長の増加とともに増加しつづける．また，光軸方向に垂直な方向の散乱点分布の幅は，光路長が平均自由行程程度の5倍程度まではほぼ0である．それより長い光路長では，垂直方向の幅も徐々に増加していくが，光軸方向の幅に比べると1/10以下と狭い．これは，媒質に垂直に光を入射し，入射点から垂直に出射する散乱光を検出する光学配置では，多重散乱の影響が強くなった場合でも光軸上の情報を取得できることを示している．

Fig.5 

Scattering points distributions of scattered light in cases of path length from L = l to L = 20l. They are calculated using path-length-assigned Monte Carlo simulation.

本章では，特定の光路長の伝搬経路のみを発生させるモンテカルロ法を用いた均一な散乱体に対する媒質解析結果を示した．この解析方法は，媒質に垂直に光を入射し，入射点から垂直に出射する散乱光のみ発生させるため，このような光学配置での散乱光の解析を，従来の方法より効率的に行うことができる．この方法では，散乱回数ごとに解析を行っていくため，考慮する散乱回数が増加すると計算時間が増加していく．また，散乱回数が増加すると計算精度も低下する．しかし，直進光，準直進光，拡散的になり始める散乱光の領域の解析では，効率的に解析ができる．また，この方法での散乱点分布の発生では，媒質の特性に関係する散乱係数，吸収係数，および，位相関数を全く使用しない．したがって，一度発生させた散乱点の分布は異なる散乱特性の媒質にも利用でき，様々な媒質の繰返しの解析はより効率的である．

5.  散乱特性に空間分布がある場合の光伝搬解析

本章では，散乱係数，減光係数，位相関数が不均一である散乱媒質に対する散乱光の解析に，特定の光路長の伝搬経路のみを発生させるモンテカルロ法を適用する方法とその解析例を示す．

散乱係数，減光係数，位相関数が位置の関数である場合，（13）と（14）式で表されたn回散乱光の光強度は，

  

$$I_n\left(0,-\widehat{k}:L\right)=A_n{I}_0\left(0,\widehat{k}\right)L^{n-1}$$（15）

  

$$A_n={\displaystyle {\int }_{{\widehat{s}}_1}^{}\cdots {\displaystyle {\int }_{{\widehat{s}}_n}^{}{\displaystyle {\int }_{{\omega }_1}\cdots {\displaystyle {\int }_{{\omega }_{n-2}}{\displaystyle \prod _{j=1}^n{\mu }_s\left(r_j\right)p\left({\widehat{s}}_j,{\widehat{s}}_{j-1},r_j\right)}\exp \left[-{\displaystyle \int {\mu }_t\left(r_j\right)ds}\right]d{\omega }_1\cdots d{\omega }_{n-2}d{\widehat{s}}_1\cdots d{\widehat{s}}_n}}}}$$（16）

となり，散乱係数と減光係数に関係する項が積分の中に残る．（16）式の積分をモンテカルロ積分で評価すれば，不均一媒質の解析ができる．この時，指数関数の中の積分もモンテカルロ積分で評価する．モンテカルロ積分の評価に必要な散乱点分布の発生は，4章で説明した均一媒質の場合と同じものを使うことができる．これは，散乱点発生の方法が散乱体の特性に依存しないためである．散乱特性に分布がある場合には，（16）式の被積分関数は位置の関数であるため，光路長ごとにモンテカルロ積分を行う必要がある．また，指数関数の中の積分には，散乱点の位置でなく，散乱光の経路が必要となる．我々ば，次の手順でモンテカルロ積分を計算する．

（1）散乱係数，減光係数，位相関数を3次元のボクセルデータとして定義する．

（2）3章で説明した方法で散乱回数ごとの散乱点分布を発生させる．光路長は1である．

（3）光路長ごとの散乱点分布を計算する．

①（2）で発生させた散乱点の座標に光路長を掛ける．

②散乱点が含まれるボクセルを決定する．

③散乱光の経路を求め，ボクセル内を光が横切る長さを記録したボクセルデータを作成する．

（4）モンテカルロ積分を実行する．

①散乱点が含まれるボクセルに対応する散乱係数と位相関数の積を計算する．

②光路長のボクセルデータと減光係数のボクセルデータの対応するボクセル同士の積を求め，それらの総和を計算する．

（2）の計算は，一度実行すれば繰り返し使用することができる．（3）の計算も光路長ごとに一度計算すればよい．光路長の分解能はボクセルの分解能とは独立に決定できる．（3）のデータは計算したい光路長ごとに保存しておく必要があり，大きな保存領域が必要となる．この2つの計算は一度実行すればよいが，多数の散乱点分布を発生させ，それを光路長ごとの散乱点と光路長のデータに変換するには長い計算時間が必要になる．しかし，媒質の特性と空間分布を変化させて繰り返し計算を行う場合には，（4）の計算のみとなり効率的に計算ができる．

Fig.6に示すような散乱媒質からの散乱光の光路長分布を計算した結果を示す．散乱媒質表面には，濃い灰色で示される散乱の強い層があり，内部にも同じ散乱の強さの直方体の領域が存在している．それ以外の薄い灰色で示される領域の散乱係数は1/100であり，吸収係数はともに0である．領域は100 × 100 × 100である．位相関数は4章と同じものを使用した．図の太い矢印で示すように，光は媒質の左側から垂直に入射され，同じ位置から垂直に出射する散乱光の光路長分布を計算する．光の入射・出射位置を図の点線で示すように変化させながら繰り返し光路長分布を計算した．Fig.7は，光の入射・検出位置が媒質の中心の場合の1から9回散乱光と全散乱光の光強度を示している．灰色で塗りつぶされた領域は，散乱が強い場所に対応する光路長の領域を示している．1回散乱光では，散乱の強い位置に対応した光路長で散乱光が強くなっている．多重散乱光では，少し長い光路長の散乱光が強くなっており，そのずれは，散乱回数が増えるにしたがって増加する．これは多重散乱光が散乱体内部を蛇行しながら進むためである．全散乱光では，散乱の強い位置に対応した光路長の散乱光が強いが，その長光路側に少し強い散乱が現れる．Fig.8は，Fig.6中に①で示すように光軸が散乱媒質の中心の場合の光路長分布と，②で示すような光軸が内部の散乱体のわずかに外側の場合の光路長分布，③で示すような光軸が内部の散乱体から遠い場合の光路長分布を示す．さらに，入射・出射位置を変化させたときの光路長0.7，4.3，6.7，12.7の散乱光の強度分布を示す．それぞれの散乱光分布は，表面の強い散乱領域，表面の下の弱い散乱領域，内部の強い散乱領域，内部の散乱領域より深い位置に対応している．内部の散乱体のわずかに外側から光を入射した場合には，内部の散乱体の影響により，対応する光路長の散乱光がわずかに増加していることがわかる．内部の散乱体から遠い場所に光を入射したときは，内部の散乱体の影響はほとんど見られない．また，光路長6.7の散乱光の分布では，内部の散乱体に対応した位置の散乱光が強くなっており，その外側もわずかに散乱光が強くなっていることが確認できる．より長い光路長では，内部の散乱体により光が強く散乱されたため，対応する散乱光が弱くなっている．

Fig.6 

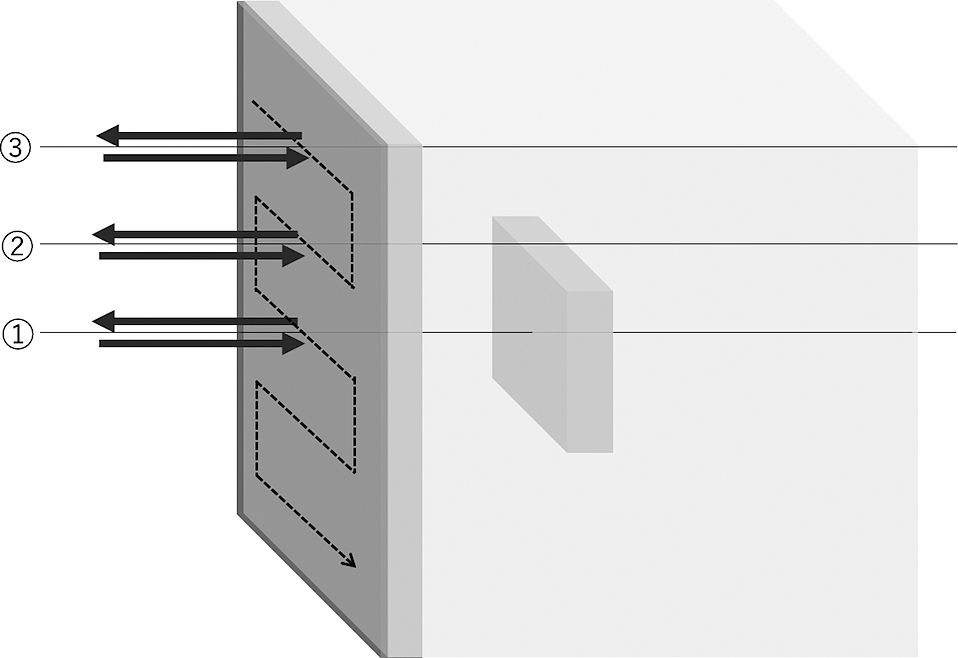
Illustration of the assumed model of scattering medium. Light is incident from left side. The surface layer shown in dark gray has scattering coefficient 100 times stronger than surroundings shown in light gray. Rectangular region shown in dark gray embedded in the scattering medium also has scattering coefficient 100 times stronger than surroundings.

Fig.7 

Path-length dependence of scattered light intensity from single scattered light to 9^th order scattered and total scattered light for the scattering medium shown in Fig.6. The incident point of light is the center of the medium. Gray regions express the pathlength corresponding to strong scattering layer.

Fig.8 

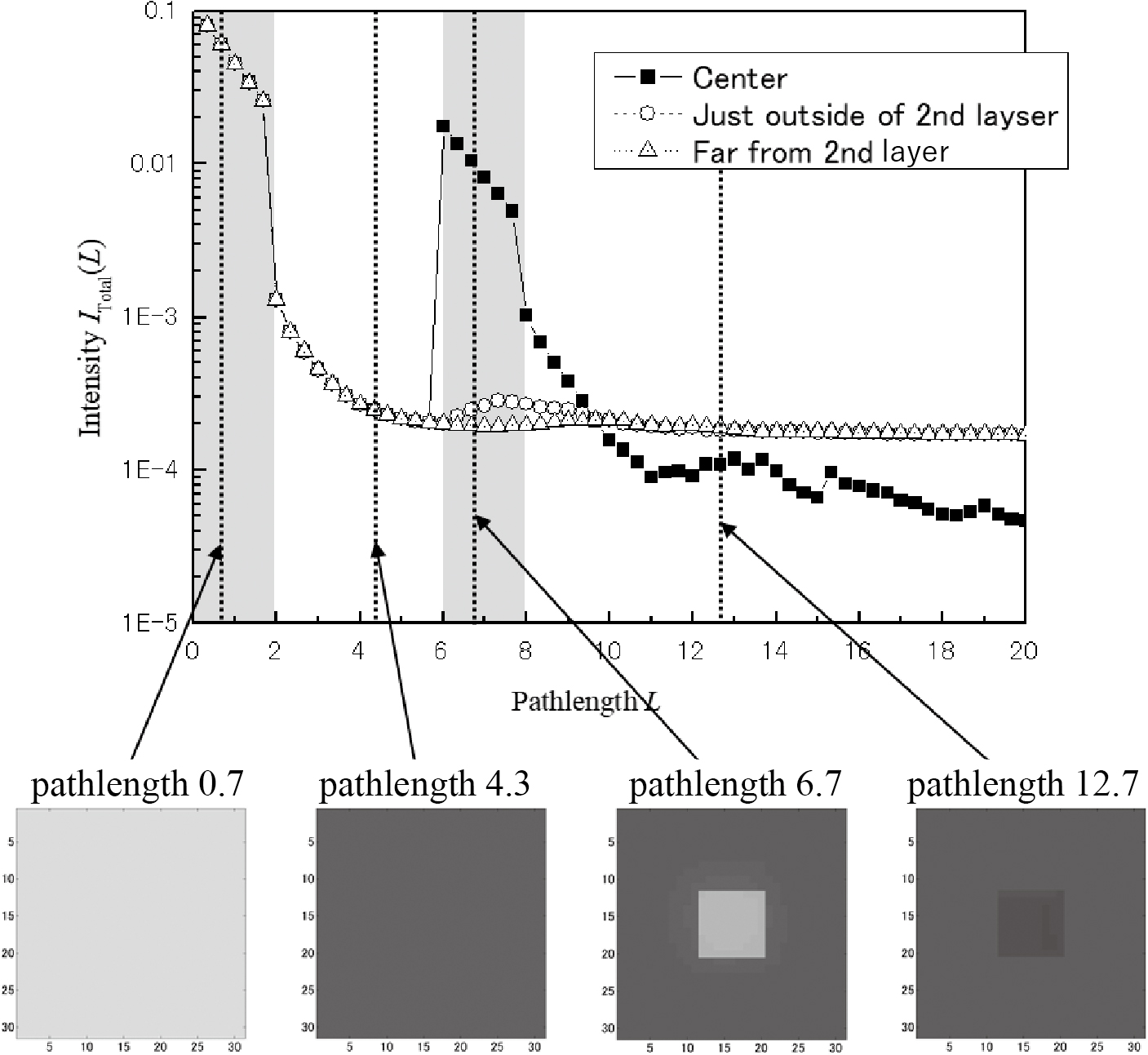
Path-length dependence of scattered light intensity in the case that ① the incident point of light is the center of the medium, ② just outside of the second layer and ③ far from the second layer. Lower figures show the dependence of the intensity of scattered light of scattered light with the path-length of 0.7, 4.3, 6.7, on the incident point.

本計算方法を用いると，光干渉断層撮影法で計測される散乱光を，多重散乱光を含めてシミュレーションすることが可能である．

6.  まとめ

本解説では，光干渉断層撮影法などの計測などで行われる，媒質に垂直に光が入射し同じ位置から垂直に出射する多重散乱光を効率的に解析するモンテカルロ法について解説した．このような特定の散乱光のみを解析する場合，通常のモンテカルロ法は散乱光の光路長と出射位置はランダムに決定するので，計算効率が悪い．紹介した方法は，対象の散乱光のみをランダムに発生できるので，効率的に散乱光の光路長分布が計算できる．散乱特性が均一な媒質に対しては，非常に少ない計算量で解析が可能である．散乱特性に空間分布がある媒質では，計算量とデータ量が増加するが，媒質を変化させながらの繰返し計算は効率的である．

利益相反の開示

利益相反なし．

引用文献

• 1)  Vo-Dinh T. (ed.) Biomedical photonics handbook: Fundamentals, Devices, and Techniques. CRC Press; 2014.
• 2)  Vo-Dinh T. (ed.) Biomedical photonics handbook: Biomedical Diagnostics. CRC Press; 2014.
• 3)   Yodh  A,  Britton  C. Spectroscopy and imaging with diffusing light. Phys Today. 1995; 48: 34-40.
• 4)   山下  優一， 牧  敦， 小泉  英明．光トポグラフィによる脳機能の無侵襲画像化．化学と工業．1996; 49: 1562-1564.
• 5)   Culver  JP,  Choe  R,  Holboke  MJ,  Zubkov  L,  Durduran  T,  Slemp  A,  Ntziachristos  V,  Chance  B,  Yodh  A. Three-dimensional diffuse optical tomography in the parallel plane transmission geometry: Evaluation of a hybrid frequency domain/continuous wave clinical system for breast imaging. Med Phys. 2003; 30: 235-247.
• 6)   Maki  A,  Yamashita  Y,  Ito  Y,  Watanabe  E,  Mayanagi  Y,  Koizumi  H. Spatial and temporal analysis of human motor activity using noninvasive NIR topography. Med Phys. 1995; 22: 1997-2205.
• 7)   Huang  D,  Swanson  EA,  Lin  CP,  Schuman  JS,  Stinson  WG,  Chang  W,  Hee  MR,  Flotte  T,  Gregory  K,  Puliafito  CA,  Fujimoto  JG. Optical coherence tomography. Science. 1991; 254: 1178-1181.
• 8)   安野  嘉晃．眼科における光干渉断層イメージングのトレンド．光学．2014; 43: 538-542.
• 9)  Ishimaru A. Wave propagation and scattering on random media; IEEE Press; 1999.
• 10)   清水  孝一．生体組織における光伝搬の解析．光学．2012; 41: 414-423.
• 11)   Wang  L,  Jacques  SL,  Zheng  L. MCML—Monte Carlo modeling of light transport in multi-layered tissues. Compt Methdos Programs Biomed. 1995; 47: 131-146.
• 12)   Ishii  K,  Iwai  T,  Nakamura  S. Numerical analysis of a path-length-resolved spectrum of time-varying scattered light field. J Opt Soc Am A. 2008; 25: 718-724.
• 13)   Ishii  K,  Nishidate  I,  Iwai  T. Analysis of light propagation in highly scattering media by path-length-assigned Monte Carlo simulations. Opt Rev. 2014; 21: 210-214.
• 14)   岡田  達弘， 西舘  泉， 石井  勝弘， 岩井  俊昭．光断層計測のモンテカルロシミュレーションにおける空間分解能の検討．第50回光波センシング技術研究会講演論文集．2012; 50: 237-243.