2021 Volume 21 Issue 2 Pages 19-41
2021 Volume 21 Issue 2 Pages 19-41
【目的】以前ベイズ推測視覚化ツールであるB. I. T. を開発・リリースした後に懸案となっていた事項のうち以下3点、マルチプラットフォームに対応することでユーザーの使用機会を拡張すること、計算に概算ではなく堅牢性を備えること、正規分布の推測以外のより多様な推測を視覚化することを実現する。
【方法】Python3とNumPy、SciPyとグラフ表示ツールであるmatplotlibを用いて、複数のコンピュータOSで動作し、事後確率の堅実な計算を担保する、新たなベイズ推測視覚化ツールを作成した。視覚化するベイズ推測は正規分布の推測以外のものを新たに収集した。
【結果】構築されたB.T.V.T.I.はWindows、MacOS、Linux上で動作した。12のベイズ推測視覚化画面を実装し、うち9つにSciPyの統計関数を実装したプログラムとなった。観測値と変数の入力と同調して事後分布のグラフ曲線と事後確率値を計算し表示するが、使用したプログラミング言語が異なるため、その操作画面はB.I.T.と異なるものとなった。
【考察】B.T.V.T.I.の他のデバイスへの今後の拡張性とSciPyの適用とその限界、現状で未引用なベイズ推測事例の今後の実装と視覚化について論じた。本ソフトを用いるにあたってベイズ推測の原理、前提や適用を理解した上で用いるのが望ましい。
Objective:To address the three pending issues that were raised after the release of B.I.T. (Bayesian inference tool). A Bayesian inference visualization tool expands the user experience by providing support to multiple platforms; it adds robustness to calculations instead of approximation and offers various inference visualization options other than the normal distribution.
Method:Using Python3, NumPy, SciPy, and the plotting tool Matplotlib, we created a new Bayesian inference visualization tool that runs on multiple operating systems and assures a robust calculation of the posterior probability. In addition, new cases of Bayesian inferences other than the normal distribution were collected for visualization.
Results:The newly developed B.T.V.T.I. (Bayesian tool for various types of inferences) runs on Windows, macOS, and Linux (Ubuntu). It is a software program with twelve Bayesian inference visualization screens, out of which nine have the statistical function implementation of SciPy. The program calculates and displays graph curves of the posterior distribution and posterior probability values at the same time as the observed values and variables are input. However, because a different programming language is used, its operation screen is different from that of B.I.T.
Discussion:The future expandability of B.T.V.T.I. to other devices, the application and limits of SciPy, and future implementation and visualization of the uncited Bayesian inference cases were discussed. Ideally, users must be familiar with the principle, premises, and applications of the Bayesian inference to use this software.
ベイズ推測は保健医療福祉分野に関するアウトカム研究のみならず、同分野の現場における意思決定にも有用である。得られた観測データから、推定したい対象の取り得る値の範囲を確信度(事後確率)として推測できることから、ベイズ推測は頻度論的統計の推定よりも臨床的な意思決定になじみやすいと考えられる。以前、著者は保健医療福祉分野で意思決定の教育においてベイズ推測を学習する際、graphical user interface(以下GUI)環境上で、一般の医療従事者、学習者が簡単に操作でき、かつ、ベイズ更新の出力結果を視覚的に理解しやすい、いわゆるデジタルダッシュボード1)的なインターフェースを有したプログラムツールが有用である2)と考え、ベイズ推測を視覚化するソフトウェアBayesian inference tool (以下B. I. T. )を開発した3)。
しかし、B. I. T. は単一のコンピュータOS(Windows)のみで動作するアプリケーションソフト(以下アプリ)だった。より多くのユーザーに提供できるよう、複数の異なるコンピュータOS(以下OS)で動作するベイズ推測視覚化ツールを開発することはB. I. T. リリース後の懸案となっていた。
また、B. I. T. の使用プログラミング言語は統計確率計算専用の関数を独自に持っておらず、B. I. T. のベイズ推測における事後確率の計算(定積分計算)はすべて概算値・近似値を出力せざるを得ない仕様となっている点において、確率計算の頑健性の面で改善の余地が残されていた。
さらに、B. I. T. はもっぱら正規分布に関するベイズ推測を扱ったものであり、当然ベイズ推測の対象となる事例は正規分布そのもの以外にも存在する。それらの中で自然共役事前分布が確率密度関数として表現できるものは、B. I. T. で実装されているベイズ推測と同様にリアルタイムの視覚化が可能であると考えられる。しかし、それらの視覚化ツールの実装と頒布は行なわれていなかった。
PythonはPCに用いられる種々のOSに対応したプログラミング言語であり、近年はGUI機能が充実している。一般商用ソフトにもPythonを用いて作られたものが増加しており4)、その可読性、メンテナンス性から今後も汎用される可能性の高い言語であると考えられる。普及の可能性以外にもPythonには以下の利点がある。まず数値計算専用のライブラリを用意しており、同ライブラリを援用することにより容易に高速な計算が行なえること、無料のオープンソースであること、基本機能以外の専門機能や拡張プログラムが豊富であること、などである5)。しかし、保健医療福祉分野において、プログラムをPythonで構築した研究が我が国では乏しく6)、さらには他のユーザー向けの頒布用に作成を行った研究はほとんどなかった。
本研究で新たなベイズ推測視覚化ツール、名称「Bayesian tool for various types of inferences;B.T.V.T.I.」を開発する目的は3つある。第1はPythonをプログラミング言語に用いて複数のOSで稼働可能とすることによって、ベイズ推測視覚化ツールの使用機会をマルチプラットフォームに拡張発展させることを狙う。第2はPythonのSciPyに多数用意された統計関数を利用することによって、より堅実な数値計算機能を提供する。第3は一般の臨床家や医学教育現場に対して初歩的で応用性の高いベイズ推測の理解を、より多様な事例を示すことで支援するために、B. I. T. で未実装であった正規分布以外のベイズ推測の視覚化の可及的多くを実装・頒布するものである。表1にてB. I. T.とB.T.V.T.I.の比較を簡潔に記した。

1 設計
B.T.V.T.I.は一般の保健医療福祉分野の従事者・学生に対する頒布を想定したプログラムである。そのベイズ推測視覚化機能自体は2)機能仕様の記載のとおり、先のB. I. T. 開発で培った経験を生かして画面構成の仕様を策定した。
1)基本的な要求仕様
B.T.V.T.I.の基本的な要求仕様を表2に示した。
基本的な要求仕様で必ず満たすべき重要な仕様が表2の(iii)、(iv)での動作であった。このうち(iii)は本研究の第1の目的に該当した。開発に用いられるプログラミング言語であるPythonは、今後改訂のリリース予定がないPython2ではなくPython3を用いた。開発環境にはVisual Studio2019を用いた。

2)機能仕様
基本的な要求仕様に続き、B.T.V.T.I.の具体的な機能仕様をインストール、セットアップ、ユーザーインターフェース、入出力、動作、計算に分けて表3に示した。使用したプログラミング言語が異なるのですべてをB. I. T.と同じにすることは求めず、B.T.V.T.I.の機能仕様はB. I. T. を一部参考にしている。
表3の(v)で、グラフ曲線はリアルタイムにアニメーション表示される。すなわち、画面内で値を入力・指定すると、即座に事後分布のグラフ曲線と事後確率値を計算し表示し、かつ、いったん入力した値を変化させると同時に、事後分布のグラフ曲線と事後確率値を再計算し再表示する。本研究の第2の目的を満たすため表3の(vi)に示す通り事後確率の計算をPythonの科学技術計算ライブラリであるNumPy7)と連携させ、SciPy8)に担わせるものとした。

3)B.T.V.T.I.に収録されるベイズ推測
本研究第3の目的を満たすため、正規分布の母数の推測以外でベイズ推測事例を収集引用した。自然共役事前分布が確率密度関数として表現できるものである限り、そのベイズ推測はすでにB. I. T. で実現されているベイズ推測と同様に計算され事後確率曲線の視覚化が可能であると考えられた。事後分布が確率密度関数として数式化されていないものであっても、他の確率分布の確率密度関数や他の数式での近似が可能なものは収録の対象とした。本研究で視覚化されるベイズ推測はB. I. T. で実現されておらず、正規分布の母数以外のベイズ推測で、未実装・未頒布のものが集められた。
2 倫理的配慮
この研究はヒトまたは動物をいっさい被験者にしなかったため、倫理審査を要しなかった。
1 実装
1)基本的な要求仕様について
著者により構築されたB.T.V.T.I.はツール選択画面を含む、Pythonプログラムコードが記載された13個のpy形式ファイルからなり、全体ボリュームは同梱のマニュアルを除いて約200キロバイトであった。ウェブサイト(https://upload.umin.ac.jp/fileshare/registrant.cgi)からダウンロードすることができる。
プログラムの開発にはウェブアプリ形式とネイティブアプリ形式の2通りが検討されるが、画面設計にあたりボタン、スライダー(スケール)、スピンボックスなどのコントロールの配置をフォームウィンドウの特定の位置に設定することが可能なこと、サーバーの構築と運用の継続が不要になること、ウェブアプリ形式の場合、クライアント端末で入力・指定された値に基づきサーバーサイドで計算後、グラフ曲線表示までの応答に時間のずれが発生する恐れがあることからB.T.V.T.I.ではネイティブアプリ形式を選択した。プログラムはPythonで標準的に用いられているライブラリによって構成された。すなわちGUI画面をTkinter9)、計算一般をNumPy、統計関数はSciPyに担わせ、グラフ描画をmatplotlib10)に行わせるものとした。実際のSciPyの統計関数11)の採用状態は次項2)の(6)に記した。
図1から3で示す通り、Windows 10 pro、macOS Catalina(バージョン10.15.6)、Linux(Ubuntu 20.04.1 LTS)での動作を確認している。字体や配色などの細かい差異はあるものの、OSが異なることで全体としての画面表示に変化が見られないことを推測の種類の画面ごとに確認した。基本的な要求仕様で最も重要な表2の(iii)と(iv)を達成し、(iii)達成により本研究の第1の目的を満たした。
ただし、B.T.V.T.I.はPythonとNumPy、SciPy、matplotlibの連携で動作するため、NumPy、SciPy、matplotlibの各ライブラリはそれぞれ最新のバージョンのものを使用すべきである。さらに今後Python3自体に大規模なバージョンアップが生じた場合、動作検証を行い動作状況によってはB.T.V.T.I.はアップデートを要することになると思われた。


2)機能仕様について
表3の機能仕様の項目に対応させて以下記す。
(1)インストール(表3の(i))
ダウンロード後解凍したB.T.V.T.I.のフォルダを任意の場所にコピーする。B.T.V.T.I.自体のダウンロード、インストールそのものは容易であると考えられた。
(2)セットアップ(表3の(ii))
PCにはあらかじめPython3本体のインストールとmatplotlib、NumPy、SciPyのPython用各ライブラリの追加インストールが必要であった。古いバージョンのPython3がプリインストールされているPCでは、なるべく新しいバージョンのものをインストールし直す必要があった。このようにPCにPython自体の環境設定が求められるが、B.T.V.T.I.単体にはインストール後の設定は特に要さなかった。Pythonプログラムコードの集まりであるB.T.V.T.I.は、予め起動されたPython3に読み込まれて動作する。
(3)ユーザーインターフェース
機能仕様である表3の(iii)(ア)から(エ)すべてが達成できていることについて以下に述べる。収録されている、全部で12種類の推測に対して各々一つずつ画面が設けられており、初期起動画面から各ベイズ推測画面をボタンクリックにより選択し起動させる。収録されているベイズ推測は各々の操作画面上で行う(表3(iii)の(ア)に対応)。
B.T.V.T.I.のベイズ推測画面のユーザーインターフェースの基本的な配置は図1、図2、図3のいずれにも示す通りである。画面上部に説明文または表、右側に観測値等を入力し値を変化させる部分、左側にグラフ曲線を表示する部分(表3(iii)の(イ)に対応)、右下に事後確率を計算表示する部分(表3(iii)の(ウ)に対応)を配置した。
すべての入力操作をコンピュータマウスのみで行う(表3(iii)の(エ)に対応)。本研究では右手でマウスを操作する場合を想定し、B. I. T. とは異なり操作用のコントロールを画面右側に集中させた。
(4)入出力
図4から図15に示す通り、各推測の操作画面において観測値と変数の値、事後確率の範囲上限・下限を入力し(表3(iv)の(オ)に対応)、事後確率分布のグラフ曲線と、指定された範囲における事後確率の値を出力した(表3(iv)の(カ)に対応)。図4から図15の詳細については2の1)で(1)から(12)にて述べた。
(5)動作(表3の(v))
画面の動作はコンピュータマウスのみの操作で入力操作と同時に画面表示の更新が自動的に行われた。
すなわち、ベイズ推測に必要な観測値のデータと変数等を入力し指定すると、即座に事後分布のグラフ曲線と事後確率値を計算し表示した。その後、入力値を変化させると同時に、事後分布のグラフ曲線と事後確率値を再計算し再表示した。これらを連続して行うことにより、グラフ曲線はリアルタイムのアニメーション表示となった。
(6)実装・視覚化された各推測を表3に示す(以降、各推測をAからLと符号で呼ぶことにする)。同表の「SciPyの統計関数」列にて統計関数の不要なLを除くAからKの推測の中で、事後確率分布の計算にPythonの科学計算ライブラリであるSciPyに収録されている関数を適用するにあたり、HとJはSciPy内に該当する統計関数がなく、HとJでの事後確率の計算には区間求積法による概算値を算出表示するにとどまった。
以上、表3の(vi)の一部を除き表3の機能仕様に対応した実装がなされていることを確認した。








3)B.T.V.T.I.に引用・実装されたベイズ推測
本研究の第3の目的に対応するものとして方法の3)をもとに、自然共役事前分布(存在する場合)、尤度関数、事後分布の数式を有するベイズ推測の文献を著者が可及的に収集し、実装した結果を表4に示した。実装されたベイズ推測には、B. I. T.と異なりいずれも正規分布そのもののベイズ推測ではないが、事後分布が正規分布または正規分布に近似されたものや、その他の近似も見られた。
2 動作例
1)AからLの動作例を以下に示す。計算の妥当性の検証として、事後確率値をR(バージョン3.6.2)を用いて検算した。各検算で数式(ア)から(ス)に用いたRのスクリプト(グラフ曲線描画含む)はまとめて付録に記した。
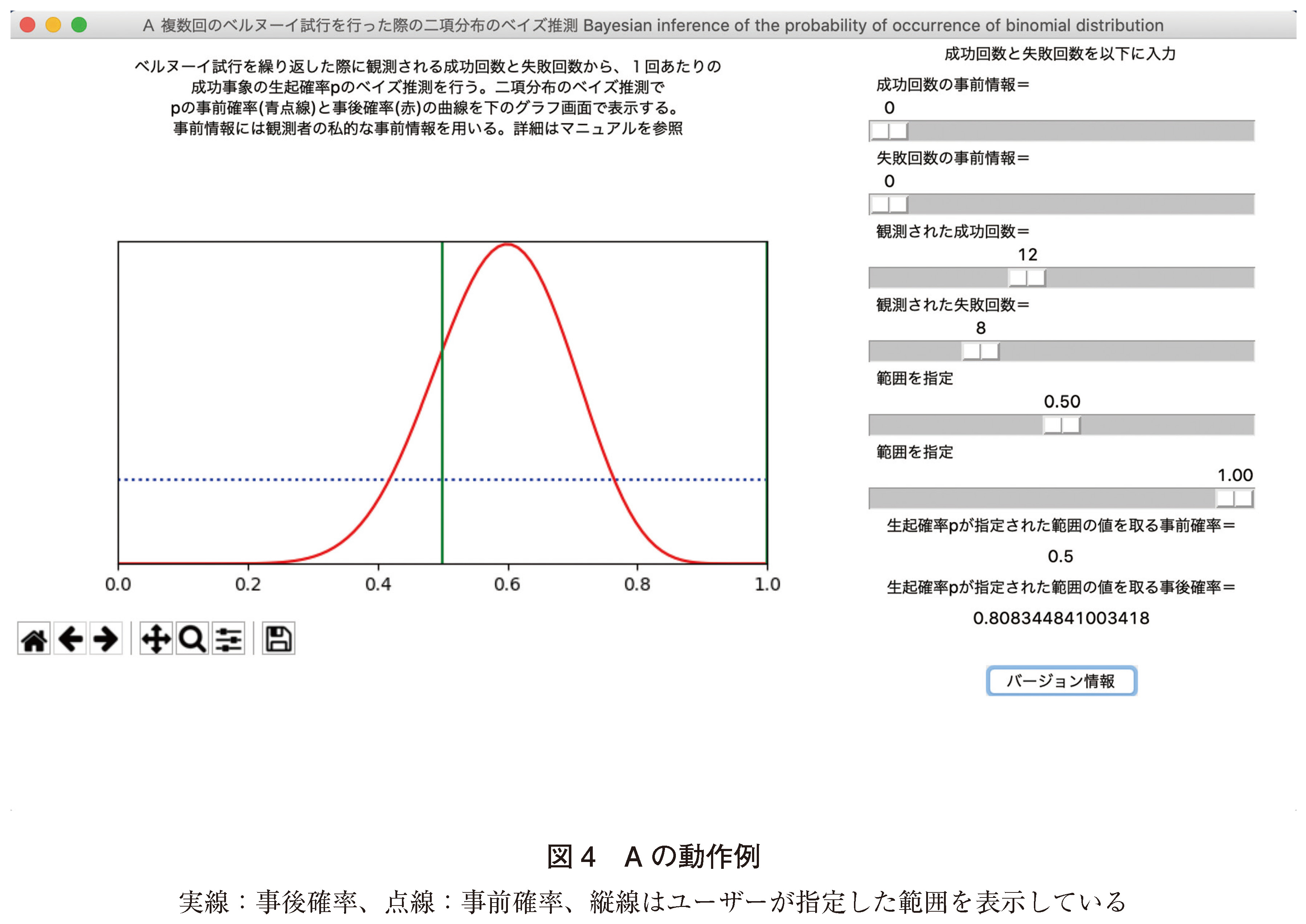
(1)A. 二項分布における生起確率の推測12)
ある治療法の有効性を推定するとき、観測されたデータは20回中12回が有効であり、無効が8回であった。私的な事前情報はこの場合では無情報とした。本治療法の有効性pが50%以上になる確率を計算する。例解:a,bの2母数のベータ分布をBe(a,b)とすると私的な事前情報は無情報であることより事前分布Be(1,1)であるので、事後分布はBe(13,9)となる。本ツールはpが0.5以上であると設定することにより、pが0.5から1の間の値を取る事後確率は80.8%(0.8083448)となった(図4)。Rの計算(付録のスクリプト(ア))ではpが0.5から1の間の値を取る事後確率は0.8083448となり、ほぼ同じ結果を示した。
(2)B. 負の二項分布における生起確率の推測
ある新薬の治験を行うとき、20回の有効を観測するまでに12回の無効を観測した。本治療法の有効率pが50%以上になる確率を計算する。なお観測者に事前のデータは無く、事前情報をLeeの記載13)の通りJeffrey’s ruleにより定めるものとする。例解:本ツールによるとpの事後分布はBe(20,12.5)となる。このときpが0.5~1の範囲を取る事後確率は91%(0.90971465)となった(図5)。Rの計算(付録のスクリプト(イ))ではpが0.5から1の間の値を取る事後確率は0.9097147となり、ほぼ同じ結果を示した。
(3)C. 三項分布における各事象の生起確率の推測14)
ある疾患に対する、ある薬物治療のアウトカムを、奏効(P1)、不変(P2)、増悪(P3)とした。各アウトカムが50%以上の確率で生起する周辺事後確信度(P1(p1 ≧ 0.5)、P2(p2 ≧ 0.5)、P3(p3 ≧ 0.5))をそれぞれ求める。観測症例数25で集計を行い、それぞれの度数8、10、7を得た。事前情報は得られていなかったとする。本ツールでは、P1(p1 ≧ 0.5)、P2(p2 ≧ 0.5)、P3(p3 ≧ 0.5)は各々2.6%(0.02611949)、12.4%(0.12389428)、1.0%(0.009578645)であると表示される(図6)。Rの計算(付録のスクリプト(ウ))ではそれぞれ0.02611949、0.1238943、0.009578645となり、ほぼ同じ結果を示した。
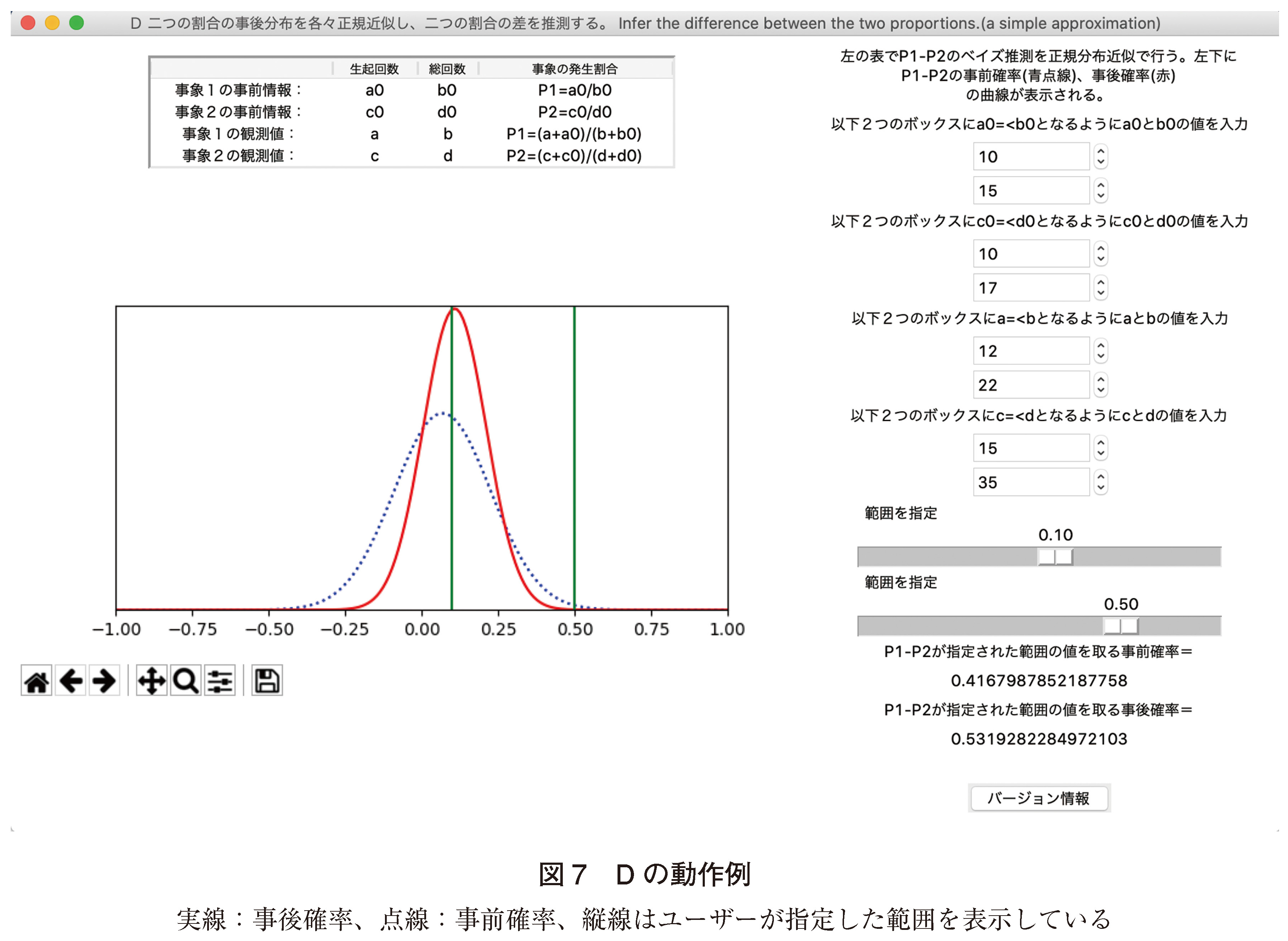
(4)D. 二つの割合の差の推測(正規分布近似)15)
疾患Xに対する、新薬の奏効割合P1=12/22、旧薬の奏効割合P2=15/35、と観測した。事前情報はそれぞれP01=10/15、P02=10/17だった。本ツールによるとP1-P2の事後確率曲線がグラフ表示され、0.1 ≦ P1-P2 ≦ 0.5となる事後確率は53.2%(0.5319282)となった(図7)。Rの計算(付録のスクリプト(エ))では、0.1 ≦ P1-P2 ≦ 0.5となる事後確率は0.5319282であり、ほぼ同じ結果となった。
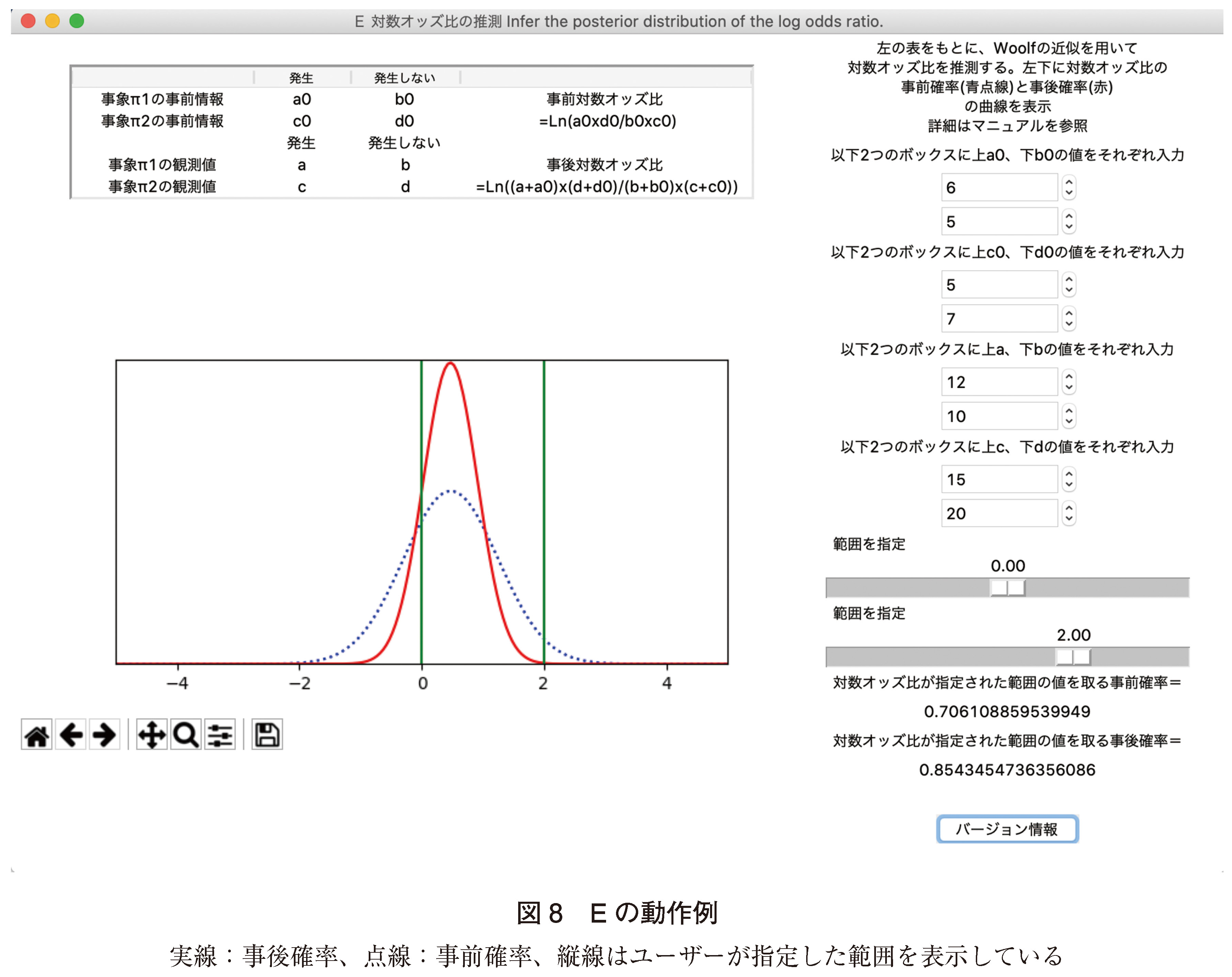
(5)E. 対数オッズ比の推測16)
疾患Xに対する、新薬の奏効オッズP1/(1-P1)=12/10、旧薬の奏効オッズP2(1-P2)=15/20が観測された。事前情報はそれぞれP01/(1-P01)=6/5、P02/(1-P02)=5/7だった。本ツールによると対数オッズ比εの事後確率曲線が表示され、0 ≦ε≦ 2となる事後確率は0.85434547(85.4%)となった(図8)。Rの計算(付録のスクリプト(オ))では0 ≦ε≦ 2となる事後確率は0.8543455でありほぼ一致した。
(6)F.ピーターセン法の推測(超幾何分布の二項分布近似)17)
総個体数Nのうち捕獲数M=200体の個体数の生物に標識した後、放流して充分拡散させたのち30体を再捕獲した。そのうち標識されていた個体は2体であった。このときp=M/Nは90%の確信度で0.03から0.20の間の値を取ることがツール画面に表示された。このpの範囲だとN=p/MよりNは90%(0.89747755)の確信度で1000から6666の間の値を取ることが推測された(図9)。Rの計算(付録のスクリプト(カ))ではpが0.03から0.20の間の値を取る事後確率は0.8974776となり、ほぼ同じ結果を示した。
(7)G. 二群の発生率比の推測(ポアソン分布近似)18)
新薬と旧薬の10万人年あたりの有害事象発生率を、各々θ1、θ2とする。新薬と旧薬の有害事象発生率を、各々6人/10万人年、2人/30万人年と観測したとき、(θ1/θ2)(1/6)(3/2)の事後確率はF(12,4)に従い19)、発生率比:θ1/θ2が3以上5以下となる事後確率は0.1307177(約13.1%)となった(図10)。Rの計算(付録のスクリプト(キ))で、3≦θ1/θ2≦5となる事後確率は0.1307177となり、ほぼ同じ結果であった。
(8)H. NNT(Number needed to treat:治療必要数)の推測20)
ある新しい治療手段の有効症例数/全実施症例数=11/20、対して従来の治療手段の有効症例数/全実施症例数=5/20であった(a=11、b=9、c=5、d=15と入力)。この場合NNTは3.3となるが、本ツール上ではNNT値の事後確率は、0.95009359(95%)の確信度で信用区間1.0から23.0の間を取ることが即座に表示された(図11)。Rの計算(付録のスクリプト(ク))ではNNTが1.0から23.0の間を取る事後確率値は0.9500936となり、ほぼ同じ結果を得た。
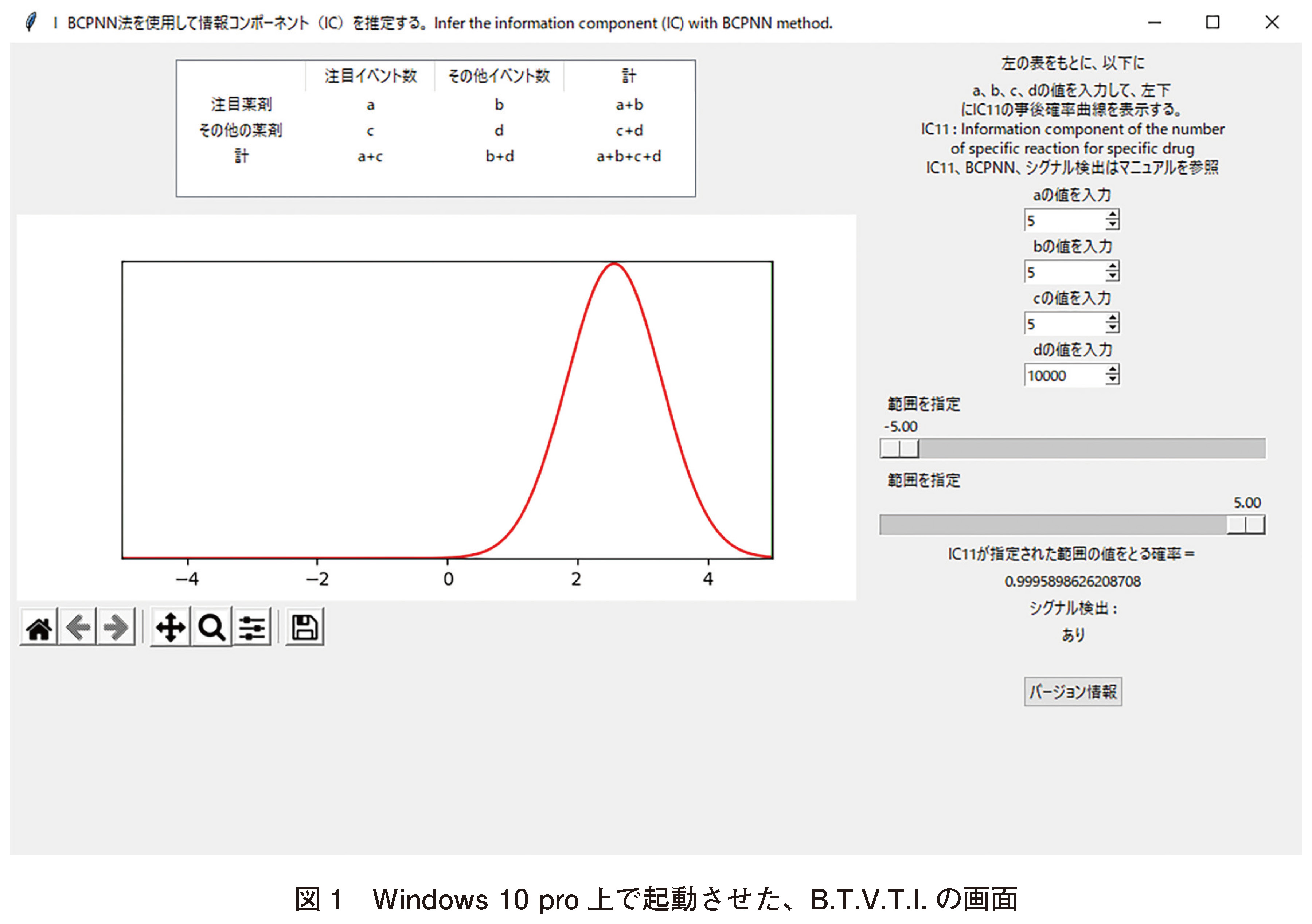
(9)I. BCPNN法によるシグナル検出の推測21)-23)
ある新薬に関する有害事象についての観測値が、(i)それぞれa=5, b=240, c=160, d=60000であった(図12)。入力に応じて操作画面上にIC11の事後分布のグラフ曲線が表示される。本プログラムでの95%信頼区間[0.64, 3.00]の下限>0となり、シグナルありと判定される。また、データセットの値を変化させることにより、シグナル検出の有無をシミュレートすることができる。
(ii)例としてa=6, b=240, c=610, d=60000 の場合はIC11の事後分布で95%信頼区間[-0.10, 2.08]の下限<0であり、シグナルなしと判定される。Rの計算では、(i)の場合(付録の数式(ケ))、IC11の事後分布は95%信頼区間[0.65, 3.03]、(ii)の場合(付録の数式(コ))、IC11の事後分布は95%信頼区間[-0.09, 2.09]となり、ほぼ同じ結果となった。
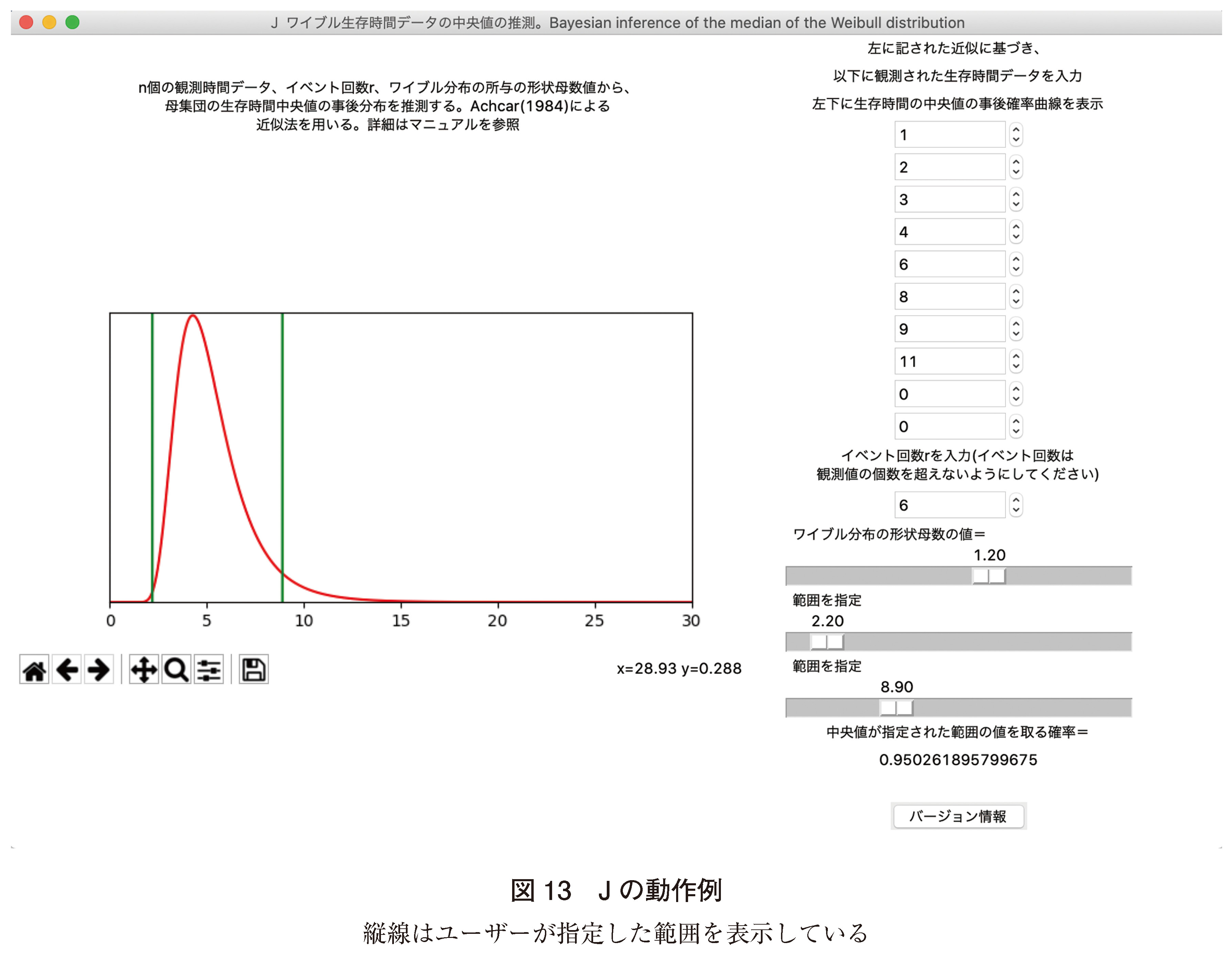
(10)J. ワイブル分布の中央値の推測24)
生存曲線がワイブル分布に従うとされる、ある集団の生存時間データ(年)を観測したところ、{1, 2, 3, 4, 6, 8, 9, 11}であり、最初の6例が死亡、後ろの2例は打ち切りであった。また、この集団の生存モデルの形状母数は1.2であった。観測データとモデルの形状母数を入力すると、本ツール上では集団の生存時間中央値は、95%(0.95026189)の確信度で2.2年から8.9年と推測されることが即座に表示された(図13)。Rの計算(付録のスクリプト(サ))で、生存時間中央値が2.2年から8.9年の間を取る事後確率は0.9502619となり、ほぼ同じ結果となった。
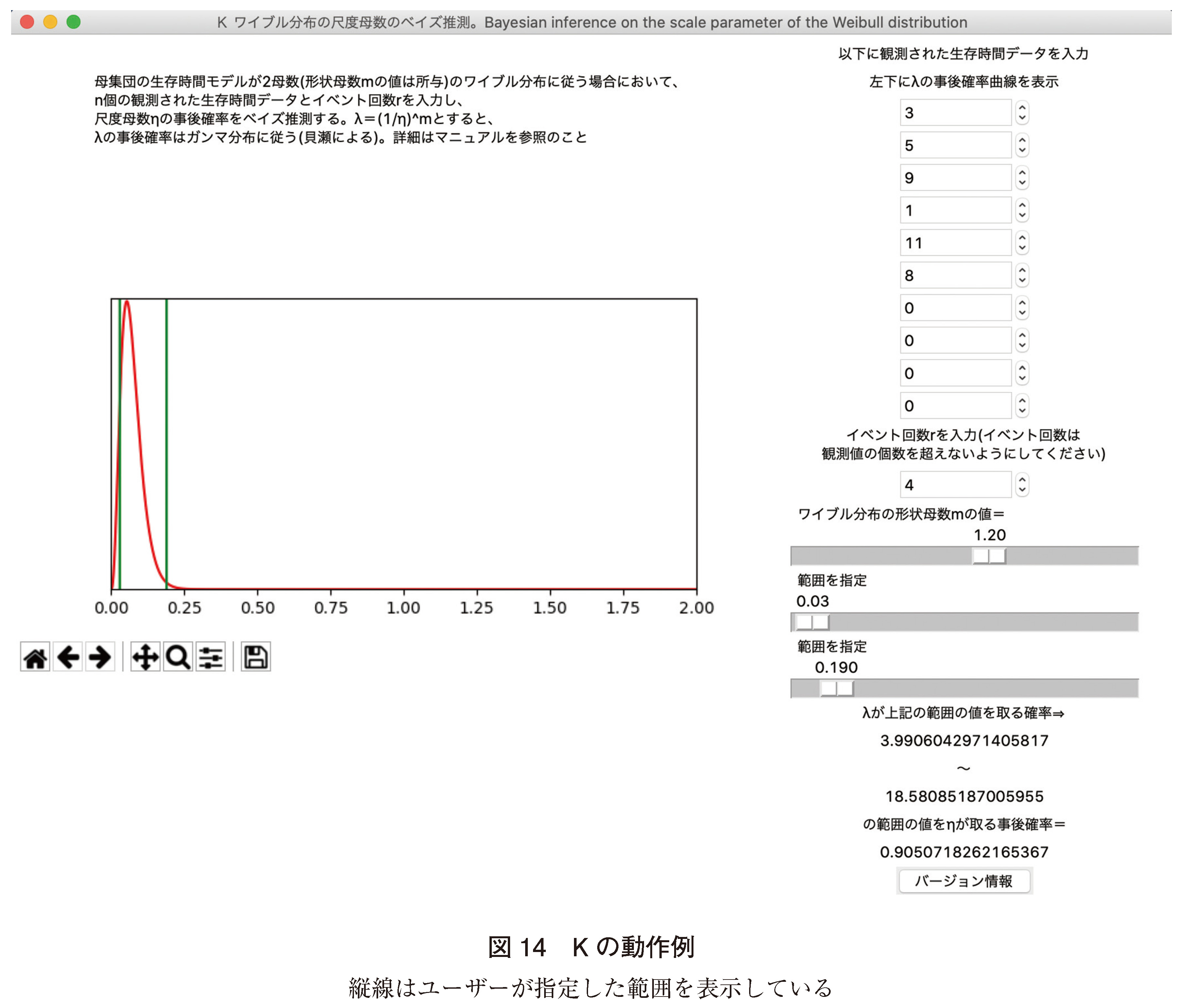
(11)K. ワイブル分布の尺度母数の推測25)
ワイブル分布型の寿命モデルを有する集団の、生存時間を観測し、サンプルデータ(単位:年)の観測値は{3, 5, 9, 1, 11, 8}であった。このうち4例は死亡、2例が打ち切りであった。母集団の形状母数m=1.2(値所与)であった。本ツール画面ではこの集団で90%(0.90507182)の確信度でλ=(1/η)mの値が0.03~0.190を取る、すなわち尺度母数ηの値が4.0~18.6を取ることが即座に表示される(図14)。Rの計算(付録のスクリプト(シ))では、λ=(1/η)mの値が0.03~0.190を取る、すなわちワイブル分布の尺度母数ηの値が4.0~18.6を取る事後確率値は0.9050718となり、ほぼ同じ値となった。
(12)L. 感度・特異度・有病率を用いた検査的中率の推測26)
ある疾患の検査の感度が80%、特異度が99%であった。有病率5%で、ある患者の検査が陽性であったとき本ツール画面ではその患者の陽性検査的中率(赤線)と陰性検査的中率(青線)の曲線が表示され、陽性検査的中率80.8%、陰性検査的中率98.9%と計算表示される(図15)。Rの計算(付録のスクリプト(ス))でも陽性検査的中率80.8%、陰性検査的中率98.9%となった。
2)本プログラムでは観測値などのデータを指定し変化させることによって、事後確率分布を自動的に計算し、事後確率分布のグラフ曲線の変化を動的なアニメーションによりベイズ推測を視覚的に理解することができ、同時にユーザーが任意の範囲で指定した、信用区間(credible interval)の事後確率も算出、表示することができた。動作例において示した事後確率値はRの検算結果とほぼ一致したことをもって、計算の妥当性を確認した。もちろんユーザーはマウスのみを操作に用い、かつ、グラフ曲線と確率の計算結果の表示をユーザーが直接変更することはできなかった。上記をマルチプラットフォームで実現した。
まず以下1から3で3つの研究目的ごとに論じ、次に4で他のソフトとの比較による本プログラムの有用性、5で本プログラムの妥当性とユーザーへのサポートについて論じた。
1 第1の目的について
B.T.V.T.I.はwindows10、macOS、Linux(Ubuntu)で稼働しており、PCにおける第1の目的を達成したと考えられる。ここではB.T.V.T.I.のPythonプログラムコードの今後の拡張性について述べる。
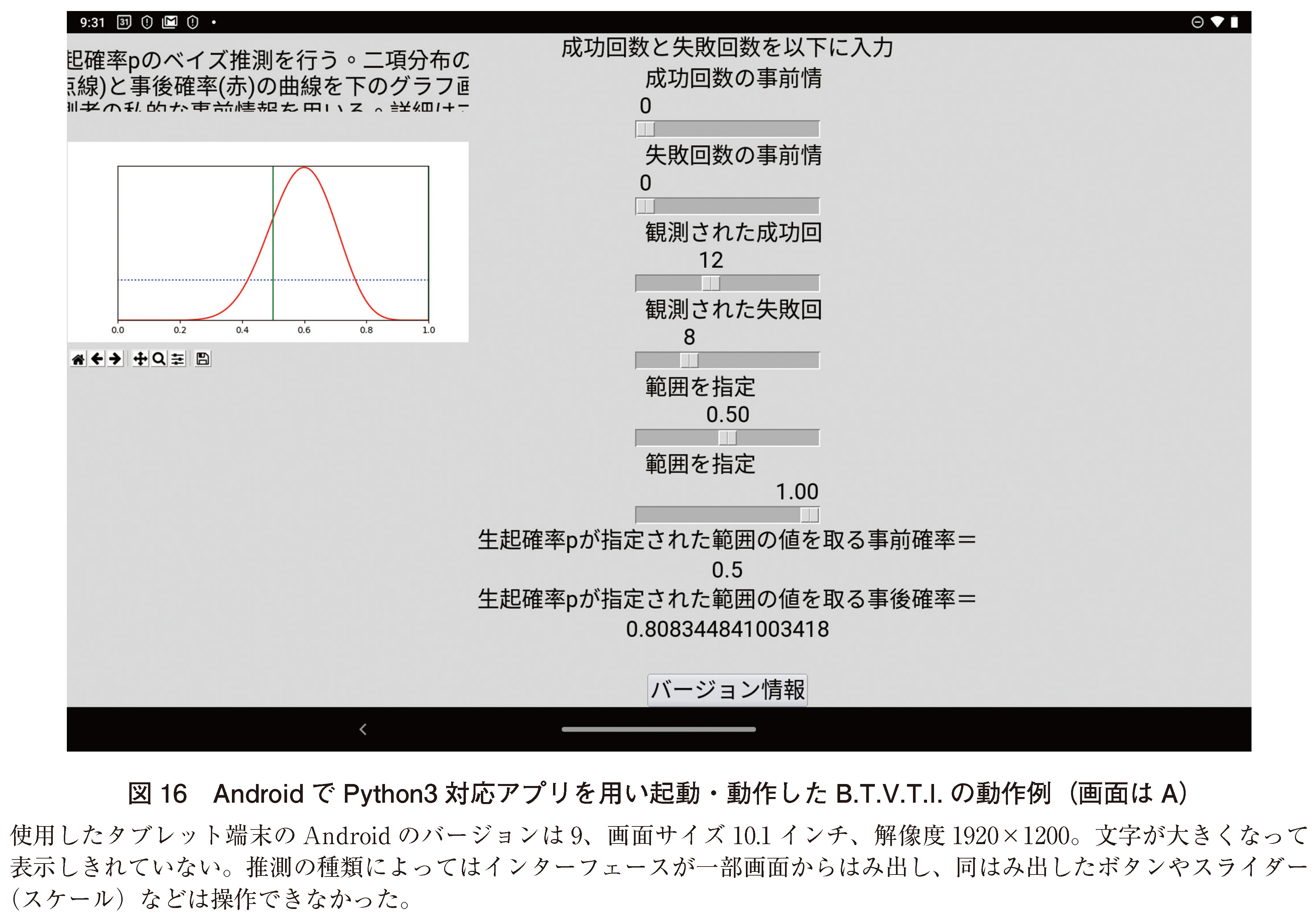
これら3者以外のOSを用いたハードウェア(デバイス)として、タブレットとスマートフォンが挙げられる。タブレットとスマートフォン向けのPython本体は現時点で公式にサポートされておらず、代わりにPythonソースファイルを読み込んで公式のPythonの動作を再現する、統合開発環境の形を取るか、もしくはJupyter Notebook27)を模した操作画面を有した、エミュレータとしてのアプリを用いることが想定される。B.T.V.T.I.にてGUIを担当しているTkinterはPythonに付与されている標準GUIツールキットであるが、iPadOS・iOSなどタブレットとスマートフォン用OS上ではこれらエミュレータとしてのアプリ28), 29)や、Jupyter Notebookを模したアプリ30), 31)はTkinterに対応していなかった32)。しかし一部のAndroid用アプリ33)ではB.T.V.T.I.のPythonプログラムコードを読み込んで、操作画面が一部タブレット画面からはみ出すものの、はみ出していない範囲でのスライダー(スケール)やスピンボックスを操作して実行することができた(図16)。今後タブレットとスマートフォンへB.T.V.T.I.の使用を拡張する際は、Kivy34)などマルチプラットフォームに対応した他のGUIツールキットを開発に用いることや、または前掲のAndroid用アプリ33)のように、現状のTkinterでも動作するアプリを使用することが考えられるが、図16が示すようにそのままでは画面と文字のサイズが大きすぎ、タブレットとスマートフォンに対応させるための文字サイズの縮小やユーザーインターフェースの再設計を含めたプログラムの大幅な改編がいずれの場合も必須であると考えられた。
2 第2の目的について
表4で示す通り、12の推測中SciPyの統計関数を用いることができた9つの推測画面は、数値計算の堅牢性がPythonによって担保されたとみなすことができよう。2つの推測画面について累積分布関数へのSciPy収録関数が不採用となり、B.T.V.T.I.は統計計算、特に事後確率の数値計算の頑健性を完全に達成するに一歩届かなかった。Lの推測は事後確率の計算に統計関数が不要であったのでさておき、Hの推測にて用いられている逆正規分布35)はいわゆる逆ガウス分布(ワルド分布)とは異なるものである。同推測でSciPyが不採用となったのはSciPyに逆正規分布35)の関数がサポートされていなかったためであった。Jにおいては事後分布の数式がAchcarによって提唱された近似式であり24)、著者が検索した限りでは特にどの確率分布にも該当しないとみなされたため、SciPyに収録されているどの統計関数も選択できなかったためであった。累積分布関数は確率密度関数を負の無限大から確率変数のある値まで定積分したものであるから、対策としてSciPyの数式を積分する関数である、scipy.integrate.quad関数36)で累積分布関数を代用する方法が挙げられる。しかしscipy.integrate.quad関数そのものが近似値を計算するものであり、根本的な解決法とするにはまだ議論の余地が残ると考えられた。SciPyの統計関数を事後確率値の計算に用いられないベイズ推測を実装する場合は、確率値に近似計算を行っている旨を当該推測ツール画面にあらかじめ表示し、ユーザーに注意を促すことが必須なのではないかと考えられた。
3 第3の目的について
B.T.V.T.I.にて視覚化されたベイズ推測は、著者が過去に情報データベース37)で検索した論文や成書のうち入手可能だったもの12)-26)から可及的に収集・引用した。このことから、まだ実装できてない推測の実在を否定することはできないと考えられた。未実装のベイズ推測の事例の存在とその検索から追加実装について論じるべきであるが、これについては表4をみるにあたり、事後確率の計算に用いられた確率分布がほぼ、指数型分布族に属するものである点に着目した。B.T.V.T.I.に実装されているような、もっぱら数式を用いた解析的手法でベイズ推測を行う場合、通常は自然共役事前分布に指数型分布族が用いられることが多い38)。よって成書や論文に様々なベイズ推測の事例を取材した際、各事例の事後確率の推測に用いられる確率分布は表4のGやKのように何らかの変数変換を用いるなどを行ったとしても、ほぼいずれかの指数型分布族をとるものと考えられる。多様な応用事例の存在は想定しえるものの、使われる数式は高々指数型分布族を構成する確率分布の種類以上には増えないものと考えることは可能かもしれない。ただし、表4のHやJのように事後確率分布に近似式を用いている場合はその限りではなく、同様の文献が未検索、未収録になっている可能性は残されていると考えられる。今後もしそのような近似が行なわれたベイズ推測の応用事例が文献上で探索された場合、引用後B.T.V.T.I.に追加実装し視覚化することが予想される。
4 他のソフトとの比較
ベイズ推測に関した機能を実装している他の代表的な製品とB.T.V.T.I.の比較を表5に記した。B.T.V.T.I.は操作の自由度や入力できる値の範囲に、画面表示の制約から来る制限がある反面、ユーザーの操作が極めて簡便であるという利点を有する。R39)、Stan+R40)、SPSS41)とB.T.V.T.I.の最大の違いは、前者が三者とも主に解析を追求するソフトであるのに対し、後者はマルチプラットフォームでベイズ的なアプローチにおいて入力値をユーザーが変更すると同時に事後情報がどのように変化するか、入力値の変化に対するグラフ曲線の同時的なリアルタイムな変動を可視化し、視覚的な理解の助けとなることに重点を置いている点にある。
一般に頒布されているプログラムでこれら仕様を満たしたものは、著者の検索する限りでは見られず、この点でB.T.V.T.I.は先進性かつ有用性を有すると考えられる。このようなB.T.V.T.I.の機能をStan+RとRについてそれぞれ実装する可能性について、Stan+RについてはStanのスクリプトのコンパイルからビルドへの過程はもちろん、いったん入力された数値をユーザーが変更するたびに、乱数列のサンプリングなどの繰り返し計算を逐次収束させるまで再計算しなければならず時間がかかり、結果のグラフ曲線の動的・同時的な瞬間的更新・再表示の実現は、特にStanが主に用いられる複雑なアルゴリズムの実行場面においては困難もしくは不適応と思われる。RについてはB.T.V.T.I.で引用されている推測法を再現する場合に限って言えば、ウェブアプリケーション用パッケージであるShiny42)と組み合わせて用いれば、かなり似たものが作成できるかもしれない。いずれR-Shiny上で類似のアプリが開発されれば、B.T.V.T.I.と競合し得ることが考えられる。

5 実装されたベイズ推測の妥当性とユーザーへのサポートについて
本プログラムに実装されたベイズ推測はすべて、実在する成書と研究論文から引用したものであり、引用した数式からグラフ曲線と事後確率計算を視覚的に再現したものであることを以て、それら推測の有用性が担保されていることを前提としている。しかし、成書や研究論文をすべて無批判に受け入れることには議論の余地がないとは言えない。本プログラムの妥当性・有用性を保守・維持・向上するためには実装するまえに一定の注意を以て当該引用元の成書・研究論文の正確性・可用性・応用可能な範囲の吟味を行うこと、また当然のことであるが実装に当たり数式のプログラムコーディングにヒューマンエラーが生じないよう幾度もチェックすること、他のソフトウェアで同じ計算を行い、結果を比較することなどで品質の管理に努めることが大切であると考えられる。
最後に、ユーザーへのサポートについて述べる。本プログラムの各操作画面にはどこに何を入力操作するか表示されているものの、その推測がどのような原理で計算されどのように結果を解釈するべきかがある程度、ユーザーに理解されている必要があると言えよう。本プログラムの操作はB.T.V.T.I.頒布に当たり作成・同梱した解説書・操作説明書(マニュアル)の精読を並行して行う必要が強く推奨されると考えられた。
新たな内容のベイズ推測を実装する、Python3を用いたベイズ推測動的視覚化ツールを構築した。マルチプラットフォームで動作し、推測の多くにSciPyを用い計算の信頼性を向上させることによって、ユーザーの使用機会を拡張発展させるものになり得ると考えられた。
本研究において著者はいかなる利益相反も有していないことをここに明言する。
検算用のRのスクリプトを以下に記した。
スクリプト(ア)
a=12 #a:有効回数
b=8 #b:無効回数
p=0.5
#事後確率値:jigo
jigo<-pbeta(1,a+1,b+1,ncp=0,lower.tail=TRUE,log.p=FALSE)-pbeta(0.5,a+1,b+1,ncp=0,lower.tail=TRUE,log.p=FALSE)
jigo
#グラフ曲線描画
jigocurve<-function(x){dbeta(x,a+1,b+1,ncp=0,log=FALSE)}
plot(jigocurve,0,1)
スクリプト(イ)
a=20 #a:有効回数
b=12 #b:無効回数
p=0.5
#事後確率値:jigo
jigo<-pbeta(1,a,b+0.5,ncp=0,lower.tail=TRUE,log.p=FALSE)-pbeta(0.5,a,b+0.5,ncp=0,lower.tail=TRUE,log.p=FALSE)
jigo
#グラフ曲線描画
jigocurve<-function(x){dbeta(x,a,b+0.5,ncp=0,log=FALSE)}
plot(jigocurve,0,1)
スクリプト(ウ)
a=8 #a:奏功回数
b=10 #b:不変回数
c=7 #c:増悪回数
p1=0.5
p2=0.5
p3=0.5
#それぞれの周辺事後確率値:P1:jigo1、P2:jigo2、P3:jigo3
jigo1<-pbeta(1,a+1,b+c+2,ncp=0,lower.tail=TRUE,log.p=FALSE)-pbeta(p1,a+1,b+c+2,ncp=0,lower.tail=TRUE,log.p=FALSE)
jigo2<-pbeta(1,b+1,a+c+2,ncp=0,lower.tail=TRUE,log.p=FALSE)-pbeta(p2,b+1,a+c+2,ncp=0,lower.tail=TRUE,log.p=FALSE)
jigo3<-pbeta(1,c+1,a+b+2,ncp=0,lower.tail=TRUE,log.p=FALSE)-pbeta(p3,c+1,a+b+2,ncp=0,lower.tail=TRUE,log.p=FALSE)
jigo1
jigo2
jigo3
#※事前無情報時のP1、P2、P3はいずれもBe(1,2)に従うものとした。
#グラフ曲線描画
jigoc1<-function(x){dbeta(x,a+1,b+c+2,ncp=0,log=FALSE)}
jigoc2<-function(x){dbeta(x,b+1,a+c+2,ncp=0,log=FALSE)}
jigoc3<-function(x){dbeta(x, c+1,a+b+2,ncp=0,log=FALSE)}
plot(jigoc1,xlim=c(0,1),ylim=c(0,5),ann=F,lty=2) #P1事後曲線を描く
par(new=T) #重ね書き指定
plot(jigoc2,xlim=c(0,1),ylim=c(0,5)) #P2事後曲線を描く
par(new=T) #重ね書き指定
plot(jigoc3,xlim=c(0,1),ylim=c(0,5)) #P3事後曲線を描く
スクリプト(エ)
a=12
a0=10
b=22-12
b0=15-10
m1=(a+a0+1)/(a+a0+b+b0+1+1) #新薬の奏効割合の事後分布(ベータ分布)の平均m1
v1=((a+a0+1)*(b+b0+1))/((a+a0+1+b+b0+1)^2*(a+a0+1+b+b0+1+1)) #新薬の奏効割合の事後分布(ベータ分布)の分散v1
c=15
c0=10
d=35-15
d0=17-10
m2=(c+c0+1)/(c+c0+d+d0+1+1) #新薬の奏効割合の事後分布(ベータ分布)の平均m2
v2=((c+c0+1)*(d+d0+1))/((c+c0+1+d+d0+1)^2*(c+c0+1+d+d0+1+1)) #新薬の奏効割合の事後分布(ベータ分布)の分散v2
m=m1-m2 #P1-P2の事後分布の平均m
v=v1+v2 #P1-P2の事後分布の分散v
jigo<-pnorm(0.5, mean=m, sd=v^0.5, lower.tail=TRUE, log.p=FALSE)-pnorm(0.1, mean=m, sd=v^0.5, lower.tail=TRUE, log.p=FALSE)
jigo
#事後確率のグラフ曲線描画
jigocurve<-function(x){dnorm(x,mean=m,sd=v^0.5,log=FALSE)}
plot(jigocurve,-1,1)
スクリプト(オ)
a=12 #新薬の奏効オッズ=a/b
b=10
c=15 #旧薬の奏効オッズ=c/d
d=20
a0=6 #新薬の奏効オッズの事前情報=a0/b0
b0=5
c0=5 #旧薬の奏効オッズの事前情報=c0/d0
d0=7
#a0,b0,c0,d0はそれぞれ回数であることからP1の事前確率~Be(a0+1,b0+1),P2の事前確率~Be(c0+1,d0+1)とした。
#事後対数オッズ比の推測。平均m、分散v
m=log(((a+a0+1-0.5)/(b+b0+1-0.5))/((c+c0+1-0.5)/(d+d0+1-0.5)))
v=1/(a+a0+1)+1/(b+b0+1)+1/(c+c0+1)+1/(d+d0+1)
#事後確率:jigo
jigo<-pnorm(2, m, v^0.5, lower.tail=TRUE, log.p=FALSE)-pnorm(0, m, v^0.5, lower.tail=TRUE, log.p=FALSE)
jigo
#事後確率のグラフ曲線描画
jigocurve<-function(x){dnorm(x,mean=m,sd=v^0.5,log=FALSE)}
plot(jigocurve,-5,5)
スクリプト(カ)
r=2 #再捕獲の中で標識されていた個体数
n=30 #再捕獲個体数
#pの取り得る範囲は0.03から0.20
#0.03から0.20の範囲のpの事後確率値:jigo
jigo<-pbeta(0.20,r+1,n-r+1,ncp=0,lower.tail=TRUE,log.p=FALSE)-pbeta(0.03,r+1,n-r+1,ncp=0,lower.tail=TRUE,log.p=FALSE)
jigo
#事後確率のグラフ曲線描画
jigocurve<-function(x){dbeta(x,r+1,n-r+1,ncp=0,log=FALSE)}
plot(jigocurve,0,1)
スクリプト(キ)
#θ1=6/(N*1)、θ2=2/(N*3)
#(θ1/θ2)(2/6)/(3/1)→(θ1/θ2)*(2/18)は自由度12、4のF分布に従う。
df1=12 #自由度その1
df2=4 #自由度その2
#率比が3から5の範囲の値を取る、すなわち、F分布の確率変数が0.34(≒3*2/18)から0.56(≒5*2/18)の範囲の値を取る事後確率値:jigo
jigo<-pf(0.56,df1,df2,ncp=0,lower.tail=TRUE,log.p=FALSE)-pf(0.34,df1,df2,ncp=0,lower.tail=TRUE,log.p=FALSE)jigo
#事後確率のグラフ曲線描画(図10に相当)
jigocurve<-function(x){df(x, df1, df2, log=FALSE)}
plot(jigocurve,0,5)
スクリプト(ク)
m1=(11+1)/(11+1+9+1) #新しい治療手段の有効症例数/全実施症例数(=11/20)の平均
m2=(5+1)/(5+1+15+1) #従来の治療手段の有効症例数/全実施症例数(=5/20)の平均
m=m1-m2 #合成された平均
v1=m1*(1-m1)/(11+9+3) #新しい治療手段の有効症例数/全実施症例数(=11/20)の分散
v2=m2*(1-m2)/(5+15+3) #従来の治療手段の有効症例数/全実施症例数(=5/20)の分散
v=v1+v2 #合成された分散
#NNTが1から23の範囲の値を取る事後確率値:jigo
f<-function(x)((1/(((2*pi*v)^0.5)*x^2))*exp(-1*((1/x)-m)*((1/x)-m)/(2*v)))
jigo<-integrate(f,1,23)
jigo$value
#事後確率のグラフ曲線描画(図11に相当)
#jigocurve<-function(x){df(x, df1, df2, log=FALSE)}
plot(f,-40,40)
スクリプト(ケ)
#γをg、E(IC11)をE、V(IC11)をV、両側95%信頼区間の下限をLCI、上限をUCIとする。
a=5
b=240
c=160
d=60000
g=1*(a+b+c+d+2)^2/((a+b+1)*(a+c+1))
E=log2((a+1)*(a+b+c+d+2)^2/((a+b+c+d+g)*(a+b+1)*(a+c+1)))
V=(1/log(2))^2*((a+b+c+d-a+g-1)/((a+1)*(1+a+b+c+d+g))+(a+b+c+d-(a+b)+1)/((a+b+1)*(a+b+c+d+3))+(a+b+c+d-(a+c)+1)/((a+c+1)*(a+b+c+d+3)))
LCI=E-1.96*V^0.5
LCI
UCI=E+1.96*V^0.5
UCI
#事後確率のグラフ曲線描画(図12の赤色曲線に相当)
jigocurve<-function(x){dnorm(x,mean=E,sd=V^0.5,log=FALSE)}
plot(jigocurve,-5,5)
スクリプト(コ)
#(ケ)でa、b、c、d、の値をそれぞれa=6、b=240、c=610、d=60000として、以下(ケ)と同じ数式で計算
a=6
b=240
c=610
d=60000
g=1*(a+b+c+d+2)^2/((a+b+1)*(a+c+1))
E=log2((a+1)*(a+b+c+d+2)^2/((a+b+c+d+g)*(a+b+1)*(a+c+1)))
V=(1/log(2))^2*((a+b+c+d-a+g-1)/((a+1)*(1+a+b+c+d+g))+(a+b+c+d-(a+b)+1)/((a+b+1)*(a+b+c+d+3))+(a+b+c+d-(a+c)+1)/((a+c+1)*(a+b+c+d+3)))
LCI=E-1.96*V^0.5
LCI
UCI=E+1.96*V^0.5
UCI
スクリプト(サ)
m=1.2 #ワイブル分布の形状母数m(値所与)
r=6 #イベント発生回数r(観測値から)
#生存時間データ(1, 2, 3, 4, 6, 8, 9, 11)
st=(1^m+2^m+3^m+4^m+6^m+8^m+9^m+11^m)*log(2)
#中央値が2.2から8.9の間を取る事後確率値:jigo
#Achcarの条件付事後確率の式は確率密度関数ではなく近似式と考えられ、積分しても1にならないので、jigo=(2.2~8.9の積分)/(0~∞の積分)でjigoを求める。
#((st/(x^m)^(r+1))*(m/x)*(1/(1*2*3*4*5*6))*exp(1)^(-1*(st/(x^m)))
f<- function(x) ((st/(x^m)^(r+1))*(m/x)*(1/(1*2*3*4*5*6))*exp(1)^(-1*(st/(x^m))))
jigo<-(integrate(f, 2.2, 8.9)$value/integrate(f, 0, Inf)$value)
jigo
#事後確率のグラフ曲線描画(図13の赤色曲線に相当)
plot(f,0,30)
スクリプト(シ)
m=1.2 #ワイブル分布の形状母数m(値所与)
r=4 #イベント発生回数r(観測値から)
#ガンマ分布の尺度母数の逆数sh(観測値から)
sh=3^m+5^m+9^m+1^m+11^m+8^m
#λが0.03から0.190の間を取る事後確率値(ワイブル分布の尺度母数ηの値が4.0~18.6の間を取る事後確率値):jigo
jigo<-pgamma(0.190,r,scale=1/sh,lower.tail=TRUE,log.p=FALSE)-pgamma(0.03,r,scale=1/sh,lower.tail=TRUE,log.p=FALSE)
jigo
#事後確率のグラフ曲線描画(図14の赤色曲線に相当)
jigocurve<-function(x){dgamma(x, r, scale=1/sh, log=FALSE)}
plot(jigocurve,0,2)
スクリプト(ス)
sen=0.8 #感度sen
sp=0.99 #特異度sp
pr=0.05 #有病率pr
#陽性検査的中率:PPV、陰性検査的中率:NPV
PPV=pr*sen/((pr*sen)+(1-pr)*(1-sp))
PPV
NPV=(1-pr)*sp/((pr*(1-sen)+(1-pr)*sp))
NPV
#PPV(図15の赤色曲線に相当)、NPV(図15の青色曲線に相当)のグラフ曲線描画
red<-function(x){x*sen/((x*sen)+(1-x)*(1-sp))} #red:PPV
blue<-function(x){1-(1-x)*sp/((x*(1-sen)+(1-x)*sp))} #blue:1-NPV
plot(red,0,1, yaxt="n",ann=F)
par(new=T) #重ね書き指定plot(blue,0,1,lty=2)