2015 Volume 91 Issue 9 Pages 501-510
2015 Volume 91 Issue 9 Pages 501-510
In conventional muography observations using two detectors for muon tracking, the accidental coincidence of vertical electromagnetic showers generates identical trajectories to the muon tracks. Although muography has favorable properties, which allow direct density measurements inside a volcano, the measured density is lower than the actual value due to these fortuitous trajectories. We performed muography of Usu volcano, and confirmed that, in comparison with a use of two detectors, background noise levels were reduced by more than one order of magnitude using seven detectors for selecting linear trajectories. The resultant muographic image showed a high-density region underneath the central region of Usu volcano. This picture is consistent with the magma intrusion model proposed in previous studies. To clarify the three-dimensional location and actual size of the detected high-density body, multidirectional muographic measurements are necessary.
To date, various methods, including seismology, geodesy, geomagnetism, and soil resistivity have been used to investigate the internal structures of various volcanoes. Muography is an emerging technique that provides information complementary to and independent from existing techniques using an elementary particle called a muon. Thus, it has been globally applied to the study of volcanoes over the last decade.1)–13) Because muon flux attenuates as a function of the density length (muon’s path length × average density along the path line), if the path length is known, the average density can be calculated by measuring the muon flux after passing through the volcano. Thus far, the technique has imaged the conduit structure beneath a lava dome at Usu volcano, Japan,6),14) degassing phenomena in conduits at Satsuma-Iwojima volcano, Japan,4) explosions of deposits at the crater floor at Asama volcano, Japan,3) three-dimensional conduit shapes at Asama volcano, Japan,2) the steam pathway inside a lava dome at La Soufrière of Guadeloupe volcano, France,11) lava dome formations at Puy de Dôme, France,15) and the conduit geometry at Etna volcano, Italy.9) However, in these studies, the target size was limited to ∼1-km path lengths due to a significant reduction of the signal-to-noise ratio.
A muon is one of the elementary particles, that can penetrate rocks thicker than 1 km. Therefore, we can image the internal structure of decameter- to kilometer-sized objects with muography, in a manner similar to X-ray imaging.
The mass of a muon is 106 MeV c−2, which is approximately 207 times heavier than an electron. The mean lifetime (τμ) of a muon is 2.2 µs. Muons do not interact via strong interactions with matter, resulting in high penetration power. Cosmic ray muons are generated after high-energy primary cosmic rays (e.g., protons, helium nuclei and others) interact with atmospheric nuclei. Mesons, such as pions and kaons, are generated by these interactions and usually decay into a muon and a muon neutrino.
Although muons decay in τμ = 2.2 µs at rest, the muons generated at the top of the atmosphere can reach the ground due to relativistic effects. A significant amount of data related to the energy spectrum of muons has been accumulated over the past 50 years16)–18) and the spectrum has been modeled.19)–22)
Because muon flux attenuates as a function of the density length as described in Sect. 1, we can calculate the muon flux after passing through the rock (penetrating muon flux) by integrating the open-sky muon flux over the range of the lowest energy, Ec, at which a muon can escape from the target to infinity. Inversely, the density length will be uniquely determined for a given penetrating muon flux at each arrival elevation angle (Fig. 1). The spatial distribution of the average density is obtained by dividing the density length by the muon path lengths for various directions.

Integrated cosmic ray muon flux after passing through a given thickness of rock. The curves are plotted against various elevation angles (0–30°).
If the penetrating muon flux decreases, the ratio of background noise to muon flux increases. If the background noise is dominant in the observation, the observed density is lower than the actual density. Therefore, background modeling helps to extract muon events from data. However, the statistical and systematic errors in the background estimate occasionally mask the density contrast in the muographic image.
The main component of the background noise is fake tracks, which are created by the accidental coincidence of vertical electromagnetic (EM) shower events consisting of multiple EM particles (electrons, positrons, and gamma rays).8) To improve the density contrast in the resultant image, a muography telescope must be designed to effectively remove such events. For this purpose, a telescope with three or more position-sensitive planes (PSPs) was designed.8) Redundant vertex points can reduce the fake tracks under the condition where events must be detected by all PSPs, which reduces the accidental coincidence rate. In this case, the number of PSPs and the noise reduction rate correlate. To further reduce the fake tracks, we selected only events that formed straight paths in the telescope. Even if EM shower particles hit all PSPs, the detected points are expected to form a random alignment rather than straight path lines.
2.2. Estimation of background caused by vertical EM shower events.To estimate background events created by vertical EM showers, we performed Monte Carlo simulations with Cosmos.23) Multiple EM particles from zenith angles of 0–20° were considered as vertical EM showers arriving at a ground surface with an area of 1.1 × 1.8 m2. The ratios of 3, 4, 5, 6, and 7 EM particles to 2 EM particles that arrived within 40 ns were 1.31 × 10−1, 3.16 × 10−2, 1.18 × 10−2, 7.07 × 10−3, and 4.11 × 10−3, respectively. Because these particles arrive vertically, each particle is expected to hit at most one PSP. Accordingly, if we use n PSPs, n EM particles should be necessary for all PSPs to detect a particle. From this simulation, the background caused by vertical EM shower events is expected to be reduced by more than two orders of magnitude using a 7-PSP telescope compared to a 2-PSP telescope.
In this study, a muography telescope with seven PSPs was used (Fig. 2(top)). The active area and the position resolution of each PSP were 1.21 m2 and 10 cm, respectively. The distance between the first and seventh PSP was 1.8 m. Therefore, the angular resolution of the telescope was ±3°. Each PSP consisted of plastic scintillator strips (ELJEN EJ-200) (1100 mm long × 100 mm wide × 20 mm thick) and photomultiplier tubes (PMTs; Hamamatsu R7724). The position resolution of each PSP corresponds to the width of the scintillator strip.

(top) Photograph of a multi-layered muography telescope. The outputs of the telescope consisting of seven muon detectors are generated by the FPGA-based muon readout module; (bottom) Principle of muon tracking in (a) side view, (b) top view, and (c) plane view of the seven detectors of the telescope. The shaded area and red grids show the tracks of muons and vertex points, respectively.
The 154 signal outputs from PMTs were generated by a FPGA-based readout module8) (Fig. 2(top)). The identification (ID) numbers and times were recorded when the readout module received the signal from the PMTs. The data were then transferred to the data acquisition computer in real time, and compressed and saved every hour. The compressed data size is ∼2.7 MB h−1.
Each of the seven PSPs was set on a bogie, which allowed it to move on both a straight rail and a circular rail. Therefore, distance and direction of the PSPs were variable. Thus, the field of view, as well as the angular resolution of the telescope, could also vary. The precision of the PSP position was 1 mm and its error corresponds to an angular resolution of 0.03° of the telescope. Because the diameter of the circular rail was 2 m and the position of the bogies was adjustable with a precision of 1 mm, it was possible to determine the telescope’s direction with a precision of 0.06°. To maintain this precision during the measurements, the bogies were fixed with screws.
The power consumption of the muography telescope was ∼300 W in total with approximate contributions from the PMTs of 164 W, from the readout electronics of 20 W, and from the data acquisition computer of 80 W. The azimuthal viewing angle was ±30° and the elevational viewing angle was 0–30°.
3.2. Muon tracking.In this paper, the telescope’s PSPs are labeled as PSP#1, PSP#2, …, and PSP#7. The muon trajectories were determined using the following algorithm. (A) The arrival direction of a muon was determined by connecting two vertex points in PSP#1 and PSP#7. (B) Only events having straight paths were selected from those recorded by process (A), and only under the following conditions: events were recognized as muons only when signals were detected by all of PSPs within a time window of 40 ns and when the five other vertex points were aligned along the straight line determined in process (A). As long as the deviations of these five points were within one half width of the scintillator, the events were recorded for track reconstruction. Because the distance of each PSP is fixed, the subtraction of the horizontal and vertical vertex positions between PSP#1 and PSP#7 yields azimuth and elevation angle information. Figure 2(bottom) shows an example of our track reconstruction.
After passing through an object larger than a few km, the muon flux is in generally very low and considerable measurement time is required to record a reasonable number of events. However, a substantial number of events is typically recorded under this condition. These events are called background events. In this study, we estimated this background level according to the following procedure. First, the theoretical muon flux was calculated by assuming lower and upper limits of the density values of the object. In the case of a mountain, the lower and upper limits were set to 1.0 and 3.0 g cm−3, respectively. Then, the number of muon counts was estimated using the detector’s geometry, including the active area, acceptance, and measurement time. If the number of recorded events was greater than 100 times the estimated value, we assumed that these events represented the background.
Ko-Usu lava dome and Oo-Usu (OU) lava dome were formed during the 1663 and the 1853 eruptions, respectively, and Showa-Shinzan (SS) lava dome was formed during the 1944 eruption. Subsequently, a newly formed upheaval (named “New Mountain”, NM) resulted from tilting of a block of near the summit during the 1977–1982 eruption.24) In addition, a major fault25) was created at the surface of the mountain. The fault (NM fault in Fig. 10)25) is shown as a gray zone (Fig. 3(top)). During this eruption, the OU lava dome rose 10 m, while the NM and Ogariyama (OY) peaks both upheaved 170 m. The Ko-Usu lava dome subsided 60 m. The Gin-numa (Gn) crater was also formed during the 1977 eruption.
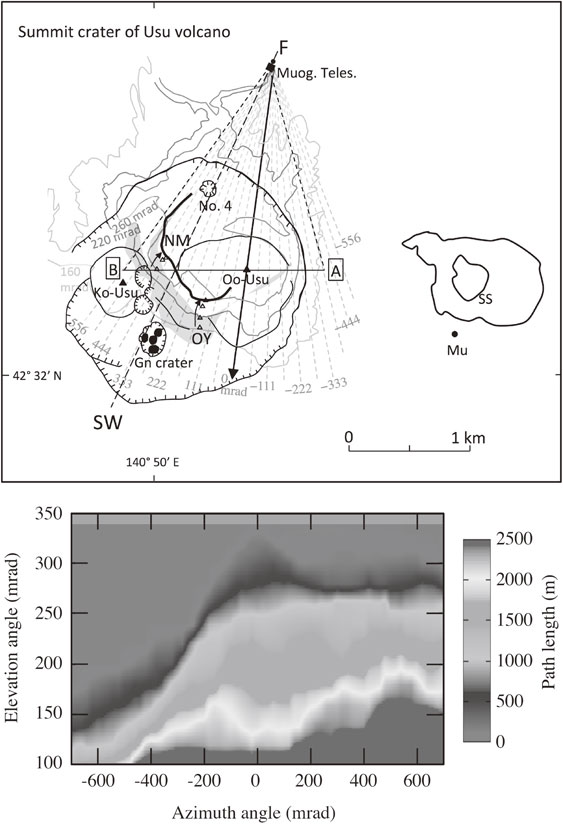
(top) Detector location (F) towards the summit of Usu volcano as of September 2015. Radial broken lines denote the viewing angles of the telescope. Solid curves indicate cross sections of the mountain at given elevation angles (160–260 mrad). The vertical cross section along line A–B is shown in Fig. 8. The heavy line connecting NM, OY, and Oo-Usu shows the ridge of the 1977–1978 upheaval. Curved arrows show the upheaval direction of NM and OY; (bottom) Path length distribution of the volcano as viewed by the telescope (F in the top figure).
Muography in this study can be compared with previous studies of the subsurface structure of Usu volcano such as magnetotellurics carried out by Ogawa et al.26) The results of ground resistivity measurements showed a resistive body underneath the NM. In addition, the measurements indicated that a 300-m wide magma body intruded and reached a height of ∼210 m relative to the observation site.26)
To obtain additional information of the subsurface structure of the volcano, the multi-layered telescope described in Sect. 3.1. was used to muographically image the internal density structure of the NM.
4.2. Location of muography telescope.The multi-layered muography telescope8) was installed at the northern foot of Usu volcano (1.75 km from the OU lava dome), and the telescope was directed toward the lava dome (Fig. 3(top)). The azimuthal viewing angle was ±30°. Figure 3(top) shows the azimuthal viewing angle used during the measurements. The OU lava dome, Ko-Usu lava dome, OY, and NM peaks were covered by this viewing angle. The elevational viewing angle covered the OU lava dome. The observation altitude was 140 m above sea level.
In this work, the muon path lengths, d(θ, ϕ), were calculated using a 1 : 25,000 topographic map,27) where θ is the elevation angle and ϕ is the azimuth angle. Figure 3(bottom) shows d(θ, ϕ) for the experimental setup.
The accuracy of the contour position was reported by Geospatial Information authority of Japan (GSI), and its standard deviation is 5 m. This level of error is negligible compared to the path lengths of Usu volcano, which exceed 1000 m.
To compare the background reduction of the multi-layered telescope with the conventional telescope, less muon flux is preferable. For this purpose, observation of a thick region of a mountain is useful because muon flux is typically low. The thickness of a mountain exponentially increases as a function of the elevation angle. In the present case, the path length of Usu volcano exceeds 2500 m if the elevation angle is less than 55 mrad. Thus, the penetrating muon flux is expected to be less than 2 × 10−8 cm−2 sr−1 s−1. By assuming the lower limit of the bulk density of the mountain (1.5 g cm−3), the density length was deduced to be 3750 meters water equivalent (m.w.e.). The penetrating muon flux was then calculated to be 2 × 10−8 cm−2 sr−1 s−1. Given the detector’s geometry, including its active area of 1.1 m2, solid angle of 0.003 sr and measurement time of 924 hours, the total muon count was estimated at 2.2.
In our actual measurement, however, 6099 and 304 counts were recorded in 924 h with two and seven PSPs, respectively. The counts were measured during the same period with the same angular resolution and active area. These counting rates were equivalent to 3 × 10−6 and 6 × 10−5 cm−2 sr−1 s−1, respectively. They were ∼150 and ∼3000 times larger than the estimated value and were interpreted as background events. Assuming these counts to be background events, the background for the 7-PSP telescope was reduced to 5% of the conventional 2-PSP telescope.28) Figure 4 shows the azimuthal dependence of the normalized events at elevation angles of 55 and 111 mrad. As shown in this figure, the normalized events are independent from the thickness distribution of the target mountain, showing the typical behavior of the background events.

Muon events after passing through 2500 m of rock. The data are plotted for six and seven PSPs, respectively. The muon events at elevation angles of 55 and 111 mrad are normalized by the muon events at the elevation angle of 389 mrad that corresponds to the open-sky region.
Figure 5 compares the observed azimuthal muon flux distribution with the topography of Usu volcano. The data points are plotted for different numbers of PSPs for tracking muon events. As observed in this figure, the data points have larger error bars when the muon trajectories were reconstructed with fewer of PSPs because of the larger statistical errors associated with the background events that are incorporated in the recorded data as described in the previous section. As a general trend, arises such that the muon transmission rate assumes a minimum value at an azimuthal angle of 166 mrad and a maximum value between 277 and 300 mrad. The normalized muon flux differs by a factor of two between the minimum and maximum values. At an elevation angle of ∼200 mrad, the average rock thickness is ∼1300 m but varies by ∼16% within an azimuthal range of −50 to 500 mrad. This correlation implies that a density anomaly in a 1300-m thick rock unit if the variation exceeds 16%.

A comparison of data obtained by each number of PSPs with the linear track selection method. Muon events are normalized relative to those from the open-sky region (389 mrad). The data are plotted for two (the second curve from the top)–seven (the bottom curve) PSPs. The error bars indicate the 1σ statistical errors. The density length distribution (solid line) was calculated from the topography of Usu volcano assuming a uniform density of 2.0 g/cm3.
Because the muography telescope was azimuthally rotatable, we compared the data collected before and after rotation (rotation angle ϕ = 111 mrad). By rotating the telescope, we can maximize the active area in the target directions. For example, when we direct the telescope toward the OU lava dome, the active area becomes smaller in the direction toward NM (from 0.75 to 0.25 m2), and vice versa. However, the rotatable telescope can optimize the observation condition in the directions of both OU lava dome and NM. Therefore, the statistics of the data are improved by adding data collected before and after rotation.
Figure 6 shows the azimuthal distribution of the transmitted muon intensities for data collected before and after rotation, which are within the statistical errors. To improve accuracy, we added these data and analyzed the added data to visualize the internal structure of the OU lava dome and NM. Figure 7 shows the added data points for θ = 222 and θ = 166 mrad with estimations for different uniform density models.

Azimuth distribution of the transmitted muon intensity measured before ( and
and  ) and after (
) and after ( and
and  ) a rotation of 6.3°. The data were collected at two different elevation angles: 222 mrad (
) a rotation of 6.3°. The data were collected at two different elevation angles: 222 mrad ( and
and  ) and 166 mrad (
) and 166 mrad ( and
and  ), respectively.
), respectively.

Comparison between the measured muon intensity and the theoretical calculation for different target densities (1.8, 2.0, 2.2, 2.4 g cm−3) and elevation angles of 222 mrad (top) and 166 mrad (bottom), respectively.
As shown in the top panel of Fig. 7, at an elevation of 222 mrad, the data points are in agreement with the 2.0-g cm−3 theoretical curve and within the statistical errors. However, those for ϕ > 500 mrad are deviate from the 2.0-g cm−3 curve by more than 1σ. As shown in the bottom panel of Fig. 7, the data points indicate higher densities at θ = 166 mrad and indicate lower densities at θ = 389 and θ = 500 mrad, at a confidence level greater than 2σ. These deviations imply a density contrast inside Usu volcano.
To visually display the results shown in Fig. 7, we plotted the spatial distribution of average densities as a color map (Fig. 8). When expressing density values in the two-dimensional color map, it is difficult to show the statistical density fluctuations. Therefore, we plotted the values only when they deviated from the 2.0-g cm−3 curve shown in Fig. 7 by more than 2σ (Fig. 8). If the deviations from the 2.0-g cm−3 curve were within 2σ, we plotted 2.0-g cm−3 as the density value in this map. The density of the white region in Fig. 8 was not calculated because the open sky flux masks the signals from the mountain.
As shown in Fig. 8, a high-density region extends beneath the intermediate region between the OU lava dome and NM. However, because the observation was unidirectional, it is difficult to judge whether the high-density region is located along the A–B line and what the actual size of this region is. To clarify these issues, another muographic observation in a different direction is necessary.
In addition, because the angular resolution of the telescope was ±3°, several directions included both open-sky regions and mountain regions. Therefore, the open sky flux that masked the signals from the mountain. To solve this problem, an angular resolution of the telescope is needed to be small enough to resolve shallow regions of Usu volcano.
Because the muographic image was created from integrated fluxes of muons that traversed the somma and basement of Usu volcano as shown in Fig. 3(top), the density effects of basaltic somma lava on the northern slope, as well as the pumice flow deposit, volcanic ashes, and terrace deposit in the basement of Usu volcano29) were integrated. Despite this situation, the high-density region is visible beyond the statistical error of 2σ. This means that high-density anomalies exist at a confidence level of more than 95%. In conclusion, this high-density region might represent magma that intruded into the basement.
6.2. Future prospects.As discussed above, the present study revealed a part of the structure of Usu volcano, as it existed in 2015. However, the present unidirectional muographic observation cannot depict the three-dimensional position of the high-density body because muography only measures horizontally integrated density. To solve this problem, the use of multidirectional muography2) is necessary. For such a measurement, the eastern foot of Usu volcano (Mu in the Fig. 3(top)) would be a good location for placement of a muography telescope to obtain a projection perpendicular to those shown in Fig. 8.
In our present study, we were unable to muographically image any region deeper than the one shown in Fig. 8. As described in the previous section, we recorded a significant amount of background events. If this background could be reduced, muography could contribute to deeper understanding of Usu volcano system. The background events consist of electromagnetic components (electrons, positrons, and gamma rays) produced by muon decay processes. After muons decay in the atmosphere, the resultant particles produce air shower events. These events generally have high energies and thus are inadvertently recorded as muon events.
Figure 9 shows the calculation results of the Geant4-based Monte Carlo simulations30) to reproduce the decay electrons’ energy spectrum after the muons have traveled 1 km and 5 km through the atmosphere. As shown in Fig. 9, the shower energy peaks at 10 MeV, which is below the energy threshold of the present detector. However, 20% of the shower events are above 100 MeV, which is above the energy threshold of the detector. Therefore, these electrons can be the source of the background. To reduce this type of background, it will be necessary for us to design the telescope in such a way that it is shielded from high-energy events. The insertion of a radiation shield with sufficient thickness is one solution to significantly reduce such events.1)

Calculation results of the Geant4-based Monte Carlo simulations30) carried out to reproduce the decay electrons’ energy spectrum for muons traveling 1 km (top) and 5 km (bottom) through the atmosphere.
Here we refer to the previous studies of the 1977–1980 eruptions of Usu volcano, particularly to the interpretation of the subsurface structure of the volcano. Already in 1985, Ogawa et al.26) carried out audio-magnetotelluric measurements across the volcano including the NM peak. In the shallow part around the 1977 craters located in the summit crater, they found a conductive zone and interpreted it as the effect of steam. Furthermore, they tentatively assumed magma intrusions to interpret the upheaval of “New Mountain” as shown in Fig. 10: The magma was cool and resistive in 1985 when the measurements were made.

Models of formation of New Mountain in the summit crater of Usu volcano showing a profile along the F–SW direction seen in Fig. 3. Ogawa et al. (1988)26) tentatively assumed an intrusion of magma along a fault, which was resistive after cooling in 1985. Yokoyama and Seino (2000)24) proposed tilt movements of the northeastern block of the volcano. Point P denotes the center of rotation of the block.
On the other hand, Yokoyama and Seino24) analyzed temporal changes of the upheaval process of “New Mountain” from 1977 to 1980 and interpreted the deformation as the final result of the tilting movement of the northeastern block of the volcano (a hatched part in Fig. 10) by about 11 degrees along an arc pivoting at point P. However, they did not discuss the forces causing the tilt.
We anticipate that more a quantitative evaluation of Usu volcano is possible via multidirectional muographic measurements with a radiation shield.
We developed a multi-layered telescope for muon tracking with reduced background noise. We confirmed that the background level was reduced by more than one order of magnitude using seven detectors for selecting linear trajectories compared to conventional telescopes with two detectors. As a result of our muographic measurements, we discovered a high-density region beneath the central area of Usu volcano. This high-density region may represent a magma intrusion that had occurred during the 1977–1982 eruption. The imaged structure inside Usu volcano is consistent with the model of a tilting movement of a block near the volcano’s summit. To image deeper regions of Usu volcano, we need to develop a new technique to shield the telescope from high-energy shower particles originating from muon decay processes in the atmosphere. Finally, to image the three-dimensional position of the detected high-density body, another muography in a different direction is necessary.
We thank Dr. I. Yokoyama for discussions about the cause of the formation of New Mountain during the 1978 Usu eruption and Dr. H. Oshima and Mr. T. Maekawa at Hokkaido University for assisting with the muographic observation. We would also like to thank two anonymous reviewers for their helpful comments, which greatly improved this manuscript.