Abstract
This study aimed to evaluate the residual radioactivity in mice induced by neutron irradiation with an accelerator-based boron neutron capture therapy (BNCT) system using a solid Li target. The radionuclides and their activities were evaluated using a high-purity germanium (HP-Ge) detector. The saturated radioactivity of the irradiated mouse was estimated to assess the radiation protection needs for using the accelerator-based BNCT system. 24Na, 38Cl, 80mBr, 82Br, 56Mn, and 42K were identified, and their saturated radioactivities were (1.4 ± 0.1) × 102, (2.2 ± 0.1) × 101, (3.4 ± 0.4) × 102, 2.8 ± 0.1, 8.0 ± 0.1, and (3.8 ± 0.1) × 101 Bq/g/mA, respectively. The 24Na activation rate at a given neutron fluence was found to be consistent with the value reported from nuclear-reactor-based BNCT experiments. The induced activity of each nuclide can be estimated by entering the saturated activity of each nuclide, sample mass, irradiation time, and proton current into the derived activation equation in our accelerator-based BNCT system.
Introduction
The clinical effectiveness of boron neutron capture therapy (BNCT) has been reported in many studies,1)–10) and its effectiveness has been also reported from in vivo and in vitro experiments.11)–17) In BNCT, 10B-labeled compounds are delivered to the tumor cells, and these cells are attacked by high linear energy transfer (LET) particles produced by the 10B(n, α)7Li reaction caused by neutron irradiation. Therefore, the relative biological effectiveness of BNCT is greater than that of conventional radiotherapy with photons. For example, BNCT is expected to kill cells that are resistant to conventional radiotherapy.13),15) Boronophenylalanine (BPA) was demonstrated to be useful as a boron carrier compound because it is preferentially uptaken by melanoma by Mishima et al.,8) and clinical studies were carried out for melanoma and other cancers using the nuclear reactors including that at Kyoto University.1)–4),10) However, BNCT has not been applied routinely in clinical practice because available BNCT facilities have been limited to the sites of research nuclear reactors, which are extremely scarce.1)–3),18),19)
As a result of recent research and development projects, it has become possible for accelerator-based BNCT systems to be installed in a hospital.20)–23) For example, the National Cancer Center Hospital (NCCH), Tokyo, Japan, is installing an accelerator-based BNCT system and is aiming to perform clinical trials of accelerator-based BNCT to evaluate its significance in clinical oncology. Hence, cell-based and in vivo experiments using small animal models such as mice should be sufficiently performed with accelerator-based BNCT systems, before patients can be treated safely and effectively. Thus, in vivo experiments using animals are required as a prerequisite for the clinical application of BNCT. After BNCT treatment in a nuclear reactor, it was reported that radioactivations were observed in the patient’s blood and organs and in in vivo experiments on small animals.12),24)–26) According to these reports, the presence of 24Na was observed in both humans and small animals. An accelerator-based BNCT system focuses on increasing the epithermal neutron flux, which can penetrate inside the body and is desirable for BNCT of internal human cancers.23),27),28) Compared with thermal neutrons, which are the dominant component of the neutron flux from nuclear reactors, the neutron capture cross-section of epithermal neutrons is generally smaller.29) However, there are no reports on induced radionuclides in small animals including mice after neutron beam irradiation using an accelerator-based BNCT system. Thus, it was necessary that the induced radionuclides after neutron irradiation using the accelerator-based BNCT system were evaluated in order to perform in vivo experiments safely. This study aimed to identify induced radionuclides and quantify them in mice after neutron irradiation using an accelerator-based BNCT system with a solid Li target.
Materials and methods
Neutron irradiation.
Neutron irradiation was performed in an accelerator-based BNCT system (Cancer Intelligence Care Systems, Inc.) at the NCCH. The maximum proton current in the system was 20.0 mA. Protons with a mean energy of 2.5 MeV were bombarded onto a solid-state Li target. Thus, the maximum energy of the generated neutrons was approximately 800 keV.30) After the generated neutrons passed beam-shaping assemblies consisting of MgF2 (Nippon Light Metal Co., Ltd.),31) the neutron energies of the maximum neutron flux were moderated to about 10 keV. Depth-neutron fluences along a central axis in an acrylic phantom made of PMMA were measured using the activation detector method with a gold wire 0.5 mm in diameter and 10.0 mm in length. A set of gold wire and gold wire covered with cadmium (0.5 mm thickness, custom-made) was used. Five mice were irradiated with neutrons. The irradiation times for the mice were 20, 40, 40, 60, and 80 min, respectively. The geometry of the neutron irradiation on the mouse is shown in Fig. 1.

We used male mice aged 5–8 weeks of an inbred strain C57BL/6J (Clea Japan, Inc., Tokyo, Japan). The mice were maintained in specific-pathogen-free conditions at the National Cancer Center Research Institute. The animal studies were performed in accordance with the Guideline for Animal Experiments at the National Cancer Center, which meets the ethical standards required by the law and the guidelines on experimental animals in Japan. The body weight of each mouse and experimental descriptions are summarized in Table 1. Three types of measurements were performed. The first measurement identified the kind of induced radionuclide and quantified it using four mice. The average body weight of the five mice was 21.0 ± 0.4 g. The second measurement confirmed the half-life of the induced radionuclide. The third measurement was performed to confirm the dose rate.
Table 1. Summary of the radioactivity measurement conditions
| Irradiation time [min] |
20 |
40 |
40 |
60 |
80 |
| Mouse body weight [g] |
20.3 |
21.2 |
20.7 |
20.5 |
21.9 |
| Measurement |
a |
a |
b |
a |
a, c |
a: The measurement was performed to identify and quantify the kind of induced radionuclides.
b: The measurement was performed to confirm the half-life of the induced radionuclides.
c: The measurement was performed to confirm the dose rates.
The mice were sacrificed by cervical dislocation just before neutron irradiation and were placed in a plastic bag (ASIAKIZAI Co., Ltd.) made of polypropylene and polyethylene. The average thickness of the sacrificed mice in the measurement cup was 2.0 cm. Gold wire was placed on the mouse to measure neutron fluence.
Radioactivity measurements.
Radioactivity was measured using an HP-Ge detector (ORTEC, GEM20P4-70, Oak Ridge, U.S.A.) coupled with a multi-channel analyzer (MCA7600, SEIKO EG&G, Tokyo, Japan). Gamma-studio (SEIKO EG&G, Tokyo, Japan) was used as the software for gamma-ray spectrum analysis. In order to determine the activity of the radionuclide, it was necessary to obtain the detection efficiencies of the HP-Ge detector. We calculated the detection efficiency via Monte Carlo simulations using a GEANT4 (ver. 10.1) system.32)–35) The HP-Ge detector had been modeled in the simulation using a standard gamma source with various energies (81–1836 keV, calibrated by the Japan Radioisotope Association, Tokyo, Japan) in a previous study.35) A low-energy electromagnetic physics model (Livermore model) was applied to the simulations. The most dominant parameter for the detection efficiency of the HP-Ge detector was relative position between the HP-Ge detector and the mouse. Additionally, the elemental composition of the mouse was not clear, and the measured density of the mouse (approximately 0.7 g/cc) was close to that of water. Therefore, the elemental composition of the mouse was approximated to be 100% water. A schematic diagram of the measurement geometries, as constructed in the simulation, is shown in Fig. 2.

The activities of 198Au in gold wire and gold wire covered with cadmium were determined, and the thermal neutron flux was calculated using a cadmium ratio that was calculated using the ratio of the activation of these two wires (activation of gold wire/activation of gold wire covered with the cadmium).18)
(b) Determination of induced radionuclides.
The radionuclides were determined based on the energies of the emitted gamma rays and their half-life. Two methods were used to determine the radionuclides and their activities. (1): In order to determine the half-life of the induced radionuclide, short time-measurements were repeated, and the change in peak counts of gamma rays was monitored. The measurement time in each of the iterative measurements was 314.0 s. This is listed as “Measurement b” in Table 1. (2) In order to detect the minor nuclides, a long-duration measurement of over 12.0 h was performed. When the radionuclide emitted more than one gamma ray for a given decay, their activities were calculated using the photopeak of each gamma ray for comparison. The gamma ray with the highest peak count was selected in each nuclide to reduce the counting error. This is listed as “Measurement a” in Table 1.
(c) Activity determination.
There were three steps to evaluate the radioactivity. In the first step, the activity was evaluated at the beginning of the measurement using the HP-Ge detector. The activity (Bqm) at the beginning of the measurement was expressed as Eq. [1]:
| \begin{equation}
\mathit{Bq}_{m} = \frac{\textit{Count} \times \lambda}{\varepsilon \times \gamma \times (1 - e^{-\lambda \times T_{m}})}\ [\text{Bq}],
\end{equation}
| [1] |
where
Count is the photo peak count, λ is the decay constant of each radionuclide, ε is the detection efficiency of the gamma ray from each radionuclide, γ is the gamma ray emission probability per decay, and
Tm is the measurement time.
In the second step, the radioactivity (Bq0) at the end of the irradiation was expressed using Eq. [2]:
| \begin{equation}
\mathit{Bq}_{0} = \frac{\mathit{Bq}_{m}}{e^{-\lambda \times T_{w}}}\ [\text{Bq}],
\end{equation}
| [2] |
where
Tw is the time between the end of the neutron irradiation and the beginning of the measurement with the HP-Ge detector.
In the accelerator-based BNCT system, the induced activities were evaluated in units of Bq/g/mC to correct for the variation in beam intensity in each irradiation and the body weight of the mouse. The proton current during the irradiation was evaluated using an ammeter in a linear accelerator (LINAC) system (NPCT-CF6, Bergoz Instrumentation, Saint-Genis-Pouilly, France). When the irradiation time was divided into n, the activity (Bq/g/mC) was expressed as Eq. [3]:
| \begin{align}
&\textit{Activity} \\
&\quad= \frac{\mathit{Bq}_{0} \times \lambda}{m \times \displaystyle\sum\nolimits_{i = 1}^{n}A_{i} \times (1 - e^{-\lambda \times T_{c}}) \times (e^{-\lambda \times (n - i) \times T_{c}})}\ \\
&\quad\qquad\qquad\qquad\qquad\qquad\qquad\qquad[\textit{Bq/g/mC}],
\end{align}
| [3] |
where
m is the weight of each mouse,
A is the proton current, and
Tc is the one of the irradiation times, which have been divided into
n (this study is 5 ms). The activity of the radionuclide (Bq/g/mC) was analyzed using in-house software (Python 2.7), with which
Eqs. [1]–
[3] were applied.
On the other hand, when we assumed that the proton intensity was constant during the neutron irradiation, the induced radioactivity in arbitrary irradiation time was also expressed as Eq. [3′]:
| \begin{equation}
\textit{Activity$'$} = \frac{\mathit{Bq}_{0} \times \lambda}{m \times (1 - e^{-\lambda \times T_{f}})}\ [\text{Bq/g/s}],
\end{equation}
| [3′] |
where
Tf is the neutron irradiation time.
When the radioactivity was calculated using Eqs. [1]–[3] and [3′], the saturated radioactivity was calculated as follows:
| \begin{align}
\textit{Saturated activity} &= \textit{Activity} \times \int_{0}^{\infty}e^{- \lambda t}\mathrm{dt} \\
&= \frac{\textit{Activity}}{\lambda}\ [\text{Bq/g/mA}],
\end{align}
| [4] |
| \begin{align}
\textit{Saturated activity$'$} &= \textit{Activity$'$} \times \int_{0}^{\infty}e^{-\lambda t}\mathrm{dt} \\
&= \frac{\textit{Activity$'$}}{\lambda}\ [\text{Bq/g}],
\end{align}
| [4′] |
where
Activity was calculated from
Eqs. [1]–
[3], and
Activity′ is calculated from Eq. [3′].
Through the application of Eq. [4], the saturated activity could be easily evaluated using proton current when the accelerator-based BNCT system at NCCH was used. The evaluated radioactivity of 24Na was compared with the results of the repeated measurement, which was calculated using Eq. [4′].
Dose measurement.
The dose rate in a mouse that was irradiated for 80 min was measured using a NaI(Tl) scintillation survey meter (TCS-172B, Hitachi-Aloka Medical), which was calibrated using a gamma-ray with an energy of 662 keV (137Cs) to evaluate the radiation safety of the irradiated mice. The dose rate measurement at a distance of 20 cm from the surface of the measurement cup was performed for 11.9 min after the end of neutron irradiation.
Results
Radioactivity measurements.
(a) Neutron profile and fluence measurement.
Figure 3 shows the thermal neutron fluence and the cadmium ratio along the depth direction in the PMMA phantom. From this result, the maximum thermal neutron fluence might be observed at 2.0–2.5 cm from the surface of the mouse body. However, the densities of the PMMA phantom and water were 1.18 and 1.00 g/cc, respectively. The chemical formula of PMMA was (C5H8O2)n, and that of water is H2O. The most affected element for moderation is hydrogen. The weight fractions (%) of hydrogen in PMMA and water were 8.05 and 11.2, respectively. Therefore, the thermal neutron flux peak of the PMMA phantom would be a bit deeper than that of the water phantom. The cadmium ratio increased with depth.
(b) Determination of induced radionuclides.
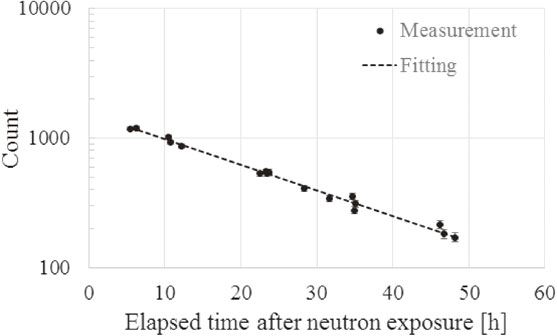
(1) Protti and colleagues reported that the highest activity was 24Na in terms of long-life nuclides for the thermal neutron irradiation of mice in the research reactor of a thermal column.12) The repeated measurements in mice focused on 24Na. Figure 4 shows the relationship between the elapsed time after 40-min neutron exposure and the measurement counts in each of the repeated measurements. According to the fitting result in Fig. 4, the half-life of the radionuclide, from which a gamma ray of 1369 keV was emitted, was 15.2 h. The literature value of the half-life and emitted gamma-ray energy of 24Na is 15.0 h and 1369 keV, respectively.24),36) Thus, it was recognized that this measured gamma ray was emitted from 24Na, and its activity was (4.3 ± 0.1) × 101 Bq/g at the end of irradiation. Because a 2754 keV gamma ray was also emitted from 24Na, the activity of 24Na was also calculated using the photo peak of the 2754 keV gamma ray, which was (4.3 ± 0.2) × 101 Bq/g at the end of irradiation. The two measured activities of 24Na agreed well with each other. The average current of a proton during irradiation was 10.0 mA. Then, the thermal neutron fluence to the mouse was (2.4 ± 0.2) × 1011 to (1.2 ± 0.1) × 1012 (average fluence: 8.1 × 1011 n/cm2).
(2) The induced radionuclides in four mice were 24Na, 38Cl, 82Br, 56Mn, and 42K. 80mBr was not detected only in the mouse irradiated for 40 min. Observed nuclides and their neutron capture reaction cross-sections and nuclear properties are listed in Table 2.37) The measured activities in units of Bq/g/mC are summarized in Table 3. The measured activity of each radionuclide for the four mice was similar. The saturated activities are summarized in Table 4. Because the maximum current of a proton was 20.0 mA in the accelerator-based BNCT system at NCCH, the maximum saturated activities of 24Na, 38Cl, 80mBr, 82Br, 56Mn, and 42K within the mouse were (5.7 ± 0.1) × 104, (9.2 ± 0.2) × 103, (1.4 ± 0.1) × 105, (1.2 ± 0.1) × 103, (3.4 ± 0.1) × 103, and (1.6 ± 0.1) × 104 Bq, respectively.
Table 2. Observed radionuclides and their properties
| Target isotope |
Abundance [%] |
Cross-section [b] |
Resonance [b] |
Product |
Half-life |
Gamma ray energy [keV] |
| 23Na |
100 |
0.530 ± 0.005 |
0.311 ± 0.10 |
24Na |
14.059 h |
1369, 2754 |
| 37Cl |
24.22 |
0.433 ± 0.006 |
0.295 ± 0.004 |
38Cl |
37.24 m |
1643, 2167 |
| 41K |
6.73 |
1.46 ± 0.03 |
1.4 ± 0.04 |
42K |
12.36 h |
313, 1525 |
| 55Mn |
100 |
13.3 ± 0.1 |
14.0 ± 0.3 |
56Mn |
2.575 h |
847, 1810 |
| 79Br |
50.686 |
11.0 ± 0.7 |
127 ± 14 |
80mBr |
4.4205 h |
37, 49 |
| 81Br |
49.314 |
2.7 ± 0.2 |
50 ± 5 |
82Br |
35.30 h |
554, 619, 777 |
Table 3. Induced radioactivity by neutron beam irradiation of mice. Unit is Bq/g/mC
| Irradiation time [min] |
80mBr |
82Br |
24Na |
38Cl |
56Mn |
42K |
| 20 |
1.8 ± 0.1 × 10−2 |
1.8 ± 0.4 × 10−5 |
1.8 ± 0.1 × 10−3 |
6.8 ± 0.2 × 10−3 |
6.8 ± 0.2 × 10−3 |
5.5 ± 0.2 × 10−4 |
| 40 |
Not detected |
1.7 ± 0.1 × 10−5 |
1.9 ± 0.1 × 10−3 |
7.1 ± 0.2 × 10−3 |
6.8 ± 0.2 × 10−3 |
6.2 ± 0.2 × 10−4 |
| 60 |
1.4 ± 0.1 × 10−2 |
1.6 ± 0.2 × 10−5 |
1.6 ± 0.1 × 10−3 |
7.0 ± 0.4 × 10−3 |
6.8 ± 0.2 × 10−3 |
5.7 ± 0.1 × 10−4 |
| 80 |
1.2 ± 0.1 × 10−2 |
1.4 ± 0.7 × 10−5 |
1.7 ± 0.1 × 10−3 |
6.4 ± 0.2 × 10−3 |
6.8 ± 0.2 × 10−3 |
5.9 ± 0.1 × 10−4 |
Table 4. Saturated radioactivity of a mouse in the accelerator-based BNCT system at the National Cancer Center Hospital, Tokyo, Japan
| Radionuclide |
80mBr |
82Br |
24Na |
38Cl |
56Mn |
42K |
| Saturated radioactivity [Bq/g/mA] |
3.4 ± 0.4 × 102 |
2.8 ± 0.1 |
1.4 ± 0.1 × 102 |
2.2 ± 0.1 × 101 |
8.0 ± 0.1 |
3.8 ± 0.1 × 101 |
| Saturated radioactivity [Bq]*1 |
1.4 ± 0.2 × 105 |
1.2 ± 0.1 × 103 |
5.7 ± 0.2 × 104 |
9.2 ± 0.2 × 103 |
3.4 ± 0.2 × 103 |
1.6 ± 0.1 × 104 |
| Quantum lower limit [Bq]*2 |
1 × 107 |
1 × 106 |
1 × 105 |
1 × 105 |
1 × 105 |
1 × 106 |
| Saturated activity/quantum lower limit |
1.4 × 10−2 |
1.2 × 10−3 |
5.9 × 10−1 |
9.2 × 10−2 |
1.4 × 10−2 |
1.6 × 10−2 |
*1: Calculated using the mean body weight of the mice and the maximum current.
*2: BSS value.
In order to compare Eqs. [4] and [4′], the saturated radioactivity was compared. According to Eq. [4] and the measurement result, the saturated activity in 24Na with a 10.0 mA proton current was calculated as (1.4 ± 0.1) × 103 Bq/g. According to Eq. [4′], the saturated activity of 24Na from repeated measurements (“measurement (1)”), for which the average proton current was 10.0 mA, was (1.4 ± 0.1) × 103 Bq/g. These two saturated radioactivities agreed with each other.
Dose measurement.
The dose rate at a distance of 20.0 cm from the surface of the measurement bag to the survey meter was 4 × 10−2 µSv/h. The dose rate was compared with an obtained dose rate, which was calculated using the measured radioactivities with the HP-Ge detector and the coefficients of a 1 cm dose equivalent rate in each of the induced radionuclides.38) The coefficient of 1 cm dose equivalent rate in each of the measured radionuclides and the obtained dose rate (which was calculated using the measured activities) are summarized in Table 5. The calculated dose rate at a distance of 20.0 cm from the surface of the measurement bag to the survey meter was (3.5 ± 0.1) × 10−2 µSv/h. The calculated dose rate was consistent with the measured dose rate.
Table 5. Calculated dose rates from a mouse irradiated for 80 min with the neutron beam
| Radionuclide |
80mBr |
82Br |
24Na |
38Cl |
56Mn |
42K |
Total |
Conversion coefficient*1
[µSv·m2·/MBq/h] |
15.3 × 10−3 |
40.6 × 10−2 |
49.2 × 10−2 |
17.8 × 10−2 |
23.6 × 10−2 |
37.3 × 10−3 |
|
Measured radioactivity
[Bq]*2 |
9.6 ± 0.1 × 103 |
1.3 ± 0.1 × 101 |
1.5 ± 0.1 × 103 |
2.3 ± 0.1 × 103 |
4.2 ± 0.1 × 102 |
5.1 ± 0.1 × 102 |
|
| Dose rate [µSv/h]*2,3 |
3.7 ± 0.1
× 10−3 |
1.3 ± 0.1
× 10−4 |
1.8 ± 0.1
× 10−2 |
1.0 ± 0.1
× 10−2 |
2.5 ± 0.1
× 10−3 |
4.7 ± 0.1
× 10−4 |
3.5 ± 0.1
× 10−2 |
*1: Coefficient of 1 cm dose equivalent rate.
*2: Each value is 11.9 min after the end of neutron beam irradiation.
*3: Dose rate at a distance of 20 cm from the surface of the measurement bag.
Discussion
Saturated activities in each induced radionuclide were measured in units of Bq/g/mA in this article. Thus, an estimation of the induced radioactivities and doses from these radionuclides could be calculated with any proton current and arbitrary irradiation time in advance. The activity (Bq) was calculated as follows:
| \begin{align}
\mathit{Bq} &= \textit{Saturated radioactivity}\ [\textit{Bq/g/mA}] \\
&\quad\times m \times A \times (1 - e^{-\lambda t})
\end{align}
| [5] |
The saturated radioactivity is calculated from
Eq. [4], where
m is the sample mass,
A is the expected proton current, λ is the decay constant in each radionuclide, and
t is the irradiation time.
According to the results of this study, if a mouse whose body weight was 21.0 g was irradiated for 60 min with the maximum proton current at NCCH, the induced radioactivities of 24Na, 38Cl, 42K, 56Mn, 80mBr, and 82Br were 2.6 × 103, 6.2 × 103, 8.6 × 102, 7.8 × 102, 2.1 × 104, and 2.3 × 101 Bq, respectively (calculated using Eq. [5]). Their dose rates at a distance of 20.0 cm from the mouse were 3.2 × 10−2, 2.8 × 10−2, 8.0 × 10−4, 4.7 × 10−3, 7.9 × 10−3, and 3.2 × 10−4 µSv/h, respectively. Figure 5 shows the relationship between the elapsed time after neutron irradiation and (a) induced radioactivity, (b) dose rate at a distance of 20.0 cm from the mouse, and (c) ratio of the radioactivity and the BSS value.39) The total dose at 1, 2, 3, 12, 24, 72, and 168 h (1 week) after neutron irradiation was reduced to 87, 77, 69, 29, 12, 1.2, and 0.0%, respectively. The main component of the dose rate was 24Na, although the highest activity of an individual radionuclide was 80mBr. Additionally, the most significant contributor to the ratio of the induced radioactivity and the activity of 38Cl was a large contribution in the activity ratio to the BSS value at the end of irradiation. The activity of 24Na became the highest contributing nuclide after 51.6 min from neutron irradiation. Therefore, in terms of radiation protection, 24Na might be most the important radionuclide induced by the accelerator-based BNCT system. The dose rate from 24Na may not be high enough to induce toxicity associated with 24Na including secondary carcinogenesis immediately. However, 24Na exists in the blood after BNCT, and Na circulates inside the body and is eliminated over a certain period. Therefore, the toxicity associated with 24Na could be dependent not only on physical half-life of 24Na, but also on the biological half-life of 24Na. The biological half-life of 24Na after BNCT is not clear. Therefore, we think that further study is needed to evaluate the long-term biological and clinical effects of 24Na on patients after BNCT.

Protti and colleagues reported no presence of 82Br in neutron-irradiated mice. However, we could detect its presence in four mice.12) 82Br is produced by the neutron capture reaction of 81Br. However, Kranda and colleagues reported that 82Br was detected from mice after neutron exposure in the thermal column of the reactor.40) They performed irradiation for 20 h at a thermal neutron flux of 5 × 1013 n/cm2/s to detect 82Br; however, Protti and colleagues performed irradiation for 15 min at a thermal neutron flux of 1.2 × 1010 n/cm2/s.12),40) In the accelerator-based BNCT system, the energies of maximum neutron fluence were ∼10 keV, and the capture cross-section between neutron and 81Br has resonances between 20 eV and 20 keV. The integral resonance of the capture cross-section and the Maxwellian average of the capture cross-section at 300 K were 46.62 and 2.358 barn, respectively.29) Therefore, differences in the neutron spectrum between this study and the report by Protti et al. might have caused the different results.
Bromine has two stable isotopes, 79Br and 81Br. 80mBr, which was induced by a reaction between a neutron and 79Br, emits gamma rays at 37.1 and 48.9 keV. As a result, 80mBr might be detected as well as 82Br. We could detect its presence in three mice, although it could not be detected in one mouse. The emitted gamma rays from 80mBr have low energy (37.1 keV and etc.). Many background events, such as Compton scattering, around this energy region could be detected in the HP-Ge detector. Comparing the mouse that received neutron irradiation for 40 min with the one that received neutron irradiation for 20 min, the measurement time in the HP-Ge detector was shorter in the mouse with neutron irradiation for 40 min. Therefore, in the mouse with neutron exposure for 40 min, the counts from 80mBr in the HP-Ge detector might be obscured. Additional studies are needed because bromine has 79Br as well as 81Br, and 82Br was detected in this study. The half-life of 80mBr was 4.4205 h. The capture cross-section between the neutron and 79Br has resonances were between 10 eV and 10 keV. The integral resonance of the capture cross-section and the Maxwellian average of the capture cross-section at 300 K were 129.1 and 11.01 barn, respectively.29) Thus, 80mBr might be hard to detect in the thermal column of the reactor.
The saturated radioactivity of 24Na was evaluated using two different methods, which considered whether there was a variation in the beam intensity or not. The saturated activities obtained using Eqs. [4] and [4′] matched well. Therefore, the induced activity might not have to consider the variation in proton current in the accelerator-based BNCT system if stable proton irradiation can be expected.
This study is the first report that has identified and quantified radionuclides after neutron irradiation with an accelerator-based BNCT system, although the report about on this topic in a research reactor has been published.12) Moreover, evaluation of induced radiation in organs, urine, blood, etc., might provide further important information on radiation protection just after BNCT in hospital. Therefore, further ongoing studies are also important. Protti and colleagues reported that the mean radioactivity of 24Na after 10 min of neutron irradiation was 253.8 Bq/g when the thermal neutron flux was 1.2 × 1010 n/cm2/s.12) Thus, the saturated radioactivity was 310.2 × 102 Bq/g. In this study, the saturated radioactivity of 24Na was 1.4 × 103 Bq/g when the thermal neutron flux was 3.4 × 108 n/cm2/s. When the ratio of the saturated radioactivity divided by the thermal neutron flux was compared in each study, the ratio in this study was 1.6 times higher than that in the report by Protti and colleagues. The discrepancy in the ratios might be associated with the size of the irradiation field. The mouse in the Protti study was shielded by a neutron attenuator, which included 95% enriched 6Li carbonate powder, but no attenuator was used in the present study. Therefore, the large field size in this study might be part of the reason that the ratio in this study was higher than that in the report by Protti and colleagues. Additionally, the discrepancy might also be associated with differences in sample thickness and the neutron distribution within the sample. The result in this study corresponded with the report by Protti and colleagues when these differences were taken into consideration. A radionuclide of Br was not detected in the thermal column of the research reactor in the previous study, although it was detected in this accelerator-based BNCT system.12) However, according to the data shown in Table 5, the highest contribution to the dose rate after neutron exposure in the accelerator-based BNCT system was 24Na. This result agreed with the thermal column of the research reactor. Therefore, in terms of radiation dose to experimenters from the induced radionuclide within the mouse body after neutron exposure, the accelerator-based BNCT system and the thermal column of the research reactor might be similar, although the induced radionuclides were not the same.
The physical dose from boron is calculated from the boron concentration and thermal neutron fluence in BNCT.1),14) Saris et al. reported that the fluence of irradiated thermal neutrons was 1.2 × 1012 n/cm2 to evaluate the survival rate of mice with malignant gliomas.11) Therefore, when the reported thermal neutron fluence is applied to the accelerator-based BNCT system at NCCH, the activity of 24Na was about 1.4 × 103 Bq (it was assumed that the neutron flux was 3.4 × 108 n/cm2/s. Therefore, the irradiation time was 1 h).
Conclusions
The induced radioactivity and the dose from that induced radioactivity can be evaluated using the proton current in the accelerator-based BNCT system, although the neutron production rate depends on each BNCT system. The induced radioactivity can be represented using Bq/g/mC, and the saturated radioactivity can be represented using Bq/g/mA. Therefore, the induced radioactivity can be predicted by the mass of the samples, required neutron fluence or required irradiation time, and by the proton current in the accelerator-based BNCT system after determining the relationship between the induced radioactivity and the integrated charge of the protons. The induced radionuclides within the mice were 24Na, 38Cl, 42K, 56Mn, 80mBr, and 82Br in these experiments. Their saturated radioactivities, which were generated by the accelerator-based BNCT system at NCCH, were (1.4 ± 0.1) × 102, (2.2 ± 0.1) × 101, (3.8 ± 0.1) × 101, 8.0 ± 0.1, (3.4 ± 0.4) × 102, and 2.8 ± 0.1 Bq/g/mA, respectively. In addition, if a required amount of neutrons is irradiated onto mice in order to evaluate survival rates or anti-tumor effects, the radioactivity of 24Na should be less than 104 Bq.
Acknowledgements
This work was supported by a JSPS Grant-in-Aid for Young Scientists (B) Grant Number 26860410. This work was partially supported by a JSPS Grant-in-Aid for Scientific Research (B) Grant Number 15H04912, by a JSPS Grant-in-Aid for Scientific Research (C) Grant Number 16K10410, by the Medical Research and Development Programs Focused on Technology Transfer: Development of Advanced Measurement and Analysis Systems (SENTAN) from the Japan Agency for Medical Research and Development, AMED (17hm0102046s0505), and by the National Cancer Center Research and Development Fund (29-A-8), (26-A-18), and (23-A-46). We thank to Dr. Hitoshi Nakagama, Dr. Yasuaki Arai, Dr. Tomomitsu Hotta, and Dr. Takamasa Kayama and other staffs in National Cancer Center for supporting our project for development of accelerator-based BNCT system.
References
- 1) Kato, I., Ono, K., Sakurai, Y., Ohmae, M., Maruhashi, A., Imahori, Y., Kirihata, M., Nakazawa, M. and Yura, Y. (2004) Effectiveness of BNCT for recurrent head and neck malignancies. Appl. Radiat. Isot. 61, 1069–1073.
- 2) Nakai, K., Yamamoto, T., Aiyama, H., Takada, T., Yoshida, F., Kageji, T., Kumada, H., Isobe, T., Endo, K., Matsuda, K., Tsurubuchi, T., Shibata, Y., Takano, S., Mizumoto, M., Tsuboi, K. and Matsumura, A. (2011) Boron neutron capture therapy combined with fractionated photon irradiation for glioblastoma: a recursive partitioning analysis of BNCT patients. Appl. Radiat. Isot. 69, 1790–1792.
- 3) Aihara, T., Morita, N., Kamitani, N., Kumada, H., Ono, K., Hiratsuka, J. and Harada, T. (2014) BNCT for advanced or recurrent head and neck cancer. Appl. Radiat. Isot. 88, 12–15.
- 4) Futamura, G., Kawabata, S., Siba, H., Kuroiwa, T., Suzuki, M., Kondo, N., Ono, K., Sakurai, Y., Tanaka, M., Todo, T. and Miyatake, S. (2014) A case of radiation-induced osteosarcoma treated effectively by boron neutron capture therapy. Radiat. Onocol. 9, 237.
- 5) Sweet, W.H. and Javid, M. (1951) The possible use of slow neutrons plus boron10 in therapy of intracranial tumors. Trans. Am. Neurol. Assoc. 56, 60–63.
- 6) Farr, L.E., Sweet, W.H., Robertson, J.S., Foster, C.G., Locksley, H.B., Sutherland, D.L., Mendelsohn, M.L. and Stickley, E.E. (1954) Neutron capture therapy with boron in the treatment of glioblastoma multiforme. Am. J. Roentgenol. Radium Ther. Nucl. Med. 71, 279–293.
- 7) Hatanaka, H. and Sano, K. (1973) A revised boron-boron neutron capture therapy for malignant brain tumors. I. Experience on terminally ill patients after Co-60 radiotherapy. Z. Neurol. 204, 309–332.
- 8) Mishima, Y., Honda, C., Ichihashi, M., Obara, H., Hiratsuka, J., Fukuda, H., Karashima, H., Kobayashi, T., Kanda, K. and Yoshino, K. (1989) Treatment of malignant melanoma by single thermal neutron capture therapy with melanoma-seeking 10B-compound. Lancet 2, 388–389.
- 9) Finkel, G.C., Poletti, C.E., Fairchild, R.G., Slatkin, D.N. and Sweet, W.H. (1989) Distribution of 10B after infusion of Na210B12H11SH into a patient with malignant astrycytoma: implications for boron neutron capture therapy. Neurosurgery 24, 6–11.
- 10) Wang, L.W., Chen, Y.W., Ho, C.Y., Hsueh, Y.W., Chou, F.I., Liu, Y.H., Liu, H.M., Peir, J.J., Jiang, S.H., Chang, C.W., Liu, C.S., Lin, K.H., Wang, S.J., Chu, P.Y., Lo, W.L., Kao, S.Y. and Yen, S.H. (2016) Fractionated boron neutron capture therapy in locally reccurent head and neck cancer: a prospective phase I/II trial. Int. J. Radiat. Oncol. Biol. Phys. 95, 396–403.
- 11) Saris, S.C., Solares, G.R., Wazer, D.E., Cano, G., Kerley, S.E., Joyce, M.A., Adelman, L.S., Harling, O.K., Madoc-Jones, H. and Zamenhof, R.G. (1992) Boron neutron capture therapy for murine malignant gliomas. Cancer Res. 52, 4672–4677.
- 12) Protti, N., Manera, S., Preta, M., Alloni, D., Ballarini, F., Tigliole, A.B., Bortolussi, S., Bruschi, P., Cagnazzo, M., Garioni, M., Postuma, I., Reversi, L., Salvini, A. and Altieri, S. (2014) Gamma residual radioactivity measurements on rats and mice irradiated in the thermal column of a TRIGA Mark II reactor for BNCT. Health Phys. 107, 534–541.
- 13) Masunaga, S., Sakurai, Y., Tanaka, H., Tano, K., Suzuki, M., Kondo, N., Narabayashi, M., Nakagawa, Y., Watanabe, T., Maruhashi, A. and Ono, K. (2014) The dependency of compound biological effectiveness factors on the type and the concentration of administrated neutron capture agents in boron neutron capture therapy. Springerplus 3, 128.
- 14) Watanabe, T., Tanaka, H., Fukutani, S., Suzuki, M., Hiraoka, M. and Ono, K. (2016) L-phenylalanine preloading reduces the 10B(n, α)7Li dose to the normal brain by inhibiting the uptake of boronophenylalanine in boron neutron capture therapy for brain tumors. Cancer Lett. 370, 27–32.
- 15) Hirota, Y., Masunaga, S., Kondo, N., Kawabata, S., Hirakawa, H., Yajima, H., Fujimori, A., Ono, K., Kuroiwa, T. and Miyatake, S. (2014) High linear-energy-transfer radiation can overcome radioresistance of glioma stem-like cells to low linear-energy-transfer radiation. J. Radiat. Res. 55, 75–83.
- 16) Sun, T., Zhang, Z., Li, B., Cheng, G., Xie, X., Wei, Y., Wu, J., Zhou, Y. and Du, Z. (2013) Boron neutron capture therapy induces cell cycle arrest and cell apotosis of glioma stem/progenitor cells in vitro. Radiat. Oncol. 8, 195.
- 17) Suzuki, M., Masunaga, S., Kinashi, Y., Takagaki, M., Sakurai, Y., Kobayashi, T. and Ono, K. (2000) The effects of boron neutron capture therapy on liver tumors and normal hepatocytes in mice. Jpn. J. Cancer Res. 91, 1058–1064.
- 18) Sakurai, Y. and Kobayashi, T. (2002) The medical-irradiation characteristics for neutron capture therapy at the Heavy Water Neutron Irradiation Facility of Kyoto University Research Reactor. Med. Phys. 29, 2328–2337.
- 19) Sakurai, Y. and Kobayashi, T. (2004) Spectrum evaluation at the filter-modified neutron irradiation field for neutron capture therapy in Kyoto University Research Reactor. Nucl. Instrum. Methods Phys. Res. A 453, 569–596.
- 20) Kamada, S., Takada, M., Suda, M., Hamano, T., Imaseki, H., Hoshi, M., Fujii, R., Nakamura, M., Sato, H., Higashimata, A. and Arai, S. (2014) Development of target system for intense neutron source of p-Li reaction. Appl. Radiat. Isot. 88, 195–197.
- 21) Kumada, H., Matsumura, A., Sakurai, H., Sakae, T., Yoshioka, M., Kobayashi, H., Matsumoto, H., Kiyanagi, Y., Shibata, T. and Nakashima, H. (2014) Project for the development of the linac based NCT facility in University of Tsukuba. Appl. Radiat. Isot. 88, 211–215.
- 22) Tanaka, H., Sakurai, Y., Suzuki, M., Masunaga, S., Mitsumoto, T., Fujita, K., Kashino, G., Kinashi, Y., Liu, Y., Takeda, M., Ono, K. and Maruhashi, A. (2011) Experimental verification of beam characteristics for cyclotron-based epithermal neutron source (C-BENS). Appl. Radiat. Isot. 89, 1642–1645.
- 23) Randers-Pehrson, G. and Brenner, D.J. (1998) A practical target system for accelerator-based BNCT which may effectively double dose rate. Med. Phys. 25, 894–896.
- 24) Fujiwara, K., Kinashi, Y., Takahashi, T., Yashima, H., Kurihara, K., Sakurai, Y., Tanaka, H., Ono, K. and Takahashi, S. (2013) Induced radioactivity in the blood of cancer patients following Boron Neutron Capture Therapy. J. Radiat. Res. 54, 769–774.
- 25) Sakurai, Y., Tanaka, H., Suzuki, Y., Kinashi, S., Masunaga, S., Maruhashi, A. and Ono, K. (2009) A feasibility study of the post-irradiation dose estimation with SPECT technique for BNCT. Appl. Radiat. Isot. 67, S218–S221.
- 26) Yasumura, S., Jones, K., Spanne, P., Schidlovsky, G., Wielopolski, L., Ren, X., Glaros, D. and Xatzikonstantinou, Y. (1993) In vivo animal models of body composition in aging. J. Nutr. 123, 459–464.
- 27) Allen, D.A. and Beynon, T.D. (1995) A design study for an accelerator-based epithermal neutron beam for BNCT. Phys. Med. Biol. 40, 807–821.
- 28) Minsky, D.M., Kreiner, A.J. and Valda, A.A. (2011) AB-BNCT beam shaping assembly based on 7Li(p, n)7Be reaction optimization. Appl. Radiat. Isot. 69, 1668–1671.
- 29) Shibata, K., Iwamoto, O., Nakagawa, T., Iwamoto, N., Ichihara, A., Kunieda, S., Chiba, S., Furutaka, K., Otsuka, N., Ohsawa, T., Murata, T., Matsunobu, H., Zukeran, A., Kamada, S. and Katakura, J. (2011) JENDL-4.0: A new library for nuclear science and engineering. J. Nucl. Sci. Technol. 48, 1–30.
- 30) Lee, C.L., Zhou, X.L., Kudchadker, R.J., Harmon, F. and Harker, Y.D. (2000) A Monte Carlo dosimetry-based evaluation of the 7Li(p, n)7Be reaction near threshold for accelerator boron neutron capture therapy. Med. Phys. 27, 192–202.
- 31) Inoue, R., Hiraga, F. and Kiyanagi, Y. (2014) Optimum design of a moderator system based on dose calculation for an accelerator driven Boron Neutron Capture Therapy. Appl. Radiat. Isot. 88, 225–228.
- 32) Agostinelli, S., Allison, J., Amako, K., Apostolakis, J., Araujo, H., Arce, P., Asai, M., Axen, D., Banerjee, S., Barrand, G., Behner, F., Bellagamba, L., Boudreau, J., Broglia, L., Brunengo, A., Burkhardt, H., Chauvie, S., Chuma, J., Chytracek, R., Cooperman, G., Cosmo, G., Degtyarenko, P., Dell’Acqua, A., Depaola, G., Dietrich, D., Enami, R., Feliciello, A., Ferguson, C., Fesefeldt, H., Folger, G., Foppiano, F., Forti, A., Garelli, S., Giani, S., Giannitrapani, R., Gibin, D., Gómez Cadenas, J.J., González, I., Gracia Abril, G., Greeniaus, G., Greiner, W., Grichine, V., Grossheim, A., Guatelli, S., Gumplinger, P., Hamatsu, R., Hashimoto, K., Hasui, H., Heikkinen, A., Howard, A., Ivanchenko, V., Johnson, A., Jones, F.W., Kallenbach, J., Kanaya, N., Kawabata, M., Kawabata, Y., Kawaguti, M., Kelner, S., Kent, P., Kimura, A., Kodama, T., Kokoulin, R., Kossov, M., Kurashige, H., Lamanna, E., Lampén, T., Lara, V., Lefebure, V., Lei, F., Liendl, M., Lockman, W., Longo, F., Magni, S., Maire, M., Medernach, E., Minamimoto, K., Mora de Freitas, P., Morita, Y., Murakami, K., Nagamatu, M., Nartallo, R., Nieminen, P., Nishimura, T., Ohtsubo, K., Okamura, M., O’Neale, S., Oohata, Y., Paech, K., Perl, J., Pfeiffer, A., Pia, M.G., Ranjard, F., Rybin, A., Sadilov, S., Di Salvo, E., Santin, G., Sasaki, T., Savvas, N., Sawada, Y., Scherer, S., Sei, S., Sirotenko, V., Smith, D., Starkov, N., Stoecker, H., Sulkimo, J., Takahata, M., Tanaka, S., Tcherniaev, E., Safai Tehrani, E., Tropeano, M., Truscott, P., Uno, H., Urban, L., Urban, P., Verderi, M., Walkden, A., Wander, W., Weber, H., Wellisch, J.P., Wenaus, T., Williams, D.C., Wright, D., Yamada, T., Yoshida, H. and Zschiesche, D. (2003) GEANT4-a simulation toolkit. Nucl. Instrum. Methods Phys. Res. A 506, 250–303.
- 33) Hurtado, S., García-León, M. and García-Tenorio, R. (2004) Monte Carlo simulation of the response of a germanium detector for low-level spectrometry using GEANT4. Appl. Radiat. Isot. 61, 139–143.
- 34) Ewa, I.O., Bodizs, D., Czifrus, S. and Molnar, Z. (2001) Monte Carlo determination of full energy peak efficiency for a HPGe detector. Appl. Radiat. Isot. 55, 103–108.
- 35) Nakamura, S., Wakita, A., Ito, M., Okamoto, H., Nishioka, S., Iijima, K., Kobayashi, K., Nishio, T., Igaki, H. and Itami, J. (2017) Modeling the detection efficiency of an HP-Ge detector for use in boron neutron capture therapy. Appl. Radiat. Isot. 125, 80–85.
- 36) Muramatsu, Y., Noda, Y., Yonehara, H., Ishiqure, N., Yoshida, S., Yukawa, M., Tagami, K., Ban-Nai, T., Uchida, S., Hirama, T., Akashi, M. and Nakamura, Y. (2001) Determination of radionuclides produced by neutrons in heavily exposed workers of the JCO criticality accident in Tokai-mura for estimating an individual’s neutron fluence. J. Radiat. Res. 42, S117–S128.
- 37) Mughabghab, S.F. (2003) Thermal neutron capture cross sections resonance integrals and g-factors. Int. At. Energy Agency (International Nuclear Data Committee (NDS)-440) 34, 1–32.
- 38) ICRP (1996) Conversion Coefficients for use in Radiological Protection against External Radiation. ICRP Publication 74. Ann. ICRP 26 (3–4).
- 39) International Atomic Energy Agency (2014) Radiation Protection and Safety of Radiation Sources: International Base Safety Standards. IAEA.
- 40) Kranda, K., KuĆera, J. and Bäurle, J. (2006) Trace elements monitored with neutron activation analysis during neurodegeneration in brains of mutant mice. J. Radioanal. Nucl. Chem. 269, 555–559.





