Towards higher-T_c superconductors

Abstract

New superconductors discovered in the Akimitsu laboratory are reviewed here. These materials can be categorized into two groups:

1) Cu-oxide superconductors.

1-1 Cu-oxide system having CuO₂ planes.

1-2 Ladder lattice superconductor.

2) Exploration of new metal-based superconductors.

2-1 MgB₂ and its application.

2-2 Y₂C₃.

2-3 Carrier-doped wide-gap semiconductors.

2-4 New superconductor with a cage-type structure: R₅T₆Sn₁₈ (R = Sc, Y, Lu; T = Rh, Ir).

Finally, all of the new superconductors discovered in our laboratory are summarized. The outlook for the high-T_c superconductors and our present work are also described.

Communicated by Sumio IIJIMA, M.J.A.

1. Superconductivity and its applications

Superconductivity was discovered in mercury (Hg) by Kamerlingh Onnes of Leiden University in 1911 (T_c = 4.2 K). That was three years after the great achievement of helium (He) liquefaction.

The three major characteristics of superconductivity are first pointed out, and then each of them is explained briefly. They are:

1. (1)    Zero electrical resistance (a current will persist indefinitely) (E = 0),
2. (2)    The Meissner effect (B = 0),
3. (3)    The Josephson effect.

(1) Zero electrical resistance.

It is well known that many free electrons exist in metals, and that an electric current is a flow of those electrons. In general, electrons are scattered by the oscillations of atoms (phonons), or by impurities in metals. This can be described by Ohm’s law. Since all metal contains impurities, and atoms oscillate, electrons are always being scattered. Thus, it seems to be impossible to ever experience zero electrical resistance. However, zero electrical resistance actually exists under superconductivity. It can thus be concluded that if an electric current is initiated in a circular superconductor, it would continue to flow indefinitely. This is a totally mysterious phenomenon and it is a puzzle that motivates many physicists to understand. Its final solution was offered by three physicists, (Bardeen, Cooper and Shrieffer), which is now known as the BCS theory.

There may be many applications of the phenomenon of zero electrical resistance, such as superconducting magnets, superconducting power transmission, and electricity storage. For example, there is a grand plan to set up global networks of electric power plants using wind-power generation, or solar batteries in deserts or waste land, and to send electricity generated in these plants to remote urban areas through superconducting cables.

Another example is linear-motor cars that run by ‘floating their bodies’, using the repulsive power of magnetic fields generated by superconducting magnets.

(2) The Meissner effect.

In addition to zero electrical resistance, superconductivity has another unique characteristic. Superconductors have no internal magnetic flux or no lines of magnetic force within their substance (B = 0). This phenomenon is called the Meissner effect, named after its discoverer, which may have many applications, such as magnetic shielding, magnetic levitation, magnetic bearings, and so on.

(3) The Josephson effect.

The third major characteristic of superconductivity is the Josephson effect. This is a phenomenon where superconducting electrons flow through between two superconductors separated by a thin barrier, without any voltage being applied. It is a quite unique phenomenon, causing superconducting electrons to flow without a voltage to drive them (DC Josephson effect) or AC current to flow when a DC voltage is applied (AC Josephson effect). In 1962, Josephson, at that time a graduate student at Cambridge University, predicted this phenomenon, specific to superconductivity, that would be a macroscopic effect of quantum mechanics. The most significant application is in a superconducting quantum interference device (SQUID). This may be used in magnetic-field sensors or super high-speed computing machines in the future.

Thus, superconductivity is not only wide and deep as fundamental aspect of physics, but also extremely important concerning applications, and it is expected to be a key to such issues as solving ‘Energy problem’. It is no exaggeration to say The 21st century is a century of superconductivity.

2. History of superconductivity exploration — before the discovery of copper oxide superconductors

As mentioned above, superconductivity is a very interesting study area, and has many possible applications. The most serious difficulty, however, is that the superconducting state is only achieved below a certain temperature, the critical temperature (T_c), which is usually very low. Nb₃Ge was a substance with the highest critical temperature obtained by 1980, at 22 K. B.T. Matthias wrote that a room-temperature superconductor is only pure science fiction. However, many scientists have continuously attempted to find superconductors with a higher T_c, and I was one of those people.

The next problem concerns what guiding principles are required to produce a higher T_c? The only clue is an equation for the superconducting transition temperature based on the BCS theory. According to the simplest BCS theory, the superconducting transition temperature (T_c) can be expressed as follows:   

\begin{equation} T_{\text{c}} \cong \Theta_{\text{D}}\,\exp\left(-\frac{1}{\lambda}\right), \end{equation} [1]

  

\begin{equation} \lambda = N(0)\cdot V, \end{equation} [2]

where Θ_D is the Debye temperature, N(0) is the state density on the Fermi surface in the normal conducting state, and V is the size of the electron-phonon interaction.

The parameters that may be easily controlled are the Debye temperature, Θ, and N(0). Matthias focused on substances having a high N(0) (the Matthias Rule). Upon systemic exploration of substances by this method, however, a breakthrough concerning the upper limit of T_c could not be obtained. Therefore, we focused on substances with a large electron-phonon interaction, V. However, when the electron-phonon interaction is increased steadily, electrons are combined in real space, form pairs in real space and stop moving, which becoming insulators. These are called charge density wave (CDW) type insulators. Figure 1 shows a schematic phase diagram, T_c vs. size of the election-phonon interaction, V. Conversely, can we obtain superconductors with a high T_c if we decrease the electron-phonon coupling constant, V, of the charge density wave-type insulators? Based on this idea, we discovered that Nb_1−xTa_xSe₃ became a superconductor when T_c = 4 K, by substituting the Ta at the Nb site to the CDW material, NbSe₃ to form Nb_1−xTa_xSe₃ and reducing V¹⁾ (Fig. 2).

Fig. 1.

Phase diagram of the electron-phonon coupling constant V vs. superconducting critical temperature T_c. (N. Tsuda, K. Nasu, J. Fujimori and K. Siratori: Electronic Conduction in Oxide (in Japanese) p. 120.).

Fig. 2.

(a) Normalized resistance as a function of the temperature for Nb_1−xTa_xSe₃ with several Ta concentrations. (b) Ta concentration dependence of T_c. Substituting Ta to CDW material NbSe₃, forming Nb_1−xTa_xSe₃ to be superconductive.¹⁾ ○ K. Kawabata,²⁾ ● Our data.¹⁾

3. Discovery of copper oxide superconductors

3-1. New Cu-oxide system having CuO₂ planes.

Meanwhile, Bednorz and Müller discovered copper oxide superconductors (1986).³⁾ The substance they found was an oxide, called La–Ba–Cu–O. It is said that they first noticed that crystals were distorted because Cu²⁺ was a Jahn-Teller ion, and they supposed that a high T_c might be obtained by changing the static distortion to a dynamic charge fluctuation. This is very similar to our idea. After that discovery, many groups figured out that this substance was two-dimensional, and that T_c was quickly increased to 160 K just a few years later.

This “revolution within the history of science” eliminated the widely accepted major prejudice that superconductivity is only possible in non magnetic materials. Leaving to other books the dramatic historical details of how a small bud germinated by Bednorz and Müller blossomed into a mainstream concept, here we describe what I did during this period. It is well known that after Bednorz and Müller discovered superconductivity in a copper oxide, a group led by Paul Chu found YBa₂Cu₃O_y (YBCO).⁴⁾ Around that time, I started studying the Cu-oxide system in earnest. My idea of how to create a new superconductor centered on the radius of ions. As shown in Table 1, I noticed that all ionic radii of elements in superconductors obtained until then were in the vicinity of 1 Å. Are there any other elements with ionic radii in that vicinity? I found that only four such ions exist: Bi³⁺, Tl³⁺, Hg²⁺, and Cd²⁺, as listed in Table 1. Surprisingly, these elements (except for Cd), were components of Bi-based, Tl-based, and Hg-based superconductors with a higher T_c.

Table 1. Ionic radius around 1 Å. Upper part (Ca²⁺ ∼ Y³⁺) shows the elements, being composed of La-Sr(Ba)-Cu-O and Y-Ba-Cu-O systems. Lower part (Bi³⁺ ∼ Cd²⁺) is the expected elements. Later, these elements Bi³⁺, Tl³⁺ and Hg²⁺ are composed of the high-T_c superconductors, called Bi-, Tl- and Hg-systems

Cation	Ionic radius [Å] (6-coordination)
Ca2+	1.02
Sr2+	1.18
Ba2+	1.38
Y3+	0.91
La3+	1.08
Bi3+	1.04
Tl3+	1.08
Hg2+	1.04
Cd2+	0.97

We now describe here some successful and unsuccessful stories. At that time, we started with the combination of Bi–Sr–Cu–O suggested by Table 1, and immediately obtained a superconductor with T_c = 6 K. Figure 3 shows its crystal structure and electrical resistance.^5),6) In a search of superconductors with a higher T_c, we replaced Nd³⁺, etc. with different valences at the site of Sr²⁺ for carrier doping. We then found signs of superconductors with T_c = 50 K, and were excitedly working on its single-phase formation. Meanwhile we heard about the discovery of Bi–Sr–Ca–Cu–O with T_c = 77 K and T_c = 105 K by Maeda et al.⁷⁾ I was disappointed by this discovery, because when one of my students tried to replace Sr²⁺ with Ca²⁺, I did not agree with his idea, because Sr²⁺ and Ca²⁺ are both divalent elements, and they would only dissolve, leading to nothing interesting chemically. However, it became clear that, in fact, when Sr and Ca are mixed, they enter into completely different sites due to their different ionic radii, resulting in different crystal structures (Fig. 4).

Fig. 3.

Temperature dependence of resistance in Bi₂Sr₂CuO₆. The inset shows the crystal structure.⁵⁾

Fig. 4.

Layered structure of (a) Bi₂Sr₂CuO₆ and (b) Bi₂Sr₂CaCu₂O₈.

Here is another example of our successful and unsuccessful cases. There is a substance, Nd₂CuO_4−δ, called a fluorite type structure, whose structure was known at that time. Unlike La₂CuO₄, it does not have oxygen above and below the copper in its crystal structure. We figured out that this substance became metallic when Ce⁴⁺ was replaced with Nd³⁺. Then, one of my students suggested, “let’s mix in Sr²⁺ in addition to Ce⁴⁺”. But I objected to this idea, saying that the number of carriers might be canceled if Sr²⁺ was mixed with Ce⁴⁺. But I remembered my previous mistake, and agreed to try this idea, in fact, a superconductor with a totally new structure emerged.^8),9) Figure 5 shows its crystal structure (called “T* structure”) and electrical resistivity.

Fig. 5.

Superconductivity in (Nd, Sr, Ce)₂CuO₄: T* structure. (a) Crystal structure of T* structure. (b) Temperature dependence of resistivity in T* structure.^8),9)

Shortly after that, however, Tokura et al. discovered a new type of superconductor,¹⁰⁾ an electron-doped type, by reducing the oxygen in (Nd_1−xCe_x)₂CuO₄. This is called the T′ structure. Figure 6 shows the “214”-type crystal structure with a different coordination having a CuO₂ plane.

Fig. 6.

Three types of “214” structure: (a) (La_1−xSr_x)₂CuO₄: T structure, (b) (Nd_1−xCe_x)₂CuO₄: T′ structure, (c) (Nd, Sr, Ce)₂CuO₄: T* structure.

Meanwhile, some essential characteristics of copper oxide superconductors had become clear.

1. The first is the existence of a CuO₂ plane consisting of Cu and O. This “parent compound” is both antiferromagnetic and insulating at the same time. This is called a Mott insulator.

2. The second characteristic is that a superconductor emerges after holes or electrons are introduced into this Mott insulator, and electricity starts flowing. Block layers adhere to the CuO₂ plane and adjust the electric charges. Figure 7 is a schematic diagram of these block layers.¹¹⁾ Superconductors with different T_c are generated by replacing these block layers.

Fig. 7.

Concept of the block layer. CuO₂ layers are inserted between block layers.¹¹⁾

The next logical step is to assemble new superconductors using these block layers. This idea is specifically to create new superconductors by finding new block layers, and combining them with existing block layers. For example, there is a substance with the crystal structure Sr₂CuO₂(CO₃).¹²⁾ This is a new copper oxide that includes a carbonate group, but this is not a superconductor itself. What should be done to dope this with a carrier? One of my doctor-course students, Masatomo Uehara (currently Yokohama National University), came up with an interesting method. It was to replace CO₃⁻² with BO₃⁻³, and thus effectively inject a carrier, and generating a new superconductor, Sr₂CuO₂(CO₃)_1−x(BO₃).¹³⁾ Figure 8 shows a phase diagram with the boron content x vs. temperature in Sr₂CuO₂(CO₃)_1−x(BO₃)_x. This superconductor is a new copper oxide that includes a carbonate group. Is it possible to create a new type superconductor by combining this crystal structures and those of existing superconductors? It was not as easy as it sounds, but we finally were able to synthesize a new superconductor under high pressure. Figure 9 shows an example of such a superconductor. We were successful in synthesizing 3 new superconductors with T_c = 55 K, 105 K and T_c = 115 K.^14),15)

Fig. 8.

Phase diagram of Sr₂CuO₄(CO₃)_1−x(BO₃)_x. Carriers can be controlled by (BO₃) content.¹³⁾

Fig. 9.

Three types of superconductor composed of different block layers including the carbonate layers. (a) Sr₂CuO₂(CO₃)_1−x(BO₃)_x (T_c = 55 K) (b) Sr₂CaCu₂O₄(CO₃)_1−x(BO₃)_x (T_c = 105 K) (c) Sr₂Ca₂CuO₄(CO₃)_1−x (BO₃)_x (T_c = 115 K).¹⁵⁾

3-2. Discovery of ladder lattice superconductors.

A common characteristic of these superconductors is having a CuO₂ plane, which does not essentially introduce any new physics. Is it possible to discover yet more superconductors that belong to new categories? To search for such a situations, we focused on a ladder lattice, which has the structure shown in Fig. 10. The Takano Group of the Institute for Chemical Research at Kyoto University discovered SrCuO₂ with a two-leg ladder lattice, and Sr₂CuO₃ with a three-leg ladder lattice. It was experimentally demonstrated that two-leg ladder lattice substances had spin gaps and three-leg ladder lattice substances had no spin gaps.¹⁶⁾ Since then, T.M. Rice,¹⁷⁾ E. Dagotto¹⁸⁾ and others have pointed out the theoretical possibility of superconductivity in ladder lattice substances. They noted that superconductivity was expressed in the even-numbered ladder lattices and that spin gaps survived.

Fig. 10.

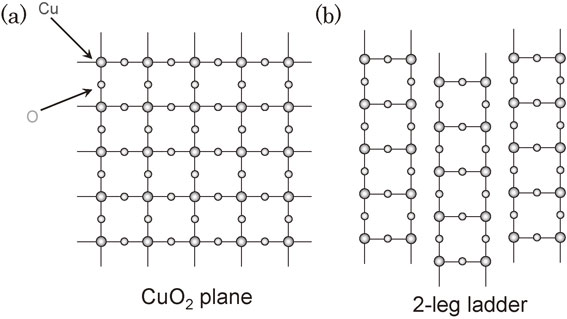
Two types of Cu-O planes. (a) Two-dimensional CuO₂ planes, (b) Two-leg ladder Cu₂O₃ planes.

Are there really such convenient ladder lattice substances? It is amazing how well things work out in nature! Such a substance does exist in reality: Sr₁₄Cu₂₄O₄₁. It is called a ‘telephone-number’ compound due to its peculiar sequence of numbers: 14–24–41. As shown in Fig. 11, this substance’s crystal structure is layered with one-dimensional chain layers on a CuO₂ plane and two-leg ladder layers on a Cu₂O₃ plane. As is evident in its valence of Cu^2.25+, many holes already exist in this substance. These holes are mainly localized in one-dimensional chain layers, and their electrical conductivity is similar to that of semiconductors. What should be done to move these holes in the chain layers to ladder layers? The easiest method is to shorten the distance between layers. To achieve this, the Sr site may simply be filled instead with Ca. In fact, when Sr is replaced by Ca in Sr_14−xCa_xCu₂₄O₄₁, its electrical resistivity decreases. In actual experiments, Ca may replace Sr only up to x = 8.4. Under a high oxygen pressure, however, Ca successfully replaced Sr up to x = 13.6. Unfortunately, however, superconductivity did not emerge. As a last resort, we measured its electrical resistivity under pressure in cooperation with Dr. Mori’s group in the Institute for Solid State Physics (ISSP) at the University of Tokyo, and in fact we found superconductivity of T_c = 12 K at 3 GPa (Fig. 12).¹⁹⁾ It was also confirmed by using the single crystal.²⁰⁾

Fig. 11.

Crystal structure of telephone number compound Sr₁₄Cu₂₄O₄₁, being composed of 1D-chain layer and 2-leg ladder layer.

Fig. 12.

(a) Temperature dependence of electrical resistivity in Sr_14−xCa_xCu₂₄O₄₁. With increasing x (Ca content), resistivity is decreased. (b) Pressure dependence of Sr_0.4Ca_13.6Cu₂₄O_41.84. Superconductivity appears at 3 GPa.¹⁹⁾

4. Exploration of metal-based new superconductors

4-1. MgB₂ and its applications.

During these explorations, we felt that we hit a dead-end with oxide superconductors, and decided to start exploring metal-based ones. Our guiding principle at that time was again the BCS theory. As shown in Eq. [1], T_c is proportional to the Debye temperature (Θ). In general, the lighter are the elements, the higher becomes the Debye temperature. It is expected that superconductivity with lighter elements would have a higher T_c. Thus, we focused on boron (B). I provided Jun Nagamatsu, an undergraduate student at that time, a research topic: to explore compounds of Mg with each of Ti and B. We included Ti because we thought that magnetic ions would play an essential role in some way, and B because it is a light element. Shortly after we began this study, Nagamatsu found a decrease in the magnetization, which was a precursory phenomenon of superconductivity. But we had a hard time to make it a single phase. Finally, Nagamatsu was able to figure out that Ti was not necessary in this superconductivity, and the essential point was to create a substance with a very simple structure, called MgB₂.²¹⁾ Figure 13 shows the electrical resistivity, and magnetic susceptibility, as a function of temperature. Figure 14 shows the crystal structure of MgB₂. There were two points that surprised us upon the discovery of this substance. First, MgB₂ was a reagent available on the market. It was surprising that a substance commercially available as a reagent is actually a superconductor with a high T_c. This was picked up in the “News and Views” section of Nature with the title “Genie in a bottle” (pp. 23–24).²¹⁾ The second interesting news was that MgB₂’s crystal structure was called the AlB₂ structure, which consists of a honeycomb structure of B and a triangular grid of Mg, the layers of which created a characteristic 2-D lattice. In fact, this type of AlB₂ structure exists in large numbers (Table 2), and most of these substances were synthesized by B.T. Matthias. Strangely, however, Matthias did not synthesize MgB₂. He would have regretted this oversight greatly if he were alive today. MgB₂ itself, obtains a high T_c through the electron-phonon interaction coupled with the strong lattice vibration of B, and it is believed that this is a typical (textbook) superconductivity, described by electron-phonon interaction. What is interesting about MgB₂ is that the band on the B plane (called σ band) and the band connecting the Boron and Mg ions (called the π band) both contribute to the superconductivity, which is called two-band superconductivity. Figure 15 shows this band structure and the Fermi surface.²²⁾

Fig. 13.

Electrical resistivity and magnetic susceptibility of MgB₂ as a function of the temperature.²¹⁾

Fig. 14.

Crystal structure of MgB₂.²¹⁾

Table 2. List of the MB₂-series materials synthesized by B.T. Matthias, except for the MgB₂

Fig. 15.

The band structure and the Fermi surface of MgB₂.²²⁾

Thus, MgB₂ is a typical BCS-type superconductor, mostly explained by the electron-phonon interaction, but its most interesting point is its applications. The critical temperature (T_c) is not the only parameter to be considered in applications. In general, superconductivity breaks down in a strong enough magnetic field, termed the critical magnetic field (H_c). Superconductivity also breaks if a large amount of electric current is applied, termed the critical current (J_c). In short, superconductivity exists in a region defined by a critical temperature, critical magnetic field and critical current. For the widest range of practical applications, superconductors with high T_c, H_c, J_c are needed. Unlike T_c, H_c and J_c may be increased by various means. For example, J_c and H_c is drastically increased by mixing in small amounts of impurities.

To be used in superconducting magnets and transmission cables, MgB₂ must be turned into wires. In that regard, MgB₂’s advantages include:

1. (1)    It may be used at a relatively high temperature (approximately 20 K), which is impossible for conventional metal-based superconducting materials.
2. (2)    Since bonding between crystal grains is strong, which makes it possible to transfer a large amount of superconducting current from one crystal grain to an adjacent one, it is not necessary to align the direction of crystal grains (as in copper oxide high-temperature superconductors). Therefore, it is relatively easy to create wires.
3. (3)    From the perspective of resources, both Mg and B are abundant raw materials that can be obtained at relatively low prices in a stable supply.

Values of H_c and J_c for MgB₂ may be enhanced with the processing procedures mentioned above. Thus, many studies have been conducted globally to create wires since the discovery of MgB₂ superconductivity, and wires longer than several km have been produced experimentally.

Some of the methods for the creation of MgB₂ wires have been proposed based on past knowhow.²³⁾ Figure 16 shows two fabrication methods: ① In situ Powder-in-tube (PIT) method and ② Internal Mg diffusion (IMD) method. Recently, the most common method has been Powder-in-Tube (PIT), where a starting powder is stuffed into metal tubes, and processed before and/or after placement in the tube. There are basically two PIT methods. One is an ex-situ method, where pre-processed MgB₂ powder is stuffed into metal tubes, such as stainless steel. The other is an in-situ method, where a mixed powder of Mg and B is stuffed in a tube to fabricate tapes, which are then heat-treated. In the ex-situ method, the greatest advantage is that a worthwhile J_c may be obtained, even without the heat-treatment process. A further heat treatment (annealing) improves the binding between crystal grains, leading to a higher J_c. In the “in-situ” method, the reactivates of Mg and B are enhanced with a heat treatment, and at the same time, unlike in the ex-situ method, there is our advantage that the crystal grains are rarely oriented.

Fig. 16.

Two fabrication methods to make a MgB₂ wire. 1) In situ powder-in-tube (PIT) method. 2) Internal Mg diffusion (IMD) method.²³⁾

Another effective method to increase the MgB₂ core density is an internal Mg diffusion (IMD) process.²⁴⁾ The IMD method is believed to provide a higher J_c due to our improved connectivity of MgB₂. The starting materials used are also important. Recently, there have been many reports that the characteristics of J_c are improved when a trace amount of minute impurities is added to a mixed powder of Mg and B. Currently, the most effective method is to add minute SiC particles that are in the nanometer range. Figure 17 shows the temperature dependence of B_c2 in MgB₂ tapes with no additives, and those with SiC added. In wires with SiC added, B_c2 for 4.2 K was as high as 30 T. This value is equal to or greater than the value of B_c2 in Nb₃Sn wires. The B_c2 in 20 K wires ranges up to 11 T. This shows that currently used utility wires may be replaced with MgB₂.

Fig. 17.

Temperature dependence of B_c2 in MgB₂ wires.²³⁾

Naturally, for use in magnet wires, the magnetic field dependence of J_c is an important factor. Figure 18 shows the present status of MgB₂ wires prepared by both the PIT and IMD methods. As shown in Fig. 18, for the practical level at 20 K and 2 T, J_c in PIT wire keeps J_c ∼ 10⁵ A/cm². Unfortunately, J_c reduces to 1.2 × 10⁴ A/cm² at 20 K and 5 T. However, there has recently been rapid progress in this area. By using the IMD method, it reached to almost 9 × 10⁴ A/cm² at 20 K and 5 T. The future is promising.

Fig. 18.

Present status of critical current density J_c (A/cm²) vs. magnetic field B (T).²³⁾

4-2. Y₂C₃.

Since discovering the MgB₂ superconductor, we have conducted broad explorations of superconductors that include light elements, such as boron (B) and carbon (C). As a result, we found that Y₂C₃ is a superconductor (T_c = 18 K) synthesized under high pressure. Figure 19 shows the temperature dependence of the resistivity and the susceptibility at ambient pressure. T_c is controllable by a synthesis condition.^25)–27) Afterwards, we found that this substance had already been reported by Krupka et al.²⁸⁾ as having a maximum T_c of 11.5 K. Figure 20 shows its crystal structure to be the Pu₂C₃-type, with a body-centered cubic structure (b.c.c.). Its Y atoms line up along the ⟨111⟩ direction, and its carbon atoms form dimers, with an extremely short C-C bond length. It is expected that its C-C stretching phonon mode is very high. Therefore, the relatively high T_c of Y₂C₃ is thought to be the result of electron-phonon coupling between high-frequency phonons and the C-C antibonding state in the vicinity of the Fermi level. A characteristic of both Y₂C₃ and La₂C₃, which has the same structure as Y₂C₃, is that they are superconductors with two gaps. This was first suggested by NMR measurement of spin-lattice relaxation.²⁹⁾ It was then clarified further in a µSR measurement.³⁰⁾ Figure 21 shows the temperature dependence of the muon spin relaxation rates of La₂C₃ and Y₂C₃. Solid and dashed lines are fitted with the s-wave’s phenomenological double-gap model.³⁰⁾ It was theoretically suggested that in the crystal structure of Y₂C₃, a strong spin-orbit interaction might lead to a mixed state of symmetric isotropic and anisotropic superconducting properties due to the lack of a space inversion symmetry. It was reported later that B_c2 is very high, at approximately 30 Tesla, which may be related to the above state.

Fig. 19.

Temperature dependence of resistivity and susceptibilities in Y₂C₃.^25),27)

Fig. 20.

Crystal structure of Y₂C₃ to be the Pu₂C₃-type with (b.c.c.) structure.

Fig. 21.

Temperature dependence of the muon spin relaxation rates of La₂C₃ and Y₂C₃. Solid and dashed lines are fitted with the s-wave’s phenomenologial double-gap model.³⁰⁾

4-3. Superconductivity of carrier-doped semiconductors.

(1) Superconductivities of boron-doped diamond and Si.

Diamonds, famously known as jewels, do not allow the flow of electricity, as is evident from their sparking. Surprisingly, however, it was discovered that diamonds become superconductive if carrier-doped (T_c = 3 K).³¹⁾ By making films even thinner, its T_c was raised to 12 K.³²⁾ The superconducting transition T_c = 0.35 K was also reported when B was doped into silicon (Si), with a similar crystal structure.³³⁾ Both substances are typical wide-gap semiconductors with the well-known diamond structure. If highly concentrated hole carriers are doped to those wide-gap semiconductors, superconductivity will be created. Since then, many theoretical studies have been actively conducted, indicating the possibility of the emergence of superconductivity at considerably higher temperatures, depending on the doped B atoms’ order or alignment.³⁴⁾

We tried to create superconductivity by B replacement (hole doping) in SiC, with characteristics similar to those of diamonds and Si, and discovered that its bulk was a superconductor with T_c = 1.4 K.³⁵⁾ We also tried to use aluminum (Al) as a hole dopant in the same manner, and verified a superconducting transition at a similar T_c (≒ 1.4 K).³⁶⁾ In the following sections, the basic physical properties that have been discovered so far are explained.

(2) Crystal structure of SiC.

SiC has a crystal structure in which C and Si are basically placed at even intervals in a diamond-type structure. However, when one looks precisely, many different structures emerge (polytype: crystal polymorphism), depending on the type of lamination layer formed. Although 200 or more polytypes have been verified currently, 3C-, 4H-, 6H-, and 15R-SiC (Ramsdell notation system) are the most important in applications, and have a high probability. In this notation system, the first number refers to the number of Si-C unit layers included in the layer direction (c, axis direction) during one cycle; C, H and R are the initial letters of crystal systems (C: cubic, H: hexagonal, R: rhombohedral). The zincblende structure that often emerges in other semiconductors is expressed as 3C, and the wurtzite structure is 2H. All band structures are of the indirect transition type, the same as that of Si. Among these polytypes, we focused on 3C-SiC and 6H-SiC (Fig. 22), and attempted hole doping in each of them.

Fig. 22.

Crystal structure of the 3C-SiC and 6H-SiC, respectively.

(3) Superconductivity of B-doped SiC.

Figure 23 shows the temperature dependence of the electrical resistivity in SiC samples (3C-SiC:B, 6H-SiC:B), where B was doped into 3C-SiC and 6H-SiC. In both, though the T_c values are low (approximately 1.4 K), a sharp superconducting transition can be observed. Also, in these transitions, substantial Meissner diamagnetism has been observed in measurements of the DC magnetic susceptibility (Fig. 23), and specific-heat jumps have been observed, confirming bulk superconductivity. It is considered that differences in T_c and the residual resistance between these substances show their disparity in reactivity, since 3C-SiC is in its low-temperature stabilized phase and 6H-SiC is in its high-temperature stabilized phase.

Fig. 23.

Temperature dependences of the electrical resistivities and magnetic susceptibilities.³⁶⁾

Figure 24 shows a magnetic field vs. temperature phase diagram of the superconducting state, as determined by measuring the electrical resistivity with changing temperature under a constant magnetic field (T-scan), and also with a changing magnetic field under a constant temperature (H-scan). As shown in Fig. 24, T_c during the cooling process starting from T > T_c and the T_c observed during the warming process do not match. This strongly suggests that B-doped SiC is a Type I superconductor. In general, simple elements, such as tin (Sn) and lead (Pb), become Type I superconductor, and Type I superconductivity in a chemical compound is very rare. The above-mentioned B-doped diamonds and B-doped Si are reported to be Type II superconductors.

Fig. 24.

H-T phase diagram for (a) B-doped 3C-SiC(3C-SiC:B) and (b) B-doped 6H-SiC(6H-SiC:B), determined from the onset of superconductivity during a T-scan and H-scan of resistivity.

(4) Superconductivity of Al-doped SiC.

Figure 25 shows the temperature vs. electrical resistivity and magnetic susceptibility in SiC samples (3C-SiC:Al), where 3C-SiC was doped with Al. T_c was approximately 1.5 K, almost equal to that of the above B-doped SiC, for which superconductivity can be verified. Also, in this transition, substantial Meissner diamagnetism has also been observed in measurements of the DC magnetic susceptibility, and a specific-heat jump has also been observed, confirming bulk superconductivity.

Fig. 25.

Temperature dependences of the electrical resistivity and magnetic susceptibility in SiC(3C-SiC:Al), where 3C-SiC was doped with Al.³⁶⁾

Figure 26 shows a magnetic field and temperature phase diagram of the superconducting state, as determined by measuring the electrical resistivity with changing the temperature under a constant magnetic field, and also with changing magnetic field under a constant temperature. Unlike the above B-doped SiC, under a finite magnetic field, that observed during the cooling process matched the T_c observed during the warming process, suggesting that this is a Type II superconductor, the same as B-doped diamond and B-doped Si.

Fig. 26.

Temperature dependence of the upper critical field H_c2 and the irreversibility field H_irr in 3C-SiC:Al.³⁶⁾

(5) Discussion and outlook.

The superconductivity of B-doped SiC involves almost the same carrier density as the superconductivity in B-doped diamond and B-doped Si, and its crystal structure is almost the same as that of diamond. It is very interesting to understand why only B-doped SiC is a Type I superconductor. Our experimental results may contribute to a qualitative understanding of this question by using the impurity level formed in semiconductors.

Table 3 summarizes the normal-state properties, including the impurity levels (E_A), and also the superconducting parameters of B-doped diamond (C:B), B-doped Si (Si:B), B-doped SiC (SiC:B), and Al-doped SiC (SiC:Al).

Table 3. Superconducting and normal state properties for SiC:Al, SiC:B, diamond (C):B and Si:B³⁶⁾

	SiC:Al	SiC:B	C:B	Si:B
n (cm−3)	7.06 × 1020	1.91 × 1021	1.80 × 1021	2.80 × 1021
γn (mJ/molK2)	0.35	0.294	0.113	—
ρ0 (mΩcm)	0.746	0.06	2.5	0.13
RRR	5.3	10.0	0.9	1.2
Tc(onset) (K)	1.5	1.45	4.50	0.35
Hc(0) (Oe)	—	115	—	—
Hsc(0) (Oe)	—	80	—	—
Hc2(0) (Oe)	432	—	4.2 × 104	4000
kF (nm−1)	2.8	3.8	3.8	—
m* (mel)	2.0	1.2	1.7	—
νF (m/s)	1.6 × 105	3.8 × 105	—	—
l (nm)	2.2	14	0.34	—
ξ(0) (nm)	87	360	80(9)	(20)
λ(0) (nm)	281	130	160	—
κGL	3.2	0.35	2(18)	—
EA (eV)	∼0.25	∼0.29	0.37	0.045

Although B-doped Si has been reported as forming Type II superconductors, recent studies suggest that they may be Type I superconductors, as revealed by samples with improved quality. B-doped Si’s Type I superconductivity may have been hidden due to the crystals’ irregularities and/or disorder, resulting in their being reported as Type II superconductivity despite the fact that it is essentially Type I superconductivity. What is observed from these parameters is that the disorder of the impurity or its level has a large impact if the acceptor level is deep, and leads to Type II superconductivity. SiC:Al may be positioned on the border of Type I and Type II superconductivities in hole-doped superconductors. Also, since the state density in the vicinity of SiC’s Fermi level is mainly due to the Si structure, it is inferred that the Si may be more important than the C for superconductivity. Based on structural analysis results, it is considered that Al may show Type II superconductivity due to the stronger impact of any disorder of Al, since it is supposed that B is then transposed to the C site and Al is transposed to the Si site.

4-4. New superconductor with a cage-type structure — R₅T₆Sn₁₈ (R = Sc, Y, Lu; T = Rh, Ir).

In this section, a new superconductor with a cage-type structure that we have worked on is briefly explained. R₅T₆Sn₁₈ (R = Sc, Y, Lu; T = Rh, Ir) was first discovered by Remeika et al.³⁷⁾ We, however, discovered a totally new experimental fact by systematically synthesizing single-crystal samples of it.³⁸⁾ R₅T₆Sn₁₈ has a cage-type structure consisting of R₅T₆Sn₁₈ (Fig. 27). This is a group in which the superconducting state changes as the R element included in the cage changes. The superconducting transition temperatures are T_c = 5, 3, or 4 K, for R = Sc, Y, or Lu, respectively. Sc, with the smallest ionic radius, has the highest T_c (Fig. 28). The most noteworthy characteristic of this group is that the superconducting gaps change substantially depending on the rare-earth ion, R.³⁸⁾ The magnetic field dependencies of the quasiparticle state densities (γ) resulting from specific-heat measurements in Lu₅Ir₆Sn₁₈ and Lu₅Rh₆Sn₁₈ at various temperatures are γ ∼ H^0.90 and γ ∼ H^1.1, respectively, representing isotropic superconducting gaps.³⁸⁾ While these isotropic superconducting gaps may be explained by the BCS theory,³⁹⁾ the magnetic-field dependencies of γ in Y₅Ir₆Sn₁₈ and Y₅Rh₆Sn₁₈ are γ − H^0.58 and γ − H^0.56, respectively, representing anisotropic superconducting gaps^38),39) (Fig. 29).

Fig. 27.

Cage-type crystal structure of R₅T₆Sn₁₈ (R = Sc, Y, Lu; T = Rh, Ir).³⁸⁾

Fig. 28.

Temperature dependence of the magnetic susceptibility in R₅Rh₆Sn₁₈ (R: Sc, Y and Lu).³⁸⁾

Fig. 29.

Quasiparticle state density (γ) vs. magnetic field.³⁸⁾

Table 4 summarizes the normal and superconducting parameters. Unfortunately, the physical reason why such a major physical property changes so substantially when rare-earth elements are changed is not yet clear.

Table 4. Superconducting parameters obtained from experiments in R₅T₆Sn₁₈ (R: Sc, Y, Lu, T: Rh, Ir). It is noted that anisotropic superconductors only appear for R = Y³⁸⁾

Space group	Sc5Rh6Sn18	Sc5Ir6Sn18	Y5Rh6Sn18	Y5Ir6Sn18	Lu5Rh6Sn18	Lu5Ir6Sn18
	I41/acd	I41/acd	I41/acd	Fm3m	I41/acd	I41/acd
Gap asymmetry	isotropic	isotropic	anisotropic	anisotropic	isotropic	isotropic
a (nm)	1.3601	1.3595	1.3792	1.3735	1.3671	1.3602
c (nm)	2.7198	2.7180	2.7498	—	2.7330	2.7315
Tc (K)	5.0	1.0	3.0	2.1	4.0	3.0
μ0Hc(0) (mT)	99.1(1)	12.2(1)	50.1(4)	30.4(1)	75.0(2)	47.6(1)
μ0Hc1(0) (mT)	5.64(1)	—	2.49(2)	1.46(1)	4.38(1)	1.87(2)
μ0Hc2(0) (T)	7.24(5)	—	4.21(6)	2.91(6)	5.58(5)	3.90(10)
λ(0) (nm)	34.2(1)	—	51.4(2)	67.2(1)	38.8(1)	59.2(2)
ξ(0) (nm)	6.74(1)	—	8.84(4)	15.9(1)	7.68(2)	13.0(1)
κ(0)	51.7(1)	—	59.1(4)	62.1(1)	50.5(1)	66.8(1)
γ (mJ/(mol·K2))	51.0(4)	27.3(4)	37.8(4)	32.1(2)	49.1(4)	31.9(1)
ΘD (K)	276(2)	246(2)	185(1)	212(2)	158(1)	193
Δ(0) (meV)	0.990(3)	0.140(1)	—	—	0.719(2)	0.544(3)
ΔCe/γnTc	2.55(36)	1.39	1.96	1.68	2.02	1.83
2Δ(0)/kBTc	4.26(3)	3.26(6)	—	—	4.12(2)	4.07(5)

5. Summary and outlook

5-1. Summary —Discovery of new superconductors—.

In the previous sections, the main topics concerning the new superconductors discovered in our laboratory are described, which can be categorized into two groups:

1. 1.    Cu-oxide superconductors.
   • 1-1    Cu-oxide system having CuO₂ planes.
   • 1-2    Ladder lattice superconductor.
2. 2.    Exploration of metal based new superconductors.
   • 2-1    MgB₂ and its application.
   • 2-2    Y₂C₃.
   • 2-3    Carrier-doped wide-gap semiconductors.
   • 2-4    New superconductor with a cage-type structure: R₅T₆Sn₁₈ (R = Sc, Y, Lu; T = Rh, Ir).

These superconductors are representative materials that we discovered.

Finally, we summarize here all of the superconductors discovered in our laboratory (Table 5).

Table 5. New superconductors discovered in the Akimitsu laboratory

Cu-oxide based new superconductors
Year	Superconductor	Tc (K)	Reference
1987	Bi-Sr-Cu-O	6	5), 6)
1988	Nd-Ce-Sr-Cu-O	28	8), 9)
1989	(Eu,Ce)-(Ba,Ln)-Cu-O (Ln = Nd, Sm, Eu)	43	40)
1992	(Y,Ca)-Sr-Cu(CO3)-O	63	41)
1992	(Bi,Pb)-Sr-Cu-(CO3)-O	41, 54	42)
1993	Sr-Ca-Cu-(CO3)-(BO3)-O	33, 55, 105, 115	14), 15)
1993	Tl-(Ba,Sr)-Cu-(CO3)-O	70	43)
1993	Hg-Ba-Sr-Cu-(CO3)-O	66	44)
1994	Ba-Ca-Cu-(CO3)-(BO3)-O	120	45)
1994	(Ca,Na)-Ca-Cu-O-Cl	49	46)
1995	(Ca,A)-Cu-O-Br (A = Na, K)	19	47)
1996	Ba-Ca-Cu-O-F	38, 106, 108
1996	Sr-Ca-Cu-O(14-24-41)	12	19)
1998	Cu-Sr-(Y,Ce)-Cu-O	43	48)
1999	Ru-Sr-Y-Cu-O	40	49)

Metal-based new superconductors
Year	Superconductor	Tc (K)	Reference
1984	(Nb,Ta)Se3	4	1)
2001	MgB2	39	21)
2003	Re-B	5	50)
2004	Y2C3	18	25)
2006	(W,Mo)-Re-(B,C)	7, 8	51)
2007	NaAlSi	7	62)
2007	SiC:B	1.4	35)
2008	SiC:Al	1.5	36)
2008	AlNx	2.8
2009	W5Si3	2.8	52)
2010	YSn3	7	53)
2010	Y3Pt4Ge6	2.6	54)
2011	W5SiB2	5.8	55)
2012	(Ta,W)5SiB2	6.5	56)
2012	KAlX (X = Si, Ge)	3.5, 4
2012	AE(TM,Si)2 (AE = Ca, Sr, Ba; TM = Ni, Pd, Pt, Cu, Ag, Au)	0.9–3.5	57)
2013	KSn2	3.2	58)
2013	A8(Al,Ge)46	4, 4.4	59)
2013	Lu2SnC	5	60)
2014	Cr2Re3B	6	61)

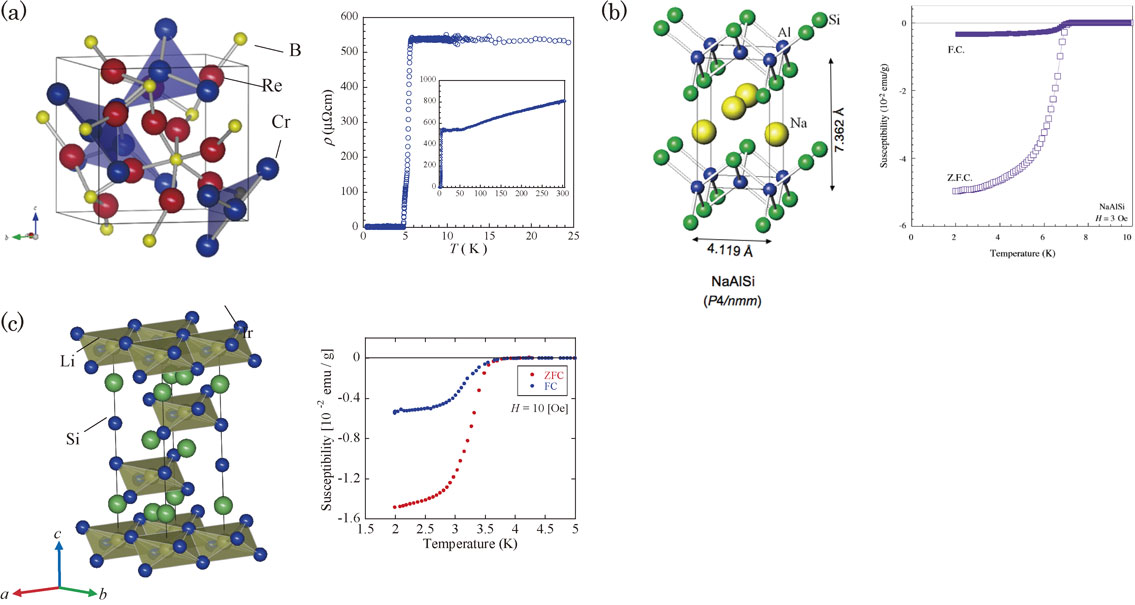
From the Table 5, we chose typical examples of superconductivities as well as crystal structures in Cr₂Re₃B,⁶¹⁾ NaAlSi⁶²⁾ and Li_xIrS₂ (Fig. 30).

Fig. 30.

Typical examples of superconductivities and crystal structures chosen from Table 5. (a) Cr₂Re₃B,⁶¹⁾ (b) NaAlSi⁶²⁾ and (c) Li_xIrSi₂.

5-2. Outlook for the higher-T_c superconductors.

In a previous section, we described what we have done. Next is our future prospects concerning what we should attack. We present here several candidates to achieve higher-T_c (T_c ≥ 100 K) superconductors.

(1) Hydride system.

The first one is the hydride system. Hydride system has long been expected to be a candidate of room-temperature superconductor. Unfortunately, however, only a moderate T_c ∼ 17 K was observed in the Pd hydrate experimentally. Recently, much attention has been paid to superconductivity at 203 K at ultra-high pressure in SH₃.⁶³⁾ Subsequently, superconductivity above 260 K (near room temperature!) has been discovered in LaH₁₀.^64),65) Disappointedly, it has only been achieved under ultra-high pressure at around 200 GPa, which is not a practical pressure. The next step is to discover a new hydride system, and to realize a high-T_c superconductor under ambient pressure.

(2) Superconductivity in 4d, 5d system.

The second big problem is that “Is there any other existing transition metal (except for Cu, Fe) oxide/chalcogenide superconducto? In particular, a high-T_c superconductor of the 4d, 5d system is unexplored?”. This will be discussed in the next section.

(3) High-T_c superconductor originated from charge fluctuation or valence skipping system.

It is well known that the origin of a high-T_c superconductor in Cu-oxide is due to magnetic fluctuation instead of some election-phonon interaction. In this sense, the charge fluctuation is another candidate to produce high-T_c superconductivity, for example Ba_1−xK_xB_iO₃ (T_c ∼ 30 K) is believed to be a charge fluctuation-mediated superconductor.

However, why can we not get a higher-T_c (T_c ≥ 100 K) superconductor mediated by charge fluctuation? This is a third big problem.

5-3. Our present work.

In this section, we briefly describe what we are presently working on.

Recently, much attention has been paid to superconductivity in the Iridate system. If superconductivity is realized in this system with the strong spin-orbit coupling (S.O.C), it will open the new dimension in condensed-matter physics. In particular, Sr₂IrO₄/Ba₂IrO₄ has been predicted to be a high-temperature superconductor upon electron doping,⁶⁶⁾ since it highly resembles the cuprate in the crystal structure and magnetic coupling constant. Particularly, the remarkable resemblance between Sr₂IrO₄/Ba₂IrO₄ and La₂CuO₄ makes a good candidate to expect unconventional HTSC in Sr₂IrO₄/Ba₂IrO₄ (Fig. 31). Indeed:

1. 1)    A low-temperature STM study⁶⁷⁾ on the K-doping (effectively election doping) in the clean surface of Sr₂IrO₄ demonstrates the clear spin gap state.
2. 2)    Moreover, Y.K. Kim et al. observed the low-temperature nodal Fermi surface and high-temperature Fermi arcs.⁶⁸⁾

These experimental results suggest clear evidence of a d-wave pairing correlation. However, direct evidence of superconductivity, such as zero resistivity (E = 0) and the Meissner effect (B = 0), can not be observed in the bulk system. We have tried to observe evidence of superconductivity in a carrier-doped bulk material. Recently, we published our present experimental data concerning this problem in the papers.^69)–71)

Fig. 31.

(a) Crystal structure of La₂CuO₄ and Sr₂IrO₄. (b) Schematic diagram of the 5d energy levels split by the crystal field (Δ), spin–orbit coupling (SOC), and on-site Coulomb repulsion (U) leading to the formation of unoccupied (upper) and occupied (lower) Hubbard bands at around the Fermi level from the J_eff = 1/2 band and the fully occupied J_eff = 3/2 band.

In particular, Terashima et al.⁶⁹⁾ demonstrated that the d-wave gapped state approaches the Fermi energy as the doped carrier increases, which shows a striking similarity with those observed for underdoped cuprate, suggesting that superconductivity can be realized with increasing the carrier concentration (Fig. 32).

Fig. 32.

(a)–(c) Second derivative of ARPES intensity plots as a function of the binding energy and wave vector on Sr_2−xLa_xIrO₄ (x = 0, 0.04 and 0.08) measured along the k direction. (d) Schematic graph of the doping-induced change in the electronic structure of Sr_2−xLa_xIrO₄ derived from our ARPES study.⁶⁹⁾

Our conclusions are summarized as follows at the present stage:

• ①    We can successfully enhance the solubility limit until x = 0.13 by using a mechanical alloying method.
• ②    The μSR measurement indicates that there is non-oscillatory signal that indicates the absence of a long-range order below T_N (Fig. 33).
• ③    At around x = 0.1, the Griffith phase (short-range A.F clusters) appears to grow upon cooling in the paramagnetic phase.
• ④    Magnetic susceptibility becomes dramatically suppressed with more fluorine substitution at on apical oxygen site.

In conclusion, however, we can not get a bulk superconductivity, probably due to insufficient carriers in the IrO₂ planes.

Fig. 33.

Magnetic phase diagram of Sr_2−xLa_xIrO₄ determined from magnetic susceptibility and µSR measurements.⁷⁰⁾

Acknowledgements

I deeply acknowledge my colleagues, Drs. H. Sawa, M. Uehara, T. Muranaka, Y. Zenitani, S. Akutagawa, K. Kawashima, K. Horigane, Z.A. Ren, S. Kuroiwa, N. Kase and all our members in my laboratory for our collaborations. In particular, I deeply acknowledge Dr. Kumakura for the discussion of applications of MgB₂. Finally, we thank to K. Horigane, M. Akimitsu, E. Sakamoto and H. Tanaka for assisting me to prepare the manuscript.

Profile

Jun Akimitsu was born in Hiroshima Prefecture in 1939. He graduated from the University of Tokyo and also received a Ph.D. from there. He became Research Associate at Institute for the Solid State Physics (ISSP), the University of Tokyo (1970–1976). He moved to Aoyama Gakuin University as Associate Professor (1976–1982), and later became Professor (1982–2015). He became the Dean of the Center for Advanced Technology, Aoyama Gakuin University (1998–2015). Meanwhile, he was a visiting professor at MIT (U.S.), and Monash University (Australia) and Guest Scientist at Brookhaven National Laboratory. After retirement from Aoyama Gakuin University, he moved to Research Institute for Interdisciplinary Science, Okayama University, in 2015. He is presently Professor (Special Appointment) of Okayama University.

He has received the following Awards; 1) 1997, Superconducting Science and Technology Award (first: For the discovery of Superconductivity in a ladder compound); 2) 1998, Nishina Memorial Award; 3) 2001, Medal with Purple Ribbon; 4) 2002, The Asahi Prize; 5) 2002, Masumoto Hakaru Award; 6) 2002, Superconducting Science and Technology Award (second: For the discovery of MgB₂); 7) 2002, Magnetic Society of Japan Award; 8) 2003, Bernd T. Matthias Prize; 9) 2007, Nishikawa Award; 10) 2008, James C. McGroddy Prize for New Materials; 11) 2012, Special Prize from the Japanese Society for Neutron Society; 12) 2014, The order of the Sacred Treasure; 13) 2019, Superconductivity Science and Technology Award (third: For distinguished contribution to the Discovery of New Superconductors).

References

• 1)   Noma,  S.,  Saito,  T.,  Ekino,  T.,  Akimitsu,  J. and  Sueno,  S. (1993) Superconducting phase in Nb_1−xTa_xSe₃ (0.135 < x < 0.16). Phys. Rev. B 48, 9620–9627.
• 2)   Kawabata,  K. (1985) Impurity effects on superconductivity and charge density waves in NbSe₃. J. Phys. Soc. Jpn. 54, 762–770.
• 3)   Bednorz,  J.G. and  Müller,  K.A. (1986) Possible high-T_c superconductivity in the Ba-La-Cu-O system. Z. Phys. B 64, 189–193.
• 4)   Wu,  M.K.,  Ashburn,  J.R.,  Torng,  C.J.,  Hor,  P.H.,  Meng,  R.L.,  Gao,  L. (1987) Superconductivity at 93 K in a new mixed-phase Y-Ba-Cu-O compound system at ambient pressure. Phys. Rev. Lett. 58, 908–910.
• 5)   Akimitsu,  J.,  Yamazaki,  A.,  Sawa,  H. and  Fujiki,  H. (1987) Superconductivity in the Bi-Sr-Cu-O system. Jpn. J. Appl. Phys. 26, L2080–L2081.
• 6)   Akimitsu,  J. (1988) Superconducting and physical properties of Bi-Sr-Cu-O system. Jpn. J. Appl. Phys. Ser. 1 Supercond. Mater. 19–23.
• 7)   Maeda,  H.,  Tanaka,  Y.,  Fukutomi,  M. and  Asano,  T. (1988) A new high-T_c oxide superconductor without a rare earth element. J. Appl. Phys. 27, L209–L210.
• 8)   Akimitsu,  J.,  Suzuki,  S.,  Watanabe,  M. and  Sawa,  H. (1988) Superconductivity in the Nd-Sr Ce-Cu-O system. Jpn. J. Appl. Phys. 27, L1859–L1860.
• 9)   Sawa,  H.,  Suzuki,  S.,  Watanabe,  M.,  Akimitsu,  J.,  Matsubara,  H.,  Watabe,  H. (1989) Unusually simple crystal structure of an Nd-Ce-Sr-Cu-O superconductor. Nature 337, 347–348.
• 10)   Tokura,  Y.,  Takagi,  H. and  Uchida,  S. (1989) A superconducting copper oxide compound with electrons as the charge carriers. Nature 337, 345–347.
• 11)   Tokura,  Y. and  Arima,  T. (1990) New classification method for layered copper compounds and its application to design of new high T_c superconductors. Jpn. J. Appl. Phys. 29, 2388–2402.
• 12)   Miyazaki,  Y.,  Yamane,  H.,  Kajitani,  T.,  Oku,  T.,  Hiraga,  K.,  Morii,  Y. (1992) Preparation and crystal structure of Sr₂CuO₂(CO₃). Physica C 191, 434–440.
• 13)   Uehara,  M.,  Nakata,  H. and  Akimitsu,  J. (1993) Superconductivity in the new compound Sr₂CuO₂(CO₃)_1−x(BO₃)_x. Physica C 216, 453–457.
• 14)   Nakata,  H.,  Uehara,  M.,  Akimitsu,  J. and  Matsui,  Y. (1994) A new family of superconductors containing carbonate group. Bull. Electrotech. Lab. 58, 468–472.
• 15)   Uehara,  M.,  Uoshima,  M.,  Ishiyama,  S.,  Nakata,  H.,  Akimitsu,  J.,  Matsui,  Y. (1994) A new homologous series of oxycarbonate superconductors Sr₂(Ca,Sr)_n−1Cu_n(CO₃)_1−x(BO₃)_xO_y (n = 1, 2 and 3). Physica C 229, 310–314.
• 16)   Azuma,  M.,  Hiroi,  Z.,  Takano,  M.,  Ishida,  K. and  Kitaoka,  Y. (1994) Observation of a spin gap in SrCu₂O₃ comprising spin-1/2 quasi-1D two-leg ladders. Phys. Rev. Lett. 73, 3463–3466.
• 17)   Rice,  T.M.,  Gopalan,  S. and  Sigrist,  M. (1993) Superconductivity, spin gaps and luttinger liquids in a class of cuprates. Europhys. Lett. 23, 445–449.
• 18)   Dagotto,  E.,  Riera,  J. and  Scalapino,  D. (1992) Superconductivity in ladders and coupled planes. Phys. Rev. B 45, 5744–5747.
• 19)   Uehara,  M.,  Nagata,  T.,  Akimitsu,  J.,  Takahashi,  H.,  Mori,  N. and  Kinoshita,  K. (1996) Superconductivity in the ladder material Sr_0.4Ca_13.6Cu₂₄O_41.84. J. Phys. Soc. Jpn. 65, 2764–2767.
• 20)   Nagata,  T.,  Uehara,  M.,  Goto,  J.,  Akimitsu,  J.,  Motoyama,  N.,  Eisaki,  H. (1998) Pressure-induced dimensional crossover and superconductivity in the hole-doped two-leg ladder compound Sr_14−xCa_xCu₂₄O₄₁. Phys. Rev. Lett. 81, 1090–1093.
• 21)   Nagamatsu,  J.,  Nakagawa,  N.,  Muranaka,  T.,  Zenitani,  Y. and  Akimitsu,  J. (2001) Superconductivity at 39 K in magnesium diboride. Nature 410, 63–64.
• 22)   Kortus,  J.,  Mazin,  I.I.,  Belashchenko,  K.D.,  Antropov,  V.P. and  Boyer,  L.L. (2001) Superconductivity of metallic boron in MgB₂. Phys. Rev. Lett. 86, 4656–4659.
• 23)   Kumakura,  H. (2012) Development of high performance MgB₂ tapes and wires. J. Phys. Soc. Jpn. 81, 011010.
• 24)   Giunchi,  G.,  Ceresara,  S.,  Ripamonti,  G.,  Di. Zenobio,  A.,  Rossi,  S.,  Chiarelli,  S. (2003) High performance new MgB₂ superconducting hollow wires. Supercond. Sci. Technol. 16, 285–291.
• 25)   Amano,  G.,  Akutagawa,  S.,  Muranaka,  T.,  Zenitani,  Y. and  Akimitsu,  J. (2004) Superconductivity at 18 K in yttrium sesquicarbide system, Y₂C₃. J. Phys. Soc. Jpn. 73, 530–532.
• 26)   Akutagawa,  S. and  Akimitsu,  J. (2007) Superconductivity of Y₂C₃ by specific heat measurement. J. Phys. Soc. Jpn. 76, 024713.
• 27)   Akutagawa,  S.,  Ohashi,  T.,  Kitano,  H.,  Maeda,  A. and  Akimitsu,  J. (2007) Microwave electrical resistivity of moderately high T_c superconductor, Y₂C₃. Physica C 460–462, 649–650.
• 28)   Krupka,  M.C.,  Giorgi,  A.L.,  Krikorian,  N.H. and  Szklartz,  E.G. (1969) High pressure synthesis and superconducting properties of yttrium sesquicarbide. J. Less Common Met. 17, 91–98.
• 29)   Harada,  A.,  Akutagawa,  S.,  Miyamichi,  Y.,  Mukuda,  H.,  Kitaoka,  Y. and  Akimitsu,  J. (2007) Multigap superconductivity in Y₂C₃: A ¹³C-NMR study. J. Phys. Soc. Jpn. 76, 023704.
• 30)   Kuroiwa,  S.,  Saura,  Y.,  Akimitsu,  J.,  Hiraishi,  M.,  Miyazaki,  M.,  Satoh,  K.H. (2008) Multigap superconductivity in sesquicarbides La₂C₃ and Y₂C₃. Phys. Rev. Lett. 100, 097002.
• 31)   Ekimov,  E.A.,  Sidorov,  V.A.,  Bauer,  E.D.,  Mel’nik,  N.N.,  Curro,  N.J.,  Thompson,  J.D. (2004) Superconductivity in diamond. Nature 428, 542–545.
• 32)   Takano,  Y.,  Nagao,  M.,  Sakaguchi,  I.,  Tachiki,  M. and  Hatano,  T. (2004) Superconductivity in diamond thin films well above liquid helium temperature. Appl. Phys. Lett. 85, 2851–2853.
• 33)   Bustarret,  E.,  Marcenat,  C.,  Achatz,  P.,  Kacmarcik,  J.,  Levy,  F.,  Huxley,  A. (2006) Superconductivity in doped cubic silicon. Nature 444, 465–468.
• 34)   Fukuyama,  H. (2006) High-temperature superconductivity by transforming bonds into bands. J. Supercond. Novel Mag. 19, 201–202.
• 35)   Ren,  Z.A.,  Kato,  J.,  Muranaka,  T.,  Akimitsu,  J.,  Kriener,  M. and  Maeno,  Y. (2007) Superconductivity in boron-doped SiC. J. Phys. Soc. Jpn. 76, 103710.
• 36)   Muranaka,  T.,  Kikuchi,  Y.,  Yoshizawa,  T.,  Shirakawa,  N. and  Akimitsu,  J. (2008) Superconductivity in carrier-doped silicon carbide. Sci. Technol. Adv. Mater. 9, 044204.
• 37)   Remeika,  J.P.,  Espinosa,  G.P.,  Cooper,  A.S.,  Barz,  H.,  Rowell,  J.M.,  McWhan,  D.B. (1980) A new family of ternary intermetallic superconducting/magnetic stannides. Solid State Commun. 34, 923–926.
• 38)   Kase,  N.,  Kittaka,  S.,  Sakakibara,  T. and  Akimitsu,  J. (2012) Superconducting gap structure of the cage compound Sc₅Rh₆Sn₁₈. J. Phys. Soc. Jpn. 81, SB016.
• 39)   Volovik,  G.E. (1993) Superconductivity with lines of GAP nodes: Density of states in the vortex. JETP Lett. 58, 469–473.
• 40)   Sawa,  H.,  Obara,  K.,  Akimitsu,  J.,  Matsui,  Y. and  Horiuchi,  S. (1989) A new family of superconducting copper oxides: (Ln_1−xCe_x)₂(Ba_1−yLn_y)₂Cu₃O_10−δ (Ln: Nd, Sm, Eu). J. Phys. Soc. Jpn. 58, 2252–2255.
• 41)   Akimitsu,  J.,  Uehara,  M.,  Ogawa,  M.,  Nakata,  H.,  Tomimoto,  K.,  Miyazaki,  Y. (1992) Superconductivity in the new compound (Y_1−xCa_x)_0.95Sr_2.05Cu_2.4(CO₃)_0.6O_y. Physica C 201, 320–324.
• 42)   Uehara,  M.,  Nakata,  H.,  Akimitsu,  J.,  Den,  T.,  Kobayashi,  T. and  Matsui,  Y. (1993) Superconductivities in the (Bi,Pb)-oxycarbonate system. Physica C 213, 51–56.
• 43)   Matsui,  Y.,  Ogawa,  M.,  Uehara,  M.,  Nakata,  H. and  Akimitsu,  J. (1993) Incommensurate and commensurate superstructures in the oxycarbonate superconductor TlSr_4−xBa_xCu₂(CO₃)O_y (x ≈ 2). Physica C 217, 287–293.
• 44)   Uehara,  M.,  Sahoda,  S.,  Nakata,  H.,  Akimitsu,  J. and  Matsui,  Y. (1994) New Hg-based oxycarbonate superconductor HgBa₂Sr₂CuO_6+δ(CO₃). Physica C 222, 27–32.
• 45)  Akimitsu, J., Uoshima, M., Ishiyama, S., Sato, M., Nakata, H., Uehara, M. et al. (1995) New oxycarbonate superconductors Sr₂(Ca,Sr)_n−1Cu_n(CO₃)O_y (n = 1, 2, 3) and Ba₂Ca_n−1Cu₂(CO₃)O_y (n = 3). In Superconductivity and Superconducting Materials Technologies (ed. Vincenzini, P.). Advances in Science and Technology, Vol. 8, Techna, Faenza, pp. 35–40.
• 46)   Zenitani,  Y.,  Inari,  K.,  Sahoda,  S.,  Uehara,  M.,  Akimitsu,  J.,  Kubota,  N. (1995) Superconductivity in (Ca,Na)₂CaCu₂O₄Cl₂ —The new simplest double-layer cuprate with apical chlorine—. Physica C 248, 167–170.
• 47)   Zenitani,  Y.,  Sahoda,  S.,  Akimitsu,  J.,  Kubota,  N. and  Ayabe,  M. (1996) New superconductor with apical bromine (Ca,A)₂CuO₂Br₂: A = Na, K. J. Jpn. Soc. Powder Powder Metall. 43, 1087–1089 (in Japanese).
• 48)   Tamura,  M.,  Sato,  M.,  Den,  T. and  Akimitsu,  J. (1998) A new superconductor with 1222 structure (Cu_1−xM_x)Sr₂(Y_1−yCe_y)₂Cu₂O_δ (M = Ti, V, Cr, Fe, Co, Ga, Ge, Mo, Ce, W and Re). Physica C 33, 1–10.
• 49)   Takagiwa,  H.,  Akimitsu,  J.,  Furukawa,  H. and  Yoshizawa,  H. (2001) Coexistence of superconductivity and (anti-)ferromagnetism in RuSr₂YCu₂O₈. J. Phys. Soc. Jpn. 70, 333–336.
• 50)   Kawano,  A.,  Mizuta,  Y.,  Takagiwa,  H.,  Muranaka,  T. and  Akimitsu,  J. (2003) The superconductivity in Re-B system. J. Phys. Soc. Jpn. 72, 1724–1728.
• 51)   Kawashima,  K.,  Kawano,  A.,  Muranaka,  T. and  Akimitsu,  J. (2006) Superconductivity in M₇Re₁₃X (M = W, Mo, X = B, C) compounds. Physica B 378–380, 1118–1119.
• 52)   Kawashima,  K.,  Muranaka,  T.,  Kousaka,  Y.,  Akutagawa,  S. and  Akimitsu,  J. (2009) Superconductivity in transition metal-silicide W₅Si₃. J. Phys. Conf. Ser. 150, 052106.
• 53)   Kawashima,  K.,  Maruyama,  M.,  Fukuma,  M. and  Akimitsu,  J. (2010) Superconducting state in YSn₃ with a AuCu₃-type structure. Phys. Rev. B 82, 094517.
• 54)   Kase,  N.,  Muranaka,  T. and  Akimitsu,  J. (2008) Superconductivity in the ternary germanide Y₃Pt₄Ge₆. J. Phys. Soc. Jpn. 77, 054714.
• 55)   Fukuma,  M.,  Kawashima,  K.,  Maruyama,  M. and  Akimitsu,  J. (2011) Superconductivity in W₅SiB₂ with the T₂ phase structure. J. Phys. Soc. Jpn. 80, 024702.
• 56)   Fukuma,  M.,  Kawashima,  K. and  Akimitsu,  J. (2012) Superconducting state in (W,Ta)₅SiB₂. Phys. Procedia 27, 48–51.
• 57)   Kawashima,  K.,  Inoue,  K.,  Ishikawa,  T.,  Fukuma,  M.,  Yoshikawa,  M. and  Akimitsu,  J. (2012) Superconductivity in Ba(TM,Si)₂ (TM = Pd, Pt, Cu, Ag and Au) with AlB₂-type structure. J. Phys. Soc. Jpn. 81, 4717.
• 58)   Miyazaki,  S.,  Kawashima,  K.,  Ipponjima,  T.,  Fukuma,  M.,  Hyakumura,  D. and  Akimitsu,  J. (2013) Superconductivity in KSn₂ with the MgZn₂-type structure. J. Korean Phys. Soc. 63, 475–476.
• 59)   Ipponjima,  T.,  Kawashima,  K.,  Miyazaki,  S.,  Hyakumura,  D.,  Yoshikawa,  M. and  Akimitsu,  J. (2013) New germanide superconductors with the type-I clathrate type structure. Physica C 494, 74–76.
• 60)   Kuchida,  S.,  Muranaka,  T.,  Kawashima,  K.,  Inoue,  K.,  Yoshikawa,  M. and  Akimitsu,  J. (2013) Superconductivity in Lu₂SnC. Physica C 494, 77–79.
• 61)   Niimura,  H.,  Kawashima,  K.,  Inoue,  K.,  Yoshikawa,  M. and  Akimitsu,  J. (2014) Superconductivity in the ternary boride Cr₂Re₃B with the β-Mn-type structure. J. Phys. Soc. Jpn. 83, 044702.
• 62)   Kuroiwa,  S.,  Kawashima,  H.,  Kinoshita,  H.,  Okabe,  H. and  Akimitsu,  J. (2007) Superconductivity in ternary silicide NaAlSi with layered diamond-like structure. Physica C 466, 11–15.
• 63)   Drozdov,  A.P.,  Eremets,  M.I.,  Troyan,  I.A.,  Ksenofontov,  V. and  Shylin,  S.I. (2015) Conventional superconductivity at 203 kelvin at high pressures in the sulfur hydride system. Nature 525, 73–76.
• 64)   Drozdov,  A.P.,  Kong,  P.P.,  Minkov,  V.S.,  Besedin,  S.P.,  Kuzovnikov,  M.A.,  Mozaffari,  S. (2019) Superconductivity at 250 K in lanthanum hydride under high pressure. Nature 569, 528–531.
• 65)   Somayazulu,  M.,  Ahart,  M.,  Mishra,  A.K.,  Geballe,  Z.M.,  Baldini,  M.,  Meng,  Y. (2019) Evidence for superconductivity above 260 K in lanthanum superhydride at megabar pressure. Phys. Rev. Lett. 122, 027001.
• 66)   Watanabe,  H.,  Shirakawa,  T. and  Yunoki,  S. (2013) Monte Carlo study of an unconventional superconducting phase in iridium oxide J_eff = 1/2 Mott insulators induced by carrier doping. Phys. Rev. Lett. 110, 027002.
• 67)   Yan,  Y.J.,  Ren,  M.Q.,  Xu,  H.C.,  Xie,  B.P.,  Tao,  R.,  Choi,  H.Y. (2015) Electron-doped Sr₂IrO₄: An analogue of hole-doped cuprate superconductors demonstrated by scanning tunneling microscopy. Phys. Rev. X 5, 041018.
• 68)   Kim,  Y.K.,  Sung,  N.H.,  Denlinger,  J.D. and  Kim,  B.J. (2016) Observation of a d-wave gap in electron-doped Sr₂IrO₄. Nat. Phys. 12, 37–41.
• 69)   Terashima,  K.,  Sunagawa,  M.,  Fujiwara,  H.,  Fukura,  T.,  Fujii,  M.,  Okada,  K. (2017) Evolution of the remnant Fermi-surface state in the lightly doped correlated spin-orbit insulator Sr_2−xLa_xIrO₄. Phys. Rev. B 96, 041106.
• 70)   Horigane,  K.,  Fujii,  M.,  Okabe,  H.,  Kobayashi,  K.,  Horie,  R.,  Ishii,  H. (2018) Magnetic phase diagram of Sr_2−xLa_xIrO₄ synthesized by mechanical alloying. Phys. Rev. B 97, 064425.
• 71)   Terashima,  K.,  Paris,  E.,  Salas-Colera,  E.,  Simonelli,  L.,  Joseph,  B.,  Wakita,  T. (2018) Determination of the local structure of Sr_2−xM_xIrO₄ (M = K, La) as a function of doping and temperature. Phys. Chem. Chem. Phys. 20, 23783–23788.