機械学習によるFe基合金のミクロ偏析生成挙動の予測

Synopsis:

A prediction method for microsegregation in Fe-based alloys was developed based on an approach of machine learning called Deep Learning. A set of model and algorithm of Deep Learning suitable for description of microsegregation was constructed by employing training data obtained by one-dimensional finite difference calculations for interdendritic microsegregation. It is shown that the developed method enables accurate prediction of the microsegregation behavior in Fe-based binary and ternary alloys with the solute atoms of C, Si, Mn, P and S. The present results demonstrate that Deep Learning offers a promising way of constructing an easy-to-use approach for prediction of microsegregation with high accuracy. Importantly, it is expected that the present method can be extended to describe effects of microstructural processes on microsegregation behavior.

1. 緒言

ミクロ偏析はデンドライト・スケールの濃度の不均一分布であり，鋳塊品質に影響を及ぼす重要な因子である。さらには，マクロ偏析の生成に直接関与するため，ミクロ偏析の生成挙動を正しく理解し，高精度に予測することが求められる。

現在までに，ミクロ偏析を予測する様々な理論や数値計算法が提案されてきた。液相内拡散，固相内拡散および固相の形態に関する近似に応じて，レバールール，Scheilモデル^1,2)，Brody-Flemingsモデル³⁾，Clyne-Kurzモデル⁴⁾，Ohnakaのモデル⁵⁾の他，様々なモデルが提案されてきた^6,7)。これらのモデルは解析式の形で与えられるため，一般に計算が簡便で低計算コストであるという利点がある。一方で，これらのモデルに導入されている組織のサイズや形態および拡散過程に関する近似が常に妥当であるとは限らないため，これらのモデルの予測精度は低い場合がある。これに対して，一次元有限差分法によるミクロ偏析の数値計算方法が提案され^8,9)，現在ではフェーズフィールド法^{10,11,12,13,14)}をはじめとする組織形成シミュレーションによって組織変化の影響も考慮したミクロ偏析の高精度解析が可能になった^15,16,17)。ただし，フェーズフィールド法をはじめとする組織形成シミュレーションはコーディングや物理モデルに関する専門的な知識を要するため，解析モデルのような簡便な利用は難しい。また，組織形成シミュレーションは高計算コストであるため，その解析には時間を要し，さらには既存のマクロ偏析モデルの計算と連成することも困難である。また，様々な合金系や様々な凝固条件を対象に組織形成シミュレーションによってミクロ偏析を解析できたとしても，その挙動を総括し，他の合金系や凝固条件での予測につなげるような手段は存在しない。

従来の解析モデルと同様に簡便で低計算コストでありつつも，組織形成シミュレーションと同等の精度でミクロ偏析挙動を算出する手法の発展が望まれる。本研究は，これらの特長を有するミクロ偏析計算手法の開発を目的とした。この目的を達成するためには，解析モデルの近似を再検討することで，より高度な物理モデルを構築する方法が考えられるが，凝固組織の複雑な時間変化を考慮した上で簡便なモデルを発展させることは容易ではない。そこで本研究では，凝固組織シミュレーションの入力値(合金の物性値および凝固条件)と，その出力値(シミュレーションから得られるミクロ偏析挙動)の関係を再現・予測する計算システム(関数と係数の組み合わせ)の構築を試みた。これは既知のデータから予測システムを開発する機械学習の試みに相当する。すなわち，シミュレーションから様々な合金系と凝固条件におけるミクロ偏析挙動を算出し，その入力値と出力値の関係を学習することで，高精度にミクロ偏析を計算可能なシステムの開発を試みた。本研究では，機械学習の方法としてディープラーニング^18,19)を用いた。次節で詳しく説明するように，ディープラーニングは非線形関係を表現する能力が著しく高く，優れた拡張性と汎化性能を有する。

本研究では，ミクロ偏析予測におけるディープラーニングの有効性を検証するとともにミクロ偏析予測に適した計算システムの構築を行った。この有効性の検証とシステムの構築においては，高計算コストの組織形成シミュレーションのデータを用いるよりも，低計算コストのデンドライト二次枝間のミクロ偏析生成挙動を対象にした一次元有限差分法のデータを用いる方が効率的である。そこで，本研究では一次元有限差分法の結果をもとにミクロ偏析予測システムの構築を試みた。対象としたのは，Fe基二元系合金と三元系合金におけるC，Si，Mn，P，Sの偏析である。続報²⁰⁾においては，本計算システムをフェーズフィールド法の結果を学習する形に拡張し，マクロ偏析シミュレーション・モデルへの実装を試みる。

2. ディープラーニング

機械学習は，画像認識，音声認識，検索エンジン等の幅広い分野で応用されており，それに応じて様々な手法が提案されている。本研究の目的は，分配係数，拡散係数といった合金の物性値，冷却速度，そして固相割合f_Sを入力することで，そのときの液相中平均濃度c_lを出力する計算システムの構築であり，回帰問題の一種である。この目的を達成するために，任意の複雑な非線形関係を表現可能な機械学習の方法であるディープラーニングを用いた。本研究の目的に関係するディープラーニングのモデルとアルゴリズムを以下に説明する。

ニューラルネットワークは脳神経系を模擬した情報処理システムであり，その代表的なモデルに多層パーセプトロン²¹⁾がある。ディープラーニングは多層パーセプトロンの発展的な情報処理システムであるため，まず多層パーセプトロンについて以下に説明する。多層パーセプトロンは入力層，中間層，出力層の3層からなる階層型ネットワークであり，入力層の信号(数値)を中間層へ，そして中間層の信号を出力層に伝えることで結果を算出する。このネットワークの模式図をFig.1に示す。これを具体的に説明するため，合金の物性値や冷却速度，f_sといったL個の入力値をx_i(i=1, 2, …, L)と表示し，さらにx=(x₁, x₂, …, x_i, …, x_L)と表す。そして，出力するM個の変数(出力値)をy=(y₁, y₂, …, y_j, …, y_M)と表す。xとyが割り当てられている層を，それぞれ入力層，出力層と呼ぶ。ここでの目的は，xからyを求めることであるが，そのために，まず以下のz_k(k=1, 2, …, N)を計算する。   

$$\begin{array}{c}{z}_k=\sigma \left(\sum _{i=1}^L{w}_{ki}^{\left(1\right)}{x}_i+b_k^{\left(1\right)}\right)\\ =\sigma \left(\sum _{i=0}^L{w}_{ki}^{\left(1\right)}{x}_i\right)\end{array}$$(1)

Fig. 1.

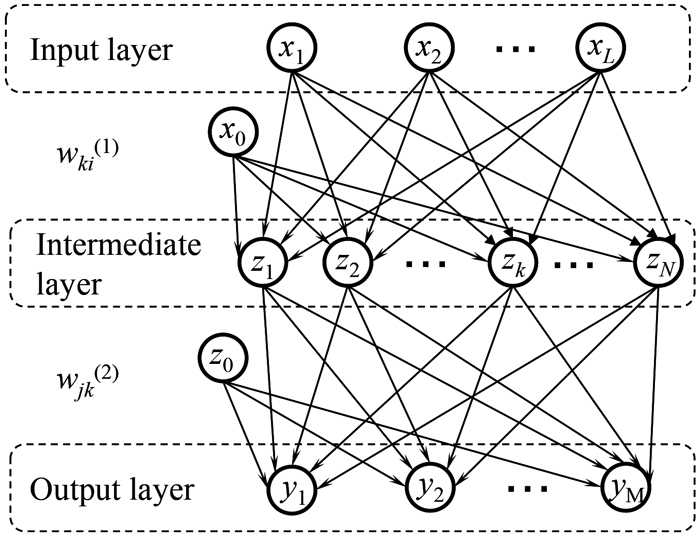
 Schematic diagram of a multilayer perceptron (MLP).

ここで，w_ki⁽¹⁾，b_k⁽¹⁾はそれぞれ結合重み，バイアス(閾値)と呼ばれる定数，σ(∙)は活性化関数と呼ばれる関数であり，シグモイド関数σ(x)=1/(1+e^−x)がよく使用される。また，二段目の式における和の演算はi=0から行うが，x₀=1，w_k0⁽¹⁾=b_k⁽¹⁾である。これらz_kが割り当てられる層が中間層であり，z_kの総数N(中間層のノード数)は学習の精度や効率に応じて調整されるパラメータである。そして，z_kを用いて，以下の式から出力値y_jを得る。   

$$\begin{array}{c}{y}_j=\sigma \left(\sum _{k=1}^N{w}_{jk}^{\left(2\right)}{z}_k+b_j^{\left(2\right)}\right)\\ =\sigma \left(\sum _{k=0}^N{w}_{jk}^{\left(2\right)}{z}_k\right)\end{array}$$(2)

ここで，z₀=1，w_j0⁽²⁾=b_j⁽²⁾であり，w_jk⁽²⁾は結合重みである。式(1)と(2)において，w_ki⁽¹⁾とw_jk⁽²⁾は未知の定数であり，これらの定数を既知のxとyの組み合わせから求める(学習する)ことになる。以下にその学習方法について説明する。

既知のxとyの組み合わせを訓練データ，その既知のyを教師データと呼ぶ。ここで，式(2)から得られるyと区別するため教師データをt=(t₁, t₂, …, t_j, …, t_M)と表す。訓練データを再現するようにw_ki⁽¹⁾とw_jk⁽²⁾を最適化することが学習の目的であり，そのために式(2)の出力値yとtの誤差(損失関数)Eを計算する。ここでは，下記の平均二乗誤差を用いる。   

$$E=\frac{1}{2}\sum _{j=1}^M{\left(t_j-y_j\right)}^2$$(3)

このEが小さくなるように，下記の式によってw_ki⁽¹⁾を更新する。   

$$w_{ki}^{\left(1\right),u+1}=w_{ki}^{\left(1\right),u}-\eta \frac{\partial E}{\partial w_{ki}^{\left(1\right)}}$$(4)

ここで，ηは学習率と呼ばれる正の定数，w_ki^(1),uは更新前，w_ki^(1),u+1は更新後のw_ki⁽¹⁾の値であり，上付文字のuは更新回数を表す。ここで，活性化関数には微分可能な関数が用いられるため，y_jはw_ki⁽¹⁾によって微分可能であり，∂E/∂w_ki⁽¹⁾は解析的に与えられる。そして，w_jk⁽²⁾に関しても式(4)と同様の方法で更新し，Eが十分小さくなるまで更新を繰り返す。式(4)に基づく最適化手法は，誤差の勾配を下るようにして誤差を最小にする方法であることから，勾配降下法と呼ばれる。ここで，詳細は割愛するが，結合重み{w}を更新する際は，w_jk⁽²⁾に関する誤差の勾配を計算してから，w_ki⁽¹⁾の誤差の勾配を計算する方が，演算回数の観点から効率的である。このとき，3種類の層を逆方向に遡る順序で演算が進むため，この方法を誤差逆伝播法と呼ぶ²¹⁾。

なお，訓練データは多数用意されていることが一般的である。その訓練データすべてに関して式(3)から誤差を算出し，その和をEとして結合重み{w}を更新する方法をバッチ処理，一つの訓練データ毎に{w}を更新して全ての訓練データを学習する方法をオンライン処理。そして全訓練データからいくつかのデータを選択して行う学習をミニバッチ処理と呼ぶ。オンライン処理およびミニバッチ処理において，訓練データの選択をランダムに行う確率的勾配降下(Stochastic Gradient Decent, SGD)法が開発されている¹⁹⁾。

上記の説明では，中間層は1層であった。その階層構造をより深くし，入力層と出力層を合わせて4層以上することも可能である。このとき，xとyの間に計算するzは，中間層の数Hに応じて増えることになる。すなわち，   

$$z_j^{\left(h+1\right)}=\sigma \left(\sum _{k=0}^{N_h}{w}_{jk}^{\left(h\right)}{z}_k^{\left(h\right)}\right)$$(5)

をh=0からh=H+1まで順に計算する。ここで，z_k⁽⁰⁾は入力値x，z_k^(H+1)は出力値yであり，z₀^(h)はh≤Hのとき1，h=H+1のとき0である。また，N_hは中間層hのノード数を表す。このような深層化によって非線形関係の表現能力が向上する。ただし，4層以上の多層パーセプトロンでは，誤差逆伝播法で{w}を学習する際に，式(4)の右辺におけるEの勾配が小さくなってしまい，実質的に{w}全体を最適化できないという問題が最近まで残されていた(勾配消失問題)。しかし，この問題を解決するモデルやアルゴリズムが近年になって開発され，そのモデルやアルゴリズムをベースにした多層パーセプトロンはディープラーニングと呼ばれている。詳細は割愛するが，事前学習によって勾配消失問題が解決可能であることが示された後，活性化関数の適切な選択によってもこの勾配消失問題の解決が可能であることが見つけられている。

本研究が対象とするディープラーニングによる回帰分析においては，上記の勾配消失問題に加えて，訓練データを過剰にフィッティングしてしまう過学習の問題，さらには真の最適解ではなく局所最適解の{w}で学習が停滞してしまう問題(局所最適解問題)が生じる。これらの問題を解消するため，本研究では以下に述べる手法の有効性を検証した。まず，勾配消失問題を解消するため，活性化関数として，シグモイド関数の他，双曲線関数σ(x)=tanh(x)とRectified Linear Unit (ReLU)関数σ(x)=x(x≥0)，0(x<0)²²⁾の三種類を使って学習を実施し，その予測精度を比較した。その結果，本研究では中間層の活性化関数に双曲線関数σ(x)=tanh(x)を用い，出力層の活性化関数には恒等関数(σ(x)=x)を用いることにした。また，過学習の問題に対しては，詳細は割愛するがL1正則化²³⁾とDropoutアルゴリズム²⁴⁾の他，学習の早期終了による過学習の抑制を試みた。その結果，学習の早期終了が本ケースにおいて効果的であったため，それを採用することにした。最後に，局所最適解の問題に対しては，いくつか有効な最適化アルゴリズムが開発されており，本研究ではAdaptive moment estimation(Adam)²⁵⁾と呼ばれるアルゴリズムを用いた。Adamにおいては，式(4)の代わりに下記の方法で{w}を更新する。   

$$w_{jk}^{\left(h\right),u+1}=w_{jk}^{\left(h\right),u}-\frac{\eta }{\sqrt{{\hat{v}}_{jk}^u}+\epsilon }{\hat{m}}_{jk}^u$$(6)

  

$${\hat{m}}_{jk}^u=m_{jk}^u/\left(1-{\left({\beta }_1\right)}^u\right)$$(7)

  

$${\hat{v}}_{jk}^u=v_{jk}^u/\left(1-{\left({\beta }_2\right)}^u\right)$$(8)

  

$$m_{jk}^u={\beta }_1{m}_{jk}^{u-1}+\left(1-{\beta }_1\right)\frac{\partial E}{\partial w_{jk}^{\left(h\right)}}$$(9)

  

$$v_{jk}^u={\beta }_2{v}_{jk}^{u-1}+\left(1-{\beta }_2\right){\left(\frac{\partial E}{\partial w_{jk}^{\left(h\right)}}\right)}^2$$(10)

ここで，m_jk⁰=0，v_jk⁰=0であり，パラメータの値としてη=0.001，β₁=0.9，β₂=0.999，ε=1.0×10⁻⁸が推奨されている²⁵⁾。本研究でもこれらの値を用いた。この方法では学習過程における誤差の勾配の履歴に応じて学習率が自動で調整されるため，E({w})空間内の鞍点や極小値における学習の停滞を回避することが可能である。

入力値や出力値の中で数値の桁が大きく異なる変数が存在する場合がある。例えば，本ケースの入力値である拡散係数と冷却速度は数桁も値が異なる。出力値である濃度も溶質元素によって大きく値が異なる場合がある。学習の入・出力値に桁の異なる変数が存在する場合には，学習において小さな値の変数の影響を十分に考慮できないことがある。そのため，学習の前処理として訓練データの正規化を行った。本研究では，訓練データの平均と標準偏差を用いて訓練データの集合が平均0および分散1になるように正規化する方法を用いた。具体的には，訓練データの集合における冷却速度の平均値${\dot{T}}_{av}$と分散$S_{\dot{T}}$を求め，以下の式で冷却速度を正規化した。   

$${\dot{T}}_{i,norm}=\frac{{\dot{T}}_i-{\dot{T}}_{av}}{S_{\dot{T}}}$$(11)

ここで，${\dot{T}}_i$は正規化前の冷却速度，${\dot{T}}_{i,norm}$は正規化後の冷却速度，これらの下付文字のiは訓練データのセットを区別している。このような処理を全ての入力値と出力値に対して施した。

本研究では，上記のディープラーニングの手法を用いてミクロ偏析計算システムの構築を試みた。ディープラーニングの実装は汎用のプログラミング言語Python 3.5で行った。特に，フレームワークchainerを用いて，GPU並列処理による学習を行った。中間層の数や学習回数は予測精度の観点から試行錯誤で調整した。その具体的な値は後述する。

3. 一次元有限差分法

ミクロ偏析予測におけるディープラーニングの有効性を検証するため，まずは一次元有限差分法によって得られる訓練データをもとに計算システムの構築を試みた。その訓練データとして，Matsumiyaらの一次元有限差分法⁸⁾を用いて二次枝間のミクロ偏析生成挙動を計算し，固相割合f_sと液相中平均濃度c_lの関係を算出した。その方法を以下に説明する。

まず，二次枝間隔λ₂の半分長さを有する一次元系をΔx間隔で離散化し，両端に鏡面対称条件を課した。左端にΔx厚さの固相を置き，残りを初期濃度c₀の液相とした。そして，液相と固相において拡散方程式を差分法により解いた。この際，空間方向は二次精度の離散化を行い，時間方向は前進オイラー法を用いた。そして，温度は空間内で均一で，一定速度$\dot{T}$で低下するものとし，固液界面における液相線温度T_l=T_m−m_lc_l*よりも温度が低下したとき，固液界面を移動させた。ここで，T_mは純鉄の融点(T_m=1811 K)，m_lは液相線勾配，c_l*は界面における液相濃度である。この界面移動の際は，固相と液相で平衡分配が成立するものとして，界面における固相濃度と液相濃度を更新した。

この計算に必要な入力値は，c₀，T_m，k_e，m_l，D_l⁰，Q_l，D_s⁰，Q_s，$\dot{T}$およびλ₂である。ここで，k_eは平衡分配係数，D_i⁰とQ_iはi相における拡散係数の振動数因子と活性化エネルギーである。本研究では，Fe基合金のフェライト凝固を対象に，溶質元素としてC，Si，Mn，P，Sを考慮した。本研究で用いたk_e，m_l，D_l⁰，Q_l，D_s⁰，Q_sの値^8,9)をTable 1に示す。また，本研究で用いた訓練データの計算条件をTable 2にまとめた。この条件に関しては次節から詳しく説明する。

Table 1. Parameters for each element employed in this study^8,9).

Element	ke	ml (K/mass%)	Dl0 (m2/s)	Ql (kJ/mol)	Ds0 (m2/s)	Qs (kJ/mol)
C	0.19	78	5.20 × 10–7	48.95	1.27 × 10–6	81.38
Si	0.77	7.6	5.14 × 10–8	38.28	8.00 × 10–4	248.9
Mn	0.77	4.9	3.85 × 10–7	69.45	7.60 × 10–5	224.4
P	0.23	34.4	1.35 × 10–6	99.16	2.90 × 10–4	230.1
S	0.05	38	4.90 × 10–8	35.98	4.56 × 10–4	214.6

Table 2. Conditions of one-dimensional finite difference calculations for training data in each system.

Alloy system	Solute	Initial concentration, c0 (mass%)	Cooling rate, $\dot{T}$　(K/s)	Secondary arm spacing, λ2 (μm)
Fe-Mn binary alloy	Mn	1.0	1, 5, 10, 15, 20, 25, 30	100
Fe-X binary alloys	C	0.01, 0.05, 0.10	0.5, 1.0, 5.0, 10	Eq. (12)
	Si	0.5, 1.0, 1.5, 2.0
	Mn
	P
	S	0.01, 0.02
Fe-X1-X2 ternary alloys	C	0.01, 0.1, 0.25, 0.50	1.0, 5.0, 10, 15	Eq. (12)
	Si	0.1, 0.5, 1.0
	Mn
	P
	S	0.001, 0.002, 0.01

4. 多層パーセプトロンとディープラーニングの比較

本章では，従来型の多層パーセプトロンとディープラーニングを比較することで本目的における後者の有効性を検証する。まず，訓練データを得るために，Fe-1.0 mass%Mn合金を対象に，λ₂を100 μmに固定して，$\dot{T}$=1，5，10，15，20，25，30 K/sの条件下でミクロ偏析挙動を計算した(Table 2参照)。この際，Δx=0.2 μm，そして時間ステップはΔt=Δx²/(3D_l*)に設定した。ここで，D_l*は初期温度における液相内拡散係数の値である。凝固中の液相中平均濃度c_lをf_sが0.008増加するごとに算出し，それを教師データとした。この解析における入力値はx=($\dot{T}$, f_s)であり，出力値はc_lである。なお，本研究では濃度を初期濃度で規格化し，c_l/c₀とした。ここで用いた全訓練データをFig.2に示す。なお，既述の通り，学習の際にはこれらのデータを平均0，分散1の集合に正規化した。

Fig. 2.

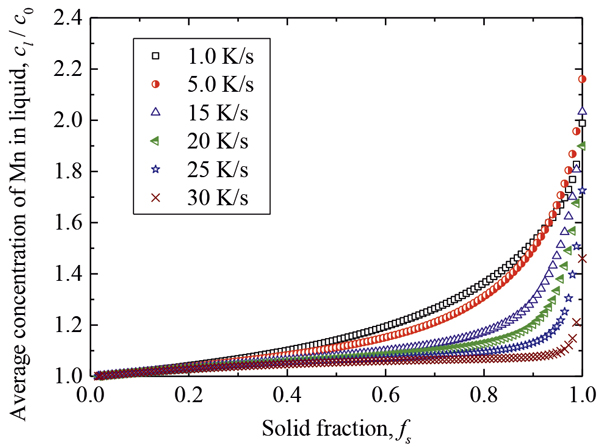
 Training data of Fe-1.0 mass%Mn alloy calculated for various cooling rates. (Online version in color.)

ディープラーニングではAdamを用いて学習を行った。その際，中間層を2層とし，それぞれのノード数を4とした。一方，従来型の多層パーセプトロンは，ノード数4の単一の中間層のみで構成し，学習アルゴリズムとしてSGD法を用い，中間層の活性化関数にシグモイド関数，出力層の活性化関数には恒等関数を用いた。いずれの場合においても，学習回数は5000回とした。

このような条件の学習過程における平均二乗誤差Eの変化をFig.3に示す。縦軸の平均二乗誤差は全訓練データから算出した値である。横軸は学習回数であり，すべての訓練データを用いて重み{w}を更新することを1 epochと呼ぶ。多層パーセプトロンに比べてディープラーニングでは誤差が速やかに減少していることが分かる。続いて，Fig.4と5に示したのは，それぞれディープラーニングと多層パーセプトロンによるミクロ偏析の予測結果である。ここには，三種類の冷却速度の結果を示したが，これらの冷却速度のデータは学習には用いていない。ディープラーニングの結果は，いずれの冷却速度においても有限差分法の結果を精度良く予測できていることが分かる。一方で，多層パーセプトロンには大きな差が現れており，特に高固相率側で予測精度が低い。以上の比較より，本研究の目的に対してはディープラーニングが有効であることが明確に示された。

Fig. 3.

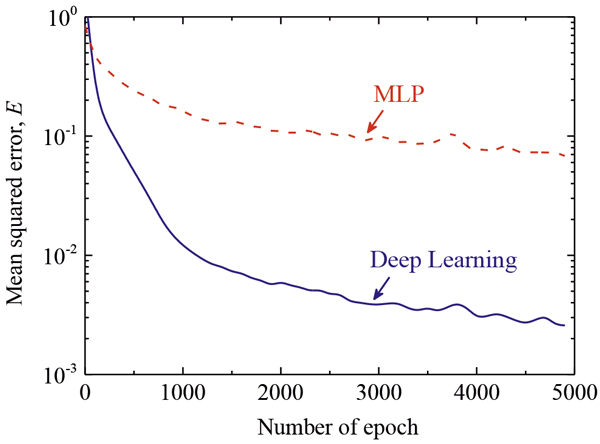
 Changes of mean squared error with the number of epoch in Deep Learning (solid line) and multilayer perceptron, MLP (dashed line). (Online version in color.)

Fig. 4.

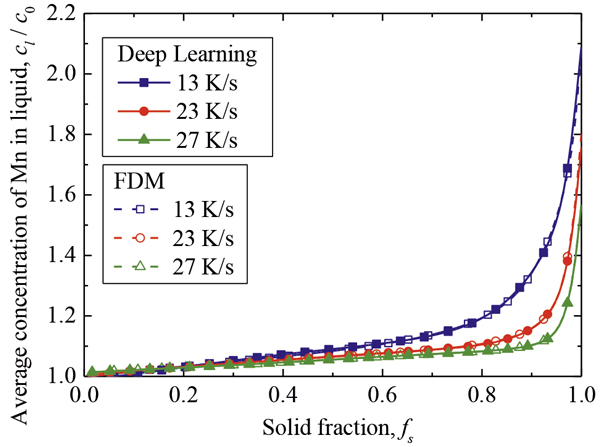
 Comparison between the results calculated by Deep Learning and Finite Difference Method (FDM) for different cooling rates. For a visual aid, only one out of every five (every six) symbols along the curve is shown for the result of Deep Learning (FDM). (Online version in color.)

Fig. 5.

 Comparison between the results calculated by multilayer perceptron (MLP) and Finite Difference Method (FDM) for different cooling rates. For a visual aid, only one out of every five (every six) symbols along the curve is shown for the result of MLP (FDM). (Online version in color.)

5. ディープラーニングによる二元系合金のミクロ偏析計算システムの構築

上記の解析においてFe-1.0 mass%Mn合金のミクロ偏析を一次元有限差分法と同等の精度で計算するシステムの開発が可能であることが示された。そこで，これを拡張し，Fe-X(X=C, Si, Mn, P, S)の複数の二元系合金におけるミクロ偏析を一次元有限差分法と同じ精度で計算するシステムの開発を試みた。

まず，一次元有限差分法によって訓練データを求めた。Table 2に示したように，Cは0.01，0.05，0.10 mass%，Si，Mn，Pは0.5，1.0，1.5，2.0 mass%，そしてSは0.01，0.02 mass%の初期濃度を対象に，それぞれの合金に対して冷却速度0.5，1.0，5.0，10 K/sの条件で訓練データを求めた。この際，二次アーム間隔の冷却速度依存性を下記の関係式²⁶⁾に基づいて考慮した。   

$${\lambda }_2=659{\left(60\dot{T}\right)}^{-0.39}$$(12)

ここで，λ₂の単位はμm，$\dot{T}$の単位はK/sである。各条件において，液相内平均濃度c_l/c₀の増加量が0.05となるように，f_sとc_l/c₀の関係を算出し，それらを訓練データとした。

一次元有限差分法の入力値は，各溶質元素のc₀，T_m，k_e，m_l，D_l⁰，Q_l，D_s⁰，Q_sと$\dot{T}$であり，このうちT_mは各合金で共通である。したがって，ディープラーニングで入力する変数は，   

$$x=\left(f_s,\dot{T},c_0,k_e,m_l,D_l{}^0,Q_l,D_s{}^0,Q_s\right)$$(13)

であり，出力値はc_l/c₀である。ディープラーニングのシステムはノード数9の中間層2層で構成し，学習回数は10000回とした。

上記の条件で学習を行い，ミクロ偏析計算システムを開発した。その予測結果をFig.6に示す。ディープラーニングの結果を実線で，そして一次元有限差分法の結果をプロットで表した。いずれも学習には用いていない初期濃度と冷却速度であり，各元素の代表的な結果を示している。C，P，Sのミクロ偏析の予測結果は一次元有限差分法の結果と良く一致している。SiとMnに関してもおおむね一致しているものの，Siにおいてはf_sが0.2程度のとき，Mnにおいてはf_sが0.3から0.8の範囲で不一致が見られる。ここで，各濃度の変化量を比較すると，学習がうまくいったC，P，Sは固相率の増加とともに比較的大きな濃度変化を示しているのに対して，学習がうまくいかなかったSiやMnの濃度変化量は小さい。このような濃度変化量の差は教師データにも存在しており，今回用いた平均0，分散1とする正規化では濃度変化量の小さな偏析を適切に学習できなかったことを意味する。そこで，本研究では正規化の方法を再検討し，次に述べる方法を採用した。まず，液相内平均濃度c_lを   

$$t=\log \left(c_l/c_0\right)$$(14)

とし，これを教師データとした。これによって異なる溶質間の濃度変化量の差を小さくした。また，入力値の拡散係数に関する値，すなわちX_in=D_s⁰，Q_s，D_l⁰，Q_lはlog(X_in)とし，さらにその値を平均0，分散1になるように正規化した。このように正規化の方法を改良し，再度同様の方法で学習を行った。その予測結果をFig.7に示す。C，P，Sに関してはほぼ同じ結果が得られたため，ここではSiとMnの結果のみをFig.7に示した。初期濃度と冷却速度はFig.6と同じものである。正規化を改良した本学習システムは，各溶質のミクロ偏析を適切に予測できていることが分かる。なお，最終凝固部の濃度に関して，一次元有限差分法の結果に対する予測結果の誤差を見積もると，C，Si，Mn，P，Sの順で3.31，6.86，1.46，0.41，0.45%であり，いずれも高精度に予測できているといえる。

Fig. 6.

 Comparison between the results of Deep Learning and FDM for (a) Fe-0.03 mass%C alloy cooled at $\dot{T}$=4 K/s, (b) Fe-0.8 mass%Si alloy cooled at $\dot{T}$=4 K/s, (c) Fe-1.3 mass%Mn alloy cooled at $\dot{T}$=4 K/s, (d) Fe-0.8 mass%P alloy cooled at $\dot{T}$=8 K/s and (e) Fe-0.15 mass%S alloy cooled at $\dot{T}$=8 K/s. In each figure, only one out of every two symbols is shown for the result of FDM. (Online version in color.)

Fig. 7.

 Comparison between the results of Deep Learning with revised normalization approach and FDM for (a) Fe-0.8 mass%Si alloy cooled at $\dot{T}$=4 K/s and (b) Fe-1.3 mass%Mn alloy cooled at $\dot{T}$=4 K/s. In each figure, only one out of every two symbols is shown for the result of FDM. (Online version in color.)

6. ディープラーニングによる三元系合金のミクロ偏析計算システムの構築

上記の通り，Fe基二元系合金におけるC，Si，Mn，P，Sのミクロ偏析を計算するシステムを開発した。本研究では，同様の手法が三元系合金にも適用可能であるかを調査した。つまり，Fe-X₁-X₂合金におけるX₁とX₂のミクロ偏析を計算可能なシステムの構築である。X₁とX₂としてC，Si，Mn，P，Sの中の二元素を考慮した。

訓練データは一次元有限差分法から算出し，その条件はCの初期濃度が0.01，0.1，0.25，0.50の四種類，Si，Mn，Pの初期濃度が0.1，0.5，1.0の各三種類，Sの初期濃度が0.001，0.002，0.01の三種類であり，それぞれの濃度で冷却速度が1.0，5.0，10，15 K/sの四種類の計算を実施した(Table 2参照)。各条件に対して，c_l/c₀が0.05増加するごとにf_sとc_l/c₀を算出し，それらを訓練データとした。ディープラーニングのシステムにおける入力値は，   

$$x=\left(f_s,\dot{T},c_{0,1},k_e{}_{,1},m_l{}_{,1},D_l{{}_{,1}}^0,Q_l{}_{,1},D_s{{}_{,1}}^0,Q_s{}_{,1},c_{0,2},k_e{}_{,2},m_l{}_{,2},D_l{{}_{,2}}^0,Q_l{}_{,2},D_s{{}_{,2}}^0,Q_s{}_{,2}\right)$$(15)

の16変数である。ここで，物性値の下付文字の1はX₁，2はX₂の物性値であることを表す。そして，このシステムの出力値はy=(c_l,1/c_0,1，c_l,2/c_0,2)である。ディープラーニングの中間層は3層，ノード数をいずれも16とし，学習回数は10000回とした。

この計算システムによる予測結果と一次元有限差分法の結果をFig.8に示す。これらの初期濃度と冷却速度のデータは学習には用いていない。いずれの三元系合金においても二つの溶質元素のミクロ偏析を精度よく予測できていることが分かる。最終凝固部の濃度に関して，一次元有限差分法の結果に対する予測結果の誤差を見積もると，Fe-C-P合金のCは0.61%，Pは0.005%，Fe-C-S合金のCは0.12%，Sは1.29%, Fe-Si-MnのSiは4.06%，Mnは2.96%，Fe-Si-SのSiは3.41%，Sは13.16%と求まった。Fe-Si-S合金におけるS濃度の誤差がやや大きいものの，全体的に高精度に予測できているといえる。したがって，本研究で構築したディープラーニングのシステムは，単一のシステムでありながら複数のFe基三元系合金のミクロ偏析を予測可能であることが示された。

Fig. 8.

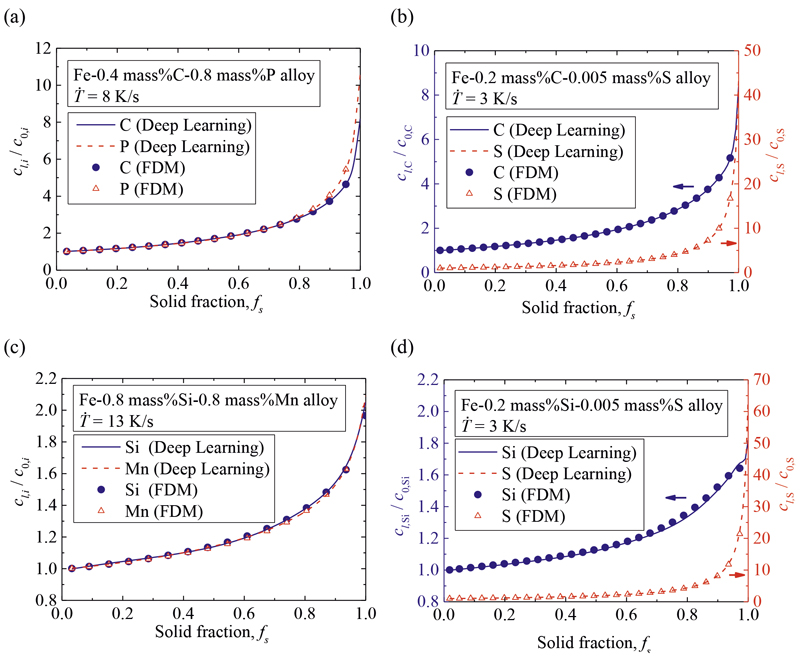
 Comparison between the results of Deep Learning and FDM for (a) Fe-0.4 mass%C-0.8 mass%P alloy cooled at $\dot{T}$=8 K/s, (b) Fe-0.2 mass%C-0.005mass%S alloy cooled at $\dot{T}$=3 K/s, (c) Fe-0.8 mass%Si-0.8mass%Mn alloy cooled at $\dot{T}$=13 K/s and (d) Fe-0.2 mass%Si-0.005 mass%S alloy cooled at $\dot{T}$=3 K/s. In each figure, only one out of every four symbols is shown for the result of FDM. (Online version in color.)

以上の結果より，本研究で構築したディープラーニングの学習システムの構成は非線形なミクロ偏析挙動を適切に学習し，精度良く予測できることが示された。本研究では，ディープラーニングの有効性の検証とミクロ偏析予測に適した計算システムの構築を目的としたため，デンドライト二次枝間のミクロ偏析生成挙動を対象にした一次元有限差分法の数値計算結果を訓練データとした。続報²⁰⁾において詳しく議論するように，本学習システムは，フェーズフィールド法による組織形成シミュレーションから得られるミクロ偏析挙動の学習と予測にも適用可能である。また，訓練データは計算結果である必要はなく，実験データを用いることも可能である。なお，本研究で構築したディープラーニングの構成は，ノード数および中間層の数が少ない非常に小規模なシステムに相当し，偏析予測に要する計算時間は数ミリ秒程度である。また，本研究で用いた活性化関数は微分可能な形式であるため，出力値を入力値で微分することも可能である。これらの点において，本計算システムはマクロ偏析シミュレーション・モデルに拡張可能であることが期待される。続報²⁰⁾において，この拡張を試みる。

7. 結言

本研究では，ミクロ偏析を高精度に計算する手法をディープラーニングに基づいて構築することを試みた。特に，従来の解析モデルと同様に簡便かつ低計算コストでありつつも，組織形成シミュ―レーションと同等の精度を有する計算システムの開発を試みた。ミクロ偏析を適切に学習し，高精度に予測するためには，学習過程における勾配消失問題に対しては活性化関数に双曲線関数を用いること，過学習の問題に対しては学習の早期終了を行うこと，そして局所最適解の問題に対してはミニバッチ型の学習アルゴリズムであるAdamを用いることが有効であることが示された。さらに，対数関数を用いた入力値と出力値の正規化が予測精度の向上に有効であることが明らかにされた。このようなモデルとアルゴリズムによって比較的小規模なシステムでも二次枝間のミクロ偏析を対象とした一次元有限差分法の結果を学習し，高精度に予測可能であることが示された。特に，Fe基二元系および三元系合金におけるC，Si，Mn，P，Sのミクロ偏析が予測可能であり，本計算システムが汎用性に優れることも示された。

本研究では，計算システムをマクロ偏析シミュレーションへ拡張することを念頭に置いたため，計算システムの出力値を液相内平均濃度のみとした。教師データとして固相内平均濃度や界面における固相濃度を用いることで，これらの固相濃度を出力値として追加可能である。凝固後の濃度不均一性を予測するためには，むしろこれらの濃度を出力値とする必要がある。また，実用的なシステムを開発するためにはフェーズフィールド法などによる組織形成シミュレーションの結果を学習する必要がある。また，本計算システムは実験データを訓練データとすることが可能であるから，実験データを主として，不足のデータをシミュレーションで補う形でシステムを構築する方法も実用的なシステムの開発に有力であると考えられる。

最後に，本研究の取り組みの発展的な内容について触れておきたい。例えば，現在では状態図計算に精通していなくても，CALPHAD法²⁷⁾によって，材料開発の現場で比較的簡便に多元系状態図を算出し，相平衡を様々な角度から解析することが可能になった。これは，自由エネルギーモデルと相平衡計算のソルバ―(熱力学計算ソフト)が開発され，種々の合金系の熱力学データベースが日々更新・拡張されているためである。本研究の取り組みを状態図計算になぞらえて表現してみれば，本研究ではミクロ偏析予測に適したモデルとソルバ―の仕様を明らかにしたことになる。そして，結合重み{w}がミクロ偏析予測のためのデータベースに相当する。すなわち，今後，各種合金系に対して実験や組織形成シミュレーションをもとにデータベース{w}を構築していくことで，例えば計算機シミュレーションに精通していない研究者や凝固・鋳造以外のプロセスを専門にする技術者であっても簡便かつ高精度に多元系合金のミクロ偏析を予測することが可能になると期待される。本研究では一次元有限差分法の結果を用いたため，さらには紙面の制約を考慮して，{w}の値を具体的に明示しなかったが，本計算システムにおいて{w}はデータベースとしての価値を有する。本研究の発展的な取り組みにおける一つの可能性として，今後蓄積されるこのようなデータベースに基づくミクロ偏析予測が考えられる。

文献

• 1)   E.  Scheil: Z. Metallkd., 34(1942), 70.
• 2)   W.G.  Pfann: Trans. AIME, 194(1952), 747.
• 3)   H.D.  Brody and  M.C.  Flemings: Trans. AIME, 236(1966), 615.
• 4)   T.W.  Clyne and  W.  Kurz: Metall. Trans. A, 12A(1981), 965.
• 5)   I.  Ohnaka: Tetsu-to-Hagané, 70(1984), S913.
• 6)   L.  Nastac and  D.M.  Stefanescu: Metall. Trans. A, 24A(1993), 2107.
• 7)   Y.-M.  Won and  B.G.  Thomas: Metall. Mater. Trans. A, 32A(2001), 1755.
• 8)   T.  Matsumiya,  H.  Kajioka,  S.  Mizoguchi,  Y.  Ueshima and  H.  Esaka: Trans. Iron Steel Inst. Jpn., 24(1984), 873.
• 9)   Y.  Ueshima,  N.  Komatsu,  S.  Mizoguchi and  H.  Kajioka: Tetsu-to-Hagané, 73(1987), 1551.
• 10)   T.  Takaki,  S.  Sakane,  M.  Ohno,  Y.  Shibuta,  T.  Shimokawabe and  T.  Aoki: Acta Mater., 118(2016), 230.
• 11)   M.  Ohno,  T.  Takaki and  Y.  Shibuta: Phys. Rev. E, 93(2016), 012802.
• 12)   Y.  Shibuta,  M.  Ohno and  T.  Takaki: JOM, 67(2015), 1793.
• 13)   T.  Takaki,  M.  Ohno,  T.  Shimokawabe and  T.  Aoki: Acta Mater., 81(2014), 272.
• 14)   T.  Takaki: ISIJ Int., 54(2014), 437.
• 15)   Q.  Du and  A.  Jacot: Acta Mater., 53(2005), 3479.
• 16)   J.  Li,  J.  Wang and  G.  Yang: J. Cryst. Growth, 311(2009), 1217.
• 17)   M.  Ohno,  T.  Takaki and  Y.  Shibuta: IOP Conf. Ser.: Mater. Sci. Eng., 84(2015), 012075.
• 18)   C.M.  Bishop: Pattern Recognition and Machine Learning, Japanese Edition First Volume, Springer Japan, Tokyo, (2007).
• 19)   Y.  LeCun,  Y.  Bengio and  G.  Hinton: Nature, 521(2015), 436.
• 20)   M.  Ohno,  D.  Kimura and  K.  Matsuura: Tetsu-to-Hagané, 103(2017), 720.
• 21)   D.E.  Rumelhart,  G.E.  Hinton and  R.J.  Williams: Nature, 323(1986), 533.
• 22)   R.  Hahnloser,  R.  Sarpeshkar,  M.A.  Mahowald,  R.J.  Douglas and  H.S.  Seung: Nature, 405(2000), 947.
• 23)   M.D.  Zeiler: arXiv, (2012), 1212.5701.
• 24)   N.  Srivastava,  G.  Hinton,  A.  Krizhevsky,  I.  Sutskever and  R.  Salakhutdinov: J. Mach. Learn. Res., 15(2014), 1929.
• 25)   D.P.  Kingma and  J.L.  Ba: arXiv, (2015), 1412.6980.
• 26)   A.  Suzuki,  T.  Suzuki,  Y.  Nagaoka and  Y.  Iwata: J. Jpn. Inst. Met., 32(1968), 1301.
• 27)   L.  Kaufmann and  H.  Bernstein: Computer Calculation of Phase Diagrams: With Special Reference to Refractory Metals, Academic Press, New York, (1970).