Elastoplastic Deformation of a Steel Tube Subjected to the Strain Paths Composed of Two Line Segments

Synopsis:

Constitutive equations play an important role for improving the accuracy of finite element analysis used in metal forming simulations. Plastic flow behavior of a steel tube is experimentally investigated in the present study. A thin-walled steel tube is subjected to linear and nonlinear loading paths. For the linear loadings, a ratio of the displacement and rotation of a grip is fixed at constant. Experimentally measured plastic flow is well predicted by the associated flow rule based on an anisotropic yield function at least for the linear loadings. In the nonlinear loadings, the specimen is subjected to the uniaxial tension followed by the simultaneous application of the axial load and torsion. The plastic flow directions in the nonlinear loadings do not agree with those for the linear loadings even though the stress states are identical. These experimental trends cannot be reproduced by the associated flow rule. We have found the linear relationship between the direction of plastic strain rate and the direction of strain rate. Therefore, the experimental data indicates that the direction of plastic flow can be represented by the direction of the strain rate as well as the stress state.

1. 緒言

近年，金型の試作段階において，有限要素解析を用いた塑性加工シミュレーションが日常的に使用されている。シミュレーションをより一層有効なものとするために，解析精度の更なる向上が期待されている。有限要素解析においては，要素の種類，要素分割方法，接触条件の取り扱い方法など多くの因子が解析結果に影響を及ぼすが，本研究では特に塑性構成則に着目する。塑性構成則は降伏関数，加工硬化則，塑性流動則を基盤としている。降伏関数に関しては盛んに研究が行われており，さまざまな異方性降伏関数が提案され，また実験検証も行われている^1,2,3)。加工硬化則はスプリングバック解析にとって極めて重要であることから，実験・モデリングともに活発に研究されている^4,5,6)。一方，塑性流動則については，1950年~1970年頃に多くの実験研究がなされたものの，統一的な見解が得られていない。また，降伏曲面上の尖り点の効果を考慮した塑性流動則が提案されており，せん断帯や座屈などの塑性不安定現象の予測への有効性が示されている^7,8,9,10,11)にも関わらず，一般的には関連流動則が適用されているのが現状である。

降伏曲面上の尖り点の形成とその塑性流動への影響は時間非依存の結晶塑性を考えると理解できる。Schmid則を適用すると，すべり系の降伏条件は応力空間において超平面によって表される。単一すべりでは，塑性ひずみ速度は超平面の法線方向を向く。一方，複数のすべり系が同時に活動する場合は応力点において複数の超平面が交差するため尖り点が形成される。そして，各超平面の法線に囲まれる領域に塑性ひずみ速度が発生する。この領域内において，塑性ひずみ速度の発生方向はすべり系の相対的な活動度合いに依存する。すなわち，塑性ひずみ速度の発生方向は，応力状態だけではなく，応力速度またはひずみ速度の影響を受けることになる。このように単結晶については，尖り点の形成ならびに塑性ひずみ速度が応力・ひずみ速度に依存することが自然に理解できる。個々の結晶粒の降伏曲面に尖り点があることから，多結晶体の巨視的な降伏曲面にも同様の尖り点があることが類推され，また，巨視的な塑性流動も応力・ひずみ速度に依存するものと推察される。

LinとIto¹²⁾の数値解析において，弾性限界によって定義された多結晶体の後続降伏曲面には明瞭な尖り点が予測されている。しかしながら，有限のオフセットひずみによって定義された降伏曲面には尖り点は現れず，丸みを帯びた形状が予測されている。オフセットひずみ法によって予負荷後の後続降伏曲面を同定した実験において，先端に丸みを帯びた尖り点が測定されており^13,14)，上記数値解析の結果に整合する。これらの結果より，多結晶体の降伏曲面上の尖り点を実験的に明確かつ正確に計測することは困難と言える。

応力経路またはひずみ経路をジグザグに変化させて，それに伴う塑性ひずみ速度の発生方向を測定した報告がある。応力経路が直角に折れ曲がるような実験^14,15,16)では，塑性流動は関連流動則に従うという結果が得られている。一方，鋭角に折れ曲がった応力経路^17,18)，もしくは折れ曲がったひずみ経路^19,20)においては，塑性ひずみ速度が応力速度方向に依存することが報告されている。したがって，このような実験においては，塑性流動に及ぼす応力・ひずみ速度の方向の影響が比較的明確に表れるようである。

最近，第一筆者は多結晶塑性モデルを使用して，種々の折れ曲がったひずみ経路に対する塑性流動を解析した²¹⁾。その結果，ひずみ速度の方向と塑性ひずみ速度の方向には明らかな相関があることが分かった。そこで，多結晶塑性モデルの解析結果を再現できる巨視的塑性流動則として，塑性ひずみ速度の方向がひずみ速度の方向に依存するモデルを構築した。

本研究では，円管試験片に様々な条件で引張とねじりを負荷し，多結晶金属の塑性流動に負荷状態が与える影響を実験的に明らかにする。その際，チャックの変位と回転を制御することで，疑似的にひずみ経路を制御する。引張とねじりの比率を一定に保った線形負荷，ならびに単軸引張を負荷した後に引張とねじりを同時に負荷する非線形負荷を実施する。線形負荷と非線形負荷において，同一の応力状態となる点での塑性ひずみ速度の発生方向を調査することで，ひずみ速度の方向が塑性流動に及ぼす影響を明らかにする。最後に，第一筆者が提案した巨視的塑性流動則と比較し，その有効性を検証する。

2. 実験方法

2・1　供試材

供試材は極低炭素量の電磁純鉄ME1F(大同特殊鋼製，JIS C 2504におけるSUY-1相当)製の円管である。丸棒に中ぐり加工を施して円管を作り，その後，外径や肉厚の寸法精度を上げるためにロール圧延を行った。最終的に焼きなまし処理を施した。公称外径は30 mm，公称肉厚は1.2 mmである。円周方向の肉厚分布は，平均値±0.01 mmの範囲であった。試験片はチャック部を除く自由変形部を90 mmとした。

2・2　ひずみと応力の同定方法

実験には引張とねじりを負荷できるサーボパルサ(島津製作所製)を用いる。負荷容量は引張・圧縮が100 kN，トルクが1 kNである。試験片の管軸方向の中央部に軸方向，円周方向，軸方向から45°方向の3方向のひずみを測定できるロゼットひずみゲージを貼り付けた。引張荷重F，トルクT，および3方向のひずみは24 bitの分解能を持つデータロガーによって0.1 s間隔で収録した。

ひずみ，応力の算出は文献²²⁾と同じ方法を用いており，以下では概略を示す。微小ひずみの仮定のもとに3方向のひずみより，せん断ひずみを算出する。その後，円管表面で測定されたひずみを肉厚中央部のひずみに変換する。変換後のひずみをε₁₁，ε₂₂，ε₁₂と記し，ひずみの代表値として以後のデータ整理に用いる。ここで，Fig.1に示すようにx₁，x₂，x₃をそれぞれ管軸，円周，肉厚方向に一致するように座標系を設定している。

Fig. 1.

 Coordinate system and stress components.

管軸方向の力のつり合いより引張応力σ₁₁を，トルクのつり合いよりせん断応力σ₁₂を以下の式で導出する。   

$${\sigma }_{11}=\frac{F}{\pi t\left(D-t\right)},{\sigma }_{12}=\frac{2T}{\pi t{\left(D-t\right)}^2}$$(1)

ここで，t，Dは肉厚および外径である。σ₁₁，σ₁₂以外の応力は生じていない。

塑性ひずみは，Hookeの法則を用いてひずみから弾性ひずみを引いて求める。   

$${\epsilon }_{11}^{\text{p}}={\epsilon }_{11}-\frac{{\sigma }_{11}}{E},{\epsilon }_{12}^{\text{p}}={\epsilon }_{12}-\frac{{\sigma }_{12}}{2G}$$(2)

ひずみおよび塑性ひずみの速度を求める際は，当該時刻の±1 sの実験値を線形近似し，その傾きをそれぞれひずみ速度，塑性ひずみ速度とする。ただし，変形経路を変更した直後は，変更直前の実験値を含めないこととする。

2・3　実験条件

本研究では，試験片端部のチャック変位速度$\dot{u}$および回転速度$\dot{\Omega }$を制御する。単軸引張において${\dot{u}}_0$=0.011 mm/sのとき，また単純せん断試験において${\dot{\Omega }}_0$=0.078°/sのとき，Misesの相当塑性ひずみ速度がおおよそ1×10⁻⁴なった。そこでこれらの変位速度と回転速度をそれぞれ基準変位速度${\dot{u}}_0$および基準回転速度${\dot{\Omega }}_0$と定義し，単軸引張および単純せん断試験を実施した。

線形負荷試験として，Fig.2(a)に示すようにチャックの変位速度と回転速度の比を一定に保持した試験を行った。変位速度と回転速度は三角関数を利用して次式で規定した。   

$$\dot{u}={\dot{u}}_0\cos \phi ,\dot{\Omega }={\dot{\Omega }}_0\sin \phi$$(3)

Fig. 2.

 Schematic illustration of applied loading paths.

φ=10, 20, 30, 40, 50, 60, 70°の7経路において線形負荷試験を行った。

次に，非線形負荷試験として，Fig.2(b)に示すような負荷経路を与えた。はじめにチャック変位がu=3.2mm(引張ひずみε₁₁≈0.03)に達するまで単軸引張を与え，その後に引張とねじりを同時に与える負荷経路に変更する。経路変更後のチャック変位速度と回転速度は式(3)を用いて規定した。φ=15, 25, 35, 45, 55, 65, 75, 90°の8経路で非線形負荷を与えた。

3. 実験結果

3・1　線形負荷試験

単軸引張試験より得られた応力−ひずみ曲線をFig.3に示す。3回の試験結果はほとんど一致しており，十分な再現性が確認できる。降伏伸びの発生により，ε₁₁<0.025の範囲では応力は一定であり，その後，加工硬化の再開が確認できる。ε₁₁>0.03の実験値を使用して，加工硬化指数は0.3，r値は0.84と同定した。また，ε₁₁=0.03まで変位速度を${\dot{u}}_0$とし，その後，100${\dot{u}}_0$に変更する実験を行い，ひずみ速度感受性指数を0.01と同定した。Young率は208 GPa，Poisson比は0.30であった。なお，単純せん断試験よりせん断弾性係数は86 GPaと同定した。

Fig. 3.

 True stress-logarithmic strain curve under uniaxial tension.

チャック変位速度，回転速度の比を一定に保った線形負荷試験を行った。試験中の相当塑性ひずみ速度は，1×10⁻⁴~1.5×10⁻⁴の範囲であった。ひずみ経路および応力経路をFig.4に示す。降伏伸びのために低ひずみ域ではひずみ経路が変動しているものの，0.03以上のひずみ範囲では直線的なひずみ経路となった。また，応力経路は負荷開始から降伏点までは直線的な経路であり，降伏伸びの発生によって直線経路から逸脱して応力経路が乱れた。降伏伸びが終了して加工硬化が再開すると再び直線的な応力経路となった。なお，降伏伸びの発生によってせん断応力が低下する現象は，Meguidらの炭素鋼を用いた実験²³⁾においても確認されている。

Fig. 4.

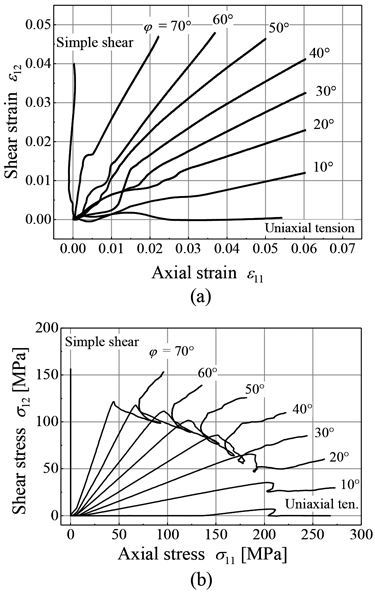
 Linear loading experiments. (a) Strain paths and (b) stress paths.

塑性異方性を調べるために次式で与えられるMisesの相当塑性ひずみを各応力経路について計算した。   

$${\overline{\epsilon }}^{\text{p}}=\int \sqrt{\left(2/3\right){\dot{\epsilon }}_{ij}^{\text{p}}{\dot{\epsilon }}_{ij}^{\text{p}}}\text{d}t$$(4)

ε^p=0.03，0.035，0.04，0.045に対する応力値を応力経路上に図示した結果をFig.5(a)に示す。図中にはMisesの降伏曲面およびBarlat-Lianの降伏曲面²⁴⁾を示す。Barlat-Lianの降伏関数に含まれる異方性係数は，実験結果の応力点を全て用いて全体的に一致するように決定した。σ₁₁>σ₁₂の範囲では，実験値はMisesの降伏曲面より内側に位置しており，一方，σ₁₁<σ₁₂の範囲では実験値がMisesの降伏曲面の外側に位置している。このように塑性流動応力の異方性が明確に確認できる。Barlat-Lianの降伏関数による予測は，十分とは言い難いが，Misesの予測結果よりは向上している。

Fig. 5.

 Stresses at constant value of (a) Mises’ equivalent plastic strain ε^p and (b) accumulated plastic work W^p.

塑性異方性や加工硬化を評価するために単位体積当たりの塑性仕事を用いることもある。Misesの相当塑性ひずみで評価した場合と比較するために，塑性仕事が一定値に達する応力点を図示した結果をFig.5(b)に示す。基準が相当塑性ひずみであるか塑性仕事であるかによって，応力値に多少の差が生じる負荷経路があるものの，全体的にはおおむね重なっている。このように，Misesの相当塑性ひずみを基準としても塑性仕事としても，本実験結果に系統的な差は生じないことを確認した。

次に，線形負荷経路に対する塑性流動と応力状態の関係を調べる。応力成分の比よりα=Arctan(σ₁₂/σ₁₁)を，塑性ひずみ速度成分の比よりβ=Arctan$\left({\dot{\epsilon }}_{12}^{\text{p}}/{\dot{\epsilon }}_{11}^{\text{p}}\right)$を定義する。線形負荷におけるαとβの関係をFig.6に示す。α=7,14°において，ε^p=0.03のときその他のひずみレベルより，βが10°程ずれている結果がある。これは降伏伸び直後であり，不安定な変形の影響を受けたためと推察される。この結果を除けば，塑性変形の進行に伴う塑性ひずみの発生方向の変化はおおよそ5°である。

Fig. 6.

 Relationship between the direction of plastic strain rate and the stress state.

MisesおよびBarlat-Lianの降伏関数を塑性ポテンシャルとみなして，関連流動則を適用して塑性ひずみの発生方向を求めた結果をFig.6に示す。Barlat-Lianの降伏関数では，ε^p=0.04において同定した異方性係数を使用した。全体的にはMisesよりもBarlat-Lianの降伏関数を用いた方が塑性ひずみの発生方向をよく予測できている。実験値と予測値の差は，応力角度αの増加とともに増えるものの，最大でも8°程度の差であった。したがって，異方性降伏関数を用いた関連流動則を適用すれば，線形負荷経路における塑性ひずみ速度の発生方向は，この程度の精度で予測できることを確認した。

3・2　非線形負荷試験

非線形負荷経路におけるひずみ経路および応力経路をFig.7に示す。はじめに単軸引張を負荷しているときに降伏伸びが発生するため，一時的にひずみ経路が乱れている。一方，負荷経路を変更した後のひずみ経路はおおよそ直線である。これに対して，応力経路は負荷経路を変更した後，非線形に曲がった経路となり，その後，放射状に直線的な経路となった。図中には負荷経路の変更点からの累積相当塑性ひずみΔε^pが一定値となる応力点を示している。応力が曲線を描きながら発展している間に発生する塑性ひずみはおおよそΔε^p=0.01である。

Fig. 7.

 Nonlinear loading experiments. (a) strain path, (b) stress path.

Fig.8には，φ=35, 55, 90°における応力経路と線形負荷の応力経路を示す。非線形負荷の応力経路は線形負荷のそれらと交差する点を複数有する。そこで，応力経路の交点における塑性ひずみ速度の発生方向を調べた。${\dot{\epsilon }}_{11}^{\text{p}}-{\dot{\epsilon }}_{12}^{\text{p}}$座標をσ₁₁−σ₁₂座標と一致させて，${\dot{\epsilon }}_{11}^{\text{p}}$と${\dot{\epsilon }}_{12}^{\text{p}}$の比を図中に直線で表している。線の長さは一定としており，塑性ひずみ速度の大きさとは無関係である。非線形負荷における塑性ひずみ速度の発生方向は，線形負荷のそれらよりも反時計回り方向に傾いている。線形負荷と非線形負荷の塑性ひずみ速度の差は，非線形負荷のφが大きいほど大きい。また，負荷経路変更後ほどその差は大きく，徐々に減少していく。以上の結果は，非線形負荷のひずみ速度の方向が線形負荷のそれから逸脱する量が大きいほど，塑性ひずみ速度の方向が反時計回りに傾くことを示している。

Fig. 8.

 Direction of plastic strain rate for the linear loadings and the nonlinear loadings with (a)φ=35°, (b) φ=55°, and (c) φ=90°.

次に，ひずみ速度と塑性ひずみ速度の発生方向の関係を定量的に検討する。応力経路の交点において，線形負荷と非線形負荷の塑性ひずみ速度の発生方向の差をθ^p，ひずみ速度の発生方向の差をθとする。θ^p，θは次式で求めた。   

$${\theta }^{\text{p}}=\mathrm{Arctan}{\left({\dot{\epsilon }}_{12}^{\text{p}}/{\dot{\epsilon }}_{11}^{\text{p}}\right)}_{\text{linear}}-\mathrm{Arctan}{\left({\dot{\epsilon }}_{12}^{\text{p}}/{\dot{\epsilon }}_{11}^{\text{p}}\right)}_{\text{nonlinear}}$$

  

$$\theta =\mathrm{Arctan}{\left({\dot{\epsilon }}_{12}/{\dot{\epsilon }}_{11}\right)}_{\text{linear}}-\mathrm{Arctan}{\left({\dot{\epsilon }}_{12}/{\dot{\epsilon }}_{11}\right)}_{\text{nonlinear}}$$

全ての非線形負荷について，線形負荷の応力経路との交点を求め，それらの応力点におけるθとθ^pの関係を導出した。その結果をFig.9に示す。多少のばらつきはあるものの，実験結果は直線的なバンド上に集中している。このように負荷経路の差異によらずθ^pとθはおおよそ比例関係にある。すなわち，本実験結果は，塑性流動は応力状態とひずみ速度の方向の2つを主要因子として表現可能であることを示している。

Fig. 9.

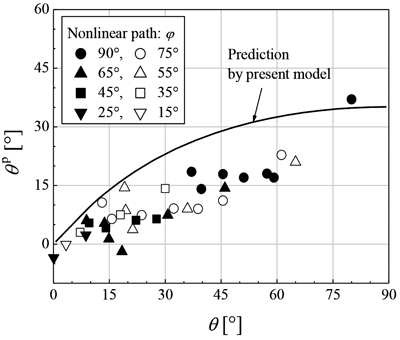
 Relationship between the direction of strain rate and that of plastic strain rate.

なお，関連流動則では塑性流動は応力状態のみで決定されるため，θにかかわらず常にθ^p=0°であり，実験結果と明らかに異なる。非線形負荷に対して，応力経路の交点におけるαとβを求めた結果をFig.6に示す。非線形負荷における結果は線形負荷のそれらとは明らかに異なっており，関連流動則では今回の実験結果を予測できないことが明白である。

4. 巨視的塑性流動則との比較

第一筆者が多結晶塑性解析をもとに構築した巨視的塑性流動則の概略を示す。ここでは擬コーナーモデルと称する。なお，詳細は文献²¹⁾を参照されたい。大変形を考慮しており，ひずみ速度(変形速度)をDと表す。降伏曲面は滑らかであると仮定し，塑性ひずみ速度をその法線方向成分D^p_nと接線方向成分D^p_tに分解する。   

$$D^{\text{p}}=D_{\text{n}}^{\text{p}}+D_{\text{t}}^{\text{p}}$$

D^p_nは降伏曲面の法線方向Nと塑性乗数$\dot{\lambda }$によって与える。   

$$D_{\text{n}}^{\text{p}}=\dot{\lambda }N$$

塑性乗数$\dot{\lambda }$は降伏条件の適応条件より求める。D^p_tは偏差ひずみ速度の接線方向成分D'_tと線形関係にあると仮定する。   

$$D_{\text{t}}^{\text{p}}=\alpha {D^{\prime }}_{\text{t}}$$

αは塑性ひずみ速度の方向を降伏曲面の法線方向からひずみ速度の発生方向に傾ける効果を有している。なお，α=0とすると関連流動則に帰着する。次式のようにαを定義すると，多結晶塑性解析の結果をよく近似できることが分かっている。   

$$\alpha =\{\begin{array}{cc}1-c_1\sqrt{\frac{g}{G}}-c_2\frac{⟨h⟩}{G}& \text{for}0\le \overline{\theta }\le {\theta }_0\\ \left(1-c_1\sqrt{\frac{g}{G}}-c_2\frac{⟨h⟩}{G}\right)\left(\frac{\pi /2-\overline{\theta }}{\pi /2-{\theta }_0}\right)& \text{for}{\theta }_0\le \overline{\theta }\le \pi /2\end{array}$$

ここで，θは降伏曲面の法線方向と偏差ひずみ速度のなす角，gは変形抵抗，Gはせん断弾性係数，hは瞬間硬化率である。c₁=0.3，c₂=0.5，θ₀=10°とすると多結晶塑性解析の結果を定量的によく再現できる。

上述の擬コーナーモデルを用いて，θとθ^pの関係を予測した結果をFig.9に示す。本流動則において，ひずみレベルが同じであれば，塑性ひずみ速度の方向はθ(偏差ひずみ速度の方向)によって決まる。そのため，θとθ^pの関係は単一曲線で表される。この点は実験結果に整合している。一方，実験におけるθとθ^pの関係が直線的であることに対して，予測値は上に凸であり，塑性ひずみ速度の方向の傾きが実験値より大きい。

最後に，φ=90°の非線形負荷経路を模擬した解析を擬コーナーモデルならびに関連流動則を用いて実施した。Fig.10に予測結果と実験結果の比較を示す。関連流動則では，塑性ひずみ速度の発生方向は実験結果よりも時計回りの方向に予測している。一方，擬コーナーモデルにおいては，塑性ひずみ速度の方向が関連流動則よりも反時計回りに傾いており実験の傾向に近い。しかしながら，全体的には傾き量がやや大きすぎるようである。これらの結果は，擬コーナーモデルの修正の必要性を示唆している。

Fig. 10.

 Stress path and plastic flow direction predicted by the present model and the associated flow rule.

5. 結論

本研究では，引張とねじりの比を一定で負荷する線形負荷，および単軸引張を負荷した後に引張とねじりを負荷する非線形負荷における塑性変形挙動を測定し，以下の点を明らかにした。

1)線形負荷における塑性ひずみ速度の発生方向は異方性降伏関数に基づいた関連流動則によっておおよそ予測可能である。

2)非線形負荷においては塑性ひずみ速度の方向は応力状態のみならず負荷状態に依存することを確認した。

3)線形負荷と非線形負荷におけるひずみ速度の方向差と塑性ひずみ速度の方向差はおおよそ比例関係にあることが明らかとなった。すなわち，本実験結果は，塑性ひずみ速度の方向は応力状態およびひずみ速度の方向を主要因子として再現できることを示している。

4)上述の実験結果は，第一筆者が提案した擬コーナーモデルによって定性的に表すことができる。しかしながら，定量的な面では精密化の余地が残っている。

謝辞

本研究は，第24回鉄鋼研究振興助成および先進的多軸応力試験による鋼板成形の高度化研究会の支援を受けて実施したものである。ここに深く謝意を表する。

文献

• 1)   F.  Barlat,  H.  Aretz,  J.W.  Yoon,  M.E.  Karabin,  J.C.  Brem and  R.E.  Dick: Int. J. Plast., 21(2005), 1009.
• 2)   F.  Yoshida,  H.  Hamasaki and  T.  Uemori: Int. J. Plast., 45(2013), 119.
• 3)   T.  Kuwabara: Int. J. Plast., 23(2007), 385.
• 4)   C.  Teodosiu and  Z.  Hu: Proc. 5th Int. Conf. on Numerical Methods in Industrial Forming Processes, Numiform '95, A.A. Balkema, Rotterdam, (1995), 173.
• 5)   F.  Yoshida and  T.  Uemori: Int. J. Plast., 18(2002), 661.
• 6)   F.  Barlat,  J.  Ha,  J.J.  Grácio,  M.-G.  Lee,  E.F.  Rauch and  G.  Vincze: Int. J. Plast., 46(2013), 130.
• 7)   V.  Tvergaard and  A.  Needleman and  K.K.  Lo: J. Mech. Phys. Solids, 29(1981), 115.
• 8)   N.  Triantafyllidis,  A.  Needleman and  V.  Tvergaard: Int. J. Solids Struct., 18(1982), 121.
• 9)   M.  Goya and  K.  Ito: JSME Int. J. Ser. 1, 33(1990), 57.
• 10)   M.  Gotoh: JSME Int. J. Ser. 1, 35(1992), 62.
• 11)   M.  Kuroda and  V.  Tvergaard: Int. J. Solids Struct., 38(2001), 8945.
• 12)   T.H.  Lin and  M.  Ito: J. Mech. Phys. Solids, 13(1965), 103.
• 13)   P.M.  Naghdi,  F.  Essenburg and  W.  Koff: J. Appl. Mech., 25(1958), 201.
• 14)   P.K.  Bertsch and  W.N.  Findley: Proc. 4th U.S. National Cong. of Applied Mechanics, ASME, New York, (1962), 893.
• 15)   B.  Paul,  W.  Chen and  L.C.  Lee: Proc. 4th U.S. National Cong. of Applied Mechanics, ASME, New York, (1962), 1031.
• 16)   E.  Shiratori and  K.  Ikegami: J. Mech. Phys. Solids, 16(1968), 373.
• 17)   P.M.  Naghdi,  J.C.  Rowley and  C.  Beadle: J. Appl. Mech., 22(1955), 416.
• 18)   A.  Phillips: Proc. 2nd Symp. on Naval Structural Mechanics, Pergamon Press, London, (1960), 202.
• 19)   A.  Phillips and  W.-Y.  Lu: J. Eng. Mater. Technol., 106(1984), 349.
• 20)   T.  Kuwabara,  M.  Kuroda,  V.  Tvergaard and  K.  Nomura: Acta Mater., 48(2000), 2071.
• 21)   K.  Yoshida: Int. J. Solids Struct., 120(2017), 213. DOI: 10.1016/j.ijsolstr.2017.05.004.
• 22)   K.  Yoshida,  A.  Ishii and  Y.  Tadano: Int. J. Plast., 53(2014), 17.
• 23)   S.A.  Meguid,  L.E.  Malvern and  J.D.  Campbell: J. Eng. Mater. Technol., 101(1979), 248.
• 24)   F.  Barlat and  K.  Lian: Int. J. Plast., 5(1989), 51.