2020 Volume 106 Issue 5 Pages 272-280
2020 Volume 106 Issue 5 Pages 272-280
In this study, a method to identify the yield surface by three types of simplified material tests is proposed. The uniaxial tensile test, hydraulic bulge test, and plane strain tensile test are used in this method. A polygon circumscribing the equal plastic work contour can be defined by assuming the associated flow rule on the direction of the plastic strain rate. The parameters of anisotropic yield function are identified as a smooth curve inscribed in this polygon. This paper describes the details of these material testing methods. The yield surface of the cold-rolled steel sheet (SPCE) is identified by the proposed method and modeled with Yld2000-2d yield function. The model is compared to the stress points which are measured by the biaxial stress tests using cruciform specimen. Both yield loci agree well. Moreover, the yield function identified by the proposed method is applied to two types of simple sheet metal forming problems, the hole expansion test and deep-drawing of cylindrical cup. The results of finite element analysis are compared with the experimental results in both problems. The thickness strain on the hole edge in the hole expansion test and the ear height of the deep-drawn cup are evaluated. The results of the analysis using the modeled yield function agree with the experimental results qualitatively.
板成形品の開発期間短縮のために,金型設計段階での事前予測による試作レス化が求められている。このためには板成形シミュレーションの高精度化が必要である。板成形解析では,材料モデリングの適否が解析精度に大きな影響を与え,特に塑性変形特性のモデル化では,異方性降伏関数を用いた精緻な材料モデルが必要となる1–3)。また,成形中に負荷方向が反転する場合は,異方性降伏関数に加えて,移動硬化または複合硬化モデルも考慮する必要がある4,5)。このような材料モデル化においては特殊な材料試験が必要となる。成形中の鋼板は二軸応力下で変形が進行するため,単軸引張試験だけでは,材料の異方性特性を適切にモデル化することはできない。これに対して,十字型試験片または円管試験片を用いた二軸応力試験が提案されている6–8)。現在,前者はISOとして規格化され9),今後の普及が期待される。一方,これらの二軸応力試験には専用の特殊試験設備が必要とされるため,現時点では,研究機関での利用が多く,設計現場での解析を対象とした材料モデリングの標準的な材料試験としては,充分に普及しているとは言い難い。
異方性降伏関数の利用拡大のために,著者らは,一般的かつ古典的な複数の材料試験法の組合せにより,異方性降伏関数を同定する簡易な方法を提案している。この方法では,「単軸引張試験」および「液圧バルジ試験」に加え,汎用の引張試験機に専用冶具を取りつけて行う「平面ひずみ引張試験」により異方性降伏曲面の外接多角形を定義し,これを用いて異方性降伏関数を同定する10–12)。この簡易同定法の妥当性については,材料試験の有限要素解析により,降伏関数が適切に同定できることを数値的に検証している13)。しかし,実験的検証は行われていない。
本報告では,各材料試験法の詳細を述べ,簡易同定法によって実際の軟鋼板の降伏曲面を測定する。この方法で得られた異方性降伏曲面モデルと既存の二軸引張試験法の実験結果14,15)を比較し,提案手法の妥当性について実験的検証を行う。また,同定した異方性降伏関数を用いて穴広げ試験および円筒深絞り加工の有限要素解析を行い,実験結果との比較にもとづき,簡易同定法による材料モデリングの有効性を示す。
提案する降伏曲面の簡易同定法では,単軸引張試験,液圧バルジ試験(等二軸応力試験)および平面ひずみ引張試験の三種類の材料試験を用いる。Fig.1に本同定法の模式説明図を示す。図は板材の圧延方向(RD)および圧延直交方向(TD)の垂直応力(σx,σy)による応力平面を示す。
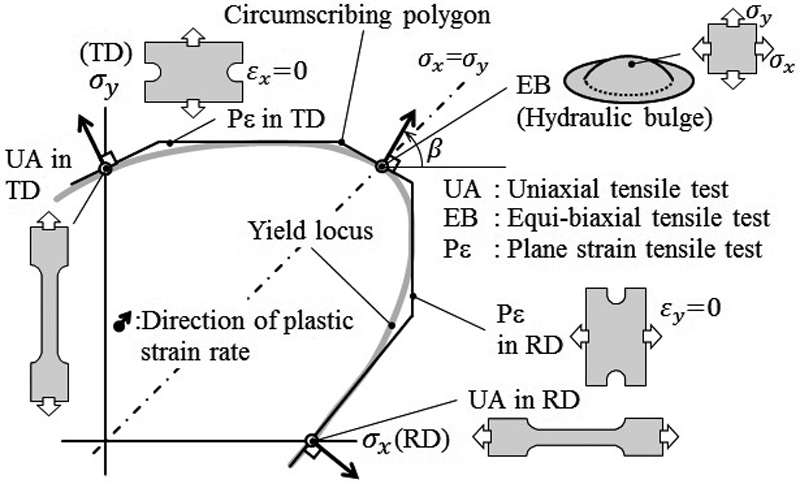
Simplified method to model anisotropic yield function.
単軸引張状態での降伏点は,各垂直応力の軸と降伏曲面の交点を示す。また,等二軸応力状態の降伏点は,σx=σyの直線と降伏曲面の交点を示す。塑性ひずみ増分{dεp}が降伏曲面の法線方向と一致すること(関連流れ則)16,17)を仮定すると,塑性ひずみ増分比の実測値から,これらの応力点における降伏曲面の接線が定まる。また,RDおよびTDの平面ひずみ引張状態では,引張り方向に直交する塑性ひずみ増分がゼロとなる。このため,降伏曲面が外に凸の滑らかな関数であることを仮定すれば,降伏曲面の各垂直応力軸方向への極大値を定めることができる。このようにして応力空間に3つの応力点と5本の外接線が定義され,これに内接する滑らかな曲線として降伏曲面を同定することができる。なお,本研究では,塑性仕事等価説16)を仮定し,同一の塑性変形仕事における応力点の集合を降伏曲面とみなして18,19),降伏曲面の外接多角形を定義する。
供試材には,公称板厚1.2 mmの深絞り加工用冷間圧延鋼板(SPCE)を用いる。この供試材は,日本鉄鋼協会「先進的多軸応力試験による鋼板成形の高度化研究会」20)で共通サンプルとして提供された鋼板であり,同一ロットの板材の降伏曲面(等塑性仕事面)が二軸応力試験によって測定されている14,15)。本研究での試験片採取のレイアウト模式図をFig.2に示す。
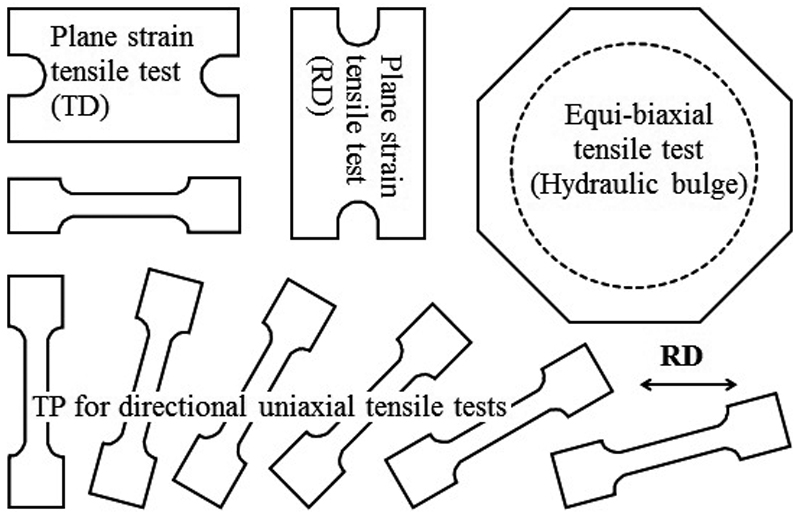
Layout of specimens for proposed materials tests.
簡易同定法で用いる3種類の材料試験方法について,以下,詳細に説明する。いずれの試験においても,ひずみの測定には,塑性域ひずみゲージ(東京測器研究所(株)製YFLA-2)を用いる。各試験を5回実施し,平均値を求める。
(1)単軸引張試験(UA:Uni-Axial tensile test)
試験にはJIS Z2241の13 B号試験片を用いる。Fig.2に示したようにRDからTDへ15°毎の計7方向の単軸引張試験を実施し,異方性主軸座標系におけるせん断応力τxyの降伏関数への寄与を測定する。いずれの試験においても試験片中央部に引張り方向および試験片幅方向の二方向のひずみゲージを貼付し,これらのひずみからLankfordのr値を測定する。
(2)液圧バルジ試験(等二軸応力試験.EB:Equi- Biaxial tensile test)
液圧バルジ試験は,周囲をビードで固定した板材の片面に液圧を加えることで,円孔ダイス側へドーム状に板材を膨らませ,頭頂部に等二軸応力を与える試験法である。板材に強い異方性がある場合,完全な等二軸応力状態をつくることは困難であることが指摘されているが21),ここでは,近似的に等二軸応力状態を仮定する。
Fig.3に試験片と金型の寸法および実験の様子を示す。試験片および金型の寸法は吉田による解析21)を参考にした。試験片中央にRDおよびTD方向のひずみゲージを貼付する。また,写真に示すように四点式(固定点3点と変位測定点1点)の曲率計を試験片頭頂部に乗せて,外表面の曲率半径を測定する。試験から得られる負荷圧力p,外表面の二軸ひずみεsx,εsyおよび外表面の曲率半径ρsを用いて,等二軸応力σEBは,以下の式により算定される。
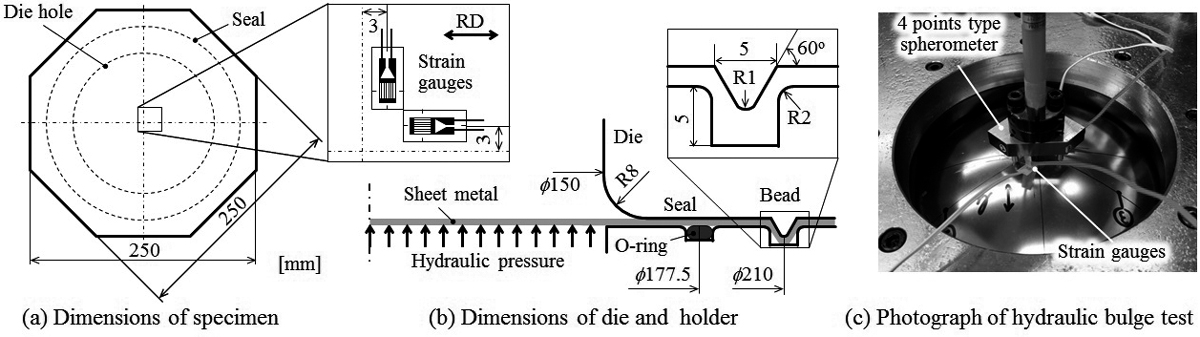
Dimensions and photograph of hydraulic bulge test.
ここで,tは板厚,ρは曲率半径を示し,下付き添字のsは外表面での測定値を,mは板厚中央面の値を示す。これらの式は非線形連立方程式となるため,数回の収束計算を行って,等二軸応力σEBを求める。
(3)平面ひずみ引張試験(Pε:Plane strain tensile test)
平面ひずみ引張試験では,幅広の試験片を短いチャック間距離で把持し,幅方向変形を拘束した状態で試験片を引っ張る22,23)。幅広試験片を把持するための専用のチャックが必要となるが,試験装置としては標準的な引張試験機で実施できる。Fig.4に平面ひずみ引張試験の試験片形状と試験の様子を示す。通常の引張試験で用いられるクサビ式チャックを参考に,最大150 mm幅の試験片を把持できるチャックを設計した。平面ひずみ引張試験はRDとTDの2方向についてそれぞれ実施する。
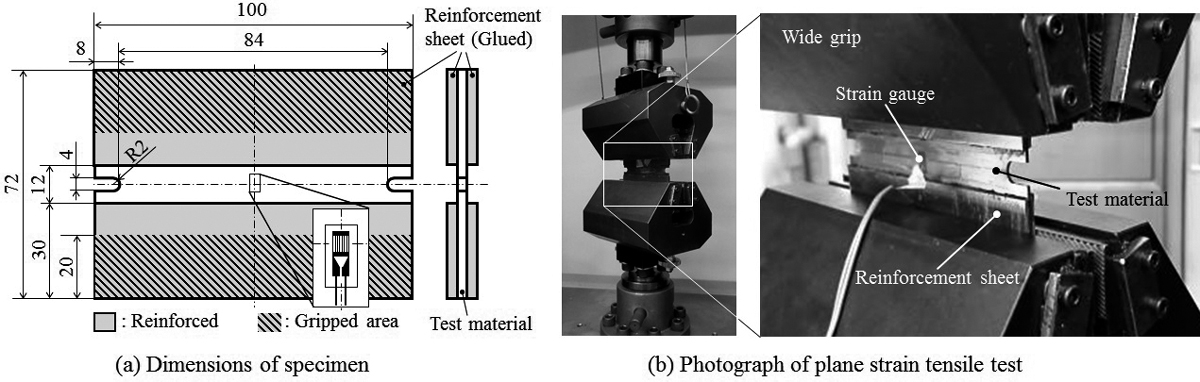
Dimensions of specimen and wide grips on plane strain tensile test.
平面ひずみ引張試験で生じる試験片の減肉は,切欠き間の応力評価部分だけにとどまらず,チャック内部でも生じる。このためチャック部から材料が引き出され,正確な平面ひずみ状態の応力測定ができない24)。これを改善するために,図に示すように応力評価領域(切欠き部)と上下4 mmを除いて試験片に補強板を接着し,試験片の変形を応力評価領域に限定させる。補強板にはチャック歯が喰い付き易いアルミ合金(A5052-H32,t=1.0 mm)を用い,2液アクリル系接着剤(セメダイン(株)製,メタルロックY611)により試験片の両面に補強板を接着した。なお,接着後に60°Cで1時間の保温を行い,接着力の安定化を図った。
また,切欠き部近傍ではひずみ場の乱れが生じるため,平面ひずみ応力の算出精度が低下することが懸念される。差分荷重による正確な平面ひずみ応力の算出についても検討しているが25,26),有限要素法解析では,試験片幅100 mmの単独の平面ひずみ引張試験でも応力の真値と測定値の誤差は1%以下であるため,今回の実験には差分荷重法は適用していない。
なお,平面ひずみ引張試験片の幅方向変形を拘束するための幅方向応力σwは実験的に測定することはできない。しかし,平面ひずみ状態であるため,幅方向の塑性ひずみ増分dεwpをゼロとすれば,幅方向応力σwは塑性仕事へ影響しない。よって,幅方向応力σwの不明は,塑性仕事算出の障壁にはならない。
以上,述べた実験方法によって得られる降伏曲面の同定誤差については,有限要素解析を用いて検証を行っている13)。
Fig.5に各試験で貼付したひずみゲージにより測定されたひずみ履歴を示す。平面ひずみ引張試験においては,試験片幅方向のひずみは小さく,目的とした平面ひずみ状態が再現されている。また,液圧バルジ試験の結果は,ややばらつきが大きいものの,ひずみ比は,ほぼ1:1となっている。Fig.6に各試験で得られた真応力-真塑性ひずみ曲線を示す。RD,TDともに単軸引張が最も低く,等二軸引張および平面ひずみ引張の真応力-真塑性ひずみ曲線は,ほぼ同程度のレベルを示している。
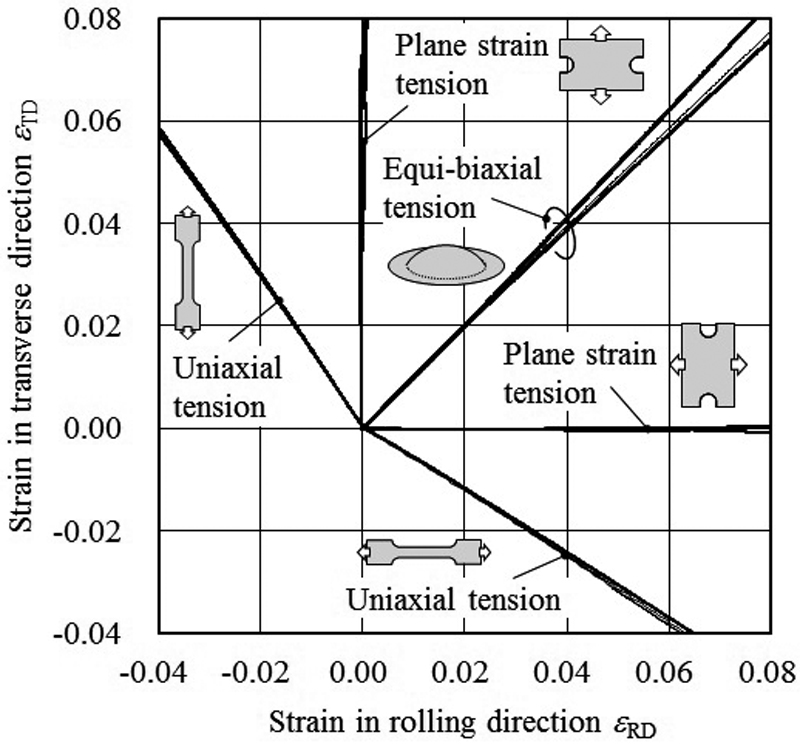
Strain paths measured by strain gages in uniaxial, plane strain and equi-biaxial tensile tests.
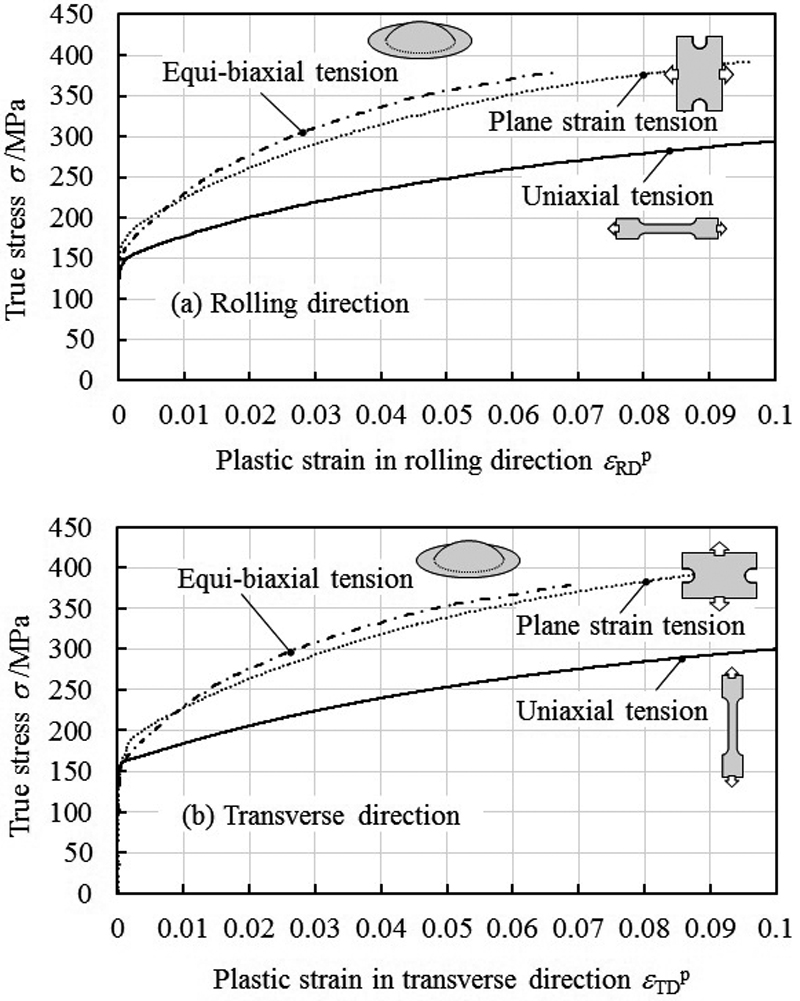
Stress-strain curves in uniaxial, plane strain and equi-biaxial tensile tests. (a) rolling direction and (b) transverse direction.
本研究では,塑性仕事等価説を仮定し,等塑性仕事面を降伏曲面とみなす。外接多角形を描くための等塑性仕事の算出方法説明図をFig.7に示す。各試験における真応力-真塑性ひずみ曲線を積分し,単位体積あたりの塑性仕事W0が等しくなる応力値を用いて外接多角形を定義する。降伏曲面は,この塑性仕事W0によって定義されるが,物理的イメージを明確にするため,RDの単軸引張試験における真塑性ひずみを基準塑性ひずみε0pとし,これを用いて塑性仕事レベルを表す8)。
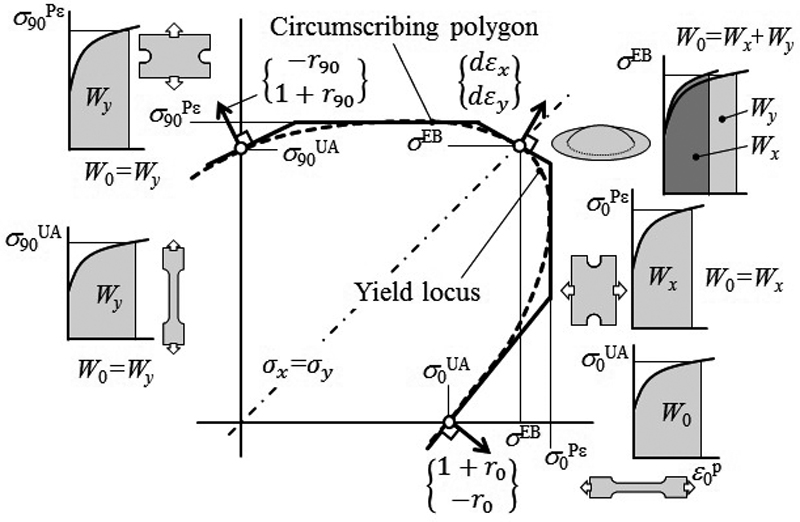
Schematic illustration for circumscribing polygon of equal plastic work contour.
Fig.8に細い実線で簡易同定法によって算出された等塑性仕事面の外接多角形を示す。図中の○印は単軸および等二軸引張試験における等塑性仕事点を示し,○につけた短い線分は塑性ひずみ増分方向(すなわち降伏曲面の法線方向)を示している。塑性仕事の小さいε0p=0.005から0.03ではわずかに外接多角形の形状変化を伴うものの,ε0p=0.03以降は大きな形状変化は見られない。
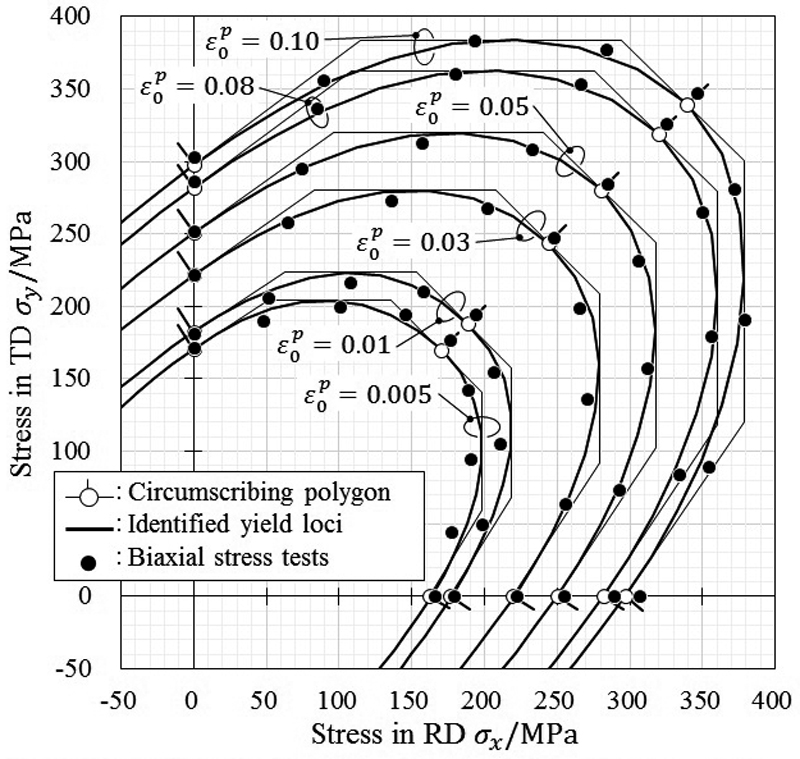
Identified yield loci by circumscribing polygons and stress points measured by biaxial stress tests.
外接多角形に内接する滑らかな曲線として降伏関数を同定する。降伏関数にはBarlatらが提案したYld2000-2d27)を用いる。Yld2000-2dの材料パラメータは,係数α1~α8と指数Mの計9個である。これらのパラメータを定めるために,実験値と降伏関数モデルの誤差の二乗和として,以下に示す誤差関数ψを定義する。
ここで,σは応力値を,βは降伏曲面の外向き法線方向(Fig.1参照)の角度をrad単位で表した値をそれぞれ示す。右上添字のUA,EBおよびPεは,それぞれ単軸引張り,等二軸引張りおよび平面ひずみ引張りの各試験での値を示す。また,右下添字は単軸および平面ひずみ引張試験におけるRDと引張り方向のなす角θ(単位は°)を示す。波線(~)付きの変数はモデル化した降伏関数の値を,波線無しの値は材料試験で測定された値を示す。wσおよびwβは応力値と法線方向のそれぞれの誤差に対する重みであり,ここではwσ/wβ=2を用いた。この値は,応力単位における約1%の誤差と塑性ひずみ増分方向における1°(0.0175 rad)の誤差をほぼ同等に評価することを意味している。
この誤差関数ψを最小化する降伏関数の材料パラメータ求めることで降伏関数を同定する。誤差最小化計算には,Microsoft社の表計算ソフトExcelに組み込まれているSolver機能の大域最適解探索ツールを用いた。
Fig.8に各等塑性仕事で同定した降伏関数モデルによる曲線を太い実線で示す。すべての等塑性仕事レベルで,3つの応力点を通り多角形に内接する滑らかな降伏曲面を,Yld2000-2d降伏関数で表現できている。また,Fig.9に引張方向を変化させた場合の単軸引張試験の流動応力とr値について実測値と降伏関数モデルの比較を示す。深絞り用鋼板であるため,流動応力の面内異方性は比較的低い。応力値についてはYld2000-2d降伏関数で精度よく近似できているが,r値については,面内分布の傾向は表現できているものの,定量的には充分な近似とは言い難い。より近似精度を向上させるためには,Yld2000-2dよりも材料パラメータ数の多い,より複雑な降伏関数28,29)を用いる必要がある。
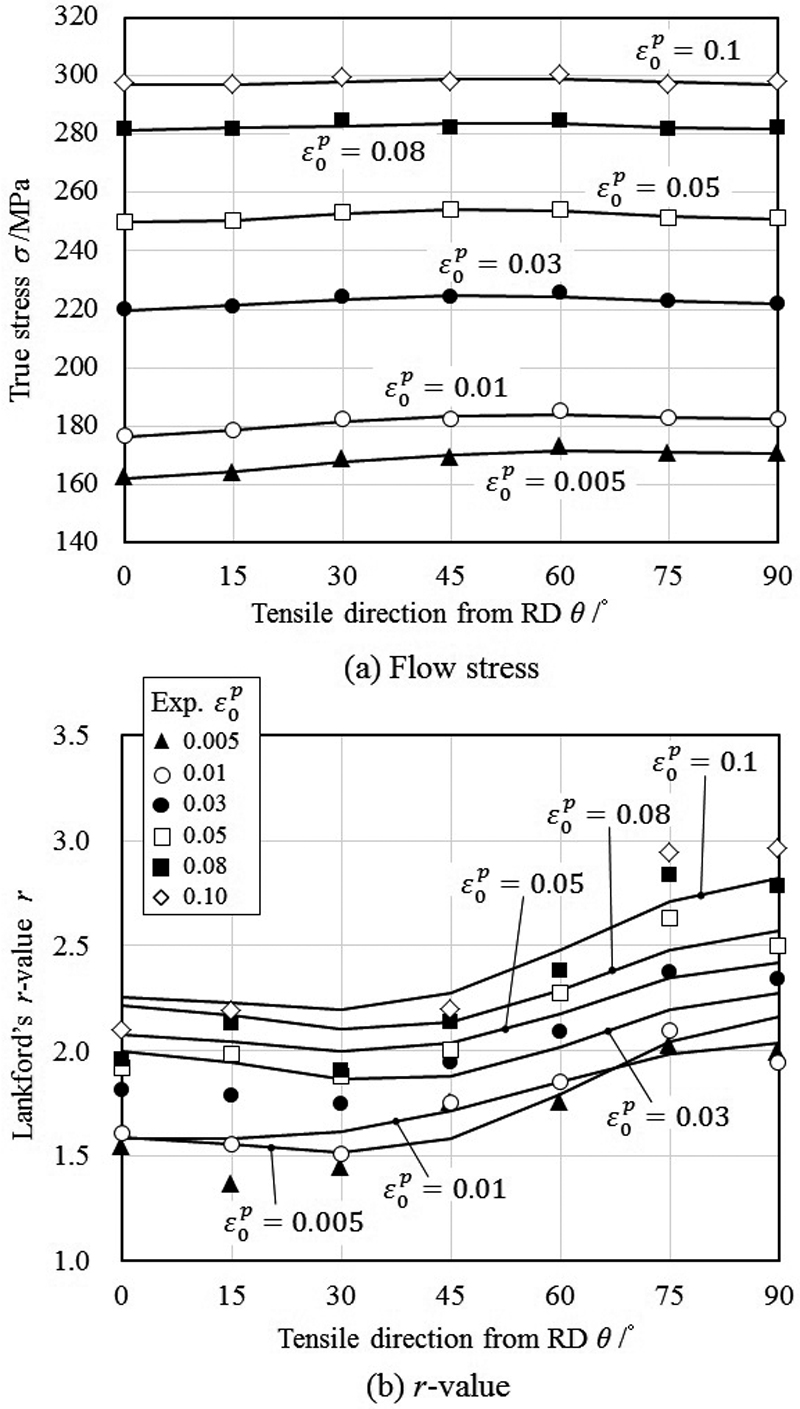
Identified yield function and uniaxial tensile test data of in-plane distribution of (a) flow stress and (b) r-value.
本研究で用いた供試材と同一ロットの鋼板の等塑性仕事点が,十字形試験片による二軸応力試験および円管試験片による二軸バルジ試験によって求められている14,15)。この結果を参照値として,本提案手法によって同定された降伏関数モデルを評価する。Fig.8に二軸応力試験で測定した参照値を●で示す。
簡易同定法で得られた降伏曲面と二軸応力試験による参照値を比較すると,塑性変形の小さいε0p=0.03までは,簡易同定法による降伏曲面の応力がやや高めにモデル化されているが,大きな塑性変形の領域では,同定された降伏曲面は,二軸応力試験の実測値とほぼ一致している。簡易同定法によって同定した降伏関数は,既存の二軸応力試験によって測定された等塑性仕事点とよい一致を示しており,本手法により適切な降伏関数が同定できる。
ここでは,基礎的な板成形実験として穴広げ試験および円筒深絞り加工を取り上げ,同定した降伏関数を用いた有限要素解析結果と成形実験結果を比較する。これにより,簡易同定法でもとめた降伏関数の板成形解析における有効性を確認する。穴広げ試験では,板材は面内二方向とも引張応力状態(応力空間の第一象限)で変形する。一方,深絞り加工のフランジ部では,成形中に引張りおよび圧縮の応力が同時に生じる(応力空間の第二および第四象限)。この二つの実験では板成形における代表的な応力状態が生じるため,これらを検証として用いる。
Table 1に簡易同定法により求めた基準塑性ひずみε0p=0.08におけるYld2000-2d降伏関数の材料パラメータを示す。また,弾性特性およびモデル化した変形抵抗曲線のパラメータを同表に示す。硬化則には等方硬化を仮定する。以下の成形解析においては,これらの材料パラメータを用いる。解析には汎用非線形有限要素解析コードMarcを用いる。対称性を考慮して1/4形状でモデル化し,板材には平面応力を仮定して薄肉シェル要素を,金型には剛体曲面を,それぞれ用いる。Yld2000-2d降伏関数は,ユーザサブルーチンライブラリUMMDpを用いて解析に組み込んだ30)。
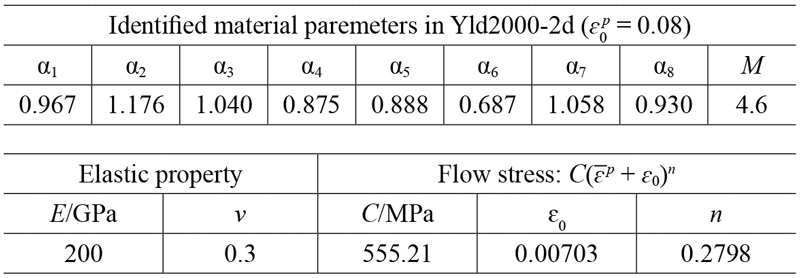
Identified material parameters for SPCE.
穴広げ試験の実験条件および解析モデルをFig.10に示す。実験結果は,今回の供試材と同一ロット材を用いた実験の文献値14)を引用する。解析における摩擦係数はμ=0.15を用いた。
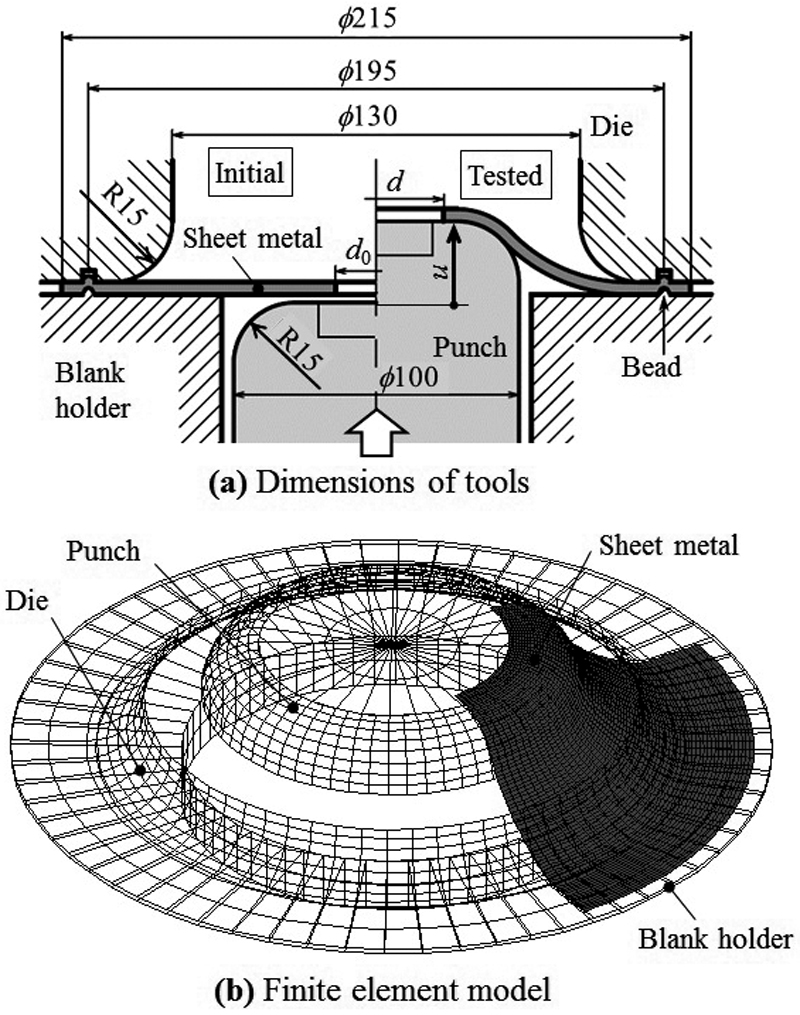
Experimental set-up and FEA model for hole expansion test.
パンチストロークu=30.0 mmまで加工した際の,変形前の孔縁から2 mmの位置における板厚方向真ひずみεzの周方向分布をFig.11に示す。実測結果を○で,解析結果を実線でそれぞれ示す。実測結果に対して全体的に解析結果の板厚減少が低く算出される傾向がある。しかし,解析による板厚ひずみεzの分布形態と変動幅は実験結果によく一致している。提案手法でモデル化した降伏関数で,板材の面内異方性の影響は定性的に表現できている。
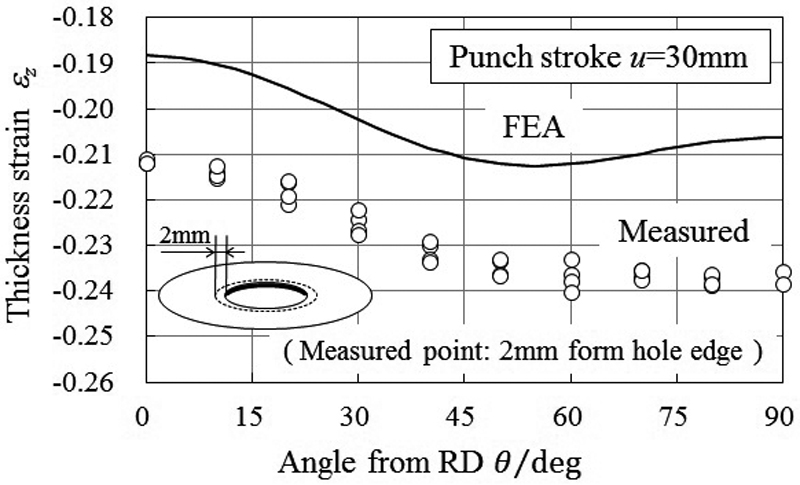
Comparison between measured and analyzed thickness strain along the hole edge.
円筒深絞り加工の成形条件および実験の様子をFig.12に示す。絞り比DR(ブランク径/パンチ径)は1.8である。実験では金型と素板の間に潤滑油を用いており,解析では摩擦係数をμ=0.0,0.1および0.2の3条件に設定した。しわ抑え力はBHF=10 kNとして,実験では写真に示すように支柱に組み込んだ圧縮ばねでしわ抑え力を与えた。
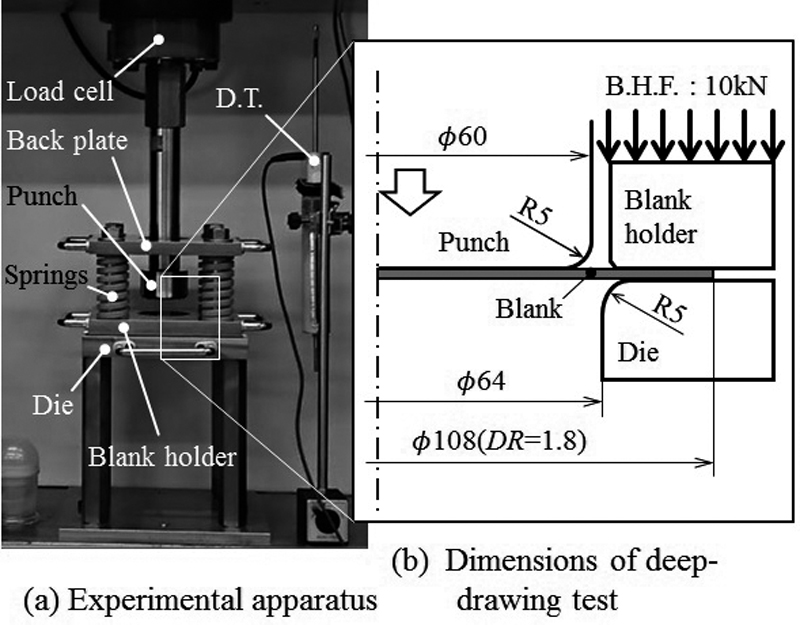
Experimental set-up for deep-drawing test.
Fig.13に実験と解析の荷重-ストローク曲線の比較を示す。実験と解析の曲線の傾向はよく一致しており,荷重の比較から摩擦係数μは概ね0.1と0.2の間にあると推定される。Fig.14に実験と解析(μ=0.1)の成形後のカップ形状の比較を示す。解析結果には相当塑性ひずみ分布を示す。面内異方性が比較的低い材料であるため,顕著な相当塑性ひずみの偏りやカップ高さの変動(耳)は見られないが,RDとTDの中間(45°方向)でわずかな谷が生じており,解析でも同様の傾向が見られる。これを定量的に評価するために試験片全周のカップ高さを測定し,解析と比較した結果を Fig.15に示す。解析には薄肉シェル要素を用いているため,板厚方向圧縮応力は考慮されていない。このため,解析結果のカップ高さは全体的にやや低く算出される傾向にある。これを考慮すれば,解析によって予測した耳高さの分布形態および変動幅は実測結果とよく一致している。
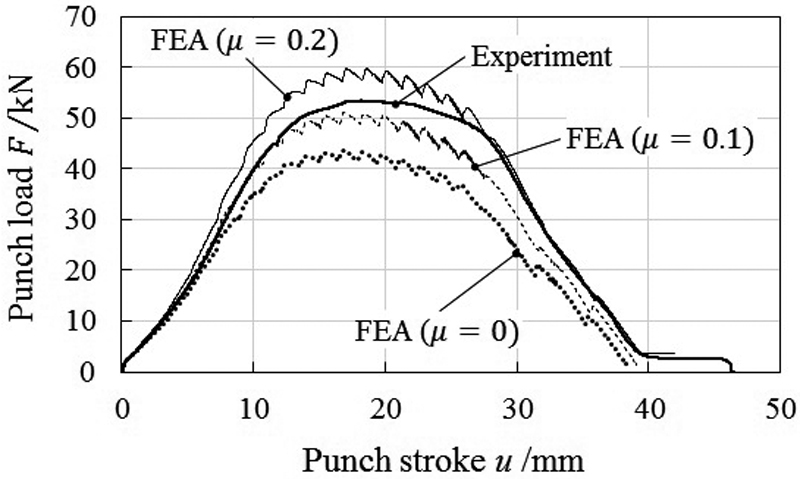
Comparison between measured and analyzed results of load-stroke curves on deep-drawing test.

Comparison between experiment and analyzed shapes of deep-drawn cup.
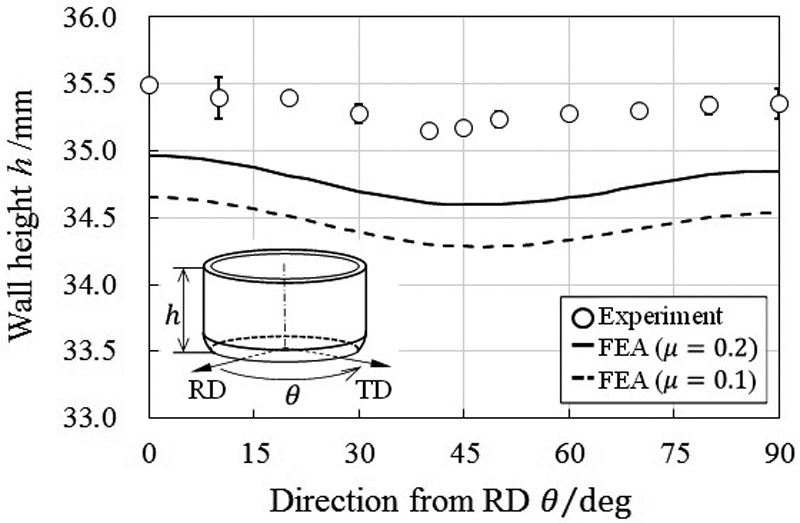
Comparison between measured and analyzed results of wall height distribution.
簡易同定法では試験法の制約から応力空間における第一象限での測定結果にもとづいて降伏曲面をモデル化している。これに対して,深絞り成形における主たる変形は,フランジ部での引張り・圧縮が混合した応力状態で進展する。このような違いがあるにもかかわらず,実験結果と解析結果は定性的な一致を示した。
降伏関数簡易同定法により,鋼板の降伏曲面をモデル化し,信頼できる二軸応力試験の結果と比較した。また,基本的な板成形問題について,同定した降伏関数を用いた解析と実験を比較した。得られた知見を以下にまとめる。
(1)等塑性仕事面の外接多角形からYld2000-2d降伏関数によってモデル化した降伏曲面と既存の二軸応力試験結果の等塑性仕事点を比較した結果,両者はよい一致を示した。提案した簡易同定法により異方性降伏関数をモデル化することが可能である。
(2)同定した降伏関数を用いて,穴広げ試験および円筒深絞り加工について有限要素解析を行い,この結果と実験結果を比較した。いずれの成形問題でも解析は実験の傾向を表現できた。簡易同定法による降伏関数モデル化は板成形解析において有効である。
(3)簡易同定法では,液圧バルジ試験機および平面ひずみ引張試験用の幅広チャックが必要となるが,いずれも比較的単純な装置・治具であるため,簡便な異方性降伏関数同定法として利用できる。
なお,反転負荷を伴う板成形解析の高精度化にはBauschinger効果を表現できる移動硬化モデルが必要である。本研究では2で述べたように,塑性仕事等価説を仮定しているため,移動硬化は考慮されていない。この点については今後の課題としたい。
本研究は,平成27年4月から平成30年3月に実施された(一社)日本鉄鋼協会「先進的多軸応力試験による鋼板成形の高度化」研究会の活動の一環として行われた。同一材料で降伏曲面を比較できたことは本研究にとって貴重な機会であった。多くの議論を頂戴した委員各位に謝意を表する。また,東京農工大学 桑原利彦 教授より二軸応力試験の実験結果を提供いただいた。ここに謝意を表する。