2024 Volume 110 Issue 8 Pages 569-589
2024 Volume 110 Issue 8 Pages 569-589
This paper reviews studies on the prediction of ductile fracture during metal forming using an ellipsoidal void model and some other models proposed by the author and some relevant studies. Section 2 discusses the research on the theory of voids for predicting ductile fracture during metal forming. Section 3 summarizes the simulation method for predicting ductile fracture during metal forming using the ellipsoidal void model, and Section 4 summarizes the simulation result on the ductile fracture prediction during metal forming using the ellipsoidal void model. Section 5 shows the applicability of the ellipsoidal void model and the simulation result on the ductile fracture prediction during metal forming using some other models.
材料が大きな塑性変形を受けた後に材料が破壊する現象を延性破壊と言う。材料の成形性は時代と共に常に改善されて来たが,生産性向上のために材料は常に材料の成形限界近くまで加工される。そのため,材料の破壊条件,すなわち如何なる条件が満足された時に材料が破壊するか,を知ることは永遠に必要になる。最近の二十年間における計算機性能および計測器性能の劇的な進歩を利用した延性破壊に関する無数の研究により,延性破壊現象が朧気ながら明らかになりつつある。しかし,これらの研究成果を実生産において十分に利用出来るとは言い難く,延性破壊に関する研究は今後も精力的に行われるであろう。
最近の十数年間に行われた延性破壊に関する研究の量は膨大であり,また研究の内容は多岐に亘る。2016年にその当時迄の延性破壊に関する研究を総括した二編の解説1,2)が発表された。これらの解説の著者数は複数であり,またこれらの解説の頁数は五十頁前後,引用文献数は三百編前後であった。その当時迄の延性破壊に関する研究の概要を把握するために,これらの解説は役に立とう。さて,2016年以降に行われた延性破壊に関する研究の量が膨大であり研究の内容が多岐に亘ることは言うまでも無い。しかし,現在迄の延性破壊に関する研究を一人の著者で総括することは困難である。
筆者は2020年に,「金属加工における延性破壊」と言う題目の専門書3)を上梓した。この本の中で筆者は,最新の研究ではなく半ば古典的な2010年頃迄に行われた代表的な研究を紹介した。また筆者は,筆者等が行っている楕円空孔モデルによる延性破壊予測のための解析法とその当時迄の解析結果を紹介した。一方,2020年にその当時迄の金属加工中の損傷を扱った解説4)が複数の著者によって執筆されたが,この解説の頁数は二十数頁,引用文献数は約二百編であり,この解説も読者の参考になろう。
従来,金属加工中の延性破壊を予測するために使用される破壊条件は,空孔や転位等の微視的視点からではなく,応力や歪等の巨視的視点から導かれた5,6,7,8)。しかし,微視的には延性破壊は空孔の発生,空孔の成長,そして空孔の合体により起きると考えられている9)。そのため,微視的な現象である延性破壊を巨視的な変数である応力や歪を使用して高精度に予測することは本質的に困難であろう。
材料が巨視的に破壊する前に変形の局所化が起こることはよく知られている10)。そして,その局所化された変形が平面歪変形であることが解析的11)および実験的12)に知られている。そのため,微視的な延性破壊の最終過程である空孔の合体は母材の平面歪変形により判定されなければならない。最近,空孔を利用して微視的な視点から延性破壊を予測することが筆者等も含む多数の研究者によって行われている13,14,15)。しかし,これらの研究において空孔の合体は基本的にThomasonの三次元変形モデル16,17)に基づいており,母材の平面歪変形により空孔の合体が判定される研究18,19)は限定される。一方,筆者等の研究では4章で説明するように,塊材加工である据込みや引抜きおよび板材加工である穴広げや二軸薄板引張りを取り扱っており,言わば金属加工全般を取り扱っている。そして,筆者等の研究以外に金属加工全般の延性破壊を取り扱った研究は無い。
先に述べた解説1,2,4)の著者数と頁数および以上を考慮して,本解説では延性破壊全般を解説するのではなく,筆者等が行っている研究およびそれに関連した研究を紹介することが現実的であり有効であろう。そこで,本解説では,筆者らが行っている研究およびその関連研究を紹介する。2章では筆者等の研究に関連した空孔理論の概要を紹介する。3章では楕円空孔モデルによる解析法を,4章では楕円空孔モデルによる解析結果を紹介する。そして,5章では楕円空孔モデルの適用限界を示すと共にその他の解析法による解析結果を紹介する。
微視的には,延性破壊は空孔の発生,空孔の成長,そして空孔の合体により起きると考えられているため9),これらの項目毎に空孔の理論を紹介する。なお,筆者の専門書3)および空孔理論による延性破壊予測に関する筆者の解説20)も参考になろう。
2・2 空孔の発生塑性変形による空孔の発生に関するGoods and Brownの解説21)に示されている様に,空孔の発生は,不純物である介在物と材料である母材の分離,あるいは介在物の破壊により起こる。Fig.1に空孔発生の概念図を示す。図(a)は介在物と母材の分離,図(b)は介在物の破壊を示す。空孔の発生が,介在物と母材の分離と介在物の破壊のいずれにより起こるかは材料に依存する。ここで,空孔の発生に関する新しい理論はここ数十年間においてあまりない。本節では,次章以降の筆者らの解析に関連した,空孔発生に関する若干の文献のみを紹介する。

Schematic diagram of void nucleation.
Gurland22)は球状化処理された過共析鋼を用いて引張試験,圧縮試験そして捩り試験を行って,セメンタイト粒子の破壊を観察した。そして,引張試験において破壊したセメンタイト粒子の割合が歪に比例することを示した。
Argonら23,24,25)は一連の研究において,中炭素鋼,銅クロム合金そしてマルエージング鋼を用いて引張試験を行うと共に,弾塑性有限要素法による解析を行って介在物と母材の界面に働く応力を求めた。そして,界面応力がある値の時に介在物と母材が分離することを示した,すなわち介在物と母材間の接合強度を求めた。
一方,Inoue and Kinoshita26,27)は様々な炭素量を持つフェライト-パーライト鋼の引張試験を行って,材料の縦断面をSEM観察した。そして,パーライト粒内のセメンタイト板が破壊して空孔が発生することを示した。ここで,パーライト粒を第二相粒子すなわち介在物と考えれば介在物破壊により空孔が発生したと言える。
本節で引用した全文献は1970年代に公表されており,空孔発生に関する実験および解析の更なる発展を期待する。最後に,空孔発生に関する古典的な解説28)および最新の解説29)を紹介する。ここで,後者の解説の頁数は五十数頁,引用文献数は約四百編であり,この解説により最新の情報が得られるであろう。
2・3 空孔の成長任意の形状の空孔が任意の応力および歪履歴を受ける場合の空孔の成長は,代表体積要素モデルを用いた有限要素解析により容易に得られる。しかし,解析にある程度の計算時間が必要なため,計算時間がほぼ零である解析的モデルが現在においても利用される。
McClintock30)は材料中心部に無限長さの円柱形空孔がある場合の空孔の成長を求めた。すなわち,材料非中心部の応力および歪と円柱形空孔の半径の関係を求めた。そして,空孔の成長速度が材料非中心部の応力三軸度に大きく依存することが示された。なお,同論文では隣接する円柱形空孔が接触する時を空孔の合体条件と仮定しているが,空孔が接触する遙か前に隣接する空孔間にある材料が局部変形により括れて空孔が合体するため,この空孔の合体条件は不適切である。
Rice and Tracey31)は材料中心部に球形空孔がある場合の空孔の成長を求めた。すなわち,材料非中心部の応力および歪と球形空孔の半径の関係を求めた。ここで,解析では球形空孔が拡張した球形空孔になる変形および楕円体形空孔になる変形が想定される。そして,空孔の成長速度が材料非中心部の応力三軸度に大きく依存することが示された。
一方,Gurson32)は球形材料の中心に球形空孔を含む材料に対する降伏関数を導いた。すなわち,Rice and Tracey31)による球形空孔を含む材料中心部の微視的な歪速度成分から,微視的な応力および歪と巨視的な応力および歪を結びつけるBishop and Hill33)の考えに従って巨視的な歪速度成分,更にエネルギ消散率が求められた。Gursonの降伏関数32)は多孔質材料の降伏関数として,筆者を含む多数の研究者によって現在でも利用されている。
2・4 空孔の合体空孔の合体は一般にエネルギ的に判定される。すなわち,隣接する空孔の間にある材料に変形が集中して空孔間の材料が括れる様な変形がエネルギ的に一番起きやすい場合,空孔が合体すると判定する。ここで,空孔間の材料が括れることを内部括れと呼ぶ。
Fig.2に平面歪引張における二つの隣接する空孔間の内部括れ領域における材料変形の単純化された表示を示す。図(a)はThomason18)に,図(b)はMelander and Ståhlberg19)による。ここで,灰色の領域が塑性変形領域を,点線が速度不連続線を表す。そして,隣接する空孔間の材料が括れる様な変形に必要なエネルギが,空孔を含む多孔質材料が一様に変形する為に必要なエネルギよりも小さい場合,空孔が合体すると判定する。ここで,紙面に垂直な方向の歪が零である平面歪変形が仮定される。更に,変形により空孔体積率が変化しないと仮定されると共に,空孔の変形勾配が材料の変形勾配に等しいと仮定される。

Simplified expression of material deformation in internal necking region between two neighboring voids in plane-strain tension.
Thomasonモデルでは,隣接する空孔間の材料が括れる様な変形に必要なエネルギを計算するためにKudo34)が鍛造の解析で用いた速度場が使用される。ここで,図中のh'/hで表される塑性変形領域の大きさはエネルギが最小化されるように最適化されるが,その最適化を行うことは煩雑である。また,後で述べる様に,その最適化されたh'/hは極めて小さいため,Melander and Ståhlbergモデルではh'/hが零と仮定される。すなわち,Melander and Ståhlbergモデルでは,速度不連続線のみが仮定されて塑性変形領域が仮定されない。
Fig.3に平面歪引張における空孔体積率の影響3)を示す。図(a)は破壊歪に,図(b)は塑性変形領域に及ぼす影響である。空孔体積率の増加と共にh'/hは増加するが,h'/hは極めて小さい。また,Melander and Ståhlbergモデルによる空孔体積率と破壊歪の関係は,Thomasonモデルによるそれと殆ど一致するため,Melander and Ståhlbergモデルの有効性が確認される。なお,Melander and Ståhlbergモデルによる空孔体積率と破壊歪の関係は,簡単な式で表現される19)。また,Thomasonモデルによる空孔体積率と破壊歪の関係は,銅合金の引張試験により得られたEdelson and Baldwin35)による空孔体積率と介在物体積率の合計と破壊歪の関係と概ね一致する18)。

Effect of void volume fraction in plane-strain tension3).
Fig.4に各時間段階における全体のシミュレーション手順の概観を示す。巨視的シミュレーションと微視的シミュレーションは連成しておらず,巨視的シミュレーションが実行された後に微視的シミュレーションが実行される。巨視的シミュレーションでは,材料の変形が剛塑性有限要素法36)により解析される。巨視的シミュレーションで計算された材料の変位勾配速度と空孔体積率速度が次の微視的シミュレーションで利用される。微視的シミュレーションでは,楕円空孔モデルにより材料の破壊が評価される。材料が破壊したか否かの情報が次の時間段階における巨視的シミュレーションで利用される。巨視的シミュレーションと微視的シミュレーションの整合性を保つために,微視的シミュレーションでは剛塑性材料が仮定される。巨視的シミュレーションと微視的シミュレーションは筆者が開発したFortran90で記述された計算機ソフトウェアを使用して実行される。

Overview of entire simulation procedure at each time step.
巨視的シミュレーションでは,Gursonの降伏関数32)が利用されるが,Gursonの降伏関数は応力の二乗の関数では無いため,剛塑性有限要素法による解析が必ずしも容易に実行されない37)。そのため,近似的なGursonの降伏関数37)が利用される。また,Gursonの降伏関数により,空孔の成長が考慮される。
なお,次節以降で述べる様に,楕円空孔モデルでは破壊に関する材料定数は唯一である。すなわち,それは空孔体積率の発展方程式における空孔発生項の中の一つの未定定数である。
3・2 空孔の発生空孔の発生は,巨視的シミュレーションの中で,空孔体積率の発展方程式において考慮される。発展方程式は材料に依存するが,以下の発展方程式のいずれかが用いられる。
| (1) |
| (2) |
| (3) |
ここで,fは空孔体積率,R ( )はランプ関数であり,x≥0の時R(x)=x,x<0の時R(x)=0である。また,A0およびA1は材料定数であり,特に指摘しない限り,引張試験において解析より得られる絞りが実験より得られる絞りに一致するようにA0およびA1が定められる。式(1),式(2),式(3)の右辺第一項は空孔の成長を表すが,右辺第二項および右辺第三項は空孔の発生を表す。そして,式(3)の空孔発生項は,式(1)の空孔発生項と式(2)の空孔発生項の和である。すなわち,式(3)は式(1)と式(2)の中間的な式である。なお,式(1)および式(2)の材料定数は一個であるが式(3)の材料定数は二個であるため,式(3)の材料定数を一個にするために式(3)においてA1=3A0と仮定される。また,ランプ関数R ( )の括弧内は応力三軸度である。
式(1)と式(2)のいずれが用いられるかに関する筆者の今までの知見を述べる。非鉄金属材料では式(1)と式(2)のいずれかが用いられる38)。ここで,式(1)が用いられる材料の特徴と式(2)が用いられる材料の特徴は特に無い。一方,鉄鋼材料では炭素量の増加と共に,用いられる式が式(1)から式(2)に変化する39)。言い換えると,低炭素鋼では空孔の発生が歪に依存する式が用いられるが,中炭素鋼では空孔の発生が歪および応力三軸度に依存する式が用いられる。なお,式(1),式(2),式(3)は非常に簡単な式であり,式(1),式(2),式(3)をあらゆる材料に適用出来るとは考え難い。空孔の発生に関する更なる研究の進展を期待する。
3・3 空孔形状および空孔配置 3・3・1 基本的な考え方介在物の有無および介在物の破壊の有無は,空孔形状および空孔配置において考慮される。
Fig.5に空孔形状および空孔配置を示す。実線は空孔の輪郭を表す,また破線は二つの隣接する空孔間の領域を二等分する線を表す。図(a)は変形前を,図(b)は変形後を示す。空孔形状および空孔配置の基本的な考え方を説明するため,介在物および空孔の発生を仮定しない。

Void shape and void configuration.
空孔形状に関して次の仮定がなされる。
空孔配置に関して次の仮定がなされる。
空孔の変位勾配が材料の変位勾配に等しいと言う仮定は必ずしも妥当ではない。しかし,その仮定は空孔形状と空孔配置の計算を容易にすると共に空孔形状と空孔配置を計算するための時間をほぼ零にするため,その仮定を採用する。介在物および空孔の発生を仮定した実在する材料の空孔形状および空孔配置を以下に説明する。
3・3・2 純金属純金属はその周りに空孔が発生する介在物を含まない。Beevers and Honeycombe40)は純アルミニウムと純銅の単結晶体および多結晶体の引張試験において,介在物がないにも拘わらず亀裂が粗いすべり帯上で発生することを示している。そこで,純金属に対する空孔形状と空孔配置が以下の様に仮定される。
空孔形状に関して次の仮定がなされる。
空孔配置に関して次の仮定がなされる。
金属加工過程の通常の非定常有限要素シミュレーションでは,全体の時間段階は多数の微小時間段階に分割されて,空孔は各時間段階において発生する。従って,上記の仮定の下で計算された空孔形状および空孔配置は唯一ではない。その中に様々な形状の空孔と様々な配置の空孔が存在する材料の破壊条件を得ることは容易ではない。従って,唯一の形状の空孔と唯一の配置の空孔が,重み付き平均を取ることによって様々な形状の空孔と様々な配置の空孔から計算される。そして,その中に唯一の形状の空孔と唯一の配置の空孔が存在する材料の破壊条件が計算される。ここで,唯一の形状の空孔と唯一の配置の空孔を使って破壊条件を計算することは一つの仮定である。
Fig.6に純金属に対する空孔形状および空孔配置を示す。ここで,(∂x/∂X)(i)(n)はi番目の時間段階後にI(単位テンソル)に等しくn番目の時間段階後に存在する変形勾配である。なお,0番目の時間段階後の状態は変形前の状態を意味する。n番目の時間段階後の唯一の空孔形状および唯一の空孔配置の変形勾配 (∂x/∂X)(n)void shape and void configuration for pure metalは, (∂x/∂X)(i)(n)にそれに対応する空孔体積率の重みをかけて平均を取ることにより計算される。

Void shape and void configuration for pure metal.
硫化マンガン(MnS)の様に介在物の強度が母材である鋼の強度よりも低い時,母材が変形中に介在物は容易に変形するが,アルミナ(Al2O3)の様に介在物の強度が母材である鋼の強度よりも高い時,母材が変形中に介在物は殆ど変形しない。今後,前者の介在物を軟質介在物,後者の介在物を硬質介在物と呼ぶ。なお,空孔は母材からの介在物の分離により発生するため,空孔の数は介在物の数に等しい,すなわち空孔数は変形中に変化しない。
Fig.7に介在物が母材から分離する合金に対する空孔形状および空孔配置を示す。ここで,空孔形状は介在物を含んだ空孔の形状である。軟質介在物に対する空孔形状は空孔が発生しない純金属に対する空孔形状に等しいと仮定される。すなわち,n番目の時間段階後の空孔形状の変形勾配 (∂x/∂X)(n)void shape for soft inclusionは (∂x/∂X)(0)(n)に等しい。一方,硬質介在物に対する空孔形状に関して次の仮定がなされる。

Void shape and void configuration for alloy in which inclusions separate from matrix.
すなわち,n番目の時間段階後の空孔形状の変形勾配 (∂x/∂X)(n)void shape for hard inclusionはI(単位テンソル)に等しい。
軟質介在物に対する空孔配置および硬質介在物に対する空孔配置は,空孔が発生しない純金属に対する空孔配置に等しいと仮定される。すなわち,n番目の時間段階後の空孔配置の変形勾配 (∂x/∂X)(n)void configuration for soft inclusionおよび (∂x/∂X)(n)void configuration for hard inclusionは (∂x/∂X)(0)(n)に等しい。
3・3・4 介在物が破壊する合金Fig.8に介在物が破壊する合金に対する空孔形状および空孔配置を示す。黒色の部分は介在物を示す,介在物によって取り囲まれた白色の部分は空孔を示す,そして二つの隣接する介在物の間に存在する白色の部分は母材を表す。なお,空孔は介在物の破壊により発生するため,空孔の数は介在物の数に等しい,すなわち空孔数は変形中に変化しない。

Void shape and void configuration for alloy in which inclusions crack.
亜共析鋼を想定するため,パーライトが介在物になる。介在物形状は,空孔が発生しない純金属に対する空孔形状に等しいと仮定される。すなわち,n番目の時間段階後の介在物形状の変形勾配 (∂x/∂X)(n)inclusion shape for inclusion crackingは (∂x/∂X)(0)(n)に等しい。一方,空孔形状に関して次の仮定がなされる。
n番目の時間段階後の空孔形状の変形勾配 (∂x/∂X)(n)void shape for inclusion crackingは基本的に (∂x/∂X)(0)(n)に等しいが,上で述べた空孔形状の仮定のために空孔形状が修正される。すなわち,修正により空孔体積率が変化しないと言う条件の下で,空孔の扁平率が0.9になるように空孔の長径と短径が修正される。
空孔配置および介在物配置は,空孔が発生しない純金属に対する空孔配置に等しいと仮定される。すなわち,n番目の時間段階後の空孔配置の変形勾配 (∂x/∂X)(n)void configuration for inclusion crackingおよび介在物配置の変形勾配 (∂x/∂X)(n)inclusion configuration for inclusion crackingは (∂x/∂X)(0)(n)に等しい。
炭素鋼の場合,パーライト粒内の亀裂発生時の亀裂の長軸方向が,材料の最大剪断応力の方向に一致することが知られている41)。従って,変形前の空孔の長軸方向が材料の最大剪断応力の方向に一致すると仮定される。
3・4 空孔合体楕円空孔モデルの核心が空孔合体にある。
Thomasonモデル18)およびMelander and Ståhlbergモデル19)では次の仮定がなされる。
しかし,前者の仮定は非現実的であり,後者の仮定は金属加工過程において一般に成立しない。そこで,楕円空孔モデルでは次の仮定がなされる。
Fig.9に楕円空孔モデルにおける材料変形を示す。すなわち,図(a)に均一変形を,図(b)に内部括れ変形を示す。図(b)にはホドグラフも示される。図(a)において点線で囲まれた領域が均一変形をするために必要なエネルギは,空孔体積率をf,母材の剪断降伏応力をkとすれば (1−f ) 4kv0Lである。一方,図(b)において点線が速度不連続線になり,二つの隣接する空孔の間にある母材のみが変形する内部括れ変形が起こるために必要なエネルギは4kv0 (l1 sin θ2+l2 sin θ1) /sin (θ1+θ2) である。従って,均一変形のためのエネルギが内部括れ変形のためのエネルギに一致すると言う破壊条件は次式で与えられる。
| (4) |

Material deformation in ellipsoidal void model.
便宜上,均一変形のためのエネルギに対する内部括れ変形のためのエネルギの比Eは次式で定義される。
| (5) |
破壊条件はEが1よりも小さい時に満足される。
l2がl1に等しく,θ2がθ1に等しい時,式(4)より破壊条件は次式で与えられる。
| (6) |
Fig.10に楕円空孔モデルにおける破壊条件の概略図を示す。l1/cos θ1の長さがLの長さの (1−f ) 倍に等しい時,均一変形のためのエネルギが内部括れ変形のためのエネルギに一致するため,破壊条件が満足される。

Schematic presentation of fracture criterion in ellipsoidal void model.
Fig.9では,速度不連続線が二つの隣接する空孔の接線に一致すると仮定された。しかし,速度不連続線が二つの隣接する空孔の接線に一致する時に,内部括れ変形のためのエネルギが必ずしも最小化されない。従って,内部括れ変形のためのエネルギが最小化されるように,速度不連続線の位置が最適化される。
3・5 空孔合体領域たとえ空孔合体の条件が座標軸と二つの隣接する空孔を結ぶ線の間のある角度に対して微視的に満足されるとしても,材料は必ずしも巨視的に破壊するとは限らない。微視的な空孔合体の条件が以下の様に巨視的な材料破壊の条件に関連付けられる。
ϕが座標軸と二つの隣接する空孔を結ぶ線の間の角度として加工前の空孔形状および空孔配置において定義される。ϕがある角度に指定された時,比Eが加工後の空孔形状および空孔配置において二つの隣接する空孔に対して計算される。比Eが1以下になるϕの範囲として,dϕが加工前の空孔形状および空孔配置において定義される。六個の空孔が中央の空孔を取り囲むため,dϕがπ/6 (=(2π/6)/2) に等しい時,指定されたある角度ϕに対して比Eが1以下になる確率は半分である。従って,空孔合体の巨視的な確率は半分であり,dϕがπ/6に等しいことは巨視的な材料破壊に対する合理的な条件であると考える。そこで,dϕがπ/6に等しい時,材料が巨視的に破壊すると仮定される。
3・6 予歪最初の加工において材料に与える歪である予歪を,予歪付与後に材料に生じる歪と区別する。予歪を与える過程における空孔形状の取扱いは,予歪付与後の過程における空孔形状の取扱いと同じであり,予歪を与える過程における空孔配置の取扱いは,予歪付与後の過程における空孔配置の取扱いと同じである。従って,予歪を与える過程におけるシミュレーション方法は予歪付与後の過程におけるシミュレーション方法と同じであり,予歪を与える過程において解析を実行するために如何なる特別な解析方法も必要とされない。
平面歪引張り,単軸引張り,そして単純剪断の三つの塑性変形様式に対して,楕円空孔モデルによる解析および代表体積要素モデルを用いた有限要素解析が行われた42)。ここで,内部括れ変形のためのエネルギ計算において速度不連続線が二つの隣接する空孔の接線に一致すると仮定された。また,代表体積要素モデルを用いた有限要素解析では空孔の発生が考慮されないため,楕円空孔モデルによる解析でも空孔の発生が考慮されない。
Fig.11に単純剪断における解析42)を示す。図(a)に座標軸と記号,図(b)に初期空孔体積率と公称破壊歪の関係を示す。変形前の二つの隣接する空孔を結ぶ線とx軸のなす角度をφと定義する。まず,変形中に最小主歪方向が変化するため,φが最適化された解析結果が示された。初期空孔体積率の増加と共に,公称破壊歪は単調に減少する。次に,変形開始時に最小主歪方向とx軸のなす角度が−π/4であるため,φが−π/4に固定された解析結果が比較のために示された。初期空孔体積率が0.2近傍で公称破壊歪は無限大になる。代表体積要素モデルを用いた単純剪断の有限要素解析43)では空孔配置が解析前に決定されているため,変形中にφが最適化されない。しかし,破壊歪を求めるために変形中にφを最適化することは必須である。

Analysis in simple shear42).
Fig.12に単軸引張りにおける代表体積要素に対する座標軸と記号42)を示す。図(a)に球形空孔,図(b)に球形空孔とドーナツ形空孔を示す。Fig.13に単軸引張りにおける初期空孔体積率と公称破壊歪の関係42)を示す。楕円空孔モデルによる解析結果は,球形空孔とドーナツ形空孔の代表体積要素モデルを用いた有限要素解析の結果と概ね一致するが,球形空孔のみの代表体積要素モデルを用いた有限要素解析の結果と全く一致しない。この一致および不一致の理由は,球形空孔とドーナツ形空孔を用いた解析では空孔の合体が考慮されるが,球形空孔のみを用いた解析では空孔が一つのため空孔の合体が考慮されないからである。次に述べる様に,楕円空孔モデルによる解析結果は,単軸引張りの実験結果35)と概ね一致する。そのため,球形空孔の代表体積要素モデルを用いた有限要素解析44)による単軸引張りの結果が,単軸引張りの実験結果と一致しないことは明らかである。

Coordinates and notation for representative volume element in uniaxial tension42).

Relationship between initial void volume fraction and nominal fracture strain in uniaxial tension42).
Fig.14に単軸引張りにおける初期空孔体積率と公称破壊歪の関係45)を示す。ここで,内部括れ変形のためのエネルギが最小化されるように,速度不連続線の位置が最適化された。図には,速度不連続線の位置が二つの隣接する空孔の接線に一致するように決定された場合の解析結果,Edelson and Baldwinによる実験結果35)そしてThomasonモデル18)による解析結果が補足された。図より,速度不連続線の位置が最適化された場合の解析結果は実験結果と良く一致するため,速度不連続線の位置を最適化することは必須である。
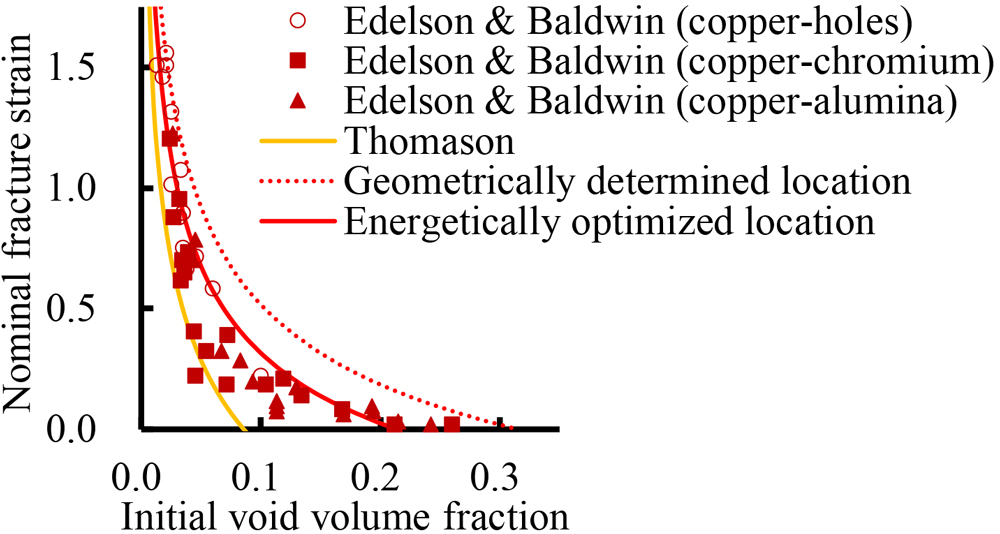
Relationship between initial void volume fraction and nominal fracture strain in uniaxial tension45).
穴広げ試験は薄板の伸びフランジ成形性を評価するための試験であり,従来穴広げ試験時の材料破壊が様々な破壊条件式を用いて評価されている46,47)。そこで,鉄鋼材料および非鉄金属材料を用いて穴広げ試験が行われて,穴広げ試験時の材料破壊が評価された48,49)。ここで,実験室において圧延加工により予歪が与えられた薄板が穴広げ試験されて,予歪が穴広げ率に及ぼす影響が求められた。
Fig.15に冷間圧延鋼板SPCCに対する予歪と穴広げ率の関係を示す48)。図(a)では式(2),図(b)では様々な従来の延性破壊条件式,が用いられた。ここで,原論文ではランプ関数がMacauleyの括弧と呼ばれている。SPCCには主に軟質介在物が含まれるが,軟質介在物を仮定した解析結果および硬質介在物を仮定した解析結果は実験結果と概ね一致する。

Relationship between prestrain and hole expansion ratio for SPCC48).
Freudenthalの破壊条件式5)を用いた場合,解析より求まる予歪が穴広げ率に及ぼす影響は,実験より求まるそれよりも大きい。一方,Cockcroft and Lathamの破壊条件式6),Brozzo等による破壊条件式7),そしてOyaneの破壊条件式8)を用いた場合,解析より求まる穴広げ率は予歪に殆ど依存しない。ここで,これらの破壊条件式では,応力のある関数を歪履歴に沿って積分した値がある値になった時に,材料が破壊すると仮定される。解析では簡単のため,薄板の圧延加工ではなく平面歪圧縮により予歪が付与されるため,予歪付与時に最大主応力σmaxが零,応力三軸度σkk/3σが
続報49)においては,ステンレス鋼SUS304およびSUS430の圧延まま材が持つと予想される予歪を仮定することにより,軟質介在物および硬質介在物を仮定して得られた予歪が穴広げ率に及ぼす影響が,実験より得られたそれに近づくことが確認された。更に,純アルミニウムA1050および純銅C1100において,純金属を仮定して得られた予歪が穴広げ率に及ぼす影響が,実験より得られたそれに概ね一致することが確認された。
4・3 引抜き加工時の内部割れ丸棒の引抜き加工において加工条件が過酷な場合,引抜き方向に周期的に内部割れが発生する。この内部割れはカッピーや内部破裂と呼ばれて,古くから実験的に知られている50,51)。また,上界法による内部割れの予測52),および有限要素法による従来の破壊条件式を用いた内部割れの予測53)あるいは周期的な内部割れの数値シミュレーション54)が行われている。そこで,亜共析鋼である機械構造用炭素鋼S15C, S35C, S45C, S55Cの多段引抜き加工が行われて,引抜き加工時の内部割れが評価された55)。ここで,亜共析鋼ではパーライト粒内のセメンタイト板が破壊して空孔が発生するため26,27),パーライト粒を介在物と考えて介在物破壊が仮定された。
Fig.16にS55Cに対する中央破裂時の空孔形状および空孔配置を示す55)。図(a)では介在物破壊が,図(b)では軟質介在物が仮定された。ここで,パーライト粒の体積率は炭素量により決定される。介在物破壊により発生した空孔の扁平率は,軟質介在物と母材の分離により発生したそれよりも大きい。そのため,中央破裂時において,介在物破壊により発生した空孔の体積率は,軟質介在物と母材の分離により発生したそれよりも小さい。

Void shape and void configuration at central burst for S55C55).
Fig.17にS55Cに対する中央破裂前の半径方向の材料密度分布を示す55)。図(a)では介在物破壊が,図(b)では軟質介在物が仮定された。ここで,凡例において各引抜き加工におけるダイス全角および断面減少率が示される。また,アルキメデス法により材料密度が測定された。介在物破壊を仮定した場合の解析より得られた半径方向の材料密度分布は実験より得られたそれと概ね一致するが,軟質介在物を仮定した場合の解析より得られた半径方向の材料密度分布は実験より得られたそれと大きく異なる。

Material density distribution in radial direction before central burst for S55C55).
図示しないが,S15Cに対して中央破裂時において介在物破壊により発生した空孔の体積率は,軟質介在物と母材の分離により発生したそれとほぼ等しい。そして,介在物破壊を仮定した場合の解析より得られた半径方向の材料密度分布および軟質介在物を仮定した場合の解析より得られたそれは実験より得られたそれと概ね一致する。
4・4 切欠き試験片の引張り試験時の絞り丸棒および薄板の引張り試験において,試験片の括れ部の応力および歪分布は括れ部の曲率半径に依存する56)。従って,丸棒および薄板の切欠き試験片の引張り試験において,試験片の切欠き部の応力および歪分布は切欠き底半径に依存する。そこで,鉄鋼材料および非鉄金属材料を用いて丸棒および薄板の切欠き試験片の引張り試験が行われて,引張り試験時の絞りが評価された38,39)。ここで,実験室において圧延加工により予歪が与えられた薄板および引抜き加工により予歪が与えられた丸棒が引張り試験されて,予歪が絞りに及ぼす影響が求められた。なお,破壊に関する唯一の材料定数は,解析より求まる無予歪および切欠き底半径5 mmの切欠き試験片の引張り試験時の絞りが,実験より求まるそれに一致するように定められる。
Fig.18に切欠き底の曲率半径と絞りの関係を示す38)。図(a)ではアルミニウム合金A5056丸棒が,図(b)では純銅C1100丸棒が取り扱われる。凡例に予歪を示す。A5056に対して軟質介在物が仮定されると共に式(2)が利用された,またC1100に対して純金属が仮定されると共に式(1)が利用された。解析より求まる予歪が絞りに及ぼす影響は実験より求まるそれと概ね一致する。

Relationship between curvature of notch root and reduction in area38).
Fig.19に切欠き底の曲率半径と絞りの関係を示す39)。図(a)では熱間圧延鋼板SPHCが,図(b)では一般構造用圧延鋼材SS400丸棒が取り扱われる。凡例に予歪を示す。SPHCおよびSS400に対して軟質介在物が仮定されると共に式(1)が利用された。解析より求まる予歪が絞りに及ぼす影響は実験より求まるそれと概ね一致する。

Relationship between curvature of notch root and reduction in area39).
円柱の据込み加工時に材料表面に現れる亀裂に関する研究は,塊材の金属加工における代表的な材料破壊に関する研究であり,数多くの実験的研究57,58,59,60)が行われている。また,有限要素法による従来の破壊条件式を用いた表面亀裂の予測61,62)が行われている。そこで,鉄鋼材料を用いて円柱の据込み加工が行われて,据込み加工時の材料破壊が評価された63)。ここで,実験室において引抜き加工により予歪が与えられた丸棒から切り出された円柱が据込み加工されて,予歪が破壊歪に及ぼす影響が求められた。また,材料が亜共析鋼であるため,介在物破壊が仮定された。一方,据込み加工前に材料表面に正方格子が焼き付けられて,材料破壊時の変形した正方格子および予歪から破壊開始時の軸方向歪と円周方向歪が求められた。なお,破壊に関する唯一の材料定数は,無予歪の円柱の据込み加工時において,解析より求まる破壊開始時の軸方向歪と円周方向歪が,実験より求まるそれに一致するように定められる。
Fig.20に破壊開始時の軸方向歪と円周方向歪の関係を示す63)。図(a)では機械構造用炭素鋼S55Cが,図(b)ではクロムモリブデン鋼SCM415が取り扱われる。凡例に据込み加工を行うための引抜き加工後の材料直径を示す。S55Cに対して式(3)が利用された,ただし,式(3)においてA1=A0と仮定された,またSCM415に対して式(1)が利用された。解析より求まる予歪が破壊開始時の軸方向歪と円周方向歪に及ぼす影響は実験より求まるそれと良く一致する。

Relationship between axial and circumferential strains at fracture initiation63).
Fig.21にS55Cに対して様々な従来の延性破壊条件式を使って計算された破壊開始時の軸方向歪と円周方向歪の関係を示す63)。図(a)ではCockcroft and Lathamの破壊条件式6)が,図(b)ではBrozzo等による破壊条件式7)が取り扱われる。凡例に据込み加工を行うための引抜き加工後の材料直径を示す。予歪の増加と共に,解析より求まる破壊開始時の軸方向歪および円周方向歪と実験より求まるそれの違いが増加する。

Relationship between axial and circumferential strains at fracture initiation calculated using various conventional ductile fracture criteria for S55C63).
薄板の成形加工では,括れによる成形限界64,65)がよく知られているが,それと破壊による成形限界は異なる66,67)ことが示されている。ここでは,破壊による成形限界68,69,70)が取り扱われる。そこで,鉄鋼材料および非鉄金属材料を用いて,二軸薄板引張り試験である中島試験が行われて,薄板の成形限界が評価されたs71)。ここで,実験室において圧延加工により予歪が与えられた薄板を使って中島試験を行うことにより,予歪が成形限界に及ぼす影響が求められた。一方,中島試験前に材料表面に正方格子が焼き付けられて,破断時の板厚と変形した正方格子および予歪から最大主歪と最小主歪が求められた。
Fig.22に中島試験における破断時の最大主歪と最小主歪の関係を示す71)。図(a)では冷間圧延鋼板SPCCが,図(b)では純銅C1100が取り扱われる。中島試験時の材料板厚は1 mmであるが,凡例に圧延加工前の材料板厚および予歪が与えられた試験片方向を示す。SPCCに対して式(1)が利用されると共に軟質介在物が仮定された,またC1100に対して式(1)が利用されると共に純金属が仮定された。解析より求まる予歪が破断時の最大主歪と最小主歪に及ぼす影響は実験より求まるそれと概ね一致する。

Relationship between major and minor strains at fracture in Nakajima test71).
Fig.23にSPCCに対して様々な従来の延性破壊条件式を使って計算された中島試験における破断時の最大主歪と最小主歪の関係を示す71)。図(a)ではCockcroft and Lathamの破壊条件式6)が,図(b)ではBrozzo等による破壊条件式7)が取り扱われる。凡例に圧延加工前の材料板厚および予歪が与えられた試験片方向を示す。解析より求まる予歪が破断時の最大主歪と最小主歪に及ぼす影響は実験より求まるそれと一致しない。

Relationship between major and minor strains at fracture in Nakajima test calculated using various conventional ductile fracture criteria for SPCC71).
更に,図示しないが,ステンレス鋼SUS304の圧延まま材が持つと予想される予歪を仮定することにより,軟質介在物を仮定して得られた予歪が破断時の最大主歪と最小主歪に及ぼす影響が,実験より得られたそれに近づくことが確認された。
4・7 Lodeのパラメータの影響Lode72)は,中間主応力が最大主応力および最小主応力に関係付けられるパラメータを定義した。Lodeのパラメータは,当初は降伏条件を評価するために使用されたが,最近ではそれのみならず延性破壊を評価するために利用される。まず,Lodeのパラメータが空孔の成長73)に影響を及ぼすことが示された。その後,延性破壊が応力三軸度のみならずLodeのパラメータに依存すること74,75,76,77)が認識されてきた。そこで,Lodeのパラメータが延性破壊に及ぼす影響が検討された78)。ここで,影響をより明確に把握するために空孔の発生は考慮されない。更に,軟質介在物および剛完全塑性材料が仮定されると共に,空孔合体領域を零にすることにより,空孔合体時に材料破壊が起こると仮定される。
Fig.24に応力三軸度(η)およびLodeのパラメータ(μ)が破壊時の相当歪に及ぼす影響を示す78)。Lodeのパラメータが指定された時,応力三軸度の増加と共に破壊時の相当歪は減少する。また,応力三軸度が指定された時,Lodeのパラメータの絶対値の増加と共に破壊時の相当歪は増加する。更に,指定された応力三軸度に対してLodeのパラメータの絶対値が等しい時,Lodeのパラメータが正の場合の破壊時の相当歪とLodeのパラメータが負の場合のそれは殆ど一致する。

Effects of stress triaxiality (η) and Lode parameter (μ) on equivalent strain at fracture78).
平面歪引張りおよび圧縮によりμ=0の場合の,軸対称引張りおよび圧縮によりμ=±1の場合の破壊時の相当歪が求められた。Fig.25に様々なLodeのパラメータにおける応力三軸度と破壊時の相当歪の関係を示す78)。

Relationship between stress triaxiality and equivalent strain at fracture in various Lode parameter78).
3・4節で説明された様に,最大主応力方向が指定された時,空孔合体は空孔形状および空孔配置のみにより決定される。そこで,応力三軸度が指定された時に空孔合体時の空孔形状および空孔配置がLodeのパラメータに依存しないことおよび材料の空孔体積率が変形中に変化しないことを仮定すれば,Lodeのパラメータが破壊時の相当歪に及ぼす影響は初等解析法により次式で求められる。
| (7) |
μ=0の破壊時の相当歪から式(7)を利用して求めたμ=±1のそれをFig.25に補足する。初等解析法による破壊時の相当歪は楕円空孔モデルによるそれと概ね一致する。
延性破壊は空孔の発生,空孔の成長そして空孔の合体により起こるという考え方に基づいて,楕円空孔モデルにより延性破壊が評価された。しかし,平面応力状態では応力三軸度が1/3付近で破壊歪が極大になり,零付近で破壊歪が極小になることが示されており79,80,81),それを4・7節で示した解析により示すことは出来ない。従って,応力三軸度が零付近における延性破壊を,楕円空孔モデルではなくその他のモデルにより評価することが試みられた。
5・2 予歪考慮比に基づくモデルによる薄板の面内剪断試験時の成形限界薄板の面内剪断試験では応力三軸度が零であり平面応力状態が保たれるため,従来数多くの剪断試験法82,83,84,85,86,87)が剪断応力と剪断歪の関係を求めるためにあるいは材料破壊を評価するために提案されてきた。ここで,宮内式剪断試験85)では,試験中に試験片の回転が無いため,回転による試験片内部の応力成分の変化が無く,また試験片および試験装置の製作が比較的容易である。そこで,宮内式剪断試験により薄板の成形限界が評価された88)。ここで,実験室において圧延加工により予歪が与えられた薄板を使って宮内式剪断試験を行うことにより,予歪が成形限界に及ぼす影響が求められた。
予歪考慮比は,全予歪に対する予歪付与後の加工で歪として考慮される予歪の比である。すなわち,圧延加工により材料に与えられた予歪に対する宮内式剪断試験で歪として考慮される予歪の比である。そして,予歪考慮比に基づくモデルでは歪がある値になった時に材料が破壊すると仮定される。なお,比較のために楕円空孔モデルによる解析も行われる。ここで,使用された材料である冷間圧延鋼板SPCCに対して,式(1)が利用される。
Fig.26に宮内式剪断試験における破壊時の最小主歪と最大主歪の間の関係を示す88)。図(a)に予歪考慮比に基づくモデル,図(b)に楕円空孔モデルによる結果を示す。ここで,簡単のために予歪考慮比が0と仮定される。すなわち,圧延加工により材料に与えられた予歪が剪断試験で歪として無視される。ここで,剪断試験時の板厚は1 mmであるが,凡例に圧延加工前の板厚,剪断方向に一致する圧延まま材の方向および剪断方向に一致する予歪付与材の方向を示す。予歪考慮比に基づくモデルによる解析結果は実験結果と概ね一致するが,楕円空孔モデルによる解析結果は実験結果と異なる。ただ,図(a)において解析結果が実験結果に完全には一致しないため,解析結果を実験結果により一致させるために予歪考慮比が最適化される。

Relationship between minor and major strains at fracture in Miyauchi shear testing88).
Fig.27に様々な予歪考慮比における破壊時の最小主歪と最大主歪の間の関係を示88)。図(a)に予歪考慮比が1,図(b)に予歪考慮比が0.2の結果を示す。予歪考慮比が1の場合,解析より求まる予歪が破壊歪に及ぼす影響は実験より求まるそれと一致しないが,予歪考慮比が0.2の場合,解析より求まる予歪が破壊歪に及ぼす影響は実験より求まるそれと良く一致する。なお,予歪考慮比が1の破壊条件は,歪がある値になった時に材料が破壊すると仮定するFreudenthalの破壊条件5)である。

Relationship between minor and major strains at fracture in various prestrain consideration ratios88).
宮内式剪断試験では変形域の長手方向と引張り方向のなす角度は0であるが,平面歪引張り試験ではそれはπ/2である。文献88)では変形域の長手方向と引張り方向のなす角度を0からπ/2まで変化させると言う拡張宮内式剪断試験が提案された。なお,平面歪引張り試験では,楕円空孔モデルによる解析結果は実験結果と概ね一致する。
5・3 転位密度テンソルに基づくモデルによる丸棒の捩り試験時の破壊予測予歪考慮比に基づくモデルは実用的であるが,予歪考慮比の物理的意味は明確ではない。歪は転位と関連するため,応力三軸度が零付近における延性破壊が転位に関連することが予想される。しかし,剪断応力は転位密度の平方根に比例するため89),スカラである転位密度に基づくモデルは歪または応力に基づくモデルと基本的に同じである。そこで,転位密度テンソル90,91)に基づくモデルが考案された。
丸棒の捩り試験では応力三軸度が零であり平面応力状態が保たれるため,丸棒の捩り試験により破壊が評価された92,93)。しかし,捩り試験機は一般に高価であるため,万能試験機に組み込める自作した簡易捩り試験機により丸棒の破壊が評価された94)。ここで,実験室において引抜き加工により予歪が与えられた丸棒を使って捩り試験を行うことにより,予歪が破壊に及ぼす影響が求められた。なお,実験では丸棒の横断面が破断面になったが,丸棒の縦断面が破断面になる現象はデラミネーションと呼ばれて,従来数多くのデラミネーションに関する研究が行われている95,96,97,98)。
転位密度テンソルに基づくモデルでは,転位密度テンソルのノルムがある値になった時に材料が破壊すると仮定される。材料が変形する時,材料から滑り出る可動転位があり,また同じ滑り平面上にある二つの異符号の可動転位は会合時に消滅するため99),全ての可動転位が材料内部に蓄積されるとは限らない。そこで,予歪付与時の全転位密度に対する予歪付与後の加工で転位密度として考慮される転位密度の比である転位密度考慮比が定義される。すなわちそれは,引抜き加工により材料に与えられた転位による転位密度に対する捩り試験で転位として考慮される転位による転位密度の比である。なお,比較のために予歪考慮比に基づくモデルによる解析も行われる。
予歪の無い材料において,解析より求まる破壊時の捩れ角が実験より求まるそれに一致する様に,これらのモデルにおいて転位密度テンソルのノルムのある値および歪のある値が定められる。また,予歪の有る材料において,解析より求まる破壊時の捩れ角が実験より求まるそれに概ね一致する様に,転位密度考慮比および予歪考慮比が定められる。
Fig.28にS55Cに対する捩り試験における予歪と破壊時の捩れ角の関係を示す94)。図(a)に転位密度考慮比に基づくモデル,図(b)に予歪考慮比に基づくモデルによる結果を示す。両モデルによる解析結果は実験結果と概ね一致する。ここで,転位密度考慮比は0.5であり,予歪考慮比は0.25である。後者の値は前節で最適化された予歪考慮比である0.2と概ね一致する。すなわち,予歪考慮比が加工様式にあまり依存しないことは興味深い。図示しないが,楕円空孔モデルによる解析結果は実験結果とあまり一致しない。

Relationship between prestrain and torsion angle at fracture in torsion testing for S55C94).
Fig.29にS55Cに対する捩り試験における破壊時の最小主歪と最大主歪の間の関係を示す94)。図(a)に転位密度考慮比に基づくモデル,図(b)に予歪考慮比に基づくモデルによる結果を示す。両モデルによる解析結果は実験結果と概ね一致する。図示しないが,楕円空孔モデルによる解析結果は実験結果とあまり一致しない。

Relationship between major and minor strains at fracture in torsion testing for S55C94).
転位密度考慮比は材料内部に蓄積された可動転位の割合を表すため,その物理的意味は明確であり,転位密度考慮比に関する研究の更なる進展が望まれる。
筆者等が行っている楕円空孔モデルおよびその他のモデルによる金属加工過程における延性破壊予測を紹介した。筆者等の研究のみならずそれに関連した数多くの代表的な研究を紹介した。最近の十年間における延性破壊に関する研究は非常に多く,延性破壊に関する研究は当分の間精力的に行われるであろう。本解説が延性破壊に興味を持つ方々の参考になれば幸いである。