Volume 4
Displaying 1-10 of 10 articles from this issue
- |<
- <
- 1
- >
- >|
Original Article
-
Article type: research-article
2005Volume 4 Pages 1-24
Published: 2005
Released on J-STAGE: June 25, 2020
Download PDF (3135K) -
Article type: research-article
2005Volume 4 Pages 25-47
Published: 2005
Released on J-STAGE: June 25, 2020
Download PDF (3805K) -
Article type: research-article
2005Volume 4 Pages 49-69
Published: 2005
Released on J-STAGE: June 25, 2020
Download PDF (2864K) -
Article type: research-article
2005Volume 4 Pages 71-91
Published: 2005
Released on J-STAGE: June 25, 2020
Download PDF (3182K) -
Article type: research-article
2005Volume 4 Pages 93-108
Published: 2005
Released on J-STAGE: June 25, 2020
Download PDF (2459K) -
Article type: research-article
2005Volume 4 Pages 109-124
Published: 2005
Released on J-STAGE: June 25, 2020
Download PDF (2592K) -
Article type: research-article
2005Volume 4 Pages 125-134
Published: 2005
Released on J-STAGE: June 25, 2020
Download PDF (1767K) -
Article type: research-article
2005Volume 4 Pages 135-146
Published: 2005
Released on J-STAGE: June 25, 2020
Download PDF (1653K) -
Article type: research-article
2005Volume 4 Pages 147-173
Published: 2005
Released on J-STAGE: June 25, 2020
Download PDF (4230K) -
Article type: research-article
2005Volume 4 Pages 175-191
Published: 2005
Released on J-STAGE: June 25, 2020
Download PDF (2707K)
- |<
- <
- 1
- >
- >|

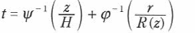
 ,
,  the inverses of the growth curves of the stem height z and of the radius r at the height z, respectively. Let us define a kind of index function u (t, z, r) of three variables age t , height z and the radius r as
the inverses of the growth curves of the stem height z and of the radius r at the height z, respectively. Let us define a kind of index function u (t, z, r) of three variables age t , height z and the radius r as 

 is a gradient of its stem curve, and the stem surface is a characteristic surface of the equation. In other words, the solution u = 1 jumps into another solution u = 0 discontinuously on the stem surface. Therefore the stem surface can be regarded as a kind of 'wave front' of its growth.
is a gradient of its stem curve, and the stem surface is a characteristic surface of the equation. In other words, the solution u = 1 jumps into another solution u = 0 discontinuously on the stem surface. Therefore the stem surface can be regarded as a kind of 'wave front' of its growth.