
- Issue 3 Pages 409-
- Issue 2 Pages 203-
- Issue 1 Pages 1-
- |<
- <
- 1
- >
- >|
-
Hideya Hashimoto, Misa Ohashi, Kazuhiro Suzuki2019Volume 42Issue 2 Pages 203-222
Published: June 27, 2019
Released on J-STAGE: July 04, 2019
JOURNAL FREE ACCESSWe give computational systems of polynomial representations of the composition maps of non-flat totally geodesic surfaces of the symmetric spaces of type A which are obtained by K. Mashimo, and the Cartan imbeddings of symmetric spaces of type A to SU(n). We obtain the relationships among the non-flat totally geodesic surfaces in symmetric spaces of types AI, AII and AIII by this methods.
View full abstractDownload PDF (164K) -
Takayuki Moriyama, Takashi Nitta2019Volume 42Issue 2 Pages 223-246
Published: June 27, 2019
Released on J-STAGE: July 04, 2019
JOURNAL FREE ACCESSA Poisson structure is a bivector whose Schouten bracket vanishes. We study a global Poisson structure on S4 associated with a holomorphic Poisson structure on CP3. The space of such Poisson structures on S4 is realised as a real algebraic variety in the space of holomorphic Poisson structures on CP3. We generalize the result to the higher dimensional case HPn by the twistor method. It is known that a holomorphic Poisson structure on CP3 corresponds to a codimension one holomorphic foliation and the space of these foliations of degree 2 has six components. In this paper we provide examples of Poisson structures on S4 associated with these components.
View full abstractDownload PDF (212K) -
Yukio Nagahata2019Volume 42Issue 2 Pages 247-273
Published: June 27, 2019
Released on J-STAGE: July 04, 2019
JOURNAL FREE ACCESSWe are interested in giving a mathematical formula of a cost in adhoc network model. In our model, the cost is formulated as an application of first-passage percolation and the motion of devices is random, and an asymptotic density of devices is formulated by hydrodynamic limit. Under some technical assumptions, we give asymptotics of a cost in adhoc network model. In order to formulate this model, we extend the results of first-passage percolation given by Howard Newman [3] to that in inhomogeneous environments.
View full abstractDownload PDF (256K) -
Kazunori Nakamoto, Yasuhiro Omoda2019Volume 42Issue 2 Pages 274-307
Published: June 27, 2019
Released on J-STAGE: July 04, 2019
JOURNAL FREE ACCESSWe introduce special classes of irreducible representations of groups: thick representations and dense representations. Denseness implies thickness, and thickness implies irreducibility. We show that absolute thickness and absolute denseness are open conditions for representations. Thereby, we can construct the moduli schemes of absolutely thick representations and absolutely dense representations. We also describe several results and several examples on thick representations for developing a theory of thick representations.
View full abstractDownload PDF (276K) -
Takeshi Harui2019Volume 42Issue 2 Pages 308-331
Published: June 27, 2019
Released on J-STAGE: July 04, 2019
JOURNAL FREE ACCESSThe author classifies finite groups acting on smooth plane curves of degree at least four. Furthermore, he gives an upper bound for the order of automorphism groups of smooth plane curves and determines the exceptional cases in terms of defining equations. This paper also contains a simple proof of the uniqueness of smooth plane curves with the full automorphism group of maximum order for each degree.
View full abstractDownload PDF (201K) -
Tomoshige Yukita2019Volume 42Issue 2 Pages 332-357
Published: June 27, 2019
Released on J-STAGE: July 04, 2019
JOURNAL FREE ACCESSIn [7], Kellerhals and Perren conjectured that the growth rates of cocompact hyperbolic Coxeter groups are Perron numbers. By results of Floyd, Parry, Kolpakov, Nonaka-Kellerhals, Komori and the author [1], [3], [8], [10], [12], [13], [21], [22], the growth rates of 2- and 3-dimensional hyperbolic Coxeter groups are always Perron numbers. Kolpakov and Talambutsa showed that the growth rates of right-angled Coxeter groups are Perron numbers [9]. For certain families of 4-dimensional cocompact hyperbolic Coxeter groups, the conjecture holds as well (see [7], [19] and also [23]). In this paper, we construct an infinite sequence of ideal non-simple hyperbolic Coxeter 4-polytopes giving rise to growth rates which are distinct Perron numbers. This is the first explicit example of an infinite family of non-compact finite volume Coxeter polytopes in hyperbolic 4-space whose growth rates are of the conjectured arithmetic nature as well.
View full abstractDownload PDF (385K) -
Alessandro Languasco, Alessandro Zaccagnini2019Volume 42Issue 2 Pages 358-375
Published: June 27, 2019
Released on J-STAGE: July 04, 2019
JOURNAL FREE ACCESSWe continue our recent work on additive problems with prime summands: we already studied the average number of representations of an integer as a sum of two primes, and also considered individual integers. Furthermore, we dealt with representations of integers as sums of powers of prime numbers. In this paper, we study a Cesàro weighted partial explicit formula for generalised Hardy-Littlewood numbers (integers that can be written as a sum of a prime power and a square) thus extending and improving our earlier results.
View full abstractDownload PDF (154K) -
Guangming Hu, Yi Qi2019Volume 42Issue 2 Pages 376-392
Published: June 27, 2019
Released on J-STAGE: July 04, 2019
JOURNAL FREE ACCESSIt is known that every finitely unbranched holomorphic covering π :
 → S of a compact Riemann surface S with genus g ≥ 2 induces an isometric embedding Φπ : Teich(S) → Teich(
→ S of a compact Riemann surface S with genus g ≥ 2 induces an isometric embedding Φπ : Teich(S) → Teich( ). By the mutual relations between Strebel rays in Teich(S) and their embeddings in Teich(
). By the mutual relations between Strebel rays in Teich(S) and their embeddings in Teich( ), we show that the augmented Teichmüller space
), we show that the augmented Teichmüller space  can be isometrically embedded in the augmented Teichmüller space
can be isometrically embedded in the augmented Teichmüller space 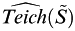 .View full abstractDownload PDF (159K)
.View full abstractDownload PDF (159K) -
Nobushige Kurokawa, Yuichiro Taguchi, Hidekazu Tanaka2019Volume 42Issue 2 Pages 393-408
Published: June 27, 2019
Released on J-STAGE: July 04, 2019
JOURNAL FREE ACCESSWe study a p-analogue of the multiple Euler constant. Then we show that it can be described by the congruence zeta function attached to powers of Gm over Fp. Moreover, we show that it converges to the multiple Euler constant as p → 1.
View full abstractDownload PDF (113K)
- |<
- <
- 1
- >
- >|