Volume 40, Issue 3
Displaying 1-14 of 14 articles from this issue
- |<
- <
- 1
- >
- >|
-
2017Volume 40Issue 3 Pages 405-420
Published: October 31, 2017
Released on J-STAGE: November 18, 2017
Download PDF (149K) -
2017Volume 40Issue 3 Pages 421-449
Published: October 31, 2017
Released on J-STAGE: November 18, 2017
Download PDF (270K) -
2017Volume 40Issue 3 Pages 450-467
Published: October 31, 2017
Released on J-STAGE: November 18, 2017
Download PDF (165K) -
2017Volume 40Issue 3 Pages 468-491
Published: October 31, 2017
Released on J-STAGE: November 18, 2017
Download PDF (185K) -
2017Volume 40Issue 3 Pages 492-517
Published: October 31, 2017
Released on J-STAGE: November 18, 2017
Download PDF (183K) -
2017Volume 40Issue 3 Pages 518-536
Published: October 31, 2017
Released on J-STAGE: November 18, 2017
Download PDF (155K) -
2017Volume 40Issue 3 Pages 537-552
Published: October 31, 2017
Released on J-STAGE: November 18, 2017
Download PDF (149K) -
2017Volume 40Issue 3 Pages 553-561
Published: October 31, 2017
Released on J-STAGE: November 18, 2017
Download PDF (96K) -
2017Volume 40Issue 3 Pages 562-576
Published: October 31, 2017
Released on J-STAGE: November 18, 2017
Download PDF (137K) -
2017Volume 40Issue 3 Pages 577-583
Published: October 31, 2017
Released on J-STAGE: November 18, 2017
Download PDF (89K) -
2017Volume 40Issue 3 Pages 584-614
Published: October 31, 2017
Released on J-STAGE: November 18, 2017
Download PDF (186K) -
2017Volume 40Issue 3 Pages 615-624
Published: October 31, 2017
Released on J-STAGE: November 18, 2017
Download PDF (110K) -
2017Volume 40Issue 3 Pages 625-637
Published: October 31, 2017
Released on J-STAGE: November 18, 2017
Download PDF (127K) -
2017Volume 40Issue 3 Pages 638-647
Published: October 31, 2017
Released on J-STAGE: November 18, 2017
Download PDF (95K)
- |<
- <
- 1
- >
- >|

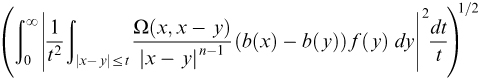 .
. satisfying certain cancellation conditions.
satisfying certain cancellation conditions.
 for all x ∈ RN is not required.
for all x ∈ RN is not required.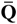 . A simple arithmetic application of this fact is also given.
. A simple arithmetic application of this fact is also given.