論文
拡張型適応的指標モデルの開発とその応用
2013 年 3 巻 1 号 p. 1-16
詳細
2013 年 3 巻 1 号 p. 1-16
臨床研究では，幾つかの測定値に基づく指標を合計した得点により，疾患の進行程度を表すことがある（例えば，大腸がんの予後を表すT 因子など）．Tian & Tibshirani (2010) は，このような得点を統計的に構成する方法，および，新規治療が有効な患者像を得点で表す方法として，適応的指標モデル（AIM: AdaptiveIndex Model）を提案している．AIM のモデルは，共変量に基づく複数のルールを指標関数により構成し，その合計値（得点）を説明変数と見做したもとで，一般化線形モデルの枠組みで構成される．その結果，応答が計量値，計数値，あるいは生存時間研究の場合などの広範に適用できる．
臨床研究では，共変量の応答への影響（主効果）とともに，治療法× 共変量の2 次交互作用（交互作用）の影響を評価することがある（例えば，がん臨床研究の予後因子と予測因子）．しかしながら，AIM では，回帰パラメータに対するスコア検定統計量がルールの選定基準に用いられるため，両方をモデルに含めることができない．さらに，既存のAIM では，前進ステップワイズ法がモデル構築（ルールの選定）に用いるため，モデルに含まれたルールの再評価は行われない（Tian & Tibshirani (2010)）．
本論文では，既存のAIM を拡張する方法，すなわち，拡張型AIM（EAIM: ExtendedAdaptive Index Model）を提案した．EAIM では，ルール評価基準に偏分残差を用いることで，主効果と交互作用を同時に推定することを可能にした．さらに，多変量適応型回帰スプライン（MARS; Multivariate Adaptive Regression Splines, Friedman, 1996）のモデル構築過程（前進ステップワイズ法によるモデル構築，後退ステップワイズ法による部分モデル系列の構成，交差確認法による最適モデルの選定）を応用することで，AIM のモデル構築過程の問題を解消した．
EAIM の有用性は，事例検討により検討し，EAIM に対するMARS アルゴリズムの有効性は，数値検証により検討した．その結果，EAIM は，主効果と交互作用を適切に捉えることができるものの，その結果は，グラフなどで精査することが重要であることがわかった．
臨床研究では，幾つかの測定値に基づく指標を合計した得点により，疾患の進行程度を表すことがある．例えば，大腸がんにおけるT 因子では，(A) 主要個数が単発，(B) 腫瘍径が2 cm以下，(C) 脈管侵襲がない，のルールがある．そして，すべてのルールに該当する場合（得点=3）をT1（予後が最も良好），そしてすべてのルールに該当しない場合（得点=0）をT4（予後が最も不良）としている．ただし，このような得点化に用いられる共変量，あるいはそのカットオフ値は，医師の経験則（主観的な得点化）に依るところが多い．Tian & Tibshirani (2010) は，このような得点化を統計的に構成する方法（客観的な得点化）として，適応的指標モデル（AIM: Adaptive IndexModel）を提案している．AIM のモデルは，共変量に基づく複数のルールを指標関数により構成し，その合計値（得点）を説明変数と見做したもとで，一般化線形モデルの枠組みで構成される．その結果，応答が計量値，計数値，あるいは生存時間研究の場合などの広範に適用できる．
また，臨床試験のなかの無作為化比較試験では，新治療（あるいは新薬）の有効性が既存治療（あるいは既存薬）との比較で示される．ただし，新治療の有効性がすべての患者に対して等く有効であるとは限らない．そのため，新治療（あるいは新薬）の適応患者像（responder）の探索を意図して，治療法× 共変量の2 次交互作用（交互作用）を評価することがある（共変量が連続尺度の場合には，任意のカットオフ値（例えば中央値）でカテゴリ化される）．Tian & Tibshirani (2010) は，適応患者像を探索するためのAIM のモデルも提案している．新治療に対する適応患者像を探索するためのAIM では，共変量に基づくルールの合計値（得点）によって，新治療の有効性への影響を提示する．これにより，「得点が高いほど有効性が高く，低いほど有効性が低い」といった解釈ができる．また，ルールが1 個の場合には，これまでの治療法× 共変量（連続尺度はカテゴリ化）の2 次交互作用（交互作用）の評価と同様であることから，得点化による適応患者像の探索は，これまでのサブセット解析を包括した接近法であると捉えることができる．
すなわち，AIM は，応答に対する共変量の影響（主効果），あるいは，治療法× 共変量の2 次交互作用（交互作用）の影響のいずれかを得点化に基づいてモデル化する方法である．このとき，AIM のモデル構築過程は，前進ステップワイズ法によって行われる．そして，各ステップで追加される指標関数（最適な共変量およびカットオフ値）の選定基準には，主効果あるいは交互作用の回帰パラメータに対するスコア検定統計量が用いられる．
他方，臨床研究では，共変量の応答への影響（主効果）とともに，治療法× 共変量の2 次交互作用（交互作用）の影響を評価することがある．例えば，がん臨床研究では，前者を予後因子（prognosis factor），後者を予測因子（predictive factor）と呼び，分子標的薬に対するバイオマーカー評価の因子として重要である．ただし，AIM では，共変量の主効果と治療法× 共変量の2 次交互作用を一つのモデルで記述することは困難である．なぜなら，AIM の選定基準では，指標関数を主効果，交互作用のいずれに追加すればよいかを評価できないためである．
本研究では，主効果と交互作用を一つのモデルで提示できる方法として，拡張型適応的指標モデル（EAIM: Extended Adaptive Index Model）法を提案する．EAIM では，AIM の評価基準に用いられている回帰パラメータのスコア検定統計量の代わりに，偏分残差の平均値に基づく基準を適用する．これにより，指標関数を主効果，交互作用のいずれに追加すればよいかを評価を選択できる．
さらに，AIM のモデル構築アルゴリズムにも問題がある．前進ステップワイズ法では，各ステップで追加された指標関数を再評価しないため，局所最適解に陥る可能性が高い．実際に，Tian & Tibshirani (2010) は，AIM のアルゴリズムの修正として，「後退あてはめ」の重要性を示唆している．そのため，EAIM では，多変量適応型回帰スプライン（MARS; Multivariate AdaptiveRegression Splines, Friedman (1991)）法の構築過程を応用する．すなわち，EAIM では，前進ステップワイズ法を用いて大きなモデルを構築し，後退ステップワイズ法を用いてモデル系列を作成する．そして，交差確認法を用いてモデル系列のなかから最適なモデルを選定する．これにより，EAIM の前進ステップワイズ法でモデルに含まれた指標関数の適切性を再評価できる．さらに，EAIM に対するMARS アルゴリズムの適用は，モデルの複雑さ（過剰適合）と解釈のし易さのトレード・オフを狙うこともできる．因に，EAIM の評価基準に偏分残差の平均値を用いることは，EAIM に対してMARS アルゴリズムを適用するためにも重要である．
EAIM の有用性および適用上の留意点は，実際の臨床試験のデータを用いて評価する．そこでは，胃全摘施行胃がん患者に対する術前免疫増強栄養食品投与の効果に対するランダム化比較第Ⅲ 相試験のデータを用いる．また，EAIM におけるMARS アルゴリズムの有効性，および，EAIM の性能の評価は，数値検証で確認する．
2節では，既存のAIM の方法について概説する．3 節では，EAIM の提案および構成のアルゴリズムを述べる．4 節では，事例検討および数値検証を通して，EAIM の評価を行う．5 節では，得られた結果を考察し，結びに代える．
Tian & Tibshirani (2010) は，AIM のモデルとして，2 種類の形式，すなわち，(1) 疾患に対する進行程度の把握を意図したモデル（モデル1），および(2) 試験治療に対する適応患者像の探索を意図したモデル（モデル2）を提案している．
いま，共変量x = (x1, x2, . . . , xP )T が与えられたとき，K 個の指標関数（ルール）によって構 成されるモデル(1) は，
で与えられる．ここに，βj(j = 0, 1) は回帰パラメータ，η(x) は一般化線形モデルにおける線形予測子，I(·) は括弧内が真ならば1，偽ならば0 を与える指標関数，p(k) はk 番目の指標関数で用いられる変数を表す添え字，cp(k) はk 番目の指標関数のなかで選択された変数
に対するカットオフ値である．そして，は，指標関数内の不等号を規定しており，
である．
すなわち，AIM は，任意の共変量をカットオフ値を用いてダミー変数に変換し，その総和をとる．つまり，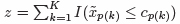
とおけば，式(1) は，η(x) = β0 + β1z となり（本論文ではx からz とおくことを得点化と呼ぶ），単一変量での一般化線形モデルと捉えることができる．このとき，線形回帰モデルはE(Y) = η(x)，ロジスティック回帰モデル（y ∈ {0, 1}) はlog(pr/(1 − pr))（ここにpr は，クラス1 の帰属確率を表す），そして，比例ハザード・モデルはλ(t, x) = λ0 exp{η(x)} である
また，モデル(2) は，
で与えられる．ここに，γ は，新治療（薬）の場合に1，既存治療（薬）の場合に0 をとるダミー変数である．モデル(2) でも，η(x) = β0 + β1γ + β2γz となることから，モデル(1) と同様に一般化線形モデルの形式で平易に表すことができる．
AIM では，回帰パラメータβj(j = 0, 1)（モデル(1) の場合），βj(j = 0, 1, 2)（モデル(2) の場合）の推定以外に，k 番目の指標関数のなかの変数およびカットオフ値cp(k) を推定しなければならない．Tian & Tibshirani (2010) は，, cp(k) の推定に，指標関数に対する回帰パラメータβ1（モデル(1) の場合），β2（モデル(2) の場合）に対するスコア検定統計量τp(k) を用いている．そして，指標関数の追加には，前進ステップワイズ法のアルゴリズムを採用している．
データ集合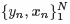
が与えられたとき，AIM のアルゴリズムを，図1 に示す．このアルゴリズムにおいて，P− に対するp(k) の削除ステップ（ステップ3e）は，モデル内に同一変数の指標関数が含まれないことを意味する．また，停止基準には，(a) 反復（ステップ3）のなかで，最大スコア検定統計量におけるp 値が事前の有意水準α 以上になる，(b) 指標関数の個数が任意の最大個数Kmax に到達する，の2 個が用いられる．
AIM は，共変量の主効果（がん臨床研究での予後因子），あるいは治療効果× 共変量の2 次交互作用（がん臨床研究での予測因子）のいずれかが評価できるものの，これらを同時にモデルに含めることができない．しかしながら，例えば，がん臨床研究における分子標的薬では，バイオマーカに対する予後因子と予測因子の評価が重要である．そのため，本論文の目標は，AIM を拡張することで，共変量に基づく主効果と治療効果× 共変量の2 次交互作用を評価できるようにAIM の拡張モデルを構成することである．本論文では，このモデルをEAIM（Extended Adaptive IndexModel）法と呼ぶ．
いま，共変量x = (x1, x2, . . . , xP )T，治療法に対するダミー変数をγ ∈ {0, 1}（1：試験治療，0：対照治療），および線形予測子をη(x) で表すとき，EAIM のモデルは
である．ここに，KM は主効果項（式(3) の第3 項）で用いられている指標関数の個数，KI は交互作用項（式(3) の第4 項）で用いられている指標関数の個数である．したがって，式(3) の第3 項が共変量に基づく効果（予後因子）を表し，第4 項が治療法× 共変量の2 次交互作用（予測因子）を表す．
2 節で述べたように，AIM では，回帰パラメータに対するスコア検定統計量が，指標関数のなかの変数およびカットオフ値の選定に用いられる．しかし，EAIM では，β2 とβ3 でスコア検定統計量が計算できるため，AIM と同様の評価基準を用いることは困難である．EAIM では，指標関数で用いられる共変量およびカットオフ値の選定基準に偏分残差（deviance residual）を用いる．
いま，式(3) をEAIM における得点化後の変数（得点化変数）
による応答y への回帰問題と見做せば，η(x) = β0 +β1γ +β2zM +β3zI となることから，EAIMでの偏分残差は，一般化線形モデルでの偏分残差をそのまま用いることができる．
データ集合
が与えられたときのxn に対する主効果に対する得点化変数を
交互作用に対する得点化変数を
とする．このとき，
に対する回帰パラメータの推定値
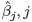= 0, 1, 2, 3 は，指標関数が与えられたもとで，最尤法により計算できる．
において，EAIM の偏分残差は，応答y が量的変数（線形回帰）のとき，
である．
また，2 値応答（yn ∈ {0, 1}) のとき，
で与えられ，ここにsign(·) は括弧内が正ならば1，負ならば-1 を与える符号関数であり，
は，yn = 1 に対する推定帰属確率，
である．
そして，
（tn は生存期間，δn は中途打ち切り指標（0：イベントなし，1：イベントあり））が与えられたとき，比例ハザード・モデルの偏分残差は，
で与えられ，ここに，
は，
である．したがって，N 個の観測値における平均偏分残差err は，
で与えられる．
AIM のモデル構築アルゴリズムは，前進ステップワイズ法のみで構成される．そのため，推定モデルが局所最適解に陥る惧れがある(Tian & Tibshirani, 2010)．他方，指標関数を打ち切りベキ乗基底関数におき代えると，式(3) のモデルは，多変量適応型回帰スプライン（MARS: MultivariateAdaptive Regression Spline）法のアルゴリズムを用いることができる．すなわち，前進ステップワイズ法において，過剰適合がするほど大きなモデルを構築し，後退ステップワイズ法において，切片まで指標関数を削除することで推定モデル系列を作成する．そして，平均偏分残差に対する交差確認推定値を用いることで，推定モデル系列のなかから最適な推定EAIM モデルを選定する．
先ず，前進ステップワイズ法のアルゴリズムを図2 に示す．ここで，
と
を個別に用いるのは，例えば，がん臨床試験における生存期間に対する予後因子（主効果）と予測因子（交互作用）は，いずれか一方であることはない．主効果と交互作用に対する共変量の重複は，このことを許容するためである．
次いで，後退ステップワイズ法のアルゴリズムを図3 に示す．後退ステップワイズ法により，推定EAIM モデル系列
= 1, 2, . . . , K0 が得られる．ここに，K0 は，前進ステップワイズ過程で得られた指標関数の最大数K0 = KM+ KI である．MARS では，最適なモデル（rightsized model）の選定に一般化交差確認法が用いられる．EAIM 法でも同様の接近法が考えられるものの，本論文では，V 重交差確認法を用いる．
いま，全データ集合
をV 分割した部分データ集合を
= 1, 2 . . . , V（テスト・データ集合）とし，残りを
= 1, 2 . . . , V（学習データ集合）とする．交差確認法では，先ず，学習データ集合
を用いて，EAIM モデルをあてはめ，
= 1, 2, . . .,K0 を推定する．次いで，モデルに対して，
番目の個体を当てはめ，偏分残差の交差確認推定値
を得る，そして，モデル系列のなかのo 番目のモデルに対する平均偏分残差の交差確認推定値
を計算する．そして，
を最小にするo∗ 番目の推定AIM モデル
を最良モデルとして選定する．あるいは，Breiman et al. (1984) に倣い，1SE ルールのもとで選定することも考えられる．
ここでは，事例検討および数値検証を通して，EAIM の性能を評価する．事例検討では，実際のデータへの応用を通して，EAIM の適用上の留意点について検討する．また，数値検証を通し て，EAIM の性能を吟味する．
ここでは，胃全摘術施行胃がん患者に対する術前免疫増強栄養食品投与の効果に関する無作為比較試験（OGSG0507）のデータを用いる．そこでは，胃全摘術施行患者に対して，術前での免疫増強栄養食品の摂取が術後感染症（SSI）割合の減少に効果があるか否かを多施設共同オープン・ラベル無作為化第Ⅲ 相試験のもとで評価された(Fujitani et al., 2012)．本解析では，γ = 1 を術前免疫増強栄養食品摂取群（N = 117）とし，γ = 0 を自由摂取群（N = 108）とする．主要評価項目（応答y）は，SSI の発現の有無（有：1，無：0）である．また，それぞれの被験者に対して，手術時間，出血量，身長，体重，BMI，体重減少量，T 因子，N 因子，ステイジ，アルブミン，白血球，手術法，再建法および根治度が共変量としてとられている．
図4 は，指標関数（本節では，解釈上の観点からルールと呼ぶ）の数に対する，平均偏分残差の交差確認推定値の推移を表している．ここで，エラーバーは，偏分残差の交差確認推定値に対する標準誤差（SE）である．1SE ルールに基づいて基底関数の数を選択するとき，最良の基底関数の個数は，5 個だった．このときの推定モデルに基づくルールを表1 に示す．
その結果，治療群γ に対する偏回帰パラメータより，術前免疫増強栄養食品の服用だけで，SSIが減少することは少ないことが示された．主効果では，出血量，ステイジ，およびBMI が選択された．すなわち，出血量，胃がんの進行程度あるいは患者の体型といった治療前および治療因子が，SSI の発現に影響があった．手術時間が増加する（480 分以上），あるいは胃がんの進行程度が進んでいない（≥Ⅱ）ような患者に対して，SSI のリスクが増大することは平易に理解できる．また，BMI が低い患者において（BMI≤23.9），SSI の発現リスクが増大した．BMI とSSI の発現に関しては，Fujitani et al. (2012) のなかでも指摘されており，EAIM は，この結果を反映している．
交互作用では，ルールに含まれるすべての共変量が主効果と同じだった（BMI およびステイジ）．偏回帰パラメータの符号より，BMI では，26.7 以上の患者に対する術前免疫増強栄養食品の服用が適さないことが示唆された．また，がんの進行程度（ステイジ）が軽微な場合（IA）にも同様の傾向が示された．すなわち，胃がんの進行程度が低い，あるいは，BMI が高い患者に，術前免疫増強栄養食品を投与することは適さないことが示唆された．
図5 は，EAIM による主効果のルールとSSI 発現割合の関係を表している．すべてのルールにおいて，ルールが真（Positive）のほうが，偽（Negative）に比べてSSI 発現割合が高かった．また，指標関数が真のとき，SSI 発現割合が最も高かったのが出血量（55.4%）であり，次いで，ステイジ（42.2%）が高かった．
図6 は，EAIM による交互作用のルールとSSI 発現割合の関係を表している．BMI が，26.7 未満のときには，SSI 発現割合が殆ど減少しなかった．また，ステイジでは，進行程度がIA を超えるときに，術前免疫増強栄養食品を投与することで，SSI 発現割合が減少するのに対して，IA のときには殆ど変化がなかった．よって，BMI の高い患者にとってインパクト投与はリスクに繋がり，Stage1A の患者にとってインパクト投与は無意味だった．つまり，EAIMでは，同じルールでも異なる解釈が必要になる場合がある．そのため，EAIM では，推定されたモデルのルールをグラフ表示し，その傾向を省察することが重要である．
4.2. 数値検証ここでは，数値検証を通して，(1) EAIM におけるMARSアルゴリズムの適切性評価，(2) EAIMが予後因子（主効果），予測因子（交互作用）を適切に捉えられるか否かの評価，を行う．
4.2.1. EAIM におけるMARS アルゴリズムの適切性評価Tian & Tibshirani (2010) では，前進ステップワイズ法に基づいてモデルを構成している．これに対して，EAIM では，前進ステップワイズ法で得られた大きなモデルを，後退ステップワイズ法により切片項まで刈り込むことで，モデル系列を構成し，交差確認法によりモデルを選択している．ここでは，EAIM のモデル構築の過程の適切性を評価する．このとき，AIM 法とEAIM法では，モデル自体が異なるため，そのままの形式では評価できない．そのため，AIM の類推として，EAIM のなかの偏分残差の代わりに，主効果および交互作用の回帰パラメータに対するスコア検定統計量のp 値を計算し，主効果と交互作用の選択には，p 値を利用した(p 値が小さい項に指標関数を追加した）．また，停止基準には，有意水準α = 0.05 を用い，いずれの回帰係数のp値においても有意にならなくなるまでアルゴリズムを停止した．因みに，この方法では，MARSアルゴリズムが利用できない．
ここでは，真のモデルとして，Tian & Tibshirani (2010) の数値検証に倣い，2 種類のモデルを考える：
ここに，xp ∼ Unif(−1, 1), p = 1, . . . , 15（Unif：連続型一様分布），γ ∼ Ber(0.5)（確率0.5 のBernoulli 分布）である．したがって，モデル1 では11 個，モデル2 では13 個が真のモデルと無関係な変数である．また，応答y は，
により算出する．モデル1 は，線形ロジスティック回帰モデルに基づいており，EAIM では真の構造を捉えることができない．他方，モデル2 は，指標関数に基づいており，EAIM を用いて真の構造を捉えることができる．本数値検証では，ロジスティック回帰解析（前進ステップワイズ法/2次交互作用までをAIC に基づいて選択），AIM アルゴリズム（スコア検定統計量/前進ステップワイズ法），およびEAIM アルゴリズム（偏分残差/MARS 法）を当てはめる．学習データの標本サイズは，NLn = 200 であり，テスト・データの標本サイズは，NTs = 500 とした．これらの設定のもとで，指標関数の最大個数（ロジスティック回帰の場合には共変量の最大個数）を変化させながら100 回シミュレートした．このとき，評価基準には，テスト・データでの平均誤分類割合とした．
（実線：EAIM（偏分残差/MARS 法），点線：AIM（スコア検定統計量/前進ステップワイズ法），破線：ロジスティック回帰分析（前進ステップワイズ法/2 次交互作用までをAIC に基づいて選択）
図7(a) は，モデル1 に対する結果である．ロジスティック回帰（破線）は，真のモデルを捉えられることから，共変量の個数P = 4 のとき，誤分類率がほぼ0 になった．これに対して，EAIM（実線）およびAIM（点線）では，真のモデルを捉えられないため，誤分類率は高かった．これは，Tian & Tibshirani (2010) でも指摘されており，AIM（およびEAIM）が予測確度の向上が目標でないことが述べられている．また，EAIM およびAIM のいずれの方法もP = 4 から上昇傾向を示した．このとき，EAIM アルゴリズムは，AIM よりも誤分類率が低かった．
図7(b) は，モデル2 に対する結果である．図7(a) と異なり，ロジスティック回帰（破線）は，真のモデルを捉えられないことから，誤分類率が高く，最大基底回数の個数P が3 以上で上昇傾向を示した．これに対して，EAIM（実線）およびAIM（点線）では，真のモデル構造の基底関数の個数P = 2 のとき，誤分類率が最小になった．AIM では，P = 4 から8 にかけて誤分類率が上昇傾向を示すだけでなく，標準偏差が大幅に上昇した．これに対して，EAIM では，最大基底関数の個数に対して，誤分類率が上昇することなく，また，標準偏差は最も低かった．よって，EAIMによるMARS アルゴリズムの導入は適切だったと考えられる．
4.2.2. 予後因子・予測因子摘出に対するEAIM の評価ここでの数値検証の目標は，(1) 生存時間研究において，適切に予後因子および予測因子を捉えることができるか，(2) EAIM の構成に影響を与える要因は何か，を検討することである．ここでは，真のモデルとして，
を考える．ここで，基線ハザードλ0(t) には，指数分布E(1) に従うとする．また，真の回帰パラメータには4 種類のパターン，すなわち，
を設定する．
このとき，標本サイズN の患者に対する共変量xjn は連続型一様Unif(0,1) に従う乱数により生成し，治療因子γn は，確率0.5 のBernoulli 分布Ber(0.5) に従う乱数により生成する．また，観測生存期間および中途打ち切り指標は，以下のように生成した．
1. いま，標本サイズN の患者のキックオフから登録までの期間が連続型一様Unif(0,T∗) に従うとしたもとで生成する（wn, n = 1, . . . , N）
2. 共変量および治療に治療因子を生成したもとで，式(5) を計算し，ハザード比λn を得る．
3. n 番目の患者真の真の生存期間un を指数分布E(1) により生成する．
4. 次式
のように観測生存期間tn, および中途打ち切り指標δm を計算した．
このとき，中途打ち切りを規定するしきい値T∗ は，100,000 回のシミュレーションによって表2 のように与えられる．本数値検証では，標本サイズN の学習標本に対してあてはめられたモデルに対して，N = 500 のテスト標本を適用し，評価基準にHarrell のC 指標を計算する．このとき，EAIM の対照手法には，Cox 比例ハザード・モデル（2 次交互作用までをモデルに含むことを許容し，前進ステップワイズ法のもとでAIC が最大になるモデルを選定），および生存時間樹木構造接近法(LeBranc & Crowley, 1992) を用いる．前者は予後因子・予測因子の評価で頻用されており，後者はEAIM と同様に結果がプロダクション・ルールで与えられることから，これらを対照手法として選択している．また，結果に影響を与える要因として，共変量の数（10, 15, 20の3 水準），学習標本の標本サイズ（100, 200, 300 の3 水準），そして，中途打ち切り割合（10%,20%の2 水準）を設定した．これらのすべての組み合わせに対して，100 回のシミュレーションを行った．これらの因子が得られた結果に及ぼす影響は，分散分析のp 値および寄与率により評価する．このとき，2 次交互作用までを解釈する．
表3 は，分散分析の結果である．手法（M）による違いが顕著であり，寄与率は56.90%だった．本数値検証における真のモデルは，EAIM 以外の手法では表現できない．このことが結果に反映されたと考えられる（前節の数値検証でも同様の示唆が与えられている）．次いで，手法（M）× モデル（T）の2 次交互作用が13.23%と高かった．つまり，予後因子・予測因子のいずれか/両方が存在する場合に，手法によって結果が大きくことなることが示された．その他の要因では，顕著な違いが認められなかった．標本サイズは，EAIM が適用される，無作為化第Ⅱ 相試験から第Ⅲ 相試験までの状況を想定したが，そのような場面では，標本サイズに殆ど依存しないことが示唆された（因に，標本サイズが小さい場合，EAIM の回帰パラメータ推定が発散する状況が散見された．このような傾向は，AIM のR パッケージaim でも同様の傾向が与えられている）．次いで，中途打ち切り割合は，今回は比較的少ない状況を想定したため，影響が小さかった．ただし，寺西他(1989) は，中途打ち切り割合が25%以上のとき，真の生存時間分布を捉えられない恐れがあることを指摘しており，過度な中途打ち切り割合での評価は不適切である．共変量の個数は，いずれの手法でも，変数選択が加味されるため，大きな影響がなかったと推察される．
図8 は，手法とその他の組み合わせ水準に対する2 次交互作用プロットである．いずれの状況においても，EAIM のC 指標が極端に高く，良好な結果が与えられた．手法× モデルの2 次交互作用では，Model.1 およびModel.2 のとき，EAIM とその他の手法（Tree, PH）の差が非常に大きかった（図8(a)）．手法× 標本サイズ（図8(b)），および手法× 共変量（図8(c)）では，いずれの手法も水準の変化に対してC 指標が殆ど変化しなかった．手法× 中途打ち切り割合では，EAIMが僅かな減少傾向を示した（図8(d)）．前述したように，EAIM では，中途打ち切りが多い場合に，分岐点候補の探索に多大な影響を与えることが想定されるため，適用する場合には注意深く検討する必要がある．
本報告では，予後因子および予測因子を同時に評価するための適応的指標モデルとして，拡張型適応的指標モデルを提案した．そこでは，多変量適応型回帰スプラインのアルゴリズムを応用することで，既存の適応的指標モデルのアルゴリズムに比べて良好な結果を示した．また，事例検討を通して，拡張型指標モデルの有用性と適応上の留意点を検討した．そして，拡張型指標モデルにより示唆された共変量のグラフィカルな省察が重要だった．さらに，数値検証を通して，拡張型適応的指標モデルの性能を吟味した．その結果，拡張型適応的指標モデルは，治療効果，予後因子および予測因子を他の手法に比べて適切に評価できるものの，真のモデルが予後因子と予測因子を含む場合には若干性能が落ちることが確認された．また，生存時間解析においては，中途打ち切り割合の影響が僅かに認められた．実地において，中途打ち切り割合が多い状況では，真の生存曲線を捉えることは困難であることから，試験自体の信頼性に疑義が持たれる場合が多い．実際に，寺西他(1989) は，中途打ち切り割合が25%以上のとき，真の生存時間分布を捉えられない恐れがあることを指摘している．このことを鑑みると，拡張型適応的指標モデルは，分子標的薬に対するバイオマーカーを伴う臨床試験のなかで注目されている，予後因子および予測因子の統計的評価に活用できそうである．
本研究は，文部科学省私立大学戦略的研究基盤形成支援事業「セキュアライフ創出のための安全知循環ネットワークに関する研究（研究代表者：堀雅洋（関西大学）」および，文部科学省科研費（若手B）「がん臨床研究におけるレスポンダーおよびシグナル検出のための統計的機械学習法の開発（研究代表者：下川敏雄（山梨大学））」の支援のもとで行われました．ここにお礼申し上げます．
