2017 年 6 巻 1 号 p. 31-45
2017 年 6 巻 1 号 p. 31-45
テストが測定すべき心理学的な特性が多様化してくるにしたがって,「テスト(項目)はそもそも何を測っているのか」という構成概念に関する精緻な検証が求められている.最近では,その手段として多次元IRTが注目されてきており,これまでそれほど測定論的な関心が注がれてこなかったテストの下位領域についての定量的な検証の必要性も指摘されている.そこで本研究では,わが国の学習指導要領に則って作成された平成18年度新潟県全県学力調査における中学校2年生数学データ (N=9,102)に対して,多次元IRTを使って下位領域特有の影響について定量的に検証した例を示す.その結果,テスト全体が測定する「数学力」よりも下位領域特有の影響を強く受けている項目は25項目中2項目存在し,その内容は定性的な観点からも妥当であることが確認できた.つまり,多次元IRTを用いることにより,テスト項目の測定内容に関して項目レベルで次元に応じた情報が得られることを意味し,今後のテストデータ分析においても,単にIRTモデルを適用するだけではなく,多次元IRT分析にもとづくより精緻な妥当性検証が可能であることが示された.
The more complicated and diverse the psychological constructs a test measures, the more sophisticated methods to study the constructs are required. Recently, multidimensional IRT is used in such studies so that the existence and structure of subscales of achievement tests are examined. The present study used the data (which had been implemented for all students in Niigata prefecture at the eighth grade level (N=9,102)) and examined in detail what the subscales measure using multidimensional IRT (bi-factor model). The results show that group factors have more impact than general factor on the 2 out of 25 items, and qualitative examination of these items confirmed the result. It is implied that multidimensional IRT can provide much item-level information compared to conventional (unidimensional) IRT and have potential for better examination of measurement constructs.
近年の大学入学者選抜に関する議論の中で,従来の知識・技能の測定にとどまらず,「思考力・判断力・表現力」といった力を測定する入学試験を目指すとされた「高大接続システム改革会議『最終報告』」( 文部科学省, 2016) に象徴されるように,わが国においてテストが測定すべき心理学的な特性は多様化してきている.実社会における様々な場面においてテストが活用されている中, 石井(2014) が指摘するように,テストが測定する構成概念についての精緻な検証を通して,「テストで評価する」だけでなく「テストを評価する」ことの重要性を再認識することが急務であるというのが現状であろう.
テストデータの分析では,わが国では歴史的に心理測定分野における「テストの専門家」が少なく,大学教育の中でもその養成に関わる講義も少ない( 木村, 2010) ことを背景としながらも,項目反応理論(item response theory)( Lord, 1952)(以下,「IRT」)を活用した研究は増加してきている.最近では,単にIRT をテストデータに適用するだけでなく,現場へのフィードバックを意識した受検者の認知的な診断を目的とした分析( 鈴木・豊田・山口・孫, 2015; 坂本・柴山, 2014)や,適応型テストのための研究( 熊谷, 2014; 熊谷・五島・中畝・柴山・佐藤・野口, 2013) などへ発展してきている.
しかしながら,これらのIRT 分析は実用的である一方で,1 次元性の仮定と局所独立の仮定の2つの条件を満たす必要があり,複数の能力を測定するような多次元性のあるテストデータは扱えないという問題があった.実際のテストには多次元性の項目反応データを生み出しうる様々な下位領域(subscales)が存在することも指摘されており( Reise, Cook, & Moore, 2015),最近ではこのような複数の能力を測定するテストの分析のために多次元IRT(multidimensional IRT) 1 ( Reckase,2009) の活用が期待されている.特に,わが国において1999 年に端緒が開かれた「学力低下論争」においても,測定領域別の平均正答率に基づく国別順位についての議論が中心となるなど( 志水,2016; 市川, 2012),テストを構成する下位領域をいかに扱うかは常にテスト結果を解釈する際の重要なポイントとなっている.この問題に対して,古典的テスト理論にもとづいて下位領域別に正答数得点を算出することやIRT 分析を通して潜在特性尺度値を推定することが行われてきたが,厳密に言えばこれらの方法は項目レベルでの下位領域間の関係性を考慮できていない.言い換えれば,ある項目が,テスト全体の測定する構成概念を反映しているのか,また下位領域特有の構成概念を反映しているのかについては従来の方法は判断不可能であった.
このような状況に対して, Reise, Morizot, & Hays (2007), Reise, Moore, & Haviland (2010), Reise, Ventura, Keefe, Baade, Gold, Greem, Kern, Gately, Nuechterlein, Seidman, & Bilder(2011), 坂本(2016) はテスト項目全体に影響を持つ一般因子(general factor)と下位領域特有の影響を示すグループ因子(group factor)を設定した多次元IRT の確認的なモデリングの一種となる双因子モデル(bifactor model)( Gibbons & Hedeker, 1992) を用いて,テストの下位領域特有の影響に関する測定論的な検証を実証的に示している.具体的には,Reise et al. ( 2007, 2010, 2011) では,一貫して双因子モデルを含む多次元IRT モデルを医療分野のデータに適用し,項目識別力パラメータを参照することによって,一般因子の影響を統制した上でのグループ因子の影響を項目レベルで相対的に比較している.特に, Reise et al. (2007) ではCAHPS2.0(ConsumerAssessment of Healthcare Providers and Systems)のデータ(N=1,000)における16 の質問項目に対し,双因子モデルを使って一般因子とグループ因子それぞれにおける心理学的な情報量を規定する項目識別力パラメータから,16 項目中2 項目が一般因子よりもグループ因子の影響を強く受けていることを明らかにした.また,学力テスト研究の分野では, 坂本(2016) がわが国の2011 年国際数学・理科教育動向調査(TIMSS)中学校2 年生数学データの214 項目(N=4,414)を対象に, Mullis, Martin, Ruddock, O’Sullivan, & Preuschoff (2009) が定める認知的領域の知識(knowledge),推論(reasoning),応用(applying)の3 領域の枠組みを用いて双因子モデルを適用した.その結果,214 項目中23 項目が,テスト全体の測定する一般因子としての「数学力」よりもグループ因子としての下位領域特有の影響を強く受けていることを明らかにしている.しかし,TIMSS は国レベルの意図されたカリキュラム,学校や教師レベルの実施されたカリキュラム,児童生徒の成果を示す達成されたカリキュラムから構成される三層構造のカリキュラムモデルに基づいている( Mullis et al. 2009) ため,わが国で行われる学習指導要領に基づいて設計される学力テストとは測定領域が異なり,測定される学力も同一ではない.
そこで本研究では,わが国の学習指導要領に基づいて設計された学力調査データを使い,その下位領域の影響について測定論的に検討することを目的とする.具体的な手順としては,まず従来の古典的テスト理論に基づく項目分析や1 次元性を仮定したIRT 分析を行う.次に,後述する4つの仮説モデルの項目パラメータを推定した後,モデルの適合度を確認し, Reise et al. (2007), 坂本(2016) と同様に,項目識別力パラメータの2 乗値によって項目レベルで測定領域についての情報量を比較する 2 .最後に,支持されたモデルから潜在特性尺度値を推定し,測定領域における学力分布を確認する.
平成18 年度新潟県全県学力調査における中学校第2 学年数学データ(N=9,102,項目数は25)を使用する 3 . 新潟県教育委員会(2007) ならびに当時の学習指導要領( 文部科学省, 2006) によれば,項目1 から項目10 は「数と式」,項目11 から項目16 は「数量関係」,そして項目17 から項目25 は「図形」を測定する項目群であり,これらが前章で述べた下位領域となる.付録 A には実際の項目例を示す.
2.2. 方法多次元IRT は一般に補償型(compensatory)モデルと非補償型(noncompensatory)モデルに大別される.補償型モデルは,複数の能力を測定するテストにおいて,ある能力が低い場合でも他の能力が十分高ければ当該の項目には正答しやすいという仮定を置くモデルである.つまり,数学的にはそれぞれの次元同士は和の関係にある.一方,非補償型モデルは当該の項目に正答するにはある特定の能力が高いだけでは達成されないことをモデル化しており,数学的にはそれぞれの次元同士の積によって正答確率を定義していることに特徴がある.本研究では,補償型多次元2 値2PL モデル(以下,多次元2PL モデル)を採用する.1 次元性を仮定した2PL モデルは, u ij を受検者 i の項目 j に対する反応, a j を項目 j における項目識別力パラメータ, b j を項目 j における項目困難度パラメータとすれば

と表せる.これを多次元空間に拡張することで多次元2PL モデル

が得られる.このとき次元数を m とすると a j は1 × m の項目 j の識別力パラメータベクトル,θ i は1 × m の受検者 i の潜在特性尺度値ベクトル, d j は困難度に関連するパラメータ(スカラー)となる.なお, d j は1次元性を仮定した項目困難度パラメータ b j と同じ解釈はできないことには注意が必要である.
多次元IRT によるテストデータの分析を行う際,測定領域に関する事前の仮説がある場合には,確認的なモデリングを行うことも可能である.その代表例とも言える双因子モデルにおける項目識別力パラメータは行列で表記すると,たとえば

となる.このように双因子モデルでは,全項目へ影響を与える一般因子と,それぞれの下位領域の影響としてのグループ因子を定めるモデルである.このモデルの特徴を利用すれば,一般因子を統制することによってグループ因子(下位領域)特有の影響を検討できることが可能となる.
また,多次元IRT でも通常のIRT と同様に項目情報量を定義することができる.項目 j に正答する確率と誤答する確率をそれぞれ P j (θ Q j (θ

と定義される.多次元IRT においては式(2) を多次元空間に拡張し,空間上の一点であるθ i とνθα iν とすると

として定義できる( Reckase & Mckinley, 1991; Reckase, 2009).当然,式(3) で定義される項目情報量関数も,式(1) より項目識別力パラメータベクトル a j ,潜在特性尺度値ベクトルθ i ,困難度に関するパラメータ d j の関数となっており,多次元の場合でも項目識別力パラメータの値によって項目情報量が規定されることがわかる.このとき,項目特性曲面(item characteristic surface)の傾きがもっとも急となる,つまり項目情報量が最大となるのは

のときとなる.式(4) より,特定の項目における同一モデル内での次元間の情報量の比較は,項目識別力パラメータの2 乗値の比較をすることで可能となることがわかる.特に,双因子モデルの場合には,テスト項目全域にわたり測定される一般因子と下位領域が測定するグループ因子の測定論的な情報量による項目レベルでの比較が可能となることが理論的に導ける( Reckase, 2009; Reise et al., 2007).
そこで本研究では, Reise et al. (2007), Rindskopf & Rose (1988), 坂本(2016) を参考にして以下の4 つのモデルを仮説として設定した.まずモデルA として1 次元性を仮定した通常の2PL モデルを設定する.このとき,テスト全体は1 つの「数学力」を測定していることを仮定することになる.次に, 新潟県教育委員会(2007) ならびに 文部科学省(2006) から,当該の項目が測定すると定められていない領域については項目識別力パラメータを0 とする確認的多次元IRT モデルをモデルB として設定する.このとき,テストの下位領域間には何らかの相関関係があると考えるのが自然であることから,下位領域間の因子間相関を認めることにする.次に,テスト全体に「数学力」因子,それに加えて下位領域特有の影響を認める双因子モデルを設定するが,このときモデルB と同様に下位領域間の関係を考慮することが可能である.そこで本研究では下位領域間の相関を許容しないモデルと相関を許容するモデルをそれぞれモデルC とモデルD とする.
テストの下位領域に関する多次元IRT 分析を行う際,その下位領域の設定によって分析結果が異なってくる.たとえば, 坂本(2016) ではTIMSS2011 中学校2 年生数学における認知的な領域の枠組みを用いて分析を行っている.その際,「知識」「推論」「応用」という領域をテストにおける「次元」(=因子(factor))とみなすことで,それ特有の影響を検証している.本研究では,わが国における学習指導要領で定められる内容的な領域をテストにおける「次元」とみなして分析を行うことになる.このような内容的な枠組みを使った測定論的な検証はこれまでほとんど試みられておらず,いわば暗黙知にその枠組みの中での平均正答率等の比較にとどまっていた.本研究では,従来のIRT 分析で扱う1 次元の構成概念としての「数学力」でのみの議論を超えて,下位領域特有の影響がある項目を抽出することや,「数学力」を統制した後の下位領域それ自体の潜在特性尺度値を推定することに繋げることを試みる.
なお,分析にはR3.1.0 におけるパッケージmirt1.7 ( Chalmers, 2015) を使用する.項目パラメータの推定法にはEM 法( Bock & Aitkin, 1981) やMetropolis-Hastings Robbins-Monro 法(MH-RM 法)( Cai, 2010) などがある.多次元IRT 分析では推定するモデルの次元数が高くなるにしたがって,EM 法にもとづく周辺最尤推定法では収束が遅くなってしまう等の課題が指摘されている.一方,MH-RM 法では,EM 法の推定精度に匹敵すること,その推定に要する時間もEM 法に比べて短いこと,また項目パラメータのリカバリの精度が高いことが知られている( Cai,2010; Han & Paek, 2014).そこで本研究では,項目パラメータの推定にはMH-RM 法を採用した.詳しくは Cai (2010), Han & Paek (2014) を参照されたい.
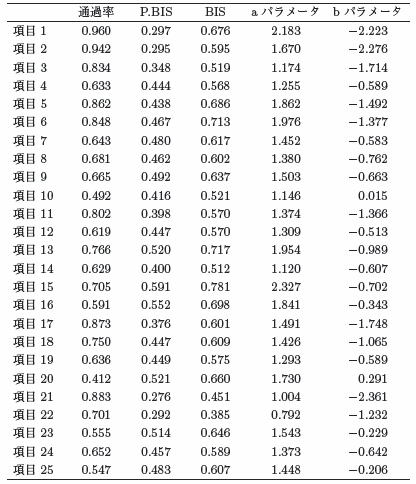
古典的テスト理論に基づいた項目ごとの通過率,点双列相関係数(point-biserial correlation),双列相関係数(biserial correlation)と,1 次元性を仮定した2PL モデルによって推定した項目識別力パラメータ(a パラメータ)と項目困難度パラメータ(b パラメータ)を表 1 に整理した.項目困難度パラメータの値から,今回のテストは比較的「易しい」項目で構成されているものの,心理測定論的に分析から除外すべき項目は含まれていない.むしろ,項目識別力パラメータの値が1.5を超えるものも25 項目中10 項目存在し,識別力の高い「良い」項目が多く含まれていることがわかる.
前節での従来の項目分析から,識別力の高い「良い」問題が多く存在していることが明らかになったものの,このテストを構成する下位領域ごとの情報はほとんど得ることができない.そこで,4つの仮説モデルの項目識別力パラメータを推定し,その結果を表 2 に整理した.ただし,モデルA については前節で行った1 次元性の仮定の下でのIRT 分析のことを指しており,項目パラメータの値も同一である.
本分析における情報量基準として,AIC(Akaike’s Information Criterion)( Akaike, 1974),BIC(Bayesian Information Criterion)( Bozdogan, 1987) を使用する.また適合度指標として,RMSEA(Root Means Square Error of Approximation)( Steiger, 1990),TLI(Tucker-Lewis Index)( Tucker & Lewis, 1973),CFI(Comparative Fit Index)( Bentler, 1990) を用いる.
表 2 より,モデルの適合度の値からモデルD がもっともあてはまりがよいことがわかる.また,モデルB において下位領域間の相関がいずれも0.8 以上あるが,モデルD においてテスト全体が測定する「数学力」を統制した後の下位領域間の相関は0.3~0.6 程度へと弱まっていることが確認できる.また,モデルD における「数と式」と「数量関係」の因子間相関0.632 は,「数と式」と「図形」,「数量関係」と「図形」のそれぞれの因子間相関0.311,0.361 より大きく推定されている.つまり,「図形」は他の測定領域と比較してやや異なる要素を測定していることを意味している.この結果は,項目レベルでみれば,項目24 と25 の「図形」の項目識別力パラメータが「数学力」のそれより大きく推定されていることにも関連していると考えられる.

実際の項目識別力パラメータは,「数学力」と「図形」は項目24 において1.612 と1.861,項目25において1.598 と1.672 である.式(4) における項目情報量の観点から,その2 乗値の比をとることで「図形」のほうが「数学力」よりも項目24 においては1.332 倍,項目25 においては1.094 倍の情報量を保有していることがわかる.付録 A の実際のテスト項目の問題内容から,これらの項目はたしかに三角形の合同条件についての知識は必要と考えられるものの,数学的証明の論旨組み立てを図形の読み取りから行い,そして推論を進めていく力が求められていることがわかる.したがって,今回の分析を通して,項目24,25 については,従来の1 次元性を仮定するIRT 分析で仮定する「数学力」よりも「図形」という領域特有の影響のほうが強いということが定量的かつ定性的に確認できたことになる.
このような項目の具体的対処としては,改めて古典的なテスト理論に基づく項目分析結果を参照し,過度に正答率が低い項目ではないか,あるいは1 次元性を仮定するIRT 分析において項目識別力パラメータの値が小さくないか,また項目困難度パラメータの値が大きくなっていないかを確認する必要がある.仮に従来の1 次元性を仮定するIRT モデルを基盤として出題されることになった(分析対象となった)場合でも,下位領域特有の影響が見られる項目は1 次元では説明できない異質な能力を測定している可能性があるので,テスト結果の解釈とその後の教育指導等には注意が必要となる.
このように,従来の1 次元性を仮定したIRT を使った項目分析では明らかにできなかった学力テストの下位領域特有の影響について,多次元IRT を基盤とした双因子モデルを使うことで定量的に明らかにすることができ,さらにそれを定性的な検討に結びつけることが示せるのである.
3.3. 潜在特性尺度値への影響次に,従来の1 次元性を仮定したIRT 分析(モデルA)とモデルD のそれぞれにおける潜在特性尺度値を,EAP 法によって推定した.その分布の広がりを確認するため,箱ひげ図を図 1,モデルA とモデルD における「数学力」潜在特性尺度値の散布図を図 2,平均と標準偏差を表 2 に整理した.
モデルD において推定される「数と式」「数量関係」「図形」の潜在特性尺度値は,「数学力」を統制した後の下位領域に関する潜在特性尺度値となっている.図 1 から,モデルA で推定された潜在特性尺度値とモデルD の「数学力」における潜在特性尺度値の分布の広がりが似通っていることがわかる.次に,「数学力」を統制することによって,モデルD におけるすべての下位領域における潜在特性尺度値の分布が「数学力」のそれより裾が短くなっていることが確認できる.その中でも,「数と式」の分布の広がりがもっとも狭く,各下位領域と比較すると相対的に「数と式」に関する学力に差がないことが示唆される.一方,3 つの下位領域の中では「図形」の分布の広がりが相対的に大きく,もっとも受検者内の能力差があることがわかる.なお,図 2 より従来の「数学力」という1 つの構成概念を仮定して行った際の潜在特性尺度値と双因子モデルで仮定する「数学力」のそれは直線状にプロットできる(相関係数=.998).
また,3 つの下位領域ごとの素点合計点とモデルD で推定した「数学力」を統制したあとの下位領域に関する学力との相関,ならびに箱ひげ図をそれぞれ表 4 と図 3~図 5 に整理した.
表 4 から,下位領域ごとに算出した素点による合計点とモデルD において「数学力」を統制したあとの下位領域に関する学力との間には0.5~0.7 程度の相関があることがわかる.素点による領域ごとの合計点には「数学力」と下位領域ごとの学力の情報が混在しているため,モデルD で推定した下位領域ごとの潜在特性尺度値とこの程度の相関が発生するのは自然である.ただし,「図形」においては相関が0.5 程度であり,相対的にその程度が低くなった.これは3.2 でも述べたように,モデルD における下位領域間の因子間相関が「図形」を含む場合に小さく推定されていたことにも関連していると考えられる(表2).この事実からも,「図形」領域は他の測定領域と比較してやや異なる要素を測定していることが示唆される.また,図 3~図 5 からは素点合計点上は同じ点数であっても,「数学力」を統制したあとの下位領域に関する学力には幅があることがわかる.




通常の項目分析やIRT 分析ではテストの1 次元性を仮定するため,厳密に言えば,測定領域としての「数学力」「数と式」「数量関係」「図形」のすべての要素(測定論的な情報)が混在しているのである.本研究では,テスト全体が測定する「数学力」を統制した後の下位領域に関する学力を推定し,従来のIRT 分析の結果や正答数得点との比較を通して,テストの測定領域(下位領域)に関する詳細な検討が可能であることを示した.多次元IRT によってテストの下位領域に関する精緻な統計量を得られる可能性があるという意味で本研究の意義となろう.



本研究では,わが国の学習指導要領に則って作成された学力テストの下位領域について,多次元IRT を用いることで,従来のIRT 分析では不可能だった構成概念に関する精緻な検証を試みた.その結果,今回使用した平成18 年度新潟県全県学力調査における中学校2 年生数学データでは,25 項目中2 項目においてテスト全体が測定する「数学力」よりも下位領域特有の影響を強く受けていることが明らかになった.また,「数学力」を統制し,下位領域特有の潜在特性尺度値を推定することで,下位領域間の学力に関する情報を得ることができることも示した.
テストデータの分析にIRT が用いられることがますます多くなってきている.しかしながら,テスト項目への反応データから推定したテトラコリック相関係数行列における固有値の減衰状況を確認し,「1 次元性を満たしている」と判断したあと,IRT のモデルを適用し,パラメータを推定する,というテストデータ分析はいわばマニュアル化しがちである.しかしながら,実際には,「1 次元性を満たす」ことを確認する方法自体も多種多様であり( Hattie, 1985),厳密に言えば「十分な1 次元性」の判断基準は明確ではない( Embretson & Reise, 2000) のである.そのため,従来の1 次元性を仮定したIRT 分析結果を報告する際にも,多次元IRT を使った分析結果も同時に報告すべきであることも指摘されている( Reise et al. 2015).本研究は,IRT の普及にともなって見落としがちな,「そのテスト(項目)はそもそも何を測っているのか」というテストデータ分析における基本的かつ重要な問いを検証するためのひとつの方法を提供したと言うことができるであろう.
今後の課題としては以下の4 点が指摘できる.まず1 点目として,本研究で明らかになった「下位領域特有の影響を受けている」ことに対するさらなる定性的な検証が必要となる.本研究では項目24,25 について下位領域(図形)特有の影響がテスト全体の測定する「数学力」よりも強いという結果であったが,項目19,20 も同様に図形領域における数学的な証明の問題であり,「三角形の内角の和180◦ である」性質から,平行な2 直線の同位角に関する問題となっている.今回,なぜ,項目19,20 ではテスト全体の測定する「数学力」の影響が強く,項目24,25 についてのみ下位領域特有の影響が強く見られたのかという定性的な要因を,教科の専門家の見解を踏まえて明らかにすることはできなかったことは本研究の限界である.しかしながら,本研究の取り組みがテスト項目の測定内容について詳細に検討できる材料となることにつながり,今後はより一層テスト分析の専門家とテスト作成者としての教科の専門家の連携が期待される.次に2 点目として,多次元IRT を適用した際に起きる項目識別力パラメータの推定値について,さらなる検証が必要である.具体的には,本研究で使用した項目21,22 の「図形」の項目識別力パラメータが,モデルC とD において0 に近い,あるいは負になる現象が確認できる.従来の1 次元性を仮定するIRT 分析ではこのような現象はそれほど発生せず,多次元IRT を使用した際に起きる重要な知見の一つであり,今後さまざまなデータへの適用を通してさらなる事例の蓄積が望まれる.3 点目は,本研究で使用したデータは正答/誤答のみであり,テストデータによっては完全正答/部分正答/誤答という多値データとなる場合もある.そのようなデータに対して,多値型の多次元IRTモデルである多次元段階反応モデル( Muraki & Carlson, 1995) や多次元一般化部分採点モデル( Yao & Schwarz, 2006) などが提案されており,実際のテストデータへの適用が望まれる.4 点目としては,双因子モデルを通して得られる一般因子とグループ因子における潜在特性尺度値を従属変数とした社会学的な分析への応用が指摘できる.今後は心理測定の専門家と教育社会学の専門家の共同研究も期待される.

なお,本研究の遂行にあたってはJSPS 科研費25380867 ならびに16H03731 の助成を受けました.また,新潟県教育委員会には貴重なデータ並びに項目等資料の使用をお認めいただきました.ここに記して深く感謝申し上げます.また,査読の先生方からは大変有意義な御指摘を賜りましたことを心から感謝申し上げます.