メンブレン型微小流体デバイスで見る，飢えゆく細菌の細胞サイズ分布法則

Abstract

細胞は，たとえ種類が同じでも，大きさはまちまちだ．そこに隠れた法則はあるだろうか．我々は，培養条件を均一に保ちつつ切替可能なデバイスを開発し，細菌細胞集団の飢餓過程を観察したところ，時間変化する細胞サイズ分布にスケール不変性という特徴を見出した．モデルによる再現，不変性の破れ，展望についても論じる．

1.  はじめに

わたしたち人間に背の高い人もそうでない人もいるのと同じように，細胞も，たとえ種類が同じでも，その大きさはまちまちだ．細胞は，成長条件下では徐々に大きくなり，小さな娘細胞に分裂する．従って，細胞の大きさを計測し，その特徴を抽出すれば，細胞の成長や分裂に関する機構のヒントが得られるだろう．このようなアプローチの代表例は，細菌細胞のサイズ制御機構に関する研究だ¹⁾．微小流体デバイスを用いた一細胞観察技術の発達により，標準的な成長条件では，分裂後の細胞が一定の長さだけ伸長したところで次の分裂が起こるとするadder modelが実験と合うことが明らかとなった．近年は，バイオマスの増大や染色体の複製など，細胞の内部機構に基づいてadder modelの出現や限界を理解すべく，活発な研究が行われている¹⁾．

個々の細胞の大きさの変化ではなく，細胞集団における大きさの分布についても興味深い報告がある．Giomettoら²⁾は，様々な単細胞真核生物に対して，種ごとに細胞体積vの分布p(v)を計測した．当然，分布p(v)は種によって異なるが，その種の平均細胞体積V = ⟨v⟩に対する体積比v/Vに注目すると，その分布p(v/V)は，調査した13種類の真核生物の全てで同じ関数形をとることが報告された．式で書けば，細胞体積vの分布p(v)について，種に依らない関数F(·)があり

  

$$p\left(v\right)=\frac{1}{v}F\left(\frac{v}{V}\right)$$（1）

のように書けるということだ．このように，Vのような単一の尺度を持ってきて比率を取ってしまえば統計的特徴が一致してしまう性質を，統計物理学では「スケール不変性」と呼んでおり，背後に単純な物理原理や普遍性があることが示唆される．細胞サイズゆらぎのような本来複雑な現象にスケール不変性が成り立つのは不思議であり，「単純な物理原理」があるならそれを理解したいと思うのは我々だけではないだろう．

このような細胞集団のサイズ分布に関する研究は，これまで定常的な培養条件下で行われてきた．そのため，周囲の環境が変化したとき，それにともない細胞サイズ分布がどう変わっていくか，スケール不変性は成り立つかなど，時間依存する条件下での分布法則の知見は極めて限られている．変動する条件下では，細胞サイズ制御の機構も変わる可能性があり，分布法則の適用限界を探求する観点から興味深いし，生物としても細胞の集団適応などの問題に繋げられる可能性がある．そのような実験を制御して行うには，大規模な細胞集団に対して均一な培養条件を維持でき，それを時間的に切り替えられるようなデバイスが望ましい．

2.  「広域マイクロ灌流系」の開発

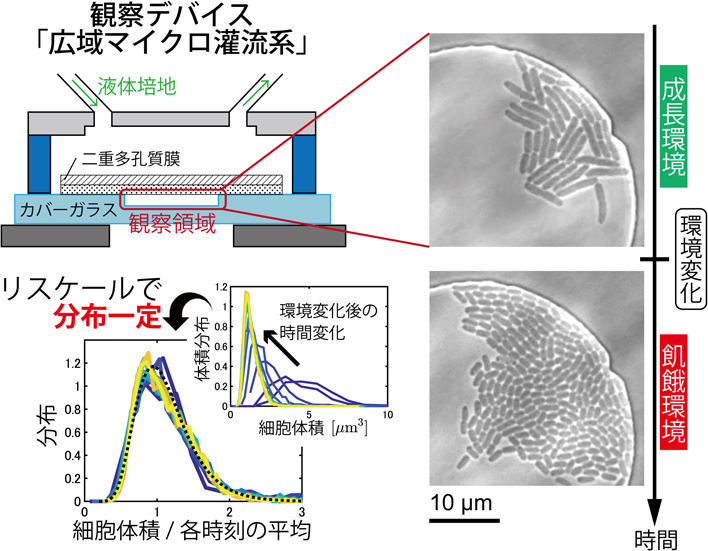
我々は，細菌細胞を主たる対象に，高密度細胞集団を広い空間で均一な環境下で培養でき，流れで細胞を乱すことなく培地を切り替えられるメンブレン型の微小流体デバイス「広域マイクロ灌流系」（図1）を開発した³⁾．このデバイスでは，カバーガラスに微細加工技術で設けた空間に細胞を入れ，多孔質膜で蓋をする．これにより，観察領域に細胞を閉じ込めたまま，新しい成長培地を細胞集団に一様に供給し続けることができる．培地を切り替えると，多孔質膜を介した拡散によって観察領域内の細胞に届けられるので，切替にともなう流体的な乱れが殆どない．また，多孔質膜として，従来デバイス⁴⁾で使われていたセルロース膜に加え，補強用のPET膜を接着した二重構造とすることで，柱なしで広い観察領域を確保できるようになった．具体的には，深さが1.1 μmの浅い観察領域でも，直径210 μmまでは実現できている³⁾．観察領域内の培地交換も3-5分程度で完了し³⁾，大腸菌の倍加時間と比べても十分短いため，環境切替に対する細胞集団の応答を計測するのに有用だろう．

図1

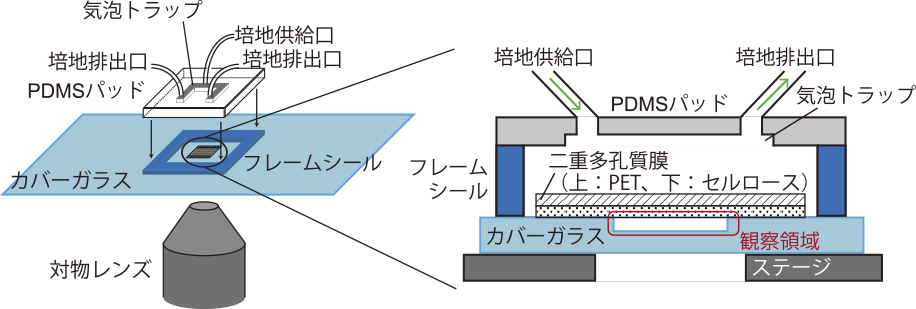
広域マイクロ灌流系の概略図³⁾．

3.  大腸菌の飢餓過程における細胞サイズゆらぎ

我々は，広域マイクロ灌流系を用いて，大腸菌集団の飢餓過程における細胞サイズゆらぎを計測した³⁾．細菌細胞は，環境が悪化し成長が鈍化・停止すると，細胞サイズが顕著に小さくなることが知られており，reductive divisionと呼ばれている⁵⁾．Reductive divisionはバッチ培養でも容易に観察できるありふれた現象だが，統計的性質や時間変化についての定量的知見は限られている．そこで我々は，広域マイクロ灌流系で大腸菌株MG1655を培養し，ある時刻で成長培地から栄養素を含まないリン酸緩衝液に切り替え，飢餓過程を引き起こした．

図2aは，成長環境と飢餓環境で細胞集団の様子を比べた写真であり，飢餓環境では細胞が短く，小さくなっていることがわかる．すなわち，reductive divisionは我々の観察でも起こっており，その時間変化を我々は計測できたということだ．そこで我々は，各時刻tで，領域内の全細胞の長さと太さを計測し，球面円柱形を仮定して細胞体積vを算出して，体積分布p(v, t)を計測した（図2b）．時間経過とともに，分布p(v, t)のピークは小さいvにシフトし，細胞体積の減少の様子がわかる．

図2

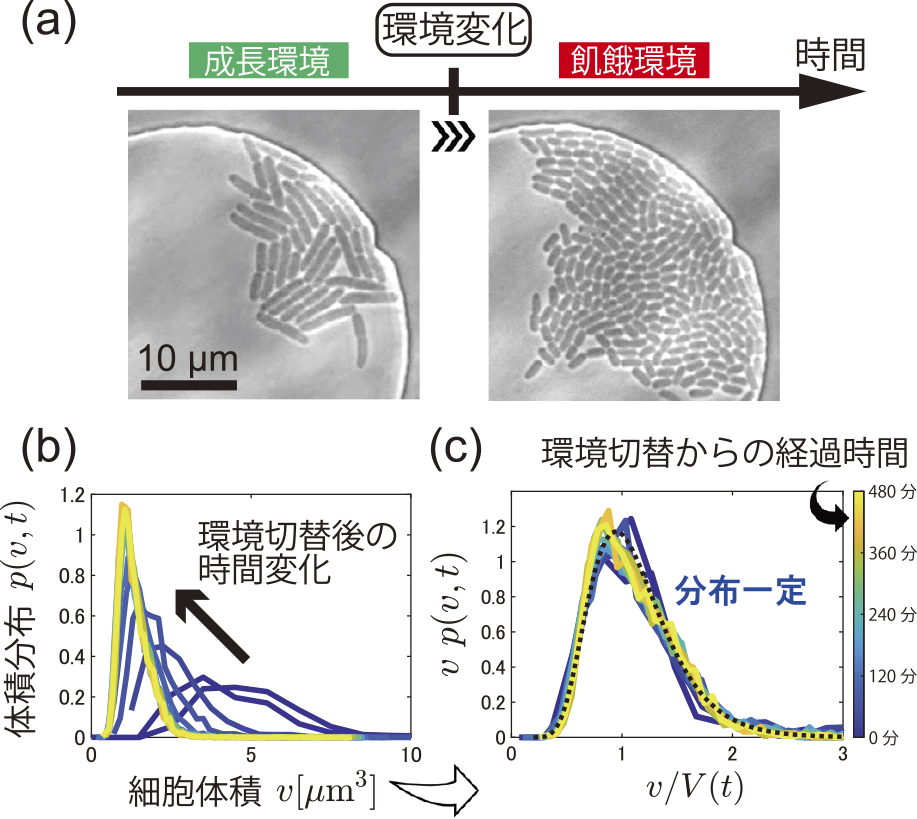
大腸菌の飢餓過程におけるreductive divisionの様子（a）と細胞サイズ分布のスケール不変性（b）（c）³⁾．写真は左が切替時，右が切替後75分時点のもの．LB培地からリン酸緩衝液に切り替えた際の結果を示す．

ここで我々は，reductive division時の細胞サイズ分布に式（1）で表すスケール不変性が成り立つかどうかを問うた．細胞の平均体積は時間変化するので，各時刻でとった平均V(t) = ⟨v⟩を使い，図2bの横軸をv/V(t)に，縦軸をvp(v, t)に変えてプロットする（図2c）．すると，図2bで見られた異なる分布関数は，全て1本の曲線に重なった．すなわち，

  

$$p\left(v,t\right)=\frac{1}{v}F\left(\frac{v}{V\left(t\right)}\right)$$（2）

が成り立ち，スケール不変性が満たされることが明らかとなった．換言すると，reductive division時のサイズ分布の時間変化（図2b）は，式（2）の関係を保つ厳しい制約のもとで起こっていたということだ．

4.  細菌の飢餓過程のシミュレーション

実験で観測されたスケール不変なreductive divisionは，細胞のどのような内部機構から生じるものだろうか．この疑問に答えるため，我々は細菌の細胞周期モデルのシミュレーションを行い，スケール不変性の検証を行った．細菌の細胞周期モデルはCooper-Helmstetter（CH）モデルがよく知られており，近年はadder機構の理解を目指して，染色体複製等に関する実験結果を取り入れながら精緻化が進んでいる^1),6)．

CHモデルで考慮するのは，細胞iの体積v_iと，染色体複製に関する細胞周期の進行度である．細胞体積v_i(t)は，成長率λで $\frac{d{v}_i}{dt}=\lambda v_i(t)$ のように増大する．細胞周期については，細菌はC期で染色体を複製し，D期で分裂する．そこでCHモデルでは，C+D期内の進行度 $X_i^{\mathrm{C}\mathrm{D}}(t)$ でこれを表現する．Witzら⁶⁾は，実験に基づき，以下の規則を採用した（図3a）．細胞iにおいて，ある時刻tで複製が始まったとする．このとき $X_i^{\mathrm{C}\mathrm{D}}(t)=0$ となり，以降は体積v_i(t)に比例する進行速度で $\frac{d{X}_i^{\mathrm{C}\mathrm{D}}}{dt}=\mu v_i(t)$ のように進む．これが終値X^CD,thに到達したら，細胞iは分裂し，娘細胞i₁，i₂になる．また，複製開始条件は，Witzら⁶⁾に従いadder的な規則で与えている．図3aに示すように，複製が始まると染色体上の複製起点oriが倍増する．その数を(#ori)とし，δをある数として，前回の複製開始から細胞体積がδ × (#ori)だけ増大したら次の複製が始まるとする（(#ori) = 2の例を図3aに示す）．これは分裂前でもよい．その場合，孫以降の代の染色体複製が始まることになるが，これは好適な成長条件下の細菌で実際に起こることが知られている．以上の規則により，細胞は図3bのように成長と分裂を繰り返す．

図3

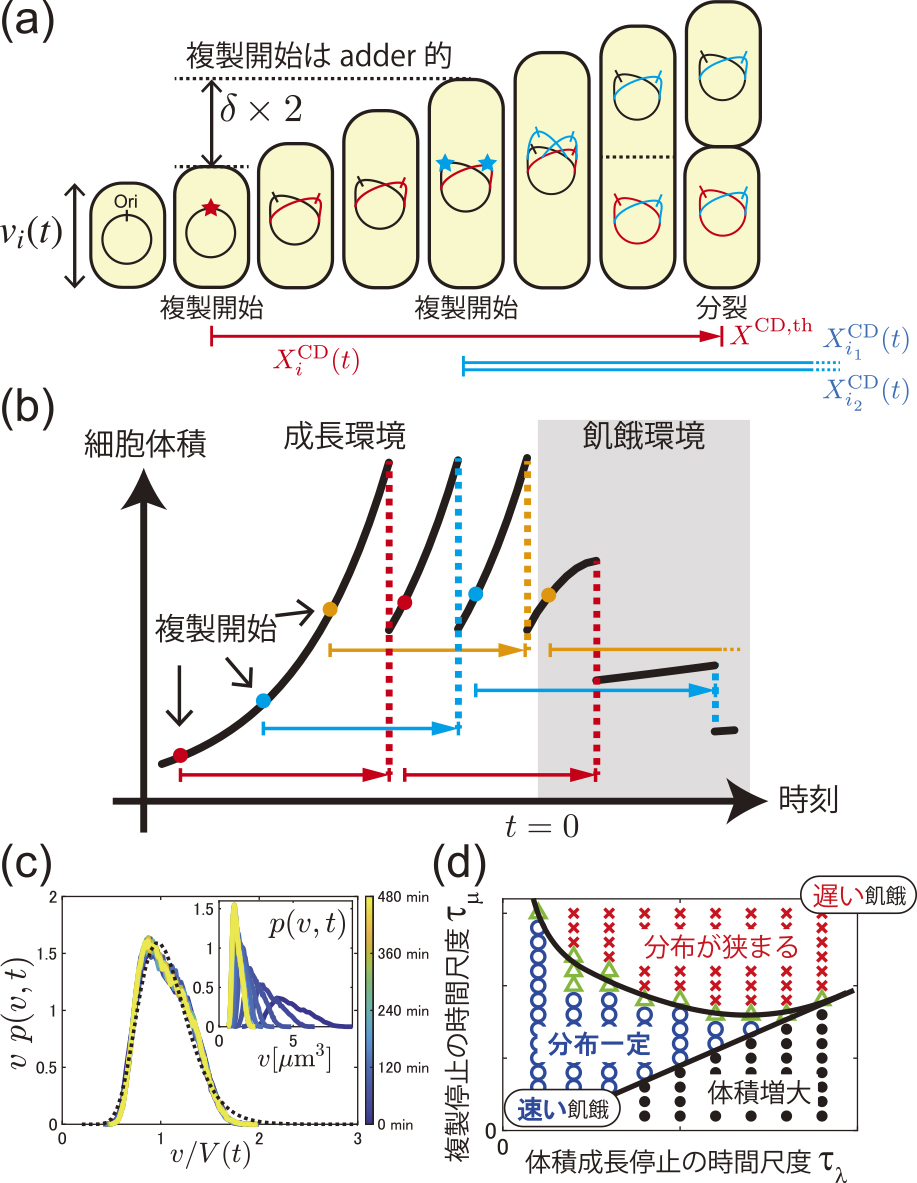
細胞周期モデルによる飢餓過程のシミュレーション³⁾．（a）モデルの定義の概略．（b）典型的な細胞体積変化の様子．（c）体積分布の結果．（d）飢餓過程の時間尺度τ_λ，τ_μを変えた場合の相図．右下の領域は，飢餓前と比べ細胞体積が増大する非現実的なパラメータ領域である．

そこで我々は，非定常な培養条件を扱えるよう，時間依存的な体積成長率λ(t)と複製進行速度の係数μ(t)を考えた³⁾．時刻t = 0で飢餓環境に切り替わると，λ(t)とμ(t)は減少してゆく．我々は，Monodの式やいくつかの素朴な仮定からλ(t)，μ(t)の関数形を決定し，実験を模したシミュレーションを実施した．その結果が図3cであり，実験（図2b, c）と同様のスケール不変なreductive divisionが確認できた．

5.  遅い飢餓過程におけるスケール不変性の破れ

以上のスケール不変性は，様々な成長培地と緩衝液の組み合わせで起こることを我々は実験で確認し，シミュレーションでも確かめている³⁾．すなわち，スケール不変性は，急激な飢餓過程において頑健に成り立つ．一方で，実験では，スケール不変な分布を表す関数F(·)（式（2））が飢餓前の成長培地によって異なることも見出された．異なる成長培地での結果は，一方の成長培地から他方の成長培地に無限にゆっくり切り替えても得られるはずだ．この結果は，ゆっくりと起こる飢餓過程ではスケール不変性が破れる可能性を示唆している．

飢餓過程の時間尺度を実験で制御することは難しいため，我々は4節のモデルで時間尺度に対する依存性を検証した．体積成長率λ(t)と複製進行速度係数μ(t)の減衰は，大雑把には指数関数的 $\lambda (t)\approx {\lambda }_0{e}^{-t/{\tau }_{\lambda }}$ ， $\mu (t)\approx {\mu }_0{e}^{-t/{\tau }_{\mu }}$ なので，ここでは指数関数を仮定し，時間尺度τ_λ，τ_μを変えてシミュレーションを行った．結果は図3dのとおりで，時間尺度が遅くなるとスケール不変性が破れる転移が起こり，体積比v/V(t)の分布が飢餓にともなって狭まっていく．これはスケール不変性の成立条件や理論的メカニズムを考察するうえで，大変興味深い結果である．

6.  むすびに

細胞のサイズ制御機構や，それを支える細胞周期動態は，特に時間依存的な条件下では未知な点が多い．本研究で見出したスケール不変性が，細胞の制御機構を探る手掛かりを与え，生物が持つ統計的性質の普遍性の理解と分類に資するような展開を期待したい．また，スケール不変性の生物的意義の考察も面白い．分布がスケール不変なら，細胞どうしの体積の関係（比）が変わらないため，力学的な接触関係も変わりづらく，細胞集団の力学的性質の頑健さ，ある種の集団適応に役立っている可能性もある．最後に，本研究で開発した広域マイクロ灌流系は，高密度細胞集団の均一培養が可能などの特長を持ち，細菌の集団応答や秩序形成，集団運動の研究など，様々な用途がありうる（例えば文献7はアクティブマター研究の例）．本デバイスが生物物理学の新たな研究に役立てば，望外の喜びである．

本研究は若本祐一氏と大倉玲子氏との共同研究の成果であり，両氏に深く感謝申し上げます．

文献

• 1)   Jun,  S. et al. (2018) Rep. Prog. Phys. 81, 056601. DOI: 10.1088/1361-6633/aaa628.
• 2)   Giometto,  A. et al. (2013) Proc. Natl. Acad. Sci. U.S.A. 110, 4646-4650. DOI: 10.1073/pnas.1301552110.
• 3)   Shimaya,  T. et al. (2021) Commun. Phys. 4, 238. DOI: 10.1038/s42005-021-00739-5.
• 4)   Inoue,  I. et al. (2001) Lab Chip 1, 50-55. DOI: 10.1039/B103931H.
• 5)   Nyström,  T. (2004) Annu. Rev. Microbiol. 58, 161-181. DOI: 10.1146/annurev.micro.58.030603.123818.
• 6)   Witz,  G. et al. (2019) eLife 8, e48063. DOI: 10.7554/elife.48063.
• 7)  Lama, H. et al. (2022) arXiv: 2205.10436. DOI: 10.48550/arXiv.2205.10436.

Biographies

竹内一将（たけうち　かずまさ）

東京大学大学院理学系研究科准教授

嶋屋拓朗（しまや　たくろう）

日本電気株式会社バイオメトリクス研究所リサーチャー