トピックス
新しいパターン伝播機構：Turingパターンは曲面上で動き出す
2024 年 64 巻 1 号 p. 38-41
詳細
2024 年 64 巻 1 号 p. 38-41
生物に見られるパターンの多くは曲面上で生じる．曲面はパターンダイナミクスを変化させ，生物学的な役割を担うことがわかってきた．私達は，曲面上でTuringパターンの振る舞いを調べることで，曲率がパターンを動かす効果を持っていることを明らかにした．平面上でパターンが止まっていても，曲面上でもそうとは限らない．
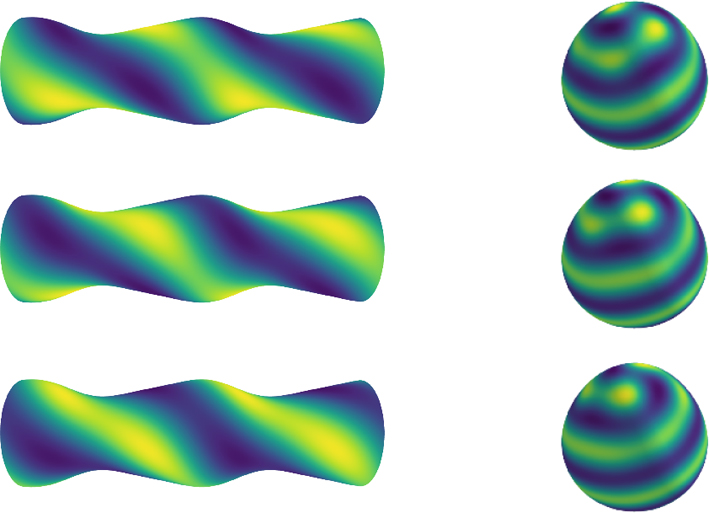
生物系に見られるパターンは，情報伝達，位置決定，細胞運動などの生体機能を担う．バクテリアの細胞分裂面を決定するMinタンパクの振動や，体節を決めるeve遺伝子のストライプパターンは良い例である．それゆえ，パターンの形成機構やダイナミクスの理解は，生物現象の解明にとって重要であり，実験的にも理論的にも多くの研究がなされてきた．
一方，生物には様々なスケールで普遍的に曲面が見られる．弯曲した膜を持つ細胞から，複雑な形態を成す組織や器官が階層的に構成される．その曲がった表面を舞台に，タンパク質や細胞が集まり，パターンを形成する．しかし，曲面上のパターンが豊富に観察されるのにも関わらず，曲面の形状がパターンに及ぼす効果には未だ謎が多い．生物は原初から曲面と付き合ってきたことを考えると，生物は曲面を巧みに使ってパターンを操っているのではないだろうか？ この素朴な問を発端として，曲面上のパターンの振る舞いを理論的，数値的に調べてきた．本稿では，著者らが発見した，曲面がパターンにもたらす新しい現象について紹介する1)．
近年の微細構造形成技術や観察技術の向上により，生物における曲面の役割が明らかになってきている．例えば，細胞集団の運動が基質の曲率により制御されることや2)，機械受容タンパクPiezo1の分布位置が膜の曲率により制限されること3)，上皮シートの厚さが基質の曲率により変化すること4)などが報告されている．
理論的な解析からも，曲面がパターンにもたらす効果が明らかになってきている．例えば，曲面の測地曲率が興奮波の速度や進行方向，形状を変化させることや5)，曲面のトポロジーが，パターンの位相特異点のダイナミクスに影響すること6)が報告されている．後者は，例えばヒドラの再生過程と関連して，形態形成における曲面の重要性が議論されている7)．
以上のように，曲面はパターンに変化をもたらす重要な因子であることがわかってきているが，その理解は発展段階である．
Turingパターンは，魚の体表模様やマウスの指の形態形成などの，空間的に周期的な構造を持つ生物系のパターンと関連して研究されてきたが，同時にその曲面上の振る舞いにも関心が持たれてきた．Alan Turingは，その著作“The Chemical Basis of Morphogenesis”8)において2種分子の化学反応系を考え，分子拡散を無視すると空間的に一様な濃度分布になる場合でも，それぞれの分子の拡散速度に違いがあると，一様でいられなくなり，空間的に周期的な構造を持つ静止パターンが形成されることを明らかにした．Turingは，胚発生を自己組織化的に誘導する機構としてこのパターン形成を捉え，この論文において既に球面上のパターンの振る舞いを考察している．Turing以降も，様々な曲面上のTuringパターンが調べられてきたが9),10)，その結果は基本的に2つにまとめられる．1つは，パターンが形成される機構は，曲面と平面でも変わらないということ．もう1つは，曲面の形状によってパターンの位置や形が調整されるということである．
数理的には，Turingパターンは次の反応拡散方程式によって記述される．
| （1） |
U = (u1, u2, …) は分子濃度，D∆Uは拡散，R(U)は反応を表す．つまり，ある分子集団が化学反応をしながら，拡散により広がっていく過程を表している．拡散速度や反応の仕方，成分数を変えることで，パターンの振る舞いが変化する．図1a, bにTuringパターンの解析によく用いられるBrusselatorモデルとその平面上でのパターンを示した．曲面上では，2点間距離が平面上のような単純な関係ではないことを反映し，拡散項が曲面の形状に応じたもの（Laplace-Beltrami演算子）に変わる．円筒や波型曲面の場合は面に沿った2点の距離関係が平面と同じことに注意してほしい．このような曲面は実際には平面と等価であり，平面と同様のパターンが現れる（図1c：パラメータは図1b左パネルと同じもの）．一方，凹凸のある曲面上では，曲面の効果が現れ，先行研究で報告されているような，曲面形状を反映した歪んだパターンとなる（図1d）．
Brusselatorモデルによる平面上と曲面上のTuringパターン．（a）Brusselatorモデル．u，vは濃度を表し，時間と空間の関数である．a，bは反応のパラメータ，Du，Dvは拡散係数．（b）平面上のTuringパターン．それぞれパラメータが異なる．（c）円筒，波型曲面上のTuringパターン．（d）凹凸のある曲面上のTuringパターン．（c, d）では，（b）の左パネルと同じパラメータを用いた．（b, c, d）明るいほどuの値が大きい．
曲面上のパターンについては，上に述べたようなパターンの変形や位置の調整はあるものの，平面であっても曲面であってもTuringパターンの振る舞いに定性的な違いはないと考えられてきた．特に，Turing以降の70年間，平面で静止しているTuringパターンは，曲面上でも静止したままであるということが想定されてきた．しかし，この想定は数学的に証明されていたわけではない．曲率が興奮波のダイナミクスを大きく変化させることを考えると，Turingパターンのような平面で静止したパターンに対しても，曲率は定性的な変化をもたらしうるのではないだろうか？
具体的な曲面とモデルの設定として，解析のしやすさから，軸対称曲面（図2a）と，Brusselator モデル（図1a）を選び，数値計算を行った．先述の通り，単なる円筒は平面と同じなので用いない．周期境界条件を用い，Turingパターンが生じる条件のもとで，曲面とモデルのパラメータを変更しながら，パターンの形状や振る舞いを調べた．その結果，これまでの想定に反して，曲面上で動き続ける進行波パターンが存在することを発見した（図2b）．平面上では静止するパラメータであるにも関わらず，曲面上では回転角θ方向への伝播を示す．また，曲面形状や境界条件，モデルパラメータの変更，モデル自体の変更（Lengyel-Epsteinモデル）など，条件を変えても伝播パターンは広く観察され，曲面上のパターン伝播が普遍的に生じる現象であることを確認した．
軸対称曲面上でのTuringパターンの伝播．（a）筒状と球状の軸対称曲面の模式図．（b）軸対称曲面上のBrusselatorモデルのTuringパターン．回転角方向に一定速度，一定形状で伝播する．図は文献1から改変．
曲面上では，静止パターンも伝播パターンも存在する．それでは，どのような条件でパターン伝播が可能となるのだろうか？ 数値計算の結果から，パターンの形状と曲面形状がともに伝播と関係していることが示唆された．パターンの形状が螺旋状の場合には伝播を示すのに対し，平行状の場合には静止したままである．この関係はドット状のパターンでも同じであり，ドットの並び方が螺旋状か平行状かで伝播が起きるかどうかが決まる．また，曲面形状の対称性も伝播に関与しており，螺旋状パターンが伝播するのは，曲面がx軸方向に鏡映対称性を持たない場合で，鏡映対称性であれば静止する．パターンの伝播と，パターン形状と曲面形状の関係をまとめると図3のようになる．
この伝播条件は，理論的解析からも示すことができる．反応拡散方程式（1）の解が，軸対称曲面上の回転角θ方向への角速度ωの進行波であるという仮定を課す（U = U(x, ρ), ρ = θ – ωt）と，速度ωは次の式（速度の式）で決まる．
| （2） |
∂ρUはUの方向微分，Rは化学反応項で，いずれもパターンUから決定される．また，dSは曲面の面積要素を表し，積分は曲面全体でとる．つまり，この式は，速度がパターンと曲面によって決まることを示しており，パターンと曲面の形状を速度の式の右辺に代入することで，静止（ω = 0）か伝播（ω ≠ 0）かを評価できる．平面上や，図3に示した曲面上で静止する条件では，パターンの形状や曲面形状は鏡映や反転対称性を持ち，この対称性を踏まえると上の速度の式が確かに0であることを示すことができる．一方，鏡映非対称曲面上の螺旋状パターンでは対称性が崩れており，速度の式は一般に0とならず，パターンの伝播が示唆される．実際，速度の式と数値計算で観察された速度はピッタリ一致し（図4），理論的にも，パターンの伝播と，パターン形状と曲面形状の関係を示すことができた．
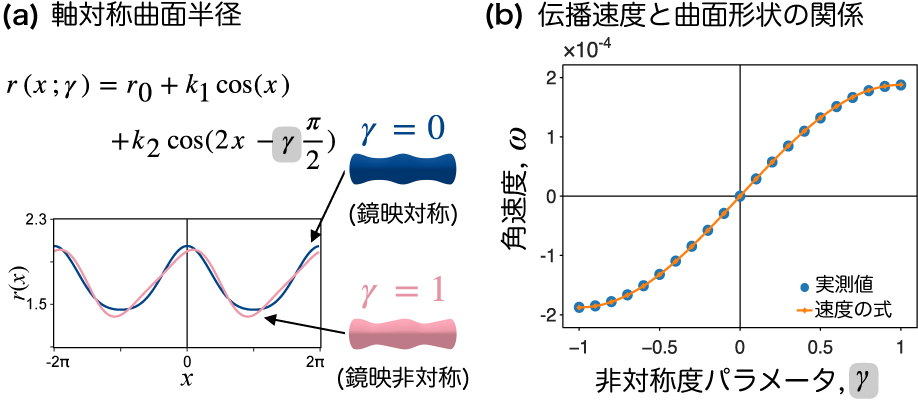
螺旋状パターンの角速度の曲面依存性．（a）軸対称曲面の半径．xは軸方向の座標，r0，k1，k2，γは曲面形状を決めるパラメータで，γは曲面の対称性を制御し，γ = 0で鏡映対称となる．（b）γに対する螺旋状パターンの速度と，速度の式（2）から計算した速度のプロット．図は文献1から改変．
Turingパターンを曲面上で調べることで，曲面上でパターンが伝播することを発見した．これは，パターン伝播を駆動するという，曲面がパターンに及ぼす新しい効果を示している．そして，パターンの伝播が，パターンと曲面の形状（対称性）から決まっていることを明らかにした．理論解析は，反応拡散系一般に対して成立するものであり，Turingパターン以外に対しても同様な機構でパターン伝播が起こることが示唆される．一定速度の伝播以外のダイナミクスや，軸対称でない曲面上で動くパターンも見出しており，曲面はパターンの振る舞いに様々な効果をもたらすようだ．
最初の問に立ち返る．生物はこのパターン伝播現象を使っているのだろうか？ 残念ながら，具体的な実例を見出しているわけではない（教えてほしい）．しかしながら，パターンの伝播自体は，情報伝達や運動機構として有用であり，曲面形状を調整することでパターンの静止と伝播を切り替えられることは，成長などに伴う組織のサイズや形状の検知や制御にも使われているかもしれない．
曲面は生物にとって普遍的かつ不可避でもあり，その上のパターンが曲面形状によって質的にも量的にも変化を受けることが明らかになってきている．本結果もその一例である．曲面上のパターンダイナミクス研究のさらなる発展が，生物現象を理解する新しい地平を開くのではないだろうか．
西出亮介（にしで りょうすけ）
東京大学大学院総合文化研究科博士課程
;%0A%09%09%09newWindow.document.open();%0A%09%09%09newWindow.document.write('<img src=%22./Graphics/64-1ie9p01.jpg%22>');%0A%09%09%09newWindow.document.close();%0A%09%09)
石原秀至（いしはら しゅうじ）
東京大学大学院総合文化研究科准教授
;%0A%09%09%09newWindow.document.open();%0A%09%09%09newWindow.document.write('<img src=%22./Graphics/64-1ie9p02.jpg%22>');%0A%09%09%09newWindow.document.close();%0A%09%09)
