Analysis of the mechanism of synaptic integration focusing on the charge held in the spine

Abstract

Successful synaptic integration is said to require that multiple excitatory postsynaptic potentials (EPSPs) occur almost simultaneously over a short period of time, so that they overlap and increase. However, if brain function is based on a chain of successful synaptic integrations, then constraints on the spacing of multiple EPSP generation must be released to allow for a higher probability of successful synaptic integration. This paper demonstrates that Ca²⁺ ions retained in spines after EPSP generation polarize spine neck fluid and dendritic fluid as a dielectric medium, that polarization is transmitted through dendrites to the cell body (soma), that polarization is enhanced by the addition of polarization from each spine, and that I propose that synaptic integration is successful when the membrane potential, as determined by the enhanced polarization and membrane capacitance, reaches the threshold of voltage-gated Na⁺ channels. Furthermore, the approach taken in this study suggests that a single neuron can integrate synapses for many combinations of synaptic inputs, that successful synaptic integration depends on spine neck capacitance and spine head size, and that spines farther from the soma are able to contribute to successful synaptic integration, and led to the elucidation of a number of important issues, including the fact that inhibitory post-synapses on dendrites suppress s effectively synaptic integration.

Significance

In this study, it was clarified that high reproducibility of synaptic integration is achieved by propagating the polarization of the medium adjacent to the charge held in each spine and adding it to raise the membrane potential. Furthermore, using the approach of this study, it was possible to clarify that spine neck capacitance and spine head size contribute significantly to synaptic integration, that distant spines are able to contribute to synaptic integration, that a single neuron is able to integrate a large number of input combinations, and that inhibitory post-synapses on dendrites effectively suppress the success of synaptic integration.

Introduction

Mechanism needed to enhance the reproducibility of the success of synaptic integration

In 1897, Cajal observed synapses for the first time and revealed the structure of a neuron connecting to another neuron [1–3]. However, the mechanism of how the action potential is generated by the synaptic integration and processing of the stimuli received at the many synapses that connect to other neurons has not been elucidated to date [1–4]. According to conventional idea, the potential in the dendrite, which is added by the overlap of multiple EPSPs as shown in Figure 1a, must reach the threshold of the voltage-gated Na⁺ channel to generate an action potential. Therefore, the interval (t) between the occurrence of the previous EPSP and the occurrence of the next EPSP must be within the duration (T) [5–7]. Figure 1b shows that the reproducibility of the action potentials by the same multiple EPSPs is very low, because the waveforms of EPSPs are difficult to add up when they occur arbitrarily. However, if the function of the brain is based on the chain of the success of synaptic integration, it is required for the reproducibility of successful synaptic integration to be high by the same multiple EPSPs, regardless of the order and interval of EPSP generation. People are able to think about the content of information obtained by long time reading, watching sports and talking. This means that the information obtained is valid in the brain for a long time. Therefore, the traces of the information obtained need to last for a long time, not for a short time like the pulsed EPSP waveform. In order to achieve this, it is necessary to have a mechanism that allows the dendritic potential raised by the EPSP to be maintained as shown in Figure 1c with a small amount of energy consumption, and allows the new potential by the next EPSP to add on the existing dendritic potential. Such a mechanism would make it possible to reproduce the success of synaptic integration based on information obtained over a long period of time. Furthermore, considering the amount of signal attenuation due to the passage through the thin, long dendrite, a mechanism utilizing dielectric properties that allows only the potential to propagate without attenuation regardless of the propagation speed is required. However, the way in which the dielectric properties are utilized seems to be in contrast to the dynamic mechanism, which utilizes the dielectric properties of the axonal fluid to enable fast conduction of action potentials [8].

Figure 1 

Sum of potentials. (a); In case of success of addition of EPSPs. (b); In case of failure of addition of EPSPs. (c); Example of the success of synaptic integration by the membrane potential increased by the polarization of three spines holding Ca²⁺ ions. And action potentials are generated in tetanus stimulus manner.

Assumptions for improving the reproducibility of the success of synaptic integration

The purpose of this study is to elucidate the mechanism that improves the reproducibility of the success of synaptic integration based on the information over a long period of time. This study is based on the assumption that Ca²⁺ ions taken into a spine are retained in the spine for some time, based on a number of previous references that mentions compartmentation of Ca²⁺ ions in the spine [9], the sudden change of the resistance of spine neck [10–13] and the long time potentiation (LTP) [1,10,14–18]. Many spines with excitatory synapses leading to dendrites have AMPA receptors, which induce Na⁺ ion influx into the spine and generate EPSPs, and NMDA receptors, which take in Ca²⁺ ions, when neurotransmitters are received from pre-synapses [19,20]. However, NMDA receptors, which received neurotransmitters, detect an increase in the electrical potential in the spine due to Na ions taken in by AMPA receptors, thereby removing the Mg blocking the channel, opening the channel, and taking Ca²⁺ ions into the spine in a sequence. As an approach to the analysis of this study, I focused on the Ca²⁺ ions that are taken in and retained in the spine after the EPSP occurs [9–13,15,16,19–21]. In other words, I focused on the effect of the statically persistent electric field E created by the charge σ due to the Ca²⁺ ions retained in the spine. The electric field E created by the isolated charge σ polarizes the surrounding medium in proportion to the dielectric constant ε of the medium, the polarization propagates through the medium in proportion to the dielectric constant ε of the medium, and the strength of the polarization appears at the boundary of the medium as potential. The dielectric constant ε of the medium is the dielectric constant ε₀ of the vacuum multiplied by the relative dielectric constant ε_r of the medium. The relative dielectric constant ε_r is the ratio of the dielectric constant ε₀ of the vacuum to the dielectric constant ε of the medium, and indicates the ease with which the medium is polarized and the ease with which the polarization is transmitted. Above relationship was expressed by Maxwell in the following equation [22].

  

$$Div\hspace{0.25em}\mathrm{\epsilon }\hspace{0.25em}\mathit{E}=Div\hspace{0.25em}{\mathrm{\epsilon }}_0\hspace{0.25em}{\mathrm{\epsilon }}_{\mathbf{r}}\hspace{0.25em}\mathit{E}=\mathrm{\sigma }$$(1)

The electric field E is in vector form, and Div is an operator that calculates the divergence of the vectors. Here, the boundary surface refers to the contact surface between media with different dielectric constants ε. Therefore, as shown in Figure 2a, we can say that boundary surfaces exist between media with different dielectric constants, such as the spine fluid, spine membrane, spine neck fluid, dendritic fluid (including soma fluid), dendritic membrane and soma membrane. And a potential corresponding to the difference in relative dielectric constant ε_r appears at each boundary surface. Therefore, the boundary surface of the media with different relative dielectric constant ε_r can be regarded as an electrode, and the capacitance is able to be set for each media. Figure 2b shows the names of the capacitance for each medium with different relative dielectric constant ε_r, Csm for the spine membrane, Csp for the spine fluid, Cn for the spine neck fluid, Cd for the dendritic fluid (including the soma fluid), Cdm for the dendrite membrane, and Csom for the soma membrane. Here the contents of the inside of the neuron are called fluid, because ion fluid has an extremely high relative dielectric constant ε_r than proteins in the neuron. On the other hand, since same kind of charges repel each other, it is difficult to contain same kind of charges in a small space. However, neurons use ion pumps to keep the intracellular concentration of Na⁺, Ca²⁺ and Cl^– ions low, and by deploying ion channels where necessary and allowing ions to flow in at the right time, they make it possible to collect same kind of charges in a narrow space like a spine. In particular, Ca²⁺ ions in the cytoplasm have a very small diffusion coefficient[a], making it difficult for them to diffuse.

Figure 2 

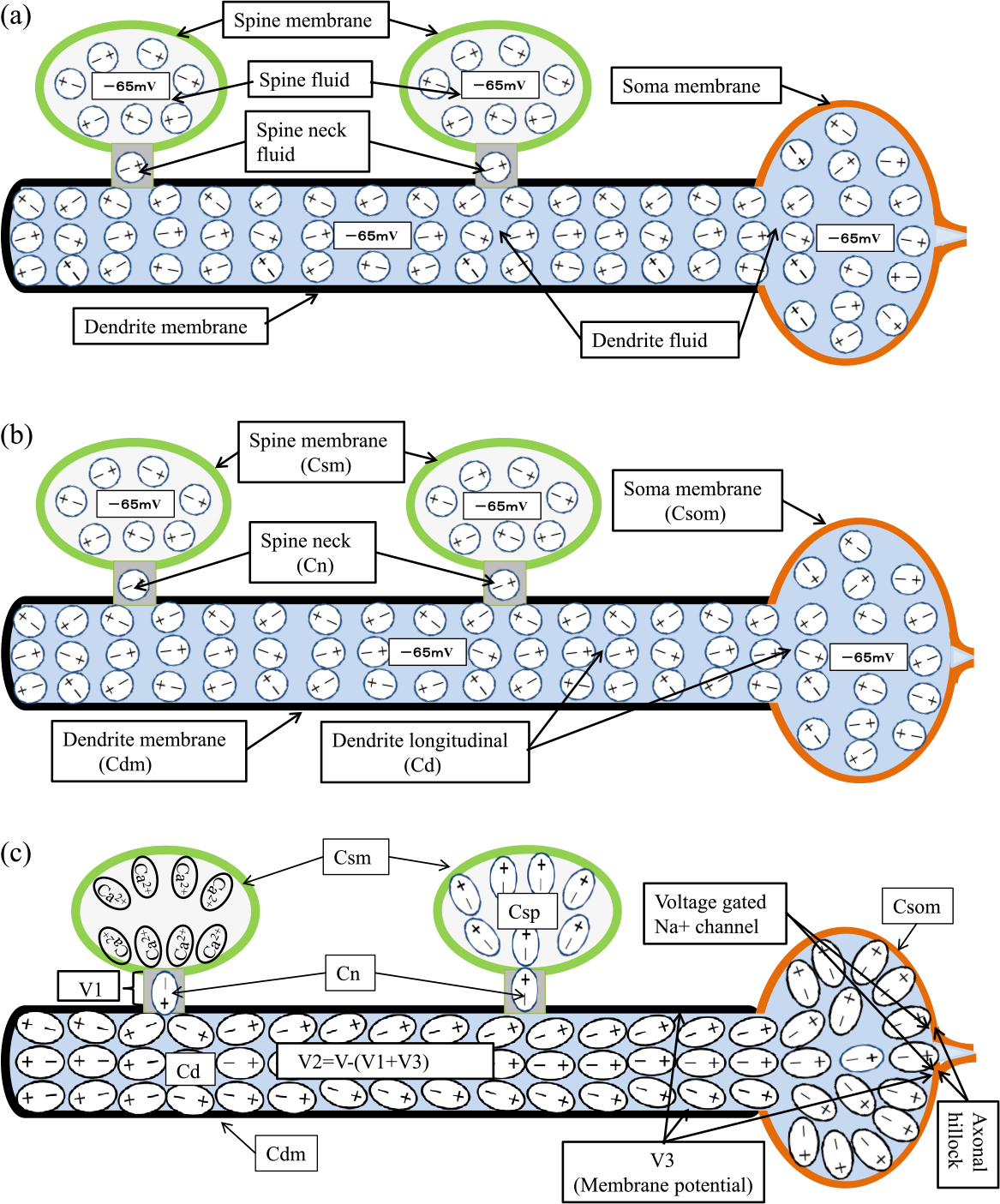
State and name of inside the dendrite and soma. (a); Name of the dielectric fluid and non polarized state. (b); Name of the capacitance and non polarized state. (c); Polarized state by the spine holding Ca²⁺ ion, and location of potential V1, V2 andV3. The ellipse represents a state of dielectric fluid polarized by Ca²⁺ ions held in the spine.

Electric current and resistance in a neuron in a rest potential state

The various ion pumps on the membrane of a neuron operate to maintain a constant difference in concentration between the inside and outside of the cell for each ion, as shown in the example in Table 1 [7]. When there is a difference in the concentration of ions inside and outside the cell, a potential difference is generated inside and outside the cell. In the case of the concentration difference shown in Table 1, we get a potential of –65 mV inside the cell compared to the outside by Goldman’s equation [7]. This potential is called the rest potential. In dendrites, spines, and axons, the concentration of each ion in the rest potential is considered to be the same. If the AMPA receptors in the spine are activated and take in Na⁺ ions, the Na⁺ ions diffuse into the dendrite through the spine neck, but after a while, the excess Na⁺ ions are discharged by the Na⁺ ion pump and the concentration difference returns to the original level, resulting in a rest potential. The same is true for the input and output of other ions. Therefore, the concentration of each ion is maintained in the dendrite at rest potential. In other words, in the rest potential state, there is no current due to the flow of ions in a specific direction, although there is random movement of ions due to thermal motion. Even if Ca²⁺ ions are retained in a spine and the potential in the spine increases, if Ca²⁺ ions cannot diffuse through the spine neck, there is no movement of charged particles of Ca²⁺ ions in the dendrite. However, by change of amount of charge Q by Ca²⁺ ions taken into the spine, a charging current flows at the moment when the degree of polarization of each medium changes [22], but when the amount of charge Q stabilizes, there is no current again. In the rest potential state, where the amount of charge Q in each spine is stable, there is no current. Therefore, in the analysis of this state, it is not necessary to consider the element of resistance, which indicates the difficulty of current flow. Figure 3 shows the equivalent circuit of a neuron for the rest potential state, where the amount of charge in each spine is stable.

Table 1  Ionic concentration outside and inside the neuron [7]

Ion	Outside (mM)	Inside (mM)	Outside : Inside
K+	5	100	1 : 20
Na+	150	15	10 : 1
Ca2+	2	0.0002	10000 : 1
Cl–	150	13	11.5 : 1

These differences of ionic concentration provide a state of the rest potential in which ion currents can be generated by opening ion channels when needed.

Figure 3 

Equivalent circuit of the neuron with one dendrite attached with m spines in which n spines holding Ca²⁺ ions. Since Csm is much smaller than Cs, Csm is ignored in the equation of electric charge. In this case, each potential is as follows, V1=n·Q/n·Cn, V2=n·Q/Cd and V3=n·Q/((m-n)Cns+Cdm+Csom).

Analysis of successful conditions for synaptic integration by equivalent circuit

After multiple spines generate EPSPs by receiving neurotransmitters from their respective pre-synapses, each spine retains Ca²⁺ ions in the spine. The Ca²⁺ ions retained in a spine, as in the spine on the left in Figure 2c, polarize the spine neck fluid, and the polarized spine neck fluid polarizes the adjacent dendritic fluid, increasing the membrane potential V3. The increased membrane potential causes the voltage-gated Na⁺ channel in the axonal hillock to be activated and generate an action potential, which is considered successful synaptic integration. In order to quantify and analyze the conditions for successful synaptic integration based on this idea, I used equivalent circuits. In the rest potential state, where the charge Q in each spine is stable, there is no need to describe resistance as described in the previous Subsection and the equivalent circuit is only capacitance, as shown in Figure 3. This equivalent circuit is used to analyze the potential difference due to the polarization between each medium caused by the static charge Q of the spine holding Ca²⁺ ions. Figure 3 shows that the spine neck capacitances Cn of n spines that hold the electric charge Q are connected in parallel to the upper side of the dendritic longitudinal capacitance Cd, and the dendritic membrane capacitance Cdm, the membrane capacitance Csom of the soma, and the spine neck capacitances Cn of m-n spines that do not hold the electric charge are connected in parallel to the lower side of the longitudinal capacitance Cd. That is, Figure 3 shows the pathway by which the polarization caused by the charge Q in the spine is transmitted to the spine neck, dendrites, and from the dendrites to the outside of the cell by capacitance.

Relationship between each capacitance and each voltage

The relationship between the amount of electric charge Q stored in the capacitance C and the voltage V appeared at both ends of the capacitance C is expressed by the following equation [22].

  

$$\mathrm{Q}=\mathrm{C}\mathrm{V}$$(2)

The amount of electric charge Q of the spine holding Ca²⁺ ions shown in Figure 3 is stored in the spine membrane capacitance Csm and the series capacitance Cs connected with the spine neck capacitance Cn, the longitudinal capacitance Cd of the dendrite and the total membrane capacitance ΣCm in serial. But, in this case since Csm is much smaller than Cs as shown later, Csm can be ignored. Therefore, the relationship of the amount of electric charge Q, voltage V and capacitances is shown by the following equation.

  

$$\mathrm{Q}=\mathrm{(}\mathrm{C}\mathrm{s}\mathrm{m}+\mathrm{C}\mathrm{s}\mathrm{)}\mathrm{V}\approx \mathrm{C}\mathrm{s}\mathrm{V}$$(3)

For a spine that does not hold Ca²⁺ ions, the spine neck capacitance Cn, capacitance of spine Csp and the spine membrane capacitance Csm are connected in series to form the series membrane capacitance Cns. In this case, since there are so many spines which do not hold Ca²⁺ ion, the capacitances Csm cannot be neglected. A Cns is connected to the longitudinal capacitance Cd of the dendrite and calculated by the following equation [22].

  

$$1/\mathrm{C}\mathrm{n}\mathrm{s}=1/\mathrm{C}\mathrm{s}\mathrm{m}+1/\mathrm{C}\mathrm{s}\mathrm{p}+1/\mathrm{C}\mathrm{n}$$(4)

The total membrane capacitance ΣCm which involves total series membrane capacitances ΣCns, total dendrite membrane capacitances ΣCdm and soma membrane capacitance Csom is connected to the longitudinal capacitance Cd and is calculated by following equation [22].

  

$$\mathrm{\Sigma }\mathrm{C}\mathrm{m}=\mathrm{\Sigma }\mathrm{C}\mathrm{n}\mathrm{s}+\mathrm{\Sigma }\mathrm{C}\mathrm{d}\mathrm{m}+\mathrm{C}\mathrm{s}\mathrm{o}\mathrm{m}$$(5)

The total series capacitance ΣCs with total spine neck capacitance ΣCn, total dendrite longitudinal capacitance ΣCd and total membrane capacitance ΣCm is obtained by the following equation.

  

$$1/\mathrm{\Sigma }\mathrm{C}\mathrm{s}=1/\mathrm{\Sigma }\mathrm{C}\mathrm{n}+1/\mathrm{\Sigma }\mathrm{C}\mathrm{d}+1/\mathrm{\Sigma }\mathrm{C}\mathrm{m}$$(6)

If the value of the charge Q due to Ca²⁺ ions held in the spines is the same, the total amount of electric charge with multiple spines can be expressed as ΣQ. According to equation (3), the relationship between the total amount of electric charge ΣQ, the total series capacitance ΣCs, and the voltage V can be expressed by the following equation.

  

$$\mathrm{V}=\mathrm{\Sigma }\mathrm{Q}/\mathrm{\Sigma }\mathrm{C}\mathrm{s}=\mathrm{\Sigma }\mathrm{Q}\mathrm{(}1/\mathrm{\Sigma }\mathrm{C}\mathrm{n}+1/\mathrm{\Sigma }\mathrm{C}\mathrm{d}+1/\mathrm{\Sigma }\mathrm{C}\mathrm{m}\mathrm{)}=\mathrm{V}1+\mathrm{V}2+\mathrm{V}3$$(7)

This equation shows that the voltage V is generated between inside and outside of the spines holding Ca²⁺ions. As shown in Figure 3, V1, V2 and V3 are calculated by the following equation. V1 is the voltage applied to both ends of the total spine neck capacitance ΣCn, which is sandwiched between the total charge ΣQ in the spine and the total dendrite longitudinal capacitance ΣCd.

  

$$\mathrm{V}1=\mathrm{\Sigma }\mathrm{Q}/\mathrm{\Sigma }\mathrm{C}\mathrm{n}$$(8)

V2 is the voltage applied to the total dendrite longitudinal capacitance ΣCd sandwiched between the total spine neck capacitance ΣCn and the total membrane capacitance ΣCm, calculated by the following equation.

  

$$\mathrm{V}2=\mathrm{\Sigma }\mathrm{Q}/\mathrm{\Sigma }\mathrm{C}\mathrm{d}$$(9)

V3 is the voltage applied to the total membrane capacitance ΣCm sandwiched between outside the neuron and inside the neuron, is called membrane potential and is calculated by the following equation.

  

$$\mathrm{V}3=\mathrm{\Sigma }\mathrm{Q}/\mathrm{\Sigma }\mathrm{C}\mathrm{m}=\mathrm{\Sigma }\mathrm{Q}/\mathrm{(}\mathrm{\Sigma }\mathrm{C}\mathrm{n}\mathrm{s}+\mathrm{\Sigma }\mathrm{C}\mathrm{d}\mathrm{m}+\mathrm{C}\mathrm{s}\mathrm{o}\mathrm{m}\mathrm{)}$$(10)

That is, the membrane potential V3 is the same at the tip of the dendrite and near the soma, and is sensed by the voltage-gated Na⁺ channel on the axonal hillock.

Conditions for the success of synaptic integration

When the membrane potential V3 rises from –65 mV, the rest potential, to –50 mV, the threshold of the voltage-gated Na+ channel on the axonal hillock, Na ions flow in, generating an action potential. Therefore, the success of synaptic integration depends on the membrane potential V3 rising by 15 mV from –65 mV to –50 mV, by the sum of the charges Q of several spines that hold Ca²⁺ ions. Therefore, the condition for successful synaptic integration is given by the following equation.

  

$$\mathrm{V}3=\mathrm{\Sigma }\mathrm{Q}/\mathrm{\Sigma }\mathrm{C}\mathrm{m}=\mathrm{\Sigma }\mathrm{Q}/\mathrm{(}\mathrm{\Sigma }\mathrm{C}\mathrm{n}\mathrm{s}+\mathrm{\Sigma }\mathrm{C}\mathrm{d}\mathrm{m}+\mathrm{C}\mathrm{s}\mathrm{o}\mathrm{m}\mathrm{)}\ge 15\hspace{0.25em}\mathrm{m}\mathrm{V}$$(11)

Therefore, if the size of each capacitance is known, the total amount of electric charge ΣQ that satisfies the condition can be determined. There are various thresholds for voltage-gated Na⁺ channels, such as –40 mV, –55 mV and –50 mV reported in [7], [15] and [16], respectively. Here, –50 mV is selected.

Electric charge quantity held in one spine

In this study, I assume that every spine holds the same amount of electric charge. As described above, the electric charge Q of the spine holding Ca²⁺ ions in Figure 3 is stored in the spine membrane capacitance Csm and the series capacitance Cs connected with the spine neck capacitance Cn, the longitudinal capacitance Cd of the dendrite and the total membrane capacitance ΣCm in serial. But, since the spine membrane capacitance Csm is much smaller than the series capacitance Cs as shown in the next section, Csm can be ignored. The series capacitance Cs of one spine is given by the following equation.

  

$$1/\mathrm{C}\mathrm{s}=1/\mathrm{C}\mathrm{n}+1/\mathrm{C}\mathrm{d}+1/\mathrm{\Sigma }\mathrm{C}\mathrm{m}$$(12)

Therefore, when V becomes –65 mV to 0 V by Ca²⁺ ions, the amount of electric charge Q retained by one spine can be calculated by the following equation according to equation (3).

  

$$\mathrm{Q}=\mathrm{V}\mathrm{C}\mathrm{s}=65\hspace{0.25em}\mathrm{m}\mathrm{V}\mathrm{C}\mathrm{s}$$(13)

Inhibitory effects of inhibitory post-synapses on synaptic integration

Most inhibitory post-synapses are located directly on dendrites or soma. Therefore, the negative charge of Cl^– ions directly flowing into the dendrites by inhibitory post-synapses is able to directly polarize the dendritic fluid, which may efficiently inhibit synaptic integration. Therefore, according to the equation (10), we calculate the amount of negative electric charge that makes the membrane potential V3, which had increased by 15 mV due to the charge in the spine, to 0 V, and verify the effect.

Verification of Ca²⁺ ion concentration when Ca²⁺ ions are retained in a spine

In order for Ca²⁺ ions to flow into the spine, the Ca²⁺ ion concentration inside the spine must be less than or equal to the Ca²⁺ ion concentration outside the spine as shown in Table 1 [7]. Therefore, I will verify the Ca²⁺ ion concentration in the spine, when Ca²⁺ ions flow into the spine and the voltage in the spine become 0 mV.

Methods

In the previous section, I could express the conditions for the success of synaptic integration in terms of equations, by assuming that Ca2+ ions are retained in the spine for a long time. I also pointed out that Cl^– ions taken in by inhibitory post-synapses may be able to effectively suppress the conditions for the success of synaptic integration by Ca²⁺ ions. In this section, I will calculate the capacitance and amount of electric charge so that the results can be obtained in the next section.

Calculation of each of the capacitance

Each of the capacitance shown in Figure 3 is obtained as follows.

Spine membrane capacitance Csm: This capacitance is calculated as the product of the surface area of the spine and the capacity per area. However, since the data for the surface area was not available, the spine was regarded as a sphere and the surface area (4πr²) of 1.0417 μm² was calculated from the average volume of the spine of 0.1 μm³ (4/3πr³) [2]. From this surface area and the capacity per area of 0.9 μF/cm² [23], we calculated a spine membrane capacitance Csm of about 0.009 pF (=9.37×10^–15F). This capacitance is a very small value, but since some dendrites have more than thousands of spines [1,2], it cannot be ignored as a factor in the total membrane capacitance.

Spine neck capacitance Cn: This capacitance is calculated using the following equation [22].

  

$$\mathrm{C}\mathrm{n}=\mathrm{\epsilon }\mathrm{S}/\mathrm{d}={\mathrm{\epsilon }}_0{\mathrm{\epsilon }}_{\mathrm{r}}\mathrm{\pi }{\mathrm{r}}^2/\mathrm{d}$$(14)

S is the cross-sectional area of the spine neck, which is calculated using the average diameter of the spine neck of 0.18 μm [2,24]. The distance d is the average spine neck length of 0.5 μm [2,24]. The data for the relative dielectric constant ε_r of the spine neck fluid is not available. However, since the relative dielectric constant ε_r of ionic fluid is proportional to the ion concentration and the resistance tends to be inversely proportional to the ion concentration, the resistance of the spine neck of the above shape is about 1 GΩ [4,11,21], while the resistance of an axon of 10 μm diameter is 140 MΩ/cm [8,25]. Therefore, I calculated that the ratio of the resistance of the spine neck fluid to that of the dendritic and axonal fluid is about 50 times greater. Therefore, the relative dielectric constant ε_r of the spine neck fluid is about 1/50 of the relative dielectric constant ε_r of the dendritic fluid and axonal fluid. The relative dielectric constant ε_r of dendritic and axonal fluids is 5×10⁷, which is the relative dielectric constant ε_r of similar gray matter in the brain at low frequencies [26,27]. Therefore, the relative dielectric constant ε_r of the spine neck fluid is 10⁶. From the product of the dielectric constant ε₀ of the vacuum, 8.854×10^–12 F/m [22], and the relative dielectric constant ε_r of the spine neck, the dielectric constant ε of the spine neck is 8.854×10^–6 F/m. Therefore, according to equation (14), the spine neck capacitance Cn was calculated to be 0.45 pF.

Spine capacitance Csp: This capacitance is calculated using the following equation.

  

$$\mathrm{C}\mathrm{s}\mathrm{p}=\mathrm{\epsilon }\mathrm{S}/\mathrm{r}=\mathrm{\epsilon }4\mathrm{\pi }{\mathrm{r}}^2/\mathrm{r}={\mathrm{\epsilon }}_0{\mathrm{\epsilon }}_{\mathrm{r}}4\mathrm{\pi }\mathrm{r}$$(15)

S is the surface area of the spine, r is the radius of the spine, ε₀ is the dielectric constant of the vacuum, and ε_r is the relative dielectric constant of the spine fluid, which is10⁶, same of the spine neck fluid. Csp is calculated 32.0 pF by ε₀ (8.854×10^–12F/m), and radius r (0.288 μm) obtained from the average spine volume of 0.1 μm³ [2.24].

Dendrite longitudinal capacitance Cd: The dendrite longitudinal capacitance Cd is calculated by the following equation based on the same idea as the definition of axonal longitudinal capacitance in the cited material [8].

  

$$\mathrm{C}\mathrm{d}=2\mathrm{\epsilon }\mathrm{S}/\mathrm{d}=2{\mathrm{\epsilon }}_0{\mathrm{\epsilon }}_{\mathrm{r}}\mathrm{\pi }{\mathrm{r}}^2/\mathrm{d}$$(16)

2 is the number of the direction propagating the polarization, S is the cross-sectional area of the dendrite, r is the radius of the dendrite, and the distance d is the distance from the start of the signal, where the dendrite connects to the spine neck, to the measurement point (axonal hillock). However, since many spines are connected to one dendrite, I determined the distance d is the average distance of half the length of the dendrite, assuming that the spines are equally spaced. Therefore, axons beyond the measurement point are not included. While, ε₀ is the dielectric constant of vacuum, 8.854×10^–12 F/m [22], and ε_r is the relative dielectric constant of the dendritic fluid, 5×10⁷, same as an axonal fluid [26,27]. Therefore, the dielectric constant ε of the dendritic fluid is 4.424×10^–4 F/m. Assume that the average dendrite diameter of CA1 pyramidal cells in the hippocampus is 1 μm and the average length is 130 μm [1]. Therefore, the dendritic longitudinal capacitance Cd is 10.7 pF according to equation (16).

Dendrite membrane capacitance Cdm: The dendrite membrane capacitance Cdm is calculated by the cylindrical capacity equation [22].

  

$$\mathrm{C}\mathrm{d}\mathrm{m}=2\mathrm{\pi }\mathrm{\epsilon }\mathrm{d}/\mathrm{l}\mathrm{n}\mathrm{(}\mathrm{D}\mathrm{o}/\mathrm{D}\mathrm{i}\mathrm{)}=2\mathrm{\pi }{\mathrm{\epsilon }}_0{\mathrm{\epsilon }}_{\mathrm{r}}\hspace{0.25em}\mathrm{d}/\mathrm{l}\mathrm{n}\mathrm{(}\mathrm{D}\mathrm{o}/\mathrm{D}\mathrm{i}\mathrm{)}$$(17)

Do is the outer diameter of the dendrite, Di is the inner diameter of the dendrite, and d is the propagation distance of the signal. If the thickness of the dendrite membrane of the CA1 pyramidal cell is 5 nm in the lipid bilayer [25] and thus the diameter is 1 μm [1], the outer diameter is 1.01 μm and thus the inner diameter is 1.00 μm. The length d shall be 130 μm[1], the same as above. If the relative dielectric constant ε_r, between 5 and 10 [25], is 7.5, the same as for the myelin sheath, the membrane capacitance Cdm of the dendrite is 5.45 pF.

Membrane capacitance of the soma Csom: The membrane capacitance of the soma Csom is determined by the product of the surface area and the capacity per area, as in the case of the membrane capacitance of the spine Csm. Therefore, Csom which is the product of the surface area (4πr²) of the soma of CA1 pyramidal cells with the average diameter 20 μm [1] and the capacity per area of 0.9 μF/cm² [23] is 11.3 pF.

Series membrane capacitance including a spine not holding Ca²⁺Ions Cns: A spine that does not hold Ca²⁺ ions in the spine is treated as a membrane capacitance connected to the dendrite. Its series membrane capacitance Cns is calculated as the series connection of the membrane capacitance of the spine Csm (0.009 pF), capacitance of spine Csp (32pF) and the capacitance of the spine neck Cn (0.45 pF) by equation (4). Therefore, the series membrane capacitance Cns is 0.0088pF.

Total membrane capacitance ΣCm: The total membrane capacitance ΣCm is the sum of the series membrane capacitance ΣCns of all spines that do not hold Ca²⁺ ions, the membrane capacitance ΣCdm of all dendrites connected to the soma, and the membrane capacitance of the soma Csom. Here, I use the capacitance values obtained above. And, I assume that there is only one dendrite with a length of 130 μm and 130 spines. I assume that there are 10 spines that hold Ca²⁺ ions and 120 spines that do not. Therefore, the total series membrane capacitance ΣCns of the 120 uncharged spines is 1.056 pF, the total dendritic membrane capacitance ΣCdm of one spine is 5.45 pF, and the soma membrane capacitance is 11.3 pF. Therefore, the total membrane capacitance ΣCm is 17.8 pF.

Calculation of the charge Q of an average spine holding Ca²⁺ ions

The series capacitance Cs of the spine in an average CA1 pyramidal cell of the hippocampus with one dendrite, which connects in series the spine neck capacitance Cn (0.45 pF), the total dendritic longitudinal capacitances ΣCd (10.7 pF), and the total membrane capacitance ΣCm (17.8 pF), is 0.42pF. And the spine membrane capacitance Csm is 0.009pF. As described in section 1.4.3, since the Csm is much smaller than the Cs, Csm is ignored in calculation of the amount of electric charge in a spine. I assumed when Ca²⁺ ions are flowed into the spine, the charge of the Ca²⁺ ions causes the voltage inside to rise from –65 mV to 0 V which is same voltage outside. Therefore, for the other parts of the rest potential in the same neuron, the amount of charge Q stored in the spine is 2.73×10^–14 coulombs, which is the product of the voltage 65×10^–3 V and the series capacitance Cs0.42×10^–12 F, according to the equation (13).

Results

This study was initiated to elucidate the mechanisms that improve the reproducibility of success of a synaptic integration, but in addition to elucidating the mechanisms, the approach of this study allowed to explain the following important issues.

- Condition for the success of synaptic integration

- Ability of integration for a huge number of synaptic input combinations by a single neuron

- Contribution of spine neck capacitance Cn to success of synaptic integration

- Contribution for success of synaptic integration by a distant spine from the soma

- The attenuation of pulse-like wave on the propagation in the dendrite

-The attenuation of back propagation of action potential (BAP) from parent dendrite to the spine

- Effective deterrence for synaptic integration by inhibitory synapses

- The spine head size and Ca²⁺ ion concentration in the spine

Condition for the success of synaptic integration

The total membrane capacitance ΣCm of an average CA1 pyramidal cell with one dendrite was calculated in the previous subsection to be 17.8pF. Therefore, the total amount of electric charge ΣQ required for the success of synaptic integration in this case, is obtained by equation (11).

  

$$\mathrm{\Sigma }\mathrm{Q}\ge 15\hspace{0.25em}\mathrm{m}\mathrm{V}\times \mathrm{\Sigma }\mathrm{C}\mathrm{m}=15\hspace{0.25em}\mathrm{m}\mathrm{V}\times 17.8\mathrm{p}\mathrm{F}=26.7\times {10}^{-14}\hspace{0.25em}\mathrm{coulombs}$$(18)

The required number of spines for the success of synaptic integration is calculated using the amount of electric charge Q of one average spine, 2.73×10^–14 coulombs calculated in the previous subsection, as below.

  

$$26.7\times {10}^{-14}\hspace{0.25em}\mathrm{coulomb}/2.73\times {10}^{-14}\hspace{0.25em}\mathrm{coulomb}=9.78$$(19)

This indicates that synaptic integration can be successfully achieved if there are 10 or more average spines holding Ca²⁺ ions in each of them. In fact, it should be noted that since there are many different shapes of spines connected to dendrites, the amount of electric charge that a spine is able to hold varies greatly from spine to spine. Figure 1c shows an example of success of synaptic integration by three spines holding Ca²⁺ ions. Furthermore, it shows action potentials are generated in a tetanus stimulus manner.

Ability of integration for a huge number of synaptic input combinations by a single neuron

As shown in above section, in a dendrite with 130 spines, at least 10 spines holding Ca²⁺ ions are required for successful synaptic integration. This is the number of combinations to select n out of m. Using the formula for combinations, if m is 130 and n is 10, the number of combinations is shown as follow.

  

$${}_{\mathrm{m}}{}^{}\mathrm{C}_{\mathrm{n}}^{}={}_{130}{}^{}\mathrm{C}_{10}^{}=2.66\times {10}^{14}$$(20)

This is a huge number of combinations. Furthermore, if m is 10,000 and n is 30, it means that a single neuron is able to handle 3.6×10⁸⁷, or an infinite number of combinations of inputs. According to the cited reference [28], it is written that there are about 16 billion (16×10⁹) neurons in the cerebrum. If we consider one neuron as one bit of memory, it means that the memory capacity is only 2Gbytes, which is much smaller than the capacity of a commercial USB memory device. However, if each neuron is able to handle _mC_n combinations of inputs, the number of 2Gbytes of neuron may be enough.

Contribution of spine neck capacitance Cn to success of synaptic integration

The above results show that the number of spines required for successful synaptic integration depends on the amount of electric charge Q stored per spine. In other words, the contribution to the success of synaptic integration is proportional to the amount of electric charge Q stored in the spine. The capacitance that stores electric charge in a spine is the capacitance Cs of the series connection, including the spine neck capacitance Cn, as shown in equation (13). In the calculation of the capacitance of the series connection, if there is a particularly small capacitance among the capacitances connected in series, the calculation result will be almost the same value as that particularly small capacitance. Therefore, while the spine neck capacitance Cn is 0.45 pF, the total dendritic longitudinal capacitance ΣCd and the total membrane capacitance ΣCm connected in series are 10.7 pF and 17.8 pF, respectively, so the capacitance Cs of the series connection including the spine neck is 0.42 pF. This means that the Capacitance Cs depends on the spine neck capacitance Cn. The spine neck capacitance Cn is shown in the equation (14), as shown in the previous section [22]. That is, it is proportional to the cross-sectional area of the spine neck (square of the radius) and inversely proportional to the length of the spine neck. Therefore, the thicker and shorter the spine neck is, the larger the spine neck capacitance Cn becomes, which contributes more to success of synaptic integration. Therefore, it is considered that the contribution of Filopodium-type spines and Mushroom-type spines [1,2,24] to the success of synaptic integration is very different.

Contribution for success of synaptic integration by a spine distant from the soma

The above analysis shows that the spine neck capacitance contributes significantly to the success of synaptic integration. On the other hand, since dendrites are long and thin, the effect of the position of the spine on the dendrite becomes an issue, even if the spine has the same shape. In other words, according to equation (13), the amount of electric charge Q that the spine is able to store depends on the series capacitance Cs. Therefore, it is necessary to analyze the relationship between the series capacitance Cs and the dendrite distance x from the parent dendrite of the spine to the soma. The dendrite longitudinal capacitance Cd is inversely proportional to the distance x from the soma as shown in equation (16), and the dendritic membrane capacitance Cdm is proportional to the distance x from the soma as shown in (17). And the series membrane capacitance Cns at 1 μm intervals, which includes spines that do not hold Ca²⁺ ions, is proportional to the distance x. Therefore, the series capacitance Cs including the spine neck capacitance Cn taking into account the distance x can be calculated by the following equation.

  

$$1/\mathrm{C}\mathrm{s}=1/\mathrm{C}\mathrm{n}+1/\mathrm{C}\mathrm{d}/x+1/\mathrm{(}x\mathrm{C}\mathrm{d}\mathrm{m}+x\mathrm{C}\mathrm{n}\mathrm{s}+\mathrm{C}\mathrm{s}\mathrm{o}\mathrm{m}\mathrm{)}$$(21)

Cn is 0.45 pF at a distance of 130 μm from the soma, Cd is 10.7 pF and Cdm is 5.45 pF, Cns is 0.0088 pF per μm, and Csom is 11.3 pF. Therefore, the relationship between Cs and distance x is:

  

$$\mathrm{C}\mathrm{s}=1/\mathrm{(}1/0.45\mathrm{p}\mathrm{F}+x/\mathrm{(}10.7\mathrm{p}\mathrm{F}·130\mathrm{)}+1/\mathrm{(}x5.45\mathrm{p}\mathrm{F}/130+x0.0088\mathrm{p}\mathrm{F}+11.3\mathrm{p}\mathrm{F}\mathrm{)}\mathrm{)}$$(22)

When the distance x from the soma is 1 μm, 100 μm, 200 μm...500 μm, the series capacitance Cs is 0.4327 pF, 0.4246 pF, 0.4145pF...0.3833 pF, respectively. As shown in Figure 4, the series capacitance Cs including the spine neck capacitance Cn is almost the same even in a spine far from the soma, so the amount of electric charge Q held in the spine is almost the same regardless of the distance x. In dendrites even with a thin diameter of 1 μm [1], the contribution of the spine to the success of synaptic integration is not significantly affected by the distance from the soma. This means that neurons utilize the advantage of the propagation properties of static polarization.

Figure 4 

Relationship between series capacitance Cs and distance from the soma. The spine is able to store amount of electric charge Q proportional to the Cs.

The attenuation of pulse-like wave

-The attenuation of pulse-like wave on the propagation in the dendrite

Pulsed EPSP and back propagation of action potential (BAP) waveforms are attenuated as they propagate through the dendrite [29,30]. For voltage-varying waveforms, the effect of displacement current, which is proportional to the product of the rate of voltage change and the capacitance, must be considered. A displacement current of (Cd) dV/dt flows in the axial direction of the dendrite, and a displacement current (leakage current) of (Cdm+Cns) dV/dt flows out through the dendritic membrane (containing Cns). The resistance of the displacement current to pass through the capacitance is represented by the impedance Z. If the rate of voltage change is expressed in terms of angular velocity ω, as in a normal electrical circuit, the impedance Z1 of the axial direction of dendrite is 1/(ωCd), and the impedance Z2 of the dendritic membrane is 1/(ωCdm+ω Cns). Therefore, if the voltage of the original waveform is V, the current I flowing through the two series-connected impedances (Z1+Z2) is I=V/(Z1+Z2), and the membrane potential Vm is Vm=IZ2. Therefore, the membrane potential Vm can be obtained by the following equation.

  

$$\begin{array}{cc}\mathrm{V}\mathrm{m}\hfill & =\mathrm{V}\mathrm{(}\mathrm{Z}2/\mathrm{(}\mathrm{Z}1+\mathrm{Z}2\mathrm{)}\mathrm{)}=\mathrm{V}\mathrm{(}1/\mathrm{(}\mathrm{\omega }\mathrm{C}\mathrm{d}\mathrm{m}+\mathrm{\omega }\mathrm{C}\mathrm{n}\mathrm{s}\mathrm{)}/\mathrm{(}\mathrm{(}1/\mathrm{(}\mathrm{\omega }\mathrm{C}\mathrm{d}\mathrm{)}+1/\mathrm{(}\mathrm{\omega }\mathrm{C}\mathrm{d}\mathrm{m}+\mathrm{\omega }\mathrm{C}\mathrm{n}\mathrm{s}\mathrm{)}\mathrm{)}\hfill \\ & =\mathrm{V}\mathrm{(}1/\mathrm{(}\mathrm{(}\mathrm{C}\mathrm{d}\mathrm{m}+\mathrm{C}\mathrm{n}\mathrm{s}\mathrm{)}/\mathrm{C}\mathrm{d}+1\mathrm{)}\mathrm{)}\hfill \end{array}$$(23)

The dendritic longitudinal capacitance Cd is inversely proportional to the distance x from the signal source according to equation (16), and the membrane capacitance of the dendrites Cdm is proportional to the distance x from the signal source from equation (17). Then, from section 2.1, Cd is 10.7 pF, Cdm is 5.45 pF when the distance from the soma is 130 μm and Cns is 1.14 pF (130 cells/130 μm). Therefore, the membrane voltage Vm for a distance x is given as below.

  

$$\mathrm{V}\mathrm{m}=\mathrm{V}\mathrm{(}1/\mathrm{(}\mathrm{(}\mathrm{C}\mathrm{d}\mathrm{m}+\mathrm{C}\mathrm{n}\mathrm{s}\mathrm{)}{\mathrm{(}x/130\mathrm{)}}^2/\mathrm{C}\mathrm{d}+1\mathrm{)}\mathrm{)}=\mathrm{V}\mathrm{(}1/\mathrm{(}6.59/10.7{\mathrm{(}x/130\mathrm{)}}^2+1\mathrm{)}$$(24)

The Vm/V ratios for distances x of 1 μm, 100 μm, 200 μm, ... 500 μm are calculated to be 1, 0.7368, 0.4093, ... 0.0924 respectively. This shows that the dynamically fluctuating pulsed waveform is greatly attenuated by distance x, as shown in Figure 5. If it is important for learning that the spines that contribute to synaptic integration receive the back propagation waveform (BAP) of the action potential, there is a problem that the BAP waveform will be small for spines that are far from the soma. Therefore, it may be related to the fact that the average length of basal dendrites of CA1 pyramidal cells is 130 μm [1]. The above calculation of attenuation can also be applied to the attenuation of the EPSP waveform from the dendrites to the soma.

Figure 5 

Relationship between distance from signal source and Attenuation ratio of the back propagation of action potential (BAP) and of the propagation of excitatory postsynaptic potential (EPSP).

On the other hand, when a voltage is generated, a current flows through the axial DC resistance of the dendrite too. The axial DC resistance of an axon with a diameter of 20 μm is 3500 MΩ/m [8,25], therefore the DC resistance per μm of a dendrite with a diameter of 1 μm is 1.4 MΩ/μm, based on the cross-sectional area ratio. On the other hand, if the rise time of the action potential is 2 m seconds, the dV/dt is 500, and the axial Cd capacitance of 10.7pF/m at a distance of 130 μm gives a resistance (impedance) per μm of 1.4378 Ω/μm. Therefore, the propagation due to the very high axial DC resistance R of the dendrite (1.4 MΩ/μm) is able to be neglected.

-The attenuation of BAP from parent dendrite to the spine

It has been reported that the back propagation of action potential (BAP) of the parent dendrite reaches the spine with almost no attenuation [31]. This phenomenon was verified by using the capacitance value calculated in section 2.1. The voltage of the BAP at the parent dendrite is called V, and the voltage of the BAP reaching the spine through the spine neck is called Vb. The path of the current from the parent dendrite to the outside via the spine neck, spine, and spine membrane can be shown by the series connection of the impedance of Zcn due to the spine neck capacitance Cn, Zcsp due to the spine capacitance Csp, and Zcsm due to the spine membrane capacitance Csm. If the rate of change of the BAP waveform is expressed in terms of angular velocity ω, the impedance C can be converted in terms of capacitance and angular velocity ω. Therefore, the current I flowing at the voltage V is calculated as below.

  

$$\mathrm{I}=\mathrm{V}/\mathrm{(}\mathrm{Z}\mathrm{c}\mathrm{n}+\mathrm{Z}\mathrm{c}\mathrm{s}\mathrm{p}+\mathrm{Z}\mathrm{c}\mathrm{s}\mathrm{m}\mathrm{)}$$(25)

And the voltage Vb in a spine is IZcsm. Therefore, Vb is calculated as below.

  

$$\begin{array}{cc}\mathrm{V}\mathrm{b}\hfill & =\mathrm{V}\mathrm{Z}\mathrm{c}\mathrm{s}\mathrm{m}/\mathrm{(}\mathrm{Z}\mathrm{c}\mathrm{n}+\mathrm{Z}\mathrm{c}\mathrm{s}\mathrm{p}+\mathrm{Z}\mathrm{c}\mathrm{s}\mathrm{m}\mathrm{)}=\mathrm{V}/\mathrm{\omega }\mathrm{C}\mathrm{s}\mathrm{m}/\mathrm{(}1/\mathrm{\omega }\mathrm{C}\mathrm{n}+1/\mathrm{\omega }\mathrm{C}\mathrm{s}\mathrm{p}+1/\mathrm{\omega }\mathrm{C}\mathrm{s}\mathrm{m}\mathrm{)}\hfill \\ & =\mathrm{V}/\mathrm{C}\mathrm{s}\mathrm{m}/\mathrm{(}1/\mathrm{C}\mathrm{n}+1/\mathrm{C}\mathrm{s}\mathrm{p}+1/\mathrm{C}\mathrm{s}\mathrm{m}\mathrm{)}\hfill \end{array}$$(26)

Substituting 0.45 pF for Cn, 32 pF for Csp, and 0.009 pF for Csm, the ratio of Vb/V is calculated to be 0.98, which means that the voltage Vb of the spine inside the spine membrane is 98% of the potential V of the parent dendrite. This means that the BAP waveform reaches the spine with almost no attenuation. Therefore, each spine holding Ca²⁺ ions is able to detect that the potential in the spine head is further increased by the BAP and recognize that it has contributed to synaptic integration. This is consistent with the Hebb Rule. On the other hand, the voltage of the EPSP that reaches the parent dendrite through the spine neck is significantly attenuated by the passage through the spine neck because the dendrite longitudinal capacitance Cd and the total membrane capacitance ΣCm of the dendrite are much larger than the spine neck capacitance Cn. However, the voltage due to the current of Na⁺ ions passing through the spine neck will be added.

Effective deterrence for synaptic integration by inhibitory synapses

The negative charge of Cl^– ions taken in by inhibitory synapses on the dendrites polarizes the dendritic fluid in a negative direction. Therefore, by equation (10), I calculate the amount of negative charge that cancels out the amount of positive charge that raises the membrane potential V3 by 15 mV. As calculated in section 3.1, the total amount of positive charge ΣQ that raises the membrane potential V3 by 15 mV is 26.7×10^–14 coulombs. To offset this amount of positive charge, 1.67×10⁶ monovalent negative Cl^– ions (1.6×10^–19 coulombs per ion) must be flowed into the dendrites. That is, the number of molecules per mole (Avogadro’s number) is 6.02×10²³, while this number is 2.77×10^–18 moles. Cl^– ions of this number of moles is contained in 4.29×10^–12 liter, which is the sum of the volume of a dendrite 130 μm long and 1 μm in diameter and a soma 20 μm in diameter [1]. Therefore, the concentration of Cl^– ions per liter is 6.46×10^–7 M (0.646 μM). Table 1 indicates that the concentration of Cl^– ions in the cell at rest potential is 13 mM, so a very small quantity in the concentration of Cl^– ions, about 1/20,000th, can efficiently offset 26.7×10^–14 coulombs of the total charge ΣQ for successful synaptic integration. However, Cl^– ions will be flowed out by the Cl^– ion pump on the dendritic membrane, and the concentration will return to the original level after a while. If enough Ca²⁺ ions are still retained in each spine at that time, synaptic integration may be successful again. However, as shown in Figure 1.c, each spine seems to reduce the amount of Ca²⁺ ions as appropriate to avoid the continuation of the high membrane potential caused by the Ca²⁺ holding spines, but the details are not known. As discussed in Section 4.2, this is a very important issue.

The spine head size and Ca²⁺ ion concentration in the spine

In order to raise the voltage in the spine from –65 mV to 0 V by introducing Ca²⁺ ions into the spine, the Ca²⁺ ion concentration in the spine at 0 V must be less than the Ca²⁺ ion concentration outside the spine. Therefore, it is necessary to verify the concentration of Ca²⁺ ions in the spine when the potential inside the spine reaches 0 V. The amount of electric charge when the voltage inside the spine reaches 0 V is 2.73×10^–14 coulombs, according to the previous section, and the number of divalent Ca²⁺ ions is 2×1.6×10^–19 coulombs per ion, so the number of Ca²⁺ ions inside the spine is 8.53×10⁴. Therefore, the number of Ca²⁺ ions in the spine is 1.42×10^–19 moles, based on 6.02×10²³ molecules per mole. Since the average volume of the spine in this study is 0.1 μm3 [2], it was verified that the concentration in the spine is 1.42 mM per liter, which is lower than the concentration of 2 mM outside the spine shown in Table 1. In order for the spine to store more electric charge, it is necessary not only to increase the spine neck capacitance Cn, but also to increase the volume of the spine head, as in a mushroom-shaped spine, so that the Ca²⁺ ion concentration is not higher than outside.

Discussion

Existence of a mechanism that stably reproduces synaptic integration

It has been said that synaptic integration is established when the temporal or spatial summation of EPSPs reaches the threshold of voltage-gated Na⁺ channels that generate action potentials [4–6,32]. Although there have been reports focusing on LTP, plasticity and compartmentation within the spine, except the addition of multiple EPSPs occurring within a short period of time [17,18,33], there are no theoretical or experimental reports of improving the reproducibility of success of synaptic integration for irregular and long receiving intervals of signals from pre-synapses that generate EPSPs. However, in reality, the brain is not affected by the order in which it receives information and the interval between the receipt of the information, and it consistently produces the same result based on the information it receives. If the brain’s decisions are based on a chain of synaptic integration results, then it is inferred that there is a mechanism that stably reproduces synaptic integration based on the multiple EPSPs involved in synaptic integration, regardless of the order and interval in which the EPSPs are generated. Therefore, I started this study to investigate the mechanism of synaptic integration from this perspective.

The influence of static electric charge of Ca²⁺ ions retained in a spine

Until now, the effect of the dynamic current like Na⁺ ions out of the spine towards the dendrite has been focused as the mechanism of synaptic integration. However, even there are no current from spine towards the dendrite, if we assume that Ca²⁺ ions taken into a spine after EPSP generation are retained in the spine for a long time, the influence of the electric charge due to the Ca²⁺ ions will last for a long time. In this study, by means of focusing on the influence by the static persistent electric charge of Ca²⁺ ions retained in the spine and the dielectric characteristic of the medium, I was able to explain not only the reproducibility of the synaptic integration process, but also some of the important issues that have been raised as described in the section of Results. On the other hand, the following problem exists. During wakefulness, neurons receive stimuli from various pre-synapses, and the number of spines holding Ca²⁺ ions increases. Therefore, the increase in the number of spines holding Ca²⁺ ions causes the problem of a persistent high membrane potential. In order to avoid this problem, each spine must release the Ca²⁺ ions it holds accordingly. But, the release and retention of Ca²⁺ ions is still not fully understood, including the phenomenon of LTP. However, it looks that each spine releases or accumulates Ca²⁺ ions reflecting own learning and activity history.

Analysis by equivalent circuit of capacitance only

Most of the analysis so far has focused on the changing voltage, current and charge. Neurons have a very complicated structure and are constantly active, but when the ions, which are charged particles in the neuron, are at a rest potential state where they do not move in a certain direction even though they undergo random thermal motion, it can be assumed that there is no current in the neuron. Therefore, as mentioned in the section of Methods, I defined capacitance for each medium, focused on the propagation pathway of polarization by capacitance, and used an equivalent circuit with only capacitance. This enabled us to formulate the relationship between capacitance and voltage with respect to the amount of electric charge. Therefore, I was able to calculate the potential of the boundary surface of the adjacent dielectric media around the amount of charge Q stored in the spine. As the result, I found that the number of spines holding the Ca²⁺ ions is related to the success of synaptic integration, that the spine neck capacitance Cn and the size of the spine head contribute to the success of synaptic integration, and that spines attached to dendrites far from the soma are able to also contribute to synaptic integration.

The basic logical functions of neurons

Computers are realized by basic logic elements such as NAND, AND, OR, and exclusive OR, and basic circuits of flip-flops (memory) to hold the processing results. These basic logic elements and basic circuits can be realized by combining only NAND in multiple stages. However, NAND, OR and exclusive OR cannot be created by combining only AND, and NAND, AND and exclusive OR cannot be created by combining only OR. A flip-flop, which is a memory, is realized by using two NAND devices to loop the signal by connecting the output of the other device to its input. Therefore, a general LSI is made by connecting a huge number of NAND elements arranged in an array, according to the logical structure. On the other hand, neurons do not output action potentials when inhibitory post-synapses are active. Therefore, it is not possible to create an AND by linking the outputs of NAND elements, as in the NAND element of a computer. However, since neurons have the basic functions of AND and OR for input, if there is an inhibitory function to suppress output, it would be considered to be able to create the desired logic circuit, including exclusive OR. That is, the fact that there are two types of neurons, excitatory neurons that output the results of AND and OR, and inhibitory neurons that suppress the output, is considered to complement to the fact that no output is produced when suppress is active. Furthermore, the output of a neuron is a pulsed release of neurotransmitter, unlike the output of a memory in a stable state. Therefore, it is necessary to realize a mechanism that memorizes the receipt of neurotransmitters from pre-synapses by the spine of post synapse by holding Ca²⁺ ions as in this proposal. On the other hand, this mechanism of retaining Ca²⁺ ions makes it possible to easily generate tetanus-stimulus like action potentials as required, as mentioned in the section of Results. Moreover, it is amazing that a neuron with many spines (m) is able to integrate synapses for _mC_n combinations of inputs (almost infinite combinations). However, if the number of spines holding Ca²⁺ ions increases in a short period of time, it may become unclear by which inputs the success of synaptic integration occurs. Anyway, if each neuron in a cerebrum was able to have such integration ability, the total processing ability for the information may be not used up in a lifetime.

Relationship to previous studies on spines

In this study, we found that a spine that can store a large amount of charge for a long period of time makes a significant contribution to the success of synaptic integration. In order to store a large amount of charge in a spine, the spine neck capacitance Cn must be large, as shown in the section of Results. In addition, a large spine head are required to prevent the Ca²⁺ ion concentration in the spine from becoming higher than outside the spine. However, there are many spines with different sized spine heads and spine necks connected to the dendrites. These spines are considered to be constantly changing according to their own activity history. For example, since the amount of stored charge is small in the spine of a small head, it is considered to be necessary to elongate the spine neck and reduce the spine neck capacitance Cn to increase the potential in the spine so that the potential-dependent proteins in the spine head can work, as shown in equation (8). A small head spine may then grow as a spine that had an experience contributing to successful synaptic integration if it is able to sense the back propagation of action potentials while the inside of the spine is highly potential by Ca²⁺ ions [34]. To date, many research results have been reported on the control of compartment and spine neck that retains Ca²⁺ ions [10,16,19,20,35]. There are also reports of the plasticity by detection of the simultaneity of EPSP and action potential back propagation [31,36,37]. Furthermore, there are reports on the long-term preservation of learning in spines [38–41]. In addition, there are many reports on morphological changes [18,42–45]. I think that it will be important in the future to investigate the relationship between the focus of this study and these valuable research reports.

Calculation of the dielectric constant and capacitances

The mechanism by which the membrane potential raised by the sum of the polarization of the medium caused by the charges held by multiple spines reaches the threshold of the voltage-gated Na⁺ channel and generates an action potential has not been studied until now. Therefore, there are little data on the dielectric properties of spines, dendrites, soma and their membranes. Therefore, I had to get dielectric constants used in this study indirectly from other relevant materials. The equation for the dielectric constant and capacitance of the dendritic fluid were taken from the axonal fluid in references [8,25–27], and the equation for the capacitance of the dendritic membrane were taken from the membrane of axon in references [8,25]. Spine membrane capacitance and soma membrane capacitance were calculated from the data of inner area [1,2] and capacity per unit area [23]. The morphology of the dendrite is based on the data of pyramidal cells in CA1 of the hippocampus, which has been well studied in the past [1]. The dielectric constant of the spine neck fluid was then derived indirectly from the relationship between the concentration of the ionic fluid and its resistance [2,4,8,11,21,24–27]. Also, the spine fluid was set to have the same dielectric constant as the spine neck fluid. However, by substituting those values into the equations derived from the proposed mechanism, I am able to confirm the validity of the proposal. However, since this proposal was logically derived based on previous research data, it is necessary to confirm it with actual biological data as much as possible.

Conclusion

The purpose of this study is to elucidate the mechanisms that improve the reproducibility of success of synaptic integration, which is the basis of brain work. Conventional analysis approaches to the mechanism of synaptic integration are concerned with the addition of dynamic waveforms of EPSPs and have not been able to explain the stable and high reproducibility of success of synaptic integration. In this study, taking into account the dielectric properties of spines, dendrites and soma, which have not been focused on so far, I have analyzed the effect of the propagation of polarization in the adjacent medium due to the charge of Ca²⁺ ions retained in spines after EPSP generation, and revealed the mechanism of the high reproducibility of success of synaptic integration. In addition, the approach of this study allowed to explain important issues, that a single neuron can realize successful synaptic integrations for a large number of input combinations, that the success of synaptic integration depends on the spine neck capacitance and size of the spine head, that contribution for success of synaptic integration by a distant spine from the soma exists, that the back propagation of the action potential(BAP) does not attenuate to the inside of the spine from parent dendrite, and that the inhibitory synapses on the dendrite deter synaptic integration effectively. However, this proposal is a theoretical one based on previous studies, and needs to be verified in vivo in the future. In addition, the relationship between successful synaptic integration and the accumulation and release of Ca²⁺ ions held in each spine needs to be studied more detail in relation to the learning effect.

Conflicts of Interest

The author declares no conflicts of interest. The authors declare no funding sources.

Author Contributions

I analyzed the mechanism of synaptic integration from my own original view point, developed and solved formulas, and drafted the article and, approved the final version of the manuscript, agreed to be accountable for all aspects of the work.

Acknowledgements

The author would like to thank Dr. Masanori Okuyama (professor emeritus of Osaka University), Dr. Naoki Yamamoto (Department of Psychiatry, Tokyo Metropolitan Tama Medical Center) and Dr. Takumi Washio (Project researcher of Future Center Initiative, The University of Tokyo).

References

• [1]  Stuart, G., Spruston, N., Häusser, M. Dendrites Third edition. (Oxford University Press, Oxford, 2016).
• [2]  Yuste, R. Dendritic Spines. (Massachusetts Institute of Technology Press, Cambridge, 2010).
• [3]   Yuste,  R.,  Tank,  D. W. Dendritic integration in mammalian neurons, a century after Cajal. Neuron 16, 701–715 (1996). https://doi.org/10.1016/S0896-6273(00)80091-4
• [4]   Tønnesen,  J.,  Nägerl,  U. V. Dendritic spines as tunable regulators of synaptic signals. Front. Psychiatry 7, 1–10 (2016). https://doi.org/10.3389/fpsyt.2016.00101
• [5]   Yuste,  R. Dendritic spines and distributed circuits. Neuron 71, 772–781 (2011). https://doi.org/10.1016/j.neuron.2011.07.024
• [6]   Magee,  J. C. Dendritic integration of excitatory synaptic input. Nat. Rev. Neurosci. 1, 181–190 (2000). https://doi.org/10.1038/35044552
• [7]  Bear, F. M., Connors, W. B., Paradiso, A. M. Neuroscience: Exploring the Brain, Third edition. (Nishimura Co., Ltd., 2007).
• [8]   Tsubo,  T.,  Kurokawa,  M. Verification of the effect of the axon fluid as a highly dielectric medium in the high-speed conduction of action potentials using a novel axon equivalent circuit. Biophys. Physicobiol. 15, 214–228 (2018). https://doi.org/10.2142/biophysico.15.0_214
• [9]   Sabatini,  B. L.,  Oertner,  T. G.,  Svoboda,  K. The life cycle of Ca²⁺ ions in dendritic spines. Neuron 33, 439–452 (2002). https://doi.org/10.1016/s0896-6273(02)00573-1
• [10]   Bloodgood,  B. L.,  Sabatini,  B. L. Neuronal activity regulates diffusion across the neck of dendritic spines. Science 310, 866–869 (2005). https://doi.org/10.1126/science.1114816
• [11]   Araya,  R.,  Vogels,  T. P.,  Yuste,  R. Activity-depend dendritic spine-neck changes are correlated with synaptic strength. Proc. Natl. Acad. Sci. U.S.A. 111, E2895–E2904 (2014). https://doi.org/10.1073/pnas.1321869111
• [12]   Majewska,  A.,  Tashiro,  A.,  Yuste,  R. Regulation of spine calcium dynamics by rapid spine motility. J. Neurosci. 20, 8262–8268 (2000). https://doi.org/10.1523/JNEUROSCI.20-22-08262.2000
• [13]   Grunditz,  Å.,  Holbro,  N.,  Tain,  L.,  Zuo,  Y.,  Oertner,  T. G. Spine-neck plasticity controls postsynaptic calcium signals through electrical compartmentalization. J. Neurosci. 28, 13457–13466 (2008). https://doi.org/10.1523/JNEUROSCI.2702-08.2008
• [14]   Bliss,  T. V. P.,  Collingridge,  G. L.,  Morris,  R. G. M.,  Reymann,  K. G. Long-term potentiation in the hippocampus: Discovery, mechanism and function. Neuroforum 24, A103–A120 (2018). https://doi.org/10.1515/nf-2017-A059
• [15]  Kandel, R. E., Schwartz, H. J., Jessell, M. T., Siegelbaum, A. S., Hudspeth, J. A. Principles of neural science Fifth edition. (The McGraw-Hill Companies, New York, 2013).
• [16]  Purves, D., Augustine, J. G., Fitzpatrick, D. Neuroscience Sixth edition. (Oxford University Press, Oxford, 2018).
• [17]   Bliss,  T. V. P.,  Collingridge,  G. L. A synaptic model of memory: Long-term potentiation in the hippocampus. Nature 361, 31–39 (1993). https://doi.org/10.1038/361031a0
• [18]   Colgan,  L. A.,  Yasuda,  R. Plasticity of dendritic spines: Subcompartmentalization of Signaling. Annu. Rev. Physiol. 76, 365–385 (2014). https://doi.org/10.1146/annurev-physiol-021113-170400
• [19]   Bloodgood,  B. L.,  Giessel,  A. J.,  Sabatini,  B. L. Biphasic synaptic Ca influx arising from compartmentalized electrical signals in dendritic spines. PLoS Biol. 7, e1000190 (2009). https://doi.org/10.1371/journal.pbio.1000190
• [20]   Higley,  M. J.,  Sabatini,  B. L. Calcium signaling in dendritic spine. Cold Spring Harb. Perspect. Biol. 4, a005686 (2012). https://doi.org/10.1101/cshperspect.a005686
• [21]   Harnett,  M. T.,  Makara,  J. K.,  Spruston,  N.,  Kath,  W. L.,  Magee,  J. C. Synaptic amplification by dendritic spines enhances input cooperativity. Nature 491, 599–602 (2012). https://doi.org/10.1038/nature11554
• [22]  Ramo, S., Whinnery, J. R. Fields and Waves in Modern Radio 2nd edition. (General Electric Company, New York, 1953).
• [23]   Gentet,  L. J.,  Stuart,  G. J.,  Clements,  J. D. Direct measurement of specific membrane capacitance in neurons. Biophys. J. 79, 314–320 (2000). https://doi.org/10.1016/S0006-3495(00)76293-X
• [24]   Arellano,  J. I.,  Benavides-Piccione,  R.,  DeFelipe,  J.,  Yuste,  R. Ultrastructure of dendritic spines: correlation between synaptic and spine morphologies. Front. Neurosci. 1, 133–143 (2007). https://doi.org/10.3389/neuro.01.1.1.010.2007
• [25]  Kenneth, S. C. Membranes ions and impulses. (University of California Press, Los Angeles, 1972).
• [26]   Gabriel,  S.,  Lau,  R. W.,  Gabriel,  C. The dielectric properties of biological tissues: II. Measurement in the frequency range 10 Hz to 20 GHz. Phys. Med. Biol. 41, 2251–2269 (1996). https://doi.org/10.1088/0031-9155/41/11/002
• [27]   Gabriel,  S.,  Lau,  R. W.,  Gabriel,  C. The dielectric properties of biological tissues: III. Parametric models for the dielectric spectrum of tissues. Phys. Med. Biol. 41, 2271–2293 (1996). https://doi.org/10.1088/0031-9155/41/11/003
• [28]   Herculano-Houzel,  S. The human brain in numbers: a linearly scaled-up primate brain. Front. Hum. Neurosci. 3, 31 (2009). https://doi.org/10.3389/neuro.09.031.2009
• [29]   Bernard,  C.,  Jonston,  D. Distance dependent modifiable threshold for action potential back-propagation in Hippocampal dendrites. J. Neurophysiol. 90, 1807–1816 (2003). https://doi.org/10.1152/jn.00286.2003
• [30]   Froemke,  R. C.,  Letzkus,  J. J.,  Kampa,  B. M.,  Hang,  G. B.,  Stuart,  G. J. Dendritic synapse location and neocortical spike-timing-dependent plasticity. Front. Synaptic Neurosci. 2, 29 (2010). https://doi.org/10.3389/fnsyn.2010.00029
• [31]   Palmer,  L. M.,  Stuart,  G. J. Membrane potential changes in dendritic spines during action potentials and synaptic input. J. Neurosci. 29, 6897–6903 (2009). https://doi.org/10.1523/JNEUROSCI.5847-08.2009
• [32]   Stuart,  G. J.,  Spruston,  N. Dendritic integration: 60 years of progress. Nat. Neurosci. 18, 1713–1721 (2015). https://doi.org/10.1038/nn.4157
• [33]   Spruston,  N. Pyramidal neurons: Dendritic structure and synaptic integration. Nat. Rev. Neurosci. 9, 206–221 (2008). https://doi.org/10.1038/nrn2286
• [34]   Bourne,  J.,  Harris,  K. M. Do thin spines learn to be mushroom spines that remember? Curr. Opin. Neurobiol. 17, 381–386 (2007). https://doi.org/10.1016/j.conb.2007.04.009
• [35]   Tønnesen,  J.,  Nägerl,  U. V. Dendritic spines as tunable regulators of synaptic signals. Front. Psychiatry 7, 101 (2016). https://doi.org/10.3389/fpsyt.2016.00101
• [36]   Kuczewski,  N.,  Porcher,  C.,  Lessmann,  V.,  Medina,  I.,  Gaiarsa,  J.-L. Back-propagating action potential. Commun. Integr. Biol. 1, 153–155 (2008). https://doi.org/10.4161/cib.1.2.7058
• [37]   Stuart,  G. J.,  Häusser,  M. Dendritic coincidence detection of EPSPs and action potential. Nat. Neurosci. 4, 63–71 (2001). https://doi.org/10.1038/82910
• [38]   Bloodgood,  B. L.,  Sabatini,  B. L. Ca²⁺ signaling in dendritic spines. Curr. Opin. Neurobiol. 17, 345–351 (2007). https://doi.org/10.1016/j.conb.2007.04.003
• [39]   Zhai,  S.,  Ark,  E. D.,  Parra-Bueno,  P.,  Yasuda,  R. Long-distance integration of nuclear ERK signaling triggered by activation of a few dendritic spines. Science 342, 1107–1111 (2013). https://doi.org/10.1126/science.1245622
• [40]   Lee,  S.-J. R.,  Escobedo-Lozoya,  Y.,  Szatmari,  E. M.,  Yasuda,  R. Activation of CaMKII in single dendritic spines during long-term potentiation. Nature 458, 299–304 (2009). https://doi.org/10.1038/nature07842
• [41]  Campanac, E., Debanne, D. Spike timing-dependent plasticity: A learning rule for dendritic integration in rat Ca1 pyramidal neurons. J. Physiol. 586, 779–793, (2008). https://doi.org/10.1113/jphysiol.2007.147017
• [42]   Berry,  K. P.,  Nedivi,  E. Spine Dynamics: Are they all the same? Neuron 96, 43–55 (2017). https://doi.org/10.1016/j.neuron.2017.08.008
• [43]   Lüscher,  C.,  Nicoll,  R. A.,  Malenka,  R. C.,  Muller,  D. Synaptic plasticity and dynamic modulation of the postsynaptic membrane. Nat. Neurosci. 3, 545–550 (2000). https://doi.org/10.1038/75714
• [44]   Korkotian,  E.,  Holcman,  D.,  Segal,  M. Dynamic regulation of spine–dendrite coupling in cultured hippocampal neurons. Eur. J. Neurosci. 20, 2649–2663 (2004). https://doi.org/10.1111/j.1460-9568.2004.03691.x
• [45]   Araya,  R. Input transformation by dendritic spines of pyramidal neurons. Front. Neuroanat. 8, 141 (2014). https://doi.org/10.3389/fnana.2014.00141