2022 Volume 19 Article ID: e190026
2022 Volume 19 Article ID: e190026
Ciliates are swimming microorganisms in aquatic environments. Habitats where ciliates accumulate include nutrient-rich solid–liquid interfaces such as pond bottom walls and waterweed surfaces. The ciliates stay near the walls to survive. We investigated the dynamics of the near-wall behavior of ciliates. In experiments, the ciliates were made to slide on a flat wall of glass substrate. When encountering the wall, the wall-side cilia of the cells stop their motion and lose their propelling activity, which indicates that the ciliates have a mechano-sensing system for cilia beating. Based on the experimental results, we hypothesized that the ciliary thrust force that propels the cell body becomes asymmetric, and the asymmetry of the thrust force generates a head-down torque to keep the cell sliding on the wall. To prove this hypothesis, we performed numerical simulations by using a developed hydrodynamic model for swimming ciliates. The model revealed that the loss of cilia activity on the wall side physically induces a sliding motion, and the aspect ratio of the cell body and effective cilium area are critical functions for the sliding behavior on a wall. In addition, we investigated the stability of the sliding motion against an external flow. We found that ciliates slide upstream on a wall. Interestingly, the dynamics of this upstream sliding, called rheotaxis, were also explained by the identical physical conditions for no-flow sliding. Only two simple physical conditions are required to explain the dynamics of ciliate survival behavior. This review article is an extended version of the Japanese article, Fluid Dynamic Model Reveals a Mechano-sensing System Underlying the Behavior of Ciliates, published in SEIBUTSU BUTSURI Vol. 61, p. 16–19 (2021).
Ciliates, one class of eukaryotic unicellular organisms, are essential for maintaining aquatic ecosystems. Quantifying their behaviors in water environments provides us with a detailed understanding of ecosystems. To identify the characteristic dynamics of ciliate behavior in nature, we performed microscopy observations and hydrodynamic simulations on swimming ciliates close to a wall and in a shear flow. As a result, mechano-sensing of cilia and an ellipsoidal cell shape dynamically described the survival behavior of ciliates efficiently. The physical approach revealed a survival strategy for swimming microorganisms.
Microorganisms are found everywhere on Earth, both in the ground and in water, and play an essential role in maintaining ecosystems [1–5]. They have survived in harsh natural environments by optimizing their biological functions and behavioral patterns. Understanding the principles of their behavior can enhance our knowledge of ecosystems and the survival strategies of microorganisms in evolution.
Although unicellular organisms do not have a nervous system, they sometimes behave in a way that is efficient for survival as if they have a will. This seems mysterious. What determines the behavior of microorganisms? The answer is reactive behaviors against stimuli that they receive from the extracellular environment. The stimuli can include concentration gradients of chemical substances, temperature gradients, light, flows, and contact with objects. For instance, microorganisms move toward prey by sensing the chemicals emitted by nutrients, and photosynthetic microorganisms move toward light, known as chemotaxis and phototaxis, respectively [6–11]. To elucidate the response mechanisms to collision, contact and flow, we must focus on an initial physical stimulus. Specifically, since contact with a boundary and an external flow can directly affect the propelling speed and direction without biochemical sensing systems, it is necessary to consider the physical dynamics of microorganisms in response to kinetic effects.
Among microorganisms, eukaryotic unicellular organisms are called protists. One class of protists, ciliates, live in ponds and swamps and are the main organisms inhabiting freshwater [12–16]. Ciliates are characterized by the presence of hair-like organelles called cilia on their entire body surface. Ciliary beating propels these bodies freely in bulk water [17–21]. During life, ciliates accumulate close to oxygen–rich liquid–air interfaces, which is often seen in experimental cultures [22,23]. On the other hand, in nature, ciliates are also seen close to solid–liquid interfaces such as the bottoms of ponds and swamps and the surfaces of stones and water plants [24–28]. Many ciliates tend to accumulate close to these “walls” to obtain sedimented nutrients such as organic matter [29–32]. While the qualitative property of this wall preference has been clarified, the mechanism remains unclear. How do swimming ciliates such as Paramecium and Tetrahymena stay near a wall? (Fig. 1)

Snapshot of T. pyriformis sliding on a glass surface. Scale bar is 20 μm.
In addition to wall preference, another mysterious property of ciliates, rheotaxis, was reported over 100 years ago [17]. Rheotaxis is a well-known property of freshwater fish living in a river, which swim against currents [33–38]. To avoid being swept away by a flow from a comfortable environment where the swimming organisms grow easily, they must resist the flow. Although the mechanisms between fish swimming and cell swimming are totally different in terms of fluid dynamics, both swimming organisms interestingly show the same resistive property against external flow. While the rheotaxis of mammalian sperm and bacterial cells was quantified by controlled experiments and mathematical simulations, the dynamics affecting the rheotaxis of ciliates have been unclear for 100 years.
In this review, we introduce a mechanical model of microbial swimming and use it to explain the dynamics using the behaviors of ciliates, which occur close to a wall and in an external flow [39–42].
Lifestyles and cell shapes of ciliates are diverse. The ciliate called Lacrymaria, which has an extendable neck and an oral apparatus on the distal end of the neck, extends the neck to 8 times longer than the cell body to catch a food source [43–45]. Euplotes have many foot-like structures termed cirrus, using which they walk on solid surfaces. They occasionally stop and create a flow parallel to the wall to feed on the food [46,47]. On the other hand, Vorticella does not move by adhering to solid surfaces with their stalk and feed by creating a feeding flow toward the surface. Stenter adheres and feeds similarly to Vorticella [48] but swims and searches for suitable sites for survival depending on the external environment [49,50]. In addition, the Spirostomum quickly contracts when it senses an extracellular stimulation. The flow induced by the contraction introduces other neighboring cells alert to the danger [51]. The cellular shapes of ciliates have diverse, not only the commonly seen oblate ellipsoid but conical, cylindrical, thin-film, string-like, branched, and even a well-developed pleated structure [52]. In this review, we focus on simple swimming ciliates with a cell shape like an oblate ellipsoid, such as Paramecium and Tetrahymena.
When ciliates are swimming, cilia beatings on a cell body are synchronized, which is called metachronal wave. The metachronal wave generates more stable flow than a stroke of single cilium and reduces the energy expenditure required for beating [53,54]. For some ciliates, the ciliary beat frequency is heterogeneous on the cell body and correlates to ciliate swimming speed [19]. The cilia on ciliates beat in a direction slightly oblique to the cell’s anterior-posterior axis [55]. Marumo et al. observed 3D helical swimming trajectories of Tetrahymena and confirmed the relationship between cilia beating pattern and the 3D trajectories experimentally [56].
Regarding interaction of ciliates with a boundary, Ferracci et al. observed Tetrahymena being entrapped at liquid-air interfaces as well as solid-liquid interfaces [22]. Manabe et al. numerically showed the entrapment comes from two parameters of cell shape which are fore-and-aft asymmetricity and constriction [23]. When ciliates are confined in solid-liquid boundaries, they show interesting responses. Paramecium in a narrow capillary tends to escape from the closed edge of the capillary defined as a dead-end [57]. Paramecium in a narrow rectangular channel changes behaviors: ballistic motion, meandering and self-bending [20]. Tetrahymena between two flat plates with a small angle tends to escape from the narrow side of space by hydrodynamic effect [58]. Tetrahymena in a small water droplet swims in a circular trajectory along the boundary of the droplet [21]. Once released from the droplet to the bulk, they continue to swim circularly with the diameter and period which are the same when swimming in the droplet.
While the above studies focus on a behavior of a single cell, collective dynamics of ciliates suspension also has been investigated. Shallow suspensions of swimming microorganisms create collective convection driven by concentration of them and form spatial patterns in a petri dish. This phenomenon is called a bioconvection. The bioconvection has been observed in suspensions of Paramecium and Tetrahymena, which have been analyzed as a macroscopic phenomenon with a convection–diffusion equation [59–62].
In 1952, Lighthill proposed a simple fluid model of microbial swimming assuming a steady Stokes flow [63]. The model, called the Squirmer model, has been developed by many researchers [64–68]. The superiority of this model lies in the fact that it divides the swimming types of microorganisms into three major patterns, independent of the species, according to the shape of the flow field generated by the microorganisms during swimming. This makes it possible to compare and discuss the swimming motions of microorganisms across species. Bacteria such as Escherichia coli and Bacillus subtilis have flagella directed toward the rear of their bodies and move like a screw boat (Fig. 2, left row). Pullers (Fig. 2 right row) such as Chlamydomonas or Euglena use flagella attached to the front of their bodies to move forward like hands doing a breaststroke. Neutral swimmers (Fig. 2 center row) such as Paramecium or Tetrahymena swim by beating cilia along their entire body surface. This simple model reproduces well the actual surrounding flow fields generated by microorganisms. It has often been used as a model to describe the long-range hydrodynamic interactions of microswimmers in multibody systems such as microbial suspensions [69–73]. We developed a squirmer model to evaluate the mechanical approach to ciliate swimming.

Schematics of cell swimming patterns. Top and bottom row represent actual cells and hydrodynamic models, respectively [41].
How does the squirmer model behave close to a boundary? When squirmers approach a solid boundary, a puller swims parallel to the boundary, but a pusher and a neutral swimmer swim away from the boundary due to repelling hydrodynamic interactions [74–78]. However, actual flagellar cells, which are described as pushers, glide on the wall [79–81]. In previous research, a complicated swimming model, with an elongated body shape and beating flagella, was required to reproduce the gliding of flagellar cells because short-range boundary interaction effects and a squirmer model are specialized for long-range hydrodynamic interactions. Namely, the wall interactions of microswimmers are not as simple as when swimming in bulk water. Ciliates, considered neutral swimmers, are known to accumulate close to walls as well, but the swimming motions of individual ciliates close to a wall have not been observed quantitatively. Therefore, we still did not know the differences between a neutral swimmer and a real ciliate, which should provide essential factors for the accumulation of ciliates.
The next question concerns rheotaxis. How does a squirmer model behave in an external flow? Assuming a continuous flow at a low Reynolds number, the squirmer would be just swept away and its orientation not affected by the flow. To change the orientation toward flow, we should realistically consider a shear flow, which rotates the orientations, and being close to a wall, which originates a shear flow. Theoretically, a puller swims against a shear flow close to a wall due to hydrodynamic interaction [82,83]. Indeed, Chlamydomonas shows rheotaxis [84,85]. A pusher does not show rheotaxis, but some actual flagellar cells are known to swim upstream [86–93]. A detailed swimming model involving dynamic flagellum found that the rheotaxis of a pusher comes from a contact interaction between an elongated cell shape and a wall. While a neutral swimmer, as expected from the wall repulsion, cannot swim against a shear flow, actual ciliates show rheotaxis [17]. We believe the ciliate rheotaxis can be understood with the detailed swimming model as well as the flagellar cells.
We investigated the dynamics under the swimming motion of ciliates near a wall by comparing an actual ciliate with a neutral swimmer. The model organisms Paramecium caudatum and Tetrahymena pyriformis were observed from the direction perpendicular to the wall, and it was found that they both slid along the wall (Fig. 3A, B) [39]. These experimental results are consistent with the fact that ciliates prefer staying close to walls. On the other hand, it is known from fluid simulations that a neutral swimmer receives the orientational torque generated by its own flow from the wall and bounces back, which clearly contradicts the experimental results. A normal neutral swimmer model is not sufficient to describe the wall preference or sliding dynamics. Therefore, to investigate more detailed wall interactions of ciliates, we performed microscopic observations of the swimming ciliates and a quantitative comparison between the actual ciliates and the model. To find the physical mechanism that causes the discrepancy between experiment and theory, we visualized the behavior of cilia beating near the wall and the flow around the cells. The cilia in contact with the wall lost their motility significantly (Fig. 3C). The flow field between the cell and the wall (the bottom area) was measured by using probe beads and particle image velocimetry (PIV). As a result, the cilia-induced flow in the bottom area was around 90% slower than that in the top area [39]. In other words, the thrust force caused by the cilia wading through the fluid is suppressed in the bottom area. From the above experimental results, we can hypothesize that the thrust force around the cell becomes asymmetric, and torque is continuously applied to the cell body to direct the cell orientation to the wall (Fig. 3D). To verify whether this hypothesis is physically realistic, we incorporated this condition into the fluid model and performed numerical calculations.
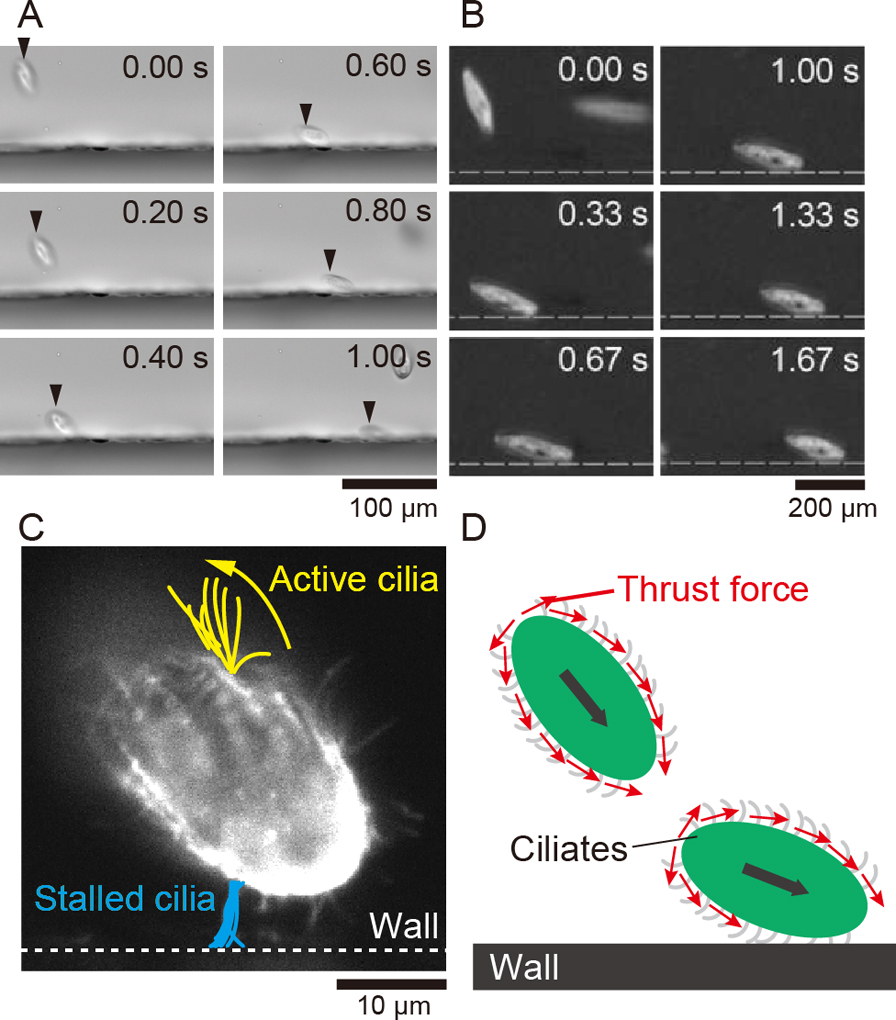
Observations of sliding ciliates. A: Snapshots of sliding T. pyriformis. B: Snapshots of sliding P. caudatum. C: Multilayered visualized cilia. D: Schematic illustration of thrust force around ciliates encountering a wall [41].
A three-dimensional boundary element method (BEM) was used for the simulation [65]. In this model, the surface of a spherical or ellipsoidal body defined as a rigid body is divided into meshes, and the thrust force of ciliated swimmers is applied to the outside of the body surface (Fig. 4A). In this model, the ellipticity of the shape of the swimmer can be changed arbitrarily. The uniform thrust force on the swimmer surface in the spherical shape represents the flow field around the neutral swimmer. Namely, this model involves the hydrodynamic feature of the neutral swimmer. Under the assumption of Stokes flow, the overall flow field is calculated by superimposing the flow field converted from the thrust force by using the Oseen tensor. The hydrodynamic interaction from the wall is incorporated by using the mirror-image method [94].

Numerical simulation setup and results [41].
To introduce the hypothesis obtained from the experiment, we defined a stop-beating area (SBA) on the wall to disturb the thrust force of the cilia contacting a wall (Fig. 4B); the thrust force in the SBA disappears, and the thrust force around the swimmer becomes asymmetric between the top and the bottom. The length of this region corresponds to the length of the cilia on the cell. Figure 4C shows numerical calculations for swimmers approaching a wall. The spherical swimmers, whose thrust force is symmetric, are repelled from the wall (Fig. 4C, upper left). When the shape was changed to an oblate ellipsoid, which is more similar to an actual ciliate, the swimmers were repelled in the same way (Fig. 4C, upper right). When the SBA was added to reproduce the asymmetric thrust force, the spherical swimmer did not repel from the wall but remained stationary on the wall (Fig. 4C, lower left). In the case of the ellipsoid with an SBA, the swimmer finally slid along the wall, as in the experiment (Fig. 4C, lower right). This result confirms our experimental hypothesis and suggests that the sliding motion of ciliates depends on the cell shape.
Why does the cell shape make a difference? The reason can be explained by examining the three separated torques applied to the sphere and ellipsoid swimmers. First, the torque is due to the repulsive flow from the wall (Figure 5, left row). Second, the torque is generated by the asymmetric thrust force (Figure 5 center row). Third, the torque is due to the elastic collision from the wall (Figure 5 right row). The first and second torques act in opposite directions. The third torque of the collision depends on the cell shape. In the case of a spherical swimmer, the collision force vector passes through the center of mass, so no torque is generated. When all the torque elements are combined, the swimming orientation will either be in the direction of vertically heading to the wall or away from the wall. On the other hand, an ellipsoidal swimmer generates a torque because the collision force vector does not pass through the center of mass. Thus, the third torque is added, which allows the ellipsoidal swimmer to maintain a balanced orientation and to slide on a wall. This balanced state is independent of the angle of incidence to a wall. Surprisingly, there are only two parameters for the sliding motion of the ciliates: the aspect ratio of the ellipsoid shape and relative length of cilia to the cell body, i.e., the size of the region where the thrust force disappears. The behavior of the swimmers in contact with the wall is roughly classified into Leaving, Sliding, and Stopping (Fig. 6A), and the phase diagram for the above two parameters shows that the swimmers exhibit sliding motion as the aspect ratio increases (Fig. 6B) [40]. The parameters of actual ciliates observed in the experiment for P. caudatum and T. pyriformis are included in the sliding region of the phase diagram, which supports the generality of the mechanism.

Schematics of torques involved in a ciliary swimmer contacting a wall [41].

Diagram of reactive motions of a ciliary swimmer [41].
We consider the swimming motion of ciliates under a shear flow close to a wall. As mentioned above, without an external flow, T. pyriformis slides on a wall. We observed T. pyriformis under a regulated shear flow with a microfluidic channel and a pressure controller. As the shear rate increased from zero, the cell orientations were gradually aligned to a flow direction and slid upstream on a wall. We found out that T. pyriformis showed rheotaxis only close to a wall. When T. pyriformis were swimming far from a wall or the shear rate was larger than a certain value, they were just swept away downstream. Using a light-sheet microscope, we visualized the cilia of ciliates on a wall under a shear flow. The cilia activity was asymmetric as well as under no-flow conditions. Therefore, the dynamics of the ciliate rheotaxis near a wall can be discussed in the same manner as the sliding motion without flow.
We performed numerical simulations of the swimming ciliates under a shear flow with the model in the former section [42]. As expected from the previous result, the swimmers without the SBA repelled from the wall and were swept away downstream. In the case of swimmers involved with the SBA as an asymmetric cilia activity, they could stay on the wall in the flow, but after a while the behaviors changed dependently on the cell shape. The spherical swimmer was swept downstream because the swimmer body was rotated by the shear flow, and the swimmer could not maintain the swimming orientation to the wall. The ellipsoidal swimmer slid upstream on the wall. Even if the ellipsoidal swimmer started to swim downstream, the swimming direction was oriented upstream, and it moved against the flow. The dynamics under this rheotaxis reproduced in the simulation were explained by considering the 3-dimensional torques. We found that only identical physical factors to explain the sliding motion were required for rheotaxis.
The sliding motion of ciliates on walls and near-wall rheotaxis are induced by two simple physical factors: the asymmetry of the thrust force by beating cilia and the ellipsoid shape of the cell. We have not yet been able to identify the cause of the ciliated beating stopping on contact with the wall. Whether the movement is mechanically impeded, whether the cilia themselves act as stress sensors, or whether there are other causes is an issue that we will pursue in the future. Here, the seemingly complex behaviors of microorganisms were based on simple physical mechanisms. We believe this result was obtained due to collaboration between physical and biological approaches, which will illuminate unclear dynamics of interesting behaviors.
All authors declare that they have no conflicts of interest.
T.O. wrote the initial manuscript. Y.N. and M.I. revised the manuscript.
We thank all the collaborators, including Mr. Junichi Manabe, Prof. Takuji Ishikawa, Prof. Shigenori Nonaka, and Dr. Atsushi Taniguchi. This work is supported by the Human Frontier Science Program LT000013/2019-C (T.O.) and JSPS KAKENHI grant Nos. 26707020, 21K03855, 22H05678 (M.I.), 21H05308 (Y.N.).