実現半分散を用いた資産配分問題

概要

近年，期待リターンの推定値を用いずに，リスクのみを考慮して資産配分を決定するリスクベース・ポートフォリオが注目されている．いくつかの先行研究は，リスクベース・ポートフォリオにおいて，従来の日次の分散などを用いるよりも，実現分散（realized variance, RV）や実現バイパワーバリエーション（realized bipower variation, BPV）といった，高頻度データから算出されるリスク指標を用いた場合に，より高いパフォーマンスが得られることを示している．一方，高頻度データを用いて資産の下方リスクを考慮するために，Barndorff-Nielsen et al. (2008)は日中の下方変動のみから算出されるリスク指標である実現半分散（realized semivariance, RS）を提案し，米国市場において実現半分散が日次リターンとの負の相関を有するとともに，高い自己相関も有することを示した．しかし，これらの特徴を資産配分問題に応用し，その有用性を検証した論文は筆者らの知る限り存在しない．そこで本研究では，実現半分散を用いて，国内株式，国内債券，国内不動産の3資産を対象としたリスクベース・ポートフォリオを構築し，従来のリスク指標を用いる場合と運用パフォーマンスを比較する．具体的には，2006年1月5日から2020年8月31日のTOPIX，長期国債先物，東証REIT指数の3資産の日中リターンを用いて，Bollerslev et al. (2020)の推定方法をもとに実現半分散を用いた分散共分散行列を推定し，リスクベース・ポートフォリオ（ボラティリティ・インバース，リスク最小化，リスクパリティ）において，従来のリスク指標（RV，BPV，日次の分散，下方半分散）を用いた場合に比べて高い運用パフォーマンスが得られることを示した．また，リターンの要因分解によって，実現半分散を用いた分散共分散行列において共分散よりも分散の方がパフォーマンスに寄与することが分かった．さらに，リスク指標の推定期間や高頻度データの観測間隔，投資ウィンドウについて感度分析を行った結果，実現半分散を用いた場合のアウトパフォーマンスが頑健であることも確認した．

1 研究の背景と目的

ポートフォリオにおける資産配分を決定する問題を資産配分問題とよび，投資信託や年金基金等の運用を行う投資家にとって非常に重要な役割を果たしている．近年，伝統的な平均分散アプローチに代わり，予測が困難な期待リターンの推定値を用いずに，一般的に推定が容易とされるリスクのみを考慮して資産配分を決定するリスクベース・ポートフォリオが注目されている．Fleming et al. (2003)やSharma and Vipul (2016)は，リスクベース・ポートフォリオにおいて，従来の日次の分散などを用いるよりも，実現分散（realized variance, RV）や実現バイパワーバリエーション（realized bipower variation, BPV）といった，高頻度データから算出されるリスク指標を用いた場合に，より高いパフォーマンスが得られることを示している．しかしRVやBPVは，正の日中リターンもリスクとして捉えることから，リスクを過大に評価してしまい，ポートフォリオ構築に適用した場合にリターンを損なう可能性がある．一方，高頻度データを用いて資産の下方リスクを考慮するために，Barndorff-Nielsen et al. (2008)は日中の下方変動のみから算出されるリスク指標である実現半分散（realized semivariance, RS）を提案し，米国市場において実現半分散が日次リターンとの負の相関を有するとともに，高い自己相関も有することを示した．したがって，実現半分散を用いてリスクベース・ポートフォリオを構築することで，従来のリスク指標を用いた場合に比べて高いパフォーマンスが得られると考えられる．しかし，そのような検証を行っている論文は，筆者らの知る限り存在しない．表1に，主な先行研究との違いをまとめておく．

表1 主な先行研究との比較

	Fleming et al. (2003)	Halbleib and Voev (2011)	Sharma and Vipul (2016)	本研究
投資資産	株式・債券・金	株式	株式	株式・債券・不動産
ポートフォリオ	リスク最小化・ 期待リターン制約付き リスク最小化	リスク最小化・ 期待リターン制約付き リスク最小化	リスク最小化・ リスクパリティ・ 最大分散度	ボラティリティインバース・ リスク最小化・ リスクパリティ
市場（国）	米国	米国	インド	日本
バックテスト期間	1984/1--2000/11	2001/1--2006/6	2009/1--2013/2	2006/1--2020/8
高頻度データの観測間隔	5分	5分	5分	1〜15分
比較対象
日次リターンの分散，共分散	○	×	○	○
実現分散（RV）	○	○	○	○
実現バイパワー 　バリエーション（BPV)	×	×	○	○
実現半分散（RS）	×	×	×	○

そこで本研究では，実現半分散を用いてリスクベース・ポートフォリオを構築し，従来のリスク指標を用いる場合と運用パフォーマンスを比較する．具体的には，2006年1月5日から2020年8月31日のTOPIX，長期国債先物，東証REIT指数の3資産の日中リターンを用いて，Bollerslev et al. (2020)の推定方法をもとに実現半分散を用いた分散共分散行列を推定し，リスクベース・ポートフォリオ（ボラティリティ・インバース，リスク最小化，リスクパリティ）において，従来のリスク指標（RV，BPV，日次リターンの分散，下方半分散）を用いた場合に比べて高い運用パフォーマンスが得られた．また，リターンの要因分解によって，実現半分散を用いた分散共分散行列において共分散よりも分散の方がパフォーマンスに寄与することが分かった．さらに，リスク指標の推定期間や高頻度データの観測間隔，投資ウィンドウについて感度分析を行った結果，実現半分散を用いた場合のアウトパフォーマンスが頑健であることも確認した．

本論文の構成は以下の通りである．2節において，高頻度データによって算出されるリスク指標の導出方法や理論的な背景について説明する．3節では，本研究で扱うリスクベース・ポートフォリオについて説明する．4節では，バックテストやリターンの要因分解を行うことで，リスクベース・ポートフォリオにおいて実現半分散を用いる有用性について議論する．5節では感度分析を行い，リスク指標の推定期間や，高頻度データの観測間隔，投資ウィンドウの変化がパフォーマンスに与える影響について考察する．最後に，6節において結論と今後の課題を述べる．

2 高頻度データに基づくリスク指標

本節では，高頻度データから算出されるリスク指標の導出方法や理論的背景について説明する．一部の記述においては，柴田(2008)，Barndorff-Nielsen and Shephard (2004a,b)，Barndorff-Nielsen et al. (2008)，Bollerslev et al. (2020)による表記方法を用いる．

2.1 実現分散

Andersen and Bollerslev (1998)により，モデルに依存しないボラティリティの推定値である実現分散（realized variance，RV)が提案された．¹以下に実現分散の導出方法を示す．

第$i$日の日次リターンを対数価格$p^*(i)$を用いて   

$$r_i=p^*(i)-p^*(i-1)$$ (1)

と表し，第$i$日内の時点$j$における日中リターンを   

$$r_{j,i}=p^*\left(i-1+\frac{j}{M}\right)-p^*\left(i-1+\frac{j-1}{M}\right),\qquad j=1,2,...,M$$ (2)

と表す．ここで$M$は1日あたりの日中リターンの観測回数である．第$i$日のRVは，日中リターンの二乗値を1日にわたって観測回数分足し合わせたものであり，   

$$RV_i=\sum_{j=1}^Mr^2_{j,i}$$ (3)

と表す．このようにRVの導出は非常に単純であるが，RVをボラティリティの推定値と考える理論的な裏付けが存在する．$p^*$が式(4)のような確率過程に従っているものとする．   

$$p^*(t)=p^*(0)+\int_{0}^{t} \mu(s)ds+\int_{0}^{t} \sigma(s)dW(s)$$ (4)

ここで，$\mu(s)$はドリフト項，$W(s)$は標準ウィーナー過程，$\sigma(s)$は瞬間的ボラティリティ²である．ある一定期間のボラティリティは，この瞬間的ボラティリティの二乗の累積値（累積ボラティリティ）として与えられる．つまり第$i$日の累積ボラティリティ$\sigma^{2*}(i)$は，式(5)のように定義される．   

$$\sigma^{2*}(i)\equiv \int_{i-1}^i\sigma^2(s)ds$$ (5)

ここで$p^*$がセミ・マルチンゲールであるという仮定をおくと，RVは観測回数を高頻度にしていくにつれ累積ボラティリティに確率収束するという性質がある．つまり$M \rightarrow \infty$のとき，RVは下記のように確率収束し，累積ボラティリティの一致推定量となる．³   

$$RV_i \stackrel{p}{\rightarrow} \sigma^{2*}(i)$$ (6)

また任意の2資産の共分散についても高頻度データから算出することができる．例えば，資産$\mathcal{A}_1$と資産$\mathcal{A}_2$の実現共分散は式(7)のように計算できる．   

$$RCV_i^{\mathcal{A}_1,\mathcal{A}_2}=\sum_{j=1}^M r^{\mathcal{A}_1}_{j,i}r^{\mathcal{A}_2}_{j,i}$$ (7)

ここで$r^{\mathcal{A}}_{j,i}$は，資産$\mathcal{A}$の第$i$日内の時点$j$における日中リターンを表す．

したがって，式(3)と式(7)のRVとRCVをそれぞれ分散共分散行列における分散部分と共分散部分に当てはめることで，RVを多変量に拡張することができる．具体的には，第$i$日，時点$j$での日中リターンから成る${N\times1}$ベクトル$\boldsymbol{r_{j,i}}=\{r_{j,i}^{\mathcal{A}_1},r_{j,i}^{\mathcal{A}_2},...,r_{j,i}^{\mathcal{A}_N}\}^\top$を考える（$N$は資産数）．このとき，第$i$日の多変量RVは   

$$\boldsymbol{RV}_i=\sum_{j=1}^M\boldsymbol{r}_{j,i}\boldsymbol{r^\top}_{j,i}$$ (8)

のように計算される$N \times N$の行列として定義される．ここで，${N\times1}$の対数価格ベクトル$\boldsymbol{P^*}(t)$が式(9)の確率過程に従うと仮定する．   

$$\boldsymbol{P^*}(t)=\boldsymbol{P^*}(0)+\int_{0}^{t} \boldsymbol{\mu}(s) d s+\int_{0}^{t} \boldsymbol{\sigma}(s) d \boldsymbol{W}(s)$$ (9)

このとき$\boldsymbol{RV}_i$は，$M \rightarrow \infty$のとき，式(10)のように確率収束する．   

$$\boldsymbol{RV}_i \stackrel{p}{\rightarrow} \int_{i-1}^{i} \boldsymbol{\sigma}(s)\boldsymbol{\sigma}^\top(s) ds$$ (10)

2.2 実現バイパワーバリエーション

一般的に，実際の価格変動は不規則で急激な変動であるジャンプを含むと考えられており，式(4)のような確率過程では実際の価格変動を十分に記述できないことが指摘されている．よって対数価格$p^*$が式(11)のような，非連続なジャンプ過程$J(t)$を含む確率過程に従うと仮定する場合が多い．   

$$p^*(t)=p^*(0)+\int_{0}^{t} \mu(s)ds+\int_{0}^{t} \sigma(s)dW(s)+J(t)$$ (11)

Barndorff-Nielsen and Shephard (2004a)は，ジャンプ成分に対して頑健なリスク指標である，実現バイパワーバリエーション（realized bipower variation, BPV）を，式(12)のように定義した．   

$$BPV_i(u, v)=M^{1-\frac{u+v}{2}} \sum_{j=1}^{M-1}\left|r_{j, i}\right|^{u}\left|r_{j+1, i}\right|^{v}$$ (12)

特に$u=v=1$のとき，   

$$BPV_i(1,1)=\sum_{j=1}^{M-1}\left|r_{j, i}\right|\left|r_{j+1, i}\right|$$ (13)

である．本研究における4節以降の分析では，$u=v=1$の場合を実現バイパワーバリエーションとして扱う．

対数価格$p^*$が式(11)の確率過程に従うとき，$M \rightarrow \infty$でBPVは以下のように確率収束する．   

$$BPV_i(u,v) \stackrel{p}{\rightarrow} \mu_{u} \mu_{v} \int_{i-1}^{i} \sigma^{u+v}(s)ds$$ (14)

ここで，   

$$\mu_{x}=2^{\frac{x}{2}} \Gamma\left(\frac{1}{2}(x+1)\right) / \Gamma\left(\frac{1}{2}\right) ,\quad \Gamma(z)=\int_{0}^{\infty} t^{z-1} e^{-t} d t$$ (15)

である．特に，$\Gamma(1)=1,\quad\Gamma(\frac{1}{2})=\sqrt{\pi}$であるため，   

$$B P V_i(1,1) \stackrel{p}{\rightarrow} \mu_{1}^2 \int_{i-1}^{i} \sigma^{2}(s) d s = \frac{2}{\pi} \int_{i-1}^{i} \sigma^{2}(s) d s$$ (16)

となり，確率過程にジャンプが含まれる場合においても，BPVを計算することで，確率過程におけるボラティリティ項のみを抽出することができ，ジャンプ成分に対して頑健なリスク指標を計算することができる．⁴

さらに，Barndorff-Nielsen and Shephard (2004b)は，資産間の実現共分散についても，ジャンプ成分に対して頑健に推定できることを示した．例えば，資産$\mathcal{A}_1,\mathcal{A}_2$のBPVの共分散部分は以下のように計算できる．   

$$B P C V_{i}^{\mathcal{A}_1, \mathcal{A}_2}=\frac{1}{4} \sum_{j=1}^{M-1}\left(\left|r_{j, i}^{\mathcal{A}_1}+r_{j, i}^{\mathcal{A}_2}\right|\left|r_{j+1, i}^{\mathcal{A}_1}+r_{j+1, i}^{\mathcal{A}_2}\right|-\left|r_{j, i}^{\mathcal{A}_1}-r_{j, i}^{\mathcal{A}_2}\right|\left|r_{j+1, i}^{\mathcal{A}_1}-r_{j+1, i}^{\mathcal{A}_2}\right|\right)$$ (17)

したがって，式(13)，式(17)を用いることでBPVを多変量に拡張することができ，ジャンプに対して頑健な分散共分散行列を推定することができる．

ここで，対数価格ベクトル$\boldsymbol{P^*}(t)$が   

$$\boldsymbol{P^*}(t)=\boldsymbol{P^*}(0)+\int_{0}^{t} \boldsymbol{\mu}(s) d s+\int_{0}^{t} \boldsymbol{\sigma}(s) d \boldsymbol{W}(s)+\boldsymbol{J}(t)$$ (18)

のようなジャンプを含む確率過程に従うと仮定するとき，多変量に拡張したBPVは，式(19)のように確率収束する．   

$$\boldsymbol{BPV}_i \stackrel{p}{\rightarrow} \mu_{1}^2\int_{i-1}^{i} \boldsymbol{\sigma}(s)\boldsymbol{\sigma}^\top(s) ds = \frac{2}{\pi}\int_{i-1}^{i} \boldsymbol{\sigma}(s)\boldsymbol{\sigma}^\top(s) ds$$ (19)

本研究においては，式(18)における累積ボラティリティを算出するため，式(13)，式(17)によって計算されるBPVとBPCVを$\mu_{1}^{-2}(=\pi/2)$倍した値を用いる．

2.3 実現半分散

Barndorff-Nielsen et al. (2008)は，高頻度データを用いて資産の下方リスクを考慮するために，日中の下方変動のみから算出されるリスク指標である実現半分散（realized semivariance, RS）を提案した．本研究においては，下方変動のみから算出される$\rm{RS^-}$と，上方変動のみから算出される$\rm{RS^+}$を用いる．第$i$日における$\rm{RS^-}$と$\rm{RS^+}$はそれぞれ下記のように定義される．   

$$R S^{-}_i=\sum_{j=1}^{M} r_{j, i}^{2} 1_{\{r_{j, i} \leq 0\}},\quad R S^{+}_i=\sum_{j=1}^{M} r_{j, i}^{2} 1_{\{r_{j, i} \geq 0\}}$$ (20)

ここで，$1_{\{X\}}$は，下付き文字内の条件$X$が成り立っているときは 1，そうでないときは 0 となる指示関数である．対数価格$p^*$が式(11)の確率過程に従うとき，$M \rightarrow \infty$でRSは下記のように確率収束する．   

$$R S^{-}_i \stackrel{p}{\rightarrow} \frac{1}{2} \int_{i-1}^{i} \sigma^{2}(s) d s+\sum_{s \in \mathcal{S}_i}(\Delta Y(s))^{2} 1_{\{\Delta Y(s) \leq 0\}}$$ (21)

  

$$R S^{+}_i \stackrel{p}{\rightarrow} \frac{1}{2} \int_{i-1}^{i} \sigma^{2}(s) d s+\sum_{s \in \mathcal{S}_i}(\Delta Y(s))^{2} 1_{\{\Delta Y(s) \geq 0\}}$$ (22)

ここで$\mathcal{S}_i$は第$i$日においてジャンプが起こった時点の集合を表す．また$\Delta Y(s)$はジャンプの変動を表し，時点$t$までのジャンプの変動の総和が$J(t)$となる．つまり，RSは累積ボラティリティの半分と下方（上方）ジャンプの二乗の総和に確率収束することがわかる．

Barndorff-Nielsen et al. (2008)は，米国株式市場における個別銘柄のRSを算出し，RSが日次リターンとの負の相関を有するとともに，高い自己相関も有することを示した．さらに，GARCHモデルやGJR-GARCHモデルを用いた時系列分析において，変数としてRSを時系列モデルに追加した場合に，モデルにおけるフィッティング精度が向上することを示した．

さらに，Bollerslev et al. (2020)は，RSについても分散共分散行列の形式に拡張した．ベクトル$\boldsymbol{x}$に対して，$p(\boldsymbol{x})=\max\{\boldsymbol{x},0\},\quad n(\boldsymbol{x})=\min\{\boldsymbol{x},0\}$とすると，第$i$日の多変量RVは以下のような3つの行列に分解することができる．⁵   

$$\boldsymbol{RV}_i=\widehat{\boldsymbol{P}}_i+\widehat{\boldsymbol{N}}_i+\widehat{\boldsymbol{M}}_i$$ (23)

  

$$\begin{eqnarray}\widehat{\boldsymbol{P}}_i\ &=&\sum_{j=1}^{M} p\left(\boldsymbol{r}_{j, i}\right) p\left(\boldsymbol{r}_{j, i}\right)^{\top},\quad \widehat{\boldsymbol{N}}_i=\sum_{j=1}^{M} n\left(\boldsymbol{r}_{j, i}\right) n\left(\boldsymbol{r}_{j, i}\right)^{\top}\\\widehat{\boldsymbol{M}}_i\ &=&\sum_{j=1}^{M} \{p\left(\boldsymbol{r}_{j, i}\right) n\left(\boldsymbol{r}_{j, i}\right)^{\top}+n\left(\boldsymbol{r}_{j, i}\right) p\left(\boldsymbol{r}_{j, i}\right)^{\top}\}\end{eqnarray}$$ (24)

ここで，対数価格ベクトル$\boldsymbol{P^*}(t)$が式(18)の確率過程に従うと仮定し，ジャンプ成分に関する行列$\boldsymbol{P^{\dagger}}_i,\boldsymbol{N^{\dagger}}_i,\boldsymbol{M^{\dagger}}_i$を下記のように定義する．   

$$\begin{eqnarray}\boldsymbol{P^{\dagger}}_i\ &=&\sum_{j \in \mathcal{S}_i} p\left(\boldsymbol{r}_{j,i}\right) p\left(\boldsymbol{r}_{j,i}\right)^{\top},\quad \boldsymbol{N^{\dagger}}_i=\sum_{j \in \mathcal{S}_i} n\left(\boldsymbol{r}_{j,i}\right) n\left(\boldsymbol{r}_{j,i}\right)^{\top}\\\boldsymbol{M^{\dagger}}_i\ &=&\sum_{j \in \mathcal{S}_i} \{ p\left(\boldsymbol{r}_{j,i}\right) n\left(\boldsymbol{r}_{j,i}\right)^{\top} + n\left(\boldsymbol{r}_{j,i}\right) p\left(\boldsymbol{r}_{j,i}\right)^{\top} \}\end{eqnarray}$$ (25)

$\boldsymbol{X}[a,b]$を行列$\boldsymbol{X}$の$a$行$b$列の要素とすると，$M \rightarrow \infty$のときに，$\widehat{\boldsymbol{P}}_i, \widehat{\boldsymbol{N}}_i, \widehat{\boldsymbol{M}}_i$は以下のように確率収束する．   

$$\begin{eqnarray}\widehat{\boldsymbol{P}}_i[a, b] \ &\stackrel{p}{\rightarrow}& \int_{i-1}^{i} v_{a, s} v_{b, s} \psi\left(\rho_{a b, s}\right) d s+\boldsymbol{P^{\dagger}}_i[a, b],\quad \widehat{\boldsymbol{N}}_i[a, b] \stackrel{p}{\rightarrow} \int_{i-1}^{i} v_{a, s} v_{b, s} \psi\left(\rho_{a b, s}\right) d s+\boldsymbol{N^{\dagger}}_i[a, b]\\\widehat{\boldsymbol{M}}_i[a, b] \ &\stackrel{p}{\rightarrow}& -2\int_{i-1}^{i} v_{a, s} v_{b, s} \psi\left(- \rho_{a b, s}\right) d s+\boldsymbol{M^{\dagger}}_i[a, b]\end{eqnarray}$$ (26)

ここで，$\psi(\rho), \boldsymbol{c}_{t}, v_{a, t}, \rho_{a b, t}$は以下のように定義される．   

$$\psi(\rho)=(2 \pi)^{-1}\left(\rho \arccos (-\rho)+\sqrt{1-\rho^{2}}\right), \boldsymbol{c}_{t}=\boldsymbol{\sigma}(t) \boldsymbol{\sigma}(t)^{\top}, c_{ab,t}=\boldsymbol{c}_{t}[a,b], v_{a, t}=\sqrt{c_{aa,t}}, \rho_{a b, t}=\frac{c_{a b, t}}{v_{a, t} v_{b, t}}$$ (27)

本研究では上記の推定方法を用いて，日中の下方，上方変動のみから算出されるリスク指標である$\rm{RS^-}$, $\rm{RS^+}$をそれぞれ$\widehat{\boldsymbol{N}}, \widehat{\boldsymbol{P}}$の分散共分散行列の形式に拡張し，リスクベース・ポートフォリオに適用した場合のパフォーマンスについて分析を行う．

3 リスクベース・ポートフォリオ

本節では，本研究で扱うリスクベース・ポートフォリオにおける投資比率の決定方法について説明する．

近年，伝統的な平均分散アプローチに代わり，予測が困難な期待リターンの推定値を用いずにリスクのみを考慮して資産配分を決定するリスクベース・ポートフォリオが注目されている．以下，本研究で扱うリスクベース・ポートフォリオについて説明する．一部の記述においては，Kato and Hibiki (2020)による表記方法を用いる．

3.1 ボラティリティ・インバースポートフォリオ

ボラティリティ・インバースポートフォリオは，リターンの分散の逆数をウェイトとするポートフォリオである．$\boldsymbol{w}=(w_1,w_2,...,w_N)^\top$を資産への投資比率を表すベクトル，$N$を資産数，$\boldsymbol{\Sigma}$を分散共分散行列とすると，ボラティリティ・インバースポートフォリオにおける各資産のウェイトは以下のように決定される．   

$$w_{i}=\frac{\frac{1}{(\rm{diag}(\boldsymbol{\Sigma}))_{\mathit{i}}}}{\sum_{i=1}^{N} \frac{1}{(\rm{diag}(\boldsymbol{\Sigma}))_{\mathit{i}}}}$$ (28)

ここで，$\rm{diag}(\boldsymbol{\Sigma})$は，行列$\boldsymbol{\Sigma}$の対角ベクトルを表し，$(\cdot)_i$はベクトルの第$i$成分のみ取り出す演算記号である．

3.2 リスク最小化ポートフォリオ

リスク最小化ポートフォリオにおいては，式(29)のような投資比率制約の下で最適化を行い，ポートフォリオ全体のリスクを最小にするウェイトを算出する．ここで，$\boldsymbol{e}=(1,\ldots,1)^\top$ である．

  

$$\begin{eqnarray}\ \boldsymbol{\text{Minimize}} \ \ \ &\boldsymbol{w^\top}&\boldsymbol{\Sigma}\boldsymbol{w}\\\ \boldsymbol{\text{subject to}} \ \ &\boldsymbol{e}^\top& \boldsymbol{w} = 1,\quad \boldsymbol{w}\geq \boldsymbol{0} \\\end{eqnarray}$$ (29)

3.3 リスクパリティポートフォリオ

平均分散アプローチにおいて，期待収益率の推定が困難であることや，最適解のパラメータに対する感応度が高いという問題点を解決するため，Qian (2005)は各資産のポートフォリオのリスク寄与度を均等にするリスクパリティポートフォリオを提案した．

資産$i$に対する投資比率が微小変化したときのポートフォリオのリスクの変化量（限界リスク）を，ポートフォリオのリスク$\sigma_P$を用いて式(30)で定義する．   

$$MRC_i=\frac{\partial \sigma_P}{\partial w_i}$$ (30)

また，資産$i$に対するリスク寄与度を，限界リスクを用いて式(31)のように定義する．   

$$RC_i=w_i \cdot MRC_i=w_i \frac{\partial \sigma_P}{\partial w_i}=\frac{\partial \sigma_P}{\partial w_i/w_i}$$ (31)

ここで，ポートフォリオ全体のリスク$\sigma_P$を   

$$\sigma_P=\sqrt{\boldsymbol{w}^\top \boldsymbol{\Sigma} \boldsymbol{w}}$$ (32)

と表すと，資産$i$のリスク寄与度は式(33)のように計算できる．   

$$RC_i=w_i \frac{(\boldsymbol{\Sigma} \boldsymbol{w})_i}{\sqrt{ \boldsymbol{w}^\top \boldsymbol{\Sigma} \boldsymbol{w}}}$$ (33)

このリスク寄与度は，各資産の投資比率の相対変化に対するポートフォリオ全体のリスク感応度と解釈できる．またオイラーの斉次関数の定理より，このポートフォリオのリスク指標が一次斉次であれば式(34)が成立する．   

$$\sigma_P=\sum^{N}_{i=1} RC_i$$ (34)

式(34)は，リスク寄与度をすべての資産について足し合わせると，ポートフォリオ全体のリスクと等しくなるということを示しており，リスク寄与度はポートフォリオ全体のリスクを個々の資産ベースに分解した値と解釈できる．

リスクパリティポートフォリオの構築においては，すべての資産のリスク寄与度が均等になるように最適化を行う．具体的には式(35)のように，ポートフォリオ全体のリスクに占める各資産のリスク寄与度の割合と，資産数の逆数の誤差二乗和を最小化することで，すべての資産にリスク寄与度を均等に配分する投資比率を算出する．⁶   

$$\begin{eqnarray}\ \boldsymbol{\text{Minimize}}\ \ \ &\sum^N_{i=1}& \left( \frac{RC_i}{\sigma_P}-\frac{1}{N} \right) ^2 \\\ \boldsymbol{\text{subject to}}\ \ &\sum^N_{i=1}& w_i =1,\quad w_i \geq 0 \quad (i=1,\ldots,N) \\\end{eqnarray}$$ (35)

3.4 高頻度データから算出される分散共分散行列の半正定値性

資産配分問題においては，分散共分散行列$\boldsymbol{\Sigma}$は半正定値性が保証されている必要がある．Andersen et al. (2003)は，資産数$N$が1日あたりの日中リターンの観測回数$M$を上回らなければ，多変量RVの半正定値性が保証されることを示した．本研究において資産数は3であり，日中リターンの観測回数を上回ることはないため，多変量RVの半正定値性は保証され，同様にRSを用いた分散共分散行列の半正定値性も保証される．一方で，Barndorff-Nielsen and Shephard (2004b)は，BPVを多変量の行列形式に拡張した場合，その分散共分散行列の半正定値性が必ずしも保証されないことを指摘している．そこでBarndorff-Nielsen and Shephard (2004b)は，Rousseeuw and Molenberghs (1993)の固有値法を用いることで，多変量BPVを半正定値性行列に変換している．具体的には，行列$\boldsymbol{S}$の固有値を並べたベクトル$\boldsymbol{\Lambda}=(\lambda_1,\lambda_2,...,\lambda_N)^\top$の負の要素を全て$0$に変換したベクトル$\boldsymbol{\Lambda}^+=(\lambda_1^+,\lambda_2^+,...,\lambda_N^+)^\top$と，$\boldsymbol{S}$の固有ベクトル$\boldsymbol{\Gamma}$を用いて，$\boldsymbol{S}$を以下のように半正定値性行列$\boldsymbol{S}^+$に変換する．   

$$ \boldsymbol{S}^+ = \boldsymbol{\Gamma}^\top \mathrm{diag} (\boldsymbol{\Lambda}^+) \boldsymbol{\Gamma}$$ (36)

ここで，$\rm{diag}$$(\boldsymbol{\Lambda}^+)$は$\boldsymbol{\Lambda}^+$を対角要素にもつ行列である．Barndorff-Nielsen and Shephard (2004b)は，日中リターンの観測回数が大きくなるにつれ，多変量BPVの固有値は非負に収束していくため，式(36)によって変換された半正定値行列も，式(19)と同様に確率収束することを示した．

4 バックテスト

本節では，実務を想定したバックテストを行い，実現半分散を用いた場合と従来のリスク指標を用いた場合のパフォーマンスを比較することで，リスクベース・ポートフォリオにおいて実現半分散を用いた場合の有用性について議論する．⁷

4.1 テスト条件

• パフォーマンス計測期間：2006年1月6日から2020年8月31日（日次リターンを用いてパフォーマンスを算出した．）
• サンプル日数：3582日
• 対象資産⁸：TOPIX，長期国債先物（以下，JGBF），東証 REIT 指数（以下，REIT）
• リスク指標：$\rm{RV}$, $\rm{BPV}$, $\rm{RS^+}$, $\rm{RS^-}$, 日次リターンの分散共分散行列（$\rm{Var\_1m}$），日次リターンの下方半分散⁹（$\rm{Var^-\_1m}$，ボラティリティ・インバースのみ）¹⁰
• リスク指標の推定ウィンドウ：日中データを用いる場合は過去1日，日次データを用いる場合は過去1か月¹¹
• 高頻度データの観測間隔：5分¹²
• 使用したリスクベース・ポートフォリオ：ボラティリティ・インバースポートフォリオ（VI），リスク最小化ポートフォリオ（MR），リスクパリティポートフォリオ（RP）
• 通貨：JPY（日本円）
• リバランス時点：推定ウィンドウの最終時点

4.2 パフォーマンス評価指標

4.2.1 最大ドローダウン

バックテストの結果，実現したポートフォリオにおける最大の下落率のことである．$P(t)$は時点$t$におけるポートフォリオの保有金額，$T$はパフォーマンス計測期間の期間数を表す．   

$$\min_{\tau\in(0,T)}\left\{ \min_{t\in(0,\tau)}\left\{ \frac{P(\tau)-P(t)}{P(t)} \right\} \right\}$$ (37)

4.2.2 95%-VaR

バックテストの結果，実現したポートフォリオの収益率$r_P$の95%のVaRである．   

$$VaR(95\%)=\min \{V:P[-r_P>V] \leq 0.05 \}$$ (38)

4.2.3 95%-CVaR

バックテストの結果，実現したポートフォリオの収益率の95%のCVaRである．   

$$CVaR(95\%)=E[-r_P|r_P \leq -VaR(95\%)]$$ (39)

4.2.4 売買回転率

バックテストの結果，実現したポートフォリオにおける売買回転率を示す．$w_i^t$と$r_i^t$はそれぞれポートフォリオにおける資産$i$の第$t$日における投資比率と実現リターンを表す．   

$$Turnover =\frac{1}{T-1} \sum_{t=1}^{T-1} \sum_{i=1}^{N}\left|w_{i}^{t+1}-w_{i}^{t}\left(1+r_{i}^{t}\right)\right|$$ (40)

4.2.5 リスクリターン

バックテストの結果，実現したポートフォリオの平均収益率 $E[r_P]$ を収益率の標準偏差$SD[r_P]$で割ることによって，ポートフォリオの効率性を表した指標である．   

$$\frac{E[r_P]}{SD[r_P]}$$ (41)

4.3 高頻度データの取り扱い

本研究では，全ての資産のデータポイントをそろえて分析を行う．TOPIXや東証REIT指数などの指数値は，9:00から11:30と，12:30から15:00までデータが開示されているが，長期国債先物については，8:45から11:00，12:30から15:00の日中の取引に加え，15:30から翌5:25までの夜間取引も行われている．本研究では，全ての資産の取引時間が重複している，9:00から11:00と，12:30から15:00の日中データを分析対象とする．例えば基本分析においては，高頻度データの観測間隔は5分として分析を行うが，TOPIX，東証REIT指数については9:00, 9:05, ..., 10:55, 11:00, 12:30, 12:35, ..., 14:55, 15:00の指数値を使用し，長期国債先物については，9:00, 9:05, ..., 10:55, 11:00, 12:30, 12:35, ..., 14:55, 15:00の各データポイントにおいて，直近の歩み値から価格変化がないものとして， その直近の歩み値を使用する．なお，長期国債先物は，全てのデータポイントにおいて，期近物の歩み値を使用する．5節においては，感度分析として様々な観測間隔で高頻度データを取得しリスク指標を算出するが，例えば観測間隔を1分とした場合は，9:00, 9:01, ..., 10:59, 11:00, 12:30, 12:31, ..., 14:59, 15:00のデータポイントについて，5分の場合と同様の手順で，各資産の日中価格データを取得している．日中価格データが取得できなかったデータポイントについては，そのデータポイントから最も近い時点で取得できたデータを用いる．

4.4 リスク指標の統計量

表2に，分析対象資産の日次リターンやリスク指標の統計量を示す．$r$は終値ベースの日次リターン，$ACF_i$は$i$日のラグをとった自己相関を表し，1日と22日（1か月）のラグをとった自己相関を表に掲載している．なお，表記方法はBarndorff-Nielsen et al. (2008)を参考にした．なお，各指標において平均値から$3\times 標準偏差$以上離れている値は外れ値として除外した．表2より，$\rm{RS^-}$と日次リターンは強い負の相関を有することがわかり，Barndorff-Nielsen et al. (2008)の分析結果と一致した．また，リスク指標同士は強い正の相関を有しているが，$\rm{RS^+}$と$\rm{RS^-}$の相関係数は相対的に小さいことがわかる．資産別にみると，JGBFは価格変動が小さいため，リスク指標が他の資産に比べて極端に小さくなっている．自己相関については，BPVが相対的に高い値となったが，RSの自己相関は，Barndorff-Nielsen et al. (2008)が示したほど高い値にはならなかった．¹³

表2 各指標の統計量

TOPIX	平均	標準偏差	相関行列						$ACF_1$	$ACF_{22}$
$r$	$2.9\times10^{-4}$	$1.2\times10^{-2}$	1.00						0.01	$-$0.01
$r^2$	$1.4\times10^{-4}$	$2.4\times10^{-4}$	$-$0.04	1.00					0.16	0.12
RV	$1.2\times10^{-4}$	$1.2\times10^{-4}$	$-$0.07	0.60	1.00				0.43	0.22
$\rm{RS^+}$	$5.5\times10^{-5}$	$6.2\times10^{-5}$	0.49	0.39	0.62	1.00			0.23	0.13
$\rm{RS^-}$	$5.7\times10^{-5}$	$8.0\times10^{-5}$	$-$0.54	0.43	0.75	0.08	1.00		0.24	0.12
BPV	$7.0\times10^{-5}$	$8.1\times10^{-5}$	$-$0.11	0.51	0.88	0.49	0.66	1.00	0.61	0.27
JGBF	平均	標準偏差	相関行列						$ACF_1$	$ACF_{22}$
$r$	$5.9\times10^{-5}$	$1.5\times10^{-3}$	1.00						$-$0.05	$-$0.01
$r^2$	$2.4\times10^{-6}$	$4.6\times10^{-6}$	$-$0.05	1.00					0.19	0.12
RV	$3.0\times10^{-6}$	$4.3\times10^{-6}$	$-$0.07	0.57	1.00				0.58	0.39
$\rm{RS^+}$	$1.5\times10^{-6}$	$2.4\times10^{-6}$	0.31	0.45	0.79	1.00			0.45	0.33
$\rm{RS^-}$	$1.5\times10^{-6}$	$2.5\times10^{-6}$	$-$0.37	0.47	0.82	0.39	1.00		0.40	0.24
BPV	$2.0\times10^{-6}$	$2.8\times10^{-6}$	$-$0.06	0.50	0.88	0.74	0.74	1.00	0.68	0.49
REIT	平均	標準偏差	相関行列						$ACF_1$	$ACF_{22}$
$r$	$1.6\times10^{-4}$	$1.1\times10^{-2}$	1.00						0.10	0.01
$r^2$	$1.4\times10^{-4}$	$3.4\times10^{-4}$	$-$0.02	1.00					0.30	0.15
RV	$1.0\times10^{-4}$	$1.5\times10^{-4}$	$-$0.06	0.57	1.00				0.65	0.38
$\rm{RS^+}$	$5.0\times10^{-5}$	$7.9\times10^{-5}$	0.26	0.47	0.82	1.00			0.51	0.33
$\rm{RS^-}$	$5.0\times10^{-5}$	$8.1\times10^{-5}$	$-$0.39	0.46	0.83	0.48	1.00		0.51	0.28
BPV	$7.9\times10^{-5}$	$1.3\times10^{-4}$	$-$0.05	0.56	0.95	0.81	0.77	1.00	0.68	0.34

4.5 バックテストの結果

表3にバックテストの結果を示す．なお，ベンチマークとして，全ての資産の投資比率を等しくする等ウェイトポートフォリオのパフォーマンスも算出している．表3より，全てのリスクベース・ポートフォリオにおいて，$\rm{RS^-}$を用いた場合に，ポートフォリオの効率性が最も大きくなった．したがって，高頻度データから算出される下方リスクの高い資産をアンダーウェイトしたことが高いパフォーマンスにつながったと解釈できる．また表4には，各資産において，日次リターンが正だが$\rm{RS^+}\leq \rm{RS^-}$となっている日の翌日のリターン$\tilde{r}$の年率平均を示している．表4より，$\tilde{r}$の平均が期間全体のリターンの平均を大きく下回っていることがわかる．日次リターンが正であっても，日中における大きな下方変動を市場参加者がリスクとして認識し，それが翌期の負のリターンとして反映されている可能性があると考えられ，$\rm{RS^-}$の高いパフォーマンスは，このような特徴を捉えることができることにも起因していると考えられる．

表3 バックテストの結果

ボラティリティ ・インバース	RV	BPV	$\rm{RS^+}$	$\rm{RS^-}$	Var_1m	$\rm{Var^-\_1m}$	等ウェイト
年率リターン	0.42%	0.26%	0.25%	1.19%	0.45%	0.24%	2.03%
年率標準偏差	2.96%	2.97%	3.66%	3.32%	2.56%	2.57%	12.88%
最大ドローダウン	$-$8.57%	$-$9.65%	$-$13.02%	$-$11.62%	$-$7.63%	$-$7.49%	$-$48.07%
95%-VaR	0.27%	0.26%	0.29%	0.29%	0.26%	0.26%	1.21%
95%-CVaR	0.47%	0.46%	0.58%	0.53%	0.43%	0.43%	2.06%
売買回転率	10.32%	8.25%	16.75%	18.95%	1.00%	1.02%	0.67%
リスクリターン	0.143	0.089	0.067	0.359	0.175	0.094	0.157
リスク最小化	RV	BPV	$\rm{RS^+}$	$\rm{RS^-}$	Var_1m	$\rm{Var^-\_1m}$	等ウェイト
年率リターン	0.54%	$-$0.58%	0.13%	1.12%	0.13%	-	2.03%
年率標準偏差	2.96%	3.29%	3.40%	3.16%	2.52%	-	12.88%
最大ドローダウン	$-$9.52%	$-$19.63%	$-$11.59%	$-$7.13%	$-$9.52%	-	$-$48.07%
95%-VaR	0.27%	0.28%	0.28%	0.29%	0.24%	-	1.21%
95%-CVaR	0.48%	0.53%	0.54%	0.51%	0.42%	-	2.06%
売買回転率	13.78%	15.52%	12.00%	14.36%	1.70%	-	0.67%
リスクリターン	0.183	$-$0.177	0.037	0.354	0.051	-	0.157
リスクパリティ	RV	BPV	$\rm{RS^+}$	$\rm{RS^-}$	Var_1m	$\rm{Var^-\_1m}$	等ウェイト
年率リターン	0.72%	0.40%	0.51%	1.59%	0.66%	-	2.03%
年率標準偏差	4.33%	4.31%	5.25%	4.90%	3.26%	-	12.88%
最大ドローダウン	$-$19.97%	$-$21.36%	$-$19.95%	$-$23.30%	$-$16.08%	-	$-$48.07%
95%-VaR	0.41%	0.41%	0.45%	0.44%	0.32%	-	1.21%
95%-CVaR	0.69%	0.69%	0.84%	0.77%	0.53%	-	2.06%
売買回転率	15.30%	13.89%	22.29%	23.66%	1.91%	-	0.67%
リスクリターン	0.166	0.092	0.097	0.324	0.203	-	0.157

表4 $\tilde{r}$の年率平均と期間全体のリターンの年率平均の比較

	年率平均		サンプル日数
	$\tilde{r}$	期間全体	$\tilde{r}$	期間全体
TOPIX	$-$42.0%	2.3%	228	3582
JGBF	$-$0.1%	0.6%	257	3582
REIT	$-$29.0%	3.2%	318	3582

一方で，RSを用いた場合，全てのリスクベース・ポートフォリオにおいて，従来のリスク指標を用いた場合に比べ売買回転率が上昇する傾向がみられる．実際に図1にてリスクベース・ポートフォリオの投資比率を確認すると，高頻度データから算出されるリスク指標を用いた場合は投資比率が急激に変化しており，特にRSにおいては投資比率の変化が激しい．これは，直近1日の日中の下方（上方）変動のみから算出されるRSのリスク水準が日ごとに大きく変化するためである．

図1 各リスクベース・ポートフォリオにおける投資比率

4.6 リターンの要因分解

ポートフォリオのリターンを式(42)に示したように，投資比率の平均要因（右辺第1項）と変動要因（右辺第2項）に分解し，それぞれの要因のパフォーマンスを確認する．表5に平均要因と変動要因のパフォーマンスを，図2にそれぞれの要因の累積リターンを示す．図表より，$\rm{RS^-}$は他の指標に比べ変動要因でリターンを獲得できていることがわかる．よって$\rm{RS^-}$を用いた場合には，動的にリバランスを行うことで相対的に高いリターンを獲得し，トータルの最終リターンも大きくなっていると解釈できる．一方で平均要因ではあまりリターンに差は見られない．   

$$\begin{eqnarray}r_{p}^{t} \ =\ &\sum_{k=1}^{N}& \bar{w}_{k} r_{k}^{t}+\sum_{k=1}^{N} \widetilde{w}_{k}^{t} r_{k}^{t}\\\ &ただし&\text{ ，}\ \bar{w}_{k} =\frac{1}{T} \sum_{t=1}^{T} w_{k}^{t},\quad \widetilde{w}_{k}^{t}=w_{k}^{t}-\bar{w}_{k} \nonumber\end{eqnarray}$$ (42)

表5 平均要因と変動要因のパフォーマンス

	ボラティリティ・インバース			リスク最小化			リスクパリティ
	総リターン	平均要因	変動要因	総リターン	平均要因	変動要因	総リターン	平均要因	変動要因
RV	0.42%	0.78%	$-$0.36%	0.54%	0.80%	$-$0.26%	0.72%	1.08%	$-$0.36%
BPV	0.26%	0.77%	$-$0.51%	$-$0.58%	0.81%	$-$1.40%	0.40%	1.08%	$-$0.68%
$\rm{RS^+}$	0.25%	0.81%	$-$0.56%	0.13%	0.70%	$-$0.57%	0.51%	1.14%	$-$0.63%
$\rm{RS^-}$	1.19%	0.82%	0.37%	1.12%	0.72%	0.40%	1.59%	1.15%	0.44%
Var_1m	0.45%	0.73%	$-$0.28%	0.13%	0.75%	$-$0.63%	0.66%	1.00%	$-$0.33%
$\rm{Var^-\_1m}$	0.24%	0.73%	$-$0.49%	-	-	-	-	-	-

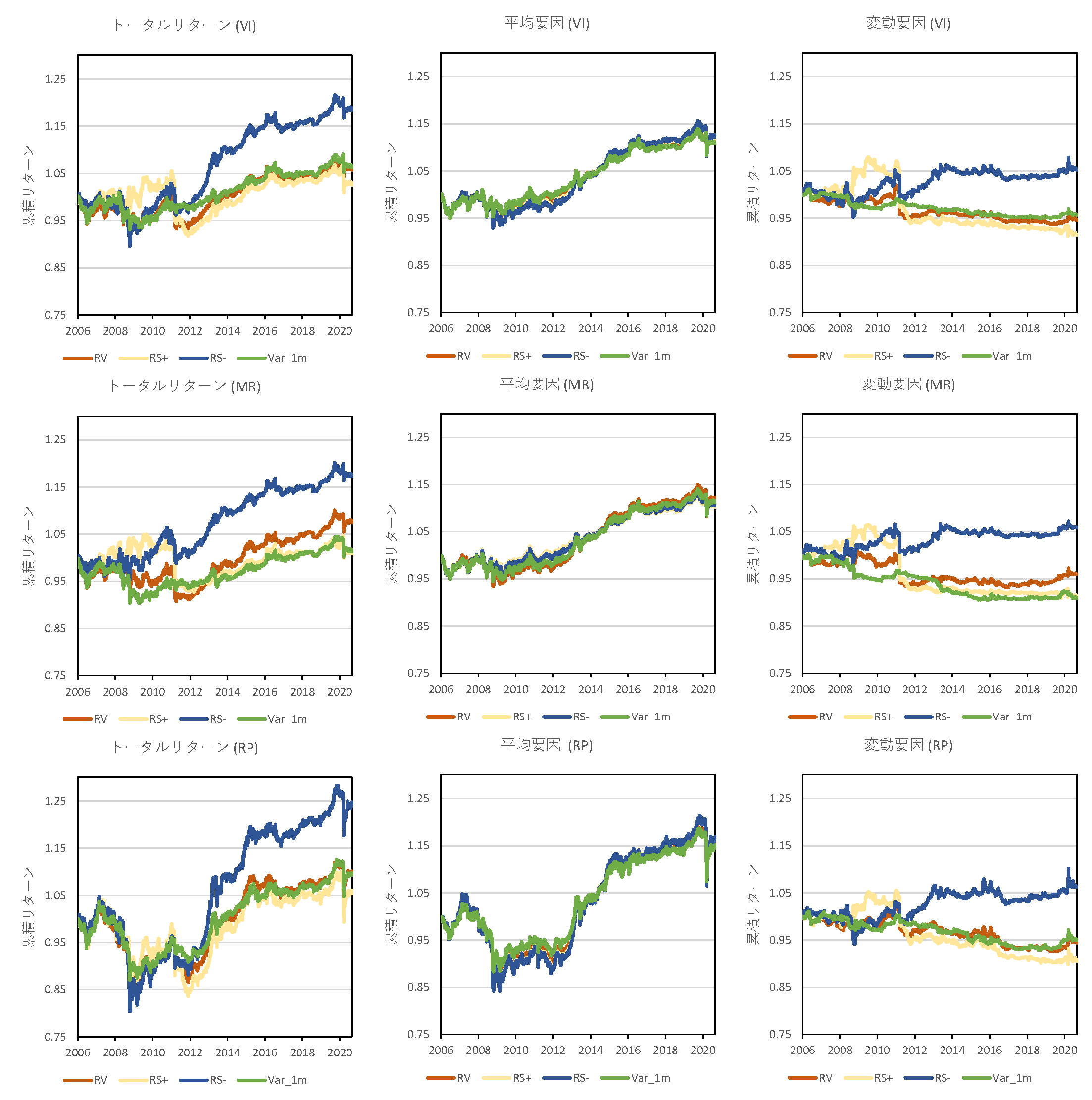
図2 平均要因，変動要因による累積リターン

4.7 $\rm{RS^-}$における分散と共分散部分のパフォーマンスへの寄与

バックテストの結果より，$\rm{RS^-}$をリスク指標として用いた場合，従来のリスク指標を用いた場合に比べて高いパフォーマンスが得られることがわかった．そこで，式(43)のように，分散共分散行列を標準偏差の部分と相関行列の部分に分解し，それぞれを日中リターンと日次リターンから推定しパフォーマンスを比較することで，$\rm{RS^-}$を用いて分散共分散行列を推定した際，行列における分散の部分と共分散の部分のどちらがパフォーマンスに寄与しているかを確認する．   

$$\boldsymbol{\Sigma}=\left(\begin{array}{ccc}\sigma_{1}^{2} & \sigma_{12} & \sigma_{13} \\\sigma_{12} & \sigma_{2}^{2} & \sigma_{23} \\\sigma_{13} & \sigma_{23} & \sigma_{3}^{2}\end{array}\right)=\boldsymbol{V}\boldsymbol{R}\boldsymbol{V}=\left(\begin{array}{ccc}\sigma_{1} & 0 & 0 \\0 & \sigma_{2} & 0 \\0 & 0 & \sigma_{3}\end{array}\right)\left(\begin{array}{ccc}1 & \frac{\sigma_{12}}{\sigma_{1} \sigma_{2}} & \frac{\sigma_{13}}{\sigma_{1} \sigma_{3}} \\\frac{\sigma_{12}}{\sigma_{1} \sigma_{2}} & 1 & \frac{\sigma_{23}}{\sigma_{2} \sigma_{3}}\\\frac{\sigma_{13}}{\sigma_{1} \sigma_{3}} & \frac{\sigma_{23}}{\sigma_{2} \sigma_{3}} & 1\end{array}\right)\left(\begin{array}{ccc}\sigma_{1} & 0 & 0 \\0 & \sigma_{2} & 0 \\0 & 0 & \sigma_{3}\end{array}\right)$$ (43)

具体的には，表6に示すデータの組み合わせが異なる4つのケースにおけるパフォーマンスを比較する．例えばケースBの場合，式(43)の$\boldsymbol{V}$については$\rm{RS^-}$から算出し，$\boldsymbol{R}$については過去22日（1か月）の日次リターンの相関行列から算出し，全体の分散共分散行列$\boldsymbol{\Sigma}$を推定する．¹⁴他のケースにおいても，日次リターンを用いて推定する際は，過去22日分の日次リターンを用いることとする．リスク最小化ポートフォリオとリスクパリティポートフォリオにおけるケースAからDのパフォーマンスは表7のようになる．表より，日中データを標準偏差部分のみに適用したケースBの場合，日中データを相関行列のみに適用したケースCに比べて高いパフォーマンスを示し，リスクパリティにおいては分散共分散行列全てを日中リターンから推定したケースDのパフォーマンスを上回った．2資産がともに下方変動した場合の日中リターンのみを足し上げる$\rm{RS^-}$の共分散部分は，時点によって十分なサンプル数が確保できない場合があるため，分散部分に比べ推定精度が悪化した可能性が高い．このサンプル数不足による推定精度の悪化によって，共分散部分を日中リターンで推定した場合のパフォーマンスが分散部分を日中リターンで推定した場合のパフォーマンスを下回ったと考えられ，$\rm{RS^-}$を用いた分散共分散行列においては，分散部分の方が共分散部分より運用パフォーマンスに寄与しているといえる．また，どちらのポートフォリオにおいても，ケースBがケースAのパフォーマンスを上回り，ケースDがケースCのパフォーマンスを上回ったことから，分散部分に関しては，日次データよりも日中データを用いて推定する方がパフォーマンスは向上すると考えられる．

表6 データの組み合わせ

		相関係数
		日次データ	日中データ
標準	日次データ	ケースA	ケースC
偏差	日中データ	ケースB	ケースD

以上の結果より，よりグローバルに投資対象を広げる場合，異なる市場のため資産間の日中リターンによる共分散が推定できない場合においても，分散部分のみをそれぞれの資産の日中リターンから算出した分散共分散行列でリスク最小化ポートフォリオやリスクパリティポートフォリオを用いる方法(表7のケースB)や，その分散のみで構築した，ボラティリティ・インバースポートフォリオを用いることで，相応のリターンを獲得できると考えられる．今後，グローバルな資産に投資した際のパフォーマンスについて分析をしていく必要がある．

表7 用いるデータの違いによるパフォーマンスへの影響

	リスク最小化				リスクパリティ
	A	B	C	D	A	B	C	D
年率リターン	0.13%	0.97%	0.46%	1.12%	0.66%	1.65%	0.46%	1.59%
年率標準偏差	2.52%	3.25%	2.72%	3.16%	3.26%	4.19%	3.72%	4.90%
最大ドローダウン	$-$9.52%	$-$10.47%	$-$6.61%	$-$7.13%	$-$16.08%	$-$18.50%	$-$20.58%	$-$23.30%
95%-VaR	0.24%	0.29%	0.27%	0.29%	0.32%	0.37%	0.36%	0.44%
95%-CVaR	0.42%	0.52%	0.45%	0.51%	0.53%	0.66%	0.60%	0.77%
売買回転率	1.70%	17.33%	2.36%	14.36%	1.91%	21.06%	3.80%	23.66%
リスクリターン	0.051	0.298	0.170	0.354	0.203	0.394	0.124	0.324

5 感度分析

5.1 リスク指標の推定期間に関する分析

本節においては，まず高頻度データから算出されるリスク指標の推定期間に関する感度分析を行い，リスク指標の推定期間がパフォーマンスに与える影響について考察する．具体的には，リスク指標の推定期間を1日，5日（1週） 10日（2週），22日（1か月），66日（3か月），120日（半年）と変化させ，4節と同様の条件でパフォーマンスを算出する．ただし，パフォーマンス算出期間は2007年1月5日から2020年8月31日とする．

図3～図5にそれぞれボラティリティ・インバース，リスク最小化，リスクパリティポートフォリオにおいて，リスク指標の推定期間を1日から半年に変化させたときのパフォーマンス指標を示す．$\rm{RS^-}$はどの推定期間においても，他の指標を用いた場合よりも高いパフォーマンスを示しており，$\rm{RS^-}$のアウトパフォーマンスは，リスク指標の推定期間に対して頑健であることがわかった．さらに$\rm{RS^-}$を用いた場合，推定期間が長くなるにつれ，平均リターンは徐々に小さくなるが，標準偏差，最大ドローダウン，CVaRなどのリスク尺度については，推定期間が1, 2週間付近で小さくなっており，ボラティリティ・インバースやリスク最小化では，推定期間が2週間の場合のリスクリターンが，推定期間を1日とした場合のリスクリターンと同等の値となった．加えて，推定期間が1日の場合は，売買回転率が非常に高い値を示していたが，推定期間が5日以上の場合には急激に売買回転率が小さくなっていることがわかる．推定期間が長くなることで，リスク指標を推定する際に各推定日でオーバーラップする期間が多くなり，リスク水準のばらつきが抑えられたことで，売買回転率やポートフォリオ全体のリスクが低下したと考えられる．

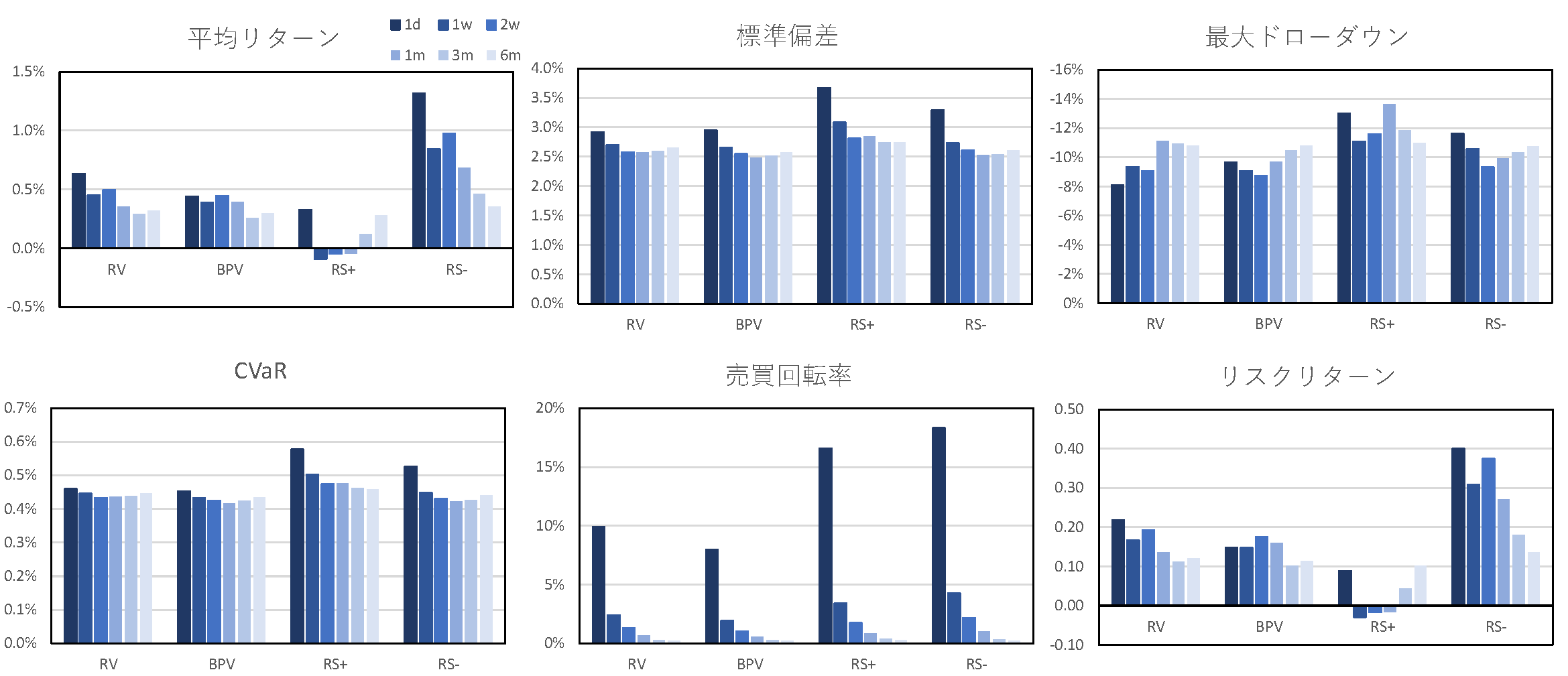
図3 リスク指標の推定期間の違いによるパフォーマンスへの影響（VI）

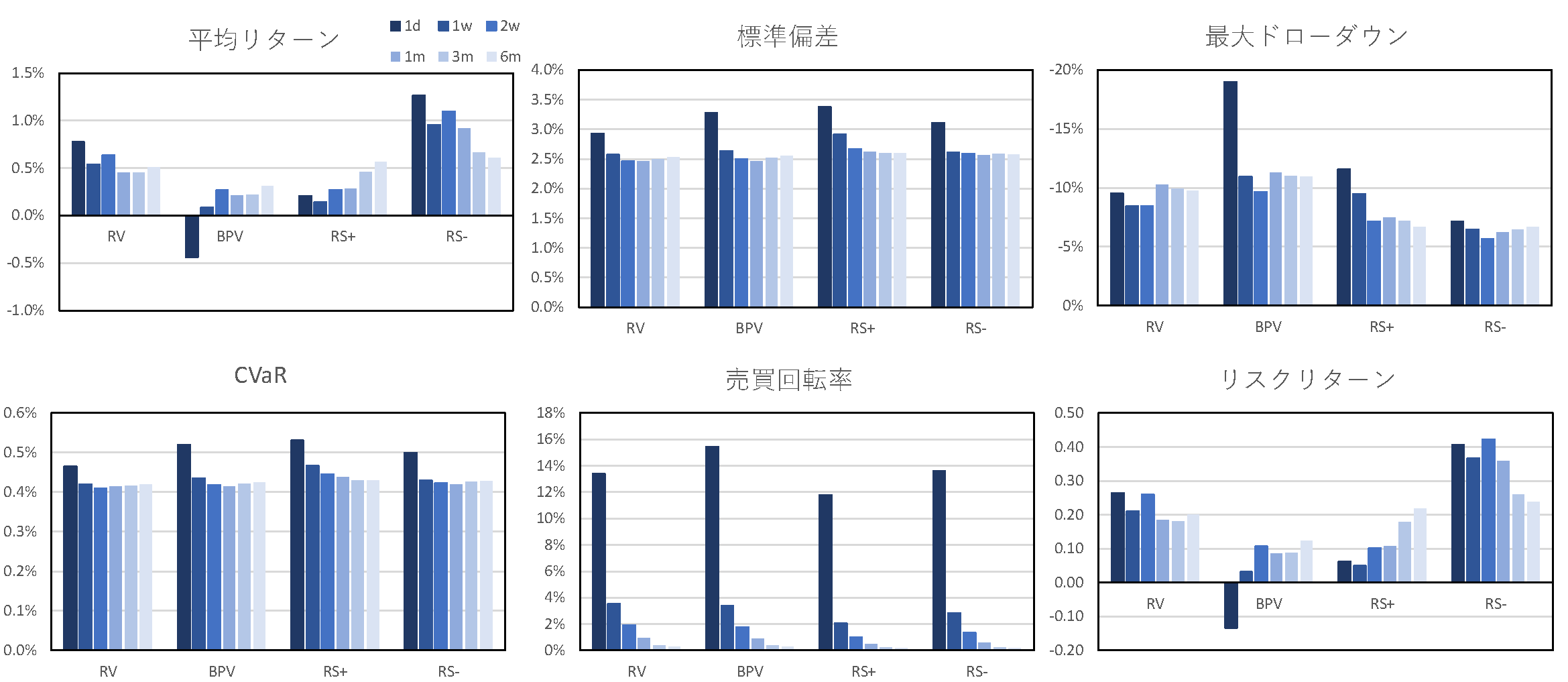
図4 リスク指標の推定期間の違いによるパフォーマンスへの影響（MR）

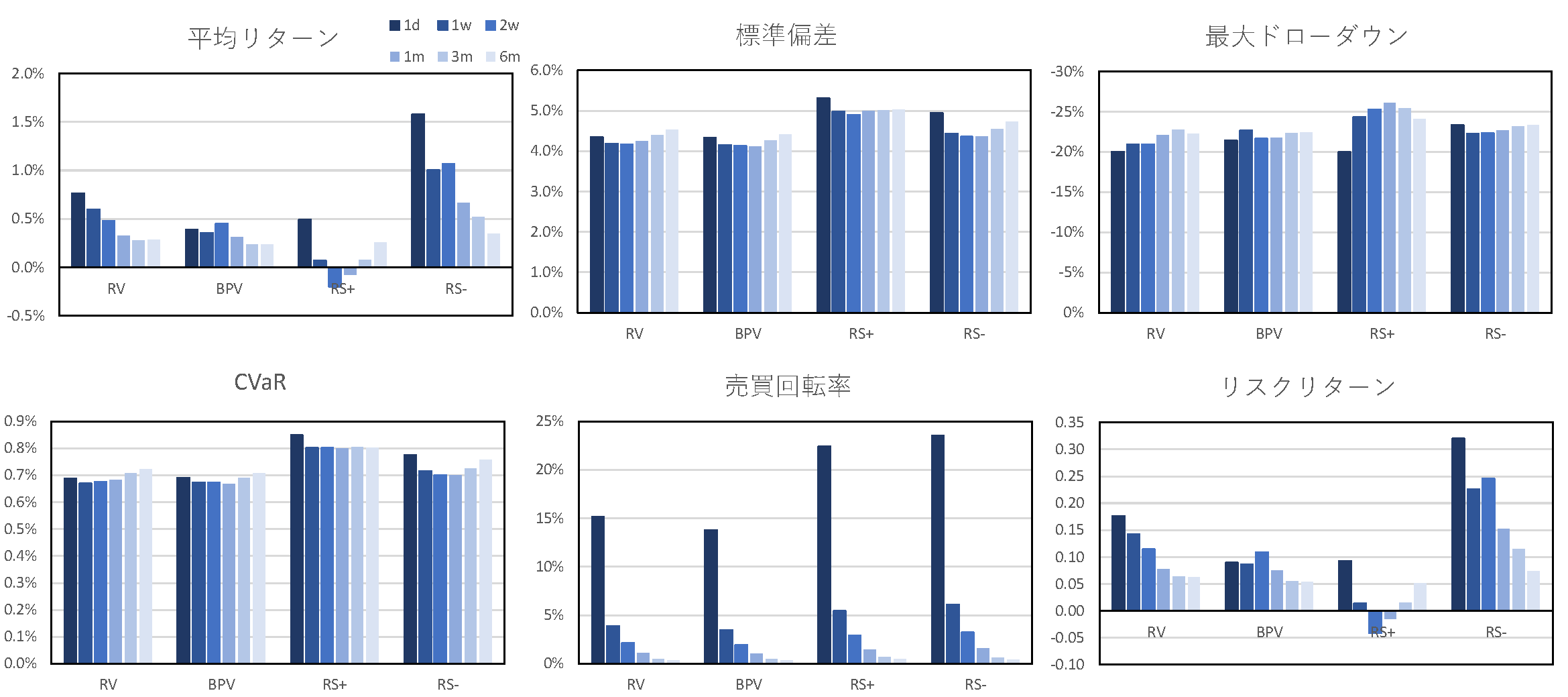
図5 リスク指標の推定期間の違いによるパフォーマンスへの影響（RP）

5.2 高頻度データの観測間隔に関する分析

次に，高頻度データの観測間隔に関する感度分析を行い，観測間隔の違いがパフォーマンスに与える影響について考察する．具体的には，観測間隔を1, 3, 5, 10, 15分と変化させ，4.5節と同様の条件でパフォーマンスを算出する．図6～図8に，各リスクパリティポートフォリオにおいて，観測間隔を1分から15分に変化させたときのパフォーマンス指標を示す．$\rm{RS^-}$はどの観測間隔においても，他の指標を用いた場合よりも高いリターンや効率性を示しており，$\rm{RS^-}$のアウトパフォーマンスは，高頻度データの観測間隔に対して頑健であることがわかった．さらに，全てのリスクベース・ポートフォリオにおいて，$\rm{RS^-}$を用いた場合，観測間隔を小さくしていくにつれ，リスクリターンは小さく，最大ドローダウン幅は大きくなる傾向がみられた．これは，観測間隔を小さくしていくにつれ，リスク指標の算出の際に，市場の制度等に起因するマイクロストラクチャーノイズなどが混入し，$\rm{RS^-}$の推定精度が悪化したためと考えられる．全体を通じて，観測間隔が10分前後のときにリスクリターンが最も高くなった．

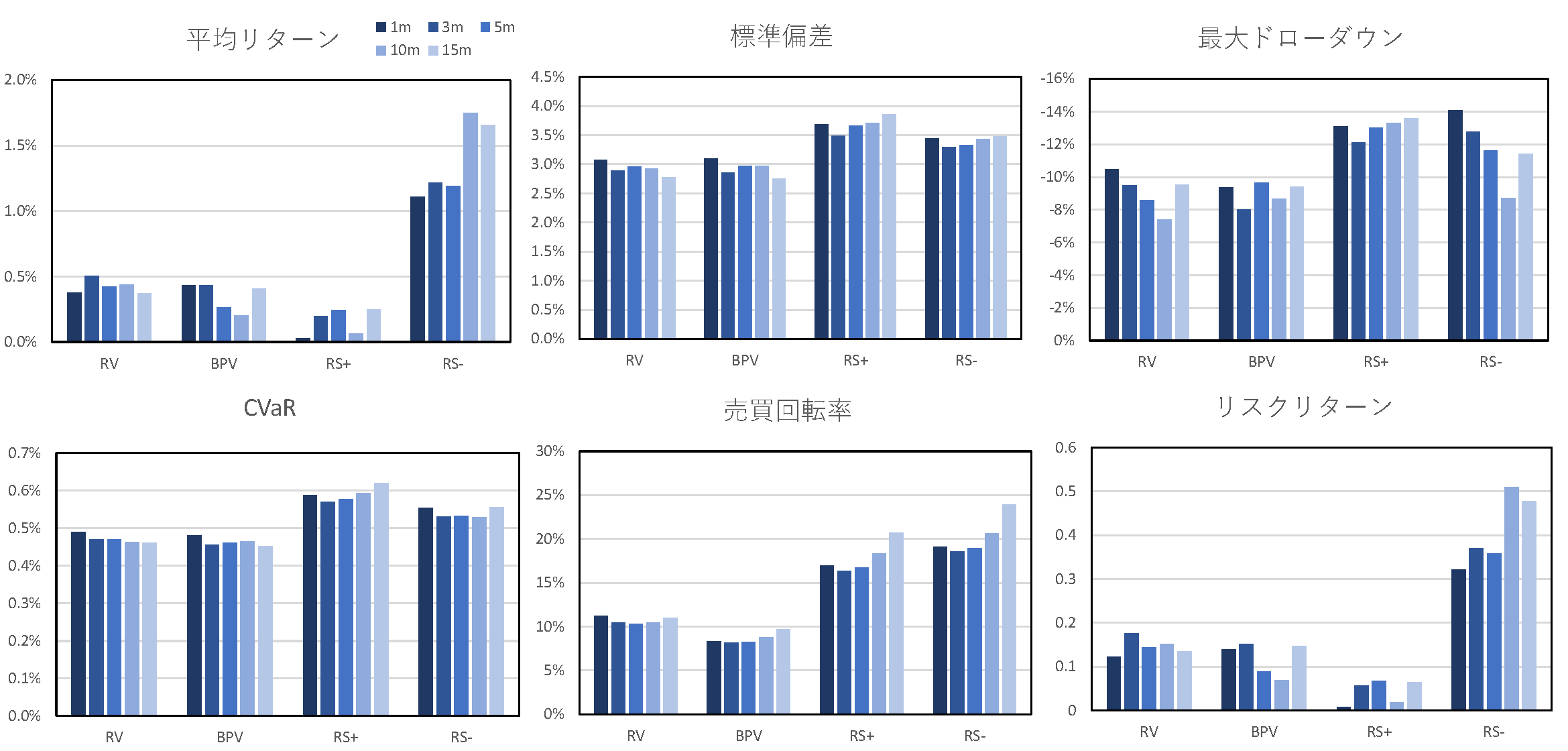
図6 リスク指標の観測間隔の違いによるパフォーマンスへの影響（VI）

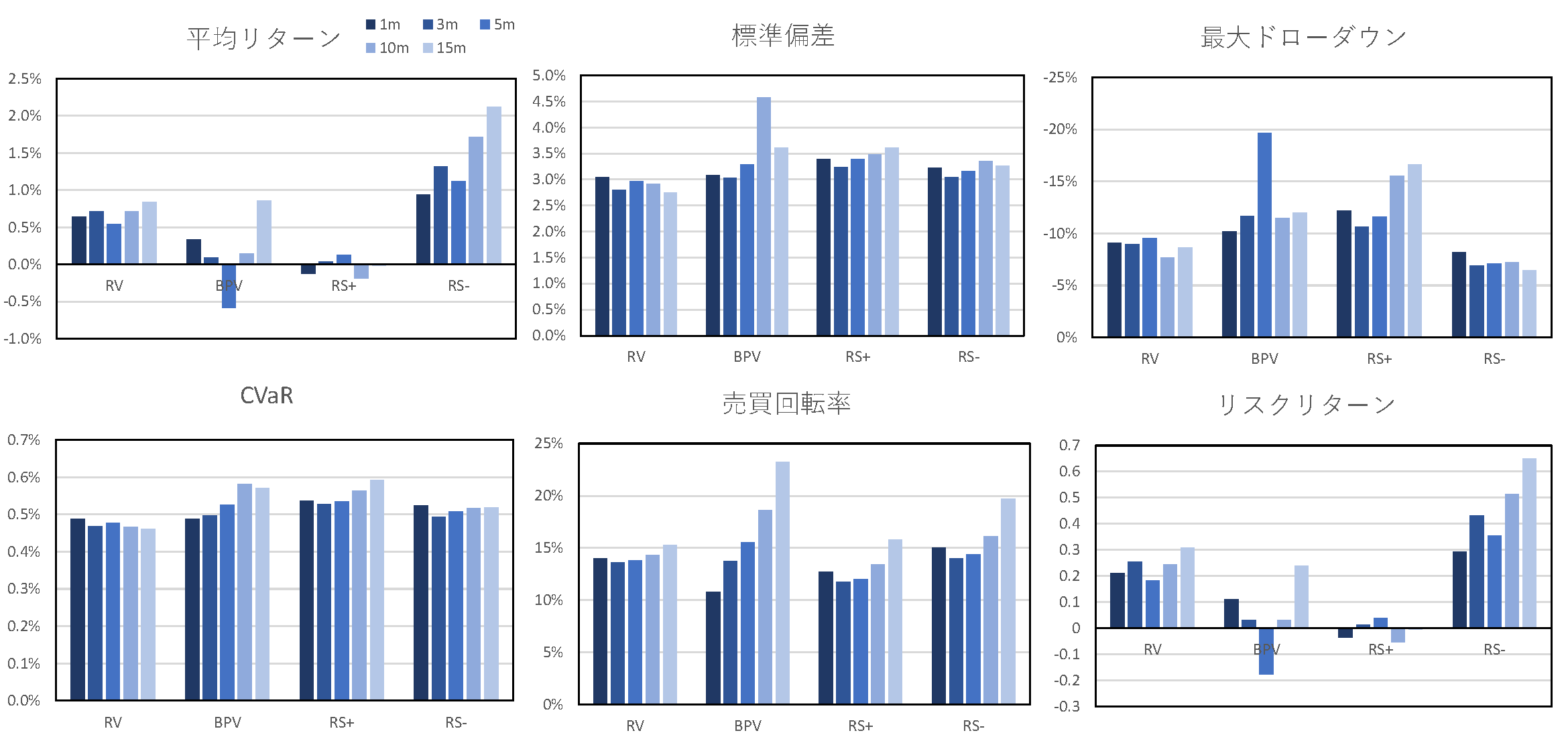
図7 リスク指標の観測間隔の違いによるパフォーマンスへの影響（MR）

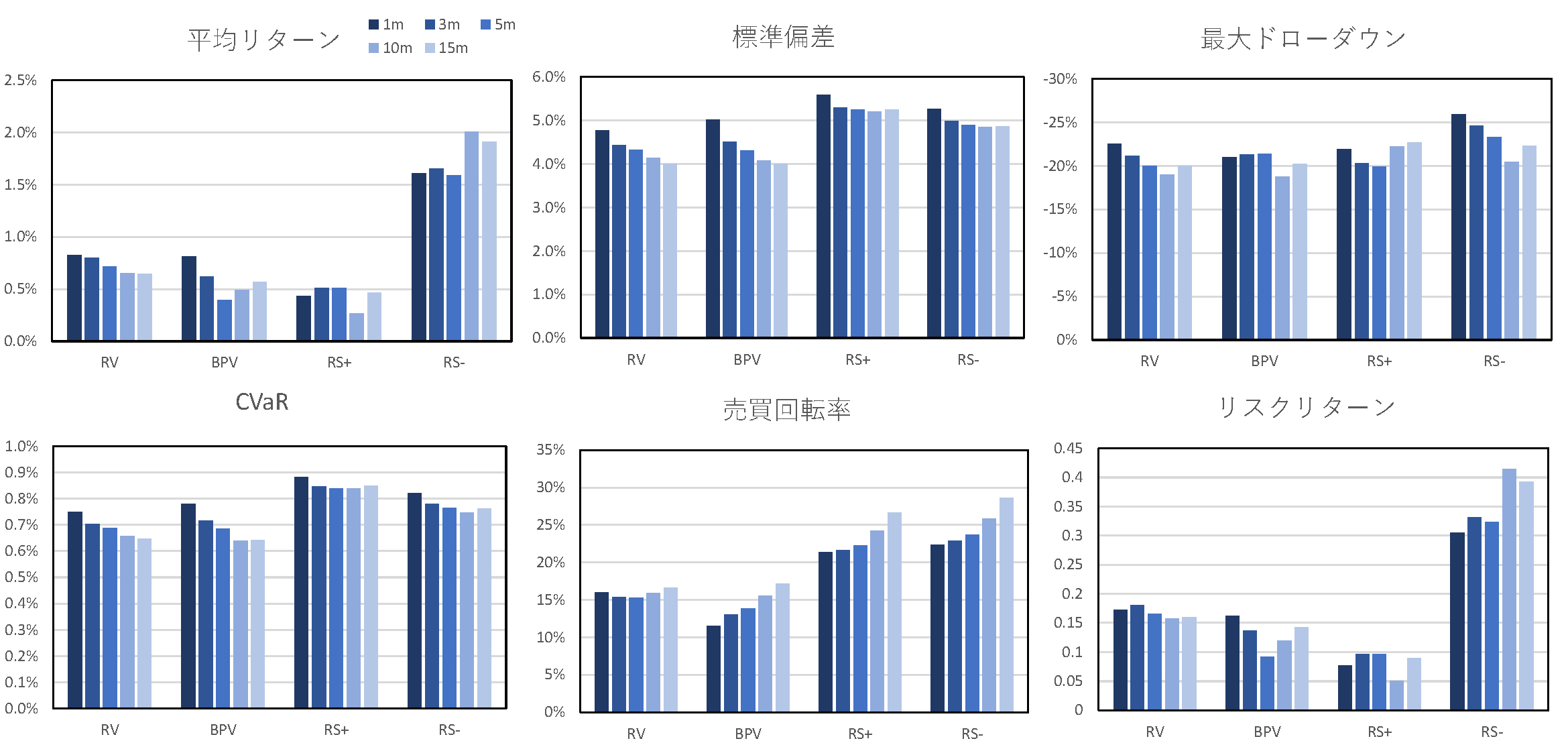
図8 リスク指標の観測間隔の違いによるパフォーマンスへの影響（RP）

5.3 投資ウィンドウに関する分析

これまでの分析では，日次リターンを用いることで投資ウィンドウを1日としてパフォーマンスを算出してきた．本節では，投資ウィンドウに関する感度分析を行い，投資ウィンドウの違いに対する$\rm{RS^-}$のアウトパフォーマンスの頑健性を確認する．具体的には，投資ウィンドウと高頻度データから算出されるリスク指標の推定期間を1日，5日（1週），10日（2週），22日（1か月）と変化させ，それぞれにおけるポートフォリオのパフォーマンスを計算する．例えば，投資ウィンドウとリスク指標の推定期間がともに5日の場合，2006年12月22日から2006年12月28日まで（5日間）の日中データから算出されたリスク指標を用いて，2006年12月28日から2007年1月12日まで（5日間）のポートフォリオのリターン（週次リターン）を計算する．そして，同様の計算を1日ずつずらして行うことで得られる，ポートフォリオの期間全体のリターンの年率平均と年率標準偏差を用いて，リスクリターンを算出する．他の条件においても，パフォーマンス算出期間は2007年1月5日から2020年8月31日とする．

表8に，リスク指標の推定期間，投資ウィンドウ別の，各リスクベース・ポートフォリオにおけるリスクリターンを示す．表より，一部のリスクベース・ポートフォリオにおいて，リスク指標の推定期間を過去1日，投資ウィンドウを10日以上とした場合を除き，ほとんどの条件において$\rm{RS^-}$を用いた場合のパフォーマンスが他のリスク指標を用いた場合のパフォーマンスを上回った．以上の結果より，投資ウィンドウの違いに対して$\rm{RS^-}$のアウトパフォーマンスが頑健であることを確認できた．一方で，$\rm{RS^-}$を用いた場合，投資ウィンドウが長くなるほど，リスクリターンは小さくなる傾向がみられる．特にリスク指標の推定期間が短いほどその傾向が顕著であり，$\rm{RS^-}$を用いて比較的長い投資ウィンドウで投資をする際は，リスクの推定期間を過去5日，10日などと長くとった方がパフォ ーマンスが向上すると考えられる．

表8 リスク推定期間・投資ウィンドウ別のリスクリターン

リスク推定期間		過去1日				過去5日				過去10日				過去22日
$\boldsymbol{ボラティリティ}\\\boldsymbol{・インバース}$		RV	BPV	$\rm{RS^+}$	$\rm{RS^-}$	RV	BPV	$\rm{RS^+}$	$\rm{RS^-}$	RV	BPV	$\rm{RS^+}$	$\rm{RS^-}$	RV	BPV	$\rm{RS^+}$	$\rm{RS^-}$
投資 ウィンドウ	1日	0.217	0.148	0.088	0.400	0.166	0.147	-0.029	0.308	0.192	0.175	-0.017	0.374	0.136	0.159	-0.017	0.27
	5日	0.237	0.228	0.063	0.270	0.197	0.217	0.042	0.345	0.225	0.230	0.037	0.384	0.165	0.192	0.043	0.293
	10日	0.258	0.257	0.090	0.227	0.247	0.264	0.054	0.364	0.202	0.241	0.016	0.349	0.161	0.190	0.037	0.294
	22日	0.161	0.189	0.047	0.128	0.162	0.190	0.060	0.221	0.155	0.176	0.047	0.241	0.135	0.148	0.050	0.222
$\boldsymbol{リスク最小化}$		RV	BPV	$\rm{RS^+}$	$\rm{RS^-}$	RV	BPV	$\rm{RS^+}$	$\rm{RS^-}$	RV	BPV	$\rm{RS^+}$	$\rm{RS^-}$	RV	BPV	$\rm{RS^+}$	$\rm{RS^-}$
投資 ウィンドウ	1日	0.264	-0.133	0.061	0.406	0.210	0.031	0.049	0.366	0.259	0.106	0.101	0.423	0.184	0.085	0.107	0.358
	5日	0.233	0.051	0.113	0.336	0.227	0.113	0.158	0.389	0.251	0.112	0.180	0.443	0.197	0.098	0.192	0.404
	10日	0.251	0.083	0.141	0.245	0.277	0.140	0.178	0.416	0.228	0.130	0.167	0.424	0.196	0.096	0.186	0.410
	22日	0.189	0.076	0.104	0.159	0.209	0.121	0.182	0.344	0.195	0.098	0.187	0.383	0.201	0.098	0.203	0.37
$\boldsymbol{リスクパリティ}$		RV	BPV	$\rm{RS^+}$	$\rm{RS^-}$	RV	BPV	$\rm{RS^+}$	$\rm{RS^-}$	RV	BPV	$\rm{RS^+}$	$\rm{RS^-}$	RV	BPV	$\rm{RS^+}$	$\rm{RS^-}$
投資 ウィンドウ	1日	0.176	0.089	0.093	0.320	0.143	0.086	0.014	0.226	0.114	0.108	-0.041	0.245	0.077	0.076	-0.015	0.152
	5日	0.144	0.098	0.079	0.166	0.106	0.127	0.023	0.183	0.117	0.131	-0.003	0.205	0.095	0.102	0.021	0.153
	10日	0.130	0.119	0.070	0.154	0.120	0.148	0.015	0.190	0.103	0.135	-0.015	0.185	0.090	0.101	0.013	0.152
	22日	0.077	0.079	0.040	0.089	0.066	0.088	0.023	0.097	0.065	0.080	0.009	0.103	0.057	0.060	0.008	0.098

6結論と今後の課題

本研究では，高頻度データから算出される下方リスク尺度である実現半分散（realized semivariance, RS）を用いて，国内株式，国内債券，国内不動産の3資産を対象としたリスクベース・ポートフォリオを構築した．その結果，日中の下方リターンから算出される実現半分散（$\rm{RS^-}$）を用いた場合，従来のリスク指標と比べて，高い運用パフォーマンスを得ることができた．また$\rm{RS^-}$を用いた分散共分散行列において，分散部分と共分散部分をそれぞれ日中データと日次データから推定してパフォーマンスを比較した結果，共分散よりも分散の方がパフォーマンスに寄与していることが分かった．感度分析においては，$\rm{RS^-}$を用いて分散共分散行列を推定した場合，リスク指標の推定期間を長くすると，平均リターンは小さくなるが，標準偏差や最大ドローダウンなどのリスク尺度や，ポートフォリオの売買回転率は小さくなることが示された．また，高頻度データの観測間隔が小さくなるほど，マイクロストラクチャーノイズなどの影響により，パフォーマンスは悪化することがわかった．さらに，投資ウィンドウが長くなるほどリスクリターンは低下し，$\rm{RS^-}$を用いて比較的長い投資ウィンドウ（1週以上）で投資を行う際は，リスクの推定期間を5日から10日とした方がパフォーマンスが向上することが示された．感度分析全体を通じて，$\rm{RS^-}$を用いた場合のアウトパフォーマンスは，リスク指標の推定期間，高頻度データの観測間隔，投資ウィンドウの変化に対して頑健であることがわかった．

本研究では，投資対象資産は国内市場のものに限られているが，グローバルにアセットクラスを拡充することで，より実務に即した検証が可能になると考える．また，実現半分散を用いた分散共分散行列を精度良く予測できる時系列モデルを考案できれば，より高い運用パフォーマンスが期待できる．

脚注

* 本研究の内容は著者が慶應義塾大学大学院理工学研究科に所属していたときに行われたものである．ここで示された内容は，野村アセットマネジメント株式会社としての見解をいかなる意味でも表さない．

1 実現分散を実現ボラティリティ，もしくはrealized volatilityと表記する先行研究もある．

2 ボラティリティは変動率を表し，通常はリターンの標準偏差に対して使われる用語であるため，$\sigma(s)$を瞬間的ボラティリティと呼ぶ．

3 厳密な証明は柴田(2008)を参照されたい．

4 厳密な証明はBarndorff-Nielsen and Shephard (2006)を参照されたい．

5 例えば，$p(\{1,2,-1\})=\{1,2,0\},\quad n(\{1,2,-1\})=\{0,0,-1\}$

6 Rのoptim 関数を用いて最適化を行ったが，解が求められなかったり，ある資産への投資比率がゼロになってしまった場合には，Chaves et al. (2012)を参考にニュートン法を用いて最適解を求めた．

7 本研究では，高頻度データ(日中データ)を用いており，全ての資産のデータポイントをそろえるために，対象資産を国内に限定した．海外資産への拡張については今後の課題としたい．

8 国内の市場データのうち，安定して高頻度データを取得できる資産クラスを選択した．また指数の始値，終値のデータについてはThomson Reutersから，日中データはJPXデータクラウドより取得した．

9 下方半分散は，$E[{|r-E[r]|_-}^2]$として計算される．ただし，$|x|_-=\max\{-x,0\}$である．

10 分散共分散行列の形で下方半分散を定義できないため，最小分散とリスクパリティでは用いない．

11 1か月は22日とした．なお，1年は240日として年率リターンや年率標準偏差を計算した．

12 多くの先行研究は高頻度データから算出されるリスク指標の算出の際に，日中リターンの観測間隔を5分としている．

13 Barndorff-Nielsen et al. (2008)は，米国の個別銘柄の$\rm{RS^-}$を算出し，ラグが1日の自己相関が0.6程度となることを示している．

14 ケースBの場合，$\sigma_1 = \sqrt{\hat{\boldsymbol{N}}[1,1]}$であり，ケースCの場合，$\sigma_{12} =\hat{\boldsymbol{N}}[1,2]$

参考文献

• 柴田舞 (2008), 「高頻度データによるボラティリティの推定：Realized Volatilityのサーベイと日本の株価指数および株価指数先物の実証分析」, 『金融研究』, 日本銀行金融研究所, 27(1), 1-54.
• Andersen, T. G., and Bollerslev, T. (1998), “Answering the skeptics: Yes, standard volatility models do provide accurate forecast,” International Economic Review, 39(4), 885-905.
• Andersen, T. G., Bollerslev, T., Diebold, F. X., and Labys, P. (2003), “Modeling and forecasting realized volatility,” Econometrica, 71(2), 529-626.
• Barndorff-Nielsen, O. E., and Shephard, N. (2004a), “Power and bipower variation with stochastic volatility and jumps,” Journal of Financial Econometrics, 2(1), 1-37.
• Barndorff-Nielsen, O. E., and Shephard, N. (2004b), “Measuring the impact of jumps in multivariate price processes using bipower covariation,” Nuffield College, Oxford University, Oxford, Discussion Paper.
• Barndorff-Nielsen, O. E., and Shephard, N. (2006), “Econometrics of testing for jumps in financial economics using bipower variation,” Journal of Financial Econometrics, 4(1), 1-30.
• Barndorff-Nielsen, O. E., Kinnebrock, S., and Shephard, N. (2008), “Measuring downside risk-realized semivariance,” The Oxford-Man Institute, University of Oxford, Working paper.
• Bollerslev, T., Li, J., Patton, A. J., and Quaedvlieg, R. (2020), “Realized semicovariances,” Econometrica, 88(4), 1515-1551.
• Chaves, D., Hsu, J., Li, F., and Shakernia, O. (2012), “Efficient algorithms for computing risk parity portfolio weights,” The Journal of Investing, 21(3), 150-163.
• Fleming, J., Kirby, C., and Ostdiek, B. (2003), “The economic value of volatility timing using “realized” volatility,” Journal of Financial Economics, 67(3), 473-509.
• Halbleib, R., and Voev, V. (2011), “Forecasting multivariate volatility using the VARFIMA model on realized covariance Cholesky factors,” Journal of Economics and Statistics, 231(1), 134-152.
• Kato, H., and Hibiki, N. (2020), “Asset allocation with asset-class-based and factor-based risk parity approaches,” Journal of the Operations Research Society of Japan, 63(4), 93-113.
• Qian, E. (2005), “Risk parity portfolios: Efficient portfolios through true diversification,” Panagora Asset Management.
• Rousseeuw, P., and Molenberghs, G. (1993), “Transformation of non positive semidefinite correlation matrices,” Communications in Statistics - Theory and Methods, 22(4), 965-984.
• Sharma, P., and Vipul. (2016), “Economic benefits of using realized covariance forecasts in risk-based portfolios,” Applied Economics, 48(6), 502-516.