観測点間相対走時差の多周波数測定

Abstract

二観測点間のP波の相対走時を異なる周波数帯で測定する手法を開発した．この手法では観測点下の地殻多重反射波によって生じる分散効果が自動的に補正される．0.03Hzから0.77Hzの周波数帯の中で狭帯域の10帯域を設定し，地殻多重反射波補正したP波波形を他方の観測点の波形と波形相関をとることで相対走時を測定する．この手法をフレンチポリネシアおよび北西太平洋に設置された広帯域海底地震計のデータ，および周辺の陸上地震観測点のデータに適用した．得られたデータに有限波長理論に基づくインバージョンを適用することにより，これまで十分な解像度が得られなかった領域において高分解能のトモグラフィーモデルを得ることに成功している．

1. はじめに

地球内部構造を調べる上で地震波形解析は有効な手段である．その中でも地震波トモグラフィーは地球内部の3次元地震波速度構造モデルを得る方法として重要な手法であり，地球内部ダイナミクスの解明に大きく貢献している．

地震波走時データを用いたP波トモグラフィーは沈み込んだスラブのような短波長の構造を明らかにし，沈み込んだスラブの複雑な形状を描写した（例えばObayashi et al., 2009; Fukao and Obayashi, 2013）．地震波の立ち上がりの時間をデータとする場合，周波数無限大を仮定した波線理論に基づいたカーネルを使ったトモグラフィーが行われてきた．しかしながら有限波長に基づくカーネルは波線理論のものとは異なり，地震波走時の地球内部構造に対する感度が地震波の周期によって異なる（Dahlen et al., 2000; Hung et al., 2000）．ただし分解能が70 kmを超えるようなグローバルトモグラフィーでは，地震波の立ち上がりの時間データを波線理論カーネルに適用する場合と，卓越周期1秒を仮定した有限波長カーネルに適用する場合とでほとんど差異が見られていない（Obayashi et al., 2013）．しかし異なる周波数バンドで観測される走時の分散関係をデータとして使い，バンド毎の地球内部構造に対する感度の違いを考慮することによって，トモグラフィーの解像度を向上させることができる（Sigloch et al., 2008; Tang et al., 2014; Obayashi et al., 2016）．

そこで，異なる二地震観測点間のP波相対走時を様々な周波数帯で波形相関法を用いて測定する手法を開発した．さらにこの手法をフレンチポリネシアおよび北西太平洋に展開された広帯域海底地震観測網のデータに適用し，分散データを得たのでここに報告する．

2. 測定方法

一つの地震に対し複数の観測点で記録が得られている場合，同じフェーズに対し異なる観測点間で時間をずらしながら対象フェーズのウィンドウで波形相互相関を取り，最大の相関係数となる時間を二観測点間の相対的な走時とする波形相互相関法で測定した．この方法を使用することにより，フェーズの立ち上がりが不明瞭な記録に対しても走時測定が可能となる．本報告では，地震イベント毎に，記録の得られている全観測点の中で，観測点間距離が20度以下となる全ての組み合わせにおいてP波波形の相関を取ることにより，観測点間の相対走時の測定を行なった．また，より多くの情報を得るため，異なる周期帯で相対走時を測定している．最長の中心周期を30秒とし，$1/\surd 2$で短周期となる周期を繰り返し1.3秒までの10バンド，すなわち30, 21.2, 15, 10.6, 7.5, 5.3, 3.7, 2.7, 1.9, 1.3秒の10バンド（Table1）を設定した．測定を行なうため，観測波形にはTable1のような10タイプのバンドパスフィルターをかけ，それぞれの周波数帯において測定を行なった．観測点下の地殻の多重反射によってP波波形は変形するため，地殻多重反射による見かけの分散が生じることがあることが知られている．地殻多重反射の補正を行うためObayashi et al.（2017）が提案する 手法を取り入れた．これは観測点下の地殻構造からP波入射に対するレスポンスを計算し，それを互いの観測波形にたすきがけで畳み込み積分してから相関を取るものである．この際の観測点下の地殻構造としてCRUST2.0（Bassin et al., 2000）を採用した．P波部分のタイムウィンドウの長さ（秒）はおよそ1周期分の波形が含まれることを目安とし，最終的には相関係数の値とリファレンス波形と観測波形との重ね合わせの図を目視で確認し決定をした．

Table 1. List of the center periods and the corner frequencies. 表1． 各周波数帯における中心周期とコーナー周波数．

Band index	1	2	3	4	5	6	7	8	9	10
Center period (sec)	30	21.2	15	10.6	7.5	5.3	3.7	2.7	1.9	1.3
Corner freq. (mHz)	23–47	33–66	47–94	66–133	94–188	133–266	188–377	266–533	377–754	533–1066

Fig.1に相互相関による相対走時測定を行なった地震波形の例を示す．観測点SOC1をリファレンスとし，SOC2とのP波の相対走時を測定した例である．リファレンス波形SOC1をシフトさせ，最大の相関係数をとる時間を二観測点間の相対的な走時とする．

Fig.1.

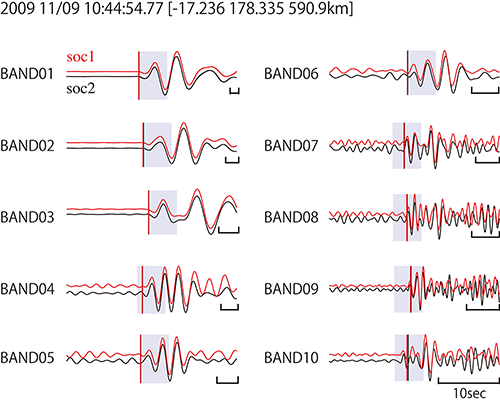
Example of seismic records used for the relative travel time measurement of P-wave between two stations at 10 frequency bands from 0.03 to 0.77 Hz. Red traces are reference waveform and black traces are observed seismogram. Vertical lines show theoretical P wave arrival time. Shaded area mean time window.

図1． 異なる二観測点間の各周波数帯におけるP波相対走時測定例． 赤はリファレンスとする観測点soc1の波形．黒は測定する観測点soc2の波形．赤，黒の縦線は，soc1, soc2それぞれの観測点におけるP波の理論到着時刻を示す．グレーの影は各周波数バンドにおけるタイムウィンドウを示す．

3. 測定した地震波データ

本報告では，フレンチポリネシアおよび北西太平洋の二地域の測定結果について報告する．

3.1 フレンチポリネシア

フレンチポリネシアでは，2003年から2010年にかけて2回の広帯域海底地震観測が行なわれている．2003年 から2005年にかけて行なわれたPolynesian BBOBS array（Suetsugu et al., 2005）では，2003年から2004年の期間で7台，2004年から2005年の期間で2台の広帯域海底地震計が設置され観測が行なわれた．また2009年から2010年にかけてはTIARES: The network for Tomographic Investigation by seafloor ARray Experiment for the Society hotspot（Suetsugu et al., 2012）により9台の広帯域海底地震計が設置され観測が行われた．本報告ではこの二つの広帯域海底地震観測網のデータに加え，2001年から2005年にかけてフレンチポリネシア地域で展開された陸上地震観測網Polynesia PLUME network（Barruol, 2002）, LDG network（Laboratoire de Geophysiue in France）, Global Seismographic Network（GSN）のデータの測定を同時に行なった．Fig.2に測定に使用した観測点を示す．

Fig.2.

Map of seismic stations in French Polynesian region and earthquakes used in this report. Red triangles show broadband ocean bottom seismometers (BBOBSs). Blue triangles indicate land stations. Red open stars mean earthquakes.

1. (a) Polynesian BBOBS array stations deployed from 2003 to 2004 and land stations.
2. (b) Polynesian BBOBS array stations deployed from 2004 to 2005 and land stations.
3. (c) TIARES network stations and land stations.

図2． フレンチポリネシアにおける地震観測点分布図．赤三角は広帯域海底地震計，青三角は陸上地震観測点，赤星は測定に使用した地震の震央を示す．

1. (a) 2003年から2004年にかけて設置されたPolynesian BBOBS arrayの観測点，および陸上地震観測点．
2. (b) 2004年から2005年にかけて設置されたPolynesian BBOBS arrayの観測点，および陸上地震観測点．
3. (c) TIARES networkの観測点，および陸上地震観測点．

3.2 北西太平洋

北西太平洋では，2010年から2014年にかけて「ふつうの海洋マントル」プロジェクトにより広帯域海底地震観測網NOMAN: Normal Oceanic Mantle Project（Utada et al., 2013） が展開され，北西太平洋シャツキー海台の北西に10台，南東に8台の広帯域海底地震計が設置され観測が行なわれた．本報告ではこのNOMANのデータに加え，NOMANの観測網に近いIRIS（Incorporated Research Institutions for Seismology）の観測点，WAKE, GUMO, YSS, PET, MIDW, ADKのデータ，および，防災科学技術研究所によって運営され日本全土に展開されているF-net（例えばOkada et al., 2004）のデータの測定を同時に行なった．Fig.3に測定に使用した観測点を示す．

Fig.3.

Map of seismic stations in Northwest Pacific region and earthquakes used in this report. Red triangles show broadband ocean bottom seismometers (BBOBSs). Blue triangles indicate F-net stations. Green triangles are land stations served by IRIS. Red open stars mean earthquakes.

図3． 北西太平洋における地震観測点分布図．赤三角は広帯域海底地震計，青三角はF-net地震観測点，緑三角はIRISによる陸上地震観測点，赤星は測定に使用した地震の震央を示す．

測定に使用した地震はフレンチポリネシア，北西太平洋共に，マグニチュード6以上，観測点からの震央距離が30から90度の範囲のものを選別した．測定に使用した地震の震央をFig.2 (d), Fig.3 (b)にそれぞれ示す．

4. 測定結果とまとめ

マグニチュード6以上の地震，全310イベント（Polynesian BBOBS array：100個，TIARES : 34個，NOMAN : 176個）の測定を行なった．本報告では測定結果の例としてTable2に示す12個のイベントを示す．

Table 2. List of events. 表2． 地震イベント一覧．

No.	date	latitude	longitude	depth (km)	Mw
1	2003/01/20/08:43:06.70	-10.490	160.770	33	7.3
2	2003/06/16/22:08:02.14	55.490	160.000	174	6.9
3	2003/12/27/22:38:01.88	-21.670	169.840	10	6.7
4	2004/09/05/10:07:07.82	33.070	136.620	14	7.0
5	2004/10/08/08:27:53.54	-10.950	162.160	36	6.9
6	2005/03/21/12:23:54.09	-24.980	-63.470	579	6.8
7	2009/02/18/21:53:45.16	-27.424	183.670	25	7.0
8	2009/08/09/10:55:55.61	33.167	137.941	297	7.1
9	2009/11/09/10:44:54.77	-17.236	178.335	590	7.3
10	2012/04/28/10:08:08.09	-18.685	185.295	134	6.6
11	2012/07/28/20:03:56.80	-4.651	153.173	41	6.5
12	2012/08/31/12:47:33.38	10.811	126.638	28	7.6

測定された観測点$i, j$間の相対走時$\Delta t_{ij}$と観測点$i,j$の走時残差$\delta t_{i}, \delta t_{j}$の関係は次のように書ける．

  

$$ \delta t_{i}-\delta t_{j}=( t_{i}^{obs}-t_{i}^{syn} )-( t_{j}^{obs}-t_{j}^{syn}) =\Delta t_{ij}-(t_{i}^{syn}-t_{j}^{syn}) $$

ここで$t^{obs}$，$t^{syn}$はそれぞれ観測走時，理論走時である．$t^{syn}$は地球内部速度構造を仮定すれば計算される．従ってすべての観測点ペアにおける上記の式に全観測点の走時残差の平均が0，すなわち$\sum\delta t_{i}=0$という仮定の条件を加えることで全観測点の走時異常$\delta t$をインバージョンで求めることができる．

Fig.4–7はそのように求めた各観測点の走時異常を示したものである．理論走時を求めるのに球対称速度構造モデルIASP91（Kennett and Engdahl, 1991）を使用した．

Fig.4.

Distribution of traveltime residuals from the average. Colored circles plotted at the locations of BBOBSs and land stations show the deviations. Red stars in lower map denote epicenters.

図4． イベント1–3の走時残差．Polynesian BBOBS array および周辺の陸上地震観測点，合わせて全22観測点の走時残差をプロットしたものである．各イベントに対し，周期30秒，15秒，7.5秒の測定結果および周期30秒と7.5秒との差を示している．

Fig.5.

Distribution of traveltime residuals from the average. Colored circles plotted at the locations of BBOBSs and land stations show the deviations. Red stars in lower map denote epicenters.

図5． イベント4–6の走時残差．Polynesian BBOBS arrayおよび周辺の陸上地震観測点，合わせて全18観測点の走時残差をプロットしたものである．各イベントに対し，周期30秒，15秒，7.5秒の測定結果および周期30秒と7.5秒との差を示している．

Fig.6.

Distribution of traveltime residuals from the average. Colored circles plotted at the locations of BBOBSs and land stations show the deviations. Red stars in lower map denote epicenters.

図6． イベント7–9の走時残差．TIARES networkおよび周辺の陸上地震観測点, 合わせて全15観測点の走時残差をプロットしたものである．各イベントに対し，周期30秒，15秒，7.5秒の測定結果および周期30秒と7.5秒との差を示している．

Fig.7.

Distribution of traveltime residuals from the average. Colored circles plotted at the locations of BBOBSs and land stations show the deviations. Red stars in lower map denote epicenters.

図7． イベント10–12の走時残差．NOMAN networkおよび周辺のIRIS陸上地震観測点，F-net観測点の走時残差をプロットしたものである．各イベントに対し，周期30秒，15秒，7.5秒の測定結果および周期30秒と7.5秒との差を示している．

Fig.4はevent1～3に関して， Polynesian BBOBS arrayおよび周辺の陸上地震観測点，合わせて全22観測点の走時残差をプロットしたものである．各イベントに対し，最長周期とその1/2，1/4にあたる30秒，15秒，7.5秒の測定結果および周期30秒と7.5秒との差を示している．

Fig.5はevent4～6に関して，Polynesian BBOBS arrayおよび陸上地震観測点，全18点での測定結果である．

Fig.6はevent7～9に関して，TIARESおよび周辺の陸上地震観測点，合わせて全15点での測定結果である．

Fig.7はevent10～12に関して，広帯域海底地震観測網NOMAN，および周辺のIRIS陸上地震観測点，日本全土に展開されているF-net観測点の測定結果である．

走時異常の全体的なパターンは，各イベント，周期30秒，15秒，7.5秒で概ね一致している．しかしパターンは同じであっても，例えばFig.6のevent8，9，Fig.7のevent11，12のように，周期によって系統的に強度が変わることから，分散が観測されていると考えられる．また，分散パターンはイベントで異なっている（例えばevent11と12）ため，伝播経路にも依存すると考えられる．従って3次元速度構造の走時異常に対する応答が波長に依って異なると考えることで，分散データはトモグラフィーの解像度の向上に寄与すると考えられる．

実際，有限波長理論に基づくインバージョンを本報告で得られた分散データを適用し，従来の波線理論に基づく地震波走時トモグラフィーに加える手法によって新たな3次元地震波速度構造モデルを得ている（Tang et al., 2014; Obayashi et al., 2016）．従来の方法では十分な解像度が得られなかったフレンチポリネシア地域において，上部マントルから深部にいたるまで高分解能のトモグラフィーモデルを得ることに成功している．

このように地震波形解析により得られた分散データを取り込むことによって，トモグラフィーの解像度を向上させることができると期待される．

謝辞

本報告の執筆にあたり大林政行氏には大変有益な助言をいただきました．査読者の深尾良夫氏，石原靖氏のコメントにより本原稿は大きく改善されました．また本解析では防災科学技術研究所によるF-netのデータを使用いたしました．ここに感謝申し上げます．

参考文献

•     Barruol,  G. (2002), PLUME investigates South Pacific superswell, Eos Trans. AGU, 83(45), 511-514, doi:10.1029/2002EO000354.
•     Bassin,  C. ,  G.  Laske , and  G.  Masters (2000), The current limits of resolution for surface wave tomography in North America, EOS Trans. AGU, 81, F897.
•     Dahlen,  F.A. ,  S.-H.  Hung , and  G.  Nolet (2000), Frechet kernels for finite-frequency traveltimes–I. Theory, Geophys. J. Int., 141, 157-174.
•     Fukao,  Y. and  M.  Obayashi (2013), Subducted slabs stagnant above, penetrating through, and trapped below the 660-km discontinuity, J. Geophys. Res., 118, 5920-5938, doi: 10.1002/2013JB010466.
•     Hung,  S.-H. ,  F.A.  Dahlen , and  G.  Nolet , (2000), Frechet kernels for finite-frequency traveltimes–II. Examples, Geophys. J. Int., 141, 175-203.
•     Kennett,  B.L.N. and  E.R.  Engdahl (1991), Traveltimes for global earthquake location and phase identification, Geophys. J. Int., 105, 429-465.
•     Obayashi,  M. ,  J.  Yoshimitsu , and  Y.  Fukao (2009), Tearing of Stagnant Slab, Science, 324(5931), 1173-1175, doi: 10.1126/science.1172496.
•     Obayashi,  M. ,  J.  Yoshimitsu ,  G.  Nolet ,  Y.  Fukao ,  H.  Shiobara ,  H.  Sugioka ,  H.  Miyamachi , and  Y.  Gao (2013), Finite frequency whole mantle P wave tomography: Improvement of subducted slab images, Geophys. Res. Lett., 40(21), 5652-5657, doi:10.1002/2013GL057401.
•     Obayashi,  M. ,  J.  Yoshimitsu ,  H.  Sugioka ,  A.  Ito ,  T.  Isse ,  H.  Shiobara ,  D.  Reymond , and  D.  Suetsugu (2016), Mantle plumes beneath the South Pacific superswell revealed by finite frequency P tomography using regional seafloor and island data, Geophys. Res. Lett., 43, 11628-11634, doi:10.1002/2016GL070793.
•     Obayashi,  M. ,  Y.  Ishihara , and  D.  Suetsugu (2017), Effects of shallow-layer reverberation on measurement of teleseismic P-wave travel times for ocean bottom seismograph data, Earth Planets Space, 69, doi:10.1186/s40623-017-0626-2.
•     Okada,  Y. ,  K.  Kasahara ,  S.  Hori ,  K.  Obara ,  S.  Sekiguchi ,  H.  Fujiwara , and  A.  Yamamoto (2004), Recent progress of seismic observation networks in Japan –Hi-net, F-net, K-NET and KiK-net–, Earth Planets Space, 56, xv- xxviii, doi:10.1186/BF03353076.
•     Sigloch,  K. ,  N.  McQuarrie , and  G.  Nolet (2008), Two-stage subduction history under North America inferred from multiple-frequency tomography, Nature Geoscience, 1, 458-462.
•     Suetsugu,  D. ,  H.  Shiobara ,  H.  Sugioka ,  G.  Barruol ,  F.  Schindele ,  D.  Reymond ,  A.  Bonneville ,  E.  Debayle ,  T.  Isse ,  T.  Kanazawa , and  Y.  Fukao (2005), Probing South Pacific mantle plumes with ocean bottom seismographs, Eos Trans. AGU, 86, 429-435, doi:10.1029/2005EO440001.
•     Suetsugu,  D. ,  H.  Shiobara ,  H.  Sugioka ,  A.  Ito ,  T.  Isse ,  T.  Kasaya ,  N.  Tada ,  K.  Baba ,  N.  Abe ,  Y.  Hamano ,  P.  Tarits ,  J.P.  Barriot , and  D.  Reymond (2012), TIARES Project– Tomographic investigation by seafloor array experiment for the Society hotspot, Earth Planets Space, 64(4), i-iv, doi:10.5047/eps.2011.11.002.
•     Tang,  U. ,  M.  Obayashi ,  F.  Niu ,  S.P.  Grand ,  Y.  Chen ,  H.  Kawakatsu ,  S.  Tanaka ,  J.  Ning , and  J.  Ni (2014), Changbaishan volcanism in northeast China linked to subduction-induced mantle upwelling, Nature Geoscience, 7, 470-475, doi:10.1038/ngeo2166.
•     Utada,  H. ,  H.  Kawakatsu ,  H.  Shiobara ,  K.  Baba ,  T.  Isse ,  D.  Suetsugu , and NOMan Project team (2013), The NOMan Project: Overview, International Workshop on “Normal Oceanic Mantle” Abstract Volume, 5-6.