Visualization of Orbitals (3) Probability Density Distributionin the Three Dimensional Representationof Hydrogen s Orbitals in a Glass Block

Abstract

水素原子の波動方程式を解く過程で得られる量子数に対応して，無数の原子軌道が導出される．これらのうち，いくつかのs軌道をガラスブロック内に実3次元で彫刻し，どのような節面が描かれるかを調べた．

1 はじめに

前回は，水素原子の1s軌道における「確率の雲」の物理的意味を解説した [1]．前回記したように，1s軌道というのは，水素原子の中の電子の最も安定な軌道，つまり，エネルギーが最も低い軌道である．水素原子のなかの電子は，より高いエネルギーの軌道への配置が無数にとれる．水素原子のシュレーディンガーの波動方程式を解くと，これら無数の軌道の数式を求めることができる．

今回は，これらの軌道を求める手続きの概略を記し，その過程で自然に求まる量子数に基づき，s, p, d, f,…などの軌道名が規定されるしくみを調べる．さらに，いくつかのs軌道を可視化する際の問題点とその解決方法について考察を加える．

2 原子軌道を求める手続き

本節には，今後必要となる最小限の数式を示した．煩わしいと思われる方は読み飛ばして，必要と思われるときに参照していただきたい．

水素原子の原子軌道を求める手続きの概略をFigure 1に示した．シュレーディンガーの波動方程式 (1) において，原子核は原点 (0, 0, 0) にあり，質量m，電荷 − eの電子が (x, y, z) に位置している． $k_0$はクーロンの法則をSI単位系で表すときの定数， h はプランク定数である．この式を解くには，まず，直交座標系 (x, y, z) から極座標系 (r, θ, φ) に変換する．これらの座標系の関係は Figure 2 に示してある．変換された式は解析的に(近似を導入せずに) 解くことができ，上記の無数の原子軌道${\chi }_{n,l,m}$の数式 (2)とそれらのエネルギー$E_n$ を求めることができる．原子軌道 (2) は， r の関数，θ の関数，および，φ の関数の積で表され，それぞれの関数は，主量子数 n, 方位量子数 lまたは，磁気量子数 m で規定される．これらの量子数は，以下に示す範囲の0または整数であることが，もとの波動方程式 (1) を解く過程で自然に導かれる．    主量子数

$n=1,2,3,\dots$(9)

   方位量子数

$0\le l\le n-1$(10)

   磁気量子数

$-l\le m\le l$(11)

Figure 1.

 A procedure to solve the Schrödinger equation of the hydrogen atom

Figure 2.

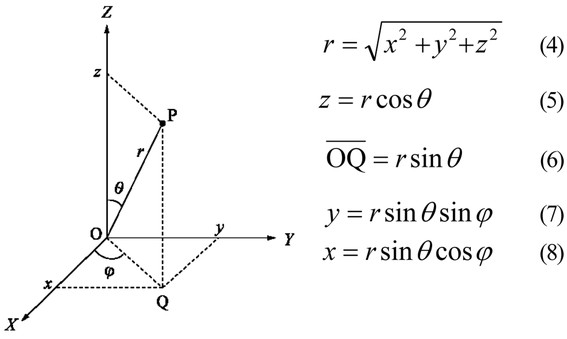
 Relationship between spherical coordinates (r, θ, φ) and Cartesian coordinates (x, y, z)

原子軌道${\chi }_{n,l,m}$ の数式 (2) は，mの値が0でない場合，複素関数(虚数単位$i\begin{array}{c}\end{array}(i^2=-1)$を含む関数)となる．これでは扱いにくい場合が多いので，原子軌道の数式 (2) を組変えて，実関数 $\chi (x,y,z)$ (3) に変換したものが使われる．

3 原子軌道の名称と量子数

原子軌道の名称と量子数の関係をTable 1に示す．1s, 2s, 2p,…などの名称における最初の数字は主量子数 n を表す．s, p,…などの英字は，方位量子数 $l$の値が0のときs, 1のときp, 2のときd, 3, 4, 5,…は，f, g, h,…とアルファベットを順次割り振る．水素原子のエネルギーは主量子数nだけで決まるので，同じエネルギーをもつ軌道の数は右端に示すように，1, 4, 9, 16,…となり, n²個ずつである．同じエネルギーをもつ軌道は，縮重(または，縮退：degenerate)していると呼ばれる．下表には4f軌道までしか示していないが，上記のことから，主量子数5の軌道は 5s, 5p, 5d, 5f, 5g であり，縮重した軌道数は，1 + 3 + 5 + 7 + 9 = 25 であることなど，高次の軌道のことが理解される．

Table 1. Names of atomic orbitals, quantum numbers n, l, m and the sum of orbitals.

4 s軌道を表す数式の特徴

Table 1. を見ると，s軌道では方位量子数 lと磁気量子数 mの値がいずれも0なので，次式となる．   

${\chi }_{n,0,0}=R_{n0}\left(r\right){\Theta }_{00}\left(\theta \right){\Phi }_0\left(\varphi \right)$(12)

上式においてθ の関数，および，φ の関数の項はたまたま定数となり，変数θ ，または，φ を含まない．したがって，s軌道の数式はどれも r だけの関数となる．

5 等値曲面表示の問題点とその対策

1s軌道はrだけの関数なので，その等値曲面は球殻状となることを，前回述べた [1]．その他のs軌道も r だけの関数なので，等値曲面はすべて球殻状である．2s 軌道の関数値は，Figure 3下図に赤線で示すように，r = 2 au のところで関数値が0となる．r の値がこれより小さいと正，大きいと負の値をとる．つまり，r = 2 auの球殻が節面となっている．この関数の最小値は，r = 4 auのところにあり，その値は −0.027 au^−3/2 である．同じ絶対値を持つ${\chi }_{\text{2s}}^{}$ = + 0.027 au^-3/2 の面は，r = 1.44 au のところにあるから，たとえば，一辺 4 au の立方体の範囲に含まれる等値曲面は，Figure 3 (a) に黄色で描いた球となる．Figure 3 (d) は， 一辺 8 au の立方体の範囲に含まれる ${\chi }_{\text{2s}}^{}$ = −0.027 au^-3/2 の面を描いたものである [2]．オレンジ色の球殻の内側には黄色の球殻が同じ絶対値を持つ面として存在するはずであるが，外側の面で覆われて全く観察できなくなる．両者を観察するには，描画範囲を狭めてFigure 3 (b), または，(c) のようにしなければならない．しかし，これらに，節面を示すr = 2 auの球殻を追加して描こうとすると，それによって関数値 = + 0.027 au^-3/2 の面が隠されてしまう．3s, 4s, 5s,…では，節面の数は，2, 3, 4,…という具合に増加するから，等値曲面で節面を含む全体のありさまを表示することはほとんど不可能である．

Figure 3.

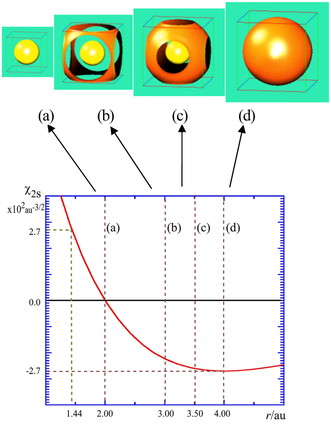
 Isosurface representation of a hydrogen 2s orbital in a (a) 4 x 4 x 4 au³, (b) 6 x 6 x 6 au³, (c) 7 x 7 x 7 au³, or (d) 8 x 8 x 8 au³ cube (top) and function value of 2s orbital vs. distance from the nucleus r(bottom)

Figure 4 は，1s, 2s, 3s軌道における電子の存在確率を，ガラスブロック内にレーザーで彫刻したものである．この方法では，節面が暗部として明瞭に観察できるだけでなく，空間全体にわたる電子の存在確率の変化の様子が，点の密度として反映されている，さらに，各軌道の広がりの比較(大きさの比較)も可能であるという特徴がある [3,4]．

Figure 4.

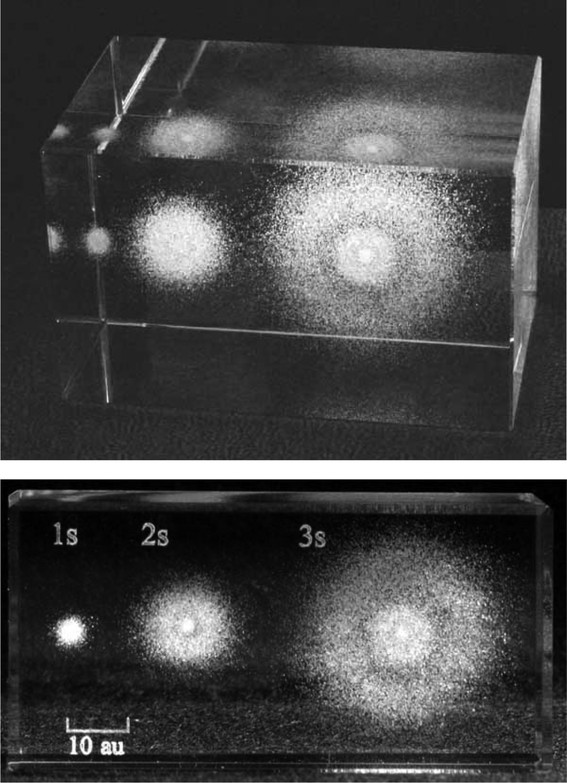
 Probability density distribution in the 3-dimensional representation of hydrogen 1s, 2s, and 3s orbitals in a 5 x 5 x 8 cm³(top) or a 4 x 4 x 8 cm³ glass block (bottom) [4]

当初は，各軌道データの1/4や1/8をカットして，節面を見やすくすることも試みた．しかし，彫刻点の数を調整することにより，カットせずとも，節面が明瞭に観察できる彫刻条件が見出せることが明らかとなった．

6 おわりに

ガラス彫刻の特徴は，節面を持つ原子軌道の場合に顕著に現れることを，s軌道について取りまとめた．原子軌道 (2) における$R_{nl}\left(r\right)$を動径波動関数という．動径波動関数の導出法と，s軌道の具体的な数式の形は，補足資料（電子付録）に示した．原子軌道の数式は，いろいろな著書 [5] やホームページ [6] で調べられるが，高次の軌道の記載は稀で，校正ミスも散見される．そこで，いかに高次の軌道でも誤りなく対応可能な方法をまとめた．数式の形から，原子軌道関数の極大，極小や，節面の位置がわかるので，適宜参照していただきたい．次回以降では，p軌道以上のさまざまな軌道のかたちや，波動性の現れ方について取扱っていく予定である．

参考文献

• 1   S. Tokita, Visualization of Orbitals (2) Probability Density Distribution in the Three Dimensional Representation of a Hydrogen 1s Orbital in a Glass Block, J. Comput. Chem. Jpn, 14, A6-A10 (2015); in Japanese;http://doi.org/10.2477/jccj.2015-0003
• 2   S. Tokita, T. Sugiyama, H. Hosoya, “A Novel Animation of Atomic Orbitals Using QTVR”, J. Comput. Aided Chem., 1, 68-75 (2000), in Japanese; http://doi.org/10.2751/jcac.1.68
• 3   S. Tokita, Kagaku (Kyoto), 65, 26 (2010), in Japanese.
• 4   http://winmostar.just-size.jp/nebula/index_cover.html
• 5   S. Tokita, "Me de Miru Ryosi Kagaku", Kodansha Ltd., (1987), p. 210–212, in Japanese.
• 6   for example: The OrbitronTM, a gallery of orbitals on the WWW, URL: http://winter.group.shef.ac.uk/orbitron/for7s: http://winter.group.shef.ac.uk/orbitron/AOs/7s/equations.html