Visualization of the Exact Solution of Dirac Equation

Abstract

水素原子のDirac方程式は厳密解が得られている．そのスピノルの形状を知ることは，重元素を含む分子での相対論効果を議論するうえで重要である．s, p, d, fの各スピノルは特徴のある形状をしているが，本論文の目的は電子密度の3D等値面図を図鑑にすることで各スピノルの特徴を一望できるようにすることにある．Schrödinger方程式の厳密解の図も併記しており，相対論では非相対論と比較して節が少なくなっていることが容易に見てとれる．Z = 100の<r > を計算し，その詳細を分析した．相対論的効果で<r > が減少するが，その効果は一様ではなく，s_1/2とp_1/2で大きい．描画と計算に用いたMathematicaノートブックは本論文とともに提供しており，改変可能な教材として利用できる．

1 はじめに

原子分子ではSchrödinger方程式 [1,2]が基礎方程式であり，水素原子の厳密解が教科書 [1,2]に掲載されている．原子軌道の可視化 [3]については本誌 [4]においても関連記事が掲載されている．ランタノイドなどの重元素を含む分子では相対論の効果が顕著になり，基礎方程式はDirac方程式 [1,2,5,6]となる．本論文ではDirac方程式の水素様原子の厳密解を扱う．

水素原子の厳密解はDirac本人ではなく，Gordon [7]とDarwin [8]により与えられた．Gordon [7]は解を合流型超幾何関数で表している．これが一般化Laguerre関数でも表現できることはPidduck [9]によって示されていたが，長らく看過されてきた [10,11]．

厳密解の可視化は，我々の知る限りWhite [12]によるものが嚆矢である．Whiteは電子密度の断面図や電子雲図を提示している．その後，Powell [13]やSzabo [14]が可視化を議論している．Grantの著書 [15]には，角度成分の密度の3D等値面図が掲載されているが，動径成分も含めた3D等値面図ではない．

Wolfram Mathematica [16]を使えば，比較的簡単に電子密度の3D等値面図を描くことができる．s, p, d, f スピノルは特徴のある形状をしており，それらの特徴を把握するには，すべての図を並べるのが最適である．しかしながら，分かりやすい図を得るには，図の大きさ，等高値などのパラメータをスピノルごとに最適なものにする必要がある．そこで，我々はスピノルの図鑑を作成することにした．これが本論文の目的である．

また，Z = 1とZ = 100の場合の<r > を計算し，スピノルの空間的な広がりを分析した．収縮に対する相対論効果を調べた．

MathematicaノートブックをSupplement 3 [30](電子付録)として提供し，ユーザがコードを改変して発展的に利用できるようにした．教材としても使われることを期待している．Mathematica環境がない場合は，CDF player [17]で閲覧ができる．

2 固有値と固有関数

水素原子のDirac方程式のHamiltonianは次の4行4列の行列で与えられる．   

$H=c\alpha ·p+(\beta -1)m_e{c}^2-\frac{Z}{r}$(1)

  

${\alpha }_i=\left(\begin{array}{cc}0& {\sigma }_i\\ {\sigma }_i& 0\end{array}\right)(i=x,y,z),\beta =\left(\begin{array}{cc}{I}_2& 0\\ 0& -I_2\end{array}\right)$(2)

ここで，cは光速度，m_e は電子の質量，Zは核電荷，σ_i はPauliスピン行列   

${\sigma }_x=\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right),{\sigma }_y=\left(\begin{array}{cc}0& -i\\ i& 0\end{array}\right),{\sigma }_z=\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right)$(3)

であり，I₂ は2行2列の単位行列である．

Hの固有関数をDyall and Faegri [6]に従って，次のように書くことにする．u₁, u₂, u₃, u₄ が4成分である．   

$\Psi =\frac{1}{r}\left(\begin{array}{c}{P}_{n\kappa }\left(r\right){\xi }_{\kappa ,m}(\theta ,\phi )\\ i{Q}_{n\kappa }\left(r\right){\xi }_{-\kappa ,m}(\theta ,\phi )\end{array}\right)=\left(\begin{array}{c}{u}_1\\ u_2\\ u_3\\ u_4\end{array}\right)$(4)

ξ は角度成分である．u₁, u₂ は大成分，u₃, u₄ は小成分と呼ばれる．動径成分の大成分g(r)，小成分f(r)は以下の如くである．   

$g\left(r\right)=\frac{P_{n\kappa }\left(r\right)}{r},f\left(r\right)=\frac{Q_{n\kappa }\left(r\right)}{r}$(5)

軌道角運動量lやスピン角運動量sはHと可換ではなく，可換であるのは j = l + s で，このjが全角運動量量子数 j を与える．なお，主量子数をn，j_zに対する固有値をmとする．量子数κ はTable 1で与えられる．

Table 1. Quantum numbers and labels.

l	0	1	1	2	2	3	3
j	1/2	1/2	3/2	3/2	5/2	5/2	7/2
κ	–1	1	–2	2	–3	3	–4
Labels	s1/2	p1/2	p3/2	d3/2	d5/2	f5/2	f7/2
Labels	s+	p–	p+	d–	d+	f–	f+

角度成分を顕わに書き下すと，4成分は以下のようになる．j = l + 1/2 に対して，   

$\begin{array}{c}{u}_1=g\left(r\right)\sqrt{\frac{l+m+1/2}{2l+1}}{Y}_{l,m-1/2}(\theta ,\varphi ),\\ u_2=g\left(r\right)\sqrt{\frac{l-m+1/2}{2l+1}}{Y}_{l,m+1/2}(\theta ,\varphi ),\\ u_3=-if\left(r\right)\sqrt{\frac{l-m+3/2}{2l+3}}{Y}_{l+1,m-1/2}(\theta ,\varphi ),\\ u_4=if\left(r\right)\sqrt{\frac{l+m+3/2}{2l+3}}{Y}_{l+1,m+1/2}(\theta ,\varphi ).\end{array}$(6)

j = l − 1/2 に対して，   

$\begin{array}{c}{u}_1=-g\left(r\right)\sqrt{\frac{l-m+1/2}{2l+1}}{Y}_{l,m-1/2}(\theta ,\varphi ),\\ u_2=g\left(r\right)\sqrt{\frac{l+m+1/2}{2l+1}}{Y}_{l,m+1/2}(\theta ,\varphi ),\\ u_3=if\left(r\right)\sqrt{\frac{l+m-1/2}{2l-1}}{Y}_{l-1,m-1/2}(\theta ,\varphi ),\\ u_4=if\left(r\right)\sqrt{\frac{l-m-1/2}{2l-1}}{Y}_{l-1,m+1/2}(\theta ,\varphi ).\end{array}$(7)

Y_l',m' (θ,ϕ) は球面調和関数である．その具体的な表式は，たとえばPauling and Wilson [18]を参照されたい．f₊ までの角度成分の詳細はTable 2のようになる．

Table 2. The angular part of the exact solution of the Dirac equation.*

Labels	mj = 1/2	mj = 3/2	mj = 5/2	mj = 7/2
s1/2 (s+)	$\begin{array}{c}\left(\begin{array}{c}{Y}_{0,0}\\ 0\end{array}\right)\\ \frac{1}{\sqrt{3}}\left(\begin{array}{c}-Y_{1,0}\\ \sqrt{2}{Y}_{1,1}\end{array}\right)\end{array}$
p1/2 (p–)	$\begin{array}{c}\frac{1}{\sqrt{3}}\left(\begin{array}{c}-Y_{1,0}\\ \sqrt{2}{Y}_{1,1}\end{array}\right)\\ \left(\begin{array}{c}{Y}_{0,0}\\ 0\end{array}\right)\end{array}$
p3/2 (p+)	$\begin{array}{c}\frac{1}{\sqrt{3}}\left(\begin{array}{c}\sqrt{2}{Y}_{1,0}\\ Y_{1,1}\end{array}\right)\\ \frac{1}{\sqrt{5}}\left(\begin{array}{c}-\sqrt{2}{Y}_{2,0}\\ \sqrt{3}{Y}_{2,1}\end{array}\right)\end{array}$	$\begin{array}{c}\frac{1}{\sqrt{3}}\left(\begin{array}{c}\sqrt{3}{Y}_{1,1}\\ 0\end{array}\right)\\ \frac{1}{\sqrt{5}}\left(\begin{array}{c}-Y_{2,1}\\ \sqrt{4}{Y}_{2,2}\end{array}\right)\end{array}$
d3/2 (d–)	$\begin{array}{c}\frac{1}{\sqrt{5}}\left(\begin{array}{c}-\sqrt{2}{Y}_{2,0}\\ \sqrt{3}{Y}_{2,1}\end{array}\right)\\ \frac{1}{\sqrt{3}}\left(\begin{array}{c}\sqrt{2}{Y}_{1,0}\\ Y_{1,1}\end{array}\right)\end{array}$	$\begin{array}{c}\frac{1}{\sqrt{5}}\left(\begin{array}{c}-Y_{2,1}\\ \sqrt{4}{Y}_{2,2}\end{array}\right)\\ \frac{1}{\sqrt{3}}\left(\begin{array}{c}\sqrt{3}{Y}_{1,1}\\ 0\end{array}\right)\end{array}$
d5/2 (d+)	$\begin{array}{c}\frac{1}{\sqrt{5}}\left(\begin{array}{c}\sqrt{3}{Y}_{2,0}\\ \sqrt{2}{Y}_{2,1}\end{array}\right)\\ \frac{1}{\sqrt{7}}\left(\begin{array}{c}-\sqrt{3}{Y}_{3,0}\\ \sqrt{4}{Y}_{3,1}\end{array}\right)\end{array}$	$\begin{array}{c}\frac{1}{\sqrt{5}}\left(\begin{array}{c}\sqrt{4}{Y}_{2,1}\\ Y_{2,2}\end{array}\right)\\ \frac{1}{\sqrt{7}}\left(\begin{array}{c}-\sqrt{2}{Y}_{3,1}\\ \sqrt{5}{Y}_{3,2}\end{array}\right)\end{array}$	$\begin{array}{c}\frac{1}{\sqrt{5}}\left(\begin{array}{c}\sqrt{5}{Y}_{2,2}\\ 0\end{array}\right)\\ \frac{1}{\sqrt{7}}\left(\begin{array}{c}-Y_{3,2}\\ \sqrt{6}{Y}_{3,3}\end{array}\right)\end{array}$
f5/2 (f–)	$\begin{array}{c}\frac{1}{\sqrt{7}}\left(\begin{array}{c}-\sqrt{3}{Y}_{3,0}\\ \sqrt{4}{Y}_{3,1}\end{array}\right)\\ \frac{1}{\sqrt{5}}\left(\begin{array}{c}\sqrt{3}{Y}_{2,0}\\ \sqrt{2}{Y}_{2,1}\end{array}\right)\end{array}$	$\begin{array}{c}\frac{1}{\sqrt{7}}\left(\begin{array}{c}-\sqrt{2}{Y}_{3,1}\\ \sqrt{5}{Y}_{3,2}\end{array}\right)\\ \frac{1}{\sqrt{5}}\left(\begin{array}{c}\sqrt{4}{Y}_{2,1}\\ Y_{2,2}\end{array}\right)\end{array}$	$\begin{array}{c}\frac{1}{\sqrt{7}}\left(\begin{array}{c}-Y_{3,2}\\ \sqrt{6}{Y}_{3,3}\end{array}\right)\\ \frac{1}{\sqrt{5}}\left(\begin{array}{c}\sqrt{5}{Y}_{2,2}\\ 0\end{array}\right)\end{array}$
f7/2 (f+)	$\begin{array}{c}\frac{1}{\sqrt{7}}\left(\begin{array}{c}\sqrt{4}{Y}_{3,0}\\ \sqrt{3}{Y}_{3,1}\end{array}\right)\\ \frac{1}{\sqrt{9}}\left(\begin{array}{c}-\sqrt{4}{Y}_{4,0}\\ \sqrt{5}{Y}_{4,1}\end{array}\right)\end{array}$	$\begin{array}{c}\frac{1}{\sqrt{7}}\left(\begin{array}{c}\sqrt{5}{Y}_{3,1}\\ \sqrt{2}{Y}_{3,2}\end{array}\right)\\ \frac{1}{\sqrt{9}}\left(\begin{array}{c}-\sqrt{3}{Y}_{4,1}\\ \sqrt{6}{Y}_{4,2}\end{array}\right)\end{array}$	$\begin{array}{c}\frac{1}{\sqrt{7}}\left(\begin{array}{c}\sqrt{6}{Y}_{3,2}\\ Y_{3,3}\end{array}\right)\\ \frac{1}{\sqrt{9}}\left(\begin{array}{c}-\sqrt{2}{Y}_{4,2}\\ \sqrt{7}{Y}_{4,3}\end{array}\right)\end{array}$	$\begin{array}{c}\frac{1}{\sqrt{7}}\left(\begin{array}{c}\sqrt{7}{Y}_{3,3}\\ 0\end{array}\right)\\ \frac{1}{\sqrt{9}}\left(\begin{array}{c}-Y_{4,3}\\ \sqrt{8}{Y}_{4,4}\end{array}\right)\end{array}$

* The upper and lower parts denote the large and small components, respectively.

P_nκ，Q_nκ は次のようになる．   

$\begin{array}{c}{P}_{n\kappa }\left(r\right)=N_{n\kappa }{e}^{-x/2}{x}^{\gamma }\\ \times N_P\left[\right(N_{\kappa }-\kappa \left)F\right(-n_r,2\gamma +1,x)\\ -n_{r}F(-n_r+1,2\gamma +1,x)]\end{array}$(8)

  

$\begin{array}{c}{Q}_{n\kappa }\left(r\right)=N_{n\kappa }{e}^{-x/2}{x}^{\gamma }\\ \times N_Q\left[\right(N_{\kappa }-\kappa \left)F\right(-n_r,2\gamma +1,x)\\ +n_{r}F(-n_r+1,2\gamma +1,x)]\end{array}$(9)

ここで，Fは合流型超幾何関数，   

$\gamma =\sqrt{{\kappa }^2-{\left(\alpha Z\right)}^2},k=\left|\kappa \right|,n_r=n-k,$(10)

  

$N_{\kappa }=\sqrt{n^2-2n_r(k-\gamma )},\lambda =Z/N_{\kappa },$(11)

  

$x=2\lambda r,$(12)

  

$N_{n\kappa }=\frac{1}{N_{\kappa }\Gamma (2\gamma +1)}\sqrt{\frac{Z\Gamma (2\gamma +1+n_r)}{2n_r!(N_{\kappa }-\kappa )},}$(13)

  

$E_{n\kappa }=-\frac{1}{{\alpha }^2}\left(1-\sqrt{1-{\left(\frac{\alpha Z}{N_{\kappa }}\right)}^2}\right),$(14)

  

$N_P=\sqrt{2+E_{n\kappa }{\alpha }^2},N_Q=\sqrt{-E_{n\kappa }{\alpha }^2}.$(15)

固有値 E_n,κ は式(14)で表され，n, κ に依存する．換言すると，n, j に依存するが，l には依らない．たとえば，2s₊ と2p_– は同じエネルギー値を与える．α は微細構造定数で，1/137.03599を用いた．原子単位系ではc = 1/αである．

一方，Schrödinger方程式の厳密解ψ_nlm(r,θ,ϕ)は次式で与えられる．   

$\begin{array}{c}{\psi }_{nlm}(r,\theta ,\varphi )=R_{nl}\left(r\right)Y_{lm}(\theta ,\varphi ),\\ R_{nl}\left(r\right)=\\ \frac{1}{(2l+1)!}\sqrt{\frac{(n+l)!}{(n-l-1)!2n}}{\left(\frac{2Z}{n}\right)}^{\frac{3}{2}}\\ \times e^{-\frac{Zr}{n}}{\left(\frac{2Zr}{n}\right)}^{l}F\left(-n+l+1,2l+2,\frac{2Zr}{n}\right)\end{array}$(16)

式(8, 9, 16)の中の合流型超幾何関数は，次の関係式を用いて一般化Laguerre関数L_n^(a)(x)で表すこともできる．Dirac方程式の場合，aは非整数となるので注意されたい．   

$\begin{array}{c}{L}_n^{\left(a\right)}\left(x\right)=\frac{\Gamma (n+a+1)}{n!\Gamma (a+1)}F(-n,a+1,x)\\ =\frac{{(a+1)}_n}{n!}F(-n,a+1,x)\end{array}$(17)

Γ(x)はガンマ関数，(a)_nはポッホハマー記号(Pochhammer symbol)である．

Dirac方程式の解の規格化密度関数ρ_rel，Schrödinger方程式の解の規格化密度関数ρ_nonrelはそれぞれ，   

${\rho }_{\text{rel}}(r,\theta ,\varphi )=u_1{u}_1^{*}+u_2{u}_2^{*}+u_3{u}_3^{*}+u_4{u}_4^{*},$(18)

  

${\rho }_{\text{nonrel}}(r,\theta ,\varphi )={\psi }_{nlm}{\psi }_{nlm}^{*}$(19)

で表され，z軸に対して対称になる．通常の分子軌道法では，ψ_nlmの角度成分Y_l,mを実数化してCartesian座標系で扱うことが多いが，ここでは複素関数のまま扱っている．

3 Mathematicaによるプロット

2節で述べた各種の数学関数は，Mathematicaにすべて用意されている．使用したMathematica関数を列挙する．

○球面調和関数   

$Y_{lm}(\theta ,\varphi )\to \text{SphericalHarmonicY}[l,m,\theta ,\varphi ]$

○合流型超幾何関数   

$F(a,b,x)\to \text{Hypergeometric1F1}[a,b,x]$

○ガンマ関数   

$\Gamma \left(x\right)\to \text{Gamma}\left[x\right]$

○ポッホハマー記号   

${\left(a\right)}_n\to \text{Pochhammer}[a,n]$

○一般化Laguerre関数   

$L_n^{\left(a\right)}\left(x\right)\to \text{LaguerreL}[n,a,x]$

Table 3に電子密度のプロットに適用したMathematicaのコードの主要部分を示す．完全なMathematicaノートブックはSupplement 3 [30]に載せている．

Table 3.  Mathematica code for density plot.

4 スピノル図鑑

Figures 1–16に1s₊∼4f₊スピノルの規格化密度関数のyz面での断面図(左)，3D等値面図(右)を与える．密度は動径成分と角度成分両方の寄与から成る全電子密度である．上段が非相対論，下段が相対論の図である．α，βスピン成分の両方からの寄与があるが，紙面の都合上，大成分での角度成分の寄与が大きい方に対応する非相対論の密度図(l, m)だけを上段に配置した．例えば，4f_7/2,1/2にはαスピン成分からl = 3, m = 0，4f_5/2,1/2にはβスピン成分からl = 3, m = 1を選んでいる．

Figure 1.

 1s₊ density.

1s(l = 0, m = 0 α)/1s₊ (j = 1/2, m_j = 1/2)

Figure 2.

 2p_– density.

2p(l = 1, m = 1 β)/2p_– (j = 1/2, m_j = 1/2)

Figure 3.

 2p₊ density.

2p(l = 1, m = 1 α)/2p₊ (j = 3/2, m_j = 3/2)

規格化密度関数の等高線図，3D等値面表示に用いたパラメータはTable 4の通りである．表中のhは表示範囲(–h, h (単位はa.u.) cmaxは等高線のうちの最高密度値，ncは等高線数，vは3D等値面図の密度値である．

Table 4. Parameters for density plot.

Labels	h	cmax	nc	v
1s	1	2.04E-1	6	1.E-4
2p	6	2.04E-3	6	3.E-4
3d	13	2.04E-4	6	3.E-5
4f	22	2.64E-5	6	1.E-4
5g	40	1.30E-5	6	4.E-6

gスピノルはRydberg状態 [19]や励起状態で占有されることがあるが，基底状態は超アクチノイド元素でしか占有されないため，関連図を s~fスピノルの図とともにSupplement 1 [28]に収めた．

1s₊∼5g₊スピノルの動径成分，動径密度関数のグラフはSupplement 2 [29]に収めてある．動径成分の小成分は，Zα でスケーリングしてある．動径成分は非相対論の動径関数にきわめて近い．なお，Burke and Grant [20]にはZ = 80の場合の動径密度関数のグラフが掲載されている．

5 節の減少

Schrödinger方程式の解に慣れた化学者にとって，Dirac方程式の解には戸惑う点が幾つかある．その1つが節の減少である．White [12]は，非相対論で見られた動径成分の節の多くが，Dirac方程式においては消失することを指摘した．実際，2p_3/2,1/2(Figure 4)では節が消失している．yz断面図からも節が消失している状況が観取できる．

Figure 4.

 2p₊ density.

2p(l = 1, m = 0 α)/2p₊ (j = 3/2, m_j = 1/2)

Figure 5.

 3d_– density.

3d(l = 2, m = 2 β)/3d_– (j = 3/2, m_j = 3/2)

Figure 6.

 3d_– density.

3d(l = 2, m = 1 β)/3d_– (j = 3/2, m_j = 1/2)

Figure 7.

 3d₊ density.

3d(l = 2, m = 2 α)/3d₊ (j = 5/2, m_j = 5/2)

Figure 8.

 3d₊ density.

3d(l = 2, m = 1 α)/3d₊ (j = 5/2, m_j = 3/2)

Figure 9.

 3d₊ density.

3d(l = 2, m = 0 α)/3d₊ (j = 5/2, m_j = 1/2)

Figure 10.

 4f_– density .

4f(l = 3, m = 3 β)/4f_– (j = 5/2, m_j = 5/2)

Figure 11.

 4f_– density

4f(l = 3, m = 2 β)/4f_– (j = 5/2, m_j = 3/2)

Figure 12.

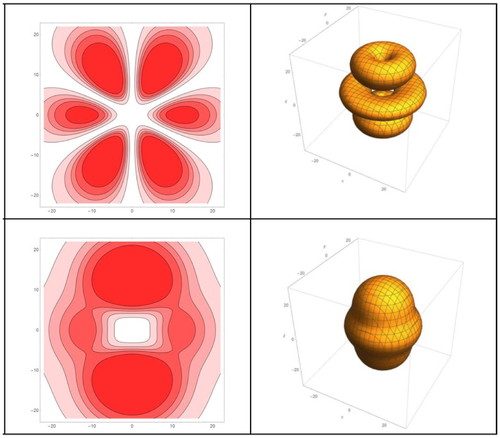
 4f_– density

4f(l = 3, m = 1 β)/4f_– (j = 5/2, m_j = 1/2)

Figure 13.

 4f₊ density .

4f(l = 3, m = 3 α)/4f₊ (j = 7/2, m_j = 7/2)

Figure 14.

 4f₊ density

4f(l = 3, m = 2 α)/4f₊ (j = 7/2, m_j = 5/2)

Figure 15.

 4f₊ density

4f(l = 3, m = 1 α)/4f₊ (j = 7/2, m_j = 3/2)

Figure 16.

 4f₊ density

4f(l = 3, m = 0 α)/4f₊ (j = 7/2, m_j = 1/2)

我々は非相対論において，波動関数の分類に節の数 [21]が使えることを示してきたが，相対論ではその利用が制限される．

Whiteは，p_1/2,1/2 (Figure 2)の密度が真球状であることも指摘している．p_1/2,1/2の大成分の角度部分のαスピン成分(t₁)，βスピン成分(t₂)Table 2に与えてあるが，t₁t₁* + t₂t₂* は [Y_1,0Y_1,0* + 2Y_1,1Y_1,1*]/3 = 1/(4π) となり，(θ, ϕ)に依らない．加えて，小成分の角度部分はs型で，これも(θ, ϕ)に依らない．

節が消失する主要な理由は，大成分•小成分内で同じl値を持ち，異なるm値を持つ角度成分がスピンとの相互作用で混じり，かつ大成分•小成分からの異なったl値をもった角度分布成分が混じることである．もう1つの理由は，動径成分の4成分の節の位置が一致しないことである．大成分の節のところに小成分からの寄与のために電子密度が僅かに生じる．これをSzabo [14]はpseudo-nodeと呼んでいる．

なお，2p_3/2,3/2(Figure 3)では，零となるのは相対論でも非相対論でもz軸上のみである．

6 平均半径に対する相対論的効果

< r > , <r²> の表式はGarstang and Mayers [22]によって与えられている．水素原子とFm⁹⁹⁺(Z = 100)の厳密解に対して<r > を計算しTables 5–6にまとめた．Table 6の中性Fm原子([Rn]5f¹² 7s²)の<r > はHartree-Fock計算 [23,24,25]に基づく．uncontracted GTF (28s 21p 15d 13f) による計算と相対論的numerical Hartree-Fock [25]である．相対論のHartree-Fock計算 [23,25]では，原子核に対してuniform charge distribution [23]またはpoint charge model [25]を適用している．両者の差はほとんどない．得られた知見を以下に述べる．

Table 5. Expectation values of r for Z = 1.

		<r >		<r2>
Labels	n	rel	nonrel	rel	nonrel
s+	1	1.4999734	1.5	2.9999068	3
	2	5.9998835	6.0	41.998496	42
	3	13.499802	13.5	206.99421	207
	4	23.999721	24.0	647.98545	648
	5	37.499641	37.5	1574.9706	1575
	6	53.999561	54.0	3257.9481	3258
p–	2	4.9998835	5.0	29.998735	30
	3	12.499802	12.5	179.99461	180
	4	22.999721	23.0	599.98601	600
	5	36.499641	36.5	1499.9713	1500
	6	52.999561	53.0	3149.9490	3150
p+	2	4.999973	5.0	29.999707	30
	3	12.499926	12.5	179.99804	180
	4	22.999884	23.0	599.99430	600
	5	36.499842	36.5	1499.9877	1500
	6	52.999802	53.0	3149.9774	3150
d–	3	10.499926	10.5	125.99836	126
	4	20.999884	21.0	503.99478	504
	5	34.499842	34.5	1349.9883	1350
	6	50.999802	51.0	2933.9782	2934
d+	3	10.499973	10.5	125.99940	126
	4	20.999941	21.0	503.99739	504
	5	34.499912	34.5	1349.9936	1350
	6	50.999884	51.0	2933.9874	2934
f–	4	17.999941	18.0	359.99779	360
	5	31.499912	31.5	1124.9941	1125
	6	47.999884	48.0	2609.9881	2610
f+	4	17.999973	18.0	359.99899	360
	5	31.499949	31.5	1124.9966	1125
	6	47.999926	48.0	2609.9925	2610

Table 6. Expectation values of r for Z = 100.

		Fm99+ (exact)			Fm (Hartree-Fock)
Labels	n	<r > rel	<r > nonrel	Cont. (%) a	<r > relb	<r > nonrelc	Cont. (%) a	<r > rel-NHFd
s+	1	0.0118	0.015	21.1	0.0120	0.0151	20.6	0.0120
	2	0.0468	0.060	22.1	0.0495	0.0630	21.5	0.0493
	3	0.1121	0.135	16.9	0.1293	0.1558	17.0	0.1291
	4	0.2076	0.240	13.5	0.2790	0.3265	14.5	0.2786
	5	0.3331	0.375	11.2	0.5716	0.6630	13.8	0.5708
	6	0.4886	0.540	9.5	1.2748	1.5426	17.4	1.2724
	7	0.6741	0.735	8.3	4.1333	4.9329	16.2	4.1226
p–	2	0.0368	0.050	26.5	0.0396	0.0531	25.5	0.0395
	3	0.1021	0.125	18.3	0.1209	0.1476	18.1	0.1209
	4	0.1976	0.230	14.1	0.2761	0.3247	15.0	0.2761
	5	0.3231	0.365	11.5	0.5895	0.6871	14.2	0.5894
	6	0.4786	0.530	9.7	1.4085	1.7422	19.2	1.4102
p+	2	0.0472	0.050	5.5	0.0509	0.0531	4.2	0.0509
	3	0.1174	0.125	6.1	0.1411	0.1476	4.4	0.1411
	4	0.2180	0.230	5.2	0.3136	0.3247	3.4	0.3136
	5	0.3488	0.365	4.4	0.6677	0.6871	2.8	0.6678
	6	0.5096	0.530	3.8	1.6989	1.7422	2.5	1.6994
d–	3	0.0974	0.105	7.2	0.1213	0.1276	4.9	0.1213
	4	0.1980	0.210	5.7	0.3076	0.3182	3.3	0.3076
	5	0.3288	0.345	4.7	0.7329	0.7513	2.5	0.7330
d+	3	0.1023	0.105	2.6	0.1271	0.1276	0.4	0.1271
	4	0.2040	0.210	2.8	0.3185	0.3182	–0.1	0.3185
	5	0.3361	0.345	2.6	0.7606	0.7513	–1.2	0.7607
f–	4	0.1740	0.180	3.3	0.3017	0.2998	–0.6	0.3017
	5	0.3061	0.315	2.8	1.0751	1.0043	–7.0	1.0757
f+	4	0.1773	0.180	1.5	0.3069	0.2998	–2.3	0.3069
	5	0.3098	0.315	1.6	1.1184	1.0043	–11.4	1.1192

^a Contraction ratio, i.e., (<r > _nonrel − <r > _rel)/<r > _nonrel ×100.

^b Ref [23].

^c Ref [24].

^d Numerical Hartree-Fock. Ref [25].

6.1 H原子

< r > , <r²>について，相対論と非相対論の差はほとんどない．

6.2 Fm⁹⁹⁺

(i) 相対論的効果を取り入れることにより全てのスピノルで収縮が見られる．

(ii) 収縮の度合いを ((<r > _nonrel − <r > _rel)/<r > _nonrel ×100)とすると，厳密解の場合，収縮の度合いもエネルギーと同様に主量子数nと角運動量jで識別される．依存するのはlではなく，jである点に注意されたい．Figure 17にn = 3, j = 1/2 (s₊, p_–), j = 3/2 (p₊, d_–), j = 5/2 (d₊) に対する収縮の度合いをHからFm⁹⁹⁺まで与えてある．jによる区分けは明瞭である．収縮の度合いはj = 1/2つまりs₊, p_– が他に比べてかなり大きく，Fm⁹⁹⁺ (Z = 100) の3s₊では16.9%，3p_–で18.3%である．一方，3p₊では6.1%，3d_–で7.2%である．3p₊と3d_–の収縮の度合いはほぼ等しい．

Figure 17.

 Contraction ratio (<r > _nonrel − <r > _rel)/<r > _nonrel ×100) versus Z.

(iii) j，nが大きいほど相対論的効果は小さくなる．これはすべての原子について言える．Figure 17にはn = 3の場合のj = 1/2と3/2が与えてあるが，両者の差は核電荷の増大とともに大きくなる．収縮の度合いが5%を超えるのは，3s₊でCe⁵⁸⁺，3p_–でBa⁵⁵⁺，3p₊でU⁹¹⁺である．図には出していないが，収縮の度合いが5%を超えるのは，1s₊でI⁵²⁺，2s₊でSb⁵⁰⁺，2p_–でPd⁴⁵⁺であり，3s₊, 3p_–と比較して小さな核荷電を持つ原子イオンとなる．

6.3 Fm原子

(i) 相対論的な計算でも非相対論的計算でもFmの<r > は対応するFm⁹⁹⁺の<r > より大きく，電子間反発の重要性が分かる．

(ii) Fm⁹⁹⁺と同じく，収縮の度合いは，j = 1/2つまりs₊とp_–が他に比べてかなり大きい．Fm⁹⁹⁺との違いは，s₊，p_–ではnが大きくなっても相対論的効果が大きいことである．

(iii) j = 3/2以降ではFm原子のスピノルの収縮の度合いはFm⁹⁹⁺に比べ小さくなる．4d₊以降では相対論的効果は減少し，<r > _relは<r > _nonrelより大きくなる．電子間反発相互作用の効果(遮蔽効果)が相対論的効果を上回り，スピノルを押し広げている．

(iv) Hg²⁺電子殻(5s² 5p⁶ 5d¹⁰ 4f¹⁴)からの電子反発により，特にFmの5fは非相対論の場合と比べてより大きく押し出されている．

7 おわりに

本論文では，水素原子Dirac方程式の厳密解の規格化密度関数の3D等値面表示を行った．スピノルの形状を表現する方法としては4成分の各成分を表示する方法 [26,27]もある．

References

• [1]   W. R. Johnson, "Atomic Structure Theory: Lectures on Atomic Physics", Springer, Berlin (2006).
• [2]   H. A. Bethe, E. E. Salpeter, "Quantum Mechanics of One- and Two-Electron Atoms", Dover Publ. Inc., Mineola, NY (2008).
• [3]   K. Suzuki, O. Kikuchi, "Denshi no Kido", Kyoritsu Shuppan, Tokyo (1984), in Japanese.
• [4]   S. Tokita, J. Comput. Chem. Jpn., 15, A7 (2016).
• [5]   P. A. M. Dirac, Proc. R. Soc. Lon. Ser.-A 117, 610–624 (1928).
• [6]   K. G. Dyall, K. Faegri, Jr., "Introduction to Relativistic Quantum Chemistry", Oxford Univ. Press, New York (2007).
• [7]   W. Gordon, Z. Phys., 48, 11 (1928).
• [8]   C. G. Darwin, Proc. R. Soc. Lon. Ser.-A 118, 654–680 (1928).
• [9]   F. D. Pidduck, J. Lond. Math. Soc., s1-4, 163 (1929).
• [10]   J. Mawhin, A. Ronveaux, Arch. Hist. Exact Sci., 64, 429 (2010).
• [11]   R. P. Martínez-y-Romero, Am. J. Phys., 68, 1050 (2000).
• [12]   H. E. White, Phys. Rev., 38, 513 (1931).
• [13]   R. E. Powell, J. Chem. Educ., 45, 558 (1968).
• [14]   A. Szabo, J. Chem. Educ., 46, 678 (1969).
• [15]   I. P. Grant, "Relativistic Quantum Theory of Atoms and Molecules", Springer, New York (2007).
• [16]   Wolfram Research, Inc., Mathematica, Version 10.3, Champaign, IL (2015).
• [17]   http://www.wolfram.com/cdf-player/
• [18]   L. Pauling, E. B. Wilson, Jr., "Introduction to Quantum Mechanics", Dover Publ. Inc., Mineola, NY (1985).
• [19]   S. Yamamoto, H. Tatewaki, Chem. Phys., 295, 47 (2003).
• [20]   V. M. Burke, I. P. Grant, Proc. Phys. Soc., 90, 297 (1967).
• [21]   N. Takeda, Y. Hatano, S. Yamamoto, H. Tatewaki, Comput. Theor. Chem., 1045, 99 (2014).
• [22]   R. H. Garstang, D. F. Mayers, Proc. Camb. Philos. Soc., 62, 777 (1966).
• [23]   T. Koga, H. Tatewaki, O. Matsuoka, J. Chem. Phys., 119, 1279 (2003), See also http://www.nsc.nagoya-cu.ac.jp/~htatewak/uncntrct_rel_gtf.html.
• [24]   T. Koga, H. Tatewaki, T. Shimazaki, Chem. Phys. Lett., 328, 473 (2000), We have calculated <r> using the HF orbitals given at http://www.nsc.nagoya-cu.ac.jp/~htatewak/uncontracted_gtf.html.
• [25]   L. Visscher, K. G. Dyall, At. Data Nucl. Data Tables, 67, 207 (1997), See also http://www.few.vu.nl/~visscher/FiniteNuclei/FiniteNuclei.htm.
• [26]   H. Moriyama, H. Tatewaki, S. Yamamoto, J. Chem. Phys., 138, 224310 (2013).
• [27]   H. Tatewaki, S. Yamamoto, H. Moriyama, "Low-lying excited states of lanthanide diatomics studied by four-component relativistic configuration interaction methods", in: "Computational methods in lanthanide and actinide chemistry", M. Dolg (Ed.), 89–119, Wiley, UK (2015).
• [28]   Supplement 1. 5g_density.and.Figures.zip.
• [29]   Supplement 2. radial_density.pdf.
• [30]   Supplement 3. Dirac.Hdens.plot.v0d.nb.