The Analysis of Defect Structure of Sn-based Perovskite Solar Cell Materials Using First-principles Calculations

Abstract

While Sn-based perovskite solar cells have photoelectronic properties comparable to those of lead halide perovskites, their low photoelectric conversion efficiency is a problem. The main cause of this problem is the defect level caused by the presence of defects in the crystal. In this study, we analyzed the defect structures in FASnI₃ and MASnI₃ perovskites using first-principles calculations and focused on the correlation between the photoelectric conversion efficiency and defect levels.

In both structures, the defect formation energy of V_Sn was low and tin tended to be easily removed. In FASnI₃, by changing the chemical potential to the Sn-rich, I-poor condition, the defect levels that were easy to form in the Sn-poor, I-rich condition became defect levels that were hard to form. It was also found that MASnI₃ has a wide range of thermodynamically stable regions with no defect levels that are prone to form under any chemical potential condition. Therefore, from the viewpoint of structural stability and structural defects, MA is preferable to FA as the A-site cation of Sn-based perovskite.

1 Introduction

Perovskite solar cells, which use perovskite crystals in the light-absorbing layer, are expected to become the next-generation solar cells because they have achieved high photoelectric conversion efficiency comparable to that of silicon-based solar cells. Currently, among perovskite solar cells, lead halide perovskite has achieved the highest photoelectric conversion efficiency [1], but the toxicity of lead has become a problem from the viewpoint of practical use, and lead-free solar cells are required. Therefore, Sn-based perovskite solar cells are attracting attention as a lead-free perovskite because of their high stability and resistance to heat and light [2]. However, Sn-based perovskite solar cells suffer from low photoelectric conversion efficiency. One of the main reasons for this is "defects". The presence of defects in the crystal causes the appearance of deep levels in the band gap (defect levels), which trap carriers and induce carrier recombination, leading to low photoelectric conversion efficiency [3]. In this study, we analyze the defect structures of FASnI₃, which contains formamidinium with high thermal stability at the A site, and MASnI₃, which contains methylammonium, the most widely studied, using first-principles calculations, and discuss the influence of the A-site cations on the defect levels [4].

2 Methods

In FASnI₃ and MASnI₃, we focused on a series of point defects [5], namely atomic vacancies, self-interstitial atoms, and anti-site defects, and considered the defect levels that are formed. First-principles calculations were performed using the DFT calculation package VASP (Vienna ab initio package) under the condition that the cutoff energy of the plane-wave expansion is 520 eV. DFT calculations were performed using the PBE (Perdew-Burke-Ernzerhof) exchange-correlation functional along with Grimme's D3 dispersion correction [6]. Defect structures for FASnI₃ and MASnI₃ were created using 2×2×2 supercells containing 8 stoichiometric units. The k-point sampling of the Brillouin zone was performed with a Γ-centered Monkhorst-Pack scheme and determined to have a density of 2×2×2 grids for 2×2×2 supercells in the case of defect structures and 2π×0.02 Å^-1 for all other cases. The point-defect calculations were conducted using Pydefect, a robust and open-source Python library [7].

3 Results and Discussion

We carried on structural optimization of FASnI₃ and MASnI₃ in primitive cell. The space groups of FASnI₃ and MASnI₃ are Amm2 and Pnma. The band gaps of FASnI₃ and MASnI₃ are 0.60 eV and 0.70 eV, respectively, confirming a direct transition band gap in both cases. The effective masses of holes and electrons were calculated to be 0.09 m₀ and 0.214 m₀ for FASnI₃ and 0.115 m₀ and 0.101 m₀ for MASnI₃. These values are similar to the results of a band gap of 0.65 eV with an effective mass of about 0.11 m₀ and 0.28 m₀ for FASnI₃ [8], and a band gap of about 0.4-0.8 eV with an effective mass of 0.101 m₀ and 0.062 m₀ for MASnI₃ [9], respectively.

A chemical potential phase diagram is created by conditions under which FASnI₃ and MASnI₃ are thermodynamically stable. For example, in the case of drawing the chemical potential phase diagram of FASnI₃, we can calculate the formation energy ΔH_f of competing phases such as FA, Sn, I, FAI, SnI₂, and SnI₄. Therefore, the condition under which FASnI₃ is thermodynamically stable [10] is,

  

${\mu }_{FA}+{\mu }_{Sn}{+3\mu }_I=∆H_f\left({FASnI}_3\right)$

and the conditions for not generating other competing phases such as FAI, SnI₂ and SnI₄ are,

  

${\mu }_{FA}+{\mu }_I<∆H_f\left(FAI\right)$

  

${\mu }_{Sn}+2{\mu }_I<∆H_f\left({SnI}_2\right)$

  

${\mu }_{Sn}+4{\mu }_I<∆H_f\left({SnI}_4\right).$

Similarly, for MASnI₃, the formation energies ΔH_f of competing phases such as MA, Sn, I, MAI, SnI₂, and SnI₄ were calculated. A phase diagram was prepared considering the conditions for thermodynamically stable formation of MASnI₃ and the conditions to avoid the formation of other competing phases such as MAI, SnI₂, and SnI₄.

Figure 1 shows the chemical potential phase diagram of (a) FASnI₃ and (b) MASnI₃. The horizontal axis is the chemical potential of Sn, and the vertical axis is the chemical potential of I. The red area indicates the stable region of FASnI₃ and MASnI₃. Compared to MASnI₃, the region of FASnI₃ is significantly narrower. In other words, FASnI₃ is more dependent on the chemical potential of the constituent elements than MASnI₃. Therefore, it was found that the crystal growth conditions must be carefully controlled when synthesizing FASnI₃.

Figure 1

 Phase diagrams of (a)FASnI₃ and (b)MASnI₃.

Figure 2 shows the defect formation energies of FASnI₃. Defect levels that easily form are those with a valence change at a defect formation energy of 0 eV or less. In particular, since defect levels appearing in the band gap affect the photoelectric conversion efficiency, we focused on the defect formation energy of defect levels appearing in the band gap. Under the Sn-poor, I-rich condition (Figure 2 (a)), I_Sn(3-/1-) defect levels, which are tin-depleted and iodine-infused defects, tend to form. However, in the Sn-rich, I-poor condition (Figure 2 (b)), the defect formation energy of I_Sn(3-/1-) is above 0 eV, indicating that this defect level is difficult to form. Therefore, in the Sn-rich, I-poor condition, there is not a defect level that is easy to form. On the other hand, MASnI₃ does not show any defect levels that affect the photoelectric conversion efficiency, because no levels are easily formed under any growth conditions, including the Sn-poor, I-rich condition (Figure 3 (a)), the Sn-rich, I-poor condition (Figure 3 (b)).

Figure 2

 Defect formation energy diagrams of native defects in FASnI₃; (a)Sn-poor, I-rich, and (b)Sn-rich, I-poor.

Figure 3

 Defect formation energy diagrams of native defects in MASnI₃; (a)Sn-poor, I-rich, and (b)Sn-rich, I-poor.

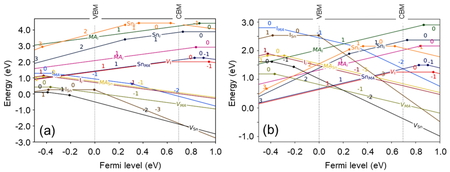
Figure 4 shows the defect level (thermodynamic ionization levels) diagrams for each structure; for FASnI₃, eight defect levels appear in the band gap. However, except for I_Sn(3-/1-),the seven defect levels are difficult to form under all growth conditions, and I_Sn(3-/1-) is also difficult to form under Sn-rich and I-poor conditions. In MASnI₃, six defect levels were found in the band gap, all of which are difficult to form under any growth conditions. In all structures, the V_Sn defect formation energy was found to be low and tin tends to be easily released. This may be attributed to the antibonding nature of the Sn-5s and I-5p orbitals at the upper end of the conduction band in each structure.

Figure 4

 Thermodynamic ionization levels of native defects in (a) FASnI₃ and (b) MASnI₃. (-/0), etc., refer to defect levels generated by charge transitions at defect sites.

4 Conclusion

From the above results, we may conclude that the formation of defect levels can be controlled in FASnI₃ by setting Sn-rich, I-poor conditions, which is expected to improve the photoelectric conversion efficiency. In MASnI₃, it was found that defect levels were less likely to form in the bandgap under any conditions, and that thermodynamically stable range for equilibrium growth was a wider than that of FASnI₃. Therefore, in terms of structural stability and strong defect resistance, MA is considered a more suitable A-site cation for tin perovskite solar cell materials than FA.

Acknowledgement

This research is supported by NEDO project of Research and Development Program for Promoting Innovative Clean Energy Technologies Through International Collaboration. We are very grateful to Prof. Shuji Hayase, University of Electro-Communications, for his helpful discussions. The DFT calculations were carried out at the Research Center for Computational Science, Okazaki, Japan (Project: 22-IMS-C064) and the Center for Computational Materials Science, Institute for Materials Research, Tohoku University for the use of MASAMUNE-IMR, (Project No. 202303-SCKXX-0025).

References

• [1]Best Research-Cell Efficiency Chart | Photovoltaic Research | NREL, (n.d.).
• [2]   G. Nasti, A. Abate, Adv. Energy Mater., 10, 1902467 (2020). doi:10.1002/aenm.201902467
• [3]   D. Meggiolaro, D. Ricciarelli, A. A. Alasmari, F. A. S. Alasmary, F. De Angelis, J. Phys. Chem. Lett., 11, 3546 (2020). doi:10.1021/acs.jpclett.0c00725 PMID:32298590
• [4]   N. Liu, C. Yam, Phys. Chem. Chem. Phys., 20, 6800 (2018). doi:10.1039/C8CP00280K PMID:29473061
• [5]   I. Yonenaga, OYO BUTURI, 86, 1040 (2017).
• [6]   S. Grimme, J. Antony, S. Ehrlich, H. Krieg, J. Chem. Phys., 132, 154104 (2010). doi:10.1063/1.3382344 PMID:20423165
• [7]   Y. Kumagai, N. Tsunoda, A. Takahashi, F. Oba, Phys. Rev. Mater., 5, 123803 (2021). doi:10.1103/PhysRevMaterials.5.123803
• [8]   M. Roknuzzaman, J. A. Alarco, H. Wang, A. Du, T. Tesfamichael, K. K. Ostrikov, Comput. Mater. Sci., 169, 109118 (2019). doi:10.1016/j.commatsci.2019.109118
• [9]   M. S. Ozório, M. Srikanth, R. Besse, J. L. F. Da Silva, Phys. Chem. Chem. Phys., 23, 2286 (2021). doi:10.1039/D0CP06090A PMID:33443529
• [10]   T. Shi, H. S. Zhang, W. Meng, Q. Teng, M. Liu, X. Yang, et al., J. Mater. Chem. A Mater. Energy Sustain., 5, 15124 (2017). doi:10.1039/C7TA02662E