J-PARCミュオンビームで拓く基礎物理実験

飯沼 裕美

doi:10.2477/jccj.2020-0023

Abstract

J-PARC MLF H-Lineとハドロンホール南実験棟で行われている3つの基礎物理実験とその相互関係を紹介します．なぜミュオンが標準模型を超えた新しい物理学へのアプローチに有用なのか，ミュオンのスピンを駆使して初期宇宙の謎を探る方法をご紹介します．

1 はじめに

スピン依存した崩壊により，自らのスピンの状態を語る性質を持つミュオンは，物質中の局所的な磁場を知る極小磁気プローブとして広く用いられています．又，ミュオンは物質世界の根源を追求する基礎物理分野に於いても，サブppm (parts per million)レベルやそれ以上の精度を狙う超精密プローブとして有用です．大強度かつ，クリーンなミュオンビームを実現するJ-PARCミュオンビームラインは，近い将来にミュオン基礎物理実験のメッカになるでしょう．

本記事では，Figure 1に示すJ-PARC MLF H-Lineや，ハドロンホール南実験棟で進行中のミュオン基礎物理実験のうちの3つを取り上げ，実験の概要と実験相互の関連性を簡単に紹介します．なぜミュオンを使って標準理論を超える新物理に迫れるのか，スピンという離散的対称性の破れ探索に適したプローブを駆使して宇宙初期の謎にどうやって迫るのか，等を筆者の観点から議論します．

Figure 1.

Preparation of new muon beam lines for precise particle physics experiments are ongoing at J-PARC MLF H-Line and Hadron Hadron hall (south).

2 離散的対称性の破れとスピン

素粒子の標準理論は我々の世界の素粒子現象の"ほぼ"全てを説明します．予言されたヒッグス粒子の存在が実験的に実証されたことは記憶に新しいです．しかし，物質優勢の宇宙の起源の全てを解明しておらず，過去数十年にわたり各地で，標準理論を越えた未知の物理事象探索は続いています．

系に連続的な対称性がある場合はそれに対応する保存則が存在すると述べるネーターの定理は，■ エネルギー・運動量の保存 → 空間・時間の並進対称性■ 角運動量の保存 → 空間の回転対称性を示します．これらは古典的な描像が成り立つ世界でも，素粒子の量子化された世界でも成り立ちます．一方，離散的な対称性は空間対称性Pと時間反転対称性Tなどがあり，ニュートン力学ではどちらに対しても不変です．しかし，素粒子の世界では破れることがあります．素粒子の基本量子数の一つである「スピン」は以下に示すように，この離散的対称性の破れを検出する強力なプローブです．離散的対称性の例を挙げましょう．

「空間反転対称性;パリティ(P)対称性の破れ」は，コバルト原子核崩壊(中性子のβ崩壊)により出てくる電子の空間分布がスピン依存することにより発見されました．「荷電共益(C)対称性の破れ」は，ニュートリノは全て左巻き，反ニュートリノは全て右巻きであり，左巻き or 右巻きというスピンの入れ替えができないことから示されます．このように，スピンは弱い相互作用に係る物理事象の離散的対称性の破れ検出に実績があると言えます．

時間反転 (T) 対称性は，現実の世界だけでなく素粒子ミクロの世界でも破られることはないと信じられていました．また，量子場の理論とローレンツ不変性(光速度不変原理と特殊相対性原理から導かれる．マクスウェル方程式はローレンツ不変．)が正しいという前提からCとPとTの同時変換のCPT対称性を持たなければなりません．よって，個々の離散的対称性が破れることがあっても，CとPの二つを同時に破らない;CP対称性は破れない，と長らく信じられてきました．しかし，CP対称性の破れも，中性K中間子や，中性B中間子が弱い相互作用により崩壊する過程で実験的に検出されています．理論的には小林-益川によるクォーク混合行列で説明されました．更に，最近ではニュートリノと反ニュートリノに係る物理事象の発生確率の有意な差がCP破れを示唆するとの実験結果も報告されています．

CP対称性の破れは，現在の物質優勢の宇宙の謎を解くカギになります．しかし小林-益川行列による効果だけではCPの破れの大きさを説明できません．宇宙初期ビックバン直後は物質と反物質が同数あったはずなのに，なぜ現在は反物質が圧倒的に少ないのか?を説明する有力な手掛かりとして素粒子物理学の重要なトピックスの一つになっています．

3 時間反転対称性の破れとスピン

素粒子の基本量子数の一つである「スピン」をプローブにして先に紹介しました時間反転対称性の破れを実験的に解明する方法があります．Figure 2に示すように，個々の素粒子は極小磁石としての性質=磁気双極子能率を持ち，質量・電荷・スピンの3つの基本量子数から記述されます．

Figure 2.

Definitions of magnetic moment and electric moment of elementary particle. They include mass, charge and spin. Magnetic moment includes g-factor.

さて，電荷をもった素粒子が仮に電荷分布を持ち，電気双極子能率はスピン軸に平行と想定します．素粒子はスピンに係る磁気双極子能率と電気双極子能率の二つのベクトル矢印を持ちます．Figure 3の左側に示すように，二つのベクトルが素粒子スピンに平行である場合を初期状態とします．

Figure 3.

Charge distribution won't change under time reversal as shown in purple arrow. However, electric dipole moment d → does change.

ここで，時間反転をします．スピンの向きは反転しますが，電荷の空間分布は時間反転に対し不変ですので，時間反転後の電気双極子能率の符号も反転します．物理描像が変化するのです．電気双極子能率は磁気双極子能率と共に電場磁場の双対性を仮定すると自然に導かれる物理量ですが，CP対称性が厳密に成り立てば電気双極子能率(以下，EDMと書く)は存在できません．即ち，存在そのものが標準理論を越えたものになるのです．

実験環境の電磁場操作によって二つの双極子能率の精密測定が可能なのは素粒子レプトンの電子とミュオンです．そして，重い粒子ほど新粒子と結合しやすいと考えられるため，ミュオンは電子よりも標準理論を越えた物理に対する感度は電子の200² =4万倍強いと期待されます．

ミュオンEDMの実験上限値は10⁻¹⁹[e.cm]です．これは1990年代後半∼2000年代初頭にかけて行われた米国BNL E821実験 [1]で与えられています．素粒子ミュオンは10⁻¹⁹cmサイズまでは，電荷の分布を持つような内部構造がない，ということを示す実験結果です．

4 ミュオンがEDM探索や新物理探索に適する理由

先に述べたように，ミュオンを用いれば実験環境の電磁場操作により，Figure 2で紹介した二つの双極子能率を同時に，独立に精密測定が可能です．磁場中でミュオンはサイクロトロン運動の角運動量を持ち，さらにスピン歳差運動を行います．これらの角速度ベクトルの差をアノマリー振動数と呼び，下式1となります．そこに，二つの双極子能率に関わるパラメータが現れます:

ω → = − e m [ g − 2 2 B → + η 2 ( β → × B → ) ] ( 1 )

(1)

第1項のg因子は磁気双極子能率とスピン角運動量を関連づける無次元量の比例定数です．内部構造を持たないディラック粒子のg因子は相対論的量子力学では正確に2で，ηはゼロです．すると， ω → は常にゼロで，二つの角運動量ベクトルが常に一致することになります．今のところ，現実の電子やミュオンの η の実験値は非常に小さい値の上限値(ほぼゼロ)があります．g因子は2からズレており，この相対的なズレ(g-2)/2を"g−2 "と呼びます．その主成分は量子電気力学(QED)で記述可能で，Schwingerによって1946年に示されています [2]．現在の理論値は強い相互作用，弱い相互作用からの寄与を含めて，サブppmレベルで求められています(the Muon g-2 Theory Initiative White Paper [3])．先に紹介した米国BNLのE821実験 [4]は，g-2のCODATA値の主要元になる実験であり，標準理論との差異が4標準偏差，すなわち，新物理の存在を示唆するものです．この差異は素粒子物理分野20年来の謎です．もし，本当に標準模型を超えた物理があるならば，その差異は実験データや理論計算の不確かさを小さくすれば有意差は大きくなるはずです．更なる精密測定によってg-2の差異の謎の決着をつけることは，これからの素粒子物理(理論，実験のどちらも)の研究の方向性を決定するという強い意義があります．

式1に示す磁場中のアノマリー振動数 ω → の第2項は，Figure 4に示すように，第1項と直交するベクトルです．信号強度は第1項に比べ1000分の1程度の寄与ですが，原理的にEDM信号をg-2 信号と分離して検出できることを示します．アノマリー振動数 ω → は，μSRと同様にミシェル崩壊の陽電子の時間スペクトルを検出して得られます．300MeV/c 高エネルギーミュオンを用いますので，崩壊陽電子のうち高エネルギー側を検出すれば，自動的にミュオンのスピンの向きを知ることになります．実験の精度は，外部磁場 B → とミュオンの運動量ベクトル β → の精密制御技術に大きくかかわります．

Figure 4.

ω → is obtained summation of orthogonal two angular moments related to magnetic and electric dipole moments.

筆者は，2008年より式1の第2項に現れるEDM信号の直接検出実験の実現に関わってきました [5, 6]．ミュオンg-2・EDM実験(J-PARC E34)についての解説は [7]もご覧ください．

新物理探索のもうひとつの重要トピックスは荷電レプトンフレーバーの破れ探索実験(CLFV)です．これは，TeVスケールにおける物理のフレーバー対称性の破れの構造を探ることになります．

ミュオンのフレーバー破れ変換:μ→ eは標準理論によると10⁴⁰∼10⁵⁰に1回の頻度でしか起こりません．しかし，標準理論を越える新物理があるとすると，稀事象発生確率は上がるはずで，例えば超対称性を仮定すると，10¹¹∼10¹⁵に1回の頻度になります．

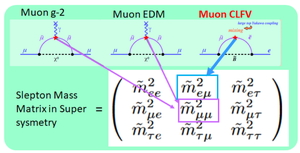
このような稀事象を実験的に測定可能なのはミュオンが弱い相互作用のみで崩壊し，その崩壊様式のほぼ100%が通常のミュオン崩壊: μ → e ν ν ¯ であり，単純かつクリーンであるからです．この節のまとめとして，Figure 5にミュオンを用いた標準理論を越える新物理探索を示します．ミュオンEDMとCLFVは存在そのものが新物理になり，ミュオンg-2は標準理論とのズレが新物理存在を示唆します．

Figure 5.

Muon is strong probe to explore the beyond standard model in fundamental physics.

5 ミュオンがQED計算の精査に適する理由

J-PARC MLFのミュオンビームラインの強みは，ほぼ静止状態のミュオンビームを大強度で生成可能なことです．磁場や電場により"束縛された系の基底状態"を実験的に実現可能になります．Figure 6に示す磁気双極子能率に係るg因子，電荷質量比や微細構造定数αなどの基礎物理量の精密測定が同時に可能になると，QED計算を実験的に評価する超精密実験プローブを手にすることになります．

Figure 6.

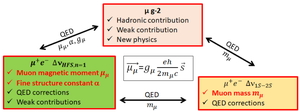
Muon probes fundamental physics values in precise QED calculations

ミュオンと電子の束縛状態であるミュオニウム (Mu)の"基底状態"をほぼ真空の電磁場中に作ることができます．

ミュオニウムの基底状態の有効ハミルトニアンは

H = h I → ⋅ J → + μ B e g J J → ⋅ H → − μ B μ g μ I → ⋅ H →

ここで， I → はミュオンスピン， J → はミュオニウムの全角運動量， μ B e は電子のボーア磁子， μ B e は電子質量をミュオン質量に置き換えたもの，g_J,g_μ はそれぞれミュオニウム中での電子とミュオンの束縛g因子と呼ばれる量です．又，Figure 7にMuの超微細構造 Δν を示します．外部磁場 H → の強さ変化に伴う，基底状態のエネルギー固有値の変化を精密に測定し，ミュオンのg因子と電荷質量比を含む磁気モーメントそのものを直接測定することができます．

Figure 7.

Hyper Fine structure of Muonium.

さらに，ほぼ静止状態のミュオンを捕獲(トラップ)する実験計画もあります．磁場中に"束縛"され非相対論的速度で周回するミュオンスピン歳差運動を精密測定します．適切な高周波を与えてミュオンスピンをサイクロトロン運動方向と垂直に制御し，ミュオンの荷電粒子としての電磁場内運動のシグナルとして得れば，そこからミュオンのg因子や電荷質量比を求めることができます．同時に，ミュオン寿命も測定することができれば，フェルミ定数も実験的に測定可能になります．

前節で紹介したg-2・EDM実験 (J-PARC E34) は，磁場中に"蓄積"された300MeV/c ミュオンの"励起状態"のサイクロトロン運動とスピンの向きがほぼ同じ平面上にあるため，g因子そのものではなく，差のg-2だけを測定する実験でした．一方，ミュオントラップ実験は，Figure 8に示すように，ミュオンが持つ3通りの周波数を独立に計測することになります．(スピン歳差運動からg-2をシグナルとして見ることは可能ですが，g-2の差だけを測定する場合に比べ，精度は劣ります．)

Figure 8.

An image to explain difference of experimental method between muon beam storage and trap.n_c is principle quantum number of Landau level.

6 まとめ

本記事では，J-PARCミュオンビームを駆使した基礎物理実験を紹介しました．大強度パルス，かつ運動量の制御が自在なJ-PARC MLFミュオンビームはミュオンに係る基本量を幅広く網羅する実験計画を可能にします．同じ実験施設の共通ビーム源を用いて，様々な角度から素粒子ミュオンの基本量を精密理解する事は，今後の基礎物理分野の進むべき方向性を決める知見をもたらすと共に，新しい実験技術の確立は，磁気プローブとしてのミュオンの可能性を更に広げていくものと期待します．

謝辞

本研究は，科学研究助成事業(科研費) JP19H00673，JP26287055および，JP23740216のサポートを受けています．

Reference

Corresponding author

Funder information

1.Fund name: Japan Society for the Promotion of Science

Register with J-STAGE for free!