2021 Volume 85 Issue 1 Pages 40-48
2021 Volume 85 Issue 1 Pages 40-48
A plasticity resistance by a grain boundary was evaluated by nanoindentation measurement in the vicinity of the grain boundary for austenitic stainless steels. Converting a load (P) - displacement (h) relation to a P/h - h curve, the plasticity resistance can be evaluated in the parameter α with hardness dimension obtained as the slope on the loading curve. The slope α is constant until the plastic zone underneath the indenter reaches to the grain boundary at a certain penetration depth (stage I), and then turns into a higher value in the deeper penetration depth range (stage II). The lower α in the stage I (αI) means the deformation resistance in the grain interior, and that in the stage II (αII) includes the deformation resistances of both the grain interior and the grain boundary. Therefore, Δα = αII − αI could correspond to the plasticity resistance by the grain boundary. It has been found that the average of Δα is higher for the nitrogen-added sample than that for the nitrogen-free one, suggesting a nitrogen effect including segregation on the plasticity resistance by a grain boundary.
多結晶金属材料におけるマクロな力学特性は,ミクロ領域の様々な強化機構の複合効果によって発現している.強化機構の中には,現象としては広く理解されているものの,素過程の理論的解釈が不確定な場合がある.例えば,降伏強度や破壊応力の粒径依存性を定式化したホールペッチの関係1,2)は,結晶粒微細化強化として経験的に成り立つことが広く知られており実用的にも活用されているが,発現機構の詳細は未解明である.この関係式は,次のように記述される.
| \begin{equation} \sigma = \sigma_{0} + kd^{-\frac{1}{2}} \end{equation} | (1) |
理論モデルの精度を上げるためには,微小スケールにおける転位―粒界相互作用の素過程を明らかにする必要がある.実験的にこれを達成するためには,従来のマクロな力学評価に加えて,単一の粒界を対象としたミクロな力学評価を行う必要がある.単一の粒界を対象とした力学試験としては,押込み硬さ試験を活用することが多い.従来は,粒界近傍のマイクロインデンテーション試験による微小硬さを指標として,粒界性格や隣接粒間の方位差9,10),偏析9)が粒界による硬度の上昇に影響を及ぼすことが指摘されている.近年では,測定技術の発達によりさらに微小な領域の力学特性を評価できるナノインデンテーション法を用いた取り組みが広く行なわれている.ナノインデンテーション法は,µNオーダの荷重分解能とnmオーダの押込み深さ分解能を持つ圧入試験である.走査プローブ顕微鏡(Scanning Probe Microscope:SPM)を併設しており,押込みと走査を同じ圧子で行うことによって高い精度で位置決めした箇所に押込むことができる.そのため,従来手法では評価が困難であった微細な第二相や析出物,粒界などを対象として力学応答を直接的に評価することが可能である11).
ナノインデンテーション法では,最大荷重に対応する硬さに加え,負荷・除荷過程における荷重-変位関係が得られ,これによって様々な力学情報を得ることができる.例えば,負荷曲線からは力学特性の深さ方向の分布を,弾性回復が支配的な除荷曲線からはヤング率を評価することができる.押込み時の特徴的な力学応答の1つとして,荷重制御条件で押込んだ場合にポップインと呼ばれる変位バースト現象が観察されることが知られている.ポップインは,圧子下における転位の生成と増殖に対応することが実験12,13),シミュレーション14-16)の双方から報告されており,最近ではポップイン挙動を解析することで,転位と格子欠陥との関係を明らかにしようとする研究が多数なされている17-20).転位―粒界相互作用に関しては,粒界直上や近傍に押込んだ際のポップイン挙動から粒界の影響が議論されている.Ohmuraらは,Interstitial Free鋼を用いてポップイン発生の臨界荷重(Pc)を粒内と粒界直上の場合で比較し,粒界直上に押込んだ場合のPcが粒内よりも低下することを明らかにして粒界が転位源として働くことを示した21).
粒界ポップイン(grain boundary pop-in)によって転位―粒界相互作用を明らかにしようとする試みもなされている22-25).粒界ポップインとは,粒界近傍に押込んだ際,第一ポップインに続いて塑性変形が進行した後に現れる2回目の大きな変位バースト現象である.塑性変形が隣接粒に伝播する瞬間に現れる現象であると考えられており22-26),先述の転位生成と増殖に起因するポップインよりも明らかに高い荷重で発生する.Wangらは,Nbを供試材として粒界近傍に押込むことで粒界ポップインの発生有無を調査し,粒界を跨ぐ2つの結晶粒のすべり面とすべり方向が近いほど粒界ポップインが発生しやすいことを明らかにしている22).また,Brittonらは,隣接する粒界を挟む2つの結晶粒のすべり面法線およびすべり方向の方位差に起因するlocal misorientation factor(m′)27)が粒界ポップインの臨界応力を高めることを示している28).Tsurekawaらは,Fe-3%Si双結晶および三結晶を用いた実験において,粒界ポップインの発生頻度がランダム粒界で比較的高いのに対して小角粒界や対応粒界ではほとんど発生しないことを示した23).また,粒界からの距離の逆数と硬さを式(1)に準えて整理し,その関係から局所的なホールペッチ係数knを求め,knと粒界 ポップインの発生頻度の間には負の相関があることを示した.これらの結果から,粒界の転位源の活性化臨界応力が高いほど粒界 ポップインが発生し難いと考察している.Javaidらは,タングステンを用い,粒界ポップイン直後に除荷した圧痕周辺を電子線チャネリングイメージ法で観察する手法で粒界への転位のpile-upと隣接粒側に転位が発生していることを明らかにしている24).Soerらは,粒界ポップインの発生が粒界と圧痕との距離に強く依存し,粒界から離れると粒界への負荷応力が小さいために粒界ポップインが現れず,近いと圧痕が粒界を跨いでしまうために正確な評価が難しいなどの測定面での課題を指摘している25).
転位―粒界相互作用を直接的に観察する試みも行われている.Ohmuraらは,Fe-0.4 at%Cマルテンサイト鋼を対象として透過型電子顕微鏡内で圧縮試験を行い,転位―粒界相互作用のin-situ測定を行っている26).小角粒界の場合は,粒内に生成した転位の粒界へのpile-upを経て隣接粒に転位が伝播するのに対し,大角粒界の場合は転位が粒界に吸収されて粒界へのpile-upや隣接粒への伝播は確認されないとしている.
Woらは,硬さを指標としてNi3Alにおいて粒界からの距離や最大荷重を変えて押込む方法で評価し27),最大荷重や粒界からの距離などの押込み条件によらず,硬さには粒界の影響が現れなかったとしている.これに対して,押込み後の試料表面のSPM像には押込みにより形成されたすべり線が粒界を超えて隣接粒に伝播していることが確認されている.さらに,このすべり線の伝播は,上述のm′と強い相関を示すことが指摘されている.
このように,ナノインデンテーションを用いた様々な手法で転位―粒界相互作用を評価する試みがなされている.この中で,粒界ポップインの解析によって評価する研究が多くなされているが,上述のように粒界性格や測定条件によっては粒界ポップインが現れないことがあり,一般的な評価手法としては課題が多い.また,TEM内でのin-situ測定は,力学応答と組織変化を直接的に評価できる点で現象の理解を深めやすい利点があるが,様々な粒界を対象として多くのデータを取得する系統的な取り組みには適さない.転位―粒界相互作用の素過程の理解を深めるためには,多くの因子に対する系統的な評価が必要であり,多様な粒界に対して簡便かつ高い精度で評価できる手法が要求される.そこで本論文では,ナノインデンテーションで得られる荷重―変位曲線を直接的に解析する方法で粒界の塑性変形抵抗を評価する新たな手法を提案し,その精度や再現性を確認する.さらに,本手法をオーステナイト系ステンレス鋼に適用し,個々の粒界における隣接粒間の方位差や添加元素の影響を調査する.
上述のように,微小スケールにおける転位―粒界相互作用の素過程を明らかにするためには,個々の粒界に対して高い精度で簡便に力学挙動を評価できる手法の開発が必要である.本研究では,ナノインデンテーション法で得られる荷重―変位曲線の解析方法について,従来の硬さ算出よりも簡便でありながら高い精度で評価できる手法の開発を試みた.
一般に,錐型圧子を用いた場合,弾性変形および塑性変形の理論的な荷重―変位関係は次式で表される29-31).
| \begin{equation} P_{\text{t}} = \alpha h^{2} \end{equation} | (2) |
式(2)が理想的なP - h関係を表すのに対して,実測される荷重(Pm)は圧子の先端形状や試験機剛性などの影響を表すh項を加えて次式のように表される33).
| \begin{equation} P_{\text{m}} = \beta h + \alpha h^{2} \end{equation} | (3) |
| \begin{equation} P_{\text{m}}/h = \beta + \alpha h \end{equation} | (4) |
供試材として,窒素濃度が異なる2種類のオーステナイト系ステンレス鋼を用いた.Table 1に化学組成を示す.本論文では,N添加材を1N材,無添加材を0N材と呼ぶ.1N材は,溶解時に合金元素を添加した後,チャンバー内の窒素分圧を6.7 × 10−2 Paで1 h保持することで溶鋼中に窒素を添加した.溶製したインゴットはアルゴン雰囲気中で1523 K,1 hの溶体化処理を施し,板厚30 mmから5 mmまで熱間圧延に供した.次いで,板厚3 mmまで両面研削により減厚した後,1 mmまで冷間圧延した.冷間圧延材を真空中で1273 K,1 h焼鈍し,ヘリウムガスで室温まで急冷した.

熱処理後,ND面を機械研磨により鏡面に仕上げた後に,表面の加工層を除去するために電解研磨を施した.次いで,ナノインデンテーション時に測定位置を走査型プローブ顕微鏡(SPM)で識別しやすくするように,電解エッチングで粒界をわずかに腐食した.電解研磨は,293 Kの5%過塩素酸エタノール溶液を用い,印可電圧約30 Vで10-20 s研磨した.粒界腐食は,硝酸,塩酸および水を1 : 1 : 1で混合した試薬で10-30 s腐食した.
ナノインデンテーションに先立って,電解放出型走査電子顕微鏡(FE-SEM)を用いた電子後方散乱回折(Electron backscatter diffraction,以下EBSD)法でND(Normal Direction)面の結晶方位を求めた.ナノインデンテーションは,Bruker社製Hysitron Tribo Indenter(TI900)を用い,300 Kの室温下で荷重制御方式により実施した.Berkovich型ダイヤモンド圧子を用い,最大荷重は3000 µNとした.負荷および除荷速度は100 µN/s,最高荷重における保持時間は10 sで,SPM像上で位置決めした結晶粒界近傍に押込んだ.
Fig. 1に,EBSD測定で得られた供試材の結晶方位マップを示す.焼鈍双晶も含めて等軸に換算した平均粒径は80 µm程度であり,直線的な粒界が多く観察される.また,結晶粒内に焼鈍双晶が認められる.ナノインデンテーション装置に併設のSPMを用いて表面の凹凸情報から粒界の位置を特定し,粒界からの距離をその場で任意に決定して押込み変形を行った.Fig. 2(a)に押込み変形後の試料表面のSPM像を,また,その図上に示された線分ABに対応する断面の表面高さプロファイルをFig. 2(b)に示す.粒界からの距離dsは,三角錐型の圧痕の最深部を試料表面に投影した位置(SPM像の三角形の重心)から粒界までの最短距離と定義した.圧子下の塑性域は,圧子先端と試料の接触位置を中心とする半球状に広がると考えられるため,3次元的な位置関係から粒界との距離を決めるのが理想的である.しかし,各点における粒界面方位を測定することは極めて非効率なため,実際には試料表面のSPM像の2次元情報をもとにdsを定めた.したがって,粒界面が試料表面に対して浅い角度で存在する可能性がある場合などは考慮が必要である.本研究で用いた供試材の場合,平均粒径が80 µmと粗大であること,粒界が直線的であることから,同一の粒界を対象とする場合は面方位や試料内部の粒界面の状態はほぼ同じと判断した.

EBSD-IPF map for the sample used.

(a) SPM image after indentation, the cross section profile along A-B which is indicated in (b) the SPM image and (c) EBSD-KAM map.
次に,塑性域サイズの算出について述べる.永久くぼみの圧痕サイズから塑性域サイズを求めるモデルとしては,Itokazuらによる方法36)と,Johnsonらによる方法37)が代表的である.前者では,三角錐Berkovich型の圧子を用いた場合の圧子下の塑性域を半球状と仮定し,その直径が押込み深さの10倍程度であると示されている.試料表面に形成される圧痕三角形の1辺の長さは,Berkovich型圧子の幾何学条件に基づくと押込み深さの約7倍であるため,塑性域サイズはそれよりもやや大きなサイズと見積られる.後者のJohnsonモデルでは,圧子の接触圧力が水平方向に等方的に作用する軸対称の半球状の塑性域とその塑性域を取り囲む弾性域を仮定するモデルである.このモデルを用いると,Berkovich型圧子と同じ頂角に対して,塑性域の半径(rpz)とcavityの半径(rc)との比率(rpz/rc)は3.0程度となる.この関係を用いると,塑性域の直径は,押込み深さの13.2倍程度と見積もられる.これらのモデルを本研究の試料において検証するため,圧痕の周囲をSEM-EBSDによって解析した.Fig. 2(c)に,Fig. 2(a)に示した圧痕周辺のEBSD-KAM(Kernel Average Misorientation)マップを示す.KAM値は,EBSDの測定点におけるあるピクセルと最近接の6つのピクセルとの方位差の平均値を示しており,微小領域の塑性ひずみ勾配を表す指標として用いられることが多い38).Fig. 2(c)に示されるように圧痕周辺はKAM値が高くなっており,塑性域が粒界にまで達していることがわかる.また,その大きさを圧痕三角形の重心からの最大距離とすると約1.3 µmと見積もられ,この時の押し込み深さが約270 nmであることから,Itokazuモデルにほぼ一致することが確かめられる.なお,KAM値は圧痕の3辺近傍で高い傾向があるため,粒界からの距離が同一であっても圧痕三角形の1辺と粒界線のなす角度が変形挙動に影響を及ぼす可能性がある.したがって,本研究では,粒界線に対する圧子の向きがほぼ同じになるように試験を行った.
4.2 粒界力学挙動の解析ナノインデンテーションで得られるP/h - h関係から,粒界が圧入変形挙動に与える影響を定量的に求める方法について述べる.
本論文の方法との比較のため,従来方法で最も一般的な指標である硬さを用いて,これを粒界からの距離dsに対してプロットした関係をFig. 3に示す.なお,ここでの硬さは,ナノインデンテーション法により求めたナノ硬さ(Nanohardness:Hn)を用いる.dsがおよそ2.5 µm付近よりも深い領域ではほぼ一定の値を示すのに対し,逆に浅い領域では粒界に近づくほど硬さがわずかに上昇する傾向を示す.また,粒界から10 µm以上離れた粒内における測定結果を図中に示す.36点の測定点に対する硬さの平均値と標準偏差は2.0 ± 0.05 GPaであり,最大値と最小値の差が0.2 GPa程度の範囲に測定値が分散する.粒内硬さに対する粒界付近の硬さの上昇率は,最も高い測定値で約21%,多くのプロット点で20%程度以下に過ぎない.これは,粒内の測定値の分散範囲よりもわずかに大きい程度であることから,粒界による変形抵抗の上昇を測定する指標としては十分な精度ではない.

Relationship between hardness and the distance to the grain boundary.
硬さよりも高い精度で粒界強度を評価する手法として,2節で述べたP/h - h関係の解析方法を検討した.Fig. 4(a)に,粒界からの距離dsが0.8 µm位置(Fig. 3において矢印で示した測定点)と粒界から10 µm以上離れた粒内に押込んだ際の荷重-変位曲線を示す.押込み深さが約124 nm(矢印)以下の範囲ではどちらの曲線も重なっている.一方,これよりも深い領域では2つの曲線は乖離し,粒界近傍に押込んだ場合の傾きが大きくなる.この変化をより詳細に解析するため,Fig. 4(a)で示した2つのP - h曲線の負荷過程を変換したP/h - h関係をFig. 4(b)に示す.押込み深さが80 nm程度までの浅い領域ではプロット点が離散的であるが,これはFig. 4(a)で見られるように弾性変形から弾塑性変形への遷移であるポップインが現れていることなどの影響と考えられ,したがって,80 nm以降の領域を解析の対象とした.粒内に押込んだ場合,プロット点は短い周期で上下の変化を頻繁に繰り返すものの,60-150 nmの長範囲ではほぼ線形的であり,その間の最小二乗近似で得られる傾きαは0.037 µN/nm2と求められる.これに対して,粒界近傍に押込んだ場合は,60-124 nmの範囲では粒内とほぼ同じ値の0.041 µN/nm2を示し,124 nm以降では約50%高い0.062 µN/nm2に上昇する.このαが変化する押込み深さ124 nmに対応する塑性域サイズをItokazuモデルで求めると,半径は深さの5倍であるので約0.62 µmと算出される.粒界からの距離dsは0.5 µmであり両者はほぼ一致することから,αの変化点は塑性域が粒界に達した時点で現れると判断される.以上より,粒界近傍に押込んだ場合,押込み初期において塑性域が粒界に達しない条件では粒界の影響を受けずに粒内と同じ変形抵抗を示し(以下,stage Iとする),塑性域が粒界に達した後は粒界からの影響を受けて変形抵抗が増加し(以下,stage IIとする),P/h - h関係の傾きが上昇したと考えられる.ここで重要なことは,P/h - h関係の傾きを用いた変形抵抗の指標は,硬さの指標に対して定量的な精度が高い点である.Fig. 4(b)で検出されたP/h - h関係の傾きαIとαIIの変化率は50%程度であるのに対し,Fig. 3で示した硬さの指標では上昇率が最大で20%程度であった.前述のように,ナノ硬さの20%の変化では優位な差と判断するには難しい場合もあるが,Fig. 4(b)に示される傾きの変化は明らかに優位であると判断できる.

(a) Typical load (P)-displacement (h) curves for grain interior and near grain boundary and (b) P/h-h curves for grain interior and near grain boundary.
P/h - h関係の解析を用いると精度が高くなる理由について,以下のように考察する.錐型圧子による圧入変形で得られる荷重Pと変位hの関係は,式(3)に示されるようにαh2項とβh項の加算で表現されることがFig. 4(b)の結果などから明確である.前述のように,この2項のうちαh2項は材料の本質的な変形抵抗に対応するのに対してβh項は圧子先端の不完全性や試料表面が平坦でないために実験誤差として発生する項である.硬さを算出する場合は,これら2つの項をともに含んだhから求めるため,特にhが小さい領域でβh項の影響は相対的に大きく現れる.これに対してP/h - h関係の傾きからαを求める方法は,βをy切片に分離することによって本質的な材料の変形抵抗のみの挙動を抽出することが可能である.βの影響は,圧子形状の不完全性を校正したとしても試料表面粗さによって発生するため,実験上は不可避である.局所的に凸形状の部分に圧入を加える場合は,平坦な場合と比較して同一荷重に対して変位が大きく現れ,逆に凹部の場合は変位が小さく測定される.試料表面の凹凸はある分布をもって分散していると考えられ,その分散が硬さ値に反映されてしまう.P/h - h関係の傾きからαを求める場合は,ある荷重―変形抵抗のつり合い状態から次の状態へ移る際の変化率を基に算出されており,それ以前の変形履歴はほとんど影響しないため試料表面による誤差を含み難いと考えられる.
この解析方法の再現性や精度をさらに確認するために,Fig. 4とは異なる1つの粒界に対して粒界からの距離を変えて圧入変形を行った結果を次に述べる.粒界からの距離をA:0.7 µm,B:0.8 µm,C:0.9 µmと変化させ,同一の最大荷重3000 µNで圧入変形を加えた際の負荷過程のP/h - h関係をFig. 5に示す.挿入されたSPM像上において,圧痕サイズと粒界からの距離を確認することができる.各プロットの形状は,Fig. 4(b)における粒界近傍の場合と同様に,stage Iと判断される押込み深さまでほぼ一定の傾きを示し,stage IIでは傾きが大きくなる.この傾向は,すべてのプロットで共通しており,かつ,αI,αIIの大きさ,すなわち粒内の変形抵抗および粒界の影響を受けた変形抵抗は,5%程度の範囲内でばらつくものの,粒界からの距離によらず同程度とみなせる.圧痕Aのプロットが圧痕B,圧痕Cに重ならない理由は,式(3),式(4)およびFig. 4で述べたように,圧子先端の不完全性や試料表面の影響を受けるβ項によるものと考えられる.その傾きの上昇率は約160%と算出され,Fig. 4(b)と同様,粒界の抵抗を定量的に評価することが可能であることを示している.Fig. 4(b)よりも上昇率が高い点については,粒界によって本質的な変形抵抗が異なること,粒界面と塑性域の3次元的な距離が異なることや粒界面に対する三角錐の向きなどが関係している可能性がある.P/h - hプロット中の破線片矢印は傾きが変化する深さをそれぞれ示しており,各圧痕について,A:146 nm,B:158 nm,C:181 nmと求められる.この値を5倍して見積もられる塑性域サイズの半径はA:730 nm,B:790 nm,C:905 nmと算出され,SPM像から求められるそれぞれのdsとほぼ一致する.以上の結果より,塑性域に粒界を含む条件で圧入変形を加えた場合,P/h - h関係の解析によって粒界が寄与する変形抵抗を従来よりも高い精度で評価できることが明らかになった.

P/h-h curves for the samples with different distances to the grain boundary.
本手法を用いることによって,多結晶材料であっても単一の粒界の変形抵抗を抽出して評価できるので,粒界の幾何学条件や偏析・析出などの組織条件などによる効果がより明確に捉えられる.αIは粒内の変形抵抗であり,αIIは粒内と粒界の変形抵抗が重畳した値であるので,これらの差分であるΔαが粒界の変形抵抗に相当すると考えられる.また,式(1)に示すホールペッチの関係に基づくと,αIは粒内の変形抵抗であるのでσ0に対応し,αIIは粒内と粒界の両方の寄与を含むσに相当すると考えられる.また,塑性域に含まれる粒界の数はいずれの条件でも1つであり,かつFig. 5に示すようにαIIは粒界からの距離に依存しないことから,粒径の寄与は一定とみなして式(1)のdを定数化できる.以上の仮説に基づくと,stage Iとstage IIの差分であるΔαは,ホールペッチ係数kに相当する因子であるとみなすことができ,すなわち単独粒界のkを直接的に評価できる.
4.3 P/h-hによる解析の適用例前節で述べたP/h - hプロットによる解析手法の適用例として,窒素添加量が異なるオーステナイト系ステンレス鋼における種々の粒界の抵抗値とそれらに及ぼす影響因子について述べる.Fig. 6は,窒素濃度が異なる0Nおよび1N試料において,圧入変形で得られたP/h - hプロットである.変形抵抗に及ぼす結晶方位の影響を可能な限り排除するため,それぞれの試料において試料表面の法線方向が<001>にほぼ平行な結晶粒を選択し,その結晶粒を取り囲む種々の粒界に対して圧入変形を加えた.粒界からの距離dsより逆算される押込み深さを境にして,1N試料では105 nm,0N試料では173 nm以上をstage IIと判断した.Fig. 7は,P/h - hプロットから求めたαI,αIIの平均値,およびこれらの差分Δαを粒界ごとに示した図である.各粒界における測定点数は4点であり,その分布の標準偏差をαI,αIIのエラーバーとして示している.それらの標準偏差の平均値は,0.002 µN/nm2程度であるため,Δαの精度は0.005 µN/nm2程度と判断される.0Nと1Nを比較すると,αI,αIIの値はともに窒素を添加した方が大きい.さらに,これらの差分であるΔαは,粒界ごとに大きさが異なるものの,0Nと1Nを比較すると平均的には1Nの窒素添加材の方が大きな値を示している.
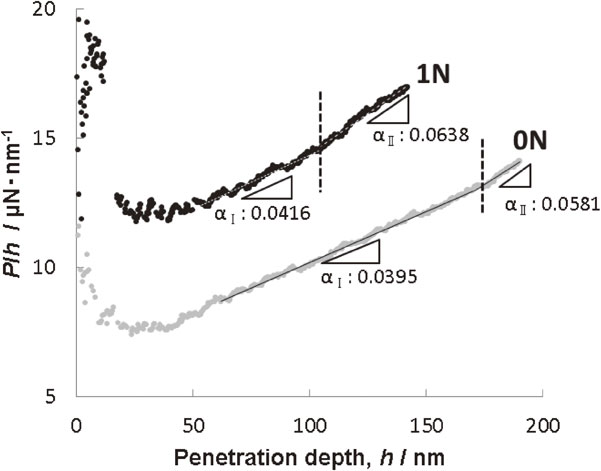
Typical P/h-h curves for 0N and 1N.

Typical P/h-h curves for 0N and 1N.
αIが窒素添加によって上昇した理由は,固溶強化あるいはCrNなどの析出強化によるものと考えられる.αIIも粒内と同様に窒素添加によって上昇しているが,粒内と粒界の変形抵抗の和であるため,これだけでは窒素添加によって粒界強度が上昇したとは判断できない.したがって,粒界強度はstage Iとstage IIの差分であるΔαで判断すべきである.
そのΔαは窒素添加によって上昇する傾向を示すが,粒界によっては窒素を含まない粒界と同程度の大きさの場合もある.Δαは,個々の粒界の変形抵抗の指標に相当するため,同一材料であっても粒界ごとに変形抵抗が異なる可能性があり,これを反映した結果と考えられる.粒界の変形抵抗に及ぼす因子として,主として幾何学条件と偏析が挙げられる.以下にこれらの因子について考察する.
幾何学的条件として,Fig. 1のEBSD測定によって得られる相対方位差(θ)に着目し,これに対してΔαをプロットした図をFig. 8に示す.相対方位差の範囲は,約20-60°である.窒素添加の有無によらず,隣接粒間の方位差とΔαとの間に明確な関係は見られない.ここで,方位差60°付近の粒界は双晶界面と判断される点に注意が必要であるが,これを除いたランダム粒界の結果のみにおいても明確な方位依存性は確認できない.本研究の結果では,相対方位差の範囲が大角粒界に限定されることや粒界面などの他の因子が考慮されていないこともあり,幾何学的な因子の影響に対する明確な結論は得られなかった.これは,IF(Interstitial Free)鋼の解析において,粒界の幾何学因子と変形抵抗に強い相関はないとする結果と一致している39)

Relationship between Δα and misorientation angle.
次に,偏析の影響について考察する.Fig. 7およびFig. 8に示すように,窒素添加によってΔαが上昇する傾向が確認できる結果より,窒素の粒界偏析によって変形抵抗が上昇したことが示唆される.理想的には,偏析量を測定して定量的に検討することが必要であるが,一般的に窒素などの軽元素の偏析濃度を高い精度で測定することは極めて難しく,著者らの取り組みでも明確化に至っていない.双晶境界は試料表面から奥行き方向に2通りの双晶面の広がりを持つため,幾何学因子が必ずしも同じではないが,Fig. 8における双晶境界の結果が示すように,いずれの結果も窒素添加材のΔαが無添加材よりも高い傾向にあり,その差は最大で10倍以上であることから,窒素添加の効果は優位であると判断される.また,TEMおよびSEMによる観察では,観察視野内において粒界に析出物などの第2相は形成されていないことが確認されており,したがって,窒素添加による粒界変形抵抗の上昇は,窒素の偏析に起因することが強く示唆される.粒界偏析による変形抵抗の上昇については,Arakiらが,粒界から隣接粒に転位を放出する臨界応力(臨界粒界せん断応力)とこれに及ぼす偏析元素の影響について,Fe-C二元合金およびこれに低温時効を施して粒界への炭素偏析を促進させた時効材を供試材として報告している40).粒界直上にナノインデンテーションを行うことで得られたポップイン発生の最大せん断応力を臨界粒界せん断応力と見なすと,時効材において臨界粒界せん断応力が比較的に高いことを示している.圧入変形の導入方法が本研究とは異なるが,隣接粒への変形伝播の素過程として粒界への応力集中と粒界転位源の活性化を仮説としている点は共通しており,どちらも粒界偏析が粒界転位源の活性化臨界応力を高めた結果と考察される.また,粒界偏析と幾何学因子の影響についてもいくつかの報告がある.Herbigらは,Fe-C系ナノ結晶材料に対する3次元アトムプローブ解析によって,粒界偏析量が隣接粒間の方位差によって異なることを実験的に示している41).ただし,Herbigらの報告によると,相対方位差が15°以下の小角粒界では方位差にほぼ比例して偏析量が増加するのに対して,15°以上の大角粒界では方位差と偏析量は相関しない.小角粒界の場合,偏析に及ぼす隣接粒間の方位差の影響が大きいのに対して,大角粒界の場合は,粒界面や回転軸などの他の影響が大きい可能性が指摘されている.Rittnerらは,リンを添加したニッケルの傾角粒界へのリン偏析に及ぼす粒界性格の影響をモンテカルロシミュレーションにより調査し,共通回転軸を固定した場合に粒界偏析量が傾角に応じて変化することを示している42).この結果から,上述のHerbigらの報告では,共通回転軸の影響は考慮されていないため,大角粒界における方位差と偏析量に相関が見られなかった可能性が考えられる.また,FCC金属では,整合双晶界面は粒界エネルギーが0と考えられるので,理想的には偏析が起こらないはずであるが,本実験結果では,0Nは59.99°とほぼ理想的な方位差であるのに対し,1Nでは59.60°と理想的な方位差から若干ずれている.このことから,理想的な方位差からのずれを許容するように2次転位が導入され,その転位上に窒素が偏析した可能性も考えられる.Moritaらは43),Mo双結晶を用いて,対応粒界からのずれ角を補償するように2次転位が導入されるとし,2次転位の転位間隔を求めている.焼鈍双晶であること,EBSDによって求められた理想的な方位差からのずれが焼鈍双晶における傾角成分のずれであると仮定し,本実験結果においても,理想的な方位差からのずれから2次転位の転位間隔を求めると,約20-30 nmと見積もれる.本仮説を検証するためには,粒界の直接観察が必要ではあるが,理想的な方位差からのずれを補うように2次転位が導入され,この転位に窒素が偏析することで,Δαが上昇した可能性が考えられる.
以上に述べたように,P/h - hプロットを解析する手法は高い精度で粒界の変形抵抗値を求めることが可能である.また,本手法を用いて種々の粒界の変形抵抗値を求め,粒界ごとにそれらの値が異なることを実験的に示した.これによって,今後は,隣接粒間の方位差,粒界構造などの幾何学因子や偏析量などの化学因子と粒界の変形抵抗値との関係をより定量的に議論でき,粒界強度の素過程である転位―粒界相互作用の更なる理解につながると考える.
局所領域の力学特性を評価できるナノインデンテーション法を用い,単一の粒界の変形抵抗値を評価することが可能な手法を提示した.さらに,本手法を用いて窒素濃度が異なるオーステナイト系ステンレス鋼の種々の粒界の変形抵抗値を評価した.以下に得られた結果をまとめて述べる.
(1) 本研究で用いたオーステナイト系ステンレス鋼の場合,粒界からの距離dsを種々変えて圧入変形を行った結果,粒界近傍における硬さの上昇率は20%程度に過ぎない.この変化率は,粒界から離れた粒内の測定値の分散範囲と同程度であり,硬さを指標として粒界の変形抵抗を評価することは測定精度の面で不十分であることを示唆する.
(2) 硬さに代わる指標として,P/h - hプロットのslopeをパラメータαとする解析方法を提示した.粒界近傍に押込んだ場合,押込み深さの上昇に伴ってある深さを境にαが上昇する挙動が現れ,その変化率は100%程度に達した.圧子下に形成される塑性域サイズを求めると,塑性域が粒界に到達する押込み深さとαの変化点がよく一致することから,これよりも深い領域では粒界の影響を反映していると判断される.
(3) αの変化点前後をそれぞれstage Iおよびstage IIとすると,stage Iは粒内単独の変形抵抗(αI)を,stage IIは粒内と粒界の複合的な変形抵抗(αII)を反映すると考えられる.したがって,これらの差分であるΔαが粒界の変形抵抗を表す指標と判断される.
(4) 同一の粒界に対して粒界からの距離dsを種々変化させて圧入変形を行い,P/h - hプロットの解析を行ったところ,αI,αIIはともにdsによらず同じ大きさを示した.αIIの値がdsに依存しないことは,ホールペッチ式における粒径項を定数とみなせることを意味しており,αI,αIIがそれぞれσ0とσに対応すると考えられるので,Δαはk値に対応するパラメータであると考えられる.
(5) 窒素濃度が異なるオーステナイト系ステンレス鋼の種々の粒界に対してP/h - hプロットの解析を行ったところ,Δαの大きさは個々の粒界で異なる値を示し,窒素添加材は無添加材よりも大きい傾向を示した.相対方位差の依存性が明確でない一方,同じ双晶境界において特に窒素添加の差が顕著に現れることから,粒界偏析の影響が強く示唆される.