2024 年 1 巻 2 号 p. 82-101
2024 年 1 巻 2 号 p. 82-101
ラフ集合の方法は、決定規則の縮約によく利用されている。ラフ集合を用いた具体的な技術は、決定規則の抽出方法として用いられる。しかし、多くの決定規則を扱う際には、計算負荷が問題になる。すべての最小長の決定規則を計算する問題は、組み合わせ爆発が生じ、NP困難な問題である。この計算の課題を扱うために、本解説では、バイオ・コンピューティング技術を導入する方法を解説する。この手法は、決定規則の縮約に、DNA分子技術を応用したもので、問題の計算処理の複雑さを効果的に軽減できる。1998年にL.M. Adlemanが、生物学的計算パラダイムの概念を開拓して以来、この技術は、既存のアルゴリズムに活用及び実装することで、新しい問題解決アルゴリズムを開発する能力を提供してきた。しかし、経営工学の意思決定問題に対する学際的なDNA分子技術を用いたアルゴリズムは、いまだDNAの利用が限られた分野に限定されており、計算技術としてはそれほど広く用いられているとは言えない。本解説では、DNA分子構造や特性を操作する分子工学のメカニズムとその技術を解説し、一般的な分子アルゴリズムの利用を紹介している。特に、我々が開発したラフ集合の最小ルール探索のための決定ルールを最小化するアルゴリズムを説明している。
【解説論文】
ラフ集合・ルールリダクションへの バイオ計算技術の導入
Introduction of Bio Computing Technology
To Rule Reduction for Rough Set Method
和多田 淳三 1 酒井 浩1 松本 義之1
Junzo Watada Hiroshi Sakai Yoshiyuki Matsumoto
1下関市立大学
Shimonoseki City University
要旨
ラフ集合の方法は、決定規則の縮約によく利用されている。ラフ集合を用いた具体的な技術は、決定規則の抽出方法として用いられる。しかし、多くの決定規則を扱う際には、計算負荷が問題になる。すべての最小長の決定規則を計算する問題は、組み合わせ爆発が生じ、NP困難な問題である。この計算の課題を扱うために、本解説では、バイオ・コンピューティング技術を導入する方法を解説する。この手法は、決定規則の縮約に、DNA分子技術を応用したもので、問題の計算処理の複雑さを効果的に軽減できる。1998年にL.M. Adlemanが、生物学的計算パラダイムの概念を開拓して以来、この技術は、既存のアルゴリズムに活用及び実装することで、新しい問題解決アルゴリズムを開発する能力を提供してきた。しかし、経営工学の意思決定問題に対する学際的なDNA分子技術を用いたアルゴリズムは、いまだDNAの利用が限られた分野に限定されており、計算技術としてはそれほど広く用いられているとは言えない。本解説では、DNA分子構造や特性を操作する分子工学のメカニズムとその技術を解説し、一般的な分子アルゴリズムの利用を紹介している。特に、我々が開発したラフ集合の最小ルール探索のための決定ルールを最小化するアルゴリズムを説明している。
キーワード: DNA計算、決定ルール削減、NP困難問題、有向グラフ、DNAラフ集合計算、エンコーディングプロセス、デオキシリボ核酸、含窒素塩基、水素結合
Abstract
Rough set methods are often used to reduce decision rules. Specific techniques using rough sets are used as a method for extracting decision rules. However, when dealing with many decision rules, the computational load becomes an issue. The problem of calculating all minimum-length decision rules is a NP-hard problem with combinatorial explosion. To address this computational challenge, this article describes a method to introduce biocomputing technology. This method applies DNA molecular technology to the reduction of decision rules, and can effectively reduce the computational complexity of the problem. Since L.M. Adleman pioneered the concept of the biological computing paradigm in 1998, this technology has provided the ability to develop new problem-solving algorithms by utilizing and implementing them in existing algorithms. However, algorithms using interdisciplinary DNA molecular technology for industrial engineering decision-making problems are still limited to areas where DNA is used in a limited way, and it cannot be said that they are widely used as a computational technology. This article describes the mechanisms and techniques of molecular engineering that manipulate DNA molecular structures and properties, and introduces the use of general molecular algorithms. In particular, we describe an algorithm we developed to minimize decision rules for minimum rule searches of rough sets.
Keywords: DNA computation, decision rule reduction, NP-hard problems, directed graphs, DNA rough set computation, encoding process, deoxyribonucleic acid,
nitrogenous bases, hydrogen bonds
1.はじめに
本解説では、ラフ集合計算にバイオ・コンピューティング技術を導入する方法を解説する。この手法は、決定規則の縮約に、DNA分子技術を応用したもので、問題の計算処理の複雑さを効果的に軽減できる。1998年にL.M. Adleman [1]が、生物学的計算パラダイムの概念を開拓して以来、この技術は、既存のアルゴリズムに活用及び実装することで、新しい問題解決アルゴリズムを開発する能力を提供している。
機械学習、データマイニング、およびその他の情報処理タスクで遭遇する問題に対しそれらの課題や問題を解決するには、多様なテータベースと情報技術を必要としている[2], [3]。これらを考慮すると、ラフセットのとアルゴリズムフレームワークは、問題解決のための有効な代替手段となる。ラフセットは、オブジエクトとその値、および決定属性から構成される決定表を利用し、種々の分類タスクを解決する手段を提供している。この手段を用いると、与えられたオブジェクトとそれらの属性の情報から簡略化された規則を抽出することができる[4]。得られる規則は、if-then型の論理式の集合であり、結論部が未知のデータの条件部が規則の条件部に合致すれば、未知データの結論部を規則の結論部で推定・補完する。これは得られた規則による意思決定支援の枠組みになる。ニューラルネットワーク系の結論付けでは結論付けの根拠の面に弱点があると考えられているが、規則を扱う体系では結論付けの根拠は用いた規則であり、説明機能を果たす。この性質から、現在、ラフセット理論は大規模データセットにおける理解可能で透明性のある意思決定のための基盤とも認識されている。
現在、ラフ集合とその応用に関する種々の研究が広く行われている。その中には、Slowinskiによって提案された一般化手法[5]が含まれる。データ解析の不確実性の管理に焦点を当てた一連の応用がある。Grzymala-Busse[6]は、エキスパートシステムにおけるデータの不確実性を管理する最小長の決定規則の計算手法を開発した。その後、Ziarko[7]は、新しいタイプの決定システム行列を提案して、決定規則の縮約方法を提供している。さらに、Skowron とRauszer [8]は、判別行列に基づく決定システム行列を応用した増分識別アルゴリズムを提案した。別の増分アルゴリズムは、Shan とZiarko [9]によって研究され、異なる方法で決定規則を形成した。多くの異なるタイプの決定規則は、いくつかの意味のある特性(オブジェクト、属性とその値、および決定属性の対応)を導いている。
それぞれの提案では、規則のすべてを求める場合と一部の規則を求める場合があるが、すべての規則を求める場合、2の属性数乗に依存する計算が必要であり、すべての最小長の決定規則を計算する問題はNP困難な問題であることが示されている[10]。これは、ラフセット理論における唯一の不都合な側面である。このような背景において、第一著者はDNA計算の手法を応用する全く斬新な手法を提案し、本手法により選択された各決定クラスの下近似部分集合を決定できることを初めて示した。これにより最小長の決定規則を導出できることを明らかにした。
著者らのうち酒井は、ラフセットの理論研究貢献している[30],[31],32].また、マレーシアのUTP研究グループは、酒井の方法を用いて、地質データの分析にラフセットの分析で得られたルールを適用して成果を得ている[32x]。地質データの解析にUTPグループは通常のラフセットによるルール抽出に基づいた解析で成果を上げてきた[49],[49x]。さらに、松本らは、経済分析、FinTech,投資問題の知識獲得に、ラフセットによるルール抽出を適用して成果を上げてきた[50],[51],[52],[53],[55],[56]。特に、和多田は、2003年ごろから、組み合わせ最適化の問題を解く方法として、DNAの化学反応が有効であることを種々して召してきた[42],[43],[46],[44],[47],[48]。
本解説では、ラフセットにおける計算の不都合性を解決するためDNA分子技術を用い提案した計算手法をサーベイし、「DNAラフセット計算」と名付けた枠組みを概説する。DNAラフセット計算は伝統的なラフセットの数学概念とDNA計算手法を融合した新たな枠組みであり、新たなデータ解析法を提供している。本解説ではその計算の効率性も評価する。尚、ページ数の制限により、一論文にまとめることが難しいため、本編においてはDNAコンピューティングの基本技術を中心に述べる。続編を検討している。
本解説は、DNAコンピューティングの基本技術を解説し、以下のように構成されている:
– 節1 研究の背景を示す。
– 節2 提案手法の理解を深めるためにDNA分子の基本について説明する。
– 節3 いくつかの関連するDNA分子技術を説明する。
– 節4 ラフセットの基本的な概念とモデル決定表について述べる。
– 節5 我々の研究で提案してきた新しいDNAラフセット計算方法を説明する。
2.方法 図など
2 デオキシリボ核酸
生物体の細胞に存在する生物ポリマー材料は、一般的にデオキシリボ核酸として知られ、DNAと略称されている[40]。DNA分子は、生物の発達と生命維持に関連するさまざまな機能を果たしている。DNA分子の機能を計算の観点から利用する主な利点は、これらの分子がナノメートルスケールで記憶を実現しながらデータを長期保存できる高容量のメモリとして機能する能力にある。本節では、DNA分子、また窒素含有塩基とも呼ばれるDNA分子の構成要素、およびDNA分子に存在する二つの重要な自然結合について簡単に説明する。
2.1 窒素含有塩基
基本的なレベルでは、一本のDNA分子はリン酸、および4種類の異なる窒素含有塩基から構成されており、アデニン(A)、チミン(T)、グアニンG)、シトシン(C)と呼ぶ。これら四つの窒素含有塩基のそれぞれを図1に構造式とともに示している。図1(a)と(c)は、それぞれ二重環構造をもつアデニン(A)とグアニン(G)を示しており、これらは、また、プリンと呼ばれる。図1(b)と(d)は、それぞれ一重環構造をもつチミン(T)とシトシン(C)を示している。これらはピリミジンと呼ばれる[41]。DNA計算の分子技術では、これら四つの窒素含有塩基A,T,G,Cを効果的に操作して意味のある処理を行う。
プリン鎖が常にピリミジン鎖に結びついているため、ベースの次元がDNA分子の長さと同じになる。したがって、二つのプリンは任意に二つのピリミジンと結合できる。言い換えれば、一つの相補的ベニスペアリングはAとTから成り、もう一つの相補的ベースペアリングはGとCから成る。これら二つの相補的ベースペアリングから、糖リン酸の骨格グループは明確に設定された向きを持ち、最終的にDNA分子のどのベースも同じ構造を想定することを可能にする。ベースペアの形成は対称的なプロセスであり、二本鎖(DNAasDNA)で右巻きへリックスを形成する。したがって、DNA分子の対称性は、単ーポリヌクレオチド鎖が正確に反対方向に走ってasDNAへリックスを形成することに関連している[43],[1]。二つの異なるタイプの相補的ベースは、図1(a)に示すように二つの水素結合でAとTを保持する。さらに、二つの異なるタイフの相補的ベースは、図1(b)に示すように三つの水素結合でGとCを保持する。ホスホジエステル結合での強い結合を示す。
2.2 ホスホジエステル結合
四つの窒素含有塩基のそれぞれは、デオキシリボースと共にリン酸で結合できる。デオキシリボースがリン酸と結びついて核酸を形成する場合、ヌクレオチドである。ヌクレオチドがポリヌクレオチド鎖に結合するためには、リン酸が5炭素の最初の糖と結びついて、ヒドロキシル基が3炭素の第二糖に結びついている結合を取る必要がある。これらの化学的結合を通じて、リン酸エステル結合を形成する隣接するヌクレオチドの糖が結びついて構成している[41]。さらに、ホスホジエステル結合で化学化合物が非金属要素で構築される。
2.3 図1の説明
DNAの四つの有塩基の構造式:(2)アデニン(A)(二重環構造);(D)チミン(T)(一重環構造);(c)グアニン(G)(二重環構造);(d)シトシン(C)(一重環構造) プリン鎖が常にピリミジン鎖に結びついているため、ベースの次元がDNA分子の長さと同じになる。したがって、二つのプリンは任意に二つのピリミジンと結合できる。言い換えれば、一つの相補的ベニスペアリングはAとTから成り、もう一つの相補的ベースペアリングはGとCから成る。これら二つの相補的ベースペアリングから、糖リン酸の骨格グループは明確に設定された向きを持ち、最終的にDNA分子のどのベースも同じ構造を想定することを可能にする。ベースペアの形成は対称的なプロセスであり、二本鎖DNAasDNA)で右巻きへリックスを形成する。したがって、DNA分子の対称性は、単ーポリヌクレオチド鎖が正確に反対方向に走ってasDNAへリックスを形成することに関連している[15]、[16]。二つの異なるタイプの相補的ベースは、図1(a)に示すように二つの水素結合でAとTを保持する。さらに、二つの異なるタイフの相補的ベースは、図1(b)に示すように三つの水素結合でGとCを保持する。ホスホジエステル結合での強い結合を示す。
2.4 水素結合
DNA分子では、二つの異なるポリヌクレオチド鎖が溶液内で結びついて、二つの負の原子の水素を使用して形成される。ポリヌクレオチドの二本鎖の間の結合は、水素結合と呼ばれる結合グループによって構築される。特に、水素結合はDNA分子の右巻きヘリックスの重要な形成など、DNA分子の高次構造を構築する役割を果たしている。水素結合は特定の結合パターンを通じて起こり、それによって通常のベースペア(bp)が形成される。すなわち、塩基Aは常に塩基Tにのみ結合し、Gは常にCにのみ結合できる。この現象はワトソン・クリック相補性として知られている[14]。1953年にワトソンとクリックは最初にDNA分子再構成モデルを構築した。
DNA分子では、2つの異なるポリヌクレオチド鎖が溶液内で結合され、2つの負の原子の共有水素原子を使用して形成される。2つの単一のポリヌクレオチド鎖間の接続は、水素結合と呼ばれる結合グループによって構築される。特に、水素結合は、右巻きのヘリックスなどのDNA分子の高次構造の形成によって主要な役割を果たす。水素結合は、通常の塩基対(bp)を通じて発生する。つまり、塩基Aは常に塩基Tにのみ結合し、Gは常にCにのみ結合する。この現象はワトソン・クリックの相補性と呼ばれている。
プリン鎖は常にピリミジン鎖にのみ結合するため、塩基の寸法はDNA分子の長さと同じになる。したがって、2つのプリンのいずれかは、2つのピリミジンのいずれかと選択的に結合する。言い換えると、1つの相補的な塩基対はAとTから構成され、もう1つの相補的な塩基対はGとCから構成される。これら2つの相補的な塩基対から、すべての糖リン酸のバックボーングループは明確な方向性を持ち、DNA分子がDNA配列の任意の塩基に対して同じ構造を想定することを可能にする。塩基対の形成は対称的なプロセスであり、二本鎖のDNA(dsDNA:double string DNA) の右巻きのヘリックスを形成することは重要である。したがって、DNA分子の対称性は、2つの単一のポリヌクレオチド鎖に関連し、それぞれが正確に反対方向に走り、dsDNAヘリックスを形成する。
2種類の異なる相補的な塩基は、図3(a)でその構造式と共に示しているように、2つの水素結合でAとTを結合させる。さらに、2種類の異なる相補的な塩基は、図3(b)でその構造式と共に示しているように、3つの水素結合でGとCを結合させている。ホスホジエステル結合の強い結合と水素結合の弱い結合の組み合わせにより、特徴的なDNA分子構造が形成される。
二重らせんの説明の節では、DNAラフセットコンピューティングを開発するためのDNA分子の操作方法について、いくつかの重要なDNA分子技術を説明する。特に、次節で、制限酵素技術とライゲーションについて述べる。

図1: DNAにおける四つの窒素含有塩基の構造式:(a)アデニン(A)(二重環構造);
(b)チミン(T)(一重環構造);(c)グアニン(G)(二重環構造);(d)シトシン(C)(一重環構造)

主構(major groove)と副構造(minor groove)が示されている。出典:wikipedia:
図2:DNAの二重らせん構造(二重らせん状)

図3: ワトソン-クリック相補性における水素結合をその構造式で表したもの:(a)アデニン(A)とチミン(T)は2つの異なる相補的塩基で、2つの水素結合に関与している;(b)グアニン(G)とシトシンcは3つの水素結合に関与する2つの異なる相補的塩基である技術、ポリメラーゼ連鎖反応(PCR)技術、親和性分離技術、およびゲル電気泳動技術の5種類のDNA分子技術について詳述している。これらの分子技術はそれぞれ、DNA分子を操作するための重要な機能を持っており、そのためには堅牢なDNAラフセットコンピューティングを構築するために必要である。
3 DNA分子技術
この節では、DNA分子技術の手法を説明し、DNAラフ集合計算を開発するためのDNA分子の操作を示している。具体的には、この節では制限酵素技術、リガーゼ技術、ポリメラーゼ連鎖反応(PCR)技術、親和性分離技術、およびゲル電気泳動技術の5種類の異なるDNA分子技術について述べる。これらの分子技術は、それぞれDNA分子を操作する。DNAラフ集合計算を構成するために必要不可欠である。
3.1 制限酵素技術
組換え DNA を生成するには、目的とする DNA 分子の特定の部位を切断し、特定の DNA フラグメントを分離する必要がある。これには、DNA の分子技術である制限酵素技術が使用される。この技術では、特定の DNA 配列を標的にすることで、DNA 分子を意図的に複数の断片に切り分ける。このような制限酵素の認識部位は、通常、4〜6個のヌクレオチドで構成されており、それぞれが対応する塩基対を含んでいる[41]。異なる長さの DNA フラグメントは、異なる種類のDNA 塩基配列を増幅し、制限酵素技術を用いてそれらを別々の断片に切断することで生成される。つまり、制限酵素は特定の DNA 塩基配列を認識し、指定された位置でそれを切断する。
制限酵素はヌクレアーゼとして働き、DNA 内部の特定の位置 (タイプ II 制限エンドヌクレアーゼ) で切断する。4つの塩基 (A, T, G, C) の可能性を考慮すると、任意の DNA 塩基配列で得られる予想頻度は 4のn乗になる。ここで n は認識される配列の長さであり、3 種類の異なる長さの部位が予測される。第一に、256 塩基対の各部位が四ヌクレオチド部位を示す。第二に、1024 塩基対の各部位が五ヌクレオチド部位を示す。最後に、4096 塩基対の各部位が六ヌクレオチド部位を示す。さらに、制限酵素技術における切断の機構は、粘着末端(sticky-ended)または平滑末端(blunt-ended)で行われる。図4は、制限酵素 (EcoRI) の機構の例を示している。
3.2 リガーゼ技術
一本のDNA鎖または二本の異なる逆方向の一本のDNA鎖に含まれる不安定なdsDNAまたはdsDNAは、リガーゼ技術を用いて修復できる。リガーゼは、リコンビナントDNAプロセスにおいて重要なリン酸エステル結合の形成を触媒できる。生化学的手順でDNAブラスミドベクターはリガーゼプロセスで1つのDNA分子に融合できる。
14リガーゼ[44]は、リン酸エステル結合を触媒するために一本のDNA鎖のギャップを封じるために使用される。リガーゼブロセスでは、T4リガーゼは粘着末端型と鈍端型の両方に対応できる。プロセスに使用されるリガーゼバッファーには、一般的な室温下で不安定なアデノシン三リン酸(ATP)が含まれている[45]。凍結庫から取り出した後、すべての酵素の種類とバッファーは氷上に保管されている。
3.3 ポリメラーゼ連鎖反応(PCR)技術
PCRは、体外で行われるDNA分子技術であり、特定のDNA配列を同時にコンプリメントするプライマーの使用によって約50万個まで増幅できる。PCR技術はDNA分子の特性を分析するために開発された。PCR技術は、DNA分子の特定の領域を制限してその増幅を行う。その後、PCR技術は耐熱性ポリメラーゼを含めることによって、DNA塩基配列のテンプレート固有の合成反応を繰り返しできる。図5は一般的に使われているPCR装置の例を示している。

図4:5-G|AATTC-3`と5-G|AATTC-3`を表すDNA塩基配列の切断を示す
DNA塩基対の制限酵素(EcoRI)の機能例


PCR技術は、エネルギーとヌクレオシドを使用してDNA分子を合成するバッファー、プライマー、ホリメラーゼ、およびテンプレートが必要である。特に、天然の酵素であるポリメラーゼは修復およびDNA分子の形成を触媒する中心的な部分である[46]。DNA分子の合成の主要なステップが繰り返され、最新の合成されたDNA分子は明確に分離され、それらをプライマーの形成を可能にするために冷やし、そのDNA補完的配列を対象としている。
加熱と冷却の各サイクルにより、DNA分子の数はプライマーの拡張により大幅に増加できる。主要な反応ではDNA分子が生成され、数サイクル後にプライマー拡張されたものが含まれている。加熱と冷却サイクル中、DNA分子数は増加し続けるが、酵素が適切な数のDNA分子を合成しない可能性があるか、反応が突然弱まることがある。最適な増幅に必要なサイクル数は非常に変動が大きく、各増幅ステップまたは含まれている初期の材料の数に依存する。
PCR技術の特徴は、強い反応が高温で繰り返される際に安定性を維持するために確立された。したがって、酵素Thermus aquaticus Taq)ポリメラーゼ[47]を使用して安定性を維持する必要がある。
3.4 親和性分離技術
親和性分離は、特定のDNA配列を他のものから分離し、1つまたは複数の特定のDNA配列を抽出するために使用する一種のDNA分子技術である[48]。化学的目的抽出、細胞質、および発酵ブロセスからの複雑な混合物を扱う親和性分離技術は、磁気ビーズを使用して水溶液で材料を収集および分散するために使用される。この抽出技術はまた、生化学的物質を抽出および分離するために使用される。別のタイプの親和性分離技術では、蛍光標識されたDNA断片を磁気ビーズに結合させることでDNA分子を抽出することができる[49]。この特定のタイプの親和性分離では、蛍光標識されたDNA断片は磁気ビーズに結合されるリガーゼの特定のベース配列をもちいている。この分離技術は、磁気ビーズに付着させる機能と、DNA断片の長さを示す固定化された磁気ビーズごとに識別する。この分離技術は同時に抽出およびテストされる多数のDNA分子を扱うことができる。多くの親和性分離技術は自動化されることが期待できる。
3.5 ゲル電気泳動技術
この技術を用いてDNA分子の長さを推定できる。ゲル竜気泳動技術には、アカロースゲル電気承動が一般的に使用される。ゲル電気泳動はDNA分子の長さを測定するだけでなく、DNAE 片をその構造から切り離すのにも非常に有効である[50]。図6は一般的に使用されるアガロースゲル電気泳動装置の例を示している。最近導入されたゲル電気泳動技術は、DNA分子の長さを測定するだけでなく、核酸を分析して分子データを提供できる。この新しい装置は各単一のDNA鎖と断片を自動的に測定し、その長さを示し、明確な線形帯を表示できる。
4 ラフ集合とモデル決定表
このセクションでは、ラフ集合理論の基本概念を簡単に再確認する。この内容は、DNA ラフ集合コンピューティングによる決定ルールの縮約を説明するのに役立つ。また、決定表の例を与え、この例のDNA ラフ集合コンピューティングによる解法を示す。
4.1 ラフ集合理論の概念
ラフ集合理論はPawlakによって、集合論の概念に基づいて導入された[23]。Pawlakは、グラニュラー・コンピューティングの基礎や、新しい形式の計算機、知識発見の方法など、数多くの新しいアルゴリズムを初めて提案した[30]。
ラフ集合理論の枠組みを示す[31]。対象の集合をUとし、U上の関係をRとする。Rは直積集合U×UÆ{(x,y)|x,y∈U}の部分集合と同一視され、この部分集合をRとかく。特に、下記の3要件を満たす関係Rは同値関係と呼ばれる。
(1) (x,x)∈R(反射性)
(2) (x,y)∈Rならば(y,x)∈R(対称性)
(3) (x,y)∈Rかつ(y,z)∈Rならば(x,z)∈R(推移性)
さらにこのとき、[s]={(s,t)|s,t∈U}と決めると異なる対象sとtについて[s]=[t]かつ[s]∩[t]={}の一方が成立する。この性質を利用し、対象集合Uを非交差集合(共通部分の無い集合)の和集合に直せる。これを関係Rによる対象集合Uの分割または識別関係とよび、各集合[s]を対象sを含む同値類とよぶ。対象集合U、その同値関係Ξ、およびUの部分集合X(ターゲット集合とよぶ)が与えられたとき、ターゲット集合Xに依存して下記の集合を決める。
(1) 下近似集合(クラス1)ΞA(X)={[s]|s∈U,[s]⊂X}
(2) 上近似集合(クラス3)ΞA(X)={[s]|s∈U,[s]∩X≠{}}=∅,
(3) 境界領域集合(クラス2)ΞB(X)=ΞA(X)−ΞA(X),
任意のターゲット集合X⊆Uに対するこれらの集合は、対象が確実にX内に位置するもの(クラス1)、確実にはXに含まれないもの(クラス2)、またはX内に存在する可能性があるもの(クラス3)を表わす[32],[33]。下近似集合は集合Xによって自動的に決まる。著者らはDNAラフ集合コンピューティング法を使用して、この下近似集合から得られる最小長の決定ルールを得る。
4.2 モデルとしての決定表
ラフ集合では、通常、決定システムDSに基づいて構築される決定表を扱っている。決定システム(DS)をDS = (U,Γ,ε,Ψ)と定義し、下記のように定める。
・U={x1,x2,…,xn}とし、各要素x1,x2,…,xnを対象とよぶ。
・Γ={ζ1,ζ2,…,ζm}とし、各要素ζ1,ζ2,…,ζmを条件属性とよぶ。また特定の属性
εを導入し、これを決定属性とよぶ。属性ζiにおける属性値の和集合をIcζiとかく。
各条件属性の属性値の和集合をIνとかき、決定属性εの属性値の集合をDνとする。
・Ψ:U×(Γ∪{ε})→Iν∪Dνにより、各対象と属性から値への対応付けを行う。
これにより、各対象xiに対する属性値が決まり、それらをΨζ1(xi),Ψζ2(xi),…,Ψζm(xi),
Ψε(xi)とかく。
最終的に、n個の対象とm個の条件属性値のそれぞれの組に対して1つの属性値が定まる。これは直感的には一枚の表を与えることに相当する。特に、決定属性値集合がDν= {τ1,τ2,…,τn}のとき、決定属性値によって決まるUの部分集合を決定クラスとよび、Dντ1,Dντ2,…,Dντnなどで表わす。決定クラスは4.1節におけるターゲット集合に相当する。
この研究で実験に使うモデル決定表に触れておく。決定表は8つの対象、4つの条件属性とその条件属性値、1つの決定属性とその決定値から構成される。これらの決定ルールは、最小長を示すように縮約される必要がある。決定ルールを縮約することで、この決定表の特性が明らかになる。モデル決定表の枠組みを次のように表わす。
モデル決定表の詳細は以下の通りである。

図7: モデルDNA有向グラフの表現
図ではx1からx8はObject-1からObject-8と表示されている。
4.3 DNA有向グラフによるルール生成の例
上記のモデル決定表に対して、図7に示すようなDNA有向グラフを作る。DNA有向グラフの表現は、決定ルールを縮約するために使用される。モデル決定表から変換されたDNA有向グラフを図7に示す。ここで、5つの対ノード (∗,4)、 (#,1)、(#,3)、(■,1)、(■,2) は複数の方向に関連している。モデルDNA有向グラフは、8つの対象ノードU={x1,x2,…,x8}と4つの条件属性ζ1,ζ2,ζ3,ζ4から構成される。ここで、3つの条件属性ζ1,ζ2,ζ3は4つの条件属性値を取り、条件属性ζ4は3つの条件属性値を取る。モデルペア行列は、与えられた対ノードのDNA配列を一本鎖DNA(ssDNA)としてエンコードする際に主に使用される。図7に言及する。
上記の環境において、DNAの化学的な性質を用い条件部が最小長の13個のルールを得た。
条件部が1個のルールは下記の3個。
(■,2)==>(ω,0), (*,1)==>(ω,1), (■,3)==>(ω,1).
条件部が2個のルールは下記の10個。
(*,4)&(#,1)==>(ω,0), (*,4)&(■,1)==>(ω,0), (*,4)&(●,1)==>(ω,0),
(*,4)&(●,3)==>(ω,0), (#,3)&(■,1)==>(ω,0), (#,3)&(●,1)==>(ω,0),
(*,4)&(●,2)==>(ω,1), (#,3)&(●,2)==>(ω,1), (#,1)&(■,1)==>(ω,1),
(■,1)&(●,3)==>(ω,1).
5 DNAラフ集合コンピューティング
4節において、DNAラフ集合コンピューティングとルール生成の簡単な例を示した。本節では前節4.2の内容を一般化した体系について述べる。決定表DS = (U,Γ,ε,Ψ)の定義に従って、DNA有向グラフを決める。
5.1 DNAにおける有向グラフ
3つの異なる要素があり、それを対象要素、条件属性要素、条件属性値要素とする。決定表の有向グラフを作成するために、条件属性要素と条件属性値要素を一体化して「対要素」と呼ばれる単一の要素にする。したがって、1つの対要素は条件属性要素と条件属性値要素を含んでいる。この2つの異なる要素(対象要素と対要素)を用いることで、これら2種類の要素から成る新しいタイプの有向グラフ、いわゆるDNA有向グラフ図8を作成する。以下では、DNA有向グラフに関する対象要素と対要素を対象ノードおよび対ノードと呼ぶ。
DNA有向グラフにおいて、決定表と同様にn個の対象ノードx1,x2,…,xnからなる集合U={x1,x2,…,xn}、m個の条件属性Γ={ζ1,ζ2,…,ζm}、IνとDνを考える。対ノード集合をペア行列として表現しPsとする。DNA有向グラフの構造はn個の対象ノードとn個の対ノードで構成されている。ここで、一部の条件属性は他の条件属性よりも少ない条件属性値をもつ対ノードが1つ以上存在する。この空のエントリを表すために、特定の記号「φ」を使用する。図7は一般のDNA有向グラフ図8の特別な場合である。
図8について言及する。
(1)aは、n個の対象ノードx1, x2, ⋯ ,xnからn個の対ノード(ζ1,Ψ1ζ1), (ζ1,Ψ2ζ1), ⋯ , (ζ1,Ψmζ1) への方向を表す。
(2) bは、n個の対象ノードx1, x2, ⋯ , xn からn個の対ノード(ζ2,Ψ1ζ2), (ζ2,Ψ2ζ2),⋯ ,(ζ2,Ψmζ2) への双方向の方向を表す。
(3) c は、n個の対ノード (ζ1,Ψ1ζ1),(ζ1,Ψ2ζ1),⋯ ,(ζ1,Ψmζ1),から n個の対ノード
(ζ2,Ψζ21),(ζ2,Ψζ22),⋯ ,(ζ2,Ψζ2m) への方向を表す。
(4) d は、n個の対ノード (ζ1,Ψ1ζ1), (ζ1,Ψ2ζ1),⋯ , (ζ1,Ψmζ1)からその他のn個の対ノード (ζn,Ψ1ζn), (ζn,Ψ2ζn),⋯ , (ζn,Ψmζn) への方向を表す。
(5) e は、n個の対ノード (ζ1,Ψ1ζ1), (ζ1,Ψ2ζ1),⋯ , (ζ1,Ψmζ1) から n個の対ノード (ζn,Ψ1ζn), (ζn,Ψ2ζn),⋯ , (ζn,Ψmζn) への方向を表す。
(6) f は、n個の対ノード (ζ2,Ψ1ζ2), (ζ2,Ψ2ζ2),⋯ (ζ2,Ψmζ2),からその他の n個の対ノード (ζn,Ψ1ζn), (ζn,Ψ2ζn),⋯ (ζn,Ψmζn) への方向を表す。
(7) g は、n個の対ノード (ζ2,Ψ1ζ2), (ζ2,Ψ2ζ2),⋯ , (ζ2,Ψmζ2) から n個の対ノード(ζn,Ψ1ζn), (ζn,Ψ2ζn),⋯ , (ζn,Ψmζn) への方向を表す。
(8) h は、その他の n個の対ノード …,…,… から n個の対ノード (ζn,Ψ1ζn), (ζn,Ψ2ζn),⋯ , (ζn,Ψmζn) への方向を表す。
(9) i は、その他の n個の対ノード …,…,… から n個の対象ノード x1, x2, ⋯ , xn への双方向の方向を表す。
(10) j は、n個の対ノード (ζn,Ψ1ζn),(ζn,Ψ2ζn),⋯ ,(ζn,Ψmζn)(ζn,Ψ1ζn), (ζn,Ψ2ζn), … , (ζn,Ψmζn) から n個の対象ノード x1, x2, ⋯ , xnへの方向を表している。
第1のケースでは、対象ノードxiが対ノード(ζα,ψζαα)に対して有向関係をもつ場合であり、xie(ζα, ψαζα)を表し、xi¯e(ζα, ψαζα)には有向関係がない。
第2のケースでは、対ノード(ζβ, ψζββ)が対象ノードxjに対して有向関係をもつ場合であり、(ζβ, ψβζβ)exjを表し、(ζβ, ψβζβ)¯exjには有向関係がない。
最終的なケースでは、対ノード(ζα, ψαζα)が対ノード(ζβ, ψβζβ)に対して有向関係をもつ場合であり、(ζα, ψαζα)e(ζβ, ψβζβ)を表し、(ζα, ψαζα)¯e(ζβ, ψβζβ)には有向

図8: DNA有向グラフの表現


図9:タイプ1のダブルエンコードサブストリング表現

図10:タイプ2のダブルエンコードサブストリング表現

図11:タイプ3のダブルエンコードサブストリング表現
しており、これによりdsDNAへの明確な結合が可能になる。図9から図15までが、各サブストリングタイプの詳細な図解を示している。

図12:タイプ4のダブルエンコードサブストリング表現

図13:タイプ5のダブルエンコードサブストリング表現

図14:タイプ6のダブルエンコードサブストリング表現
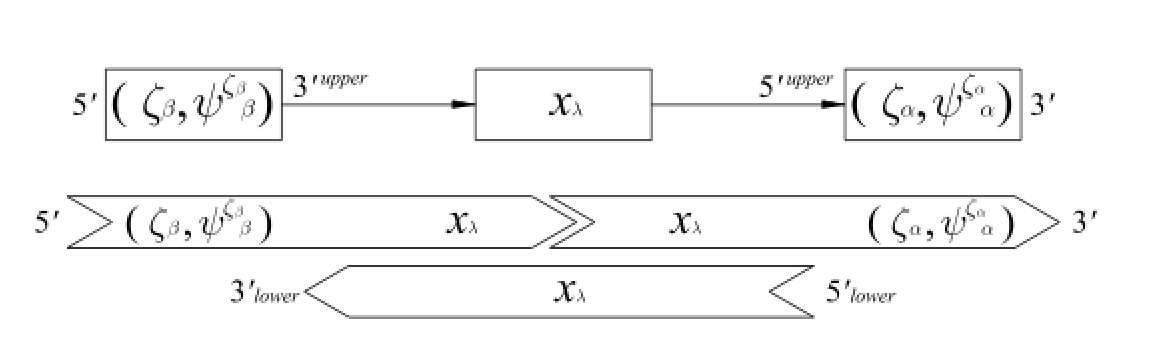
図15:タイプ7のダブルエンコードサブストリング表現
6 結論
本解説では、DNA分子計算を用いてラフ集合を計算する方法を提案した。DNAの有向グラフを用いて決定表のオブジェクトと属性値の関係を表現し、分子計算により下近似集合を識別し、決定ルールを縮約する手法を示した。簡単な例を示し、実際に得られるルールを示した。この方法により、計算効率が向上し、複雑な決定問題に対する解決策が提供した。将来的には、この手法をさらに発展させ、より広範な応用を目指すことが期待される。
謝辞
この研究は、2007年から2011年までの北九州産業科学技術振興財団(FAIS)(アジアの大学間の科学技術協力のためのFAIS R&D基金)によって部分的に支援されました。ここに記して、謝意を表す。
参考文献
[4] Z. Pawlak (1982) “rough sets,”International Journal of Computer and Information Sciences, 11(5):341-–356. http://dx.doi.org/10.1007/BF01001956
[5] Roman Slowinski, editor (1992) “Intelligent Decision Support,” pages 363-–372. Kluwer Academic Publishers, Dordrecht. ISBN:3030963195, 9783030963194
[6] J.W. Grzymala Busse (2003)“a comparison of tree strategies to rule induction from data with numerical attributes,”Electronic Notes in Theoretical Computer Science, 82(4):132-–140. https://doi.org/10.1016/S1571-0661(04)80712-6
[7] W. Ziarko (1993)“variable precision rough set model”. Journal of Computer and System Sciences, 46(1):39–59. https://doi.org/10.1016/0022-0000(93)90048-2
[8] A. Skowron and C. Rauszer (1992) “The discernibility matrices and functions in information systems.”In R.Slowinski(ed.),Intelligent Decision Support: Handbook of Application and Advances of the Rough Sets Theory, pages 331–362. Kluwer Academic Publishers, Dordrecht. https://doi.org/10.1007/978-94-015-7975-9_21
[9] N. Shan and W. Ziarko (1995)“data-based acquisition and incremental modification of classification rules”. Computational Intelligence, 11(2):357–370. doi.org/10.1111/j.1467-8640.1995.tb00038.x
[11] James D. Watson, Tania A. Baker, Stephen P. Bell, Alexander Gann,Michael Levine, and Righard Losick (2008) Molecular Biology of the Gene(6th edition) Pearson Eduction, Inc. 日本語訳:ワトソン、遺伝子の分子生物学、第6版、監訳:中村桂子、役者:滋賀陽子、中塚公子、宮下悦子、東京電機大学出版局、2010年、ISBN:978-4-501-62570-2 C3045. ISBN-13:978-0805395921
[12] Hiroshi Sakai, Michinori Nakata, Junzo Watada (2020) “ NIS-Apriori-based rule generation with three-way decisions and its application system in SQL”. Information Sciences, 507:755-771. https://doi.org/10.1016/j.ins.2018.09.008
[13] 酒井浩, 中田典規, 和多田淳三 (2020) “ ラフ集合非決定情報解析とNIS-アプリオリシステム ―可能世界意味論に基づくルール生成システム―”.知能と情報 32(4):747-758. https://doi.org/10.3156/jsoft.32.4_747
[14] Hiroshi Sakai (2021) “ Studies on Association Rule-based Table Data Analysis and Its Applications - New Mathematics for Data Sciences –”. Journal of Combinatorics, Information & System Sciences 46(1-4):115-230. https://doi.org/ 10.32381/JCISS.2021.46.1-4.3
[15] Touhid Mohammad Hossain, Junzo Watada, Izzatdin A Aziz, and Maman Hermana.(2020) "Machine learning in electrofacies classification and sub-surface lithology interpretation: A rough set theory approach". Applied Sciences, 10(17):5940, 2020. https://doi.org/10.3390/app10175940.
[16] Hiroshi Sakai, Zhiwen Jian, Touhid Mohammad Hossain, and Junzo Watada.(2020) "Rule-based functionality for decision making with reasoning and its application: Case studies on three data sets.". Journal of Combinatorics, Information & System Sciences, 45(1–4):157–173, 2020. https://doi.org/10.32381/JCISS.2020.45.1-4.2.
[17] Touhid Mohammad Hossain, Junzo Watada, Izzatdin Abdul Aziz, Maman Hermana, Sheikh Tanzim Meraj, and Hiroshi Sakai.(2021) "Lithology prediction using well logs: A granular computing approach". Int. J. Innov. Comput. Inf. Control (IJICIC), 17(1):225–244, 2021.
[18] Yoshiyuki Matsumoto and Junzo Watada.(2009) "Knowledge acquisition from time series data through rough sets analysis". (IJICIC) International Journal of Innovative Computing Information and Control, 5(12):4885–4897, 2009. https://doi.org/10.14864/fss.24.0.144.0.
[19] Yoshiyuki Matsumoto and Junzo Watada.(2011) "Rough sets based prediction model of tick-wise price fluctuations". Journal of Advanced Computational Intelligence and Intelligent Informatics, 15(4):449–453, 2011. https://doi.org/10.20965/jaciii.2011.p0449.
[20] Yoshiyuki Matsumoto and Junzo Watada.(2012) "Rough set-based market knowledge acquisition from tick-wise price movement data". International Journal of Intelligent Technologies and Applied Statistics, 5(3):267–280, 2012. https://doi.org/10.6148/IJITAS.2012.05.03.03.
[21] Yoshiyuki Matsumoto and Junzo Watada.(2015) "Rough set model based knowledge acquisition of market movements from economic data". In Information Granularity, Big Data, and Computational Intelligence, vol.8:375–388. Springer, Cham, 2015. https://doi.org/10.1007/978-3-319-08254-7_18
[22] Yoshiyuki Matsumoto and Junzo Watada.(2018) "Knowledge acquisition from rough sets using merged decision rules". Journal of Advanced Computational Intelligence and Intelligent Informatics, 22(3):404–410, 2018. https://doi.org/10.20965/jaciii.2018.p0404
[23] Jianxiong Yang and Junzo Watada. (2012) "Rough set based optimization for data mining: an improved fuzzy clustering approach". SICE Journal of Control, Measurement, and System Integration, 5(4):210–217, 2012.
[24] Muhammad Faiz Mohamed Saaid, Zuwairie Ibrahim, Zulkifli Md Yusof, and Junzo Watada.(2010) "Automation of a DNA computing readout method based on real-time PCR implemented on a light cycler system". International Journal of Innovative Computing Information and Control (IJICIC), 6(10): 4263–4272, 2010.
[25] Don Jyh-Fu Jeng, Ikno Kim, and Junzo Watada.(2008) "Bio-soft computing with fixed-length DNA to a group control optimization problem". Soft computing, 12:223–228, 2008. https://doi.org/10.1007/s00500-007-0202-y,
[26] Rohani Binti Abu Bakar, Junzo Watada, and Witold Pedrycz.(2008) "A proximity approach to DNA based clustering analysis". International Journal of Innovative Computing Information and Control (IJICIC), 4(5):1203–1212, 2008.
[27] Rohani binti Abu Bakar and Junzo Watada.(2008) "DNA computing and its applications: survey". ICIC Express Letters ICIC International, 2(1):101–108, 2008.
[28] Rohani Binti Abu Bakar, Junzo Watada, and WitoldPedrycz.(2008) "DNA approach to solve clustering problem based on a mutual order". Biosystems, 91(1):1–13, 2008. https://doi.org/10.1016/j.biosystems.2007.06.002,
[29] Rohani Binti Abu Bakar and Junzo Watada.(2011) "Empirical robustness evaluation of DNA-based clustering methods". International Journal of Intelligent Computing in Medical Sciences & Image Processing, 4(1):45303,2011.
[30] Rohani Abu Bakar, Chu Yu-Yi, and Junzo Watada.(2011) "Robustness of DNA-based clustering". In New Advances in Intelligent Signal Processing, pages75–92. Springer, Berlin, Heidelberg, 2011。
https://doi.org/10.1007/978-3-642-11739-8_4
[31] Ikno Kim, Don Jyh-Fu Jeng, and Junzo Watada.(2006) "Redesigning subgroupsin a personnel network based on DNA computing". International Journal of Innovative Computing Information and Control (IJICIC), 2(4):885–896,2006.
[32] Ikno Kim, Junzo Watada, and Witold Pedrycz.(2008) "A DNA-based algorithm for arranging weighted cliques". Simulation Modelling Practice and Theory, 16(10):1561–1570, 2008. https://doi.org/10.1016/j.simpat.2007.11.003},.
[33] Kim Ikno and Junzo Watada.(2009) "Decision making with an interpretive structural modeling method using a DNA-based algorithm". IEEE Trans. on Nanobioscience, 8(2):181–191, 2009. https://doi.org/10.1109/TNB.2009.2023788.
[34] Ikno Kim and Junzo Watada. (2009) "Decision making with an interpretive structural modeling method using a DNA-based algorithm". IEEE Trans on Nanobioscience, 8(2):181–191, 2009 . https://doi.org/10.1109/TNB.2009.2023788},
[35] Ikno Kim and Junzo Watada.(2009) "a fuzzy density analysis of subgroups by means of DNA oligonucleotides". In Intelligent Systems and Technologies: Methods and Applications, pages 31–45. Springer, 2009.
[36] Ikno Kim, Yu-Yi Chu, Junzo Watada, Jui-Yu Wu, and Witold Pedrycz.(2011) "A DNA-based algorithm for minimizing decision rules: A rough sets approach". IEEE Trans on NanoBioscience, 10(3):139–151, 2011. https://doi.org/10.1109/TNB.2011.2168535,
[37] Ikno Kim, Junzo Watada, Witold Pedrycz, and Jui-Yu Wu.(2012) "Pattern clustering with statistical methods using a DNA-based algorithm". IEEE Trans on NanoBioscience, 11(2):100–110, 2012. https://doi.org/10.1109/TNB.2012.2190618.
[38] Ikno Kim, Junzo Watada, and Witold Pedrycz.(2013) "DNA rough-set computing in the development of decision rule reducts". In Rough Sets and Intelligent Systems-Professor Zdzislaw Pawlak in Memoriam: Volume 1, pages 409–438. Springer, 2013.
[39] Junzo Watada.(2008) "DNA computing and its application". In Computational Intelligence: A Compendium, pages 1065–1089. Springer, 2008.
[40] D.L. Hartl and E.W. Jones (2009) Genetics: Analysis of Genes and Genomes , pages 431–445. Jones and Bartlett Publishers Inc. 7th edn. ISBN-13:978-0763772154
[41] D.L. Hartl and E.W. Jones (2002) Essential genetics (3rd edn.), pages 90–412. Jones and Bartlett Publishers Inc.2002. ISBN-13:978-0763708382
[42] J.D. Watson and F.H.C. Crick (1953) “Molecular structure of nucleic acids, a structure for deoxyribose nucleic acid,”Nature, 171(4356):737–738, 1953. https://doi.org/10.1038/171737a0
[43] J.D.Watson, R.M. Myers, A.A. Caudy, and J.A.Witkowski (2007) Recombinant DNA. W.H. Freeman and Company. Genes and genomes - a short course, 3rd edn. ISBN:9780716728665, https://books.google.com/books/about/Recombinant_D.
[44] W.L. Jorgensen and J.D. Madura (1985)“temperature and size dependence for monte carlo simulation of tip4p water. molecular physics,”An International Journal at the Interface between Chemistry and Physics, 56(6):1381–1392. https://doi.org/10.1080/00268978500103111
[44] J.J. Greene and V.B. Rao.(1996) Recombinant DNA principles and methodologies.Marcel Dekker Inc. ISBN-13:978-0824799892
[45] L. Kari, G. Paun, G. Rozenberg, A. Salomaa, and S. Yu (1998)“ DNA computing, sticker systems, and universality,”Acta Informatica, 35(5):401–420. https://doi.org/: 10.1007/s002360050125
[46] P. Rabinow (1996) Making PCR: A story of biotechnology. The University of Chicago Press, Chicago. https://doi.org/ 10.1525/ae.1999.26.3.783
[47] M.J. McPherson, P. Quirke, and G.R. Taylor (1991) PCR 1, pages 1–14. Oxford University Press Inc. https://doi.org/10.1093/oso/9780199631964.001.0001,
[48] P. Matejtschuk (1997) Affinity separations,pages 2–38. Oxford University Press Inc. ISBN-13:978-0199635504
[49] E.R. Goedken, M. Levitus, A. Johnson, C. Bustamante, M.OfDonnell, and J. Kuriyan (2004)“fluorescence measurements on the e. coli DNA polymerase clamp loader implications for conformational changes during atp and clamp binding,” Journal of Molecular Biology, 336(5):1047–1059. https://doi.org/ 10.1016/j.jmb.2003.12.074
[50] D.A. Micklos, G.A. Freyer, and D.A. Crotty (2003) DNA science. Cold Spring Harbor Laboratory Press. A first course, 2nd edn. ISBN(Hardback):0-87969-636-2
[51] Z. Pawlak (1984) “rough classification,”International Journal of Man-Machine Studies, 20(5):469–483. https://doi.org/10.1016/S0020-7373(84)80022-X
[52] J.F. Peters and A. Skowron (2007)“zdzis aw pawlak life and work (1926-2006),”. Information Sciences, 177:1–2. https://doi.org/ 10.1007/11847465_1
[53] L. Polkowski and A. Skowron (1998) Rough Sets in Knowledge Discovery 1.Methodology and Applications. Physica-Verlag, Heidelberg.ISBN:379081119X,9783790811193
[54] Z. Pawlak, S.K.M. Wong, and W. Ziarko (1988) “rough sets:, probabilistic versus deterministic approach”. International Journal of Man-Machine Studies, 29(1):81–95, https://doi.org/10.1016/S0020-7373(88)80032-4
この研究は、2007年から2011年までの北九州産業科学技術振興財団(FAIS)(アジアの大学間の科学技術協力のためのFAIS R&D基金)によって部分的に支援されました。ここに記して、謝意を表す。